Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-22T11:33:45.941Z Has data issue: false hasContentIssue false
  • English
  • Français

On Kloosterman Sums with Oscillating Coefficients

Published online by Cambridge University Press:  20 November 2018

Peiming Deng
Peiming Deng*
Affiliation:
Department of Mathematics The Normal University of Guangxi Guilin, Guangxi 541004 P.R. China
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we prove: for any positive integers 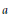$a$ and 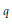$q$ with 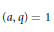$\left( a,\,q \right)\,=\,1$, we have uniformly

$$\sum\limits_{\begin{matrix} n\le N \\ (n,q)=1,n\bar{n}\equiv 1(\,\bmod \,q) \\ \end{matrix}}{\mu (n)e(\frac{a\bar{n}}{q})\ll Nd(q)\left\{ \frac{{{\log }^{\frac{5}{2}}}N}{{{q}^{\frac{1}{2}}}}+\frac{{{q}^{\frac{1}{5}}}{{\log }^{\frac{13}{5}}}N}{{{N}^{\frac{1}{5}}}} \right\}.}$$

This improves the previous bound obtained by D. Hajela, A. Pollington and B. Smith [5].

Keywords

10G10Kloosterman sumsoscillating coefficientsestimate
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 3 , 01 September 1999 , pp. 285 - 290
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Apostol, T., Introduction to Analytic Number Theory. Springer-Verlag, 1976.Google Scholar
[2] Davenport, H., Multiplicative Number Theory. Springer-Verlag, 1980.Google Scholar
[3] Deshouillers, J. M. and Iwaniec, H., Kloosterman Sums and Fourier Coefficients of Cusp Forms. Invent.Math. 70 (1982), 219–288.Google Scholar
[4] Elliott, P. D. T. A., Arithmetic Functions and Integer Products. Springer-Verlag, 1984.Google Scholar
[5] Hajela, D., Pollington, A. and Smith, B., On Kloosterman Sums with Oscillating Coefficients. Canad. Math. Bull. (1) 31 (1988), 32–36.Google Scholar
[6] Hooley, C., On the Brun-Titchmarsh Theorem. J. Reine Angew.Math. 225 (1972), 60–79.Google Scholar
[7] Vaughan, R. C., An Elementary Method in Prime Number Theory. Recent Progress in Analytic Number Theory, Academic Press, 1981.Google Scholar