Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-22T02:36:52.988Z Has data issue: false hasContentIssue false
  • English
  • Français

On semidirectly closed pseudovarieties of finite semigroups and monoids

Part of: Semigroups

Published online by Cambridge University Press:  02 August 2021

Jiří Kad’ourek
Jiří Kad’ourek*
Affiliation:
Department of Mathematics and Statistics, Masaryk University, Kotlářská 2, 611 37 Brno, Czech Republic
*
e-mail: kadourek@math.muni.cz
Get access Rights & Permissions [Opens in a new window]

Abstract

For every pseudovariety 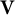$\mathbf {V}$ of finite monoids, let 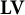$\mathbf {LV}$ denote the pseudovariety of all finite semigroups all of whose local submonoids belong to 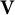$\mathbf {V}$ . In this paper, it is shown that, for every nontrivial semidirectly closed pseudovariety 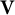$\mathbf {V}$ of finite monoids, the pseudovariety 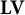$\mathbf {LV}$ of finite semigroups is also semidirectly closed if, and only if, the given pseudovariety 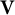$\mathbf {V}$ is local in the sense of Tilson. This finding resolves a long-standing open problem posed in the second volume of the classic monograph by Eilenberg.

Keywords

semidirect product of semigroupssemidirectly closed pseudovariety of finite semigroupslocal pseudovariety of finite monoids

MSC classification

Primary: 20M07: Varieties and pseudovarieties of semigroups
Secondary: 20M50: Connections of semigroups with homological algebra and category theory
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 3 , September 2022 , pp. 612 - 627
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research has been supported by the Grant Agency of the Czech Republic under the project GA19-12790S.

References

Almeida, J., Finite Semigroups and Universal Algebra, Series in Algebra, 3, World Scientific, Singapore, 1994.Google Scholar
Almeida, J., A syntactical proof of locality of DA . Internat. J. Algebra Comput. 6(1996), 165–177.CrossRefGoogle Scholar
Almeida, J. and Weil, P., Profinite categories and semidirect products . J. Pure Appl. Algebra. 123(1998), 1–50.CrossRefGoogle Scholar
Eilenberg, S., Automata, Languages and Machines. Vol. B, Pure and Applied Mathematics, 59, Academic Press, New York, 1976.Google Scholar
Jones, P. R. and Trotter, P. G., Locality of DS and associated varieties . J. Pure Appl. Algebra. 104(1995), 275–301.CrossRefGoogle Scholar
Kad’ourek, J., On the locality of the pseudovariety DG . J. Inst. Math. Jussieu. 7(2008), 93–180.Google Scholar
Kad’ourek, J., On a locality-like property of the pseudovariety J . Period. Math. Hungar. 76(2018), 1–46.CrossRefGoogle Scholar
Kad’ourek, J., On semidirectly closed non-aperiodic pseudovarieties of finite monoids . Proc. Edinb. Math. Soc. (2). 63(2020), 913–928.CrossRefGoogle Scholar
Stiffler, P. Jr., Extension of the fundamental theorem of finite semigroups . Adv. Math. 11(1973), 159–209.CrossRefGoogle Scholar
Tilson, B., Categories as algebra: an essential ingredient in the theory of monoids . J. Pure Appl. Algebra. 48(1987), 83–198.10.1016/0022-4049(87)90108-3CrossRefGoogle Scholar