Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-30T01:14:52.549Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Average Number of Square-Free Values of Polynomials

Published online by Cambridge University Press:  20 November 2018

Igor E. Shparlinski
Igor E. Shparlinski*
Affiliation:
Department of Computing, Macquarie University, NSW 2109, Australia e-mail: igor.shparlinski@mq.edu.au
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We obtain an asymptotic formula for the number of square-free integers in 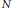$N$ consecutive values of polynomials on average over integral polynomials of degree at most $k$ and of height at most 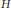$H$, where 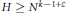$H\,\ge \,{{N}^{k-1+\varepsilon }}$ for some fixed $\varepsilon \,>\,0$. Individual results of this kind for polynomials of degree 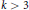$k\,>\,3$, due to A. Granville (1998), are only known under the 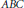$ABC$-conjecture.

Keywords

11N32polynomialssquare-free numbers
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 4 , 01 December 2013 , pp. 844 - 849
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Cutter, P., Granville, A., and Tucker, T. J., The number of fields generated by the square root of values of a given polynomial. Canad. Math. Bull. 46 (2003), no. 1, 71–79. http://dx.doi.org/10.4153/CMB-2003-007-0 Google Scholar
[2] Granville, A., ABC means we can count squarefrees. Internat. Math. Res. Notices 19 (1998), no. 19, 991–1009.Google Scholar
[3] Hooley, C., On the power-free values assumed by polynomial. Hardy-Ramanujan J. 26 (2003), 30–55.Google Scholar
[4] Luca, F. and Shparlinski, I. E., Quadratic fields generated by polynomials. Archiv Math. 91 (2008), no. 5, 399–408. http://dx.doi.org/10.1007/s00013-008-2656-2 Google Scholar
[5] Poonen, B., Squarefree values of multivariable polynomials. Duke Math. J. 118 (2003), no. 2, 353–373. http://dx.doi.org/10.1215/S0012-7094-03-11826-8 Google Scholar