Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T16:54:27.791Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Dichotomy of the Evolution Families: A Discrete-Argument Approach

Published online by Cambridge University Press:  20 November 2018

Ciprian Preda  and
Ciprian Sipos
Ciprian Preda
Affiliation:
Department of Mathematics, University of California, Los Angeles, CA 90095, U.S.A. e-mail: ciprian.preda@feaa.uvt.ro
Ciprian Sipos
Affiliation:
Department of Economics, West University of Timişoara, Timişoara 300115, Romania e-mail: ciprian.sipos@feaa.uvt.ro
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We establish a discrete-time criteria guaranteeing the existence of an exponential dichotomy in the continuous-time behavior of an abstract evolution family. We prove that an evolution family 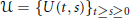$\mathcal{U}\,=\,{{\{U(t,\,s)\}}_{t\ge s\ge 0}}$ acting on a Banach space 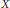$X$ is uniformly exponentially dichotomic (with respect to its continuous-time behavior) if and only if the corresponding difference equation with the inhomogeneous term from a vector-valued Orlicz sequence space 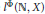${{l}^{\Phi }}(\mathbb{N},\,X)$ admits a solution in the same 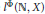${{l}^{\Phi }}(\mathbb{N},\,X)$. The technique of proof effectively eliminates the continuity hypothesis on the evolution family (i.e., we do not assume that 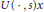$U(\,\cdot \,,\,s)x$ or 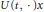$U(t,\,\cdot \,)x$ is continuous on 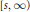$[s,\,\infty )$, and respectively 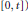$[0,\,t])$. Thus, some known results given by Coffman and Schaffer, Perron, and Ta Li are extended.

Keywords

34D0547D0693D20evolution familiesexponential dichotomyOrlicz sequence spacesadmissibility
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 3 , 01 September 2011 , pp. 527 - 537
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Ben-Artzi, A. and Gohberg, I., Dichotomy of systems and invertibility of linear ordinary differential operators. In: Time-variant systems and interpolation, Oper. Theory Adv. Appl., 56, Birkhäuser, Basel, 1992, pp. 90–119.Google Scholar
[2] Chicone, C. and Latushkin, Y., Evolution semigroups in dynamical systems and differential equations. Mathematical Surveys andMonographs, 70, American Mathematical Society, Providence, RI, 1999.Google Scholar
[3] Coffman, C. V. and Schäffer, J. J., Dichotomies for linear difference equations. Math. Ann. 172(1967), 139–166. doi:10.1007/BF01350095Google Scholar
[4] Daleckii, J. L, Kreĭn, M. G., Stability of solutions of differential equations in Banach space. Translations of Mathematical Monographs, 43, American Mathematical Society, Providence, RI, 1974.Google Scholar
[5] Henry, D., Geometric theory of semilinear parabolic equations. Lecture Notes in Mathematics, 840, Springer-Verlag, Berlin-New York, 1981.Google Scholar
[6] LaSalle, J. P., The stability and control of discrete processes. Applied Mathematical Sciences, 62, Springer-Verlag, New York, 1986.Google Scholar
[7] Latushkin, Y. and Montgomery-Smith, S., Evolutionary semigroups and Lyapunov theorems in Banach spaces. J. Funct. Anal. 127(1995), no. 1, 173–197. doi:10.1006/jfan.1995.1007Google Scholar
[8] Latushkin, Y. and Randolph, T., Dichotomy of differential equations on Banach spaces and an algebra of weighted translation operators. Integral Equations Operator Theory 23(1995), no. 4, 472–500. doi:10.1007/BF01203919Google Scholar
[9] Massera, J. L. and Schäffer, J. J., Linear differential equations and function spaces. Pure and Applied Mathematics, 21, Academic Press, New York-London, 1966.Google Scholar
[10] Megan, M. and Preda, P., Admissibility and dichotomies for linear discrete-time systems in Banach spaces. An. Univ. Timişoara Ştiint Mat. 26(1988), 45–54.Google Scholar
[11] van Minh, N., Räbiger, F., and Schnaubelt, R., Exponential stability, exponential expansiveness, and exponential dichotomy of evolution equations on the half-line. Integral Equations Operator Theory 32(1998), no. 3, 332–353. doi:10.1007/BF01203774Google Scholar
[12] van Minh, N., On the proof of characterizations of the exponential dichotomy. Proc. Amer. Math. Soc. 127(1999), no. 3, 779–782. doi:10.1090/S0002-9939-99-04640-7Google Scholar
[13] Perron, O., Die Stabilitätsfrage bei Differentialgeighungen. Math. Z. 32(1930), no. 1, 703–728. doi:10.1007/BF01194662Google Scholar
[14] Pinto, M., Discrete dichotomies. Advances in difference equations. Comput. Math. Appl. 28(1994), no. 1–3, 259–270. doi:10.1016/0898-1221(94)00114-6Google Scholar
[15] Preda, C., A discrete Perron-Ta Li type theorem for the dichotomy of evolution operators. J. Math. Anal. Appl. 332(2007), no. 1, 727–734. doi:10.1016/j.jmaa.2006.10.056Google Scholar
[16] Preda, P., On a Perron condition for evolutionary processes in Banach spaces. Bull. Math. Soc. Sci. Math. R.S. Roumanie (N.S.) 32(80)(1988), no. 1, 65–70.Google Scholar
[17] Przyluski, K. M. and Rolewicz, S., On stability of linear time-varying infinite-dimensional discrete-time systems. Systems Control Lett. 4(1984), no. 5, 307–315. doi:10.1016/S0167-6911(84)80042-0Google Scholar
[18] Sasu, B. and Sasu, A. L., Exponential dichotomy and (lp, lq )-admissibility on the half-line. J. Math. Anal. Appl. 316(2006), no. 2, 397–408. doi:10.1016/j.jmaa.2005.04.047Google Scholar
[19] Schnaubelt, R., Sufficient conditions for exponential stability and dichotomy of evolution equations. Forum Math. 11(1999), no. 5, 543–566. doi:10.1515/form.1999.013Google Scholar
[20] Li, Ta, Die Stabilitätsfrage bei Differenzgleichungen. Acta Math. 63(1934), 99–141. doi:10.1007/BF02547352Google Scholar