Let 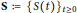$\mathbf{S}:={{\{S(t)\}}_{t\ge 0}}$ be a 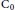${{\text{C}}_{0}}$-semigroup of quasinilpotent operators (i.e., 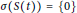$\sigma (S(t))=\{0\}$ for each 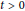$t>0$). In dynamical systems theory the above quasinilpotency property is equivalent to a very strong concept of stability for the solutions of autonomous systems. This concept is frequently called superstability and weakens the classical finite time extinction property (roughly speaking, disappearing solutions). We show that under some assumptions, the quasinilpotency, or equivalently, the superstability property of a 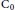${{\text{C}}_{0}}$-semigroup is preserved under the perturbations of its infinitesimal generator.