Hostname: page-component-cb9f654ff-w5vf4 Total loading time: 0 Render date: 2025-08-16T07:05:29.431Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive Definite Sequence of Operators and a Fixed Point Theorem

Published online by Cambridge University Press:  20 November 2018

A. T. Dash
A. T. Dash*
Affiliation:
University of Guelph, Guelph, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this note is to prove the following:

Theorem. Let {A n} be a positive definite sequence of operators on a Hilbert space H with A 0=1. If A1 f=f for some f in H, then A n f=f for all n.

Note that a bilateral sequence of operators {An:n = 0, ±1, ±2,…} on H is positive definite if

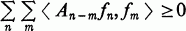
for every finitely nonzero sequence {fn} of vectors in H [1].

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 15 , Issue 2 , June 1972 , pp. 295
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Riesz, F. and Sz.-Nagy, B., Appendix to functional analysis, Ungar, New York.Google Scholar