Let F be a field of characteristic 0 and G a group such that each element of the group ring F[G] is either (right) invertible or a (left) zero divisor. Then G is locally finite.

This answers a question of Herstein [1, p. 36] [2, p. 450] in the characteristic 0 case. The proof can be informally summarized as follows: Let gl,…,gn be a finite subset of G, and let

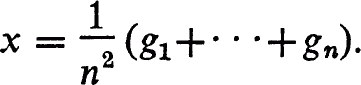
1—x is not a zero divisor so it is invertible and its inverse is 1+x+x3+⋯. The fact that this series converges to an element of F[G] (a finite sum) forces the subgroup generated by g1,…,gn to be finite, proving the theorem. The formal proof is via epsilontics and takes place inside of F[G].