Let 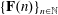$\{\mathbf{F}(n)\}_{n\in \mathbb{N}}$ and 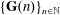$\{\mathbf{G}(n)\}_{n\in \mathbb{N}}$ be linear recurrence sequences. It is a well-known Diophantine problem to determine the finiteness of the set 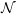${\mathcal{N}}$ of natural numbers such that their ratio 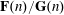$\mathbf{F}(n)/\mathbf{G}(n)$ is an integer. In this paper we study an analogue of such a divisibility problem in the complex situation. Namely, we are concerned with the divisibility problem (in the sense of complex entire functions) for two sequences 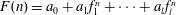$F(n)=a_{0}+a_{1}f_{1}^{n}+\cdots +a_{l}f_{l}^{n}$ and 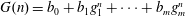$G(n)=b_{0}+b_{1}g_{1}^{n}+\cdots +b_{m}g_{m}^{n}$, where the 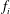$f_{i}$ and 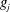$g_{j}$ are nonconstant entire functions and the 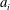$a_{i}$ and 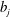$b_{j}$ are non-zero constants except that 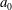$a_{0}$ can be zero. We will show that the set 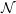${\mathcal{N}}$ of natural numbers such that 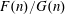$F(n)/G(n)$ is an entire function is finite under the assumption that 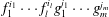$f_{1}^{i_{1}}\cdots f_{l}^{i_{l}}g_{1}^{j_{1}}\cdots g_{m}^{j_{m}}$ is not constant for any non-trivial index set 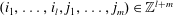$(i_{1},\ldots ,i_{l},j_{1},\ldots ,j_{m})\in \mathbb{Z}^{l+m}$.