Hostname: page-component-76c49bb84f-t7r7g Total loading time: 0 Render date: 2025-07-01T12:29:49.589Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on Hopf Images and Quantum Permutation Groups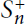$S_{n}^{+}$

Published online by Cambridge University Press:  20 November 2018

Paweł Józiak
Paweł Józiak*
Affiliation:
Institute of Mathematics of the Polish Academy of Sciences, ul. Sniadeckich 8, 00-656 Warszawa, Poland and Institute of Mathematics, University of Wrocław, pl. Grunwaldzki 2/4, 50–384 Wrocław, Poland, e-mail: pjoziak@impan.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Motivated by a question of A. Skalski and P. M. Sołtan (2016) about inner faithfulness of S. Curran’s map of extending a quantum increasing sequence to a quantum permutation, we revisit the results and techniques of T. Banica and J. Bichon (2009) and study some group-theoretic properties of the quantum permutation group on points. This enables us not only to answer the aforementioned question in the positive for the case where 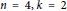$n\,=\,4,\,k\,=\,2$, but also to classify the automorphisms of 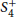$S_{4}^{+}$, describe all the embeddings 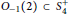${{O}_{-1}}(2)\,\subset \,S_{4}^{+}$ and show that all the copies of 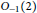${{O}_{-1}}(2)$ inside 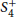$S_{4}^{+}$are conjugate. We then use these results to show that the converse to the criterion we applied to answer the aforementioned question is not valid.

Keywords

20G4281R5046L8916W35Hopf imagequantum permutation groupcompact quantum group

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 2 , 01 June 2018 , pp. 301 - 317
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Banica, T., Symmetries ofa generic coaction. Math. Ann. 314(1999), no. 4, 763–780.http://dx.doi.org/10.1007/s002080050315 Google Scholar
[2] Banica, T., Truncation and duality resultsfor Hopf image algebras. Bull. Pol. Acad. Sei. Math. 62(2014), 161–180.http://dx.doi.org/10.4064/ba62-2-5 Google Scholar
[3] Banica, T. and Bichon, J., Quantum groups acting on 4 points. J. Reine Angew. Math. 626(2009), 75–114.http://dx.doi.org/10.1515/CRELLE.2009.003 Google Scholar
[4] Banica, T., Hopf Images and inner faithful representations. Glasg. Math. J. 52(2010), 677–703.http://dx.doi.Org/10.1017/S001 7089510000510 Google Scholar
[5] Banica, T. and Speicher, R., Liberation of orthogonal Lie groups. Adv. Math. 222(2009), 1461–1501.http://dx.doi.Org/10.1016/j.aim.2009.06.009 Google Scholar
[6] Bichon, J., Quelques nouvelles déformations du groupe symétrique. C. R. Acad. Sei. Paris Sér. I Math. 330(2000), 761–764.http://dx.doi.org/10.1016/S0764-4442(00)00275-5 Google Scholar
[7] Bichon, J. and Yuncken, R., Quantum subgroups ofthe compact quantumgroup SU−1(3). Bull. Lond. Math. Soc. 46(2014), 315–328.http://dx.doi.Org/10.1112/blms/bdt105 Google Scholar
[8] Brannan, M., Collins, B., and Vergnioux, R., The Connes embedding property for quantum group von Neumann algebras. Trans. Amer. Math. Soc. 369(2017), no. 6, 3799–3819. http://dx.doi.Org/10.1090/tran/6752 Google Scholar
[9] Curran, S., A characterization offreeness by invariance under quantum spreading. J. Reine Angew. Math. 659(2011), 43–65. http://dx.doi.Org/10.1515/CRELLE.2O11.066 Google Scholar
[10] Daws, M., Kasprzak, P., Skalski, A., and Soltan, P. M., Closed quantum subgroups oflocally compact quantum groups. Adv. Math. 231(2012), 3473–3501.http://dx.doi.Org/10.1016/j.aim.2O12.09.002 Google Scholar
[11] Doi, Y., Braided bialgebras and quadratic bialgebras. Comm. Algebra 21(1993), 1731–1749.http://dx.doi.org/10.1080/00927879308824649 Google Scholar
[12] Golubitsky, M., Stewart, I., and Schaeffer, D. G., Singularities and groups in bifurcation theory. Vol. II. Applied Mathematical Sciences, 69, Springer-Verlag, New York, 1988.http://dx.doi.Org/10.1007/978-1-4612-4574-2 Google Scholar
[13] Józiak, P., Hopf Images in Locally compact quantum groups. PhD thesis, Institute of Mathematics Polish Academy of Sciences, 2016.Google Scholar
[14] Józiak, P., Kasprzak, P., and So łtan, P. M., Hopf images in locally compact quantum groups. J. Math. Anal. Appl. 455(2017), 141–166.http://dx.doi.Org/10.1016/j.jmaa.2017.05.047 Google Scholar
[15] Kadison, R. V. and Ringrose, J. R., Fundamentals ofthe theory of Operator algebras. Vol. II. Pure and Applied Mathematics, 100, Academic Press, Inc., Orlando, FL, 1986.http://dx.doi.org/10.1016/S0079-8169(08)60611-X Google Scholar
[16] Kalantar, M. and Neufang, M., From quantum groups to groups. Canad. J. Math. 65(2013), 1073–1094.http://dx.doi.org/10.4153/CJM-2012-047-X Google Scholar
[17] Köstler, C. and Speicher, R., A noncommutative de Finetti theorem: invariance under quantum permutations is equivalent tofreeness with amalgamation. Comm. Math. Phys. 291(2009), 473–490.http://dx.doi.org/10.1007/s00220-009-0802-8 Google Scholar
[18] Kyed, D. and Soltan, P. M., Property (T) and exotic quantum group norms. J. Noncommut. Geom. 6(2012), 773–800.http://dx.doi.org/10.4171/JNCC/105 Google Scholar
[19] Patri, I., Normal subgroups, center and inner automorphisms ofcompact quantum groups. Internat. J. Math. 24(2013), 1350071, 37.http://dx.doi.org/10.1142/S0129167X13500717 Google Scholar
[20] Podles, P., Symmetries of quantum Spaces. Subgroups and quotient Spaces of quantum SU(2) and SO(3) groups. Comm. Math. Phys. 170(1995), 1–20.http://dx.doi.Org/10.1007/BF02099436 Google Scholar
[21] Schauenburg, P., Hopf bi-Galois extensions. Comm. Algebra 24(1996), 3797–3825.http://dx.doi.org/10.1080/00927879608825788 Google Scholar
[22] Skalski, A. and Soltan, P. M., Quantum families ofinvertible maps and related problems. Canad. J. Math. 68(2016), 698–720.http://dx.doi.org/10.4153/CJM-2015-037-9 Google Scholar
[23] Wang, S., Quantum symmetry groups offinite Spaces. Comm. Math. Phys. 195(1998), 195–211.http://dx.doi.Org/10.1007/s00220005O385 Google Scholar
[24] Woronowicz, S. L., Compact matrix pseudogroups. Comm. Math. Phys. 111(1987), 613–665.http://dx.doi.Org/10.1007/BF01219077 Google Scholar
[25] Woronowicz, S. L., Compact quantum groups. In: Symétries quantiques (Les Houches, 1995), North-Holland, Amsterdam, 1998, pp. 845–884.Google Scholar