Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-15T06:17:47.311Z Has data issue: false hasContentIssue false
  • English
  • Français

Representation Theories for the Laplace Transform

Published online by Cambridge University Press:  20 November 2018

H. P. Heinig
H. P. Heinig*
Affiliation:
McMaster University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Widder-Post real inversion operator [4[ is defined by

1.1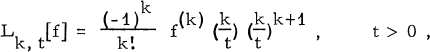

k = 1, 2,…. Utilizing this inversion operator one can obtain the following representation theorem (see e.g. [4[ Chapter VII, Theorem 15a).

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 10 , Issue 3 , August 1967 , pp. 333 - 345
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Lorentz, G. G., Bernstein Polynomials. Toronto (1955).Google Scholar
2. Rooney, P. G., A Generalization of some Theorems of Hardy. Trans. Royal Soc. Can., Ser III, Sect. Ill (XLIX), (1955).Google Scholar
3. Taylor, A. E., Introduction to Functional Analysis. New York (1955).Google Scholar
4. Widder, D. V., The Laplace Transform. Princeton (1944).Google Scholar
5. Zygmund, A., Trigonometric Series. Vol. I. Cambridge (1955).Google Scholar