Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T05:38:57.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of Real C*-Algebras

Published online by Cambridge University Press:  20 November 2018

Jeffrey L. Boersema  and
Efren Ruiz
Jeffrey L. Boersema
Affiliation:
Department of Mathematics, Seattle University, Seattle, WA 98122, U.S.A.e-mail: boersema@seattleu.edu
Efren Ruiz
Affiliation:
Department of Mathematics, University of Hawaii Hilo, Hilo, Hawaii 96720, U.S.A.e-mail: ruize@hawaii.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We will give a characterization of stable real 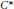${{C}^{*}}$-algebras analogous to the one given for complex 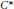${{C}^{*}}$-algebras by Hjelmborg and Rørdam. Using this result, we will prove that any real 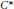${{C}^{*}}$-algebra satisfying the corona factorization property is stable if and only if its complexification is stable. Real 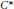${{C}^{*}}$-algebras satisfying the corona factorization property include 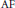$\text{AF}$-algebras and purely infinite C*-algebras. We will also provide an example of a simple unstable C*-algebra, the complexification of which is stable.

Keywords

46L05stabilityreal C*-algebras
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 4 , 01 December 2011 , pp. 593 - 606
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Bhat, B. V. R., Elliott, G. A., and Fillmore, P. A., eds., Lectures on operator theory. Fields Institute Monographs, 13, American Mathematical Society, Providence, RI, 1999.Google Scholar
[2] Boersema, J. L., The range of united K-theory. J. Funct. Anal. 235(2006), no. 2, 701–718.Google Scholar
[3] Boersema, J. L. and Stacey, P. J., Correction to the paper: “Real structure in purely infinite C*-algebras” [J. Operator Theory 49(2003), no. 1, 77–84]. J. Operator Theory 53(2005), no. 2, 441–442.Google Scholar
[4] Brown, L. G., Stable isomorphism of hereditary subalgebras of C*-algebras. Pacific J. Math. 71(1977), no. 2, 335–348.Google Scholar
[5] Brown, L. G., Semicontinuity and multipliers of C*-algebras. Canad. J. Math. 40(1988), no. 4, 865–988. doi:10.4153/CJM-1988-038-5Google Scholar
[6] Brown, L. G. and Pedersen, G. K., C*-algebras of real rank zero. J. Funct. Anal. 99(1991), no. 1, 131–149. doi:10.1016/0022-1236(91)90056-BGoogle Scholar
[7] Cuntz, J., K-theory for certain C*-algebras. Ann. of Math. (2) 113(1981), no. 1, 181–197. doi:10.2307/1971137Google Scholar
[8] Hjelmborg, J. v. B. and Rørdam, M., On stability of C*-algebras. J. Funct. Anal. 155(1998), no. 1, 153–170. doi:10.1006/jfan.1997.3221Google Scholar
[9] Murphy, G. J., C*-algebras and operator theory. Academic Press Inc., Boston, MA, 1990.Google Scholar
[10] Ng, P. W., The corona factorization property. In: Operator theory, operator algebras, and applications, Contemporary Mathematics, 414, American Mathematical Society, Providence, RI, 2006, pp. 97–110.Google Scholar
[11] Pedersen, G. K., C*-algebras and their automorphism groups. London Mathematical Society Monographs, 14. Academic Press, Inc., London-New York, 1979.Google Scholar
[12] Rieffel, M., Dimension and stable rank in the K-theory of C*-algebras. Proc. London Math. Soc. 46(1983), no. 2, 301–333. doi:10.1112/plms/s3-46.2.301Google Scholar
[13] Rørdam, M., Stability of C*-algebras is not a stable property.. Doc. Math. 2(1997), 375–386.Google Scholar
[14] Rørdam, M., Stable C*-algebras. In: Operator algebras and applications, Advanced Studies in Pure Mathematics, 38, Math. Soc. Japan, Tokyo, 2004, pp. 177–199.Google Scholar
[15] Schröder, H., K-theory for real C*-algebras and applications. Pitman Research Notes Mathematics Series, 290, Longman, Scientific, & Technical, Harlow, 1993.Google Scholar
[16] Stacey, P. J., Real structure in purely infinite C*-algebras. J. Operator Theory 49(2003), no. 1, 77–84.Google Scholar
[17] Villadsen, J., Simple C*-algebras with perforation. J. Funct. Anal. 154(1998), no. 1, 110–116. doi:10.1006/jfan.1997.3168Google Scholar
[18] Zhang, S., On the structure of projections and ideals of corona algebras. Canad. J. Math. 41(1989), no. 4, 721–742. doi:10.4153/CJM-1989-033-4Google Scholar
[19] Zhang, S., Certain C*-algebras of real rank zero and their corona and multiplier algebras. I. Pacific J. Math. 155(1992), no. 1, 169–197.Google Scholar