Hostname: page-component-5c6d5d7d68-xq9c7 Total loading time: 0 Render date: 2024-08-16T11:11:05.318Z Has data issue: false hasContentIssue false
  • English
  • Français

A Szpilrajn–Marczewski Type Theorem for Concentration Dimension on Polish Space

Published online by Cambridge University Press:  20 November 2018

Józef Myjak ,
Tomasz Szarek  and
Maciej Śleçzka
Józef Myjak
Affiliation:
WMS AGH, Al. Mickiewicza 30, 30-059 Krakow, Poland e-mail: myjak@univaq.it
Tomasz Szarek
Affiliation:
Institute of Mathematics, Silesian University, Bankowa 14, 40-007 Katowice, Poland e-mail: szarek@ux2.math.us.edu.plsleczka@ux2.math.us.edu.pl
Maciej Śleçzka
Affiliation:
Institute of Mathematics, Silesian University, Bankowa 14, 40-007 Katowice, Poland e-mail: szarek@ux2.math.us.edu.plsleczka@ux2.math.us.edu.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 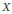$X$ be a Polish space. We will prove that

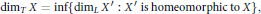$${{\dim}_{T}}X=\inf \left\{ {{\dim}_{L}}{X}'\,:\,{X}'\,\text{is homeomorphic to }X\, \right\},$$

where 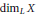${{\dim}_{L}}\,X$ and 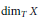${{\dim}_{T}}\,X$ stand for the concentration dimension and the topological dimension of 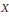$X$, respectively.

Keywords

11K5528A78Hausdorff dimensiontopological dimensionLévy concentration functionconcentration dimension
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 2 , 01 June 2006 , pp. 247 - 255
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Billingsley, P., Convergence of Probability Measures. John Wiley, New York, 1968.Google Scholar
[2] Engelking, R., Dimension Theory. Biblioteka Matematyczna, Warszawa, 1981.Google Scholar
[3] Falconer, K. J., Techniques in Fractal Geometry. John Wiley and Sons, Chichester, 1997.Google Scholar
[4] Foguel, S. R., The Ergodic Theory of Markov Processes. Van Nostrand Mathematical Studies 21, Van Nostrand Reinhold, New York, 1969.Google Scholar
[5] Ford, L. R. and Fulkerson, R. D., Maximal flow through a network. Canad. J. Math. 8(1956), 399–404.Google Scholar
[6] Frostman, O., Potential d’équilibre et capacité des ensembles avec quelques applications á la théorie des fonctions Maddel. Lunds Univ. Mat. Sem. 3(1935), 1–118.Google Scholar
[7] Hengartner, W. and Theodorescu, R., Concentration Functions. Probability and Mathematical Statistics 20, Academic Press, New York, 1973.Google Scholar
[8] Howroyd, J. D., On dimension and on the existence of sets of finite positive Hausdorff measure. Proc. London Math. Soc. 70(1995), no. 3, 581–604.Google Scholar
[9] Hurewicz, W. and Wallman, H., Dimension Theory. Princeton Mathematical Series 4, Princeton University Press, Princeton, NJ, 1941.Google Scholar
[10] Joyce, H., A relationship between packing and topological dimensions. Mathematika 45(1998), no. 1, 43–53.Google Scholar
[11] Lasota, A. and Myjak, J., On a dimension of measures. Bull. Polish Acad. sci. Math. 50(2002), no. 2, 221–235.Google Scholar
[12] Myjak, J. and Szarek, T., Szpilrajn type theorem for concentration dimension. Fund. Math. 172(2002), no. 1, 19–25.Google Scholar
[13] Myjak, J. and Szarek, T., Some generic properties of concentration dimension of measure. UnioneMat. Ital. Sez. B Artic. Ric. Mat. 8(2003), no. 1, 211–219.Google Scholar
[14] Nöbeling, V. G., Hausdorffische und mengentheoretische Dimension. In: Menger, K., Ergebnisse eines Mathematischen Kolloquiums, Springer-Verlag, Vienna, 1998, pp. 24–25.Google Scholar
[15] Rogers, C. A., Hausdorff Measures. Cambridge University Press, London, 1970.Google Scholar
[16] Szpilrajn, E., La dimension et la mesure. Fund. Math. 27(1937), 81–89.Google Scholar