Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gilkey, P. B.
1984.
The eta invariant and theK-theory of odd dimensional spherical space forms.
Inventiones Mathematicae,
Vol. 76,
Issue. 3,
p.
421.
1988.
The Homology of Hopf Spaces.
Vol. 40,
Issue. ,
p.
449.

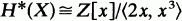 where dim
where dim 