Article contents
Balls-in-Bins Processes with Feedback and Brownian Motion
Published online by Cambridge University Press: 01 January 2008
Abstract
In a balls-in-bins process with feedback, balls are sequentially thrown into bins so that the probability that a bin with n balls obtains the next ball is proportional to f(n) for some function f. A commonly studied case where there are two bins and f(n) = np for p > 0, and our goal is to study the fine behaviour of this process with two bins and a large initial number t of balls. Perhaps surprisingly, Brownian Motions are an essential part of both our proofs.
For p > 1/2, it was known that with probability 1 one of the bins will lead the process at all large enough times. We show that if the first bin starts with 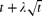 balls (for constant λ∈ℝ), the probability that it always or eventually leads has a non-trivial limit depending on λ.
balls (for constant λ∈ℝ), the probability that it always or eventually leads has a non-trivial limit depending on λ.
For p ≤ 1/2, it was known that with probability 1 the bins will alternate in leadership. We show, however, that if the initial fraction of balls in one of the bins is > 1/2, the time until it is overtaken by the remaining bin scales like Θ(t1+1/(1-2p)) for p < 1/2 and exp(Θ(t)) for p = 1/2. In fact, the overtaking time has a non-trivial distribution around the scaling factor, which we determine explicitly.
Our proofs use a continuous-time embedding of the balls-in-bins process (due to Rubin) and a non-standard approximation of the process by Brownian Motion. The techniques presented also extend to more general functions f.
Information
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2007
References
- 10
- Cited by

