Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-25T20:53:00.482Z Has data issue: false hasContentIssue false
  • English
  • Français

Decision Trees and Influences of Variables Over Product Probability Spaces

Published online by Cambridge University Press:  01 May 2009

HAMED HATAMI
HAMED HATAMI*
Affiliation:
Department of Computer Science, University of Toronto, Ontario M5S 3G4, Canada (e-mail: hamed@cs.toronto.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

A celebrated theorem of Friedgut says that every function f : {0, 1}n → {0, 1} can be approximated by a function g : {0, 1}n → {0, 1} with 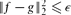, which depends only on eO(If / ε) variables, where If is the sum of the influences of the variables of f. Dinur and Friedgut later showed that this statement also holds if we replace the discrete domain {0, 1}n with the continuous domain [0, 1]n, under the extra assumption that f is increasing. They conjectured that the condition of monotonicity is unnecessary and can be removed.

We show that certain constant-depth decision trees provide counter-examples to the Dinur–Friedgut conjecture. This suggests a reformulation of the conjecture in which the function g : [0, 1]n → {0, 1}, instead of depending on a small number of variables, has a decision tree of small depth. In fact we prove this reformulation by showing that the depth of the decision tree of g can be bounded by eO(If / ε2).

Furthermore, we consider a second notion of the influence of a variable, and study the functions that have bounded total influence in this sense. We use a theorem of Bourgain to show that these functions have certain properties. We also study the relation between the two different notions of influence.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 18 , Issue 3 , May 2009 , pp. 357 - 369
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Beckner, W. (1975) Inequalities in Fourier analysis. Ann. of Math. (2) 102 159–182.CrossRefGoogle Scholar
[2]Bonami, A. (1970) Études des coefficients Fourier des fonctiones de L p(g). Ann. Inst. Fourier 20 335–402.CrossRefGoogle Scholar
[3]Bourgain, J. (2002) On the distributions of the Fourier spectrum of Boolean functions. Israel J. Math. 131 269–276.CrossRefGoogle Scholar
[4]Bourgain, J., Kahn, J., Kalai, G., Katznelson, Y. and Linial, N. (1992) The influence of variables in product spaces. Israel J. Math. 77 55–64.CrossRefGoogle Scholar
[5]Dinur, I., Regev, O. and Smyth, C. D. (2005) The hardness of 3-uniform hypergraph coloring. Combinatorica 25 519–535.CrossRefGoogle Scholar
[6]Dinur, I. and Safra, S. (2005) On the hardness of approximating minimum vertex cover. Ann. of Math. (2) 162 439–485.CrossRefGoogle Scholar
[7]Friedgut, E. (1998) Boolean functions with low average sensitivity depend on few coordinates. Combinatorica 18 27–35.CrossRefGoogle Scholar
[8]Friedgut, E. (1999) Sharp thresholds of graph properties, and the k-sat problem. J. Amer. Math. Soc. 12 1017–1054.CrossRefGoogle Scholar
[9]Friedgut, E. (2004) Influences in product spaces: KKL and BKKKL revisited. Combin. Probab. Comput. 13 17–29.CrossRefGoogle Scholar
[10]Friedgut, E. and Kalai, G. (1996) Every monotone graph property has a sharp threshold. Proc. Amer. Math. Soc. 124 2993–3002.CrossRefGoogle Scholar
[11]Friedgut, E., Kalai, G. and Naor, A. (2002) Boolean functions whose Fourier transform is concentrated on the first two levels. Adv. Appl. Math. 29 427–437.CrossRefGoogle Scholar
[12]Hatami, H. (2006) A remark on Bourgain's distributional inequality on the Fourier spectrum of Boolean functions. Online J. Analytic Combin. 1.Google Scholar
[13]Kahn, J., Kalai, G. and Linial, N. (1988) The influence of variables on Boolean functions. In Proc. 29th Annual Symposium on Foundations of Computer Science, pp. 68–80.CrossRefGoogle Scholar
[14]Khot, S. and Regev, O. (2008) Vertex cover might be hard to approximate to within 2-ε. J. Comput. System Sci. 74 335–349.CrossRefGoogle Scholar
[15]Linial, N., Mansour, Y. and Nisan, N. (1993) Constant depth circuits, Fourier transform, and learnability. J. Assoc. Comput. Mach. 40 607–620.CrossRefGoogle Scholar
[16]Margulis, G. A. (1974) Probabilistic characteristics of graphs with large connectivity. Problemy Peredači Informacii 10 101–108.Google Scholar
[17]O'Donnell, R., Saks, M. and Schramm, O. (2005) Every decision tree has an influential variable. In FOCS'05: Proc. 46th Annual IEEE Symposium on Foundations of Computer Science, IEEE Computer Society, Washington, DC, pp. 31–39.CrossRefGoogle Scholar
[18]O'Donnell, R. and Servedio, R. (2007) Learning monotone decision trees in polynomial time. SIAM J. Comput. 37 827–844.CrossRefGoogle Scholar
[19]Russo, L. (1981) On the critical percolation probabilities. Z. Wahrsch. Verw. Gebiete 56 229–237.CrossRefGoogle Scholar
[20]Talagrand, M. (1989) Isoperimetry and integrability of the sum of independent Banach-space valued random variables. Ann. Probab. 17 1546–1570.CrossRefGoogle Scholar
[21]Talagrand, M. (1994) On Russo's approximate zero-one law. Ann. Probab. 22 1576–1587.CrossRefGoogle Scholar