Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bourgain, Jean
2008.
Roth’s theorem on progressions revisited.
Journal d'Analyse Mathématique,
Vol. 104,
Issue. 1,
p.
155.
GREEN, BEN
and
TAO, TERENCE
2009.
A NOTE ON THE FREIMAN AND BALOG–SZEMERÉDI–GOWERS THEOREMS IN FINITE FIELDS.
Journal of the Australian Mathematical Society,
Vol. 86,
Issue. 1,
p.
61.
GREEN, BEN
and
TAO, TERENCE
2009.
Freiman's Theorem in Finite Fields via Extremal Set Theory.
Combinatorics, Probability and Computing,
Vol. 18,
Issue. 3,
p.
335.
Шкредов, Илья Дмитриевич
and
Shkredov, Il'ya Dmitrievich
2010.
Анализ Фурье в комбинаторной теории чисел.
Успехи математических наук,
Vol. 65,
Issue. 3,
p.
127.
Iosevich, Alex
Morgan, Hannah
and
Pakianathan, Jonathan
2011.
On Directions Determined by Subsets of Vector Spaces over Finite Fields.
Integers,
Vol. 11,
Issue. 6,
Lovett, Shachar
2012.
Equivalence of polynomial conjectures in additive combinatorics.
Combinatorica,
Vol. 32,
Issue. 5,
p.
607.
Ben-Sasson, Eli
Lovett, Shachar
and
Ron-Zewi, Noga
2012.
An Additive Combinatorics Approach Relating Rank to Communication Complexity.
p.
177.
EVEN-ZOHAR, CHAIM
2012.
On Sums of Generating Sets in ℤ2n.
Combinatorics, Probability and Computing,
Vol. 21,
Issue. 6,
p.
916.
Even-Zohar, Chaim
and
Lev, Vsevolod F.
2013.
Small asymmetric sumsets in elementary abelian 2-groups.
Discrete Mathematics,
Vol. 313,
Issue. 5,
p.
689.
Dell, Holger
and
Van Melkebeek, Dieter
2014.
Satisfiability Allows No Nontrivial Sparsification unless the Polynomial-Time Hierarchy Collapses.
Journal of the ACM,
Vol. 61,
Issue. 4,
p.
1.
Even-Zohar, Chaim
and
Lovett, Shachar
2014.
The Freiman–Ruzsa theorem over finite fields.
Journal of Combinatorial Theory, Series A,
Vol. 125,
Issue. ,
p.
333.
Ben-Sasson, Eli
Lovett, Shachar
and
Ron-Zewi, Noga
2014.
An Additive Combinatorics Approach Relating Rank to Communication Complexity.
Journal of the ACM,
Vol. 61,
Issue. 4,
p.
1.
FREIMAN, GREGORY
HERZOG, MARCEL
LONGOBARDI, PATRIZIA
and
MAJ, MERCEDE
2014.
SMALL DOUBLING IN ORDERED GROUPS.
Journal of the Australian Mathematical Society,
Vol. 96,
Issue. 3,
p.
316.
Shkredov, Ilya Dmitrievich
2015.
Структурные теоремы в аддитивной комбинаторике.
Успехи математических наук,
Vol. 70,
Issue. 1(421),
p.
123.
Xie, Ning
Xu, Shuai
and
Xu, Yekun
2021.
Computer Science – Theory and Applications.
Vol. 12730,
Issue. ,
p.
460.
Xie, Ning
Xu, Shuai
and
Xu, Yekun
2023.
A generalization of a theorem of Rothschild and van Lint.
Theoretical Computer Science,
Vol. 955,
Issue. ,
p.
113802.

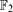 . Specifically we show that if
. Specifically we show that if 