Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T18:15:47.069Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the Brown–Erdős–Sós conjecture in groups

Part of: Graph theory

Published online by Cambridge University Press:  03 February 2020

Jason Long
Jason Long*
Affiliation:
Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, Oxford OX2 6GG, UK Email: Jason.Long@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that a dense subset of a sufficiently large group multiplication table contains either a large part of the addition table of the integers modulo some k, or the entire multiplication table of a certain large abelian group, as a subgrid. As a consequence, we show that triples systems coming from a finite group contain configurations with t triples spanning 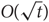$ O(\sqrt t )$ vertices, which is the best possible up to the implied constant. We confirm that for all t we can find a collection of t triples spanning at most t + 3 vertices, resolving the Brown–Erdős–Sós conjecture in this context. The proof applies well-known arithmetic results including the multidimensional versions of Szemerédi’s theorem and the density Hales–Jewett theorem.

This result was discovered simultaneously and independently by Nenadov, Sudakov and Tyomkyn [5], and a weaker result avoiding the arithmetic machinery was obtained independently by Wong [11].

MSC classification

Primary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Secondary: 05C35: Extremal problems 05C65: Hypergraphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 29 , Issue 4 , July 2020 , pp. 633 - 640
Check for updates
Copyright
© Cambridge University Press 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brown, W. G., Erdős, P. and Sós, V. T. (1973) Some extremal problems on r-graphs. In New Directions in the Theory of Graphs (Harary, F., ed.), Academic Press.Google Scholar
Dodos, P., Kanellopoulos, V. and Tyros, K. (2014) A simple proof of the density Hales–Jewett theorem. Int. Math. Res. Not. 12 3340–3352.CrossRefGoogle Scholar
Furstenberg, H. and Katznelson, Y. (1978) An ergodic Szemerédi theorem for commuting transformations. J. Analyse Math. 38 275–291.CrossRefGoogle Scholar
Furstenberg, H. and Katznelson, Y. (1989) A density version of the Hales–Jewett Theorem for k = 3. Discrete Math. 75 227–241.Google Scholar
Nenadov, R., Sudakov, B. and Tyomkyn, M. (2019) Proof of the Brown–Erdős–Sós conjecture in groups. Math. Proc. Cam. Phil. Soc. 1–11.CrossRefGoogle Scholar
Pyber, L. (1997) How abelian is a finite group? In The Mathematics of Paul Erdős I (Graham, R. L. et al., eds), Vol. 13 of Algorithms and Combinatorics, Springer, pp. 372–384.Google Scholar
Ruzsa, I. and Szemerédi, E. (1978) Triple systems with no six points carrying three triangles. Coll. Math. Soc. J. Bolyai 18 939–945.Google Scholar
Sárközy, G. N. and Selkow, S. (2004) An extension of the Ruzsa–Szemerédi theorem. Combinatorica 25 77–84.CrossRefGoogle Scholar
Solymosi, J. (2015) The (7, 4) -conjecture in finite groups. Combin. Probab. Comput. 24 680–686.Google Scholar
Solymosi, J. and Wong, C. (2019) The Brown–Erdős–Sós conjecture in finite abelian groups. Discrete Appl. Math.CrossRefGoogle Scholar
Wong, C. (2019) On the existence of dense substructures in finite groups. Preprint.Google Scholar