Hostname: page-component-7479d7b7d-68ccn Total loading time: 0 Render date: 2024-07-14T00:21:54.192Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted Interlace Polynomials

Published online by Cambridge University Press:  10 August 2009

LORENZO TRALDI
LORENZO TRALDI*
Affiliation:
Lafayette College, Easton, Pennsylvania 18042, USA (e-mail: traldil@lafayette.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

The interlace polynomials introduced by Arratia, Bollobás and Sorkin extend to invariants of graphs with vertex weights, and these weighted interlace polynomials have several novel properties. One novel property is a version of the fundamental three-term formula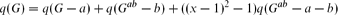 that lacks the last term. It follows that interlace polynomial computations can be represented by binary trees rather than mixed binary–ternary trees. Binary computation trees provide a description of q(G) that is analogous to the activities description of the Tutte polynomial. If G is a tree or forest then these ‘algorithmic activities’ are associated with a certain kind of independent set in G. Three other novel properties are weighted pendant-twin reductions, which involve removing certain kinds of vertices from a graph and adjusting the weights of the remaining vertices in such a way that the interlace polynomials are unchanged. These reductions allow for smaller computation trees as they eliminate some branches. If a graph can be completely analysed using pendant-twin reductions, then its interlace polynomial can be calculated in polynomial time. An intuitively pleasing property is that graphs which can be constructed through graph substitutions have vertex-weighted interlace polynomials which can be obtained through algebraic substitutions.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 19 , Issue 1 , January 2010 , pp. 133 - 157
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aigner, M. and van der Holst, H. (2004) Interlace polynomials. Linear Alg. Appl. 377 11–30.CrossRefGoogle Scholar
[2]Anderson, C., Cutler, J. D., Radcliffe, A. J., and Traldi, L. On the interlace polynomials of forests. Discrete Math., to appear.Google Scholar
[3]Arratia, R., Bollobás, B., and Sorkin, G. B. (2000) The interlace polynomial: A new graph polynomial. In Proc. 11th Annual ACM–SIAM Symposium on Discrete Algorithms (San Francisco 2000), ACM, New York, pp. 237–245.Google Scholar
[4]Arratia, R., Bollobás, B., and Sorkin, G. B. (2004) The interlace polynomial of a graph. J. Combin. Theory Ser. B 92 199–233.CrossRefGoogle Scholar
[5]Arratia, R., Bollobás, B., and Sorkin, G. B. (2004) A two-variable interlace polynomial. Combinatorica 24 567–584.CrossRefGoogle Scholar
[6]Balister, P. N., Bollobás, B., Cutler, J. and Pebody, L. (2002) The interlace polynomial of graphs at —1. Europ. J. Combin. 23 761–767.CrossRefGoogle Scholar
[7]Bari, R. A. (1979) Chromatic polynomials and the internal and external activities of Tutte. In Graph Theory and Related Topics (Waterloo 1977), Academic Press, New York, pp. 41–52.Google Scholar
[8]Bläser, M. and Hoffmann, C. (2008) On the complexity of the interlace polynomial. In STACS 2008: 25th International Symposium on Theoretical Aspects of Computer Science (Bordeaux 2008), pp. 97–108. Available at http://www.stacs-conf.org/.Google Scholar
[9]Boesch, F. T., Satyanarayana, A. and Suffel, C. L. (1988) Some recent advances in reliability analysis using graph theory: A tutorial. Congr. Numer. 64 253–276.Google Scholar
[10]Bollobás, B. (1998) Modern Graph Theory, Springer, New York.CrossRefGoogle Scholar
[11]Bouchet, A. (1987) Digraph decompositions and Eulerian systems. SIAM J. Alg. Disc. Meth. 8 323–337.CrossRefGoogle Scholar
[12]Bouchet, A. (1987) Reducing prime graphs and recognizing circle graphs. Combinatorica 7 243–254.CrossRefGoogle Scholar
[13]Bouchet, A. (1994) Circle graph obstructions. J. Combin. Theory Ser. B 60 107–144.CrossRefGoogle Scholar
[14]Bouchet, A. (2001) Multimatroids III: Tightness and fundamental graphs. Europ. J. Combin. 22 657–677.CrossRefGoogle Scholar
[15]Colbourn, C. J. (1987) The Combinatorics of Network Reliability, Oxford University Press, Oxford.Google Scholar
[16]Courcelle, B. (2008) A multivariate interlace polynomial and its computation for graphs of bounded clique-width. Electron. J. Combin. 15 #R69.CrossRefGoogle Scholar
[17]Courcelle, B. (2008) Circle graphs and monadic second-order logic. J. Appl. Logic 6 416–442.CrossRefGoogle Scholar
[18]Crapo, H. (1967) A higher invariant for matroids. J. Combin. Theory 2 406–417.CrossRefGoogle Scholar
[19]Cunningham, W. H. (1982) Decomposition of directed graphs. SIAM J. Alg. Disc. Meth. 3 214–228.CrossRefGoogle Scholar
[20]Ellis-Monaghan, J. A. and Sarmiento, I. (2007) Distance hereditary graphs and the interlace polynomial. Combin. Probab. Comput. 16 947–973.CrossRefGoogle Scholar
[21]Gordon, G. and McMahon, E. (1997) Interval partitions and activities for the greedoid Tutte polynomial. Adv. Appl. Math. 18 33–49.CrossRefGoogle Scholar
[22]Gordon, G. and Traldi, L. (1990) Generalized activities and the Tutte polynomial. Discrete Math. 85 167–176.CrossRefGoogle Scholar
[23]Kauffman, L. H. (1989) A Tutte polynomial for signed graphs. Discrete Appl. Math. 25 105–127.CrossRefGoogle Scholar
[24]Kotzig, A. (1968) Eulerian lines in finite 4-valent graphs and their transformations. In Theory of Graphs (Tihany 1966), Academic Press, New York, pp. 219–230.Google Scholar
[25]Murasugi, K. (1989) On invariants of graphs with applications to knot theory. Trans. Amer. Math. Soc. 314 1–49.CrossRefGoogle Scholar
[26]Oxley, J. G. and Welsh, D. J. A. (1992) Tutte polynomials computable in polynomial time. Discrete Math. 109 185–192.CrossRefGoogle Scholar
[27]Traldi, L. (1989) A dichromatic polynomial for weighted graphs and link polynomials. Proc. Amer. Math. Soc. 106 279–286.CrossRefGoogle Scholar
[28]Traldi, L. (2000) Series and parallel reductions for the Tutte polynomial. Discrete Math. 220 291–297.CrossRefGoogle Scholar
[29]Tutte, W. T. (1984) Graph Theory, Cambridge University Press, Cambridge.Google Scholar
[30]White, N., ed. (1992) Matroid Applications, Cambridge University Press, Cambridge.CrossRefGoogle Scholar