Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T14:46:28.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Applications of the Semi-Definite Method to the Turán Density Problem for 3-Graphs

Published online by Cambridge University Press:  07 December 2012

VICTOR FALGAS-RAVRY  and
EMIL R. VAUGHAN
VICTOR FALGAS-RAVRY
Affiliation:
Institutionen för matematik och matematisk statistik, Umeå Universitet, 901 87 Umeå, Sweden (e-mail: victor.falgas-ravry@math.umu.se)
EMIL R. VAUGHAN
Affiliation:
School of Electronic Engineering and Computer Science, Queen Mary, University of London, Mile End Road, London E1 4NS, UK (e-mail: emil79@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove several new Turán density results for 3-graphs with independent neighbourhoods. We show:

\begin{align*} \pi (K_4^-, C_5, F_{3,2})=12/49, \pi (K_4^-, F_{3,2})=5/18 \textrm {and} \pi (J_4, F_{3,2})=\pi (J_5, F_{3,2})=3/8, \end{align*}
where Jt is the 3-graph consisting of a single vertex x together with a disjoint set A of size t and all $\binom{|A|}{2}$ 3-edges containing x. We also prove two Turán density results where we forbid certain induced subgraphs: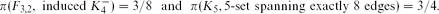
\begin{align*} \pi (F_{3,2}, \textrm { induced }K_4^-)=3/8 \textrm {and} \pi (K_5, 5\textrm {-set spanning exactly 8 edges})=3/4. \end{align*}
 The latter result is an analogue for K5 of Razborov's result that
\begin{align*} \pi (K_4, 4\textrm {-set spanning exactly 1 edge})=5/9. \end{align*}
We give several new constructions, conjectures and bounds for Turán densities of 3-graphs which should be of interest to researchers in the area. Our main tool is ‘Flagmatic’, an implementation of Razborov's semi-definite method, which we are making publicly available. In a bid to make the power of Razborov's method more widely accessible, we have tried to make Flagmatic as user-friendly as possible, hoping to remove thereby the major hurdle that needs to be cleared before using the semi-definite method. Finally, we spend some time reflecting on the limitations of our approach, and in particular on which problems we may be unable to solve. Our discussion of the ‘complexity barrier’ for the semi-definite method may be of general interest.

Keywords

Primary 05D05Secondary 05C65
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 1 , January 2013 , pp. 21 - 54
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]JSON standard. http://tools.ietf.org/html/rfc4627.Google Scholar
[2]The on-line encyclopedia of integer sequences. http://oeis.org.Google Scholar
[3]Alon, N. and Shapira, A. (2003) Testing subgraphs in directed graphs. In Proc. 35th Annual ACM Symposium on Theory of Computing, ACM, pp. 700–709.Google Scholar
[4]Alon, N. and Shapira, A. (2005) A characterization of the (natural) graph properties testable with one-sided error. In 46th Annual IEEE Symposium on Foundations of Computer Science, 2005, IEEE, pp. 429–438.Google Scholar
[5]Baber, R. (2011) Some results in extremal combinatorics. PhD thesis, University College London.Google Scholar
[6]Baber, R. and Talbot, J. (2011) Hypergraphs do jump. Combin. Probab. Comput. 20 161–171.Google Scholar
[7]Baber, R. and Talbot, J. (2012) New Turán densities for 3-graphs. Electron. J. Combin. 19 #19.Google Scholar
[8]Balogh, J. (2002) The Turán density of triple systems is not principal. J. Combin. Theory Ser. A 100 176–180.CrossRefGoogle Scholar
[9]Bollobás, B. (1974) Three-graphs without two triples whose symmetric difference is contained in a third. Discrete Math. 8 21–24.Google Scholar
[10]Bollobás, B., Leader, I. and Malvenuto, C. (2011) Daisies and other Turán problems. Combin. Probab. Comput. 20 743–747.Google Scholar
[11]Borchers, B. (1999) CSDP: A library for semidefinite programming. Optim. Methods Software 11 613–623.CrossRefGoogle Scholar
[12]Brown, W. G. (1983) On an open problem of Paul Turán concerning 3-graphs. In Studies in Pure Mathematics: To the Memory of Paul Turán, Birkhäuser, pp. 91–93.Google Scholar
[13]de Caen, D. and Füredi, Z. (2000) The maximum size of 3-uniform hypergraphs not containing a Fano plane. J. Combin. Theory Ser. B 78 274–279.Google Scholar
[14]Erdős, P. and Stone, A. H. (1946) On the structure of linear graphs. Bull. Amer. Math. Soc 52 1087–1091.Google Scholar
[15]Falgas-Ravry, V. and Vaughan, E. R. A note on stability and the semi-definite method. Preprint.Google Scholar
[16]Falgas-Ravry, V. and Vaughan, E. R. (2011) On applications of Razborov's flag algebra calculus to extremal 3-graph theory. arXiv:1110.1623Google Scholar
[17]Falgas-Ravry, V. and Vaughan, E. R. (2012) Turán H-densities for 3-graphs. Electron. J. Combin. 19 #40.CrossRefGoogle Scholar
[18]Fon-Der-Flaass, D. G. (1988) Method for construction of (3, 4)-graphs. Math. Notes 44 781–783.Google Scholar
[19]Frankl, P. and Füredi, Z. (1983) A new generalization of the Erdős–Ko–Rado theorem. Combinatorica 3 341–349.Google Scholar
[20]Frankl, P. and Füredi, Z. (1984) An exact result for 3-graphs. Discrete Math. 50 323–328.Google Scholar
[21]Frohmader, A. (2008) More constructions for Turán's (3, 4)-conjecture. Electron. J. Combin. 15 R137.Google Scholar
[22]Füredi, Z., Pikhurko, O. and Simonovits, M. (2005) On triple systems with independent neighbourhoods. Combin. Probab. Comput. 14 795–813.Google Scholar
[23]Goldberg, D. (1991) What every computer scientist should know about floating-point arithmetic. ACM Computing Surveys (CSUR) 23 5–48.Google Scholar
[24]Grzesik, A. (2012) On the maximum number of C 5's in a triangle-free graph. J. Combin. Theory Ser. B 102 1061–1066.Google Scholar
[25]Hirst, J. (2011) The inducibility of graphs on four vertices. arXiv:1109.1592Google Scholar
[26]Keevash, P. (2011) Hypergraph Turán problems. In Surveys in combinatorics 2011, Cambridge University Press, pp. 83–140.Google Scholar
[27]Keevash, P. and Mubayi, D. (2012) The Turán number of F 3, 3. Combin. Probab. Comput. 21 451–456.Google Scholar
[28]Kostochka, A. V. (1982) A class of constructions for Turán's (3, 4)-problem. Combinatorica 2 187–192.Google Scholar
[29]Mubayi, D. Personal communication.Google Scholar
[30]Mubayi, D. and Pikhurko, O. (2008) Constructions of non-principal families in extremal hypergraph theory. Discrete Math. 308 4430–4434.Google Scholar
[31]Mubayi, D. and Rödl, V. (2002) On the Turán number of triple systems. J. Combin. Theory Ser. A 100 136–152.Google Scholar
[32]Pikhurko, O. Personal communication.Google Scholar
[33]Pikhurko, O. (2010) An analytic approach to stability. Discrete Math. 310 2951–2964.Google Scholar
[34]Pikhurko, O. (2011) The minimum size of 3-graphs without a 4-set spanning no or exactly three edges. Europ. J. Combin. 32 1142–1155.Google Scholar
[35]Pikhurko, O. (2012) On possible Turán densities. arXiv:1204.4423Google Scholar
[36]Razborov, A. A. (2007) Flag algebras. J. Symbolic Logic 72 1239–1282.Google Scholar
[37]Razborov, A. A. (2010) On 3-hypergraphs with forbidden 4-vertex configurations. SIAM J. Discrete Math. 24 946–963.CrossRefGoogle Scholar
[38]Razborov, A. A. (2011) On the Fon-der-Flaass interpretation of extremal examples for Turán's (3, 4)-problem. Proc. Steklov Inst. Math. 274 247–266.Google Scholar
[39]Rödl, V. and Schacht, M. (2009) Generalizations of the removal lemma. Combinatorica 29 467–501.Google Scholar
[40]Sidorenko, A. (1995) What we know and what we do not know about Turán numbers. Graphs Combin. 11 179–199.Google Scholar
[41]Simonovits, M. (1968) A method for solving extremal problems in graph theory, stability problems. In Theory of Graphs: Proc. Colloq., Tihany, 1966, Academic, pp. 279–319.Google Scholar
[42]Vaughan, E. R. (2012) Flagmatic User's Guide, version 1.0. http://maths.qmul.ac.uk/~ev/flagmatic/usersguide.pdf.Google Scholar