Hostname: page-component-77f85d65b8-7lfxl Total loading time: 0 Render date: 2026-04-17T17:56:07.525Z Has data issue: false hasContentIssue false
  • English
  • Français

Exit Frequency Matrices for Finite Markov Chains

Published online by Cambridge University Press:  14 May 2010

ANDREW BEVERIDGE  and
LÁSZLÓ LOVÁSZ
ANDREW BEVERIDGE
Affiliation:
Department of Mathematics and Computer Science, Macalester College, Saint Paul, MN 55105, USA (e-mail: abeverid@macalester.edu)
LÁSZLÓ LOVÁSZ
Affiliation:
Institute of Mathematics, Eötvös Loránd University, Budapest, Hungary (e-mail: lovasz@cs.elte.hu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the 'Save PDF' action button.

Consider a finite irreducible Markov chain on state space S with transition matrix M and stationary distribution π. Let R be the diagonal matrix of return times, Rii = 1/πi. Given distributions σ, τ and k ∈ S, the exit frequency xk(σ, τ) denotes the expected number of times a random walk exits state k before an optimal stopping rule from σ to τ halts the walk. For a target distribution τ, we define Xτ as the n × n matrix given by (Xτ)ij = xj(i, τ), where i also denotes the singleton distribution on state i.

The dual Markov chain with transition matrix 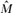= RM⊤R−1 is called the reverse chain. We prove that Markov chain duality extends to matrices of exit frequencies. Specifically, for each target distribution τ, we associate a unique dual distribution τ*. Let 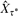denote the matrix of exit frequencies from singletons to τ* on the reverse chain. We show that 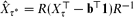, where b is a non-negative constant vector (depending on τ). We explore this exit frequency duality and further illuminate the relationship between stopping rules on the original chain and reverse chain.

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 19 , Issue 4 , July 2010 , pp. 541 - 560
Copyright
Copyright © Cambridge University Press 2010

References

[1]Aldous, D. J. and Fill, J.Reversible Markov Chains and Random Walks on Graphs. To appear. http://www.stat.berkeley.edu/~aldous/RWG/book.html.Google Scholar
[2]Aldous, D., Lovász, L. and Winkler, P. (1997) Mixing times for uniformly ergodic Markov chains. Stochastic Processes Appl. 71 165–185.CrossRefGoogle Scholar
[3]Beveridge, A. (2009) Centers for random walks on trees. SIAM J. Discrete Math. 23 300–318.Google Scholar
[4]Beveridge, A. and Lovász, L. (1998) Random walks and the regeneration time. J. Graph Theory 29 57–62.Google Scholar
[5]Coppersmith, D., Tetali, P. and Winkler, P. (1993) Collisions among random walks on a graph. SIAM J. Discrete Math. 6 363–374.CrossRefGoogle Scholar
[6]Doyle, P. and Snell, J. L. Random walks and electric networks. http://arxiv.org/abs/math/0001057. Derived from Random Walks and Electric Networks (1984), Carus Monographs, Mathematical Association of America.Google Scholar
[7]Häggström, O. (2002) Finite Markov Chains and Algorithmic Applications, Cambridge University Press.CrossRefGoogle Scholar
[8]Lancaster, P. and Tismenetsky, M. (1985) The Theory of Matrices, Academic Press, Orlando.Google Scholar
[9]Lovász, L. (1996) Random walks on graphs: A survey. In Combinatorics: Paul Erdős is Eighty, Vol. II (Miklós, D., Sós, V. T. and Szőnyi, T., eds), János Bolyai Mathematical Society, pp. 353–397.Google Scholar
[10]Lovász, L. and Winkler, P. (1995) Efficient stopping rules for Markov chains. In Proc. 27th ACM Symposium on the Theory of Computing, pp. 76–82.CrossRefGoogle Scholar
[11]Lovász, L. and Winkler, P. (1995) Mixing of random walks and other diffusions on a graph. In Surveys in Combinatorics (Rowlinson, P., ed.), Vol. 218 of London Mathematical Society Lecture Notes, Cambridge University Press, pp. 119–154.Google Scholar
[12]Lovász, L. and Winkler, P. (1998) Reversal of Markov chains and the forget time. Combin. Probab. Comput. 7 189–204.Google Scholar
[13]Lovász, L. and Winkler, P. (1998) Mixing times. In Microsurveys in Discrete Probability (Aldous, D. and Propp, J., eds), DIMACS Series in Discrete Mathematics and Theoretical Computer Science, AMS, pp. 85–133.Google Scholar
[14]Pitman, J. W. (1977) Occupation measures for Markov chains. Adv. Appl. Probab. 9 69–86.CrossRefGoogle Scholar