Hostname: page-component-5c6d5d7d68-xq9c7 Total loading time: 0 Render date: 2024-08-15T11:25:08.518Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Strong Chromatic Number of Random Graphs

Published online by Cambridge University Press:  01 March 2008

PO-SHEN LOH  and
BENNY SUDAKOV
PO-SHEN LOH
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ 08544, USA (e-mail: ploh@math.princeton.edu)
BENNY SUDAKOV
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ 08544, USA and Institute for Advanced Study, Princeton, USA (e-mail: bsudakov@math.princeton.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a graph with n vertices, and let k be an integer dividing n. G is said to be strongly k-colourable if, for every partition of V(G) into disjoint sets V1 ∪ ··· ∪ Vr, all of size exactly k, there exists a proper vertex k-colouring of G with each colour appearing exactly once in each Vi. In the case when k does not divide n, G is defined to be strongly k-colourable if the graph obtained by adding 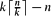isolated vertices is strongly k-colourable. The strong chromatic number of G is the minimum k for which G is strongly k-colourable. In this paper, we study the behaviour of this parameter for the random graph Gn,p. In the dense case when p ≫ n−1/3, we prove that the strong chromatic number is a.s. concentrated on one value Δ + 1, where Δ is the maximum degree of the graph. We also obtain several weaker results for sparse random graphs.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 17 , Issue 2 , March 2008 , pp. 271 - 286
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aharoni, R., Berger, E. and Ziv, R. Independent systems of representatives in weighted graphs. Combinatorica, to appear.Google Scholar
[2]Aharoni, R. and Holzman, R. (2005) Private communication.Google Scholar
[3]Alon, N. (1988) The linear arboricity of graphs. Israel J. Math. 62 311–325.CrossRefGoogle Scholar
[4]Alon, N. (1992) The strong chromatic number of a graph. Random Struct. Alg. 3 1–7.CrossRefGoogle Scholar
[5]Alon, N. (2003) Problems and results in extremal combinatorics I. Discrete Math. 273 31–53.CrossRefGoogle Scholar
[6]Alon, N. and Krivelevich, M. (1997) The concentration of the chromatic number of random graphs. Combinatorica 17 303–313.CrossRefGoogle Scholar
[7]Alon, N. and Spencer, J. (2000) The Probabilistic Method, 2nd edn, Wiley, New York.CrossRefGoogle Scholar
[8]Bohman, T. and Holzman, R. (2002) On a list coloring conjecture of Reed. J. Graph Theory 41 106–109.CrossRefGoogle Scholar
[9]Bollobás, B. (2001) Random Graphs, 2nd edn, Vol. 73 of Cambridge Studies in Advanced Mathematics, Cambridge University Press, Cambridge.CrossRefGoogle Scholar
[10]Bollobás, B., Erdős, P. and Szemerédi, E. (1975) On complete subgraphs of r-chromatic graphs. Discrete Math. 13 97–107.CrossRefGoogle Scholar
[11]Fellows, M. (1990) Transversals of vertex partitions in graphs. SIAM J. Discrete Math. 3 206–215.CrossRefGoogle Scholar
[12]Fleischner, H. and Stiebitz, M. (1992) A solution to a colouring problem of P. Erdős. Discrete Math. 101 39–48.CrossRefGoogle Scholar
[13]Fleischner, H. and Stiebitz, M. (1997) Some remarks on the cycle plus triangles problem. In The Mathematics of Paul Erdős, Vol. II, Algorithms and Combinatorics 14 136–142.CrossRefGoogle Scholar
[14]Haxell, P. (2001) A note on vertex list colouring. Combin. Probab. Comput. 10 345–348.CrossRefGoogle Scholar
[15]Haxell, P. (2004) On the strong chromatic number. Combin. Probab. Comput. 13 857–865.CrossRefGoogle Scholar
[16]Haxell, P. (2005) Private communication.Google Scholar
[17]Haxell, P. and Szabó, T. (2006) Odd transversals are odd. Combin. Probab. Comput. 15 193–211.CrossRefGoogle Scholar
[18]Jin, G. (1992) Complete subgraphs of r-partite graphs. Combin. Probab. Comput. 1 241–250.CrossRefGoogle Scholar
[19]Loh, P. and Sudakov, B. Independent transversals in locally sparse graphs. J. Combin. Theory Ser. B, to appear.Google Scholar
[20]Łuczak, T. (1991) A note on the sharp concentration of the chromatic number of random graphs. Combinatorica 11 295–297.CrossRefGoogle Scholar
[21]Matula, D. (1970) On the complete subgraphs of a random graph. In Proc. Second Chapel Hill Conf. on Combinatorial Mathematics and its Applications, University of North Carolina, Chapel Hill, NC, pp. 356–369.Google Scholar
[22]Meshulam, R. (2003) Domination numbers and homology. J. Combin. Theory Ser. A 102 321–330.CrossRefGoogle Scholar
[23]Reed, B. (1999) The list colouring constants. J. Graph Theory 31 149–153.3.0.CO;2-#>CrossRefGoogle Scholar
[24]Reed, B. and Sudakov, B. (2002) Asymptotically the list colouring constants are 1. J. Combin. Theory Ser. B 86 27–37.CrossRefGoogle Scholar
[25]Shamir, E. and Spencer, J. (1987) Sharp concentration of the chromatic number on random graphs G n,p. Combinatorica 7 121–129.CrossRefGoogle Scholar
[26]Szabó, T. and Tardos, G. (2006) Extremal problems for transversals in graphs with bounded degree. Combinatorica 26 333–351.CrossRefGoogle Scholar
[27]Yuster, R. (1997) Independent transversals in r-partite graphs. Discrete Math. 176 255–261.CrossRefGoogle Scholar