Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-28T21:20:00.589Z Has data issue: false hasContentIssue false
  • English
  • Français

Powers of paths in tournaments

Part of: Graph theory

Published online by Cambridge University Press:  23 March 2021

Nemanja Draganić ,
François Dross ,
Jacob Fox ,
António Girão ,
Frédéric Havet ,
Dániel Korándi ,
William Lochet ,
David Munhá Correia ,
Alex Scott  and
Benny Sudakov
Nemanja Draganić
Affiliation:
Department of Mathematics, ETH Zurich, Zurich, Switzerland
François Dross
Affiliation:
Université de Bordeaux, CNRS, Bordeaux INP, LaBRI, UMR 5800, Talence, France
Jacob Fox
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA, USA
António Girão
Affiliation:
Institut für Informatik, Universität Heidelberg, Germany
Frédéric Havet
Affiliation:
CNRS, Université Côte d’Azur, I3S, INRIA, Sophia Antipolis, France
Dániel Korándi*
Affiliation:
Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, Oxford, United Kingdom
William Lochet
Affiliation:
Department of Informatics, University of Bergen, Norway
David Munhá Correia
Affiliation:
Department of Mathematics, ETH Zurich, Zurich, Switzerland
Alex Scott
Affiliation:
Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, Oxford, United Kingdom
Benny Sudakov
Affiliation:
Department of Mathematics, ETH Zurich, Zurich, Switzerland
*
*Corresponding author. Email: korandi@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

In this short note we prove that every tournament contains the k-th power of a directed path of linear length. This improves upon recent results of Yuster and of Girão. We also give a complete solution for this problem when k=2, showing that there is always a square of a directed path of length 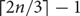, which is best possible.

MSC classification

Primary: 05C35: Extremal problems 05C20: Directed graphs (digraphs), tournaments
Secondary: 05C38: Paths and cycles
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 6 , November 2021 , pp. 894 - 898
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research supported in part by SNSF grant 200021_196965

‡

Research supported in part by ERC grant No 714704

§

Research supported by a Packard Fellowship and by NSF award DMS-185563.

Research supported by DFG under Germany’s Excellence Strategy EXC-2181/1 - 390900948.

ǁ

Research supported in part by Agence Nationale de la Recherche under contract Digraphs ANR-19-CE48-0013-01.

††

Supported by SNSF Postdoc.Mobility Fellowship P400P2_186686.

‡‡

Research supported by ERC grant No 819416.

References

Bollobás, B. and Häggkvist, R., Powers of Hamilton cycles in tournaments, J. Combin. Theory Ser. B 50 (1990), 309–318.CrossRefGoogle Scholar
Dirac, G., Some theorems on abstract graphs, Proc. London Math. Soc. 2 (1952), 69–81.CrossRefGoogle Scholar
Erdős, P. and Gallai, T., On maximal paths and circuits of graphs, Acta Math. Hungar., 10 (1959), 337–356.CrossRefGoogle Scholar
Girão, A., A note on long powers of paths in tournaments, arXiv:2010.02875 preprint.Google Scholar
Komlós, J., Sárközy, G.N. and Szemerédi, E., Proof of the Seymour conjecture for large graphs, Ann. Comb. 2 (1998), 43–60.CrossRefGoogle Scholar
West, D., Introduction to Graph Theory, 2nd ed., Prentice Hall, 2001.Google Scholar
Yuster, R., Paths with many shortcuts in tournaments, Discrete Math. 334 (2021), 112168.CrossRefGoogle Scholar