This special issue is devoted to papers from the meeting on Combinatorics, Probability and Computing, held at the Mathematisches Forschungsinstitut in Oberwolfach from the 23$^{\rm rd}$ to the 29$^{\rm th}$ of September 2001. As is typical of meetings at Oberwolfach, this was an exciting and stimulating conference; there was a large number of excellent talks, many of which provoked a great deal of interest and discussion among the participants.

In this paper we study random linear systems with $k > 3$ variables per equation over the finite field GF(2), or equivalently k-XOR-CNF formulas. In a previous paper Creignou and Daudé proved that there exists a phase transition exhibiting a sharp threshold, for the consistency (satisfiability) of such systems (formulas). The control parameter for this transition is the ratio of the number of equations to the number of variables, and the scale for which the transition occurs remains somewhat elusive. In this paper we establish, for any $k > 3$, non-trivial lower and upper estimates of the value of the control ratio for which the phase transition occurs. For $k=3$ we get 0.89 and 0.93, respectively. Moreover, we give experimental results for $k=3$ suggesting that the critical ratio is about 0.92. Our estimates are clearly close to the critical ratio.

In this paper we consider a bipartite version of Schütte's well-known tournament problem. A bipartite tournament $T=(A,B,E)$ with teams $A$ and $B$, and set of arcs $E$, has the property $S_{k,l}$ if for any subsets $K\subseteq A$ and $L\subseteq B$, with $|K| =k$ and $| L | =l$, there exist conquerors of $K$ and $L$ in opposite teams. The task is to estimate, for fixed $k$ and $l$, the minimum number $f(k,l)=| A | + | B | $ of players in a tournament satisfying property $S_{k,l}$. We achieve this goal by reformulating the problem in terms of intersecting set families and applying probabilistic as well as constructive methods. Intriguing connections with some famous problems of this area have emerged in this way, leading to new open questions.

It has been shown [2] that if n is odd and m1,…,mt are integers with mi[ges ]3 and [sum ]i=1tmi=|E(Kn)| then Kn can be decomposed as an edge-disjoint union of closed trails of lengths m1,…,mt. This result was later generalized [3] to all sufficiently dense Eulerian graphs G in place of Kn. In this article we consider the corresponding questions for directed graphs. We show that the complete directed graph <?TeX \displaystyle{\mathop{K}^{\raise-2pt\hbox{$\scriptstyle\leftrightarrow$}}}_{n}?> can be decomposed as an edge-disjoint union of directed closed trails of lengths m1,…,mt whenever mi[ges ]2 and <?TeX \sum_{i=1}^t m_{i}=\vert E({\leftrightarrow}_{n})\vert ?>, except for the single case when n=6 and all mi=3. We also show that sufficiently dense Eulerian digraphs can be decomposed in a similar manner, and we prove corresponding results for (undirected) complete multigraphs.

In this article we introduce combinatorial multicolour discrepancies and generalize several classical results from $2$-colour discrepancy theory to $c$ colours ($c \geq 2$). We give a recursive method that constructs $c$-colourings from approximations of $2$-colour discrepancies. This method works for a large class of theorems, such as the ‘six standard deviations’ theorem of Spencer (1985), the Beck–Fiala (1981) theorem, the results of Matoušek, Wernisch and Welzl (1994) and Matoušek (1995) for bounded VC-dimension, and Matoušek and Spencer's (1996) upper bound for the arithmetic progressions. In particular, the $c$-colour discrepancy of an arbitrary hypergraph ($n$ vertices, $m$ hyperedges) is \[ \OO\Bigl(\sqrt{\tfrac n c\,\log m}\Bigr). \] If $m = \OO(n)$, then this bound improves to \[ \OO\Bigl(\sqrt{\tfrac n c\,\log c}\Bigr). \]

On the other hand there are examples showing that discrepancy in $c$ colours can not be bounded in terms of two-colour discrepancies in general, even if $c$ is a power of 2. For the linear discrepancy version of the Beck–Fiala theorem, the recursive approach also fails.

Here we extend the method of floating colours via tensor products of matrices to multicolourings, and prove multicolour versions of the Beck–Fiala theorem and the Bárány–Grinberg theorem. Using properties of the tensor product we derive a lower bound for the $c$-colour discrepancy of general hypergraphs. For the hypergraph of arithmetic progressions in $\{1, \ldots, n\}$ this yields a lower bound of $\frac{1}{25 \sqrt c} \sqrt[4]{n}$ for the discrepancy in $c$ colours. The recursive method shows an upper bound of $\OO(c^{-0.16} \sqrt[4]{n})$

The results of this paper concern the ‘large spectra’ of sets, by which we mean the set of points in ${\bb F}_p^{\times}$ at which the Fourier transform of a characteristic function $\chi_A$, $A\subseteq {\bb F}_p$, can be large. We show that a recent result of Chang concerning the structure of the large spectrum is best possible. Chang's result has already found a number of applications in combinatorial number theory.

We also show that if $|A|=\lfloor {p/2}\rfloor$, and if $R$ is the set of points $r$ for which $|\hat{\chi}_A(r)|\geqslant \alpha p$, then almost nothing can be said about $R$ other than that $|R|\ll \alpha^{-2}$, a trivial consequence of Parseval's theorem.

The name of Frank Ramsey is universally known amongst combinatorial mathematicians, but our casual mental picture of him can easily be an unimpressive one – the man who almost stumbled across the theorem that now bears his name, thereby anticipating Erdős and Szekeres, who of course gave the proper proof. Such an idea of Ramsey is entirely false: he was an absolutely brilliant man, who would certainly have become even more famous had he not died so young, and who would surely, it could easily be argued, have made yet further remarkable contributions to philosophy, economics and logic – and to combinatorics.

We analyse a randomized pursuit-evasion game played by two players on a graph, a hunter and a rabbit. Let $G$ be any connected, undirected graph with $n$ nodes. The game is played in rounds and in each round both the hunter and the rabbit are located at a node of the graph. Between rounds both the hunter and the rabbit can stay at the current node or move to another node. The hunter is assumed to be restricted to the graph $G$: in every round, the hunter can move using at most one edge. For the rabbit we investigate two models: in one model the rabbit is restricted to the same graph as the hunter, and in the other model the rabbit is unrestricted, i.e., it can jump to an arbitrary node in every round.

We say that the rabbit is caught as soon as hunter and rabbit are located at the same node in a round. The goal of the hunter is to catch the rabbit in as few rounds as possible, whereas the rabbit aims to maximize the number of rounds until it is caught. Given a randomized hunter strategy for $G$, the escape length for that strategy is the worst case expected number of rounds it takes the hunter to catch the rabbit, where the worst case is with regard to all (possibly randomized) rabbit strategies. Our main result is a hunter strategy for general graphs with an escape length of only $\O(n \log (\diam(G)))$ against restricted as well as unrestricted rabbits. This bound is close to optimal since $\Omega(n)$ is a trivial lower bound on the escape length in both models. Furthermore, we prove that our upper bound is optimal up to constant factors against unrestricted rabbits.

A general spectral bound for the sizes of some vertex subsets, which are mutually at a given minimum distance in a graph, is derived. This unifies and improves some previous results. Some applications to the study of certain metric parameters of the graph are then discussed.

It is known that random $k$-Sat instances with at least $(2^k \cdot \ln 2)\cdot n$ random clauses are unsatisfiable with high probability. This result is simply obtained by showing that the expected number of satisfying assignments tends to $0$ when the number of variables $n$ tends to infinity. This proof does not directly provide us with an efficient algorithm certifying the unsatisfiability of a given random formula. Concerning efficient algorithms, it is essentially known that random formulas with $n^\varepsilon \cdot n^{k/2}$ clauses with $k$ literals can be efficiently certified as unsatisfiable. The present paper is the result of trying to lower this bound. We obtain better bounds for some specialized satisfiability problems. These results are based on discrepancy investigations for hypergraphs.

Further, we show that random formulas with a linear number of clauses can be efficiently certified as unsatisfiable in the Not-All-Equal-$3$-Sat sense. A similar result holds for the non-$3$-colourability of random graphs with a linear number of edges. We obtain these results by direct application of approximation algorithms.

A celebrated theorem of Turán asserts that every graph on n vertices with more than $\frac{r\,{-}\,1}{2r}n^2$ edges contains a copy of a complete graph $K_r+1$. In this paper we consider the following more general question. Let G be a $K_r+1-free graph of order n and let α be a constant, 0<α≤1. How dense can every induced subgraph of G on αn vertices be? We prove the following local density extension of Turán's theorem.

For every integer $r\geq 2$ there exists a constant $c_r < 1$ such that, if $c_r < \alpha < 1$ and every αn vertices of G span more than

\[ \frac{r\,{-}\,1}{2r}(2\alpha -1)n^2\vspace*{7pt} \]

edges, then G contains a copy of $K_r+1$. This result is clearly best possible and answers a question of Erdős, Faudree, Rousseau and Schelp [5].

In addition, we prove that the only $K_r+1-free graph of order n, in which every αn vertices span at least $\frac{r\,{-}\,1}{2r}(2\alpha -1)n^2$ edges, is a Turán graph. We also obtain the local density version of the Erdős–Stone theorem.

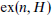For a graph H and an integer n, the Turán number is the maximum possible number of edges in a simple graph on n vertices that contains no copy of H. H is r-degenerate if every one of its subgraphs contains a vertex of degree at most r. We prove that, for any fixed bipartite graph H in which all degrees in one colour class are at most r, . This is tight for all values of r and can also be derived from an earlier result of Füredi. We also show that there is an absolute positive constant c such that, for every fixed bipartite r-degenerate graph H, This is motivated by a conjecture of Erdős that asserts that, for every such H,

For two graphs G and H, the Ramsey number is the minimum number 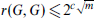n such that, in any colouring of the edges of the complete graph on n vertices by red and blue, there is either a red copy of G or a blue copy of H. Erdős conjectured that there is an absolute constant c such that, for any graph G with m edges, . Here we prove this conjecture for bipartite graphs 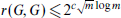G, and prove that for general graphs G with m edges, for some absolute positive constant c.

These results and some related ones are derived from a simple and yet surprisingly powerful lemma, proved, using probabilistic techniques, at the beginning of the paper. This lemma is a refined version of earlier results proved and applied by various researchers including Rödl, Kostochka, Gowers and Sudakov.

The sizes of the cycles and unicyclic components in the random graph $G(n, n/2\pm s)$, where $n^{2/3}\ll s \ll n$, are studied using the language of point processes. This refines several earlier results by different authors. Asymptotic distributions of various random variables are given: these distributions include the gamma distributions with parameters 1/4, 1/2 and 3/4, as well as the Poisson–Dirichlet and GEM distributions with parameters 1/4 and 1/2.

For a random graph on n vertices where the edges appear with individual rates, we give exact formulas for the expected time at which the number of components has gone down to k and the expected length of the corresponding minimal spanning forest.

For a random bipartite graph we give a formula for the expected time at which a k-assignment appears. This result has a bearing on the random assignment problem.

Let $G$ be a cyclic group of order $n$ and let $\mu = \{x_1,x_2, \dots, x_m\}$ be a sequence of elements of $G$. Let $k$ be the number of distinct values taken by the sequence $\mu$. Let $n\wedge \mu$ be the set of the $n$-subsequence sums.

We show that one of the following conditions holds:

1. $\mu$ has a value repeated $n-k+3$ times

2. $n\wedge \mu$ contains a non-null subgroup

3. $|n\wedge \mu|\geq m-n+k-2.$

We conjecture that the last condition could be improved to $|n\wedge \mu|\geq m-n+k-1$. This conjecture generalizes several known results. We also obtain a generalization of a recent result due to Bollobás and Leader.

For an integer $s\ges 2$, a property $\P^{(s)}$ is an infinite class of s-uniform hypergraphs closed under isomorphism. We say that a property $\P^{(s)}$ is \emph{hereditary\/} if~$\P^{(s)}$ is closed under taking induced subhypergraphs. Thus, for some `forbidden class' $\FF=\{\F_i^{(s)}\:i\in I\}$ of s-uniform hypergraphs, $\P^{(s)}$ is the set of all s-uniform hypergraphs not containing any $\F_i^{(s)}\in\FF$ as an induced subhypergraph. Let $\P^{(s)}_n$ be those hypergraphs of $\P^{(s)}$ on some fixed n-vertex set. For a set of s-uniform hypergraphs $\FF=\{\F_i^{(s)}\:i\in I\}$, let

\[ \exind(n,\FF)=\max\bigl|[n]^s{\setminus}(\M\cup\N)\vphantom{\big|}\bigr|, \]

where the maximum is taken over all $\M$ and $\N\subseteq[n]^s$ with $\M\cap\N=\emptyset$ such that, for all $\G\subseteq[n]^s{\setminus}(\M\cup\N)$, no $\F_i^{(s)}\in\FF$ appears as an induced subhypergraph of $\G\cup\M$. We show that

\[ \log_2\big|\P^{(3)}_n\big|=\exind(n,\FF)+o(n^3) \]

holds for $s=3$ and any hereditary property $\P^{(3)}$, where $\FF$ is a forbidden class associated with $\P^{(3)}$. This result complements a collection of analogous theorems already proved for graphs (i.e., $s=2$).

A proper vertex coloring of a graph is called equitable if the sizes of colour classes differ by at most 1. In this paper, we find the minimum number l=l(d, Δ) such that every d-degenerate graph with maximum degree at most Δ admits an equitable t-colouring for every t[ges ]l when Δ[ges ]27d.

A subgraph H in an edge-colouring is properly coloured if incident edges of H are assigned different colours, and H is rainbow if no two edges of H are assigned the same colour. We study properly coloured subgraphs and rainbow subgraphs forced in edge-colourings of complete graphs in which each vertex is incident to a large number of colours.

In this paper we consider a random star $d$-process which begins with $n$ isolated vertices, and in each step chooses randomly a vertex of current minimum degree $\delta$, and connects it with $d - \delta$ random vertices of degree less than $d$. We show that, for $d \geqslant 3$, the resulting final graph is connected with probability $1 - o(1)$, and moreover that, for suficiently large $d$, it is $d$-connected with probability $1 - o(1)$.