Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T16:31:51.720Z Has data issue: false hasContentIssue false
  • English
  • Français

On the topology of Diophantine approximation spectra

Part of: Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  02 May 2017

Damien Roy
Damien Roy*
Affiliation:
Département de Mathématiques, Université d’Ottawa, 585 King Edward, Ottawa, Ontario K1N 6N5, Canada email droy@uottawa.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Fix an integer 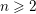$n\geqslant 2$. To each non-zero point 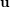$\mathbf{u}$ in 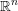$\mathbb{R}^{n}$, one attaches several numbers called exponents of Diophantine approximation. However, as Khintchine first observed, these numbers are not independent of each other. This raises the problem of describing the set of all possible values that a given family of exponents can take by varying the point 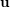$\mathbf{u}$. To avoid trivialities, one restricts to points 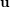$\mathbf{u}$ whose coordinates are linearly independent over 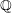$\mathbb{Q}$. The resulting set of values is called the spectrum of these exponents. We show that, in an appropriate setting, any such spectrum is a compact connected set. In the case 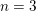$n=3$, we prove moreover that it is a semi-algebraic set closed under component-wise minimum. For 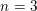$n=3$, we also obtain a description of the spectrum of the exponents 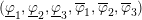$(\text{}\underline{\unicode[STIX]{x1D711}}_{1},\text{}\underline{\unicode[STIX]{x1D711}}_{2},\text{}\underline{\unicode[STIX]{x1D711}}_{3},\overline{\unicode[STIX]{x1D711}}_{1},\overline{\unicode[STIX]{x1D711}}_{2},\overline{\unicode[STIX]{x1D711}}_{3})$ recently introduced by Schmidt and Summerer.

Keywords

parametric geometry of numberssuccessive minimaexponents of Diophantine approximationspectrumtopology

MSC classification

Primary: 11J13: Simultaneous homogeneous approximation, linear forms
Secondary: 11J82: Measures of irrationality and of transcendence
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 7 , July 2017 , pp. 1512 - 1546
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

German, O. N., Intermediate Diophantine exponents and parametric geometry of numbers , Acta Arith. 154 (2012), 79–101.CrossRefGoogle Scholar
Jarník, V., Über einen Satz von A. Khintchine , Práce Mat.-Fiz. 43 (1935), 151–166.Google Scholar
Jarník, V., Über einen Satz von A. Khintchine II , Acta Arith. 2 (1936), 1–22.CrossRefGoogle Scholar
Jarník, V., Zum Khintchineschen ‘Übertragungssatz’ , Trav. Inst. Math. Tbilissi 3 (1938), 193–212.Google Scholar
Jarník, V., Contributions à la théorie des approximations diophantiennes linéaires et homogènes , Czechoslovak Math. J. 4 (1954), 330–353; (in Russian, with French summary).CrossRefGoogle Scholar
Keita, A., On a conjecture of Schmidt for the parametric geometry of numbers , Mosc. J. Comb. Number Theory 6 (2016), 282–292.Google Scholar
Khintchine, A. Y., Zur metrischen Theorie der diophantischen Approximationen , Math. Z. 24 (1926), 706–714.CrossRefGoogle Scholar
Khintchine, A. Y., Über eine Klasse linearer diophantischer Approximationen , Rend. Circ. Mat. Palermo 50 (1926), 170–195.CrossRefGoogle Scholar
Laurent, M., Exponents of Diophantine approximation in dimension two , Canad. J. Math. 61 (2009), 165–189.CrossRefGoogle Scholar
Laurent, M., On transfer inequalities in Diophantine approximation , in Analytic number theory in honour of Klaus Roth (Cambridge University Press, Cambridge, 2009), 306–314.Google Scholar
Marnat, A., About Jarník’s-type relation in higher dimension, Preprint (2015),arXiv:1510.06334 [math.NT].Google Scholar
Moshchevitin, N. G., Proof of W. M. Schmidt’s conjecture concerning successive minima of a lattice , J. Lond. Math. Soc. (2) 86 (2012), 129–151.CrossRefGoogle Scholar
Moshchevitin, N. G., Exponents for three-dimensional simultaneous Diophantine approximations , Czechoslovak Math. J. 62 (2012), 127–137.CrossRefGoogle Scholar
Roy, D., On Schmidt and Summerer parametric geometry of numbers , Ann. of Math. (2) 182 (2015), 739–786.CrossRefGoogle Scholar
Roy, D., Spectrum of the exponents of best rational approximation , Math. Z. 283 (2016), 143–155.CrossRefGoogle Scholar
Schmidt, W. M., On heights of algebraic subspaces and diophantine approximations , Ann. of Math. (2) 85 (1967), 430–472.CrossRefGoogle Scholar
Schmidt, W. M., Open problems in Diophantine approximations , in Approximations diophantiennes et nombres transcendants (Luminy 1982), Progress in Mathematics, vol. 31 (Birkhäuser, Boston, MA, 1983), 271–287.Google Scholar
Schmidt, W. M. and Summerer, L., Parametric geometry of numbers and applications , Acta Arith. 140 (2009), 67–91.CrossRefGoogle Scholar
Schmidt, W. M. and Summerer, L., Diophantine approximation and parametric geometry of numbers , Monatsh. Math. 169 (2013), 51–104.CrossRefGoogle Scholar
Schmidt, W. M. and Summerer, L., Simultaneous approximation to three numbers , Mosc. J. Comb. Number Theory 3 (2013), 84–107.Google Scholar
Schmidt, W. M. and Summerer, L., The generalization of Jarnik’s identity , Acta Arith. 175 (2016), 119–136.Google Scholar
Schmidt, W. M. and Summerer, L., Simultaneous approximation to two reals: bounds for the second successive minimum, Mathematika, to appear (special issue in memoriam of Klaus Roth).Google Scholar
Seidenberg, A., A new decision method for elementary algebra , Ann. of Math. (2) 60 (1954), 365–374.CrossRefGoogle Scholar