Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T14:21:36.702Z Has data issue: false hasContentIssue false
  • English
  • Français

Positivity properties of the bundle of logarithmic tensors on compact Kähler manifolds

Part of: Complex manifolds Pluripotential theory

Published online by Cambridge University Press:  21 September 2016

Frédéric Campana  and
Mihai Păun
Frédéric Campana
Affiliation:
Institut Elie Cartan, Nancy, Université de Lorraine, France email Frederic.Campana@univ-lorraine.fr KIAS scholar, KIAS, 85 Hoegiro, Dongdaemun-gu, Seoul 130-722, South Korea
Mihai Păun
Affiliation:
Korea Institute for Advanced Study, School of Mathematics, 85 Hoegiro, Dongdaemun-gu, Seoul 130-722, Korea email paun@kias.re.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 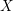$X$ be a compact Kähler manifold, endowed with an effective reduced divisor 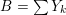$B=\sum Y_{k}$ having simple normal crossing support. We consider a closed form of 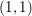$(1,1)$ -type 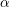$\unicode[STIX]{x1D6FC}$ on 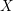$X$ whose corresponding class 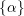$\{\unicode[STIX]{x1D6FC}\}$ is nef, such that the class 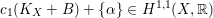$c_{1}(K_{X}+B)+\{\unicode[STIX]{x1D6FC}\}\in H^{1,1}(X,\mathbb{R})$ is pseudo-effective. A particular case of the first result we establish in this short note states the following. Let 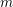$m$ be a positive integer, and let 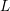$L$ be a line bundle on 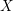$X$ , such that there exists a generically injective morphism 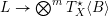$L\rightarrow \bigotimes ^{m}T_{X}^{\star }\langle B\rangle$ , where we denote by 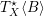$T_{X}^{\star }\langle B\rangle$ the logarithmic cotangent bundle associated to the pair 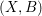$(X,B)$ . Then for any Kähler class 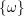$\{\unicode[STIX]{x1D714}\}$ on 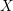$X$ , we have the inequality

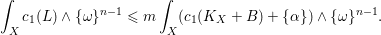$$\begin{eqnarray}\displaystyle \int _{X}c_{1}(L)\wedge \{\unicode[STIX]{x1D714}\}^{n-1}\leqslant m\int _{X}(c_{1}(K_{X}+B)+\{\unicode[STIX]{x1D6FC}\})\wedge \{\unicode[STIX]{x1D714}\}^{n-1}.\end{eqnarray}$$
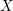If $X$ is projective, then this result gives a generalization of a criterion due to Y. Miyaoka, concerning the generic semi-positivity: under the hypothesis above, let 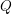$Q$ be the quotient of 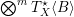$\bigotimes ^{m}T_{X}^{\star }\langle B\rangle$ by 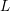$L$ . Then its degree on a generic complete intersection curve 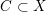$C\subset X$ is bounded from below by
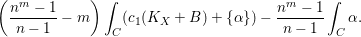$$\begin{eqnarray}\displaystyle \biggl(\frac{n^{m}-1}{n-1}-m\biggr)\int _{C}(c_{1}(K_{X}+B)+\{\unicode[STIX]{x1D6FC}\})-\frac{n^{m}-1}{n-1}\int _{C}\unicode[STIX]{x1D6FC}.\end{eqnarray}$$
 As a consequence, we obtain a new proof of one of the main results of our previous work [F. Campana and M. Păun, Orbifold generic semi-positivity: an application to families of canonically polarized manifolds, Ann. Inst. Fourier (Grenoble) 65 (2015), 835–861].

Keywords

tensorscurvatureMonge–Ampère equations

MSC classification

Primary: 32Q05: Negative curvature manifolds 32Q10: Positive curvature manifolds 32Q15: Kähler manifolds 32Q20: Kähler-Einstein manifolds 32U05: Plurisubharmonic functions and generalizations
Secondary: 32U15: General pluripotential theory
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 11 , November 2016 , pp. 2350 - 2370
Copyright
© The Authors 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Birkar, C., Cascini, P., Hacon, C. and Mckernan, J., Existence of minimal models for varieties of log general type , J. Amer. Math. Soc. 23 (2010), 405–468.CrossRefGoogle Scholar
Boucksom, S., Demailly, J.-P., Păun, M. and Peternell, T., The pseudo-effective cone of a compact Kähler manifold and varieties of negative Kodaira dimension , J. Algebraic Geom. 22 (2013), 201–248.CrossRefGoogle Scholar
Campana, F., Guenancia, H. and Păun, M., Metrics with cone singularities along normal crossing divisors and holomorphic tensor fields , Ann. Sci. Éc. Norm. Supér (4) 46 (2013), 879–916.CrossRefGoogle Scholar
Campana, F. and Păun, M., Orbifold generic semi-positivity: an application to families of canonically polarized manifolds , Ann. Inst. Fourier (Grenoble) 65 (2015), 835–861.CrossRefGoogle Scholar
Demailly, J.-P., Estimations L 2 pour l’opérateur ∂̄ d’un fibré vectoriel holomorphe semi-positif au-dessus d’une variété kählérienne complète , Ann. Sci. Éc. Norm. Supér (4) 15 (1982), 457–511.CrossRefGoogle Scholar
Demailly, J.-P., Regularization of closed positive currents and intersection theory , J. Algebraic Geom. 1 (1992), 361–409.Google Scholar
Donaldson, S., Anti self-dual Yang Mills connections over complex algebraic surfaces and stable vector bundles , Proc. Lond. Math. Soc. (3) 50 (1985), 1–26.CrossRefGoogle Scholar
Enoki, I., Stability and negativity for tangent sheaves of minimal Kähler spaces , in Geometry and analysis on manifolds (Katata/Kyoto, 1987), Lecture Notes in Mathematics, vol. 1339 (Springer, Berlin, 1988), 118–126.CrossRefGoogle Scholar
Guenancia, H., Kähler–Einstein metrics with cone singularities on klt pairs , Int. J. Math. 24 (2013), 1350035.CrossRefGoogle Scholar
Guenancia, H. and Păun, M., Conic singularities metrics with prescribed Ricci curvature: the case of general cone angles along normal crossing divisors , J. Differential Geom. 103 (2016), 15–57.CrossRefGoogle Scholar
Kobayashi, S., Differential geometry of complex vector bundles (Princeton University Press, Princeton, NJ).CrossRefGoogle Scholar
Kollár, J., Lectures on resolution of singularities , Ann. of Math. Stud. (2007).Google Scholar
Miyaoka, Y., The Chern classes and Kodaira dimension of a minimal variety , in Algebraic geometry, Sendai, 1985, ed. Oda, T. (North-Holland, Amsterdam, 1987).Google Scholar
Siu, Y.-T., Lectures on Hermitian–Einstein metrics for stable bundles and Kähler–Einstein metrics (Birkhäuser, Basel, 1987).CrossRefGoogle Scholar
Yau, S.-T., On the Ricci curvature of a compact Kähler manifold and the complex Monge–Ampère equation. I. , Comm. Pure Appl. Math. 31 (1978), 339–411.CrossRefGoogle Scholar