Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T14:00:29.585Z Has data issue: false hasContentIssue false
  • English
  • Français

Shimura varieties at level 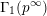$\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations

Part of: Discontinuous groups and automorphic forms Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry

Published online by Cambridge University Press:  26 May 2020

Ana Caraiani ,
Daniel R. Gulotta ,
Chi-Yun Hsu ,
Christian Johansson ,
Lucia Mocz ,
Emanuel Reinecke  and
Sheng-Chi Shih
Ana Caraiani
Affiliation:
Department of Mathematics, Imperial College London, LondonSW7 2AZ, UK email caraiani.ana@gmail.com
Daniel R. Gulotta
Affiliation:
Department of Mathematics, Columbia University, 2990 Broadway, New York, NY10027, USA
Chi-Yun Hsu
Affiliation:
Department of Mathematics, Harvard University, 1 Oxford Street, Cambridge, MA02138, USA
Christian Johansson
Affiliation:
Department of Mathematical Sciences, Chalmers University of Technology and the University of Gothenburg, SE-412 96Gothenburg, Sweden email chrjohv@chalmers.se
Lucia Mocz
Affiliation:
Mathematisches Institut der Universität Bonn, Endenicher Allee 60, 53115Bonn, Germany
Emanuel Reinecke
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI48109, USA email reinec@umich.edu
Sheng-Chi Shih
Affiliation:
University of Lille, CNRS, UMR 8524 – Laboratoire Paul Painlevé, 59000Lille, France email sheng-chi.shih@univ-lille.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the compactly supported cohomology of certain 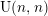$\text{U}(n,n)$- or 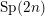$\text{Sp}(2n)$-Shimura varieties with 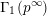$\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$-level vanishes above the middle degree. The only assumption is that we work over a CM field 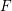$F$ in which the prime 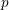$p$ splits completely. We also give an application to Galois representations for torsion in the cohomology of the locally symmetric spaces for 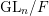$\text{GL}_{n}/F$. More precisely, we use the vanishing result for Shimura varieties to eliminate the nilpotent ideal in the construction of these Galois representations. This strengthens recent results of Scholze [On torsion in the cohomology of locally symmetric varieties, Ann. of Math. (2) 182 (2015), 945–1066; MR 3418533] and Newton–Thorne [Torsion Galois representations over CM fields and Hecke algebras in the derived category, Forum Math. Sigma 4 (2016), e21; MR 3528275].

Keywords

locally symmetric spacesperfectoid spacesGalois representations

MSC classification

Primary: 11F75: Cohomology of arithmetic groups 11F80: Galois representations 11G18: Arithmetic aspects of modular and Shimura varieties 14G22: Rigid analytic geometry
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 6 , June 2020 , pp. 1152 - 1230
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Current address: Mathematical Institute, University of Oxford, Oxford OX2 6GG, UK email Daniel.Gulotta@maths.ox.ac.uk

2

Current address: Department of Mathematics, University of California, Los Angeles, Box 95155, Los Angeles, CA 90095, USA email cyhsu@math.ucla.edu

3

Current address: Department of Mathematics, University of Chicago, 5734 S. University Ave., Chicago, IL 60637, USA email lmocz@math.uchicago.edu

A.C. was supported in part by a Royal Society University Research Fellowship and by ERC Starting Grant 804176. C.-Y.H. is partially supported by a Government Scholarship to Study Abroad from Taiwan. C.J. was supported in part by the Herchel Smith Foundation. E.R. was partially supported by NSF Grant No. DMS-1501461.

References

Allen, P. B., Calegari, F., Caraiani, A., Gee, T., Helm, D., Le Hung, B. V., Newton, J., Scholze, P., Taylor, R. and Thorne, J. A., Potential automorphy over CM fields, Preprint (2018), arXiv:1812.09999.Google Scholar
Ash, A. and Stevens, G., $p$-adic deformations of arithmetic cohomology, Preprint (2008), http://math.bu.edu/people/ghs/preprints/Ash-Stevens-02-08.pdf.Google Scholar
Bartenwerfer, W., Der erste Riemannsche Hebbarkeitssatz im nichtarchimedischen Fall, J. Reine Angew. Math. 286–287 (1976), 144–163.Google Scholar
Bernstein, J. and Lunts, V., Equivariant sheaves and functors, Lecture Notes in Mathematics, vol. 1578 (Springer, Berlin); MR 1299527.CrossRefGoogle Scholar
Bhatt, B. and Scholze, P., Prisms and prismatic cohomology, Preprint (2019), arXiv:1905.08229.Google Scholar
Birkbeck, C., Feng, T., Hansen, D., Hong, S., Li, Q., Wang, A. and Ye, L., Extensions of vector bundles on the Fargues–Fontaine curve, J. Inst. Math. Jussieu, to appear. Preprint (2017), arXiv:1705.00710.Google Scholar
Borel, A. and Serre, J.-P., Corners and arithmetic groups, Comment. Math. Helv. 48 (1973), 436–491, with an appendix: Arrondissement des variétés à coins, by A. Douady and L. Hérault; MR 0387495.CrossRefGoogle Scholar
Borel, A. and Tits, J., Groupes réductifs, Publ. Math. Inst. Hautes Études Sci. 27 (1965), 55–150; MR 0207712.CrossRefGoogle Scholar
Boyer, P., Sur la torsion dans la cohomologie des variété de Shimura de Kottwitz–Harris–Taylor, J. Inst. Math. Jussieu 18 (2019), 499–517; MR 3936639.CrossRefGoogle Scholar
Brown, M., Locally flat imbeddings of topological manifolds, Ann. of Math. (2) 75 (1962), 331–341.CrossRefGoogle Scholar
Calegari, F. and Emerton, M., Completed cohomology—a survey, in Non-abelian fundamental groups and Iwasawa theory, London Mathematical Society Lecture Note Series, vol. 393 (Cambridge University Press, Cambridge, 2012), 239–257; MR 2905536.Google Scholar
Calegari, F. and Geraghty, D., Modularity lifting beyond the Taylor–Wiles method, Invent. Math. 211 (2018), 297–433; MR 3742760.CrossRefGoogle Scholar
Calegari, F., Geraghty, D. and Harris, M., Bloch–Kato conjectures for automorphic motives. Appendix to “Minimal modularity lifting for nonregular symplectic representations” [in Duke Math. J., 169 (2020), 801–896] by F. Calegari and D. Geraghty, Duke Math. J. 169 (2020), 880–891; MR 4079417.Google Scholar
Caraiani, A. and Scholze, P., On the generic part of the cohomology of compact unitary Shimura varieties, Ann. of Math. (2) 186 (2017), 649–766; MR 3702677.CrossRefGoogle Scholar
Caraiani, A. and Scholze, P., On the generic part of the cohomology of non-compact unitary Shimura varieties, Preprint (2019), arXiv:1909.01898.Google Scholar
Chenevier, G., The p-adic analytic space of pseudocharacters of a profinite group and pseudorepresentations over arbitrary rings, in Automorphic forms and Galois representations, Vol. 1, London Mathematical Society Lecture Note Series, vol. 414 (Cambridge University Press, Cambridge, 2014), 221–285; MR 3444227.CrossRefGoogle Scholar
Deligne, P., Travaux de Shimura, in Séminaire Bourbaki, 23ème année (1970/71), Exp. No. 389, Lecture Notes in Mathematics, vol. 244 (Springer, Berlin, 1971), 123–165; MR 0498581.CrossRefGoogle Scholar
Emerton, M., Ordinary parts of admissible representations of p-adic reductive groups I. Definition and first properties, Astérisque 331 (2010), 355–402; MR 2667882.Google Scholar
Emerton, M., Ordinary parts of admissible representations of p-adic reductive groups II. Derived functors, Astérisque 331 (2010), 403–459; MR 2667883.Google Scholar
Emerton, M., Completed cohomology and the p-adic Langlands program, in Proceedings of the International Congress of Mathematicians, vol. II (Kyung Moon Sa, Seoul, 2014), 319–342.Google Scholar
Faltings, G., Almost étale extensions, Astérisque 279 (2002), 185–270.Google Scholar
Faltings, G. and Chai, C.-L., Degeneration of abelian varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 22 (Springer, Berlin, 1990), with an appendix by David Mumford; MR 1083353.CrossRefGoogle Scholar
Fernandez-Alcober, G. A., Kazachkov, I. V., Remeslennikov, V. N. and Symonds, P., Comparison of the discrete and continuous cohomology groups of a pro-p group, St. Petersburg Math. J. 19 (2008), 961–973.CrossRefGoogle Scholar
Gabber, O. and Ramero, L., Almost ring theory, Lecture Notes in Mathematics, vol. 1800 (Springer, Berlin, 2003); MR 2004652.CrossRefGoogle Scholar
Gee, T. and Newton, J., Patching and the completed homology of locally symmetric spaces, J. Inst. Math. Jussieu, to appear. Preprint (2016), arXiv:1609.06965.Google Scholar
Hansen, D., Quotients of adic spaces by finite groups, Math. Res. Lett., to appear. Preprint (2016), http://www.math.columbia.edu/∼hansen/adicgpquotient.pdf.Google Scholar
Hansen, D., Universal eigenvarieties, trianguline Galois representations, and p-adic Langlands functoriality, J. Reine Angew. Math. 730 (2017), 1–64, with an appendix by James Newton; MR 3692014.CrossRefGoogle Scholar
Hill, R., On Emerton’s p-adic Banach spaces, Int. Math. Res. Not. IMRN 2010 (2010), 3588–3632; MR 2725506.CrossRefGoogle Scholar
Huber, R., A generalization of formal schemes and rigid analytic varieties, Math. Z. 217 (1994), 513–551; MR 1306024.CrossRefGoogle Scholar
Jantzen, J. C., Representations of algebraic groups, Mathematical Surveys and Monographs, vol. 107, second edition (American Mathematical Society, Providence, RI, 2003); MR 2015057.Google Scholar
Kashiwara, M. and Schapira, P., Sheaves on manifolds, Grundlehren der mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 292 (Springer, Berlin, 1994), with a chapter in French by Christian Houzel, corrected reprint of the 1990 original; MR 1299726.Google Scholar
Kedlaya, K. S. and Liu, R., Relative p-adic Hodge theory, I: Foundations, Astérisque 371 (2015), 239; MR 3379653.Google Scholar
Kedlaya, K. S. and Liu, R., Relative $p$-adic Hodge theory, II: Imperfect period rings, Preprint (2016), arXiv:1602.06899.Google Scholar
Khare, C. B. and Thorne, J. A., Potential automorphy and the Leopoldt conjecture, Amer. J. Math. 139 (2017), 1205–1273; MR 3702498.CrossRefGoogle Scholar
Kottwitz, R. E., Points on some Shimura varieties over finite fields, J. Amer. Math. Soc. 5 (1992), 373–444; MR 1124982.CrossRefGoogle Scholar
Lan, K.-W., Arithmetic compactifications of PEL-type Shimura varieties, London Mathematical Society Monographs, vol. 36 (Princeton University Press, Princeton, NJ, 2013); MR 3186092.Google Scholar
Lan, K.-W. and Stroh, B., Compactifications of subschemes of integral models of Shimura varieties, Forum Math. Sigma 6 (2018), e18; MR 3859178.CrossRefGoogle Scholar
Lan, K.-W. and Suh, J., Vanishing theorems for torsion automorphic sheaves on compact PEL-type Shimura varieties, Duke Math. J. 161 (2012), 1113–1170; MR 2913102.CrossRefGoogle Scholar
Lan, K.-W. and Suh, J., Vanishing theorems for torsion automorphic sheaves on general PEL-type Shimura varieties, Adv. Math. 242 (2013), 228–286; MR 3055995.CrossRefGoogle Scholar
Ludwig, J., A quotient of the Lubin–Tate tower, Forum Math. Sigma 5 (2017), e17; MR 3680340.CrossRefGoogle Scholar
Mumford, D., Abelian varieties, Tata Institute of Fundamental Research Studies in Mathematics, vol. 5 (Oxford University Press, London, 1970).Google Scholar
Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of number fields, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 323, second edition (Springer, Berlin, 2008); MR 2392026.CrossRefGoogle Scholar
Newton, J. and Thorne, J. A., Torsion Galois representations over CM fields and Hecke algebras in the derived category, Forum Math. Sigma 4 (2016), e21; MR 3528275.CrossRefGoogle Scholar
Pink, R., Arithmetical compactification of mixed Shimura varieties, Bonner Mathematische Schriften [Bonn Mathematical Publications], vol. 209 (Universität Bonn, Mathematisches Institut, Bonn, 1990); Dissertation, Rheinische Friedrich-Wilhelms-Universität Bonn, Bonn, 1989; MR 1128753.Google Scholar
Scheiderer, C., Quasi-augmented simplicial spaces, with an application to cohomological dimension, J. Pure Appl. Algebra 81 (1992), 293–311; MR 1179103.CrossRefGoogle Scholar
Scholze, P., Perfectoid spaces, Publ. Math. Inst. Hautes Études Sci. 116 (2012), 245–313; MR 3090258.CrossRefGoogle Scholar
Scholze, P., p-adic Hodge theory for rigid-analytic varieties, Forum Math. Pi 1 (2013), e1; MR 3090230.CrossRefGoogle Scholar
Scholze, P., Perfectoid spaces: a survey, in Current Developments in Mathematics, 2012 (International Press, Somerville, MA, 2013), 193–227; MR 3204346.Google Scholar
Scholze, P., On torsion in the cohomology of locally symmetric varieties, Ann. of Math. (2) 182 (2015), 945–1066; MR 3418533.CrossRefGoogle Scholar
Scholze, P., Étale cohomology of diamonds, Preprint (2017), arXiv:1709.07343.Google Scholar
Scholze, P. and Weinstein, J., Moduli of p-divisible groups, Cambridge J. Math. 1 (2013), 145–237.CrossRefGoogle Scholar
Scholze, P. and Weinstein, J., Berkeley lectures on p-adic geometry, Annals of Mathematics Studies, 207 (Princeton University Press, Princeton, NJ, 2020).Google Scholar
The Stacks Project Authors, Stacks Project, http://stacks.math.columbia.edu.Google Scholar
Wedhorn, T., Ordinariness in good reductions of Shimura varieties of PEL-type, Ann. Sci. Éc. Norm. Supér (4) 32 (1999), 575–618; MR 1710754.CrossRefGoogle Scholar