Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T04:31:20.090Z Has data issue: false hasContentIssue false
  • English
  • Français

Spinor groups with good reduction

Part of: Algebraic number theory: global fields Forms and linear algebraic groups

Published online by Cambridge University Press:  07 March 2019

Vladimir I. Chernousov ,
Andrei S. Rapinchuk  and
Igor A. Rapinchuk
Vladimir I. Chernousov
Affiliation:
Department of Mathematics, University of Alberta, Edmonton, Alberta T6G 2G1, Canada email vladimir@ualberta.ca
Andrei S. Rapinchuk
Affiliation:
Department of Mathematics, University of Virginia, Charlottesville, VA 22904-4137, USA email asr3x@virginia.edu
Igor A. Rapinchuk
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, MI 48824, USA email rapinchu@msu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 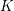$K$ be a two-dimensional global field of characteristic 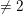$\neq 2$ and let 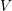$V$ be a divisorial set of places of 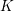$K$. We show that for a given 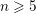$n\geqslant 5$, the set of 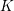$K$-isomorphism classes of spinor groups 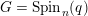$G=\operatorname{Spin}_{n}(q)$ of nondegenerate $n$-dimensional quadratic forms over 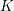$K$ that have good reduction at all 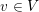$v\in V$ is finite. This result yields some other finiteness properties, such as the finiteness of the genus 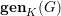$\mathbf{gen}_{K}(G)$ and the properness of the global-to-local map in Galois cohomology. The proof relies on the finiteness of the unramified cohomology groups 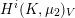$H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V}$ for 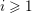$i\geqslant 1$ established in the paper. The results for spinor groups are then extended to some unitary groups and to groups of type 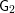$\mathsf{G}_{2}$.

Keywords

algebraic groupsGalois cohomologygood reductionHasse principlesunramified cohomology

MSC classification

Primary: 11E72: Galois cohomology of linear algebraic groups
Secondary: 11R34: Galois cohomology
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 3 , March 2019 , pp. 484 - 527
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by the Canada Research Chairs Program and by an NSERC research grant. The second author was partially supported by the Simons Foundation. During the preparation of the final version of the paper, he visited Princeton University and the Institute for Advanced Study, and would like to thankfully acknowledge the hospitality of both institutions. The third author was partially supported by an AMS-Simons Travel Grant. We are grateful to P. Gille and M. Rapoport for useful conversations. Last but not least, we would like to express our gratitude to all anonymous referees whose comments, insights and suggestions helped to improve the original paper significantly.

References

Berhuy, G., Finiteness of R-equivalence groups of some adjoint classical groups of type 2 D 3 , J. Algebra 309 (2007), 360–366.Google Scholar
Berhuy, G., An introduction to Galois cohomology and its applications, London Mathematical Society Lecture Note Series, vol. 377 (Cambridge University Press, Cambridge, 2010).Google Scholar
Bloch, S. and Ogus, A., Gersten’s conjecture and the homology of schemes , Ann. Sci. Éc. Norm. Supér. (4) 7 (1974), 181–201.Google Scholar
Brussel, E., On Saltman’s p-adic curves papers , in Quadratic forms, linear algebraic groups, and cohomology, Developments in Mathematics, vol. 18 (Springer, New York, 2010), 13–39.Google Scholar
Cassels, J. W. S. and Fröhlich, A. (eds), Algebraic number theory, second edition (London Mathematical Society, London, 2010).Google Scholar
Chernousov, V. I., Gille, P. and Pianzola, A., Torsors over the punctured affine line , Amer. J. Math. 134 (2012), 1541–1583.Google Scholar
Chernousov, V. I., Neher, E., Pianzola, A. and Yahorau, U., On conjugacy of Cartan subalgebras in extended affine Lie algebras , Adv. Math. 290 (2016), 260–292.Google Scholar
Chernousov, V. I., Rapinchuk, A. S. and Rapinchuk, I. A., The genus of a division algebra and the unramified Brauer group , Bull. Math. Sci. 3 (2013), 211–240.Google Scholar
Chernousov, V. I., Rapinchuk, A. S. and Rapinchuk, I. A., Division algebras with the same maximal subfields , Russian Math. Surveys 70 (2015), 91–122.Google Scholar
Chernousov, V. I., Rapinchuk, A. S. and Rapinchuk, I. A., On the size of the genus of a division algebra , Proc. Steklov Inst. Math. 292 (2016), 63–93.Google Scholar
Chernousov, V. I., Rapinchuk, A. S. and Rapinchuk, I. A., On some finiteness properties of algebraic groups over finitely generated fields , C. R. Math. Acad. Sci. Paris, Ser. I 354 (2016), 869–873.Google Scholar
Chernousov, V. I., Rapinchuk, A. S. and Rapinchuk, I. A., The finiteness of the genus of a finite-dimensional division algebras, and some generalizations, Israel J. Math., to appear.Google Scholar
Chernousov, V. I., Rapinchuk, A. S. and Rapinchuk, I. A., Algebraic groups with the same tori, weakly commensurable Zariski-dense subgroups, and good reduction, in preparation.Google Scholar
Colliot-Thélène, J.-L., Birational invariants, purity and the Gersten conjecture , in K-theory and algebraic geometry: connections with quadratic forms and division algebras (Santa Barbara, CA, 1992), Proceedings of Symposia in Pure Mathematics, vol. 58 (American Mathematical Society, Providence, RI, 1995), 1–64.Google Scholar
Colliot-Thélène, J.-L., Quelques résultats de finitude pour le groupe SK 1 d’une algèbre de biquaternions , J. K-Theory 10 (1996), 31–48.Google Scholar
Colliot-Thélène, J.-L., Hoobler, R. and Kahn, B., The Bloch–Ogus–Gabber theorem , in Algebraic K-theory (Toronto, ON, 1996), Fields Institute Communications, vol. 16 (American Mathematical Society, Providence, RI, 1997), 31–94.Google Scholar
Colliot-Thélène, J.-L., Parimala, R. and Suresh, V., Patching and local-global principles for homogeneous spaces over function fields of p-adic curves , Comment. Math. Helv. 87 (2012), 1011–1033.Google Scholar
Colliot-Thélène, J.-L. and Sansuc, J.-J., Fibrés quadratiques et composantes connexes réelles , Math. Ann. 244 (1979), 105–134.Google Scholar
Colliot-Thélène, J.-L., Sansuc, J.-J. and Soulé, C., Torsion dans le groupe de Chow de codimension deux , Duke Math. J. 50 (1983), 763–801.Google Scholar
Conrad, B., Non-split reductive groups over , in Autour des schémas en groupes, Vol. II, Panoramas et Synthèses, vol. 46 (Soc. Math. France, Paris, 2015), 193–253.Google Scholar
Cutkosky, S. D., Introduction to Algebraic Geometry, Graduate Studies in Mathematics, vol. 188 (American Mathematical Society, Providence, RI, 2018).Google Scholar
Faltings, G., Endlichkeitssätze für abelsche Varietäten über Zahlkörpern , Invent. Math. 73 (1983), 349–366.Google Scholar
Garibaldi, S., Merkurjev, A. and Serre, J.-P., Cohomological invariants in Galois cohomology, University Lecture Series, vol. 28 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Gerstein, L. J., Basic quadratic forms, Graduate Studies in Mathematics, vol. 90 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Gille, P. and Szamuely, T., Central simple algebras and Galois cohomology (Cambridge University Press, Cambridge, 2006).Google Scholar
Gross, B. H., Groups over , Invent. Math. 124 (1996), 263–279.Google Scholar
Harder, G., Halbeifache Gruppenschemata über Dedekindringen , Invent. Math. 4 (1967), 165–191.Google Scholar
Hartshorne, R., Algebraic geometry, Geometry & Topology Monographs, vol. 52 (Springer, Berlin, 1977).Google Scholar
Jannsen, U., Principe de Hasse cohomologique , in Séminaire de Théorie des Nombres (Soc. Math. France, Paris, 1989–90), 121–140.Google Scholar
Jannsen, U., Hasse principles for higher-dimensional fields , Ann. of Math. (2) 183 (2016), 1–71.Google Scholar
Jannsen, U., Sato, S. and Saito, K., Étale duality for constructible sheaves on arithmetic schemes , J. reine angew. Math. 688 (2014), 1–65.Google Scholar
Javanpeykar, A. and Loughran, D., Good reduction of algebraic groups and flag varieties , Arch. Math. 104 (2015), 133–143.Google Scholar
Kahn, B., Sur le groupe des clsses d’un schéma arithmétiques , Bull. Soc. Math. France 134 (2006), 395–415.Google Scholar
Kato, K., A Hasse principle for two dimensional global fields , J. reine angew. Math. 366 (1986), 142–183, with an appendix by J.-L. Colliot-Thélène.Google Scholar
Knus, M.-A., Merkurjev, A., Rost, M. and Tignol, J.-P., The book of involutions, Colloquium Publications, vol. 44 (American Mathematical Society, Providence, RI, 1998).Google Scholar
Lam, T. Y., Introduction to quadratic forms over fields, Graduate Studies in Mathematics, vol. 67 (American Mathematical Society, Providence, RI, 2005).Google Scholar
Merkurjev, A. S. and Suslin, A. A., K-cohomology of Severi-Brauer varieties and the norm residue homomorphism , Izv. Akad. Nauk SSSR Ser. Mat. 46 (1982), 1011–1046.Google Scholar
Milne, J. S., Étale cohomology (Princeton University Press, Princeton, NJ, 1980).Google Scholar
Milnor, J., Algebraic K-theory and quadratic forms , Invent. Math. 9 (1970), 318–344.Google Scholar
Orlov, D., Vishik, A. and Voevodsky, V., An exact sequence for K M /2 with applications to quadratic forms , Ann. of Math. (2) 165 (2007), 1–13.Google Scholar
Parimala, R., A Hasse principle for quadratic forms over function fields , Bull. Amer. Math. Soc. (N.S.) 51 (2014), 447–461.Google Scholar
Parimala, R. and Suresh, V., Isotropy of quadratic forms over function fields of p-adic curves , Publ. Math. Inst. Hautes Études Sci. 88 (1998), 129–150.Google Scholar
Parimala, R. and Suresh, V., The u-invariant of the function fields of p-adic curves , Ann. of Math. (2) 172 (2010), 1391–1405.Google Scholar
Platonov, V. P. and Rapinchuk, A. S., Algebraic groups and number theory (Academic Press, New York, 1994).Google Scholar
Prasad, G. and Rapinchuk, A. S., Existence of irreducible -regular elements in Zariski-dense subgroups , Math. Res. Lett. 10 (2003), 21–32.Google Scholar
Prasad, G. and Rapinchuk, A. S., Weakly commensurable arithmetic groups and isospectral locally symmetric spaces , Publ. Math. Inst. Hautes Études Sci. 109 (2009), 113–184.Google Scholar
Prasad, G. and Rapinchuk, A. S., Weakly commensurable groups, with applications to differential geometry , in Handbook of Group Actions, Vol. I, Advanced Lectures in Mathematics, vol. 32 (International Press, Somerville, MA, 2015), 495–524.Google Scholar
Prasad, G. and Rapinchuk, A. S., Generic elements of a Zariski-dense subgroup form an open subset , Trans. Moscow Math. Soc. 78 (2017), 299–314.Google Scholar
Raghunathan, M. S. and Ramanathan, A., Principal bundles on the affine line , Proc. Indian Acad. Sci. Math. Sci. 93 (1984), 137–145.Google Scholar
Rapinchuk, A. S., Towards the eigenvalue rigidity of Zariski-dense subgroups , in Proceedings of the international congress of mathematicians (Seoul 2014), Vol. II (Kyung Moon Sa, Seoul, 2014), 247–269.Google Scholar
Rapinchuk, A. S. and Rapinchuk, I. A., On division algebras having the same maximal subfields , Manuscripta Math. 132 (2010), 273–293.Google Scholar
Rapinchuk, I. A., A generalization of Serre’s condition (F) with applications to the finiteness of unramified cohomology , Math. Z. (2018), doi:10.1007/s00209-018-2079-0.Google Scholar
Rapinchuk, I. A., On residue maps for affine curves , J. Pure Appl. Algebra 223 (2019), 965–975.Google Scholar
Samuel, P., A propos du théorèm des unités , Bull. Sci. Math. (2) 90 (1966), 89–96.Google Scholar
SGA 1: Revêtements étales et groupe fondamentale, Lecture Notes in Mathematics, vol. 224 (Springer, Berlin, 1971).Google Scholar
Artin, M., Deligne, P., Grothendieck, A. and Verdier, J.-L., SGA 4, tome 3, Lecture Notes in Mathematics, vol. 305 (Springer, New York, 1973).Google Scholar
Deligne, P., Cohomologie étale , in SGA 4½, Lecture Notes in Mathematics, vol. 569 (Springer, 1977).Google Scholar
Serre, J.-P., Galois cohomology (Springer, Berlin, 1997).Google Scholar
The Stacks Project (2019) Étale cohomology. https://stacks.math.columbia.edu/tag/03N1.Google Scholar
Voevodsky, V., Motivic cohomology with /2-coefficients , Publ. Math. Inst. Hautes Études Sci. 98 (2003), 59–104.Google Scholar
Voevodsky, V., On motivic cohomology with /ℓ-coefficients , Ann. of Math. (2) 174 (2011), 401–438.Google Scholar