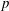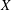Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Choudhury, Utsav
and
Skowera, Jonathan
2016.
Motivic Decomposition for Relative Geometrically Cellular Stacks.
Communications in Algebra,
Vol. 44,
Issue. 2,
p.
648.
Kerz, Moritz
and
Strunk, Florian
2017.
On the vanishing of negative homotopy K-theory.
Journal of Pure and Applied Algebra,
Vol. 221,
Issue. 7,
p.
1641.
Kerz, Moritz
Strunk, Florian
and
Tamme, Georg
2018.
Algebraic K-theory and descent for blow-ups.
Inventiones mathematicae,
Vol. 211,
Issue. 2,
p.
523.
Pepin Lehalleur, Simon
2019.
Triangulated categories of relative 1-motives.
Advances in Mathematics,
Vol. 347,
Issue. ,
p.
473.
KELLY, SHANE
2019.
A BETTER COMPARISON OF - AND -COHOMOLOGIES.
Nagoya Mathematical Journal,
Vol. 236,
Issue. ,
p.
183.
Sadhu, Vivek
2020.
On the vanishing of relative negative K-theory.
Journal of Algebra and Its Applications,
Vol. 19,
Issue. 08,
p.
2050152.
Kelly, Shane
and
Morrow, Matthew
2021.
K-theory of valuation rings.
Compositio Mathematica,
Vol. 157,
Issue. 6,
p.
1121.