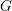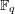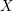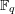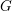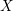Introduction
Let  $X$ be a smooth projective geometrically connected curve over a finite field
$X$ be a smooth projective geometrically connected curve over a finite field  $\mathbb{F}_{q}$. We denote by
$\mathbb{F}_{q}$. We denote by  $F$ its function field, by
$F$ its function field, by  $\mathbb{A}$ the ring of adèles of
$\mathbb{A}$ the ring of adèles of  $F$ and by
$F$ and by  $\mathbb{O}$ the ring of integral adèles.
$\mathbb{O}$ the ring of integral adèles.
Let  $G$ be a connected split reductive group over
$G$ be a connected split reductive group over  $\mathbb{F}_{q}$. For simplicity, we assume in the introduction that the center of
$\mathbb{F}_{q}$. For simplicity, we assume in the introduction that the center of  $G$ is finite.
$G$ is finite.
We consider the space of automorphic forms  $C_{c}(G(F)\backslash G(\mathbb{A})/G(\mathbb{O}),\mathbb{C})$. On the one hand, there is the notion of cuspidal automorphic form. An automorphic form is said to be cuspidal if its image under the constant term morphism along any proper parabolic subgroup of
$C_{c}(G(F)\backslash G(\mathbb{A})/G(\mathbb{O}),\mathbb{C})$. On the one hand, there is the notion of cuspidal automorphic form. An automorphic form is said to be cuspidal if its image under the constant term morphism along any proper parabolic subgroup of  $G$ is zero. A theorem of Harder [Reference HarderHar74, Theorem 1.2.1] says that the space of cuspidal automorphic forms has finite dimension. The proof uses the Harder–Narasimhan truncations and the contractibility of deep enough strata.
$G$ is zero. A theorem of Harder [Reference HarderHar74, Theorem 1.2.1] says that the space of cuspidal automorphic forms has finite dimension. The proof uses the Harder–Narasimhan truncations and the contractibility of deep enough strata.
On the other hand, the space of automorphic forms is equipped with an action of the Hecke algebra  $C_{c}(G(\mathbb{O})\backslash G(\mathbb{A})/G(\mathbb{O}),\mathbb{Q})$ by convolution on the right. An automorphic form is said to be (rationally) Hecke-finite if it belongs to a finite-dimensional subspace that is stable under the action of the Hecke algebra.
$C_{c}(G(\mathbb{O})\backslash G(\mathbb{A})/G(\mathbb{O}),\mathbb{Q})$ by convolution on the right. An automorphic form is said to be (rationally) Hecke-finite if it belongs to a finite-dimensional subspace that is stable under the action of the Hecke algebra.
In [Reference LafforgueLaf18, Proposition 8.23], Vincent Lafforgue proved that the space of cuspidal automorphic forms and the space of Hecke-finite automorphic forms are equal. In fact, the space of cuspidal automorphic forms is stable under the action of the Hecke algebra and is finite-dimensional, and thus it is included in the space of Hecke-finite automorphic forms. The converse direction follows from the following fact: any non-zero image of the constant term morphism along a proper parabolic subgroup  $P$ with Levi quotient
$P$ with Levi quotient  $M$ is supported on the components indexed by a cone in the lattice of the cocharacters of the center of
$M$ is supported on the components indexed by a cone in the lattice of the cocharacters of the center of  $M$. Hence it generates an infinite-dimensional vector space under the action of the Hecke algebra of
$M$. Hence it generates an infinite-dimensional vector space under the action of the Hecke algebra of  $M$. Thus a non-cuspidal automorphic form can not be Hecke-finite for the Hecke algebra of
$M$. Thus a non-cuspidal automorphic form can not be Hecke-finite for the Hecke algebra of  $M$.
$M$.
Let  $\ell$ be a prime number not dividing
$\ell$ be a prime number not dividing  $q$. In [Reference DrinfeldDri78] and [Reference DrinfeldDri87], Drinfeld introduced the stacks classifying
$q$. In [Reference DrinfeldDri78] and [Reference DrinfeldDri87], Drinfeld introduced the stacks classifying  $\text{GL}_{n}$-shtukas for the representation
$\text{GL}_{n}$-shtukas for the representation  $\text{St}\boxtimes \text{St}^{\ast }$ of
$\text{St}\boxtimes \text{St}^{\ast }$ of  $\text{GL}_{n}\times \text{GL}_{n}$, where
$\text{GL}_{n}\times \text{GL}_{n}$, where  $\text{St}$ is the standard representation of
$\text{St}$ is the standard representation of  $\text{GL}_{n}$ and
$\text{GL}_{n}$ and  $\text{St}^{\ast }$ is its dual, and considered their
$\text{St}^{\ast }$ is its dual, and considered their  $\ell$-adic cohomology. These were also used by Laurent Lafforgue in [Reference LafforgueLaf97]. Later in [Reference VarshavskyVar04], Varshavsky defined the stacks classifying
$\ell$-adic cohomology. These were also used by Laurent Lafforgue in [Reference LafforgueLaf97]. Later in [Reference VarshavskyVar04], Varshavsky defined the stacks classifying  $G$-shtukas
$G$-shtukas  $\operatorname{Cht}_{G,I,W}$ for general
$\operatorname{Cht}_{G,I,W}$ for general  $G$ and for an arbitrary representation
$G$ and for an arbitrary representation  $W$ of
$W$ of  $\widehat{G}^{I}$, where
$\widehat{G}^{I}$, where  $\widehat{G}$ is the Langlands dual group of
$\widehat{G}$ is the Langlands dual group of  $G$ over
$G$ over  $\mathbb{Q}_{\ell }$ and
$\mathbb{Q}_{\ell }$ and  $I$ is a finite set (Drinfeld considered the case
$I$ is a finite set (Drinfeld considered the case  $G=\text{GL}_{n}$,
$G=\text{GL}_{n}$,  $I=\{1,2\}$ and
$I=\{1,2\}$ and  $W=\text{St}\boxtimes \text{St}^{\ast }$). Varshavsky also defined the degree
$W=\text{St}\boxtimes \text{St}^{\ast }$). Varshavsky also defined the degree  $j$ cohomology group with compact support
$j$ cohomology group with compact support  $H_{G,I,W}^{j}$ of the
$H_{G,I,W}^{j}$ of the  $\ell$-adic intersection complex of
$\ell$-adic intersection complex of  $\operatorname{Cht}_{G,I,W}$ (this stack is smooth in the case of Drinfeld but not in general). In particular, when
$\operatorname{Cht}_{G,I,W}$ (this stack is smooth in the case of Drinfeld but not in general). In particular, when  $I=\emptyset$ and
$I=\emptyset$ and  $W=\mathbf{1}$ is the one-dimensional trivial representation of the trivial group
$W=\mathbf{1}$ is the one-dimensional trivial representation of the trivial group  $\widehat{G}^{\emptyset }$, the cohomology group
$\widehat{G}^{\emptyset }$, the cohomology group  $H_{G,\emptyset ,\mathbf{1}}^{0}$ coincides with
$H_{G,\emptyset ,\mathbf{1}}^{0}$ coincides with  $C_{c}(G(F)\backslash G(\mathbb{A})/G(\mathbb{O}),\mathbb{Q}_{\ell })$.
$C_{c}(G(F)\backslash G(\mathbb{A})/G(\mathbb{O}),\mathbb{Q}_{\ell })$.
The Hecke algebra  $C_{c}(G(\mathbb{O})\backslash G(\mathbb{A})/G(\mathbb{O}),\mathbb{Z}_{\ell })$ acts on the cohomology group
$C_{c}(G(\mathbb{O})\backslash G(\mathbb{A})/G(\mathbb{O}),\mathbb{Z}_{\ell })$ acts on the cohomology group  $H_{G,I,W}^{j}$. In [Reference LafforgueLaf18], Vincent Lafforgue defined the subspace
$H_{G,I,W}^{j}$. In [Reference LafforgueLaf18], Vincent Lafforgue defined the subspace  $H_{G,I,W}^{j,\;\operatorname{Hf}}$ of
$H_{G,I,W}^{j,\;\operatorname{Hf}}$ of  $H_{G,I,W}^{j}$ which consists of the cohomology classes
$H_{G,I,W}^{j}$ which consists of the cohomology classes  $c$ for which
$c$ for which  $C_{c}(G(\mathbb{O})\backslash G(\mathbb{A})/G(\mathbb{O}),\mathbb{Z}_{\ell })\cdot c$ is a finitely generated
$C_{c}(G(\mathbb{O})\backslash G(\mathbb{A})/G(\mathbb{O}),\mathbb{Z}_{\ell })\cdot c$ is a finitely generated  $\mathbb{Z}_{\ell }$-submodule of
$\mathbb{Z}_{\ell }$-submodule of  $H_{G,I,W}^{j}$. When
$H_{G,I,W}^{j}$. When  $I=\emptyset$ and
$I=\emptyset$ and  $W=\mathbf{1}$, the space
$W=\mathbf{1}$, the space  $H_{G,\emptyset ,\mathbf{1}}^{0,\,\operatorname{Hf}}$ coincides with the space of Hecke-finite automorphic forms, and thus coincides with the space of cuspidal automorphic forms. Vincent Lafforgue used
$H_{G,\emptyset ,\mathbf{1}}^{0,\,\operatorname{Hf}}$ coincides with the space of Hecke-finite automorphic forms, and thus coincides with the space of cuspidal automorphic forms. Vincent Lafforgue used  $H_{G,I,W}^{0,\;\operatorname{Hf}}$ to construct the excursion operators on the space of cuspidal automorphic forms and obtained a canonical decomposition of this space indexed by the Langlands parameters.
$H_{G,I,W}^{0,\;\operatorname{Hf}}$ to construct the excursion operators on the space of cuspidal automorphic forms and obtained a canonical decomposition of this space indexed by the Langlands parameters.
We can also define a subspace  $H_{G,I,W}^{j,\;\operatorname{Hf-rat}}$ of
$H_{G,I,W}^{j,\;\operatorname{Hf-rat}}$ of  $H_{G,I,W}^{j}$ which consists of the cohomology classes
$H_{G,I,W}^{j}$ which consists of the cohomology classes  $c$ for which
$c$ for which  $C_{c}(G(\mathbb{O})\backslash G(\mathbb{A})/G(\mathbb{O}),\mathbb{Q}_{\ell })\cdot c$ is a finite-dimensional
$C_{c}(G(\mathbb{O})\backslash G(\mathbb{A})/G(\mathbb{O}),\mathbb{Q}_{\ell })\cdot c$ is a finite-dimensional  $\mathbb{Q}_{\ell }$-vector subspace of
$\mathbb{Q}_{\ell }$-vector subspace of  $H_{G,I,W}^{j}$. By definition, we have
$H_{G,I,W}^{j}$. By definition, we have  $H_{G,I,W}^{j,\;\operatorname{Hf}}\subset H_{G,I,W}^{j,\;\operatorname{Hf-rat}}$. When
$H_{G,I,W}^{j,\;\operatorname{Hf}}\subset H_{G,I,W}^{j,\;\operatorname{Hf-rat}}$. When  $I=\emptyset$ and
$I=\emptyset$ and  $W=\mathbf{1}$, it is easy to see that they are equal.
$W=\mathbf{1}$, it is easy to see that they are equal.
In this paper, we are interested in the constant term morphism of the cohomology of stacks of shtukas, analogous to the case of automorphic forms. For any parabolic subgroup  $P$ of
$P$ of  $G$, let
$G$, let  $M$ be its Levi quotient. As in [Reference VarshavskyVar04], we can define the stack of
$M$ be its Levi quotient. As in [Reference VarshavskyVar04], we can define the stack of  $P$-shtukas
$P$-shtukas  $\operatorname{Cht}_{P,I,W}$ and the stack of
$\operatorname{Cht}_{P,I,W}$ and the stack of  $M$-shtukas
$M$-shtukas  $\operatorname{Cht}_{M,I,W}$. The morphisms
$\operatorname{Cht}_{M,I,W}$. The morphisms  $G{\hookleftarrow}P{\twoheadrightarrow}M$ induce a correspondence
$G{\hookleftarrow}P{\twoheadrightarrow}M$ induce a correspondence
 $$\begin{eqnarray}\operatorname{Cht}_{G,I,W}\leftarrow \operatorname{Cht}_{P,I,W}\rightarrow \operatorname{Cht}_{M,I,W}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{G,I,W}\leftarrow \operatorname{Cht}_{P,I,W}\rightarrow \operatorname{Cht}_{M,I,W}\!.\end{eqnarray}$$From this we construct a constant term morphism
 $$\begin{eqnarray}C_{G}^{P,\,j}:H_{G,I,W}^{j}\rightarrow H_{M,I,W}^{j}.\end{eqnarray}$$
$$\begin{eqnarray}C_{G}^{P,\,j}:H_{G,I,W}^{j}\rightarrow H_{M,I,W}^{j}.\end{eqnarray}$$ Then we define the cuspidal cohomology  $H_{G,I,W}^{j,\;\operatorname{cusp}}\subset H_{G,I,W}^{j}$ as the intersection of the kernels of the constant term morphisms for all proper parabolic subgroups.
$H_{G,I,W}^{j,\;\operatorname{cusp}}\subset H_{G,I,W}^{j}$ as the intersection of the kernels of the constant term morphisms for all proper parabolic subgroups.
This construction was suggested by Vincent Lafforgue. He also conjectured the following.
– The cuspidal cohomology is of finite dimension.
– The following three
 $\mathbb{Q}_{\ell }$-vector subspaces of
$\mathbb{Q}_{\ell }$-vector subspaces of  $H_{G,I,W}^{j}$ are equal:
$H_{G,I,W}^{j}$ are equal:  $$\begin{eqnarray}H_{G,I,W}^{j,\;\operatorname{Hf}}=H_{G,I,W}^{j,\;\operatorname{Hf-rat}}=H_{G,I,W}^{j,\;\operatorname{cusp}}.\end{eqnarray}$$
$$\begin{eqnarray}H_{G,I,W}^{j,\;\operatorname{Hf}}=H_{G,I,W}^{j,\;\operatorname{Hf-rat}}=H_{G,I,W}^{j,\;\operatorname{cusp}}.\end{eqnarray}$$
In this paper, we prove these conjectures except for the equality with  $H_{G,I,W}^{j,\;\operatorname{Hf}}$, which we plan to treat in a future paper. The main results are as follows.
$H_{G,I,W}^{j,\;\operatorname{Hf}}$, which we plan to treat in a future paper. The main results are as follows.
Theorem 0.0.1 (Theorem 5.0.1).
The  $\mathbb{Q}_{\ell }$-vector space
$\mathbb{Q}_{\ell }$-vector space  $H_{G,I,W}^{j,\;\operatorname{cusp}}$ has finite dimension.
$H_{G,I,W}^{j,\;\operatorname{cusp}}$ has finite dimension.
Proposition 0.0.2 (Proposition 6.0.1).
The two  $\mathbb{Q}_{\ell }$-vector subspaces
$\mathbb{Q}_{\ell }$-vector subspaces  $H_{G,I,W}^{j,\;\operatorname{cusp}}$ and
$H_{G,I,W}^{j,\;\operatorname{cusp}}$ and  $H_{G,I,W}^{j,\;\operatorname{Hf-rat}}$ of
$H_{G,I,W}^{j,\;\operatorname{Hf-rat}}$ of  $H_{G,I,W}^{j}$ are equal.
$H_{G,I,W}^{j}$ are equal.
As a consequence,  $H_{G,I,W}^{j,\;\operatorname{Hf}}$ has finite dimension.
$H_{G,I,W}^{j,\;\operatorname{Hf}}$ has finite dimension.
In particular, when  $I=\emptyset$ and
$I=\emptyset$ and  $W=\mathbf{1}$, the constant term morphism
$W=\mathbf{1}$, the constant term morphism  $C_{G}^{P,\,0}$ coincides with the usual constant term morphism for automorphic forms. In this case, Theorem 0.0.1 coincides with Theorem 1.2.1 in [Reference HarderHar74], and Proposition 0.0.2 coincides with [Reference LafforgueLaf18, Proposition 8.23] mentioned before.
$C_{G}^{P,\,0}$ coincides with the usual constant term morphism for automorphic forms. In this case, Theorem 0.0.1 coincides with Theorem 1.2.1 in [Reference HarderHar74], and Proposition 0.0.2 coincides with [Reference LafforgueLaf18, Proposition 8.23] mentioned before.
Let  $N\subset X$ be a finite subscheme. Theorem 0.0.1 and Proposition 0.0.2 are still true for the cohomology with level structure on
$N\subset X$ be a finite subscheme. Theorem 0.0.1 and Proposition 0.0.2 are still true for the cohomology with level structure on  $N$.
$N$.
Structure of the paper
In §1 we construct the parabolic induction diagram and define Harder–Narasimhan truncations which are compatible with the parabolic induction. In §2 we recall the cohomology of the stacks of  $G$-shtukas and define the cohomology of the stacks of
$G$-shtukas and define the cohomology of the stacks of  $M$-shtukas. In §3 we construct the constant term morphism using the compatibility of the geometric Satake equivalence with the constant term functors for the Beilinson–Drinfeld affine grassmannians.
$M$-shtukas. In §3 we construct the constant term morphism using the compatibility of the geometric Satake equivalence with the constant term functors for the Beilinson–Drinfeld affine grassmannians.
The idea of the proofs of Theorem 0.0.1 and Proposition 0.0.2 is analogous to the case of automorphic forms. The goal of §§4 and 5 is to prove Theorem 0.0.1. In §4 we prove the contractibility of deep enough horospheres. In §5 we use this result and an argument by induction on the semisimple rank to prove the finiteness of cuspidal cohomology. In §6 we show that the constant term morphism commutes with the action of the Hecke algebra, and we prove Proposition 0.0.2.
Notation and conventions
0.0.3
Let  $G$ be a connected split reductive group over
$G$ be a connected split reductive group over  $\mathbb{F}_{q}$. Let
$\mathbb{F}_{q}$. Let  $G^{\text{der}}$ be the derived group of
$G^{\text{der}}$ be the derived group of  $G$ and
$G$ and  $G^{\text{ab}}:=G/G^{\text{der}}$ the abelianization of
$G^{\text{ab}}:=G/G^{\text{der}}$ the abelianization of  $G$. Let
$G$. Let  $Z_{G}$ be the center of
$Z_{G}$ be the center of  $G$ and
$G$ and  $G^{\text{ad}}$ the adjoint group of
$G^{\text{ad}}$ the adjoint group of  $G$ (equal to
$G$ (equal to  $G/Z_{G}$).
$G/Z_{G}$).
0.0.4
We fix a discrete subgroup  $\unicode[STIX]{x1D6EF}_{G}$ of
$\unicode[STIX]{x1D6EF}_{G}$ of  $Z_{G}(\mathbb{A})$ such that
$Z_{G}(\mathbb{A})$ such that  $\unicode[STIX]{x1D6EF}_{G}\cap Z_{G}(\mathbb{O})Z_{G}(F)=\{1\}$, the quotient
$\unicode[STIX]{x1D6EF}_{G}\cap Z_{G}(\mathbb{O})Z_{G}(F)=\{1\}$, the quotient  $Z_{G}(F)\backslash Z_{G}(\mathbb{A})/Z_{G}(\mathbb{O})\unicode[STIX]{x1D6EF}_{G}$ is finite and the composition of morphisms
$Z_{G}(F)\backslash Z_{G}(\mathbb{A})/Z_{G}(\mathbb{O})\unicode[STIX]{x1D6EF}_{G}$ is finite and the composition of morphisms  $\unicode[STIX]{x1D6EF}_{G}{\hookrightarrow}Z_{G}(\mathbb{A}){\hookrightarrow}G(\mathbb{A}){\twoheadrightarrow}G^{\text{ab}}(\mathbb{A})$ is injective. Note that the volume of
$\unicode[STIX]{x1D6EF}_{G}{\hookrightarrow}Z_{G}(\mathbb{A}){\hookrightarrow}G(\mathbb{A}){\twoheadrightarrow}G^{\text{ab}}(\mathbb{A})$ is injective. Note that the volume of  $G(F)\backslash G(\mathbb{A})/G(\mathbb{O})\unicode[STIX]{x1D6EF}_{G}$ is finite. We write
$G(F)\backslash G(\mathbb{A})/G(\mathbb{O})\unicode[STIX]{x1D6EF}_{G}$ is finite. We write  $\unicode[STIX]{x1D6EF}:=\unicode[STIX]{x1D6EF}_{G}$.
$\unicode[STIX]{x1D6EF}:=\unicode[STIX]{x1D6EF}_{G}$.
0.0.5
We fix a Borel subgroup  $B\subset G$. By a parabolic subgroup we will mean a standard parabolic subgroup (i.e. a parabolic subgroup containing
$B\subset G$. By a parabolic subgroup we will mean a standard parabolic subgroup (i.e. a parabolic subgroup containing  $B$), unless explicitly stated otherwise.
$B$), unless explicitly stated otherwise.
0.0.6
Let  $H$ be a connected split reductive group over
$H$ be a connected split reductive group over  $\mathbb{F}_{q}$ with a fixed Borel subgroup. Let
$\mathbb{F}_{q}$ with a fixed Borel subgroup. Let  $\unicode[STIX]{x1D6EC}_{H}$ (respectively
$\unicode[STIX]{x1D6EC}_{H}$ (respectively  $\widehat{\unicode[STIX]{x1D6EC}}_{H}$) denote the weight (respectively coweight) lattice of
$\widehat{\unicode[STIX]{x1D6EC}}_{H}$) denote the weight (respectively coweight) lattice of  $H$. Let
$H$. Let  $\langle ~,~\rangle :\widehat{\unicode[STIX]{x1D6EC}}_{H}\times \unicode[STIX]{x1D6EC}_{H}\rightarrow \mathbb{Z}$ denote the natural pairing between the two.
$\langle ~,~\rangle :\widehat{\unicode[STIX]{x1D6EC}}_{H}\times \unicode[STIX]{x1D6EC}_{H}\rightarrow \mathbb{Z}$ denote the natural pairing between the two.
Let  $\widehat{\unicode[STIX]{x1D6EC}}_{H}^{+}\subset \widehat{\unicode[STIX]{x1D6EC}}_{H}$ denote the monoid of dominant coweights and
$\widehat{\unicode[STIX]{x1D6EC}}_{H}^{+}\subset \widehat{\unicode[STIX]{x1D6EC}}_{H}$ denote the monoid of dominant coweights and  $\widehat{\unicode[STIX]{x1D6EC}}_{H}^{\text{pos}}\subset \widehat{\unicode[STIX]{x1D6EC}}_{H}$ the monoid generated by positive simple coroots. Let
$\widehat{\unicode[STIX]{x1D6EC}}_{H}^{\text{pos}}\subset \widehat{\unicode[STIX]{x1D6EC}}_{H}$ the monoid generated by positive simple coroots. Let  $\widehat{\unicode[STIX]{x1D6EC}}_{H}^{\mathbb{Q}}:=\widehat{\unicode[STIX]{x1D6EC}}_{H}\underset{\mathbb{Z}}{\otimes }\mathbb{Q}$. Let
$\widehat{\unicode[STIX]{x1D6EC}}_{H}^{\mathbb{Q}}:=\widehat{\unicode[STIX]{x1D6EC}}_{H}\underset{\mathbb{Z}}{\otimes }\mathbb{Q}$. Let  $\widehat{\unicode[STIX]{x1D6EC}}_{H}^{\text{pos},\mathbb{Q}}$ and
$\widehat{\unicode[STIX]{x1D6EC}}_{H}^{\text{pos},\mathbb{Q}}$ and  $\widehat{\unicode[STIX]{x1D6EC}}_{H}^{+,\mathbb{Q}}$ denote the rational cones of
$\widehat{\unicode[STIX]{x1D6EC}}_{H}^{+,\mathbb{Q}}$ denote the rational cones of  $\widehat{\unicode[STIX]{x1D6EC}}_{H}^{\text{pos}}$ and
$\widehat{\unicode[STIX]{x1D6EC}}_{H}^{\text{pos}}$ and  $\widehat{\unicode[STIX]{x1D6EC}}_{H}^{+}$. We use analogous notation for the weight lattice.
$\widehat{\unicode[STIX]{x1D6EC}}_{H}^{+}$. We use analogous notation for the weight lattice.
We use the partial order on  $\widehat{\unicode[STIX]{x1D6EC}}_{H}^{\mathbb{Q}}$ defined by
$\widehat{\unicode[STIX]{x1D6EC}}_{H}^{\mathbb{Q}}$ defined by  $\unicode[STIX]{x1D707}_{1}\leqslant \text{}^{H}\unicode[STIX]{x1D707}_{2}\Leftrightarrow \unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D707}_{1}\in \widehat{\unicode[STIX]{x1D6EC}}_{H}^{\text{pos},\mathbb{Q}}$ (i.e.
$\unicode[STIX]{x1D707}_{1}\leqslant \text{}^{H}\unicode[STIX]{x1D707}_{2}\Leftrightarrow \unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D707}_{1}\in \widehat{\unicode[STIX]{x1D6EC}}_{H}^{\text{pos},\mathbb{Q}}$ (i.e.  $\unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D707}_{1}$ is a linear combination of simple coroots of
$\unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D707}_{1}$ is a linear combination of simple coroots of  $H$ with coefficients in
$H$ with coefficients in  $\mathbb{Q}_{{\geqslant}0}$).
$\mathbb{Q}_{{\geqslant}0}$).
We will apply these notations to  $H=G$,
$H=G$,  $H=G^{\text{ad}}$ or
$H=G^{\text{ad}}$ or  $H=$ some Levi quotient
$H=$ some Levi quotient  $M$ of
$M$ of  $G$.
$G$.
0.0.7
We denote by  $\unicode[STIX]{x1D6E4}_{G}$ the set of simple roots of
$\unicode[STIX]{x1D6E4}_{G}$ the set of simple roots of  $G$ and by
$G$ and by  $\widehat{\unicode[STIX]{x1D6E4}}_{G}$ the set of simple coroots. The standard parabolic subgroups of
$\widehat{\unicode[STIX]{x1D6E4}}_{G}$ the set of simple coroots. The standard parabolic subgroups of  $G$ are in bijection with the subsets of
$G$ are in bijection with the subsets of  $\unicode[STIX]{x1D6E4}_{G}$ in the following way. To a parabolic subgroup
$\unicode[STIX]{x1D6E4}_{G}$ in the following way. To a parabolic subgroup  $P$ with Levi quotient
$P$ with Levi quotient  $M$, we associate the subset
$M$, we associate the subset  $\unicode[STIX]{x1D6E4}_{M}$ in
$\unicode[STIX]{x1D6E4}_{M}$ in  $\unicode[STIX]{x1D6E4}_{G}$ equal to the set of simple roots of
$\unicode[STIX]{x1D6E4}_{G}$ equal to the set of simple roots of  $M$.
$M$.
0.0.8
Let  $N\subset X$ be a finite subscheme. We denote by
$N\subset X$ be a finite subscheme. We denote by  ${\mathcal{O}}_{N}$ the ring of functions on
${\mathcal{O}}_{N}$ the ring of functions on  $N$ and write
$N$ and write  $K_{G,N}:=\operatorname{Ker}(G(\mathbb{O})\rightarrow G({\mathcal{O}}_{N}))$.
$K_{G,N}:=\operatorname{Ker}(G(\mathbb{O})\rightarrow G({\mathcal{O}}_{N}))$.
Let  $H$ be an algebraic group over
$H$ be an algebraic group over  $\mathbb{F}_{q}$. We denote by
$\mathbb{F}_{q}$. We denote by  $H_{N}$ the Weil restriction
$H_{N}$ the Weil restriction  $\operatorname{Res}_{{\mathcal{O}}_{N}/\mathbb{F}_{q}}H$.
$\operatorname{Res}_{{\mathcal{O}}_{N}/\mathbb{F}_{q}}H$.
0.0.9
If not specified, all schemes are defined over  $\mathbb{F}_{q}$ and all the fiber products are taken over
$\mathbb{F}_{q}$ and all the fiber products are taken over  $\mathbb{F}_{q}$.
$\mathbb{F}_{q}$.
0.0.10
For any scheme  $S$ over
$S$ over  $\mathbb{F}_{q}$ and
$\mathbb{F}_{q}$ and  $x$ an
$x$ an  $S$-point of
$S$-point of  $X$, we denote by
$X$, we denote by  $\unicode[STIX]{x1D6E4}_{x}\subset X\times S$ the graph of
$\unicode[STIX]{x1D6E4}_{x}\subset X\times S$ the graph of  $x$.
$x$.
0.0.11
For any scheme  $S$ over
$S$ over  $\mathbb{F}_{q}$, we denote by
$\mathbb{F}_{q}$, we denote by  $\operatorname{Frob}_{S}:S\rightarrow S$ the Frobenius morphism over
$\operatorname{Frob}_{S}:S\rightarrow S$ the Frobenius morphism over  $\mathbb{F}_{q}$. For any
$\mathbb{F}_{q}$. For any  $G$-bundle
$G$-bundle  ${\mathcal{G}}$ on
${\mathcal{G}}$ on  $X\times S$, we denote by
$X\times S$, we denote by  $^{\unicode[STIX]{x1D70F}}{\mathcal{G}}$ the
$^{\unicode[STIX]{x1D70F}}{\mathcal{G}}$ the  $G$-bundle
$G$-bundle  $(\operatorname{Id}_{X}\times _{\mathbb{F}_{q}}\operatorname{Frob}_{S})^{\ast }{\mathcal{G}}$.
$(\operatorname{Id}_{X}\times _{\mathbb{F}_{q}}\operatorname{Frob}_{S})^{\ast }{\mathcal{G}}$.
0.0.12
We use [Reference Laumon and Moret-BaillyLMB99, Definitions 3.1 and 4.1] for prestacks, stacks and algebraic stacks.
0.0.13
As in [Reference Laumon and Moret-BaillyLMB99, §18], [Reference Laszlo and OlssonLO08] and [Reference Laszlo and OlssonLO09], for  ${\mathcal{X}}$ an algebraic stack locally of finite type over
${\mathcal{X}}$ an algebraic stack locally of finite type over  $\mathbb{F}_{q}$, we denote by
$\mathbb{F}_{q}$, we denote by  $D_{c}^{b}({\mathcal{X}},\mathbb{Q}_{\ell })$ the bounded derived category of constructible
$D_{c}^{b}({\mathcal{X}},\mathbb{Q}_{\ell })$ the bounded derived category of constructible  $\ell$-adic sheaves on
$\ell$-adic sheaves on  ${\mathcal{X}}$. We have the notion of six operators and perverse sheaves.
${\mathcal{X}}$. We have the notion of six operators and perverse sheaves.
If  $f:{\mathcal{X}}_{1}\rightarrow {\mathcal{X}}_{2}$ is a morphism of finite type of schemes (respectively algebraic stacks) locally of finite type, we will denote by
$f:{\mathcal{X}}_{1}\rightarrow {\mathcal{X}}_{2}$ is a morphism of finite type of schemes (respectively algebraic stacks) locally of finite type, we will denote by  $f_{!}$,
$f_{!}$,  $f_{\ast }$,
$f_{\ast }$,  $f^{\ast }$,
$f^{\ast }$,  $f^{!}$ the corresponding functors between
$f^{!}$ the corresponding functors between  $D_{c}^{b}({\mathcal{X}}_{1},\mathbb{Q}_{\ell })$ and
$D_{c}^{b}({\mathcal{X}}_{1},\mathbb{Q}_{\ell })$ and  $D_{c}^{b}({\mathcal{X}}_{2},\mathbb{Q}_{\ell })$, always understood in the derived sense.
$D_{c}^{b}({\mathcal{X}}_{2},\mathbb{Q}_{\ell })$, always understood in the derived sense.
0.0.14
We will work with étale cohomology. So for any stack (respectively scheme) (for example  $\operatorname{Cht}_{G,N,I,W}$ and
$\operatorname{Cht}_{G,N,I,W}$ and  $\operatorname{Gr}_{G,I,W}$), we consider only the reduced substack (respectively subscheme) associated to it.
$\operatorname{Gr}_{G,I,W}$), we consider only the reduced substack (respectively subscheme) associated to it.
1 Parabolic induction diagram of stacks of shtukas
The goal of this section is to introduce the parabolic induction diagram of stacks of shtukas without a bound on the modifications at paws in §§1.1–1.3 and to introduce the Harder–Narasimhan stratification for the parabolic induction diagram in §§1.4–1.7.
In §§1.1–1.3 we work in the context of prestacks (see 0.0.12).
1.1 Reminder of stacks of shtukas and Beilinson–Drinfeld affine grassmannians
This subsection is based on [Reference VarshavskyVar04, §2] and [Reference LafforgueLaf18, §§1 and 2]. All the results are well known.
Definition 1.1.1. We define  $\operatorname{Bun}_{G,N}$ to be the prestack that associates to any affine scheme
$\operatorname{Bun}_{G,N}$ to be the prestack that associates to any affine scheme  $S$ over
$S$ over  $\mathbb{F}_{q}$ the groupoid
$\mathbb{F}_{q}$ the groupoid

1.1.2
 $\operatorname{Bun}_{G,N}$ is a smooth algebraic stack over
$\operatorname{Bun}_{G,N}$ is a smooth algebraic stack over  $\mathbb{F}_{q}$, locally of finite type.
$\mathbb{F}_{q}$, locally of finite type.
Definition 1.1.3. We define  $\operatorname{Hecke}_{G,N,I}$ to be the prestack that associates to any affine scheme
$\operatorname{Hecke}_{G,N,I}$ to be the prestack that associates to any affine scheme  $S$ over
$S$ over  $\mathbb{F}_{q}$ the groupoid
$\mathbb{F}_{q}$ the groupoid  $\operatorname{Hecke}_{G,N,I}(S)$ that classifies the following data:
$\operatorname{Hecke}_{G,N,I}(S)$ that classifies the following data:
(i)
 $(x_{i})_{i\in I}\in (X\smallsetminus N)^{I}(S)$;
$(x_{i})_{i\in I}\in (X\smallsetminus N)^{I}(S)$;(ii)
 $({\mathcal{G}},\unicode[STIX]{x1D713}),({\mathcal{G}}^{\prime },\unicode[STIX]{x1D713}^{\prime })\in \operatorname{Bun}_{G,N}(S)$;
$({\mathcal{G}},\unicode[STIX]{x1D713}),({\mathcal{G}}^{\prime },\unicode[STIX]{x1D713}^{\prime })\in \operatorname{Bun}_{G,N}(S)$;(iii) an isomorphism of
 $G$-bundles
$G$-bundles  $\unicode[STIX]{x1D719}:\left.{\mathcal{G}}\vphantom{\big|}\right|_{(X\times S)\smallsetminus (\bigcup _{i\in I}\unicode[STIX]{x1D6E4}_{x_{i}})}\overset{{\sim}}{\rightarrow }\left.{\mathcal{G}}^{\prime }\vphantom{\big|}\right|_{(X\times S)\smallsetminus (\bigcup _{i\in I}\unicode[STIX]{x1D6E4}_{x_{i}})}$ which preserves the
$\unicode[STIX]{x1D719}:\left.{\mathcal{G}}\vphantom{\big|}\right|_{(X\times S)\smallsetminus (\bigcup _{i\in I}\unicode[STIX]{x1D6E4}_{x_{i}})}\overset{{\sim}}{\rightarrow }\left.{\mathcal{G}}^{\prime }\vphantom{\big|}\right|_{(X\times S)\smallsetminus (\bigcup _{i\in I}\unicode[STIX]{x1D6E4}_{x_{i}})}$ which preserves the  $N$-level structure, i.e.
$N$-level structure, i.e.  $\unicode[STIX]{x1D713}^{\prime }\circ \left.\unicode[STIX]{x1D719}\vphantom{\big|}\right|_{N\times S}=\unicode[STIX]{x1D713}$.
$\unicode[STIX]{x1D713}^{\prime }\circ \left.\unicode[STIX]{x1D719}\vphantom{\big|}\right|_{N\times S}=\unicode[STIX]{x1D713}$.
1.1.4
The prestack  $\operatorname{Hecke}_{G,N,I}$ is an inductive limit of algebraic stacks over
$\operatorname{Hecke}_{G,N,I}$ is an inductive limit of algebraic stacks over  $(X\smallsetminus N)^{I}$. We define the morphism of paws
$(X\smallsetminus N)^{I}$. We define the morphism of paws  $\operatorname{Hecke}_{G,N,I}\rightarrow (X\smallsetminus N)^{I}$ by sending
$\operatorname{Hecke}_{G,N,I}\rightarrow (X\smallsetminus N)^{I}$ by sending  $((x_{i})_{i\in I},({\mathcal{G}},\unicode[STIX]{x1D713})\xrightarrow[{}]{\unicode[STIX]{x1D719}}({\mathcal{G}}^{\prime },\unicode[STIX]{x1D713}^{\prime }))$ to
$((x_{i})_{i\in I},({\mathcal{G}},\unicode[STIX]{x1D713})\xrightarrow[{}]{\unicode[STIX]{x1D719}}({\mathcal{G}}^{\prime },\unicode[STIX]{x1D713}^{\prime }))$ to  $(x_{i})_{i\in I}$.
$(x_{i})_{i\in I}$.
1.1.5
We denote by  $\operatorname{pr}_{0}$ (respectively
$\operatorname{pr}_{0}$ (respectively  $\operatorname{pr}_{1}$) the projection
$\operatorname{pr}_{1}$) the projection  $\operatorname{Hecke}_{G,N,I}\rightarrow \operatorname{Bun}_{G,N}$ which sends
$\operatorname{Hecke}_{G,N,I}\rightarrow \operatorname{Bun}_{G,N}$ which sends  $((x_{i})_{i\in I},({\mathcal{G}},\unicode[STIX]{x1D713})\xrightarrow[{}]{\unicode[STIX]{x1D719}}({\mathcal{G}}^{\prime },\unicode[STIX]{x1D713}^{\prime }))$ to
$((x_{i})_{i\in I},({\mathcal{G}},\unicode[STIX]{x1D713})\xrightarrow[{}]{\unicode[STIX]{x1D719}}({\mathcal{G}}^{\prime },\unicode[STIX]{x1D713}^{\prime }))$ to  $({\mathcal{G}},\unicode[STIX]{x1D713})$ (respectively to
$({\mathcal{G}},\unicode[STIX]{x1D713})$ (respectively to  $({\mathcal{G}}^{\prime },\unicode[STIX]{x1D713}^{\prime })$).
$({\mathcal{G}}^{\prime },\unicode[STIX]{x1D713}^{\prime })$).
Let  $\operatorname{Frob}:\operatorname{Bun}_{G,N}\rightarrow \operatorname{Bun}_{G,N}$ be the Frobenius morphism over
$\operatorname{Frob}:\operatorname{Bun}_{G,N}\rightarrow \operatorname{Bun}_{G,N}$ be the Frobenius morphism over  $\mathbb{F}_{q}$. With the notation in 0.0.11, for any affine scheme
$\mathbb{F}_{q}$. With the notation in 0.0.11, for any affine scheme  $S$ over
$S$ over  $\mathbb{F}_{q}$, the morphism
$\mathbb{F}_{q}$, the morphism  $\operatorname{Frob}:\operatorname{Bun}_{G,N}(S)\rightarrow \operatorname{Bun}_{G,N}(S)$ is given by
$\operatorname{Frob}:\operatorname{Bun}_{G,N}(S)\rightarrow \operatorname{Bun}_{G,N}(S)$ is given by  $({\mathcal{G}},\unicode[STIX]{x1D713})\rightarrow (\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}},^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713})$.
$({\mathcal{G}},\unicode[STIX]{x1D713})\rightarrow (\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}},^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713})$.
Definition 1.1.6. We define the prestack of shtukas  $\operatorname{Cht}_{G,N,I}$ to be the following fiber product.
$\operatorname{Cht}_{G,N,I}$ to be the following fiber product.

1.1.7
Concretely,  $\operatorname{Cht}_{G,N,I}$ is the prestack which associates to any affine scheme
$\operatorname{Cht}_{G,N,I}$ is the prestack which associates to any affine scheme  $S$ over
$S$ over  $\mathbb{F}_{q}$ the groupoid
$\mathbb{F}_{q}$ the groupoid  $\operatorname{Cht}_{G,N,I}(S)$ classifying the following data:
$\operatorname{Cht}_{G,N,I}(S)$ classifying the following data:
(i)
 $(x_{i})_{i\in I}\in (X\smallsetminus N)^{I}(S)$;
$(x_{i})_{i\in I}\in (X\smallsetminus N)^{I}(S)$;(ii)
 $({\mathcal{G}},\unicode[STIX]{x1D713})\in \operatorname{Bun}_{G,N}(S)$;
$({\mathcal{G}},\unicode[STIX]{x1D713})\in \operatorname{Bun}_{G,N}(S)$;(iii) an isomorphism of
 $G$-bundles
$G$-bundles  $\unicode[STIX]{x1D719}:\left.{\mathcal{G}}\vphantom{\big|}\right|_{(X\times S)\smallsetminus (\bigcup _{i\in I}\unicode[STIX]{x1D6E4}_{x_{i}})}\overset{{\sim}}{\rightarrow }\left.\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}}\vphantom{\big|}\right|_{(X\times S)\smallsetminus (\bigcup _{i\in I}\unicode[STIX]{x1D6E4}_{x_{i}})}$ which preserves the
$\unicode[STIX]{x1D719}:\left.{\mathcal{G}}\vphantom{\big|}\right|_{(X\times S)\smallsetminus (\bigcup _{i\in I}\unicode[STIX]{x1D6E4}_{x_{i}})}\overset{{\sim}}{\rightarrow }\left.\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}}\vphantom{\big|}\right|_{(X\times S)\smallsetminus (\bigcup _{i\in I}\unicode[STIX]{x1D6E4}_{x_{i}})}$ which preserves the  $N$-level structure, i.e.
$N$-level structure, i.e.  $^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}\circ \left.\unicode[STIX]{x1D719}\vphantom{\big|}\right|_{N\times S}=\unicode[STIX]{x1D713}$.
$^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}\circ \left.\unicode[STIX]{x1D719}\vphantom{\big|}\right|_{N\times S}=\unicode[STIX]{x1D713}$.
We define the morphism of paws  $\mathfrak{p}_{G}:\operatorname{Cht}_{G,N,I}\rightarrow (X\smallsetminus N)^{I}$ by sending
$\mathfrak{p}_{G}:\operatorname{Cht}_{G,N,I}\rightarrow (X\smallsetminus N)^{I}$ by sending  $((x_{i})_{i\in I},({\mathcal{G}},\unicode[STIX]{x1D713})\xrightarrow[{}]{\unicode[STIX]{x1D719}}(\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}},^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}))$ to
$((x_{i})_{i\in I},({\mathcal{G}},\unicode[STIX]{x1D713})\xrightarrow[{}]{\unicode[STIX]{x1D719}}(\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}},^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}))$ to  $(x_{i})_{i\in I}$.
$(x_{i})_{i\in I}$.
1.1.8
The prestack  $\operatorname{Cht}_{G,N,I}$ is an inductive limit of algebraic stacks over
$\operatorname{Cht}_{G,N,I}$ is an inductive limit of algebraic stacks over  $(X\smallsetminus N)^{I}$.
$(X\smallsetminus N)^{I}$.
1.1.9
We will omit the index  $N$ if
$N$ if  $N=\emptyset$.
$N=\emptyset$.
We will need a local model of  $\operatorname{Cht}_{G,N,I}$. For this, we recall the definition of Beilinson–Drinfeld affine grassmannians.
$\operatorname{Cht}_{G,N,I}$. For this, we recall the definition of Beilinson–Drinfeld affine grassmannians.
1.1.10
For  $(x_{i})_{i\in I}\in X^{I}(S)$,
$(x_{i})_{i\in I}\in X^{I}(S)$,  $d\in \mathbb{N}$, we denote by
$d\in \mathbb{N}$, we denote by  $\unicode[STIX]{x1D6E4}_{\sum dx_{i}}$ the closed subscheme of
$\unicode[STIX]{x1D6E4}_{\sum dx_{i}}$ the closed subscheme of  $X\times S$ whose ideal is generated by
$X\times S$ whose ideal is generated by  $(\prod _{i\in I}t_{i})^{d}$ locally for the Zariski topology, where
$(\prod _{i\in I}t_{i})^{d}$ locally for the Zariski topology, where  $t_{i}$ is an equation of the graph
$t_{i}$ is an equation of the graph  $\unicode[STIX]{x1D6E4}_{x_{i}}$. We define
$\unicode[STIX]{x1D6E4}_{x_{i}}$. We define  $\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}:=\mathop{\varinjlim }\nolimits_{d}\unicode[STIX]{x1D6E4}_{\sum dx_{i}}$ to be the formal neighborhood of
$\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}:=\mathop{\varinjlim }\nolimits_{d}\unicode[STIX]{x1D6E4}_{\sum dx_{i}}$ to be the formal neighborhood of  $\bigcup _{i\in I}\unicode[STIX]{x1D6E4}_{x_{i}}$ in
$\bigcup _{i\in I}\unicode[STIX]{x1D6E4}_{x_{i}}$ in  $X\times S$.
$X\times S$.
A  $G$-bundle on
$G$-bundle on  $\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}$ is a projective limit of
$\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}$ is a projective limit of  $G$-bundles on
$G$-bundles on  $\unicode[STIX]{x1D6E4}_{\sum dx_{i}}$ as
$\unicode[STIX]{x1D6E4}_{\sum dx_{i}}$ as  $d\rightarrow \infty$.
$d\rightarrow \infty$.
Definition 1.1.11. We define the Beilinson–Drinfeld affine grassmannian  $\operatorname{Gr}_{G,I}$ to be the ind-scheme that associates to any affine scheme
$\operatorname{Gr}_{G,I}$ to be the ind-scheme that associates to any affine scheme  $S$ over
$S$ over  $\mathbb{F}_{q}$ the set
$\mathbb{F}_{q}$ the set  $\operatorname{Gr}_{G,I}(S)$ classifying the following data:
$\operatorname{Gr}_{G,I}(S)$ classifying the following data:
(i)
 $(x_{i})_{i\in I}\in X^{I}(S)$;
$(x_{i})_{i\in I}\in X^{I}(S)$;(ii)
 ${\mathcal{G}},{\mathcal{G}}^{\prime }$ two
${\mathcal{G}},{\mathcal{G}}^{\prime }$ two  $G$-bundles on
$G$-bundles on  $\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}$;
$\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}$;(iii) an isomorphism of
 $G$-bundles
$G$-bundles  $\unicode[STIX]{x1D719}:\left.{\mathcal{G}}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}\smallsetminus (\bigcup _{i\in I}\unicode[STIX]{x1D6E4}_{x_{i}})}\overset{{\sim}}{\rightarrow }\left.{\mathcal{G}}^{\prime }\vphantom{\big|}\right|_{\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}\smallsetminus (\bigcup _{i\in I}\unicode[STIX]{x1D6E4}_{x_{i}})}$ where the precise meaning is given in [Reference LafforgueLaf18, Notation 1.7];
$\unicode[STIX]{x1D719}:\left.{\mathcal{G}}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}\smallsetminus (\bigcup _{i\in I}\unicode[STIX]{x1D6E4}_{x_{i}})}\overset{{\sim}}{\rightarrow }\left.{\mathcal{G}}^{\prime }\vphantom{\big|}\right|_{\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}\smallsetminus (\bigcup _{i\in I}\unicode[STIX]{x1D6E4}_{x_{i}})}$ where the precise meaning is given in [Reference LafforgueLaf18, Notation 1.7];(iv) a trivialization
 $\unicode[STIX]{x1D703}:{\mathcal{G}}^{\prime }\overset{{\sim}}{\rightarrow }G$ on
$\unicode[STIX]{x1D703}:{\mathcal{G}}^{\prime }\overset{{\sim}}{\rightarrow }G$ on  $\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}$.
$\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}$.
1.1.12
We have the morphism of paws:  $\operatorname{Gr}_{G,I}\rightarrow X^{I}$. The fiber over
$\operatorname{Gr}_{G,I}\rightarrow X^{I}$. The fiber over  $(x_{i})_{i\in I}\in X_{\overline{\mathbb{F}_{q}}}^{I}$ is
$(x_{i})_{i\in I}\in X_{\overline{\mathbb{F}_{q}}}^{I}$ is  $\prod _{y\in \{x_{i}|i\in I\}}\operatorname{Gr}_{G,y}$, where
$\prod _{y\in \{x_{i}|i\in I\}}\operatorname{Gr}_{G,y}$, where  $\operatorname{Gr}_{G,y}$ is the usual affine grassmannian, i.e. the fpqc quotient
$\operatorname{Gr}_{G,y}$ is the usual affine grassmannian, i.e. the fpqc quotient  $G_{{\mathcal{K}}_{y}}/G_{{\mathcal{O}}_{y}}$, where
$G_{{\mathcal{K}}_{y}}/G_{{\mathcal{O}}_{y}}$, where  ${\mathcal{O}}_{y}$ is the complete local ring on
${\mathcal{O}}_{y}$ is the complete local ring on  $y$ and
$y$ and  ${\mathcal{K}}_{y}$ is its field of fractions.
${\mathcal{K}}_{y}$ is its field of fractions.
(a) For any
 $d\in \mathbb{N}$, we define
$d\in \mathbb{N}$, we define  $G_{I,d}$ to be the group scheme over
$G_{I,d}$ to be the group scheme over  $X^{I}$ that associates to any affine scheme
$X^{I}$ that associates to any affine scheme  $S$ over
$S$ over  $\mathbb{F}_{q}$ the set consisting of pairs
$\mathbb{F}_{q}$ the set consisting of pairs  $((x_{i})_{i\in I},f)$, where
$((x_{i})_{i\in I},f)$, where  $(x_{i})_{i\in I}\in X^{I}(S)$ and
$(x_{i})_{i\in I}\in X^{I}(S)$ and  $f$ is an automorphism of the trivial
$f$ is an automorphism of the trivial  $G$-bundle on
$G$-bundle on  $\unicode[STIX]{x1D6E4}_{\sum dx_{i}}$.
$\unicode[STIX]{x1D6E4}_{\sum dx_{i}}$.(b) We define the group scheme
 $G_{I,\infty }:=\underset{\longleftarrow }{\lim }\,G_{I,d}$.
$G_{I,\infty }:=\underset{\longleftarrow }{\lim }\,G_{I,d}$.
1.1.14
The fiber of  $G_{I,\infty }$ over
$G_{I,\infty }$ over  $(x_{i})_{i\in I}\in X_{\overline{\mathbb{F}_{q}}}^{I}$ is
$(x_{i})_{i\in I}\in X_{\overline{\mathbb{F}_{q}}}^{I}$ is  $\prod _{y\in \{x_{i}|i\in I\}}G_{{\mathcal{O}}_{y}}$.
$\prod _{y\in \{x_{i}|i\in I\}}G_{{\mathcal{O}}_{y}}$.
1.1.15
The group scheme  $G_{I,\infty }$ acts on
$G_{I,\infty }$ acts on  $\operatorname{Gr}_{G,I}$ by changing the trivialization
$\operatorname{Gr}_{G,I}$ by changing the trivialization  $\unicode[STIX]{x1D703}$. We denote by
$\unicode[STIX]{x1D703}$. We denote by  $[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}]$ the quotient prestack. For any affine scheme
$[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}]$ the quotient prestack. For any affine scheme  $S$ over
$S$ over  $\mathbb{F}_{q}$,
$\mathbb{F}_{q}$,  $[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}](S)$ is the groupoid classifying the data (i), (ii) and (iii) in Definition 1.1.11.
$[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}](S)$ is the groupoid classifying the data (i), (ii) and (iii) in Definition 1.1.11.
1.1.16
We have a morphism of prestacks:
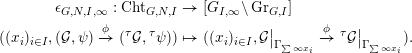
Remark 1.1.17. The prestack  $[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}]$ is not an inductive limit of algebraic stacks. But we can still use it for the construction in §§1.2 and 1.3. We will construct a variant of morphism (1.2) for algebraic stacks in 2.4.1.
$[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}]$ is not an inductive limit of algebraic stacks. But we can still use it for the construction in §§1.2 and 1.3. We will construct a variant of morphism (1.2) for algebraic stacks in 2.4.1.
The following definition will be used in §4.
(a) We define
 $\operatorname{Bun}_{G,N,I,d}$ to be the prestack that associates to any affine scheme
$\operatorname{Bun}_{G,N,I,d}$ to be the prestack that associates to any affine scheme  $S$ over
$S$ over  $\mathbb{F}_{q}$ the groupoid classifying the following data:
$\mathbb{F}_{q}$ the groupoid classifying the following data: (i)
 $(x_{i})_{i\in I}\in (X\smallsetminus N)^{I}(S)$;
$(x_{i})_{i\in I}\in (X\smallsetminus N)^{I}(S)$;(ii)
 ${\mathcal{G}}$: a
${\mathcal{G}}$: a  $G$-bundle over
$G$-bundle over  $X\times S$;
$X\times S$;(iii) a level structure on the divisor
 $(N\times S)+\unicode[STIX]{x1D6E4}_{\sum dx_{i}}$, i.e. an isomorphism of
$(N\times S)+\unicode[STIX]{x1D6E4}_{\sum dx_{i}}$, i.e. an isomorphism of  $G$-bundles:
$G$-bundles:  $\unicode[STIX]{x1D713}:\left.{\mathcal{G}}\vphantom{\big|}\right|_{(N\times S)+\unicode[STIX]{x1D6E4}_{\sum dx_{i}}}\overset{{\sim}}{\rightarrow }\left.G\vphantom{\big|}\right|_{(N\times S)+\unicode[STIX]{x1D6E4}_{\sum dx_{i}}}$.
$\unicode[STIX]{x1D713}:\left.{\mathcal{G}}\vphantom{\big|}\right|_{(N\times S)+\unicode[STIX]{x1D6E4}_{\sum dx_{i}}}\overset{{\sim}}{\rightarrow }\left.G\vphantom{\big|}\right|_{(N\times S)+\unicode[STIX]{x1D6E4}_{\sum dx_{i}}}$.
(b) We define
 $\operatorname{Bun}_{G,N,I,\infty }:=\underset{\longleftarrow }{\lim }~\operatorname{Bun}_{G,N,I,d}$.
$\operatorname{Bun}_{G,N,I,\infty }:=\underset{\longleftarrow }{\lim }~\operatorname{Bun}_{G,N,I,d}$.
1.1.19
 $\operatorname{Bun}_{G,N,I,d}$ is a smooth algebraic stack over
$\operatorname{Bun}_{G,N,I,d}$ is a smooth algebraic stack over  $(X\smallsetminus N)^{I}$. Its fiber over a point
$(X\smallsetminus N)^{I}$. Its fiber over a point  $(x_{i})_{i\in I}\in (X\smallsetminus N)^{I}(\mathbb{F}_{q})$ is
$(x_{i})_{i\in I}\in (X\smallsetminus N)^{I}(\mathbb{F}_{q})$ is  $\operatorname{Bun}_{G,N+\sum dx_{i}}$.
$\operatorname{Bun}_{G,N+\sum dx_{i}}$.
1.1.20
The definitions and constructions in this subsection work for all affine smooth geometrically connected algebraic groups over  $\mathbb{F}_{q}$ (we will use these for parabolic subgroups of
$\mathbb{F}_{q}$ (we will use these for parabolic subgroups of  $G$ and their Levi quotients).
$G$ and their Levi quotients).
1.2 Parabolic induction diagrams
1.2.1
Let  $P$ be a parabolic subgroup of
$P$ be a parabolic subgroup of  $G$ and let
$G$ and let  $M$ be its Levi quotient. Applying the definitions and constructions in §1.1 to
$M$ be its Levi quotient. Applying the definitions and constructions in §1.1 to  $P$ and
$P$ and  $M$, respectively, we define
$M$, respectively, we define  $\operatorname{Bun}_{P,N}$,
$\operatorname{Bun}_{P,N}$,  $\operatorname{Cht}_{P,N,I}$,
$\operatorname{Cht}_{P,N,I}$,  $\operatorname{Gr}_{P,I}$,
$\operatorname{Gr}_{P,I}$,  $P_{I,\infty }$,
$P_{I,\infty }$,  $\unicode[STIX]{x1D716}_{P,N,I,\infty }$ and
$\unicode[STIX]{x1D716}_{P,N,I,\infty }$ and  $\operatorname{Bun}_{M,N}$,
$\operatorname{Bun}_{M,N}$,  $\operatorname{Cht}_{M,N,I}$,
$\operatorname{Cht}_{M,N,I}$,  $\operatorname{Gr}_{M,I}$,
$\operatorname{Gr}_{M,I}$,  $M_{I,\infty }$,
$M_{I,\infty }$,  $\unicode[STIX]{x1D716}_{M,N,I,\infty }$.
$\unicode[STIX]{x1D716}_{M,N,I,\infty }$.
Remark 1.2.2. When  $N$ is non-empty, the prestack
$N$ is non-empty, the prestack  $\operatorname{Cht}_{P,N,I}$ defined above is not the same as the one defined in [Reference VarshavskyVar04, 2.28]. We will describe the difference in Remark 3.4.4.
$\operatorname{Cht}_{P,N,I}$ defined above is not the same as the one defined in [Reference VarshavskyVar04, 2.28]. We will describe the difference in Remark 3.4.4.
1.2.3
The morphisms of groups  $G{\hookleftarrow}P{\twoheadrightarrow}M$ induce morphisms of prestacks over
$G{\hookleftarrow}P{\twoheadrightarrow}M$ induce morphisms of prestacks over  $\operatorname{Spec}\mathbb{F}_{q}$:
$\operatorname{Spec}\mathbb{F}_{q}$:
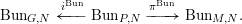 $$\begin{eqnarray}\operatorname{Bun}_{G,N}\xleftarrow[{}]{i^{\text{Bun}}}\operatorname{Bun}_{P,N}\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\text{Bun}}}\operatorname{Bun}_{M,N}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{G,N}\xleftarrow[{}]{i^{\text{Bun}}}\operatorname{Bun}_{P,N}\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\text{Bun}}}\operatorname{Bun}_{M,N}\!.\end{eqnarray}$$Construction 1.2.4. The morphisms of groups  $G{\hookleftarrow}P{\twoheadrightarrow}M$ induce morphisms of prestacks over
$G{\hookleftarrow}P{\twoheadrightarrow}M$ induce morphisms of prestacks over  $(X\smallsetminus N)^{I}$.
$(X\smallsetminus N)^{I}$.

More concretely, for any affine scheme  $S$ over
$S$ over  $\mathbb{F}_{q}$:
$\mathbb{F}_{q}$:
 $i:\operatorname{Cht}_{P,N,I}(S)\rightarrow \operatorname{Cht}_{G,N,I}(S)$ is given by
$i:\operatorname{Cht}_{P,N,I}(S)\rightarrow \operatorname{Cht}_{G,N,I}(S)$ is given by  $({\mathcal{P}}\rightarrow ^{\unicode[STIX]{x1D70F}}{\mathcal{P}})\mapsto ({\mathcal{P}}\overset{P}{\times }G\rightarrow ^{\unicode[STIX]{x1D70F}}{\mathcal{P}}\overset{P}{\times }G)$ where the level structure
$({\mathcal{P}}\rightarrow ^{\unicode[STIX]{x1D70F}}{\mathcal{P}})\mapsto ({\mathcal{P}}\overset{P}{\times }G\rightarrow ^{\unicode[STIX]{x1D70F}}{\mathcal{P}}\overset{P}{\times }G)$ where the level structure  $\unicode[STIX]{x1D713}:\left.{\mathcal{P}}\vphantom{\big|}\right|_{N\times S}\overset{{\sim}}{\rightarrow }\left.P\vphantom{\big|}\right|_{N\times S}$ is sent to
$\unicode[STIX]{x1D713}:\left.{\mathcal{P}}\vphantom{\big|}\right|_{N\times S}\overset{{\sim}}{\rightarrow }\left.P\vphantom{\big|}\right|_{N\times S}$ is sent to  $\unicode[STIX]{x1D713}\overset{P}{\times }G$;
$\unicode[STIX]{x1D713}\overset{P}{\times }G$;
 $\unicode[STIX]{x1D70B}:\operatorname{Cht}_{P,N,I}(S)\rightarrow \operatorname{Cht}_{M,N,I}(S)$ is given by
$\unicode[STIX]{x1D70B}:\operatorname{Cht}_{P,N,I}(S)\rightarrow \operatorname{Cht}_{M,N,I}(S)$ is given by  $({\mathcal{P}}\rightarrow ^{\unicode[STIX]{x1D70F}}{\mathcal{P}})\mapsto ({\mathcal{P}}\overset{P}{\times }M\rightarrow ^{\unicode[STIX]{x1D70F}}{\mathcal{P}}\overset{P}{\times }M)$ where the level structure
$({\mathcal{P}}\rightarrow ^{\unicode[STIX]{x1D70F}}{\mathcal{P}})\mapsto ({\mathcal{P}}\overset{P}{\times }M\rightarrow ^{\unicode[STIX]{x1D70F}}{\mathcal{P}}\overset{P}{\times }M)$ where the level structure  $\unicode[STIX]{x1D713}$ is sent to
$\unicode[STIX]{x1D713}$ is sent to  $\unicode[STIX]{x1D713}\overset{P}{\times }M$.
$\unicode[STIX]{x1D713}\overset{P}{\times }M$.
1.2.5
The morphisms of groups  $G{\hookleftarrow}P{\twoheadrightarrow}M$ induce morphisms of ind-schemes over
$G{\hookleftarrow}P{\twoheadrightarrow}M$ induce morphisms of ind-schemes over  $X^{I}$:
$X^{I}$:
 $$\begin{eqnarray}\operatorname{Gr}_{G,I}\xleftarrow[{}]{i^{0}}\operatorname{Gr}_{P,I}\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{0}}\operatorname{Gr}_{M,I}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Gr}_{G,I}\xleftarrow[{}]{i^{0}}\operatorname{Gr}_{P,I}\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{0}}\operatorname{Gr}_{M,I}\!.\end{eqnarray}$$1.2.6
Let  ${\mathcal{X}}$ (respectively
${\mathcal{X}}$ (respectively  ${\mathcal{Y}}$) be an (ind-)scheme over a base
${\mathcal{Y}}$) be an (ind-)scheme over a base  $S$ that is equipped with an action of a group scheme
$S$ that is equipped with an action of a group scheme  $A$ (respectively
$A$ (respectively  $B$) over
$B$) over  $S$ from the right. Let
$S$ from the right. Let  $A\rightarrow B$ be a morphism of group schemes over
$A\rightarrow B$ be a morphism of group schemes over  $S$. Let
$S$. Let  ${\mathcal{X}}\rightarrow {\mathcal{Y}}$ be a morphism of (ind-)schemes over
${\mathcal{X}}\rightarrow {\mathcal{Y}}$ be a morphism of (ind-)schemes over  $S$ which is
$S$ which is  $A$-equivariant (where
$A$-equivariant (where  $A$ acts on
$A$ acts on  ${\mathcal{Y}}$ via
${\mathcal{Y}}$ via  $A\rightarrow B$). This morphism induces a morphism of quotient prestacks
$A\rightarrow B$). This morphism induces a morphism of quotient prestacks
 $$\begin{eqnarray}[A\backslash {\mathcal{X}}]\rightarrow [B\backslash {\mathcal{Y}}].\end{eqnarray}$$
$$\begin{eqnarray}[A\backslash {\mathcal{X}}]\rightarrow [B\backslash {\mathcal{Y}}].\end{eqnarray}$$1.2.7
Applying 1.2.6 to  $i^{0}:\operatorname{Gr}_{P,I}\rightarrow \operatorname{Gr}_{G,I}$ and
$i^{0}:\operatorname{Gr}_{P,I}\rightarrow \operatorname{Gr}_{G,I}$ and  $P_{I,\infty }{\hookrightarrow}G_{I,\infty }$, we obtain a morphism of prestacks:
$P_{I,\infty }{\hookrightarrow}G_{I,\infty }$, we obtain a morphism of prestacks:
 $$\begin{eqnarray}\overline{i^{0}}:[P_{I,\infty }\backslash \operatorname{Gr}_{P,I}]\rightarrow [G_{I,\infty }\backslash \operatorname{Gr}_{G,I}].\end{eqnarray}$$
$$\begin{eqnarray}\overline{i^{0}}:[P_{I,\infty }\backslash \operatorname{Gr}_{P,I}]\rightarrow [G_{I,\infty }\backslash \operatorname{Gr}_{G,I}].\end{eqnarray}$$ Applying 1.2.6 to  $\unicode[STIX]{x1D70B}^{0}:\operatorname{Gr}_{P,I}\rightarrow \operatorname{Gr}_{M,I}$ and
$\unicode[STIX]{x1D70B}^{0}:\operatorname{Gr}_{P,I}\rightarrow \operatorname{Gr}_{M,I}$ and  $P_{I,\infty }{\twoheadrightarrow}M_{I,\infty }$, we obtain a morphism of prestacks:
$P_{I,\infty }{\twoheadrightarrow}M_{I,\infty }$, we obtain a morphism of prestacks:
 $$\begin{eqnarray}\overline{\unicode[STIX]{x1D70B}^{0}}:[P_{I,\infty }\backslash \operatorname{Gr}_{P,I}]\rightarrow [M_{I,\infty }\backslash \operatorname{Gr}_{M,I}].\end{eqnarray}$$
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D70B}^{0}}:[P_{I,\infty }\backslash \operatorname{Gr}_{P,I}]\rightarrow [M_{I,\infty }\backslash \operatorname{Gr}_{M,I}].\end{eqnarray}$$1.2.8
The following diagram of prestacks is commutative.

1.3 Quotient by  $\unicode[STIX]{x1D6EF}$
$\unicode[STIX]{x1D6EF}$
1.3.1
Let  $Z_{G}$ be the center of
$Z_{G}$ be the center of  $G$ as defined in 0.0.3. We have an action of
$G$ as defined in 0.0.3. We have an action of  $\operatorname{Bun}_{Z_{G}}$ on
$\operatorname{Bun}_{Z_{G}}$ on  $\operatorname{Bun}_{G,N}$ by twisting a
$\operatorname{Bun}_{G,N}$ by twisting a  $G$-bundle by a
$G$-bundle by a  $Z_{G}$-bundle, i.e. the action of
$Z_{G}$-bundle, i.e. the action of  ${\mathcal{T}}_{Z}\in \operatorname{Bun}_{Z_{G}}$ is given by
${\mathcal{T}}_{Z}\in \operatorname{Bun}_{Z_{G}}$ is given by  ${\mathcal{G}}\mapsto ({\mathcal{G}}\times {\mathcal{T}}_{Z})/Z_{G}$. Similarly,
${\mathcal{G}}\mapsto ({\mathcal{G}}\times {\mathcal{T}}_{Z})/Z_{G}$. Similarly,  $\operatorname{Bun}_{Z_{G}}$ acts on
$\operatorname{Bun}_{Z_{G}}$ acts on  $[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}]$, i.e. the action of
$[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}]$, i.e. the action of  ${\mathcal{T}}_{Z}\in \operatorname{Bun}_{Z_{G}}$ is given by
${\mathcal{T}}_{Z}\in \operatorname{Bun}_{Z_{G}}$ is given by
 $$\begin{eqnarray}({\mathcal{G}}\xrightarrow[{}]{\unicode[STIX]{x1D719}}{\mathcal{G}}^{\prime })\mapsto (({\mathcal{G}}\times \left.{\mathcal{T}}_{G}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}})/Z_{G}\xrightarrow[{}]{\unicode[STIX]{x1D719}}({\mathcal{G}}^{\prime }\times \left.{\mathcal{T}}_{G}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}})/Z_{G}).\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{G}}\xrightarrow[{}]{\unicode[STIX]{x1D719}}{\mathcal{G}}^{\prime })\mapsto (({\mathcal{G}}\times \left.{\mathcal{T}}_{G}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}})/Z_{G}\xrightarrow[{}]{\unicode[STIX]{x1D719}}({\mathcal{G}}^{\prime }\times \left.{\mathcal{T}}_{G}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}})/Z_{G}).\end{eqnarray}$$ For  ${\mathcal{T}}_{Z}\in \operatorname{Bun}_{Z_{G}}(\mathbb{F}_{q})$, we have a canonical identification
${\mathcal{T}}_{Z}\in \operatorname{Bun}_{Z_{G}}(\mathbb{F}_{q})$, we have a canonical identification  ${\mathcal{T}}_{Z}\simeq ^{\unicode[STIX]{x1D70F}}{\mathcal{T}}_{Z}$. Thus
${\mathcal{T}}_{Z}\simeq ^{\unicode[STIX]{x1D70F}}{\mathcal{T}}_{Z}$. Thus  $\operatorname{Bun}_{Z_{G}}(\mathbb{F}_{q})$ acts on
$\operatorname{Bun}_{Z_{G}}(\mathbb{F}_{q})$ acts on  $\operatorname{Cht}_{G,N,I}$ by twisting a
$\operatorname{Cht}_{G,N,I}$ by twisting a  $G$-bundle by a
$G$-bundle by a  $Z_{G}$-bundle, i.e. the action of
$Z_{G}$-bundle, i.e. the action of  ${\mathcal{T}}_{Z}\in \operatorname{Bun}_{Z_{G}}(\mathbb{F}_{q})$ is given by
${\mathcal{T}}_{Z}\in \operatorname{Bun}_{Z_{G}}(\mathbb{F}_{q})$ is given by  $({\mathcal{G}}\xrightarrow[{}]{\unicode[STIX]{x1D719}}\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}})\mapsto (({\mathcal{G}}\times {\mathcal{T}}_{Z})/Z_{G}\xrightarrow[{}]{\unicode[STIX]{x1D719}}\text{}^{\unicode[STIX]{x1D70F}}({\mathcal{G}}\times {\mathcal{T}}_{Z})/Z_{G})$.
$({\mathcal{G}}\xrightarrow[{}]{\unicode[STIX]{x1D719}}\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}})\mapsto (({\mathcal{G}}\times {\mathcal{T}}_{Z})/Z_{G}\xrightarrow[{}]{\unicode[STIX]{x1D719}}\text{}^{\unicode[STIX]{x1D70F}}({\mathcal{G}}\times {\mathcal{T}}_{Z})/Z_{G})$.
The group  $\unicode[STIX]{x1D6EF}$ defined in 0.0.4 acts on
$\unicode[STIX]{x1D6EF}$ defined in 0.0.4 acts on  $\operatorname{Bun}_{G,N}$,
$\operatorname{Bun}_{G,N}$,  $\operatorname{Cht}_{G,N,I}$ and
$\operatorname{Cht}_{G,N,I}$ and  $[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}]$ via
$[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}]$ via  $\unicode[STIX]{x1D6EF}\rightarrow Z_{G}(\mathbb{A})\rightarrow \operatorname{Bun}_{Z_{G}}(\mathbb{F}_{q})$.
$\unicode[STIX]{x1D6EF}\rightarrow Z_{G}(\mathbb{A})\rightarrow \operatorname{Bun}_{Z_{G}}(\mathbb{F}_{q})$.
1.3.2
Note that the morphism  $\unicode[STIX]{x1D716}_{G,N,I,\infty }$ defined in (1.2) is
$\unicode[STIX]{x1D716}_{G,N,I,\infty }$ defined in (1.2) is  $\unicode[STIX]{x1D6EF}$-equivariant.
$\unicode[STIX]{x1D6EF}$-equivariant.
Now applying Definition 1.1.13 to  $Z_{G}$ (respectively
$Z_{G}$ (respectively  $G^{\text{ad}}$), we define a group scheme
$G^{\text{ad}}$), we define a group scheme  $(Z_{G})_{I,\infty }$ (respectively
$(Z_{G})_{I,\infty }$ (respectively  $G_{I,\infty }^{\text{ad}}$) over
$G_{I,\infty }^{\text{ad}}$) over  $X^{I}$. We have
$X^{I}$. We have  $G_{I,\infty }^{\text{ad}}=G_{I,\infty }/(Z_{G})_{I,\infty }$. The group scheme
$G_{I,\infty }^{\text{ad}}=G_{I,\infty }/(Z_{G})_{I,\infty }$. The group scheme  $(Z_{G})_{I,\infty }$ acts trivially on
$(Z_{G})_{I,\infty }$ acts trivially on  $\operatorname{Gr}_{G,I}$, so the action of
$\operatorname{Gr}_{G,I}$, so the action of  $G_{I,\infty }$ on
$G_{I,\infty }$ on  $\operatorname{Gr}_{G,I}$ factors through
$\operatorname{Gr}_{G,I}$ factors through  $G_{I,\infty }^{\text{ad}}$. We use this action to define the quotient prestack
$G_{I,\infty }^{\text{ad}}$. We use this action to define the quotient prestack  $[G_{I,\infty }^{\text{ad}}\backslash \operatorname{Gr}_{G,I}]$. The morphism
$[G_{I,\infty }^{\text{ad}}\backslash \operatorname{Gr}_{G,I}]$. The morphism  $G_{I,\infty }{\twoheadrightarrow}G_{I,\infty }^{\text{ad}}$ induces a morphism
$G_{I,\infty }{\twoheadrightarrow}G_{I,\infty }^{\text{ad}}$ induces a morphism  $[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}]\rightarrow [G_{I,\infty }^{\text{ad}}\backslash \operatorname{Gr}_{G,I}]$, which is
$[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}]\rightarrow [G_{I,\infty }^{\text{ad}}\backslash \operatorname{Gr}_{G,I}]$, which is  $\unicode[STIX]{x1D6EF}$-equivariant for the trivial action of
$\unicode[STIX]{x1D6EF}$-equivariant for the trivial action of  $\unicode[STIX]{x1D6EF}$ on
$\unicode[STIX]{x1D6EF}$ on  $[G_{I,\infty }^{\text{ad}}\backslash \operatorname{Gr}_{G,I}]$.
$[G_{I,\infty }^{\text{ad}}\backslash \operatorname{Gr}_{G,I}]$.
Hence the composition of morphisms
 $$\begin{eqnarray}\operatorname{Cht}_{G,N,I}\xrightarrow[{}]{\unicode[STIX]{x1D716}_{G,N,I,\infty }}[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}]\rightarrow [G_{I,\infty }^{\text{ad}}\backslash \operatorname{Gr}_{G,I}]\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{G,N,I}\xrightarrow[{}]{\unicode[STIX]{x1D716}_{G,N,I,\infty }}[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}]\rightarrow [G_{I,\infty }^{\text{ad}}\backslash \operatorname{Gr}_{G,I}]\end{eqnarray}$$ is  $\unicode[STIX]{x1D6EF}$-equivariant. Thus it factors through
$\unicode[STIX]{x1D6EF}$-equivariant. Thus it factors through
 $$\begin{eqnarray}\unicode[STIX]{x1D716}_{G,N,I,\infty }^{\unicode[STIX]{x1D6EF}}:\operatorname{Cht}_{G,N,I}/\unicode[STIX]{x1D6EF}\rightarrow [G_{I,\infty }^{\text{ad}}\backslash \operatorname{Gr}_{G,I}].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}_{G,N,I,\infty }^{\unicode[STIX]{x1D6EF}}:\operatorname{Cht}_{G,N,I}/\unicode[STIX]{x1D6EF}\rightarrow [G_{I,\infty }^{\text{ad}}\backslash \operatorname{Gr}_{G,I}].\end{eqnarray}$$We will construct a variant of morphism (1.7) for algebraic stacks in 2.4.1.
1.3.3
 $Z_{G}$ acts on a
$Z_{G}$ acts on a  $P$-bundle via
$P$-bundle via  $Z_{G}{\hookrightarrow}P$. Just as in 1.3.1, we have an action of
$Z_{G}{\hookrightarrow}P$. Just as in 1.3.1, we have an action of  $\operatorname{Bun}_{Z_{G}}$ on
$\operatorname{Bun}_{Z_{G}}$ on  $\operatorname{Bun}_{P,N}$ by twisting a
$\operatorname{Bun}_{P,N}$ by twisting a  $P$-bundle by a
$P$-bundle by a  $Z_{G}$-bundle. This leads to an action of
$Z_{G}$-bundle. This leads to an action of  $\unicode[STIX]{x1D6EF}$ on
$\unicode[STIX]{x1D6EF}$ on  $\operatorname{Bun}_{P,N}$,
$\operatorname{Bun}_{P,N}$,  $\operatorname{Cht}_{P,N,I}$ and
$\operatorname{Cht}_{P,N,I}$ and  $[P_{I,\infty }\backslash \operatorname{Gr}_{P,I}]$ via
$[P_{I,\infty }\backslash \operatorname{Gr}_{P,I}]$ via  $\unicode[STIX]{x1D6EF}\rightarrow Z_{G}(\mathbb{A})\rightarrow \operatorname{Bun}_{Z_{G}}(\mathbb{F}_{q})$.
$\unicode[STIX]{x1D6EF}\rightarrow Z_{G}(\mathbb{A})\rightarrow \operatorname{Bun}_{Z_{G}}(\mathbb{F}_{q})$.
Using the morphism  $Z_{G}{\hookrightarrow}M$, we similarly obtain an action of
$Z_{G}{\hookrightarrow}M$, we similarly obtain an action of  $\unicode[STIX]{x1D6EF}$ on
$\unicode[STIX]{x1D6EF}$ on  $\operatorname{Bun}_{M,N}$,
$\operatorname{Bun}_{M,N}$,  $\operatorname{Cht}_{M,N,I}$ and
$\operatorname{Cht}_{M,N,I}$ and  $[M_{I,\infty }\backslash \operatorname{Gr}_{M,I}]$.
$[M_{I,\infty }\backslash \operatorname{Gr}_{M,I}]$.
1.3.4
Applying Definition 1.1.13 to  $\overline{P}:=P/Z_{G}$ (respectively
$\overline{P}:=P/Z_{G}$ (respectively  $\overline{M}:=M/Z_{G}$), we define a group scheme
$\overline{M}:=M/Z_{G}$), we define a group scheme  $\overline{P}_{I,\infty }$ (respectively
$\overline{P}_{I,\infty }$ (respectively  $\overline{M}_{I,\infty }$) over
$\overline{M}_{I,\infty }$) over  $X^{I}$. We have
$X^{I}$. We have  $\overline{P}_{I,\infty }=P_{I,\infty }/(Z_{G})_{I,\infty }$ and
$\overline{P}_{I,\infty }=P_{I,\infty }/(Z_{G})_{I,\infty }$ and  $\overline{M}_{I,\infty }=M_{I,\infty }/(Z_{G})_{I,\infty }$.
$\overline{M}_{I,\infty }=M_{I,\infty }/(Z_{G})_{I,\infty }$.
The morphism  $\unicode[STIX]{x1D716}_{P,N,I,\infty }$ defined in 1.2.1 is
$\unicode[STIX]{x1D716}_{P,N,I,\infty }$ defined in 1.2.1 is  $\unicode[STIX]{x1D6EF}$-equivariant. Since the group scheme
$\unicode[STIX]{x1D6EF}$-equivariant. Since the group scheme  $(Z_{G})_{I,\infty }$ acts trivially on
$(Z_{G})_{I,\infty }$ acts trivially on  $\operatorname{Gr}_{P,I}$, the action of
$\operatorname{Gr}_{P,I}$, the action of  $P_{I,\infty }$ on
$P_{I,\infty }$ on  $\operatorname{Gr}_{P,I}$ factors through
$\operatorname{Gr}_{P,I}$ factors through  $\overline{P}_{I,\infty }$. We denote by
$\overline{P}_{I,\infty }$. We denote by  $[\overline{P}_{I,\infty }\backslash \operatorname{Gr}_{P,I}]$ the resulting quotient prestack. The morphism
$[\overline{P}_{I,\infty }\backslash \operatorname{Gr}_{P,I}]$ the resulting quotient prestack. The morphism  $P_{I,\infty }{\twoheadrightarrow}\overline{P}_{I,\infty }$ induces a morphism
$P_{I,\infty }{\twoheadrightarrow}\overline{P}_{I,\infty }$ induces a morphism  $[P_{I,\infty }\backslash \operatorname{Gr}_{P,I}]\rightarrow [\overline{P}_{I,\infty }\backslash \operatorname{Gr}_{P,I}]$, which is
$[P_{I,\infty }\backslash \operatorname{Gr}_{P,I}]\rightarrow [\overline{P}_{I,\infty }\backslash \operatorname{Gr}_{P,I}]$, which is  $\unicode[STIX]{x1D6EF}$-equivariant for the trivial action of
$\unicode[STIX]{x1D6EF}$-equivariant for the trivial action of  $\unicode[STIX]{x1D6EF}$ on
$\unicode[STIX]{x1D6EF}$ on  $[\overline{P}_{I,\infty }\backslash \operatorname{Gr}_{P,I}]$. Hence the composition of morphisms
$[\overline{P}_{I,\infty }\backslash \operatorname{Gr}_{P,I}]$. Hence the composition of morphisms  $\operatorname{Cht}_{P,N,I}\xrightarrow[{}]{\unicode[STIX]{x1D716}_{P,N,I,\infty }}[P_{I,\infty }\backslash \operatorname{Gr}_{P,I}]\rightarrow [\overline{P}_{I,\infty }\backslash \operatorname{Gr}_{P,I}]$ is
$\operatorname{Cht}_{P,N,I}\xrightarrow[{}]{\unicode[STIX]{x1D716}_{P,N,I,\infty }}[P_{I,\infty }\backslash \operatorname{Gr}_{P,I}]\rightarrow [\overline{P}_{I,\infty }\backslash \operatorname{Gr}_{P,I}]$ is  $\unicode[STIX]{x1D6EF}$-equivariant. Thus it factors through
$\unicode[STIX]{x1D6EF}$-equivariant. Thus it factors through
 $$\begin{eqnarray}\unicode[STIX]{x1D716}_{P,N,I,\infty }^{\unicode[STIX]{x1D6EF}}:\operatorname{Cht}_{P,N,I}/\unicode[STIX]{x1D6EF}\rightarrow [\overline{P}_{I,\infty }\backslash \operatorname{Gr}_{P,I}].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}_{P,N,I,\infty }^{\unicode[STIX]{x1D6EF}}:\operatorname{Cht}_{P,N,I}/\unicode[STIX]{x1D6EF}\rightarrow [\overline{P}_{I,\infty }\backslash \operatorname{Gr}_{P,I}].\end{eqnarray}$$ Similarly, the composition of morphisms  $\operatorname{Cht}_{M,N,I}\xrightarrow[{}]{\unicode[STIX]{x1D716}_{M,N,I,\infty }}[M_{I,\infty }\backslash \operatorname{Gr}_{M,I}]\rightarrow [\overline{M}_{I,\infty }\backslash \operatorname{Gr}_{M,I}]$ is
$\operatorname{Cht}_{M,N,I}\xrightarrow[{}]{\unicode[STIX]{x1D716}_{M,N,I,\infty }}[M_{I,\infty }\backslash \operatorname{Gr}_{M,I}]\rightarrow [\overline{M}_{I,\infty }\backslash \operatorname{Gr}_{M,I}]$ is  $\unicode[STIX]{x1D6EF}$-equivariant for the trivial action of
$\unicode[STIX]{x1D6EF}$-equivariant for the trivial action of  $\unicode[STIX]{x1D6EF}$ on
$\unicode[STIX]{x1D6EF}$ on  $[\overline{M}_{I,\infty }\backslash \operatorname{Gr}_{M,I}]$. Thus it factors through
$[\overline{M}_{I,\infty }\backslash \operatorname{Gr}_{M,I}]$. Thus it factors through
 $$\begin{eqnarray}\unicode[STIX]{x1D716}_{M,N,I,\infty }^{\unicode[STIX]{x1D6EF}}:\operatorname{Cht}_{M,N,I}/\unicode[STIX]{x1D6EF}\rightarrow [\overline{M}_{I,\infty }\backslash \operatorname{Gr}_{M,I}].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}_{M,N,I,\infty }^{\unicode[STIX]{x1D6EF}}:\operatorname{Cht}_{M,N,I}/\unicode[STIX]{x1D6EF}\rightarrow [\overline{M}_{I,\infty }\backslash \operatorname{Gr}_{M,I}].\end{eqnarray}$$1.3.5
The morphisms  $i$ and
$i$ and  $\unicode[STIX]{x1D70B}$ in (1.6) are
$\unicode[STIX]{x1D70B}$ in (1.6) are  $\unicode[STIX]{x1D6EF}$-equivariant. Diagram (1.6) induces a commutative diagram of prestacks.
$\unicode[STIX]{x1D6EF}$-equivariant. Diagram (1.6) induces a commutative diagram of prestacks.

In the remaining part of §1, we introduce the Harder–Narasimhan stratification (compatible with the action of 𝛯) for the parabolic induction diagram (1.4). In order to do so, we use the Harder–Narasimhan stratification for the parabolic induction diagram (1.3). From now on we work in the context of algebraic (ind-)stacks.
In §1.4, we recall the usual Harder–Narasimhan stratification  $\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}}\subset \operatorname{Bun}_{G}$ and a variant
$\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}}\subset \operatorname{Bun}_{G}$ and a variant  $\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}\subset \operatorname{Bun}_{G}$ which is compatible with the action by
$\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}\subset \operatorname{Bun}_{G}$ which is compatible with the action by  $\unicode[STIX]{x1D6EF}$.
$\unicode[STIX]{x1D6EF}$.
In §1.5, we introduce the Harder–Narasimhan stratification  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}\subset \operatorname{Bun}_{M}$, which allows us to construct in §1.6 the truncated parabolic induction diagrams (1.26):
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}\subset \operatorname{Bun}_{M}$, which allows us to construct in §1.6 the truncated parabolic induction diagrams (1.26):
 $$\begin{eqnarray}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\leftarrow \operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\rightarrow \operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\leftarrow \operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\rightarrow \operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}.\end{eqnarray}$$In §1.7, we define the Harder–Narasimhan stratification on the stacks of shtukas using §§1.4–1.6.
1.4 Harder–Narasimhan stratification of  $\operatorname{Bun}_{G}$
$\operatorname{Bun}_{G}$
In 1.4.1–1.4.10, we recall the Harder–Narasimhan stratification of  $\operatorname{Bun}_{G}$ defined in [Reference SchiederSch15] and [Reference Drinfeld and GaitsgoryDG15, §7]. (In these papers, the group is reductive over an algebraically closed field. Since our group
$\operatorname{Bun}_{G}$ defined in [Reference SchiederSch15] and [Reference Drinfeld and GaitsgoryDG15, §7]. (In these papers, the group is reductive over an algebraically closed field. Since our group  $G$ is split over
$G$ is split over  $\mathbb{F}_{q}$, we use Galois descent to obtain the stratification over
$\mathbb{F}_{q}$, we use Galois descent to obtain the stratification over  $\mathbb{F}_{q}$.)
$\mathbb{F}_{q}$.)
In 1.4.11–1.4.17, we recall a variant of the Harder–Narasimhan stratification of  $\operatorname{Bun}_{G}$ which is compatible with the quotient by
$\operatorname{Bun}_{G}$ which is compatible with the quotient by  $\unicode[STIX]{x1D6EF}$, as in [Reference VarshavskyVar04, §2] and [Reference LafforgueLaf18, §1].
$\unicode[STIX]{x1D6EF}$, as in [Reference VarshavskyVar04, §2] and [Reference LafforgueLaf18, §1].
1.4.1
Applying 0.0.6 to group  $G$, we define
$G$, we define  $\widehat{\unicode[STIX]{x1D6EC}}_{G}$,
$\widehat{\unicode[STIX]{x1D6EC}}_{G}$,  $\widehat{\unicode[STIX]{x1D6EC}}_{G}^{+}$,
$\widehat{\unicode[STIX]{x1D6EC}}_{G}^{+}$,  $\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\text{pos}}$,
$\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\text{pos}}$,  $\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}$,
$\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}$,  $\widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}$,
$\widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}$,  $\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\text{pos},\mathbb{Q}}$ and the partial order ‘
$\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\text{pos},\mathbb{Q}}$ and the partial order ‘ ${\leqslant}\text{}^{G}$’ on
${\leqslant}\text{}^{G}$’ on  $\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}$.
$\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}$.
1.4.2
[Reference SchiederSch15, 2.1.2] Let  $P$ be a parabolic subgroup of
$P$ be a parabolic subgroup of  $G$ and
$G$ and  $M$ its Levi quotient. Consider the sublattice
$M$ its Levi quotient. Consider the sublattice  $\widehat{\unicode[STIX]{x1D6EC}}_{[M,M]_{\text{sc}}}\subset \widehat{\unicode[STIX]{x1D6EC}}_{G}$ spanned by the simple coroots of
$\widehat{\unicode[STIX]{x1D6EC}}_{[M,M]_{\text{sc}}}\subset \widehat{\unicode[STIX]{x1D6EC}}_{G}$ spanned by the simple coroots of  $M$. We define
$M$. We define
 $$\begin{eqnarray}\widehat{\unicode[STIX]{x1D6EC}}_{G,P}:=\widehat{\unicode[STIX]{x1D6EC}}_{G}/\widehat{\unicode[STIX]{x1D6EC}}_{[M,M]_{\text{sc}}}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\unicode[STIX]{x1D6EC}}_{G,P}:=\widehat{\unicode[STIX]{x1D6EC}}_{G}/\widehat{\unicode[STIX]{x1D6EC}}_{[M,M]_{\text{sc}}}.\end{eqnarray}$$ Let  $\widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\mathbb{Q}}:=\widehat{\unicode[STIX]{x1D6EC}}_{G,P}\otimes _{\mathbb{Z}}\mathbb{Q}$. We denote by
$\widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\mathbb{Q}}:=\widehat{\unicode[STIX]{x1D6EC}}_{G,P}\otimes _{\mathbb{Z}}\mathbb{Q}$. We denote by  $\widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\text{pos}}$ the image of
$\widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\text{pos}}$ the image of  $\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\text{pos}}$ in
$\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\text{pos}}$ in  $\widehat{\unicode[STIX]{x1D6EC}}_{G,P}$, and by
$\widehat{\unicode[STIX]{x1D6EC}}_{G,P}$, and by  $\widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\text{pos},\mathbb{Q}}$ the image of
$\widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\text{pos},\mathbb{Q}}$ the image of  $\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\text{pos},\mathbb{Q}}$ in
$\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\text{pos},\mathbb{Q}}$ in  $\widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\mathbb{Q}}$. We introduce the partial order on
$\widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\mathbb{Q}}$. We introduce the partial order on  $\widehat{\unicode[STIX]{x1D6EC}}_{G,P}$ by
$\widehat{\unicode[STIX]{x1D6EC}}_{G,P}$ by

1.4.3
[Reference SchiederSch15, 2.1.3], [Reference Drinfeld and GaitsgoryDG15, 7.1.3, 7.1.5] Let  $Z_{M}$ be the center of
$Z_{M}$ be the center of  $M$. Let
$M$. Let  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}}$ be the coweight lattice of
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}}$ be the coweight lattice of  $Z_{M}$, i.e.
$Z_{M}$, i.e.  $\operatorname{Hom}(\mathbb{G}_{m},Z_{M})$. Note that it equals to
$\operatorname{Hom}(\mathbb{G}_{m},Z_{M})$. Note that it equals to  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}^{0}}=\operatorname{Hom}(\mathbb{G}_{m},Z_{M}^{0})$, where
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}^{0}}=\operatorname{Hom}(\mathbb{G}_{m},Z_{M}^{0})$, where  $Z_{M}^{0}$ is the neutral connected component of
$Z_{M}^{0}$ is the neutral connected component of  $Z_{M}$.
$Z_{M}$.
We have a natural inclusion  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}}\subset \widehat{\unicode[STIX]{x1D6EC}}_{G}$ (because
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}}\subset \widehat{\unicode[STIX]{x1D6EC}}_{G}$ (because  $Z_{M}$ is included in the image of
$Z_{M}$ is included in the image of  $B{\hookrightarrow}P{\twoheadrightarrow}M$). The composition
$B{\hookrightarrow}P{\twoheadrightarrow}M$). The composition  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}}^{\mathbb{Q}}{\hookrightarrow}\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}{\twoheadrightarrow}\widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\mathbb{Q}}$ is an isomorphism:
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}}^{\mathbb{Q}}{\hookrightarrow}\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}{\twoheadrightarrow}\widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\mathbb{Q}}$ is an isomorphism:
 $$\begin{eqnarray}\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}}^{\mathbb{ Q}}\overset{{\sim}}{\rightarrow }\widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\mathbb{Q}}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}}^{\mathbb{ Q}}\overset{{\sim}}{\rightarrow }\widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\mathbb{Q}}.\end{eqnarray}$$We define the slope map to be the composition
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{P}:\widehat{\unicode[STIX]{x1D6EC}}_{G,P}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\mathbb{Q}}\cong \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}}^{\mathbb{ Q}}{\hookrightarrow}\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{P}:\widehat{\unicode[STIX]{x1D6EC}}_{G,P}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\mathbb{Q}}\cong \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}}^{\mathbb{ Q}}{\hookrightarrow}\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}.\end{eqnarray}$$ We define  $\operatorname{pr}_{P}$ to be the composition
$\operatorname{pr}_{P}$ to be the composition
 $$\begin{eqnarray}\operatorname{pr}_{P}:\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}{\twoheadrightarrow}\widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\mathbb{Q}}\simeq \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}}^{\mathbb{ Q}}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{pr}_{P}:\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}{\twoheadrightarrow}\widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\mathbb{Q}}\simeq \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}}^{\mathbb{ Q}}.\end{eqnarray}$$ By definition, we have  $\widehat{\unicode[STIX]{x1D6EC}}_{G,G}^{\mathbb{Q}}=\widehat{\unicode[STIX]{x1D6EC}}_{Z_{G}}^{\mathbb{Q}}$,
$\widehat{\unicode[STIX]{x1D6EC}}_{G,G}^{\mathbb{Q}}=\widehat{\unicode[STIX]{x1D6EC}}_{Z_{G}}^{\mathbb{Q}}$,  $\widehat{\unicode[STIX]{x1D6EC}}_{G,P}=\widehat{\unicode[STIX]{x1D6EC}}_{M,M}$ and
$\widehat{\unicode[STIX]{x1D6EC}}_{G,P}=\widehat{\unicode[STIX]{x1D6EC}}_{M,M}$ and 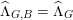 $\widehat{\unicode[STIX]{x1D6EC}}_{G,B}=\widehat{\unicode[STIX]{x1D6EC}}_{G}$. So
$\widehat{\unicode[STIX]{x1D6EC}}_{G,B}=\widehat{\unicode[STIX]{x1D6EC}}_{G}$. So  $\unicode[STIX]{x1D719}_{B}$ is just the inclusion
$\unicode[STIX]{x1D719}_{B}$ is just the inclusion  $\widehat{\unicode[STIX]{x1D6EC}}_{G}{\hookrightarrow}\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}$.
$\widehat{\unicode[STIX]{x1D6EC}}_{G}{\hookrightarrow}\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}$.
Lemma 1.4.4 [Reference SchiederSch15, Proposition 3.1].
The slope map  $\unicode[STIX]{x1D719}_{P}$ preserves the partial orders ‘
$\unicode[STIX]{x1D719}_{P}$ preserves the partial orders ‘ ${\leqslant}\text{}^{G}$’ on
${\leqslant}\text{}^{G}$’ on  $\widehat{\unicode[STIX]{x1D6EC}}_{G,P}$ and
$\widehat{\unicode[STIX]{x1D6EC}}_{G,P}$ and  $\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}$ in the sense that it maps
$\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}$ in the sense that it maps  $\widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\text{pos}}$ to
$\widehat{\unicode[STIX]{x1D6EC}}_{G,P}^{\text{pos}}$ to  $\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\text{pos},\mathbb{Q}}$.
$\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\text{pos},\mathbb{Q}}$.
1.4.5
[Reference VarshavskyVar04, Lemma 2.2], [Reference SchiederSch15, 2.2.1, 2.2.2], [Reference Drinfeld and GaitsgoryDG15, 7.2.3] The map  $\operatorname{Bun}_{P}\rightarrow \operatorname{Bun}_{M}$ in 1.2.3 induces a bijection on the set of connected components of
$\operatorname{Bun}_{P}\rightarrow \operatorname{Bun}_{M}$ in 1.2.3 induces a bijection on the set of connected components of  $\operatorname{Bun}_{P}$ and
$\operatorname{Bun}_{P}$ and  $\operatorname{Bun}_{M}$. We have
$\operatorname{Bun}_{M}$. We have  $\unicode[STIX]{x1D70B}_{0}(\operatorname{Bun}_{P})\cong \unicode[STIX]{x1D70B}_{0}(\operatorname{Bun}_{M})\cong \widehat{\unicode[STIX]{x1D6EC}}_{G,P}$. Let
$\unicode[STIX]{x1D70B}_{0}(\operatorname{Bun}_{P})\cong \unicode[STIX]{x1D70B}_{0}(\operatorname{Bun}_{M})\cong \widehat{\unicode[STIX]{x1D6EC}}_{G,P}$. Let  $\deg _{M}:\operatorname{Bun}_{M}\rightarrow \unicode[STIX]{x1D70B}_{0}(\operatorname{Bun}_{M})\cong \widehat{\unicode[STIX]{x1D6EC}}_{G,P}$ and
$\deg _{M}:\operatorname{Bun}_{M}\rightarrow \unicode[STIX]{x1D70B}_{0}(\operatorname{Bun}_{M})\cong \widehat{\unicode[STIX]{x1D6EC}}_{G,P}$ and  $\deg _{P}:\operatorname{Bun}_{P}\rightarrow \operatorname{Bun}_{M}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{G,P}$.
$\deg _{P}:\operatorname{Bun}_{P}\rightarrow \operatorname{Bun}_{M}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{G,P}$.
Definition 1.4.6 [Reference Drinfeld and GaitsgoryDG15, 7.3.3, 7.3.4].
For any  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}$, we define
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}$, we define  $\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}}$ to be the stack that associates to any affine scheme
$\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}}$ to be the stack that associates to any affine scheme  $S$ over
$S$ over  $\mathbb{F}_{q}$ the groupoid
$\mathbb{F}_{q}$ the groupoid

where a  $P$-structure of
$P$-structure of  ${\mathcal{G}}_{s}$ is a
${\mathcal{G}}_{s}$ is a  $P$-bundle
$P$-bundle  ${\mathcal{P}}$ on
${\mathcal{P}}$ on  $X_{s}$ such that
$X_{s}$ such that  ${\mathcal{P}}\overset{P}{\times }G\simeq {\mathcal{G}}_{s}$.
${\mathcal{P}}\overset{P}{\times }G\simeq {\mathcal{G}}_{s}$.
(a) By [Reference SchiederSch15, Lemma 3.3], the above Definition 1.4.6 is equivalent to
(the argument repeats the proof in [Reference SchiederSch15, Lemma 3.3] by replacing
 $\unicode[STIX]{x1D719}_{G}(\check{\unicode[STIX]{x1D706}}_{G})$ by
$\unicode[STIX]{x1D719}_{G}(\check{\unicode[STIX]{x1D706}}_{G})$ by  $\unicode[STIX]{x1D707}$).
$\unicode[STIX]{x1D707}$).(b) By [Reference SchiederSch15, Proposition 3.2 and Remark 3.2.4], the definition of
 $\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}}$ in (a) is equivalent to the Tannakian description:where
$\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}}$ in (a) is equivalent to the Tannakian description:where
 ${\mathcal{B}}_{\unicode[STIX]{x1D706}}$ is the line bundle associated to
${\mathcal{B}}_{\unicode[STIX]{x1D706}}$ is the line bundle associated to  ${\mathcal{B}}$ and
${\mathcal{B}}$ and  $B\rightarrow T\xrightarrow[{}]{\unicode[STIX]{x1D706}}\mathbb{G}_{m}$.
$B\rightarrow T\xrightarrow[{}]{\unicode[STIX]{x1D706}}\mathbb{G}_{m}$.(c) The reason why we use Definition 1.4.6 (rather than its equivalent forms) is that it will be useful for non-split groups in future works.
Lemma 1.4.8 [Reference Drinfeld and GaitsgoryDG15, 7.3.4, Proposition 7.3.5].
(a) For any
 $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}$, the stack
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}$, the stack  $\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}}$ is an open substack of
$\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}}$ is an open substack of  $\operatorname{Bun}_{G}$.
$\operatorname{Bun}_{G}$.(b) For any
 $\unicode[STIX]{x1D707}_{1}\leqslant \text{}^{G}\unicode[STIX]{x1D707}_{2}$, we have an open immersion
$\unicode[STIX]{x1D707}_{1}\leqslant \text{}^{G}\unicode[STIX]{x1D707}_{2}$, we have an open immersion  $\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}_{1}}{\hookrightarrow}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}_{2}}$.
$\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}_{1}}{\hookrightarrow}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}_{2}}$.(c) We have
 $\operatorname{Bun}_{G}=\bigcup _{\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}}$.
$\operatorname{Bun}_{G}=\bigcup _{\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}}$.(d) The open substack
 $\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}}$ is of finite type.
$\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}}$ is of finite type.
Definition 1.4.9. For any  $\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}$, let
$\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}$, let  $\operatorname{Bun}_{G}^{(\unicode[STIX]{x1D706})}\subset \operatorname{Bun}_{G}$ be the quasi-compact locally closed reduced substack defined in [Reference SchiederSch15, Theorem 2.1] and [Reference Drinfeld and GaitsgoryDG15, Theorem 7.4.3]. It is called a Harder–Narasimhan stratum of
$\operatorname{Bun}_{G}^{(\unicode[STIX]{x1D706})}\subset \operatorname{Bun}_{G}$ be the quasi-compact locally closed reduced substack defined in [Reference SchiederSch15, Theorem 2.1] and [Reference Drinfeld and GaitsgoryDG15, Theorem 7.4.3]. It is called a Harder–Narasimhan stratum of  $\operatorname{Bun}_{G}$.
$\operatorname{Bun}_{G}$.
1.4.10
[Reference Drinfeld and GaitsgoryDG15, Corollary 7.4.5] We have

where  $\operatorname{pr}_{P}$ is defined in (1.14) and
$\operatorname{pr}_{P}$ is defined in (1.14) and  $\unicode[STIX]{x1D704}:\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}}^{\mathbb{Q}}{\hookrightarrow}\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}$ is the inclusion. For any
$\unicode[STIX]{x1D704}:\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}}^{\mathbb{Q}}{\hookrightarrow}\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}$ is the inclusion. For any  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}$, we have
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}$, we have

The set  $\{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}\,|\,\unicode[STIX]{x1D706}\leqslant \text{}^{G}\unicode[STIX]{x1D707}\text{ and }\operatorname{Bun}_{G}^{(\unicode[STIX]{x1D706})}\neq \emptyset \}$ is finite. This gives another proof of Lemma 1.4.8(d).
$\{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}\,|\,\unicode[STIX]{x1D706}\leqslant \text{}^{G}\unicode[STIX]{x1D707}\text{ and }\operatorname{Bun}_{G}^{(\unicode[STIX]{x1D706})}\neq \emptyset \}$ is finite. This gives another proof of Lemma 1.4.8(d).
The above open substack  $\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}}$ is not preserved by the action of
$\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G}\unicode[STIX]{x1D707}}$ is not preserved by the action of  $\unicode[STIX]{x1D6EF}$ on
$\unicode[STIX]{x1D6EF}$ on  $\operatorname{Bun}_{G}$. Now we introduce open substacks which are preserved by the action of
$\operatorname{Bun}_{G}$. Now we introduce open substacks which are preserved by the action of  $\unicode[STIX]{x1D6EF}$.
$\unicode[STIX]{x1D6EF}$.
1.4.11
Applying 0.0.6 to group  $G^{\text{ad}}$, we define
$G^{\text{ad}}$, we define  $\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}$,
$\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}$,  $\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+}$,
$\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+}$,  $\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\text{pos}}$,
$\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\text{pos}}$,  $\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}$,
$\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}$,  $\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$,
$\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$,  $\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\text{pos},\mathbb{Q}}$ and the partial order ‘
$\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\text{pos},\mathbb{Q}}$ and the partial order ‘ ${\leqslant}\text{}^{G^{\text{ad}}}$’ on
${\leqslant}\text{}^{G^{\text{ad}}}$’ on  $\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}$.
$\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}$.
The morphism  $G{\twoheadrightarrow}G/Z_{G}=G^{\text{ad}}$ induces a morphism
$G{\twoheadrightarrow}G/Z_{G}=G^{\text{ad}}$ induces a morphism
 $$\begin{eqnarray}\unicode[STIX]{x1D6F6}_{G}:\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F6}_{G}:\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}.\end{eqnarray}$$ It maps  $\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\text{pos},\mathbb{Q}}$ to
$\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\text{pos},\mathbb{Q}}$ to  $\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\text{pos},\mathbb{Q}}$.
$\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\text{pos},\mathbb{Q}}$.
Definition 1.4.12. For any  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, we define
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, we define  $\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ to be the stack that associates to any affine scheme
$\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ to be the stack that associates to any affine scheme  $S$ over
$S$ over  $\mathbb{F}_{q}$ the groupoid
$\mathbb{F}_{q}$ the groupoid

Remark 1.4.13. For the same reason as in Remark 1.4.7, Definition 1.4.12 is equivalent to [Reference VarshavskyVar04, Notation 2.1(b)] and [Reference LafforgueLaf18, (1.3)].
1.4.14
Just as in 1.4.10, for  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, we have
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, we have
 $$\begin{eqnarray}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}=\mathop{\bigcup }_{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}},\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}\operatorname{Bun}_{G}^{(\unicode[STIX]{x1D706})}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}=\mathop{\bigcup }_{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}},\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}\operatorname{Bun}_{G}^{(\unicode[STIX]{x1D706})}\!.\end{eqnarray}$$ The set 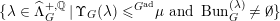 $\{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}\,|\,\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}\text{ and }\operatorname{Bun}_{G}^{(\unicode[STIX]{x1D706})}\neq \emptyset \}$ is finite modulo
$\{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}\,|\,\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}\text{ and }\operatorname{Bun}_{G}^{(\unicode[STIX]{x1D706})}\neq \emptyset \}$ is finite modulo  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{G}}$.
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{G}}$.
1.4.15
The action of  $\unicode[STIX]{x1D6EF}$ on
$\unicode[STIX]{x1D6EF}$ on  $\operatorname{Bun}_{G}$ preserves
$\operatorname{Bun}_{G}$ preserves  $\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$. We define the quotient
$\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$. We define the quotient  $\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}$.
$\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}$.
(a) For any
 $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, the stack
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, the stack  $\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ is an open substack of
$\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ is an open substack of  $\operatorname{Bun}_{G}$.
$\operatorname{Bun}_{G}$.(b) For any
 $\unicode[STIX]{x1D707}_{1}\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}_{2}$, we have an open immersion
$\unicode[STIX]{x1D707}_{1}\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}_{2}$, we have an open immersion  $\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}_{1}}{\hookrightarrow}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}_{2}}$.
$\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}_{1}}{\hookrightarrow}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}_{2}}$.(c) The stack
 $\operatorname{Bun}_{G}$ is the inductive limit of these open substacks:
$\operatorname{Bun}_{G}$ is the inductive limit of these open substacks:  $\operatorname{Bun}_{G}=\bigcup _{\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$.
$\operatorname{Bun}_{G}=\bigcup _{\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$.(d) The stack
 $\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}$ is of finite type.
$\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}$ is of finite type.
Proof. Parts (a), (b) and (c) are induced by Lemma 1.4.8 (see also [Reference VarshavskyVar04, Lemme A.3)]. Part (d) follows from 1.4.14. ◻
Remark 1.4.17. See [Reference VarshavskyVar04, Lemmas 3.1 and 3.7] for another proof of Lemma 1.4.8(d) and Lemma 1.4.16(d).
1.5 Harder–Narasimhan stratification of  $\operatorname{Bun}_{M}$
$\operatorname{Bun}_{M}$
Let  $P$ be a proper parabolic subgroup of
$P$ be a proper parabolic subgroup of  $G$ and
$G$ and  $M$ its Levi quotient.
$M$ its Levi quotient.
1.5.1
Applying 0.0.6 to group  $M$, we define
$M$, we define  $\widehat{\unicode[STIX]{x1D6EC}}_{M}$,
$\widehat{\unicode[STIX]{x1D6EC}}_{M}$,  $\widehat{\unicode[STIX]{x1D6EC}}_{M}^{+}$,
$\widehat{\unicode[STIX]{x1D6EC}}_{M}^{+}$,  $\widehat{\unicode[STIX]{x1D6EC}}_{M}^{\text{pos}}$,
$\widehat{\unicode[STIX]{x1D6EC}}_{M}^{\text{pos}}$,  $\widehat{\unicode[STIX]{x1D6EC}}_{M}^{\mathbb{Q}}$,
$\widehat{\unicode[STIX]{x1D6EC}}_{M}^{\mathbb{Q}}$,  $\widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}}$,
$\widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}}$,  $\widehat{\unicode[STIX]{x1D6EC}}_{M}^{\text{pos},\mathbb{Q}}$ and the partial order ‘
$\widehat{\unicode[STIX]{x1D6EC}}_{M}^{\text{pos},\mathbb{Q}}$ and the partial order ‘ ${\leqslant}\text{}^{M}$’ on
${\leqslant}\text{}^{M}$’ on  $\widehat{\unicode[STIX]{x1D6EC}}_{M}^{\mathbb{Q}}$.
$\widehat{\unicode[STIX]{x1D6EC}}_{M}^{\mathbb{Q}}$.
1.5.2
Sections 1.4.2–1.4.10 work also for  $M$. In particular, let
$M$. In particular, let  $P^{\prime }$ be a parabolic subgroup of
$P^{\prime }$ be a parabolic subgroup of  $M$; we have the slope map
$M$; we have the slope map  $\unicode[STIX]{x1D719}_{P^{\prime }}:\widehat{\unicode[STIX]{x1D6EC}}_{M,P^{\prime }}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{M}^{\mathbb{Q}}$ and
$\unicode[STIX]{x1D719}_{P^{\prime }}:\widehat{\unicode[STIX]{x1D6EC}}_{M,P^{\prime }}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{M}^{\mathbb{Q}}$ and  $\deg _{P^{\prime }}:\operatorname{Bun}_{P^{\prime }}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{M,P^{\prime }}$.
$\deg _{P^{\prime }}:\operatorname{Bun}_{P^{\prime }}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{M,P^{\prime }}$.
Definition 1.5.3. Applying Definition 1.4.9 to  $M$, for any
$M$, for any  $\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}}$, we define a quasi-compact locally closed substack
$\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}}$, we define a quasi-compact locally closed substack  $\operatorname{Bun}_{M}^{(\unicode[STIX]{x1D706})}\subset \operatorname{Bun}_{M}$, called a Harder–Narasimhan stratum of
$\operatorname{Bun}_{M}^{(\unicode[STIX]{x1D706})}\subset \operatorname{Bun}_{M}$, called a Harder–Narasimhan stratum of  $\operatorname{Bun}_{M}$.
$\operatorname{Bun}_{M}$.
Now we introduce  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}\subset \operatorname{Bun}_{M}$ which will be used to construct diagram (1.26).
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}\subset \operatorname{Bun}_{M}$ which will be used to construct diagram (1.26).
Definition 1.5.4. For any  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, we define
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, we define 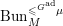 $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ to be the stack that associates to any affine scheme
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ to be the stack that associates to any affine scheme  $S$ over
$S$ over  $\mathbb{F}_{q}$ the groupoid
$\mathbb{F}_{q}$ the groupoid  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}(S):=$
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}(S):=$

where  $\unicode[STIX]{x1D6F6}_{G}:\widehat{\unicode[STIX]{x1D6EC}}_{M}^{\mathbb{Q}}=\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}$ is defined in (1.15).
$\unicode[STIX]{x1D6F6}_{G}:\widehat{\unicode[STIX]{x1D6EC}}_{M}^{\mathbb{Q}}=\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}$ is defined in (1.15).
Similarly to Lemma 1.4.16, we have
(a) For any
 $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, the stack
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, the stack  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ is an open substack of
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ is an open substack of  $\operatorname{Bun}_{M}$.
$\operatorname{Bun}_{M}$.(b) For any
 $\unicode[STIX]{x1D707}_{1}\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}_{2}$, we have an open immersion
$\unicode[STIX]{x1D707}_{1}\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}_{2}$, we have an open immersion  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}_{1}}{\hookrightarrow}\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}_{2}}$.
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}_{1}}{\hookrightarrow}\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}_{2}}$.(c) The stack
 $\operatorname{Bun}_{M}$ is the inductive limit of these open substacks:
$\operatorname{Bun}_{M}$ is the inductive limit of these open substacks:  $\operatorname{Bun}_{M}=\bigcup _{\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}}\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$.
$\operatorname{Bun}_{M}=\bigcup _{\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}}\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$.
1.5.6
The action of  $\unicode[STIX]{x1D6EF}$ on
$\unicode[STIX]{x1D6EF}$ on  $\operatorname{Bun}_{M}$ preserve
$\operatorname{Bun}_{M}$ preserve  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$. We define the quotient
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$. We define the quotient  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}$. Note that
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}$. Note that  $\unicode[STIX]{x1D6EF}$ is a lattice in
$\unicode[STIX]{x1D6EF}$ is a lattice in  $Z_{G}(F)\backslash Z_{G}(\mathbb{A})$. However,
$Z_{G}(F)\backslash Z_{G}(\mathbb{A})$. However,  $\unicode[STIX]{x1D6EF}$ is only a discrete subgroup but not a lattice in
$\unicode[STIX]{x1D6EF}$ is only a discrete subgroup but not a lattice in  $Z_{M}(F)\backslash Z_{M}(\mathbb{A})$ (since
$Z_{M}(F)\backslash Z_{M}(\mathbb{A})$ (since  $P\subsetneq G$). We will see that
$P\subsetneq G$). We will see that  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}$ is locally of finite type but not necessarily of finite type.
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}$ is locally of finite type but not necessarily of finite type.
1.5.7
Note that  $\widehat{\unicode[STIX]{x1D6EC}}_{G,P}=\widehat{\unicode[STIX]{x1D6EC}}_{M,M}$. Consider the composition of morphisms
$\widehat{\unicode[STIX]{x1D6EC}}_{G,P}=\widehat{\unicode[STIX]{x1D6EC}}_{M,M}$. Consider the composition of morphisms
 $$\begin{eqnarray}\operatorname{Bun}_{M}\xrightarrow[{}]{\deg _{M}}\widehat{\unicode[STIX]{x1D6EC}}_{M,M}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{M,M}^{\mathbb{Q}}\simeq \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}}^{\mathbb{ Q}}{\twoheadrightarrow}\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{ Q}},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{M}\xrightarrow[{}]{\deg _{M}}\widehat{\unicode[STIX]{x1D6EC}}_{M,M}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{M,M}^{\mathbb{Q}}\simeq \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}}^{\mathbb{ Q}}{\twoheadrightarrow}\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{ Q}},\end{eqnarray}$$ where  $\deg _{M}$ is defined in 1.4.5. We denote by
$\deg _{M}$ is defined in 1.4.5. We denote by  $A_{M}$ the image of
$A_{M}$ the image of  $\widehat{\unicode[STIX]{x1D6EC}}_{M,M}$ in
$\widehat{\unicode[STIX]{x1D6EC}}_{M,M}$ in  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$. For any
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$. For any  $\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$, we denote by
$\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$, we denote by  $\operatorname{Bun}_{M}^{\unicode[STIX]{x1D708}}$ its inverse image in
$\operatorname{Bun}_{M}^{\unicode[STIX]{x1D708}}$ its inverse image in  $\operatorname{Bun}_{M}$. It is non-empty if and only if
$\operatorname{Bun}_{M}$. It is non-empty if and only if  $\unicode[STIX]{x1D708}\in A_{M}$.
$\unicode[STIX]{x1D708}\in A_{M}$.
Definition 1.5.8. We define  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$ to be the intersection of
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$ to be the intersection of  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ and
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ and  $\operatorname{Bun}_{M}^{\unicode[STIX]{x1D708}}$.
$\operatorname{Bun}_{M}^{\unicode[STIX]{x1D708}}$.
1.5.9
The stack  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$ is open and closed in
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$ is open and closed in  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ and is open in
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ and is open in  $\operatorname{Bun}_{M}^{\unicode[STIX]{x1D708}}$. We have a decomposition
$\operatorname{Bun}_{M}^{\unicode[STIX]{x1D708}}$. We have a decomposition
 $$\begin{eqnarray}\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}=\underset{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{ Q}}}{\bigsqcup }\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}=\underset{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{ Q}}}{\bigsqcup }\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}\!.\end{eqnarray}$$1.5.10
Just as in 1.4.14, we have
 $$\begin{eqnarray}\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}=\underset{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}},\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}{\bigcup }\mathop{\operatorname{Bun}}_{M}^{(\unicode[STIX]{x1D706})}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}=\underset{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}},\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}{\bigcup }\mathop{\operatorname{Bun}}_{M}^{(\unicode[STIX]{x1D706})}\!.\end{eqnarray}$$1.5.11
Similarly to (1.14), we define
 $$\begin{eqnarray}\operatorname{pr}_{P}^{\text{ad}}:\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{ Q}}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{pr}_{P}^{\text{ad}}:\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{ Q}}.\end{eqnarray}$$ Taking into account that  $\widehat{\unicode[STIX]{x1D6EC}}_{G}=\widehat{\unicode[STIX]{x1D6EC}}_{M}$ and
$\widehat{\unicode[STIX]{x1D6EC}}_{G}=\widehat{\unicode[STIX]{x1D6EC}}_{M}$ and  $\widehat{\unicode[STIX]{x1D6EC}}_{G,P}=\widehat{\unicode[STIX]{x1D6EC}}_{M,M}$, for any
$\widehat{\unicode[STIX]{x1D6EC}}_{G,P}=\widehat{\unicode[STIX]{x1D6EC}}_{M,M}$, for any  $\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}},$ we deduce that
$\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}},$ we deduce that  $\operatorname{Bun}_{M}^{(\unicode[STIX]{x1D706})}\subset \operatorname{Bun}_{M}^{\unicode[STIX]{x1D708}}$ if and only if
$\operatorname{Bun}_{M}^{(\unicode[STIX]{x1D706})}\subset \operatorname{Bun}_{M}^{\unicode[STIX]{x1D708}}$ if and only if  $\unicode[STIX]{x1D708}=\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})$.
$\unicode[STIX]{x1D708}=\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})$.
1.5.12
We deduce from 1.5.10 and 1.5.11 that
 $$\begin{eqnarray}\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}=\underset{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}},\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D708}}{\bigcup }\mathop{\operatorname{Bun}}_{M}^{(\unicode[STIX]{x1D706})}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}=\underset{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}},\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D708}}{\bigcup }\mathop{\operatorname{Bun}}_{M}^{(\unicode[STIX]{x1D706})}\!.\end{eqnarray}$$1.5.13
We denote by  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\operatorname{pos},\mathbb{Q}}:=\operatorname{pr}_{P}^{\text{ad}}(\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\text{pos},\mathbb{Q}})$. We introduce the partial order on
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\operatorname{pos},\mathbb{Q}}:=\operatorname{pr}_{P}^{\text{ad}}(\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\text{pos},\mathbb{Q}})$. We introduce the partial order on  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$ by
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$ by
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{1}\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}_{2}\Leftrightarrow \unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D707}_{1}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\operatorname{pos},\mathbb{Q}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{1}\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}_{2}\Leftrightarrow \unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D707}_{1}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\operatorname{pos},\mathbb{Q}}.\end{eqnarray}$$ By definition, for  $\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{M}$, we have
$\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{M}$, we have  $\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FE}})=0$. By [Reference SchiederSch15, Proposition 3.1], for
$\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FE}})=0$. By [Reference SchiederSch15, Proposition 3.1], for  $\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}-\widehat{\unicode[STIX]{x1D6E4}}_{M}$ we have
$\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}-\widehat{\unicode[STIX]{x1D6E4}}_{M}$ we have  $\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FE}})>0$ and these
$\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FE}})>0$ and these  $\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FE}})$ are linearly independent. Thus for
$\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FE}})$ are linearly independent. Thus for  $\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}$ and
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}$ and  $\unicode[STIX]{x1D706}_{1}\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D706}_{2}$, we have
$\unicode[STIX]{x1D706}_{1}\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D706}_{2}$, we have  $\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D706}_{1})\leqslant \text{}^{G^{\text{ad}}}\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D706}_{2})$. Also, the inclusion
$\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D706}_{1})\leqslant \text{}^{G^{\text{ad}}}\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D706}_{2})$. Also, the inclusion  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}\subset \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}$ maps
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}\subset \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}$ maps  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\operatorname{pos},\mathbb{Q}}$ to
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\operatorname{pos},\mathbb{Q}}$ to  $\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\operatorname{pos},\mathbb{Q}}$.
$\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\operatorname{pos},\mathbb{Q}}$.
Lemma 1.5.14. Let  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. Then the stack
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. Then the stack  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}$ is empty unless
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}$ is empty unless  $\unicode[STIX]{x1D708}\in A_{M}$ defined in 1.5.7 and
$\unicode[STIX]{x1D708}\in A_{M}$ defined in 1.5.7 and  $\unicode[STIX]{x1D708}\leqslant \text{}^{G^{\text{ad}}}\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})$.
$\unicode[STIX]{x1D708}\leqslant \text{}^{G^{\text{ad}}}\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})$.
Proof. The first condition follows from 1.5.7. To prove the second condition, note that for the set  $\{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}}\;|\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D708}\}$ to be non-empty, by 1.5.13 we must have
$\{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}}\;|\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D708}\}$ to be non-empty, by 1.5.13 we must have  $\unicode[STIX]{x1D708}\leqslant \text{}^{G^{\text{ad}}}\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})$.◻
$\unicode[STIX]{x1D708}\leqslant \text{}^{G^{\text{ad}}}\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})$.◻
1.5.15
Let  $\overline{M}=M/Z_{G}$ as in 1.3.4. For
$\overline{M}=M/Z_{G}$ as in 1.3.4. For  $\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}$, we define
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}$, we define  $\unicode[STIX]{x1D706}\leqslant \text{}^{\overline{M}}\unicode[STIX]{x1D707}$ if and only if
$\unicode[STIX]{x1D706}\leqslant \text{}^{\overline{M}}\unicode[STIX]{x1D707}$ if and only if  $\unicode[STIX]{x1D707}-\unicode[STIX]{x1D706}$ is a linear combination of simple coroots of
$\unicode[STIX]{x1D707}-\unicode[STIX]{x1D706}$ is a linear combination of simple coroots of  $M$ with coefficients in
$M$ with coefficients in  $\mathbb{Q}_{{\geqslant}0}$ modulo
$\mathbb{Q}_{{\geqslant}0}$ modulo  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{G}}^{\mathbb{Q}}$.
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{G}}^{\mathbb{Q}}$.
1.5.16
Let  $\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}$ and
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}$ and  $\unicode[STIX]{x1D706}\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}$. We write
$\unicode[STIX]{x1D706}\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}$. We write  $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D707}-\sum _{\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}}c_{\check{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FE}})$ for some
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D707}-\sum _{\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}}c_{\check{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FE}})$ for some  $c_{\check{\unicode[STIX]{x1D6FE}}}\in \mathbb{Q}_{{\geqslant}0}$. We deduce from 1.5.13 that
$c_{\check{\unicode[STIX]{x1D6FE}}}\in \mathbb{Q}_{{\geqslant}0}$. We deduce from 1.5.13 that  $\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D706})=\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})$ if and only if
$\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D706})=\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})$ if and only if  $c_{\check{\unicode[STIX]{x1D6FE}}}=0$ for all
$c_{\check{\unicode[STIX]{x1D6FE}}}=0$ for all  $\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}-\widehat{\unicode[STIX]{x1D6E4}}_{M}$. Hence
$\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}-\widehat{\unicode[STIX]{x1D6E4}}_{M}$. Hence
 $$\begin{eqnarray}\unicode[STIX]{x1D706}\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}\quad \text{and}\quad \operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D706})=\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})\;\Leftrightarrow \;\unicode[STIX]{x1D706}\leqslant \text{}^{\overline{M}}\unicode[STIX]{x1D707}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}\quad \text{and}\quad \operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D706})=\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})\;\Leftrightarrow \;\unicode[STIX]{x1D706}\leqslant \text{}^{\overline{M}}\unicode[STIX]{x1D707}.\end{eqnarray}$$1.5.17
Let  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and  $\unicode[STIX]{x1D708}\leqslant \text{}^{G^{\text{ad}}}\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})$. For every
$\unicode[STIX]{x1D708}\leqslant \text{}^{G^{\text{ad}}}\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})$. For every  $\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}-\widehat{\unicode[STIX]{x1D6E4}}_{M}$, let
$\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}-\widehat{\unicode[STIX]{x1D6E4}}_{M}$, let  $c_{\unicode[STIX]{x1D6FE}}\in \mathbb{Q}_{{\geqslant}0}$ be the unique coefficient such that
$c_{\unicode[STIX]{x1D6FE}}\in \mathbb{Q}_{{\geqslant}0}$ be the unique coefficient such that
 $$\begin{eqnarray}\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})-\mathop{\sum }_{\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}-\widehat{\unicode[STIX]{x1D6E4}}_{M}}c_{\unicode[STIX]{x1D6FE}}\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FE}})=\unicode[STIX]{x1D708}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})-\mathop{\sum }_{\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}-\widehat{\unicode[STIX]{x1D6E4}}_{M}}c_{\unicode[STIX]{x1D6FE}}\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FE}})=\unicode[STIX]{x1D708}.\end{eqnarray}$$ We define  $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}}:=\unicode[STIX]{x1D707}-\sum _{\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}-\widehat{\unicode[STIX]{x1D6E4}}_{M}}c_{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FE}})$. As in 1.5.16, we deduce that
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}}:=\unicode[STIX]{x1D707}-\sum _{\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}-\widehat{\unicode[STIX]{x1D6E4}}_{M}}c_{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FE}})$. As in 1.5.16, we deduce that
 $$\begin{eqnarray}\unicode[STIX]{x1D706}\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}\quad \text{and}\quad \operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D708}\;\Leftrightarrow \;\unicode[STIX]{x1D706}\leqslant \text{}^{\overline{M}}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}\quad \text{and}\quad \operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D708}\;\Leftrightarrow \;\unicode[STIX]{x1D706}\leqslant \text{}^{\overline{M}}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}}.\end{eqnarray}$$1.5.18
The action of  $\unicode[STIX]{x1D6EF}$ on
$\unicode[STIX]{x1D6EF}$ on  $\operatorname{Bun}_{M}$ preserves
$\operatorname{Bun}_{M}$ preserves  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}$. We define the quotient
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}$. We define the quotient  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}$.
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}$.
Lemma 1.5.19. The stack  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}$ is of finite type.
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}$ is of finite type.
Proof. By (1.21), we have
 $$\begin{eqnarray}\{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}}\;|\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D708}\}=\{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}}\;|\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\leqslant \text{}^{\overline{M}}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}}\}.\end{eqnarray}$$
$$\begin{eqnarray}\{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}}\;|\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D708}\}=\{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}}\;|\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\leqslant \text{}^{\overline{M}}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}}\}.\end{eqnarray}$$ We deduce from 1.4.10 (applied to  $M$) that the set
$M$) that the set  $\{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}}\;|\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D708},\;\operatorname{Bun}_{M}^{(\unicode[STIX]{x1D706})}\neq \emptyset \}$ is finite modulo
$\{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}}\;|\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D708},\;\operatorname{Bun}_{M}^{(\unicode[STIX]{x1D706})}\neq \emptyset \}$ is finite modulo  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{G}}$. By Definition 1.5.3,
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{G}}$. By Definition 1.5.3,  $\operatorname{Bun}_{M}^{(\unicode[STIX]{x1D706})}$ is of finite type. From 1.5.12 we deduce the lemma.◻
$\operatorname{Bun}_{M}^{(\unicode[STIX]{x1D706})}$ is of finite type. From 1.5.12 we deduce the lemma.◻
1.5.20
By Lemma 1.5.14, the decomposition (1.17) is in fact indexed by a translated cone in  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$:
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$:
 $$\begin{eqnarray}\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}:=\{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{ Q}},\;\unicode[STIX]{x1D708}\leqslant \text{}^{G^{\text{ad}}}\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})\}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}:=\{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{ Q}},\;\unicode[STIX]{x1D708}\leqslant \text{}^{G^{\text{ad}}}\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})\}.\end{eqnarray}$$We deduce that
 $$\begin{eqnarray}\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}=\underset{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}}{\bigsqcup }\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}=\underset{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}}{\bigsqcup }\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}\end{eqnarray}$$and
 $$\begin{eqnarray}\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}=\underset{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}}{\bigsqcup }\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}=\underset{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}}{\bigsqcup }\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}.\end{eqnarray}$$1.6 Harder–Narasimhan stratification of parabolic induction
Recall that we have morphisms (1.3):  $\operatorname{Bun}_{G}\xleftarrow[{}]{i^{\text{Bun}}}\operatorname{Bun}_{P}\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\text{Bun}}}\operatorname{Bun}_{M}$.
$\operatorname{Bun}_{G}\xleftarrow[{}]{i^{\text{Bun}}}\operatorname{Bun}_{P}\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\text{Bun}}}\operatorname{Bun}_{M}$.
Definition 1.6.1. Let  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. We define
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. We define  $\operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ to be the inverse image of
$\operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ to be the inverse image of  $\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ in
$\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ in  $\operatorname{Bun}_{P}$.
$\operatorname{Bun}_{P}$.
Lemma 1.6.2. The image of  $\operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ in
$\operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ in  $\operatorname{Bun}_{M}$ is included in
$\operatorname{Bun}_{M}$ is included in  $\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$.
$\operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$.
Proof. Let  ${\mathcal{P}}\in \operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ and let
${\mathcal{P}}\in \operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$ and let  ${\mathcal{M}}$ be its image in
${\mathcal{M}}$ be its image in  $\operatorname{Bun}_{M}$. We will check that
$\operatorname{Bun}_{M}$. We will check that  ${\mathcal{M}}\in \operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$. For any parabolic subgroup
${\mathcal{M}}\in \operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$. For any parabolic subgroup  $P^{\prime }$ of
$P^{\prime }$ of  $M$, let
$M$, let  $M^{\prime }$ be its Levi quotient. Let
$M^{\prime }$ be its Levi quotient. Let  ${\mathcal{P}}^{\prime }$ be a
${\mathcal{P}}^{\prime }$ be a  $P^{\prime }$-structure of
$P^{\prime }$-structure of  ${\mathcal{M}}$ and
${\mathcal{M}}$ and  ${\mathcal{M}}^{\prime }:={\mathcal{P}}^{\prime }\overset{P^{\prime }}{\times }M^{\prime }$. By Definition 1.5.4, we need to prove that
${\mathcal{M}}^{\prime }:={\mathcal{P}}^{\prime }\overset{P^{\prime }}{\times }M^{\prime }$. By Definition 1.5.4, we need to prove that  $\unicode[STIX]{x1D6F6}_{G}\circ \unicode[STIX]{x1D719}_{P^{\prime }}\circ \operatorname{deg}_{P^{\prime }}({\mathcal{P}}^{\prime })\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}$.
$\unicode[STIX]{x1D6F6}_{G}\circ \unicode[STIX]{x1D719}_{P^{\prime }}\circ \operatorname{deg}_{P^{\prime }}({\mathcal{P}}^{\prime })\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}$.
Let  $P^{\prime \prime }:=P\underset{M}{\times }P^{\prime }$. It is a parabolic subgroup of
$P^{\prime \prime }:=P\underset{M}{\times }P^{\prime }$. It is a parabolic subgroup of  $G$ with Levi quotient
$G$ with Levi quotient  $M^{\prime }$. We have the following.
$M^{\prime }$. We have the following.

By [Reference Drinfeld and GaitsgoryDG16, Lemma 2.5.8], we can define a  $P^{\prime \prime }$-bundle
$P^{\prime \prime }$-bundle  ${\mathcal{P}}^{\prime \prime }:={\mathcal{P}}\underset{{\mathcal{M}}}{\times }{\mathcal{P}}^{\prime }$. We have
${\mathcal{P}}^{\prime \prime }:={\mathcal{P}}\underset{{\mathcal{M}}}{\times }{\mathcal{P}}^{\prime }$. We have  $\deg _{P^{\prime }}{\mathcal{P}}^{\prime }=\deg _{M^{\prime }}{\mathcal{M}}^{\prime }=\deg _{P^{\prime \prime }}{\mathcal{P}}^{\prime \prime }$. Taking into account that
$\deg _{P^{\prime }}{\mathcal{P}}^{\prime }=\deg _{M^{\prime }}{\mathcal{M}}^{\prime }=\deg _{P^{\prime \prime }}{\mathcal{P}}^{\prime \prime }$. Taking into account that  $\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}=\widehat{\unicode[STIX]{x1D6EC}}_{M}^{\mathbb{Q}}$, we deduce that
$\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}=\widehat{\unicode[STIX]{x1D6EC}}_{M}^{\mathbb{Q}}$, we deduce that  $\unicode[STIX]{x1D6F6}_{G}\circ \unicode[STIX]{x1D719}_{P^{\prime }}\circ \operatorname{deg}_{P^{\prime }}({\mathcal{P}}^{\prime })=\unicode[STIX]{x1D6F6}_{G}\,\circ \,\unicode[STIX]{x1D719}_{P^{\prime \prime }}\,\circ \,\operatorname{deg}_{P^{\prime \prime }}({\mathcal{P}}^{\prime \prime })\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}$, where the last inequality follows from the definition of
$\unicode[STIX]{x1D6F6}_{G}\circ \unicode[STIX]{x1D719}_{P^{\prime }}\circ \operatorname{deg}_{P^{\prime }}({\mathcal{P}}^{\prime })=\unicode[STIX]{x1D6F6}_{G}\,\circ \,\unicode[STIX]{x1D719}_{P^{\prime \prime }}\,\circ \,\operatorname{deg}_{P^{\prime \prime }}({\mathcal{P}}^{\prime \prime })\leqslant \text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}$, where the last inequality follows from the definition of  $\operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$.◻
$\operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}$.◻
1.6.3
By Lemma 1.6.2, morphisms (1.3) induce morphisms:
 $$\begin{eqnarray}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}\leftarrow \operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}\rightarrow \operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}\leftarrow \operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}\rightarrow \operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}.\end{eqnarray}$$ The group  $\unicode[STIX]{x1D6EF}$ acts on all these stacks. All the morphisms are
$\unicode[STIX]{x1D6EF}$ acts on all these stacks. All the morphisms are  $\unicode[STIX]{x1D6EF}$-equivariant. Thus morphisms (1.25) induce morphisms:
$\unicode[STIX]{x1D6EF}$-equivariant. Thus morphisms (1.25) induce morphisms:
 $$\begin{eqnarray}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\leftarrow \operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\rightarrow \operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\leftarrow \operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\rightarrow \operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}.\end{eqnarray}$$1.6.4
For any  $\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$, we define
$\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$, we define  $\operatorname{Bun}_{P}^{\unicode[STIX]{x1D708}}$ to be the inverse image of
$\operatorname{Bun}_{P}^{\unicode[STIX]{x1D708}}$ to be the inverse image of  $\operatorname{Bun}_{M}^{\unicode[STIX]{x1D708}}$ in
$\operatorname{Bun}_{M}^{\unicode[STIX]{x1D708}}$ in  $\operatorname{Bun}_{P}$. We define
$\operatorname{Bun}_{P}$. We define  $\operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}:=\operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}\cap \operatorname{Bun}_{P}^{\unicode[STIX]{x1D708}}$. Morphisms (1.26) induce morphisms:
$\operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}:=\operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}\cap \operatorname{Bun}_{P}^{\unicode[STIX]{x1D708}}$. Morphisms (1.26) induce morphisms:
 $$\begin{eqnarray}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\leftarrow \operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}\rightarrow \operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{G}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\leftarrow \operatorname{Bun}_{P}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}\rightarrow \operatorname{Bun}_{M}^{{\leqslant}\text{}^{G^{\text{ad}}}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}.\end{eqnarray}$$1.7 Harder–Narasimhan stratification of stack of shtukas
Notation 1.7.1. In the remaining part of the paper, we will only use the truncations indexed by ‘ ${\leqslant}\text{}^{G^{\text{ad}}}$’ (rather than ‘
${\leqslant}\text{}^{G^{\text{ad}}}$’ (rather than ‘ ${\leqslant}\text{}^{G}$’). To simplify the notation, from now on, ‘
${\leqslant}\text{}^{G}$’). To simplify the notation, from now on, ‘ ${\leqslant}$’ means ‘
${\leqslant}$’ means ‘ ${\leqslant}\text{}^{G^{\text{ad}}}$’.
${\leqslant}\text{}^{G^{\text{ad}}}$’.
Definition 1.7.2. Let  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ (respectively
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ (respectively  $\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}$). We define
$\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}}$). We define  $\operatorname{Cht}_{G,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}$ (respectively
$\operatorname{Cht}_{G,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}$ (respectively  $\operatorname{Cht}_{G,N,I}^{(\unicode[STIX]{x1D706})}$) to be the inverse image of
$\operatorname{Cht}_{G,N,I}^{(\unicode[STIX]{x1D706})}$) to be the inverse image of  $\operatorname{Bun}_{G}^{{\leqslant}\,\unicode[STIX]{x1D707}}$ (respectively
$\operatorname{Bun}_{G}^{{\leqslant}\,\unicode[STIX]{x1D707}}$ (respectively  $\operatorname{Bun}_{G}^{(\unicode[STIX]{x1D706})}$) by the morphism
$\operatorname{Bun}_{G}^{(\unicode[STIX]{x1D706})}$) by the morphism
 $$\begin{eqnarray}\operatorname{Cht}_{G,N,I}\rightarrow \operatorname{Bun}_{G},\quad ((x_{i})_{i\in I},({\mathcal{G}},\unicode[STIX]{x1D713})\xrightarrow[{}]{\unicode[STIX]{x1D719}}(\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}},^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}))\mapsto {\mathcal{G}}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{G,N,I}\rightarrow \operatorname{Bun}_{G},\quad ((x_{i})_{i\in I},({\mathcal{G}},\unicode[STIX]{x1D713})\xrightarrow[{}]{\unicode[STIX]{x1D719}}(\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}},^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}))\mapsto {\mathcal{G}}.\end{eqnarray}$$ Similarly, we define  $\operatorname{Cht}_{M,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}$ (respectively
$\operatorname{Cht}_{M,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}$ (respectively  $\operatorname{Cht}_{M,N,I}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$,
$\operatorname{Cht}_{M,N,I}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$,  $\operatorname{Cht}_{M,N,I}^{(\unicode[STIX]{x1D706})}$) using the morphism
$\operatorname{Cht}_{M,N,I}^{(\unicode[STIX]{x1D706})}$) using the morphism  $\operatorname{Cht}_{M,N,I}\rightarrow \operatorname{Bun}_{M}$ and
$\operatorname{Cht}_{M,N,I}\rightarrow \operatorname{Bun}_{M}$ and  $\operatorname{Cht}_{P,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}$ (respectively
$\operatorname{Cht}_{P,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}$ (respectively  $\operatorname{Cht}_{P,N,I}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$) using the morphism
$\operatorname{Cht}_{P,N,I}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$) using the morphism  $\operatorname{Cht}_{P,N,I}\rightarrow \operatorname{Bun}_{P}$.
$\operatorname{Cht}_{P,N,I}\rightarrow \operatorname{Bun}_{P}$.
1.7.3
The following diagram is commutative

where the first line is defined in (1.4). We deduce that  $\operatorname{Cht}_{P,N,I}^{{\leqslant}\,\unicode[STIX]{x1D707}}$ is the inverse image of
$\operatorname{Cht}_{P,N,I}^{{\leqslant}\,\unicode[STIX]{x1D707}}$ is the inverse image of  $\operatorname{Cht}_{G,N,I}^{{\leqslant}\,\unicode[STIX]{x1D707}}$ in
$\operatorname{Cht}_{G,N,I}^{{\leqslant}\,\unicode[STIX]{x1D707}}$ in  $\operatorname{Cht}_{P,N,I}$.
$\operatorname{Cht}_{P,N,I}$.
Lemma 1.7.4. The image of  $\operatorname{Cht}_{P,N,I}^{{\leqslant}\,\unicode[STIX]{x1D707}}$ in
$\operatorname{Cht}_{P,N,I}^{{\leqslant}\,\unicode[STIX]{x1D707}}$ in  $\operatorname{Cht}_{M,N,I}$ is included in
$\operatorname{Cht}_{M,N,I}$ is included in  $\operatorname{Cht}_{M,N,I}^{{\leqslant}\,\unicode[STIX]{x1D707}}$.
$\operatorname{Cht}_{M,N,I}^{{\leqslant}\,\unicode[STIX]{x1D707}}$.
1.7.5
Just as in 1.6.3 and 1.6.4, morphisms (1.4) induce morphisms:
 $$\begin{eqnarray}\displaystyle & \operatorname{Cht}_{G,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\leftarrow \operatorname{Cht}_{P,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\rightarrow \operatorname{Cht}_{M,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \operatorname{Cht}_{G,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\leftarrow \operatorname{Cht}_{P,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\rightarrow \operatorname{Cht}_{M,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}, & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \operatorname{Cht}_{G,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\leftarrow \operatorname{Cht}_{P,N,I}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}\rightarrow \operatorname{Cht}_{M,N,I}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \operatorname{Cht}_{G,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\leftarrow \operatorname{Cht}_{P,N,I}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}\rightarrow \operatorname{Cht}_{M,N,I}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}. & \displaystyle\end{eqnarray}$$We deduce from (1.24) a decomposition:
 $$\begin{eqnarray}\operatorname{Cht}_{M,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}=\underset{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}}{\bigsqcup }\operatorname{Cht}_{M,N,I}^{{\leqslant}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{M,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}=\underset{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}}{\bigsqcup }\operatorname{Cht}_{M,N,I}^{{\leqslant}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}.\end{eqnarray}$$2 Cohomology of stacks of shtukas
In §§2.1–2.5 we recall the definition of the cohomology of stacks of  $G$-shtukas with values in perverse sheaves coming from
$G$-shtukas with values in perverse sheaves coming from  $[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}]$ via
$[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}]$ via  $\unicode[STIX]{x1D716}_{G,N,I,\infty }$, i.e. coming from
$\unicode[STIX]{x1D716}_{G,N,I,\infty }$, i.e. coming from  $G_{I,\infty }$-equivariant perverse sheaves over
$G_{I,\infty }$-equivariant perverse sheaves over  $\operatorname{Gr}_{G,I}$. These sections are based on [Reference LafforgueLaf18, §§1, 2 and 4].
$\operatorname{Gr}_{G,I}$. These sections are based on [Reference LafforgueLaf18, §§1, 2 and 4].
In §2.6 we define the cohomology of stacks of  $M$-shtukas.
$M$-shtukas.
Notation 2.0.1. Our results are of geometric nature, i.e. we will not consider the action of  $\text{Gal}(\overline{\mathbb{F}_{q}}/\mathbb{F}_{q})$. From now on, we pass to the base change over
$\text{Gal}(\overline{\mathbb{F}_{q}}/\mathbb{F}_{q})$. From now on, we pass to the base change over  $\overline{\mathbb{F}_{q}}$. We keep the same notations
$\overline{\mathbb{F}_{q}}$. We keep the same notations  $X$,
$X$,  $\operatorname{Bun}_{G,N}$,
$\operatorname{Bun}_{G,N}$,  $\operatorname{Cht}_{G,N,I}$,
$\operatorname{Cht}_{G,N,I}$,  $\operatorname{Gr}_{G,I}$, etc., but now everything is over
$\operatorname{Gr}_{G,I}$, etc., but now everything is over  $\overline{\mathbb{F}_{q}}$ and the fiber products are taken over
$\overline{\mathbb{F}_{q}}$ and the fiber products are taken over  $\overline{\mathbb{F}_{q}}$.
$\overline{\mathbb{F}_{q}}$.
2.1 Reminder of a generalization of the geometric Satake equivalence
2.1.1
The geometric Satake equivalence for the affine grassmannian is established in [Reference Mirkovic and VilonenMV07] over the ground field  $\mathbb{C}$. By [Reference Mirkovic and VilonenMV07, §14], [Reference GaitsgoryGai07, §1.6] and [Reference ZhuZhu17], the constructions in [Reference Mirkovic and VilonenMV07] carries over to the case of an arbitrary algebraically closed ground field of characteristic prime to
$\mathbb{C}$. By [Reference Mirkovic and VilonenMV07, §14], [Reference GaitsgoryGai07, §1.6] and [Reference ZhuZhu17], the constructions in [Reference Mirkovic and VilonenMV07] carries over to the case of an arbitrary algebraically closed ground field of characteristic prime to  $\ell$.
$\ell$.
2.1.2
Let  $\widehat{G}$ be the Langlands dual group of
$\widehat{G}$ be the Langlands dual group of  $G$ over
$G$ over  $\mathbb{Q}_{\ell }$ defined by the geometric Satake equivalence for the affine grassmannian, as in [Reference Mirkovic and VilonenMV07, Theorem 7.3] and [Reference GaitsgoryGai07, Theorem 2.2].
$\mathbb{Q}_{\ell }$ defined by the geometric Satake equivalence for the affine grassmannian, as in [Reference Mirkovic and VilonenMV07, Theorem 7.3] and [Reference GaitsgoryGai07, Theorem 2.2].
2.1.3
[Reference Mirkovic and VilonenMV07, §2], [Reference GaitsgoryGai01, 1.1.1 and §6] The Beilinson–Drinfeld affine grassmannian  $\operatorname{Gr}_{G,I}$ is an ind-scheme. Every finite-dimensional closed subscheme of
$\operatorname{Gr}_{G,I}$ is an ind-scheme. Every finite-dimensional closed subscheme of  $\operatorname{Gr}_{G,I}$ is contained in some finite-dimensional closed subscheme of
$\operatorname{Gr}_{G,I}$ is contained in some finite-dimensional closed subscheme of  $\operatorname{Gr}_{G,I}$ stable under the action of
$\operatorname{Gr}_{G,I}$ stable under the action of  $G_{I,\infty }$.
$G_{I,\infty }$.
We denote by  $\operatorname{Perv}_{G_{I,\infty }}(\operatorname{Gr}_{G,I},\mathbb{Q}_{\ell })$ the category of
$\operatorname{Perv}_{G_{I,\infty }}(\operatorname{Gr}_{G,I},\mathbb{Q}_{\ell })$ the category of  $G_{I,\infty }$-equivariant perverse sheaves with
$G_{I,\infty }$-equivariant perverse sheaves with  $\mathbb{Q}_{\ell }$-coefficients on
$\mathbb{Q}_{\ell }$-coefficients on  $\operatorname{Gr}_{G,I}$ (for the perverse normalization relative to
$\operatorname{Gr}_{G,I}$ (for the perverse normalization relative to  $X^{I}$).
$X^{I}$).
2.1.4
As in [Reference GaitsgoryGai07, 2.5], we denote by  $P^{\widehat{G},I}$ the category of perverse sheaves with
$P^{\widehat{G},I}$ the category of perverse sheaves with  $\mathbb{Q}_{\ell }$-coefficients on
$\mathbb{Q}_{\ell }$-coefficients on  $X^{I}$ (for the perverse normalization relative to
$X^{I}$ (for the perverse normalization relative to  $X^{I}$) endowed with an extra structure given in [Reference GaitsgoryGai07].
$X^{I}$) endowed with an extra structure given in [Reference GaitsgoryGai07].
Theorem 2.1.5 [Reference GaitsgoryGai07, Theorem 2.6].
There is a canonical equivalence of categories
 $$\begin{eqnarray}\operatorname{Perv}_{G_{I,\infty }}(\operatorname{Gr}_{G,I},\mathbb{Q}_{\ell })\overset{{\sim}}{\rightarrow }P^{\widehat{G},I},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Perv}_{G_{I,\infty }}(\operatorname{Gr}_{G,I},\mathbb{Q}_{\ell })\overset{{\sim}}{\rightarrow }P^{\widehat{G},I},\end{eqnarray}$$compatible with the tensor structures defined in [Reference GaitsgoryGai07].
2.1.6
We denote by  $\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{G}^{I})$ the category of finite-dimensional
$\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{G}^{I})$ the category of finite-dimensional  $\mathbb{Q}_{\ell }$-linear representations of
$\mathbb{Q}_{\ell }$-linear representations of  $\widehat{G}^{I}$. We have a fully faithful functor
$\widehat{G}^{I}$. We have a fully faithful functor  $\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{G}^{I})\rightarrow P^{\widehat{G},I}:W\mapsto W\otimes {\mathbb{Q}_{\ell }}_{X^{I}}$. The composition of this functor and the inverse functor
$\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{G}^{I})\rightarrow P^{\widehat{G},I}:W\mapsto W\otimes {\mathbb{Q}_{\ell }}_{X^{I}}$. The composition of this functor and the inverse functor  $P^{\widehat{G},I}\overset{{\sim}}{\rightarrow }\operatorname{Perv}_{G_{I,\infty }}(\operatorname{Gr}_{G,I},\mathbb{Q}_{\ell })$ in Theorem 2.1.5 gives the following.
$P^{\widehat{G},I}\overset{{\sim}}{\rightarrow }\operatorname{Perv}_{G_{I,\infty }}(\operatorname{Gr}_{G,I},\mathbb{Q}_{\ell })$ in Theorem 2.1.5 gives the following.
Corollary 2.1.7. We have a canonical natural fully faithful  $\mathbb{Q}_{\ell }$-linear fiber functor:
$\mathbb{Q}_{\ell }$-linear fiber functor:
 $$\begin{eqnarray}\text{Sat}_{G,I}:\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{G}^{I})\rightarrow \operatorname{Perv}_{G_{I,\infty }}(\operatorname{Gr}_{G,I},\mathbb{Q}_{\ell }).\end{eqnarray}$$
$$\begin{eqnarray}\text{Sat}_{G,I}:\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{G}^{I})\rightarrow \operatorname{Perv}_{G_{I,\infty }}(\operatorname{Gr}_{G,I},\mathbb{Q}_{\ell }).\end{eqnarray}$$Definition 2.1.8. For any  $W\in \operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{G}^{I})$, we define
$W\in \operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{G}^{I})$, we define  ${\mathcal{S}}_{G,I,W}:=\text{Sat}_{G,I}(W)$. We define
${\mathcal{S}}_{G,I,W}:=\text{Sat}_{G,I}(W)$. We define  $\operatorname{Gr}_{G,I,W}$ to be the support of
$\operatorname{Gr}_{G,I,W}$ to be the support of  ${\mathcal{S}}_{G,I,W}$.
${\mathcal{S}}_{G,I,W}$.
2.1.9
When  $W=W_{1}\oplus W_{2}$, by the functoriality of
$W=W_{1}\oplus W_{2}$, by the functoriality of  $\text{Sat}_{G,I}$, we have
$\text{Sat}_{G,I}$, we have  ${\mathcal{S}}_{G,I,W}={\mathcal{S}}_{G,I,W_{1}}\oplus {\mathcal{S}}_{G,I,W_{2}}$. Then
${\mathcal{S}}_{G,I,W}={\mathcal{S}}_{G,I,W_{1}}\oplus {\mathcal{S}}_{G,I,W_{2}}$. Then  $\operatorname{Gr}_{G,I,W}=\operatorname{Gr}_{G,I,W_{1}}\cup \operatorname{Gr}_{G,I,W_{2}}$.
$\operatorname{Gr}_{G,I,W}=\operatorname{Gr}_{G,I,W_{1}}\cup \operatorname{Gr}_{G,I,W_{2}}$.
2.1.10
By [Reference LafforgueLaf18, Théroème 1.17], the above definition of  $\operatorname{Gr}_{G,I,W}$ is equivalent to [Reference LafforgueLaf18, Définition 1.12 and the definition after (1.14)] (which describes
$\operatorname{Gr}_{G,I,W}$ is equivalent to [Reference LafforgueLaf18, Définition 1.12 and the definition after (1.14)] (which describes  $\operatorname{Gr}_{G,I,W}$ as a generalization of the Zariski closure of the Schubert cell in affine grassmannian). It is well known that
$\operatorname{Gr}_{G,I,W}$ as a generalization of the Zariski closure of the Schubert cell in affine grassmannian). It is well known that  $\operatorname{Gr}_{G,I,W}$ is a closed subscheme of
$\operatorname{Gr}_{G,I,W}$ is a closed subscheme of  $\operatorname{Gr}_{G,I}$ and that it is projective (see [Reference Mirkovic and VilonenMV07, §§2–3], [Reference ZhuZhu17, Proposition 2.1.5]). The ind-scheme
$\operatorname{Gr}_{G,I}$ and that it is projective (see [Reference Mirkovic and VilonenMV07, §§2–3], [Reference ZhuZhu17, Proposition 2.1.5]). The ind-scheme  $\operatorname{Gr}_{G,I}$ is an inductive limit of
$\operatorname{Gr}_{G,I}$ is an inductive limit of  $\operatorname{Gr}_{G,I,W}$. ‘
$\operatorname{Gr}_{G,I,W}$. ‘
Remark 2.1.11. By [Reference LafforgueLaf18, Théroème 1.17], when  $W$ is irreducible, the perverse sheaf
$W$ is irreducible, the perverse sheaf  ${\mathcal{S}}_{G,I,W}$ is (not canonically) isomorphic to the intersection complex (with coefficient in
${\mathcal{S}}_{G,I,W}$ is (not canonically) isomorphic to the intersection complex (with coefficient in  $\mathbb{Q}_{\ell }$ and the perverse normalization relative to
$\mathbb{Q}_{\ell }$ and the perverse normalization relative to  $X^{I}$) of
$X^{I}$) of  $\operatorname{Gr}_{G,I,W}$.
$\operatorname{Gr}_{G,I,W}$.
2.2 Satake perverse sheaves on quotient stacks
The stacks  $[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}]$ or
$[G_{I,\infty }\backslash \operatorname{Gr}_{G,I}]$ or  $[G_{I,\infty }\backslash \operatorname{Gr}_{G,I,W}]$ are not algebraic because the group scheme
$[G_{I,\infty }\backslash \operatorname{Gr}_{G,I,W}]$ are not algebraic because the group scheme  $G_{I,\infty }$ is of infinite dimension. For technical reasons, we will need algebraic stacks.
$G_{I,\infty }$ is of infinite dimension. For technical reasons, we will need algebraic stacks.
Proposition 2.2.1 [Reference GaitsgoryGai01, 1.1.1].
For  $d\in \mathbb{Z}_{{\geqslant}0}$ large enough depending on
$d\in \mathbb{Z}_{{\geqslant}0}$ large enough depending on  $W$, the action of
$W$, the action of  $\operatorname{Ker}(G_{I,\infty }\rightarrow G_{I,d})$ on
$\operatorname{Ker}(G_{I,\infty }\rightarrow G_{I,d})$ on  $\operatorname{Gr}_{G,I,W}$ is trivial. Thus the action of
$\operatorname{Gr}_{G,I,W}$ is trivial. Thus the action of  $G_{I,\infty }$ on
$G_{I,\infty }$ on  $\operatorname{Gr}_{G,I,W}$ factors through
$\operatorname{Gr}_{G,I,W}$ factors through  $G_{I,d}$.
$G_{I,d}$.
2.2.2
For  $d$ as in Proposition 2.2.1, we define the quotient stack
$d$ as in Proposition 2.2.1, we define the quotient stack  $[G_{I,d}\backslash \operatorname{Gr}_{G,I,W}]$. Since the group scheme
$[G_{I,d}\backslash \operatorname{Gr}_{G,I,W}]$. Since the group scheme  $G_{I,d}$ is of finite dimension, the stack
$G_{I,d}$ is of finite dimension, the stack  $[G_{I,d}\backslash \operatorname{Gr}_{G,I,W}]$ is algebraic.
$[G_{I,d}\backslash \operatorname{Gr}_{G,I,W}]$ is algebraic.
2.2.3
Let  ${\mathcal{S}}_{G,I,W}$ be the
${\mathcal{S}}_{G,I,W}$ be the  $G_{I,\infty }$-equivariant perverse sheaf on
$G_{I,\infty }$-equivariant perverse sheaf on  $\operatorname{Gr}_{G,I,W}$ defined in Definition 2.1.8. By Proposition 2.2.1, the action of
$\operatorname{Gr}_{G,I,W}$ defined in Definition 2.1.8. By Proposition 2.2.1, the action of  $G_{I,\infty }$ on
$G_{I,\infty }$ on  ${\mathcal{S}}_{G,I,W}$ factors through
${\mathcal{S}}_{G,I,W}$ factors through  $G_{I,d}$. Since the kernel of
$G_{I,d}$. Since the kernel of  $G_{I,\infty }{\twoheadrightarrow}G_{I,d}$ is connected, by [Reference Beilinson, Bernstein, Deligne and GabberBBDG82, Proposition 4.2.5], we deduce that
$G_{I,\infty }{\twoheadrightarrow}G_{I,d}$ is connected, by [Reference Beilinson, Bernstein, Deligne and GabberBBDG82, Proposition 4.2.5], we deduce that  ${\mathcal{S}}_{G,I,W}$ is also
${\mathcal{S}}_{G,I,W}$ is also  $G_{I,d}$-equivariant.
$G_{I,d}$-equivariant.
Let  $\unicode[STIX]{x1D709}_{G,I,d}:\operatorname{Gr}_{G,I,W}\rightarrow [G_{I,d}\backslash \operatorname{Gr}_{G,I,W}]$ be the canonical morphism. It is smooth of dimension
$\unicode[STIX]{x1D709}_{G,I,d}:\operatorname{Gr}_{G,I,W}\rightarrow [G_{I,d}\backslash \operatorname{Gr}_{G,I,W}]$ be the canonical morphism. It is smooth of dimension  $\dim G_{I,d}$. By [Reference Beilinson, Bernstein, Deligne and GabberBBDG82, Corollaire 4.2.6.2] and the discussion after it, there exists a perverse sheaf (up to shift
$\dim G_{I,d}$. By [Reference Beilinson, Bernstein, Deligne and GabberBBDG82, Corollaire 4.2.6.2] and the discussion after it, there exists a perverse sheaf (up to shift  $[\dim G_{I,d}]$) (for the perverse normalization relative to
$[\dim G_{I,d}]$) (for the perverse normalization relative to  $X^{I}$)
$X^{I}$)  ${\mathcal{S}}_{G,I,W}^{d}$ on
${\mathcal{S}}_{G,I,W}^{d}$ on  $[G_{I,d}\backslash \operatorname{Gr}_{G,I,W}]$ such that
$[G_{I,d}\backslash \operatorname{Gr}_{G,I,W}]$ such that  ${\mathcal{S}}_{G,I,W}=\unicode[STIX]{x1D709}_{G,I,d}^{\ast }{\mathcal{S}}_{G,I,W}^{d}$.
${\mathcal{S}}_{G,I,W}=\unicode[STIX]{x1D709}_{G,I,d}^{\ast }{\mathcal{S}}_{G,I,W}^{d}$.
2.2.4
Let  $d\leqslant d^{\prime }$ be two integers large enough as in Proposition 2.2.1. Then the morphisms
$d\leqslant d^{\prime }$ be two integers large enough as in Proposition 2.2.1. Then the morphisms  $G_{I,\infty }{\twoheadrightarrow}G_{I,d^{\prime }}{\twoheadrightarrow}G_{I,d}$ induce a commutative diagram.
$G_{I,\infty }{\twoheadrightarrow}G_{I,d^{\prime }}{\twoheadrightarrow}G_{I,d}$ induce a commutative diagram.

We have  $(\unicode[STIX]{x1D709}_{G,I,d^{\prime }})^{\ast }{\mathcal{S}}_{G,I,W}^{d^{\prime }}={\mathcal{S}}_{G,I,W}=(\unicode[STIX]{x1D709}_{G,I,d})^{\ast }{\mathcal{S}}_{G,I,W}^{d}=(\unicode[STIX]{x1D709}_{G,I,d^{\prime }})^{\ast }(\operatorname{pr}_{d^{\prime }}^{d})^{\ast }{\mathcal{S}}_{G,I,W}^{d}$. By [Reference Beilinson, Bernstein, Deligne and GabberBBDG82, Proposition 4.2.5], the functor
$(\unicode[STIX]{x1D709}_{G,I,d^{\prime }})^{\ast }{\mathcal{S}}_{G,I,W}^{d^{\prime }}={\mathcal{S}}_{G,I,W}=(\unicode[STIX]{x1D709}_{G,I,d})^{\ast }{\mathcal{S}}_{G,I,W}^{d}=(\unicode[STIX]{x1D709}_{G,I,d^{\prime }})^{\ast }(\operatorname{pr}_{d^{\prime }}^{d})^{\ast }{\mathcal{S}}_{G,I,W}^{d}$. By [Reference Beilinson, Bernstein, Deligne and GabberBBDG82, Proposition 4.2.5], the functor  $(\unicode[STIX]{x1D709}_{G,I,d^{\prime }})^{\ast }$ (up to shift) is fully faithful. We deduce that
$(\unicode[STIX]{x1D709}_{G,I,d^{\prime }})^{\ast }$ (up to shift) is fully faithful. We deduce that  ${\mathcal{S}}_{G,I,W}^{d^{\prime }}=(\operatorname{pr}_{d^{\prime }}^{d})^{\ast }{\mathcal{S}}_{G,I,W}^{d}$.
${\mathcal{S}}_{G,I,W}^{d^{\prime }}=(\operatorname{pr}_{d^{\prime }}^{d})^{\ast }{\mathcal{S}}_{G,I,W}^{d}$.
2.2.5
By Proposition 2.2.1, the action of  $G_{I,\infty }^{\text{ad}}$ on
$G_{I,\infty }^{\text{ad}}$ on  $\operatorname{Gr}_{G,I,W}$ factors through
$\operatorname{Gr}_{G,I,W}$ factors through  $G_{I,d}^{\text{ad}}$. We define the quotient stack
$G_{I,d}^{\text{ad}}$. We define the quotient stack  $[G_{I,d}^{\text{ad}}\backslash \operatorname{Gr}_{G,I,W}]$.
$[G_{I,d}^{\text{ad}}\backslash \operatorname{Gr}_{G,I,W}]$.
As in the discussion after [Reference LafforgueLaf18, Définition 2.14], since  $(Z_{G})_{I,\infty }$ acts trivially on
$(Z_{G})_{I,\infty }$ acts trivially on  $\operatorname{Gr}_{G,I,W}$, the
$\operatorname{Gr}_{G,I,W}$, the  $G_{I,\infty }$-equivariant perverse sheaf
$G_{I,\infty }$-equivariant perverse sheaf  ${\mathcal{S}}_{G,I,W}$ on
${\mathcal{S}}_{G,I,W}$ on  $\operatorname{Gr}_{G,I,W}$ is also
$\operatorname{Gr}_{G,I,W}$ is also  $G_{I,\infty }^{\text{ad}}$-equivariant and
$G_{I,\infty }^{\text{ad}}$-equivariant and  $G_{I,d}^{\text{ad}}$-equivariant. Indeed, by 2.1.9 it is enough to prove this for
$G_{I,d}^{\text{ad}}$-equivariant. Indeed, by 2.1.9 it is enough to prove this for  $W$ irreducible. By Remark 2.1.11, in this case
$W$ irreducible. By Remark 2.1.11, in this case  ${\mathcal{S}}_{G,I,W}$ is isomorphic to the intersection complex of
${\mathcal{S}}_{G,I,W}$ is isomorphic to the intersection complex of  $\operatorname{Gr}_{G,I,W}$, hence is
$\operatorname{Gr}_{G,I,W}$, hence is  $G_{I,\infty }^{\text{ad}}$-equivariant.
$G_{I,\infty }^{\text{ad}}$-equivariant.
Just as in 2.2.3, let  $\unicode[STIX]{x1D709}_{G,I,d}^{\text{ad}}:\operatorname{Gr}_{G,I,W}\rightarrow [G_{I,d}^{\text{ad}}\backslash \operatorname{Gr}_{G,I,W}]$ be the canonical morphism. There exists a perverse sheaf (up to shift
$\unicode[STIX]{x1D709}_{G,I,d}^{\text{ad}}:\operatorname{Gr}_{G,I,W}\rightarrow [G_{I,d}^{\text{ad}}\backslash \operatorname{Gr}_{G,I,W}]$ be the canonical morphism. There exists a perverse sheaf (up to shift  $[\dim G_{I,d}^{\text{ad}}]$) (for the perverse normalization relative to
$[\dim G_{I,d}^{\text{ad}}]$) (for the perverse normalization relative to  $X^{I}$)
$X^{I}$)  ${\mathcal{S}}_{G,I,W}^{\text{ad},\,d}$ on
${\mathcal{S}}_{G,I,W}^{\text{ad},\,d}$ on  $[G_{I,d}^{\text{ad}}\backslash \operatorname{Gr}_{G,I,W}]$ such that
$[G_{I,d}^{\text{ad}}\backslash \operatorname{Gr}_{G,I,W}]$ such that  ${\mathcal{S}}_{G,I,W}=(\unicode[STIX]{x1D709}_{G,I,d}^{\text{ad}})^{\ast }{\mathcal{S}}_{G,I,W}^{\text{ad},\,d}$.
${\mathcal{S}}_{G,I,W}=(\unicode[STIX]{x1D709}_{G,I,d}^{\text{ad}})^{\ast }{\mathcal{S}}_{G,I,W}^{\text{ad},\,d}$.
2.3 Representability of stacks of shtukas
Definition 2.3.1. We define  $\operatorname{Cht}_{G,N,I,W}$ to be the inverse image of
$\operatorname{Cht}_{G,N,I,W}$ to be the inverse image of  $[G_{I,\infty }\backslash \operatorname{Gr}_{G,I,W}]$ in
$[G_{I,\infty }\backslash \operatorname{Gr}_{G,I,W}]$ in  $\operatorname{Cht}_{G,N,I}$ by
$\operatorname{Cht}_{G,N,I}$ by  $\unicode[STIX]{x1D716}_{G,N,I,\infty }$.
$\unicode[STIX]{x1D716}_{G,N,I,\infty }$.
2.3.2
 $\operatorname{Cht}_{G,N,I}$ is an inductive limit of closed subtacks
$\operatorname{Cht}_{G,N,I}$ is an inductive limit of closed subtacks  $\operatorname{Cht}_{G,N,I,W}$.
$\operatorname{Cht}_{G,N,I,W}$.
2.3.3
Let  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. We define
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. We define  $\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}:=\operatorname{Cht}_{G,N,I,W}\cap \operatorname{Cht}_{G,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}$, where
$\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}:=\operatorname{Cht}_{G,N,I,W}\cap \operatorname{Cht}_{G,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}$, where  $\operatorname{Cht}_{G,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}$ is defined in Definition 1.7.2. We define the quotient
$\operatorname{Cht}_{G,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}$ is defined in Definition 1.7.2. We define the quotient  $\operatorname{Cht}_{G,N,I,W}/\unicode[STIX]{x1D6EF}$ and
$\operatorname{Cht}_{G,N,I,W}/\unicode[STIX]{x1D6EF}$ and  $\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}$.
$\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}$.
Proposition 2.3.4 [Reference VarshavskyVar04, Proposition 2.16].
The stack  $\operatorname{Cht}_{G,N,I,W}$ is a Deligne–Mumford stack locally of finite type. The stack
$\operatorname{Cht}_{G,N,I,W}$ is a Deligne–Mumford stack locally of finite type. The stack  $\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}$ is a Deligne–Mumford stack of finite type.
$\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}$ is a Deligne–Mumford stack of finite type.
2.3.5
The stack 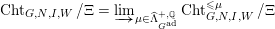 $\operatorname{Cht}_{G,N,I,W}/\unicode[STIX]{x1D6EF}=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}}\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}$ is locally of finite type.
$\operatorname{Cht}_{G,N,I,W}/\unicode[STIX]{x1D6EF}=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}}\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}$ is locally of finite type.
2.4 Satake perverse sheaf on stacks of shtukas
2.4.1
For any  $d\in \mathbb{Z}_{{\geqslant}0}$ large enough as in Proposition 2.2.1, we define
$d\in \mathbb{Z}_{{\geqslant}0}$ large enough as in Proposition 2.2.1, we define  $\unicode[STIX]{x1D716}_{G,N,I,d}$ to be the composition of morphisms
$\unicode[STIX]{x1D716}_{G,N,I,d}$ to be the composition of morphisms
 $$\begin{eqnarray}\unicode[STIX]{x1D716}_{G,N,I,d}:\operatorname{Cht}_{G,N,I,W}\xrightarrow[{}]{\unicode[STIX]{x1D716}_{G,N,I,\infty }}[G_{I,\infty }\backslash \operatorname{Gr}_{G,I,W}]\rightarrow [G_{I,d}\backslash \operatorname{Gr}_{G,I,W}].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}_{G,N,I,d}:\operatorname{Cht}_{G,N,I,W}\xrightarrow[{}]{\unicode[STIX]{x1D716}_{G,N,I,\infty }}[G_{I,\infty }\backslash \operatorname{Gr}_{G,I,W}]\rightarrow [G_{I,d}\backslash \operatorname{Gr}_{G,I,W}].\end{eqnarray}$$This is morphism (2.3) in [Reference LafforgueLaf18].
Just as in 1.3.2, we define a morphism
 $$\begin{eqnarray}\unicode[STIX]{x1D716}_{G,N,I,d}^{\unicode[STIX]{x1D6EF}}:\operatorname{Cht}_{G,N,I,W}/\unicode[STIX]{x1D6EF}\rightarrow [G_{I,d}^{\text{ad}}\backslash \operatorname{Gr}_{G,I,W}].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}_{G,N,I,d}^{\unicode[STIX]{x1D6EF}}:\operatorname{Cht}_{G,N,I,W}/\unicode[STIX]{x1D6EF}\rightarrow [G_{I,d}^{\text{ad}}\backslash \operatorname{Gr}_{G,I,W}].\end{eqnarray}$$This is morphism (2.10) in [Reference LafforgueLaf18].
2.4.2
We denote by  $\dim _{X^{I}}G_{I,d}$ the relative dimension of
$\dim _{X^{I}}G_{I,d}$ the relative dimension of  $G_{I,d}$ over
$G_{I,d}$ over  $X^{I}$ and by
$X^{I}$ and by  $|I|$ the cardinal of
$|I|$ the cardinal of  $I$. We have
$I$. We have  $\dim _{X^{I}}G_{I,d}=d\cdot |I|\cdot \operatorname{dim}G$.
$\dim _{X^{I}}G_{I,d}=d\cdot |I|\cdot \operatorname{dim}G$.
Proposition 2.4.3 [Reference LafforgueLaf18, Proposition 2.8].
The morphisms  $\unicode[STIX]{x1D716}_{G,N,I,d}$ (respectively
$\unicode[STIX]{x1D716}_{G,N,I,d}$ (respectively  $\unicode[STIX]{x1D716}_{G,N,I,d}^{\unicode[STIX]{x1D6EF}}$) is smooth of dimension
$\unicode[STIX]{x1D716}_{G,N,I,d}^{\unicode[STIX]{x1D6EF}}$) is smooth of dimension  $\dim _{X^{I}}G_{I,d}$ (respectively
$\dim _{X^{I}}G_{I,d}$ (respectively  $\dim _{X^{I}}G_{I,d}^{\text{ad}}$).
$\dim _{X^{I}}G_{I,d}^{\text{ad}}$).
2.4.4
For all  $d\in \mathbb{Z}_{{\geqslant}0}$ large enough as in Proposition 2.2.1, we have morphisms over
$d\in \mathbb{Z}_{{\geqslant}0}$ large enough as in Proposition 2.2.1, we have morphisms over  $(X\smallsetminus N)^{I}$.
$(X\smallsetminus N)^{I}$.

We deduce from Proposition 2.4.3 that  $\dim \operatorname{Cht}_{G,N,I,W}=\dim \operatorname{Gr}_{G,I,W}$. We refer to [Reference LafforgueLaf18, Proposition 2.11] for the fact that
$\dim \operatorname{Cht}_{G,N,I,W}=\dim \operatorname{Gr}_{G,I,W}$. We refer to [Reference LafforgueLaf18, Proposition 2.11] for the fact that  $\operatorname{Cht}_{G,N,I,W}$ is locally isomorphic to
$\operatorname{Cht}_{G,N,I,W}$ is locally isomorphic to  $\operatorname{Gr}_{G,I,W}$ for the étale topology. We will not use this result in this paper.
$\operatorname{Gr}_{G,I,W}$ for the étale topology. We will not use this result in this paper.
Definition 2.4.5. Let  $d\in \mathbb{Z}_{{\geqslant}0}$ large enough as in Proposition 2.2.1. We define
$d\in \mathbb{Z}_{{\geqslant}0}$ large enough as in Proposition 2.2.1. We define  ${\mathcal{F}}_{G,N,I,W}:=(\unicode[STIX]{x1D716}_{G,N,I,d})^{\ast }{\mathcal{S}}_{G,I,W}^{d}$.
${\mathcal{F}}_{G,N,I,W}:=(\unicode[STIX]{x1D716}_{G,N,I,d})^{\ast }{\mathcal{S}}_{G,I,W}^{d}$.
Remark 2.4.6. As in 2.2.4, let  $d,d^{\prime }\in \mathbb{Z}_{{\geqslant}0}$ both large enough with
$d,d^{\prime }\in \mathbb{Z}_{{\geqslant}0}$ both large enough with  $d\leqslant d^{\prime }$. Then we have
$d\leqslant d^{\prime }$. Then we have  $\unicode[STIX]{x1D716}_{G,N,I,d}=\operatorname{pr}_{d^{\prime }}^{d}\circ \,\unicode[STIX]{x1D716}_{G,N,I,d^{\prime }}$. Thus
$\unicode[STIX]{x1D716}_{G,N,I,d}=\operatorname{pr}_{d^{\prime }}^{d}\circ \,\unicode[STIX]{x1D716}_{G,N,I,d^{\prime }}$. Thus  $(\unicode[STIX]{x1D716}_{G,N,I,d})^{\ast }{\mathcal{S}}_{G,I,W}^{d}=(\unicode[STIX]{x1D716}_{G,N,I,d^{\prime }})^{\ast }(\operatorname{pr}_{d^{\prime }}^{d})^{\ast }{\mathcal{S}}_{G,I,W}^{d}=(\unicode[STIX]{x1D716}_{G,N,I,d^{\prime }})^{\ast }{\mathcal{S}}_{G,I,W}^{d^{\prime }}$. Hence
$(\unicode[STIX]{x1D716}_{G,N,I,d})^{\ast }{\mathcal{S}}_{G,I,W}^{d}=(\unicode[STIX]{x1D716}_{G,N,I,d^{\prime }})^{\ast }(\operatorname{pr}_{d^{\prime }}^{d})^{\ast }{\mathcal{S}}_{G,I,W}^{d}=(\unicode[STIX]{x1D716}_{G,N,I,d^{\prime }})^{\ast }{\mathcal{S}}_{G,I,W}^{d^{\prime }}$. Hence  ${\mathcal{F}}_{G,N,I,W}$ is independent of
${\mathcal{F}}_{G,N,I,W}$ is independent of  $d$.
$d$.
Definition 2.4.7. We define  ${\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}:=(\unicode[STIX]{x1D716}_{G,N,I,d}^{\unicode[STIX]{x1D6EF}})^{\ast }{\mathcal{S}}_{G,I,W}^{\text{ad},\,d}$.
${\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}:=(\unicode[STIX]{x1D716}_{G,N,I,d}^{\unicode[STIX]{x1D6EF}})^{\ast }{\mathcal{S}}_{G,I,W}^{\text{ad},\,d}$.
Just as in Remark 2.4.6,  ${\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}$ is independent of
${\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}$ is independent of  $d$.
$d$.
Lemma 2.4.8. The complex  ${\mathcal{F}}_{G,N,I,W}$ (respectively
${\mathcal{F}}_{G,N,I,W}$ (respectively  ${\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}$) is a perverse sheaf (for the perverse normalization relative to
${\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}$) is a perverse sheaf (for the perverse normalization relative to  $(X\smallsetminus N)^{I}$) on
$(X\smallsetminus N)^{I}$) on  $\operatorname{Cht}_{G,N,I}$ (respectively
$\operatorname{Cht}_{G,N,I}$ (respectively  $\operatorname{Cht}_{G,N,I}/\unicode[STIX]{x1D6EF}$) supported on
$\operatorname{Cht}_{G,N,I}/\unicode[STIX]{x1D6EF}$) supported on  $\operatorname{Cht}_{G,N,I,W}$ (respectively
$\operatorname{Cht}_{G,N,I,W}$ (respectively  $\operatorname{Cht}_{G,N,I,W}/\unicode[STIX]{x1D6EF}$) (in the context of 0.0.13). When
$\operatorname{Cht}_{G,N,I,W}/\unicode[STIX]{x1D6EF}$) (in the context of 0.0.13). When  $W$ is irreducible,
$W$ is irreducible,  ${\mathcal{F}}_{G,N,I,W}$ (respectively
${\mathcal{F}}_{G,N,I,W}$ (respectively  ${\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}$) is (not canonically) isomorphic to the intersection complex (with coefficient in
${\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}$) is (not canonically) isomorphic to the intersection complex (with coefficient in  $\mathbb{Q}_{\ell }$ and the perverse normalization relative to
$\mathbb{Q}_{\ell }$ and the perverse normalization relative to  $(X\smallsetminus N)^{I}$) of
$(X\smallsetminus N)^{I}$) of  $\operatorname{Cht}_{G,N,I,W}$ (respectively
$\operatorname{Cht}_{G,N,I,W}$ (respectively  $\operatorname{Cht}_{G,N,I,W}/\unicode[STIX]{x1D6EF}$).
$\operatorname{Cht}_{G,N,I,W}/\unicode[STIX]{x1D6EF}$).
2.5 Cohomology of stacks of  $G$-shtukas
$G$-shtukas
Recall that we have the morphism of paws  $\mathfrak{p}_{G}:\operatorname{Cht}_{G,I,N}/\unicode[STIX]{x1D6EF}\rightarrow (X\smallsetminus N)^{I}$.
$\mathfrak{p}_{G}:\operatorname{Cht}_{G,I,N}/\unicode[STIX]{x1D6EF}\rightarrow (X\smallsetminus N)^{I}$.
Definition 2.5.1 [Reference LafforgueLaf18, Definitions 4.1 and 4.7].
For any  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, we define
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, we define
 $$\begin{eqnarray}{\mathcal{H}}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}:=R(\mathfrak{p}_{G})_{!}(\left.{\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}\vphantom{\big|}\right|_{\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}})\in D_{c}^{b}((X\smallsetminus N)^{I},\mathbb{Q}_{\ell }).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}:=R(\mathfrak{p}_{G})_{!}(\left.{\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}\vphantom{\big|}\right|_{\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}})\in D_{c}^{b}((X\smallsetminus N)^{I},\mathbb{Q}_{\ell }).\end{eqnarray}$$ For any  $j\in \mathbb{Z}$, we define degree
$j\in \mathbb{Z}$, we define degree  $j$ cohomology sheaf (for the ordinary
$j$ cohomology sheaf (for the ordinary  $t$-structure)
$t$-structure)
 $$\begin{eqnarray}{\mathcal{H}}_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}}:=R^{j}(\mathfrak{p}_{G})_{!}(\left.{\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}\vphantom{\big|}\right|_{\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}}:=R^{j}(\mathfrak{p}_{G})_{!}(\left.{\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}\vphantom{\big|}\right|_{\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}}).\end{eqnarray}$$ This is a  $\mathbb{Q}_{\ell }$-constructible sheaf on
$\mathbb{Q}_{\ell }$-constructible sheaf on  $(X\smallsetminus N)^{I}$.
$(X\smallsetminus N)^{I}$.
The complex  ${\mathcal{H}}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}$ and the sheaf
${\mathcal{H}}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}$ and the sheaf  ${\mathcal{H}}_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}}$ depend on
${\mathcal{H}}_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}}$ depend on  $\unicode[STIX]{x1D6EF}$. We do not write
$\unicode[STIX]{x1D6EF}$. We do not write  $\unicode[STIX]{x1D6EF}$ in the index to simplify the notations.
$\unicode[STIX]{x1D6EF}$ in the index to simplify the notations.
2.5.2
Let  $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and
$\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and  $\unicode[STIX]{x1D707}_{1}\leqslant \unicode[STIX]{x1D707}_{2}$. We have an open immersion:
$\unicode[STIX]{x1D707}_{1}\leqslant \unicode[STIX]{x1D707}_{2}$. We have an open immersion:
 $$\begin{eqnarray}\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}_{1}}/\unicode[STIX]{x1D6EF}{\hookrightarrow}\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}_{2}}/\unicode[STIX]{x1D6EF}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}_{1}}/\unicode[STIX]{x1D6EF}{\hookrightarrow}\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}_{2}}/\unicode[STIX]{x1D6EF}.\end{eqnarray}$$ For any  $j$, morphism (2.4) induces a morphism of sheaves:
$j$, morphism (2.4) induces a morphism of sheaves:
 $$\begin{eqnarray}{\mathcal{H}}_{G,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}_{1}}\rightarrow {\mathcal{H}}_{G,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}_{2}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}_{G,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}_{1}}\rightarrow {\mathcal{H}}_{G,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}_{2}}.\end{eqnarray}$$Definition 2.5.3. We define

as an inductive limit in the category of constructible sheaves on  $(X\smallsetminus N)^{I}$.
$(X\smallsetminus N)^{I}$.
2.5.4
Let  $\overline{\unicode[STIX]{x1D702}^{I}}$ be a geometric point over the generic point
$\overline{\unicode[STIX]{x1D702}^{I}}$ be a geometric point over the generic point  $\unicode[STIX]{x1D702}^{I}$ of
$\unicode[STIX]{x1D702}^{I}$ of  $X^{I}$.
$X^{I}$.
Definition 2.5.5. We define
 $$\begin{eqnarray}H_{G,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}}:=\left.{\mathcal{H}}_{G,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}}\vphantom{\big|}\right|_{\overline{\unicode[STIX]{x1D702}^{I}}}\;,\quad H_{G,N,I,W}^{j}:=\left.{\mathcal{H}}_{G,N,I,W}^{j}\vphantom{\big|}\right|_{\overline{\unicode[STIX]{x1D702}^{I}}}\,.\end{eqnarray}$$
$$\begin{eqnarray}H_{G,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}}:=\left.{\mathcal{H}}_{G,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}}\vphantom{\big|}\right|_{\overline{\unicode[STIX]{x1D702}^{I}}}\;,\quad H_{G,N,I,W}^{j}:=\left.{\mathcal{H}}_{G,N,I,W}^{j}\vphantom{\big|}\right|_{\overline{\unicode[STIX]{x1D702}^{I}}}\,.\end{eqnarray}$$ By definition  $H_{G,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}}$ is a
$H_{G,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}}$ is a  $\mathbb{Q}_{\ell }$-vector space of finite dimension. We have
$\mathbb{Q}_{\ell }$-vector space of finite dimension. We have  $H_{G,N,I,W}^{j}=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}}H_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}}$.
$H_{G,N,I,W}^{j}=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}}H_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}}$.
2.6 Cohomology of stacks of  $M$-shtukas
$M$-shtukas
Let  $P$ be a proper parabolic subgroup of
$P$ be a proper parabolic subgroup of  $G$ and let
$G$ and let  $M$ be its Levi quotient.
$M$ be its Levi quotient.
2.6.1
Let  $\widehat{M}$ be the Langlands dual group of
$\widehat{M}$ be the Langlands dual group of  $M$ over
$M$ over  $\mathbb{Q}_{\ell }$ defined by the geometric Satake equivalence. The compatibility between the geometric Satake equivalence and the constant term functor along
$\mathbb{Q}_{\ell }$ defined by the geometric Satake equivalence. The compatibility between the geometric Satake equivalence and the constant term functor along  $P$ (that we will recall in Theorem 3.2.6 below) induces a canonical inclusion
$P$ (that we will recall in Theorem 3.2.6 below) induces a canonical inclusion  $\widehat{M}{\hookrightarrow}\widehat{G}$ (compatible with pinning).
$\widehat{M}{\hookrightarrow}\widehat{G}$ (compatible with pinning).
2.6.2
We view  $W\in \operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{G}^{I})$ as a representation of
$W\in \operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{G}^{I})$ as a representation of  $\widehat{M}^{I}$ via
$\widehat{M}^{I}$ via  $\widehat{M}^{I}{\hookrightarrow}\widehat{G}^{I}$. As in §§2.1–2.4, we define
$\widehat{M}^{I}{\hookrightarrow}\widehat{G}^{I}$. As in §§2.1–2.4, we define  $\operatorname{Gr}_{M,I,W}$ and
$\operatorname{Gr}_{M,I,W}$ and  $\operatorname{Cht}_{M,N,I,W}$. For
$\operatorname{Cht}_{M,N,I,W}$. For  $d\in \mathbb{Z}_{{\geqslant}0}$ large enough such that the action of
$d\in \mathbb{Z}_{{\geqslant}0}$ large enough such that the action of  $M_{I,\infty }$ on
$M_{I,\infty }$ on  $\operatorname{Gr}_{M,I,W}$ factors through
$\operatorname{Gr}_{M,I,W}$ factors through  $M_{I,d}$, we define
$M_{I,d}$, we define
 $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D716}_{M,N,I,d}:\operatorname{Cht}_{M,N,I,W}\rightarrow [M_{I,d}\backslash \operatorname{Gr}_{M,I,W}], & \displaystyle \nonumber\\ \displaystyle & \unicode[STIX]{x1D716}_{M,N,I,d}^{\unicode[STIX]{x1D6EF}}:\operatorname{Cht}_{M,N,I,W}/\unicode[STIX]{x1D6EF}\rightarrow [\overline{M}_{I,d}\backslash \operatorname{Gr}_{M,I,W}]. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D716}_{M,N,I,d}:\operatorname{Cht}_{M,N,I,W}\rightarrow [M_{I,d}\backslash \operatorname{Gr}_{M,I,W}], & \displaystyle \nonumber\\ \displaystyle & \unicode[STIX]{x1D716}_{M,N,I,d}^{\unicode[STIX]{x1D6EF}}:\operatorname{Cht}_{M,N,I,W}/\unicode[STIX]{x1D6EF}\rightarrow [\overline{M}_{I,d}\backslash \operatorname{Gr}_{M,I,W}]. & \displaystyle \nonumber\end{eqnarray}$$ We define perverse sheaf  ${\mathcal{S}}_{M,I,W}$ on
${\mathcal{S}}_{M,I,W}$ on  $\operatorname{Gr}_{M,I,W}$, perverse sheaves (up to shift)
$\operatorname{Gr}_{M,I,W}$, perverse sheaves (up to shift)  ${\mathcal{S}}_{M,I,W}^{d}$ on
${\mathcal{S}}_{M,I,W}^{d}$ on  $[M_{I,d}\backslash \operatorname{Gr}_{M,I,W}]$ and
$[M_{I,d}\backslash \operatorname{Gr}_{M,I,W}]$ and  ${\mathcal{S}}_{M,I,W}^{\text{ad},d}$ on
${\mathcal{S}}_{M,I,W}^{\text{ad},d}$ on  $[\overline{M}_{I,d}\backslash \operatorname{Gr}_{M,I,W}]$. We define
$[\overline{M}_{I,d}\backslash \operatorname{Gr}_{M,I,W}]$. We define
 $$\begin{eqnarray}{\mathcal{F}}_{M,N,I,W}:=\unicode[STIX]{x1D716}_{M,N,I,d}^{\ast }{\mathcal{S}}_{M,I,W}^{d}\quad \text{and}\quad {\mathcal{F}}_{M,N,I,W}^{\unicode[STIX]{x1D6EF}}:=(\unicode[STIX]{x1D716}_{M,N,I,d}^{\unicode[STIX]{x1D6EF}})^{\ast }{\mathcal{S}}_{M,I,W}^{\text{ad},d}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{M,N,I,W}:=\unicode[STIX]{x1D716}_{M,N,I,d}^{\ast }{\mathcal{S}}_{M,I,W}^{d}\quad \text{and}\quad {\mathcal{F}}_{M,N,I,W}^{\unicode[STIX]{x1D6EF}}:=(\unicode[STIX]{x1D716}_{M,N,I,d}^{\unicode[STIX]{x1D6EF}})^{\ast }{\mathcal{S}}_{M,I,W}^{\text{ad},d}.\end{eqnarray}$$2.6.3
Applying [Reference VarshavskyVar04, Proposition 2.16] to  $M$, we deduce that
$M$, we deduce that  $\operatorname{Cht}_{M,I,N,W}$ is a Deligne–Mumford stack locally of finite type and that for
$\operatorname{Cht}_{M,I,N,W}$ is a Deligne–Mumford stack locally of finite type and that for  $\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}}$, the Deligne–Mumford stack
$\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}}$, the Deligne–Mumford stack  $\operatorname{Cht}_{M,I,N,W}^{(\unicode[STIX]{x1D706})}$ (defined in Definition 1.7.2) is of finite type.
$\operatorname{Cht}_{M,I,N,W}^{(\unicode[STIX]{x1D706})}$ (defined in Definition 1.7.2) is of finite type.
Let  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. We define
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. We define  $\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}:=\operatorname{Cht}_{M,N,I,W}\cap \operatorname{Cht}_{M,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}$, where
$\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}:=\operatorname{Cht}_{M,N,I,W}\cap \operatorname{Cht}_{M,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}$, where  $\operatorname{Cht}_{M,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}$ is defined in Definition 1.7.2. We define the quotient
$\operatorname{Cht}_{M,N,I}^{{\leqslant}\unicode[STIX]{x1D707}}$ is defined in Definition 1.7.2. We define the quotient  $\operatorname{Cht}_{M,N,I,W}/\unicode[STIX]{x1D6EF}$ and
$\operatorname{Cht}_{M,N,I,W}/\unicode[STIX]{x1D6EF}$ and  $\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}$. As in 1.5.6,
$\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}$. As in 1.5.6,  $\unicode[STIX]{x1D6EF}$ is a lattice in
$\unicode[STIX]{x1D6EF}$ is a lattice in  $Z_{G}(F)\backslash Z_{G}(\mathbb{A})$ but only a discrete subgroup in
$Z_{G}(F)\backslash Z_{G}(\mathbb{A})$ but only a discrete subgroup in  $Z_{M}(F)\backslash Z_{M}(\mathbb{A})$. The decomposition (1.31) induces a decomposition
$Z_{M}(F)\backslash Z_{M}(\mathbb{A})$. The decomposition (1.31) induces a decomposition
 $$\begin{eqnarray}\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}=\underset{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}}{\bigsqcup }\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}=\underset{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}}{\bigsqcup }\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF},\end{eqnarray}$$ where each  $\operatorname{Cht}_{M,I,N,W}^{{\leqslant}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}$ is of finite type (just as in Lemma 1.5.19).
$\operatorname{Cht}_{M,I,N,W}^{{\leqslant}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}$ is of finite type (just as in Lemma 1.5.19).
Recall that we have the morphism of paws  $\mathfrak{p}_{M}:\operatorname{Cht}_{M,I,N}/\unicode[STIX]{x1D6EF}\rightarrow (X\smallsetminus N)^{I}$.
$\mathfrak{p}_{M}:\operatorname{Cht}_{M,I,N}/\unicode[STIX]{x1D6EF}\rightarrow (X\smallsetminus N)^{I}$.
Definition 2.6.4. For any  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and  $\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$, we define
$\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$, we define
 $$\begin{eqnarray}{\mathcal{H}}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}:=R(\mathfrak{p}_{M})_{!}(\left.{\mathcal{F}}_{M,I,N,W}^{\unicode[STIX]{x1D6EF}}\vphantom{\big|}\right|_{\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}})\in D_{c}^{b}((X\smallsetminus N)^{I},\mathbb{Q}_{\ell }).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}:=R(\mathfrak{p}_{M})_{!}(\left.{\mathcal{F}}_{M,I,N,W}^{\unicode[STIX]{x1D6EF}}\vphantom{\big|}\right|_{\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}})\in D_{c}^{b}((X\smallsetminus N)^{I},\mathbb{Q}_{\ell }).\end{eqnarray}$$ For any  $j\in \mathbb{Z}$, we define degree
$j\in \mathbb{Z}$, we define degree  $j$ cohomology sheaf
$j$ cohomology sheaf
 $$\begin{eqnarray}{\mathcal{H}}_{M,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}:=R^{j}(\mathfrak{p}_{M})_{!}(\left.{\mathcal{F}}_{M,I,N,W}^{\unicode[STIX]{x1D6EF}}\vphantom{\big|}\right|_{\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}_{M,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}:=R^{j}(\mathfrak{p}_{M})_{!}(\left.{\mathcal{F}}_{M,I,N,W}^{\unicode[STIX]{x1D6EF}}\vphantom{\big|}\right|_{\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}}).\end{eqnarray}$$2.6.5
If  $\unicode[STIX]{x1D708}\notin \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}$, by Lemma 1.5.14,
$\unicode[STIX]{x1D708}\notin \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}$, by Lemma 1.5.14,  $\operatorname{Cht}_{M,I,N,W}^{{\leqslant}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}=\emptyset$. In this case
$\operatorname{Cht}_{M,I,N,W}^{{\leqslant}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}=\emptyset$. In this case  ${\mathcal{H}}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}=0$.
${\mathcal{H}}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}=0$.
Definition 2.6.6. Let  $\overline{\unicode[STIX]{x1D702}^{I}}$ be the geometric generic point of
$\overline{\unicode[STIX]{x1D702}^{I}}$ be the geometric generic point of  $X^{I}$ fixed in 2.5.4. We define
$X^{I}$ fixed in 2.5.4. We define
 $$\begin{eqnarray}H_{M,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}:=\left.{\mathcal{H}}_{M,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}\vphantom{\big|}\right|_{\overline{\unicode[STIX]{x1D702}^{I}}}\,.\end{eqnarray}$$
$$\begin{eqnarray}H_{M,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}:=\left.{\mathcal{H}}_{M,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}\vphantom{\big|}\right|_{\overline{\unicode[STIX]{x1D702}^{I}}}\,.\end{eqnarray}$$ This is a finite-dimensional  $\mathbb{Q}_{\ell }$-vector space. We define
$\mathbb{Q}_{\ell }$-vector space. We define
 $$\begin{eqnarray}H_{M,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}}:=\mathop{\prod }_{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}}H_{M,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}.\end{eqnarray}$$
$$\begin{eqnarray}H_{M,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}}:=\mathop{\prod }_{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}}H_{M,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}.\end{eqnarray}$$2.6.7
Let  $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and
$\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and  $\unicode[STIX]{x1D707}_{1}\leqslant \unicode[STIX]{x1D707}_{2}$. We have an open immersion:
$\unicode[STIX]{x1D707}_{1}\leqslant \unicode[STIX]{x1D707}_{2}$. We have an open immersion:
 $$\begin{eqnarray}\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}_{1}}/\unicode[STIX]{x1D6EF}{\hookrightarrow}\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}_{2}}/\unicode[STIX]{x1D6EF}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}_{1}}/\unicode[STIX]{x1D6EF}{\hookrightarrow}\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}_{2}}/\unicode[STIX]{x1D6EF}.\end{eqnarray}$$ For any  $j$, morphism (2.9) induces a morphism of vector spaces:
$j$, morphism (2.9) induces a morphism of vector spaces:
 $$\begin{eqnarray}H_{M,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}_{1}}\rightarrow H_{M,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}_{2}}.\end{eqnarray}$$
$$\begin{eqnarray}H_{M,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}_{1}}\rightarrow H_{M,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}_{2}}.\end{eqnarray}$$Definition 2.6.8. We define

as an inductive limit in the category of  $\mathbb{Q}_{\ell }$-vector spaces.
$\mathbb{Q}_{\ell }$-vector spaces.
Definition 2.6.9. For any  $\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$, we define
$\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$, we define  $H_{M,N,I,W}^{j,\,\unicode[STIX]{x1D708}}:=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}}H_{M,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$ as an inductive limit in the category of
$H_{M,N,I,W}^{j,\,\unicode[STIX]{x1D708}}:=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}}H_{M,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$ as an inductive limit in the category of  $\mathbb{Q}_{\ell }$-vector spaces.
$\mathbb{Q}_{\ell }$-vector spaces.
3 Constant term morphisms and cuspidal cohomology
Let 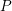 $P$ be a parabolic subgroup of
$P$ be a parabolic subgroup of  $G$ and
$G$ and  $M$ its Levi quotient. Let
$M$ its Levi quotient. Let  $W\in \operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{G}^{I})$. The goal of this section is to construct a constant term morphism from
$W\in \operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{G}^{I})$. The goal of this section is to construct a constant term morphism from  $H_{G,N,I,W}^{j}$ to
$H_{G,N,I,W}^{j}$ to  $H_{M,N,I,W}^{j}$ (in fact, to a variant
$H_{M,N,I,W}^{j}$ (in fact, to a variant  $H_{M,N,I,W}^{\prime \,j}$ of
$H_{M,N,I,W}^{\prime \,j}$ of  $H_{M,N,I,W}^{j}$ defined in §3.4 below). There are two steps.
$H_{M,N,I,W}^{j}$ defined in §3.4 below). There are two steps.
First, we will construct a commutative diagram

where the morphism  $\unicode[STIX]{x1D70B}$ is of finite type. Therefore the complex
$\unicode[STIX]{x1D70B}$ is of finite type. Therefore the complex  $\unicode[STIX]{x1D70B}_{!}i^{\ast }{\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}$ on
$\unicode[STIX]{x1D70B}_{!}i^{\ast }{\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}$ on  $\operatorname{Cht}_{M,N,I,W}/\unicode[STIX]{x1D6EF}$ is well defined in
$\operatorname{Cht}_{M,N,I,W}/\unicode[STIX]{x1D6EF}$ is well defined in  $D_{c}^{b}(\operatorname{Cht}_{M,N,I,W}/\unicode[STIX]{x1D6EF},\mathbb{Q}_{\ell })$ (in the context of 0.0.13). We will construct a canonical morphism of complexes on
$D_{c}^{b}(\operatorname{Cht}_{M,N,I,W}/\unicode[STIX]{x1D6EF},\mathbb{Q}_{\ell })$ (in the context of 0.0.13). We will construct a canonical morphism of complexes on  $\operatorname{Cht}_{M,N,I,W}/\unicode[STIX]{x1D6EF}$:
$\operatorname{Cht}_{M,N,I,W}/\unicode[STIX]{x1D6EF}$:
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{!}i^{\ast }{\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}\rightarrow {\mathcal{F}}_{M,N,I,W}^{\unicode[STIX]{x1D6EF}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{!}i^{\ast }{\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}\rightarrow {\mathcal{F}}_{M,N,I,W}^{\unicode[STIX]{x1D6EF}}.\end{eqnarray}$$ Second, the cohomological correspondence given by (3.1) and (3.2) will give a morphism from  $H_{G,N,I,W}^{j}$ to
$H_{G,N,I,W}^{j}$ to  $H_{M,N,I,W}^{j}$.
$H_{M,N,I,W}^{j}$.
3.1 Some geometry of the parabolic induction diagram
Recall that we have morphisms over  $X^{I}$ in (1.5):
$X^{I}$ in (1.5):  $\operatorname{Gr}_{G,I}\xleftarrow[{}]{i^{0}}\operatorname{Gr}_{P,I}\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{0}}\operatorname{Gr}_{M,I}$.
$\operatorname{Gr}_{G,I}\xleftarrow[{}]{i^{0}}\operatorname{Gr}_{P,I}\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{0}}\operatorname{Gr}_{M,I}$.
Proposition 3.1.1. We have  $(i^{0})^{-1}(\operatorname{Gr}_{G,I,W})\subset (\unicode[STIX]{x1D70B}^{0})^{-1}(\operatorname{Gr}_{M,I,W}),$ where the inverse images are in the sense of reduced subschemes in
$(i^{0})^{-1}(\operatorname{Gr}_{G,I,W})\subset (\unicode[STIX]{x1D70B}^{0})^{-1}(\operatorname{Gr}_{M,I,W}),$ where the inverse images are in the sense of reduced subschemes in  $\operatorname{Gr}_{P,I}$.
$\operatorname{Gr}_{P,I}$.
Proof. It is enough to prove the inclusion for each fiber over  $X^{I}$. By 1.1.12, we reduce the case of the Beilinson–Drinfeld affine grassmannian with paws indexed by
$X^{I}$. By 1.1.12, we reduce the case of the Beilinson–Drinfeld affine grassmannian with paws indexed by  $I$ to the case of the usual affine grassmannian
$I$ to the case of the usual affine grassmannian  $\operatorname{Gr}_{G}=G_{{\mathcal{K}}}/G_{{\mathcal{O}}}$.
$\operatorname{Gr}_{G}=G_{{\mathcal{K}}}/G_{{\mathcal{O}}}$.
When  $P=B$, the statement follows from [Reference Mirkovic and VilonenMV07, Theorem 3.2]. More concretely, for
$P=B$, the statement follows from [Reference Mirkovic and VilonenMV07, Theorem 3.2]. More concretely, for  $\unicode[STIX]{x1D714}$ a dominant coweight of
$\unicode[STIX]{x1D714}$ a dominant coweight of  $G$, we denote by
$G$, we denote by  $\operatorname{Gr}_{G,\unicode[STIX]{x1D714}}$ the Zariski closure of the Schubert cell defined by
$\operatorname{Gr}_{G,\unicode[STIX]{x1D714}}$ the Zariski closure of the Schubert cell defined by  $\unicode[STIX]{x1D714}$ in
$\unicode[STIX]{x1D714}$ in  $\operatorname{Gr}_{G}$. For
$\operatorname{Gr}_{G}$. For  $\unicode[STIX]{x1D708}$ a coweight of
$\unicode[STIX]{x1D708}$ a coweight of  $T$, we denote by
$T$, we denote by  $\operatorname{Gr}_{T,\unicode[STIX]{x1D708}}$ the component of
$\operatorname{Gr}_{T,\unicode[STIX]{x1D708}}$ the component of  $\operatorname{Gr}_{T}$ (which is discrete) associated to
$\operatorname{Gr}_{T}$ (which is discrete) associated to  $\unicode[STIX]{x1D708}$. We denote by
$\unicode[STIX]{x1D708}$. We denote by  $C_{\unicode[STIX]{x1D714}}$ the set of coweights of
$C_{\unicode[STIX]{x1D714}}$ the set of coweights of  $G$ which are
$G$ which are  $W$-conjugated to a dominant coweight
$W$-conjugated to a dominant coweight  ${\leqslant}\unicode[STIX]{x1D714}$ (where the order is taken in the coweight lattice of
${\leqslant}\unicode[STIX]{x1D714}$ (where the order is taken in the coweight lattice of  $G$). By [Reference Mirkovic and VilonenMV07, Theorem 3.2] the subscheme
$G$). By [Reference Mirkovic and VilonenMV07, Theorem 3.2] the subscheme  $(i^{0})^{-1}(\operatorname{Gr}_{G,\unicode[STIX]{x1D714}})\cap (\unicode[STIX]{x1D70B}^{0})^{-1}(\operatorname{Gr}_{T,\unicode[STIX]{x1D708}})$ in
$(i^{0})^{-1}(\operatorname{Gr}_{G,\unicode[STIX]{x1D714}})\cap (\unicode[STIX]{x1D70B}^{0})^{-1}(\operatorname{Gr}_{T,\unicode[STIX]{x1D708}})$ in  $\operatorname{Gr}_{B}$ is non-empty if and only if
$\operatorname{Gr}_{B}$ is non-empty if and only if  $\unicode[STIX]{x1D708}\in C_{\unicode[STIX]{x1D714}}$. Hence
$\unicode[STIX]{x1D708}\in C_{\unicode[STIX]{x1D714}}$. Hence
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}^{0}((i^{0})^{-1}(\operatorname{Gr}_{G,\unicode[STIX]{x1D714}}))=\underset{\unicode[STIX]{x1D708}\in C_{\unicode[STIX]{x1D714}}}{\bigsqcup }\operatorname{Gr}_{T,\unicode[STIX]{x1D708}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}^{0}((i^{0})^{-1}(\operatorname{Gr}_{G,\unicode[STIX]{x1D714}}))=\underset{\unicode[STIX]{x1D708}\in C_{\unicode[STIX]{x1D714}}}{\bigsqcup }\operatorname{Gr}_{T,\unicode[STIX]{x1D708}}.\end{eqnarray}$$ For general  $P$ with Levi quotient
$P$ with Levi quotient  $M$, we denote by
$M$, we denote by  $B^{\prime }$ the Borel subgroup of
$B^{\prime }$ the Borel subgroup of  $M$. We use the following diagram, where the square is Cartesian.
$M$. We use the following diagram, where the square is Cartesian.

Since the square is Cartesian, we have

For any dominant coweight  $\unicode[STIX]{x1D706}$ of
$\unicode[STIX]{x1D706}$ of  $M$, we denote by
$M$, we denote by  $\operatorname{Gr}_{M,\unicode[STIX]{x1D706}}$ the Zariski closure of the Schubert cell defined by
$\operatorname{Gr}_{M,\unicode[STIX]{x1D706}}$ the Zariski closure of the Schubert cell defined by  $\unicode[STIX]{x1D706}$ in
$\unicode[STIX]{x1D706}$ in  $\operatorname{Gr}_{M}$. Applying [Reference Mirkovic and VilonenMV07, Theorem 3.2] to
$\operatorname{Gr}_{M}$. Applying [Reference Mirkovic and VilonenMV07, Theorem 3.2] to  $\operatorname{Gr}_{M}\leftarrow \operatorname{Gr}_{B^{\prime }}\rightarrow \operatorname{Gr}_{T}$, we have
$\operatorname{Gr}_{M}\leftarrow \operatorname{Gr}_{B^{\prime }}\rightarrow \operatorname{Gr}_{T}$, we have

The subscheme  $(i_{G}^{P})^{-1}\operatorname{Gr}_{G,\unicode[STIX]{x1D714}}$ in
$(i_{G}^{P})^{-1}\operatorname{Gr}_{G,\unicode[STIX]{x1D714}}$ in  $\operatorname{Gr}_{P}$ is stable under the action of
$\operatorname{Gr}_{P}$ is stable under the action of  $P_{{\mathcal{O}}}$. The subscheme
$P_{{\mathcal{O}}}$. The subscheme  $(\unicode[STIX]{x1D70B}_{M}^{P})(i_{G}^{P})^{-1}\operatorname{Gr}_{G,\unicode[STIX]{x1D714}}$ in
$(\unicode[STIX]{x1D70B}_{M}^{P})(i_{G}^{P})^{-1}\operatorname{Gr}_{G,\unicode[STIX]{x1D714}}$ in  $\operatorname{Gr}_{M}$ is stable under the action of
$\operatorname{Gr}_{M}$ is stable under the action of  $M_{{\mathcal{O}}}$, so is a union of strata in
$M_{{\mathcal{O}}}$, so is a union of strata in  $\operatorname{Gr}_{M}$. We deduce from (3.4) and (3.5) that
$\operatorname{Gr}_{M}$. We deduce from (3.4) and (3.5) that  $\operatorname{Gr}_{M,\unicode[STIX]{x1D706}}$ can be in
$\operatorname{Gr}_{M,\unicode[STIX]{x1D706}}$ can be in  $(\unicode[STIX]{x1D70B}_{M}^{P})(i_{G}^{P})^{-1}\operatorname{Gr}_{G,\unicode[STIX]{x1D714}}$ only if
$(\unicode[STIX]{x1D70B}_{M}^{P})(i_{G}^{P})^{-1}\operatorname{Gr}_{G,\unicode[STIX]{x1D714}}$ only if  $\unicode[STIX]{x1D706}\in C_{\unicode[STIX]{x1D714}}$. Thus
$\unicode[STIX]{x1D706}\in C_{\unicode[STIX]{x1D714}}$. Thus

3.1.2
We define  $\operatorname{Gr}_{P,I,W}:=(i^{0})^{-1}(\operatorname{Gr}_{G,I,W})$. As a consequence of Proposition 3.1.1, morphisms (1.5) induce morphisms over
$\operatorname{Gr}_{P,I,W}:=(i^{0})^{-1}(\operatorname{Gr}_{G,I,W})$. As a consequence of Proposition 3.1.1, morphisms (1.5) induce morphisms over  $X^{I}$:
$X^{I}$:
 $$\begin{eqnarray}\operatorname{Gr}_{G,I,W}\xleftarrow[{}]{i^{0}}\operatorname{Gr}_{P,I,W}\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{0}}\operatorname{Gr}_{M,I,W}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Gr}_{G,I,W}\xleftarrow[{}]{i^{0}}\operatorname{Gr}_{P,I,W}\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{0}}\operatorname{Gr}_{M,I,W}.\end{eqnarray}$$3.1.3
We deduce from the commutative diagram (1.6) that
 $$\begin{eqnarray}i^{-1}(\operatorname{Cht}_{G,N,I,W})\subset \unicode[STIX]{x1D70B}^{-1}(\operatorname{Cht}_{M,N,I,W}),\end{eqnarray}$$
$$\begin{eqnarray}i^{-1}(\operatorname{Cht}_{G,N,I,W})\subset \unicode[STIX]{x1D70B}^{-1}(\operatorname{Cht}_{M,N,I,W}),\end{eqnarray}$$ where the inverse images are in the sense of reduced substacks in  $\operatorname{Cht}_{P,N,I}$. We define
$\operatorname{Cht}_{P,N,I}$. We define  $\operatorname{Cht}_{P,N,I,W}:=i^{-1}(\operatorname{Cht}_{G,N,I,W})$. Morphisms in (1.4) induce morphisms over
$\operatorname{Cht}_{P,N,I,W}:=i^{-1}(\operatorname{Cht}_{G,N,I,W})$. Morphisms in (1.4) induce morphisms over  $(X\smallsetminus N)^{I}$:
$(X\smallsetminus N)^{I}$:
 $$\begin{eqnarray}\operatorname{Cht}_{G,N,I,W}\xleftarrow[{}]{i}\operatorname{Cht}_{P,N,I,W}\xrightarrow[{}]{\unicode[STIX]{x1D70B}}\operatorname{Cht}_{P,N,I,W}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{G,N,I,W}\xleftarrow[{}]{i}\operatorname{Cht}_{P,N,I,W}\xrightarrow[{}]{\unicode[STIX]{x1D70B}}\operatorname{Cht}_{P,N,I,W}\!.\end{eqnarray}$$3.1.4
Let  $d\in \mathbb{Z}_{{\geqslant}0}$ large enough depending on
$d\in \mathbb{Z}_{{\geqslant}0}$ large enough depending on  $W$ as in Proposition 2.2.1 applied to
$W$ as in Proposition 2.2.1 applied to  $\operatorname{Gr}_{G,I,W}$ and to
$\operatorname{Gr}_{G,I,W}$ and to  $\operatorname{Gr}_{M,I,W}$. To simplify the notations, we write
$\operatorname{Gr}_{M,I,W}$. To simplify the notations, we write  $\unicode[STIX]{x1D716}_{G,d}$ for
$\unicode[STIX]{x1D716}_{G,d}$ for  $\unicode[STIX]{x1D716}_{G,N,I,d}$ defined in 2.4.1 and
$\unicode[STIX]{x1D716}_{G,N,I,d}$ defined in 2.4.1 and  $\unicode[STIX]{x1D716}_{M,d}$ for
$\unicode[STIX]{x1D716}_{M,d}$ for  $\unicode[STIX]{x1D716}_{M,N,I,d}$ defined in 2.6.2. Similarly we define
$\unicode[STIX]{x1D716}_{M,N,I,d}$ defined in 2.6.2. Similarly we define  $\unicode[STIX]{x1D716}_{P,d}$ to be the composition
$\unicode[STIX]{x1D716}_{P,d}$ to be the composition
 $$\begin{eqnarray}\operatorname{Cht}_{P,N,I,W}\rightarrow [P_{I,\infty }\backslash \operatorname{Gr}_{P,I,W}]\rightarrow [P_{I,d}\backslash \operatorname{Gr}_{P,I,W}].\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{P,N,I,W}\rightarrow [P_{I,\infty }\backslash \operatorname{Gr}_{P,I,W}]\rightarrow [P_{I,d}\backslash \operatorname{Gr}_{P,I,W}].\end{eqnarray}$$We deduce from the commutative diagram (1.6), morphisms (3.6) and (3.7) a commutative diagram of algebraic stacks.

3.1.5
The right square in (3.8) is not Cartesian. We have a commutative diagram, where the square is Cartesian.

Remark 3.1.6. Note that  $\widetilde{\operatorname{Cht}}_{M,N,I,W}$ depends on the choice of
$\widetilde{\operatorname{Cht}}_{M,N,I,W}$ depends on the choice of  $d$. We do not write
$d$. We do not write  $d$ in index to shorten the notation.
$d$ in index to shorten the notation.
Definition 3.1.7. Let  $U$ be the unipotent radical of
$U$ be the unipotent radical of  $P$. We have
$P$. We have  $P/U=M$. Applying Definition 1.1.13 to
$P/U=M$. Applying Definition 1.1.13 to  $U$, we define the group scheme
$U$, we define the group scheme  $U_{I,d}$ over
$U_{I,d}$ over  $X^{I}$.
$X^{I}$.
Lemma 3.1.8. The morphism  $\unicode[STIX]{x1D70B}_{d}$ is smooth of relative dimension
$\unicode[STIX]{x1D70B}_{d}$ is smooth of relative dimension  $\dim _{X^{I}}U_{I,d}$.
$\dim _{X^{I}}U_{I,d}$.
The following proof was suggested to the author by a referee.
Proof. Proposition 2.4.3 works also for  $P$ and
$P$ and  $M$. Hence the morphism
$M$. Hence the morphism  $\unicode[STIX]{x1D716}_{P,d}$ is smooth of relative dimension
$\unicode[STIX]{x1D716}_{P,d}$ is smooth of relative dimension  $\dim _{X^{I}}P_{I,d}$ and the morphism
$\dim _{X^{I}}P_{I,d}$ and the morphism  $\unicode[STIX]{x1D716}_{M,d}$ (hence
$\unicode[STIX]{x1D716}_{M,d}$ (hence  $\widetilde{\unicode[STIX]{x1D716}_{M,d}}$) is smooth of relative dimension
$\widetilde{\unicode[STIX]{x1D716}_{M,d}}$) is smooth of relative dimension  $\dim _{X^{I}}M_{I,d}$. Thus to prove that
$\dim _{X^{I}}M_{I,d}$. Thus to prove that  $\unicode[STIX]{x1D70B}_{d}$ is smooth, it is enough to show that it induces a surjective map between relative tangent spaces.
$\unicode[STIX]{x1D70B}_{d}$ is smooth, it is enough to show that it induces a surjective map between relative tangent spaces.
For any closed point  $x_{P}=((x_{i}),{\mathcal{P}}\rightarrow ^{\unicode[STIX]{x1D70F}}{\mathcal{P}})$ of
$x_{P}=((x_{i}),{\mathcal{P}}\rightarrow ^{\unicode[STIX]{x1D70F}}{\mathcal{P}})$ of  $\operatorname{Cht}_{P,N,I,W}$, let
$\operatorname{Cht}_{P,N,I,W}$, let  $x_{M}:=\unicode[STIX]{x1D70B}_{d}(x_{P})$. We have the canonical morphism
$x_{M}:=\unicode[STIX]{x1D70B}_{d}(x_{P})$. We have the canonical morphism
 $$\begin{eqnarray}T_{\unicode[STIX]{x1D716}_{P,d}}(x_{P})\rightarrow T_{\widetilde{\unicode[STIX]{x1D716}_{M,d}}}(x_{M}),\end{eqnarray}$$
$$\begin{eqnarray}T_{\unicode[STIX]{x1D716}_{P,d}}(x_{P})\rightarrow T_{\widetilde{\unicode[STIX]{x1D716}_{M,d}}}(x_{M}),\end{eqnarray}$$ where  $T_{\unicode[STIX]{x1D716}_{P,d}}(x_{P})$ (respectively
$T_{\unicode[STIX]{x1D716}_{P,d}}(x_{P})$ (respectively  $T_{\widetilde{\unicode[STIX]{x1D716}_{M,d}}}(x_{M})$) is the tangent space of
$T_{\widetilde{\unicode[STIX]{x1D716}_{M,d}}}(x_{M})$) is the tangent space of  $\operatorname{Cht}_{P,N,I,W}$ (respectively
$\operatorname{Cht}_{P,N,I,W}$ (respectively  $\widetilde{\operatorname{Cht}}_{M,N,I,W}$) at
$\widetilde{\operatorname{Cht}}_{M,N,I,W}$) at  $x_{P}$ (respectively
$x_{P}$ (respectively  $x_{M}$) relative to
$x_{M}$) relative to  $[P_{I,d}\backslash \operatorname{Gr}_{P,I,W}]$.
$[P_{I,d}\backslash \operatorname{Gr}_{P,I,W}]$.
Let  $y=\unicode[STIX]{x1D716}_{P,d}(x_{P})$. By the proof of [Reference LafforgueLaf18, Proposition 2.8], we have a Cartesian square
$y=\unicode[STIX]{x1D716}_{P,d}(x_{P})$. By the proof of [Reference LafforgueLaf18, Proposition 2.8], we have a Cartesian square

where  $b_{1}^{P}$ is a smooth morphism (which is the forgetful morphism of the level structure on
$b_{1}^{P}$ is a smooth morphism (which is the forgetful morphism of the level structure on  $d\sum x_{i}$) and
$d\sum x_{i}$) and  $b_{2}^{P}$ has zero differential (because it is the composition of the Frobenius morphism with some other morphism). We have
$b_{2}^{P}$ has zero differential (because it is the composition of the Frobenius morphism with some other morphism). We have  $T_{\unicode[STIX]{x1D716}_{P,d}}(x_{P})=T_{b_{1}^{p}}(x_{P})$ (see for example [Reference LafforgueLaf97, I. 2. Proposition 1]). It is well known that
$T_{\unicode[STIX]{x1D716}_{P,d}}(x_{P})=T_{b_{1}^{p}}(x_{P})$ (see for example [Reference LafforgueLaf97, I. 2. Proposition 1]). It is well known that  $\operatorname{Bun}_{P,N+d\sum x_{i}}\xrightarrow[{}]{b_{1}^{P}}\operatorname{Bun}_{P,N}$ is a
$\operatorname{Bun}_{P,N+d\sum x_{i}}\xrightarrow[{}]{b_{1}^{P}}\operatorname{Bun}_{P,N}$ is a  $P_{d\sum x_{i}}$-torsor, where
$P_{d\sum x_{i}}$-torsor, where  $P_{d\sum x_{i}}$ is defined in 0.0.8. We deduce that
$P_{d\sum x_{i}}$ is defined in 0.0.8. We deduce that  $T_{b_{1}^{p}}(x_{P})=\operatorname{Lie}(P_{d\sum x_{i}})$.
$T_{b_{1}^{p}}(x_{P})=\operatorname{Lie}(P_{d\sum x_{i}})$.
Similarly, we have a Cartesian square (taking into account that  $\widetilde{\unicode[STIX]{x1D716}_{M,d}}^{-1}(y)=\unicode[STIX]{x1D716}_{M,d}^{-1}(\overline{\unicode[STIX]{x1D70B}_{d}^{0}}(y))$)
$\widetilde{\unicode[STIX]{x1D716}_{M,d}}^{-1}(y)=\unicode[STIX]{x1D716}_{M,d}^{-1}(\overline{\unicode[STIX]{x1D70B}_{d}^{0}}(y))$)

where  $b_{1}^{M}$ is a smooth morphism (which is the forgetful morphism of the level structure on
$b_{1}^{M}$ is a smooth morphism (which is the forgetful morphism of the level structure on  $d\sum x_{i}$) and
$d\sum x_{i}$) and  $b_{2}^{M}$ has zero differential. We deduce that
$b_{2}^{M}$ has zero differential. We deduce that  $T_{\widetilde{\unicode[STIX]{x1D716}_{M,d}}}(x_{M})=T_{b_{1}^{M}}(x_{M})=\operatorname{Lie}(M_{d\sum x_{i}}),$ where
$T_{\widetilde{\unicode[STIX]{x1D716}_{M,d}}}(x_{M})=T_{b_{1}^{M}}(x_{M})=\operatorname{Lie}(M_{d\sum x_{i}}),$ where  $M_{d\sum x_{i}}$ is defined in 0.0.8.
$M_{d\sum x_{i}}$ is defined in 0.0.8.
Morphism (3.10) is the canonical morphism  $\operatorname{Lie}(P_{d\sum x_{i}})\rightarrow \operatorname{Lie}(M_{d\sum x_{i}})$ induced by
$\operatorname{Lie}(P_{d\sum x_{i}})\rightarrow \operatorname{Lie}(M_{d\sum x_{i}})$ induced by  $P{\twoheadrightarrow}M$. Hence it is surjective. We deduce also that the relative tangent space of
$P{\twoheadrightarrow}M$. Hence it is surjective. We deduce also that the relative tangent space of  $\unicode[STIX]{x1D70B}_{d}$ is
$\unicode[STIX]{x1D70B}_{d}$ is  $\operatorname{Lie}(U_{d\sum x_{i}})$.◻
$\operatorname{Lie}(U_{d\sum x_{i}})$.◻
3.2 Compatibility of the geometric Satake equivalence and parabolic induction
The goal of this section is to recall (3.17) and deduce (3.20), which is the key ingredient for the next section.
3.2.1
We apply Definition 1.1.11 to  $\mathbb{G}_{m}$ and denote by
$\mathbb{G}_{m}$ and denote by  $\operatorname{Gr}_{\mathbb{G}_{m},I}$ the associated reduced ind-scheme. We denote by
$\operatorname{Gr}_{\mathbb{G}_{m},I}$ the associated reduced ind-scheme. We denote by  $\unicode[STIX]{x1D70C}_{G}$ (respectively
$\unicode[STIX]{x1D70C}_{G}$ (respectively  $\unicode[STIX]{x1D70C}_{M}$) the half sum of positive roots of
$\unicode[STIX]{x1D70C}_{M}$) the half sum of positive roots of  $G$ (respectively
$G$ (respectively  $M$). Since
$M$). Since  $2(\unicode[STIX]{x1D70C}_{G}-\unicode[STIX]{x1D70C}_{M})$ is a character of
$2(\unicode[STIX]{x1D70C}_{G}-\unicode[STIX]{x1D70C}_{M})$ is a character of  $M$, the morphism
$M$, the morphism  $2(\unicode[STIX]{x1D70C}_{G}-\unicode[STIX]{x1D70C}_{M}):M\rightarrow \mathbb{G}_{m}$ induces a morphism
$2(\unicode[STIX]{x1D70C}_{G}-\unicode[STIX]{x1D70C}_{M}):M\rightarrow \mathbb{G}_{m}$ induces a morphism  $\operatorname{Gr}_{M,I}\rightarrow \operatorname{Gr}_{\mathbb{G}_{m},I}$ by sending a
$\operatorname{Gr}_{M,I}\rightarrow \operatorname{Gr}_{\mathbb{G}_{m},I}$ by sending a  $M$-bundle
$M$-bundle  ${\mathcal{M}}$ to the
${\mathcal{M}}$ to the  $\mathbb{G}_{m}$-bundle
$\mathbb{G}_{m}$-bundle  ${\mathcal{M}}\overset{M}{\times }\mathbb{G}_{m}$. We have a morphism
${\mathcal{M}}\overset{M}{\times }\mathbb{G}_{m}$. We have a morphism  $\operatorname{deg}:\operatorname{Gr}_{\mathbb{G}_{m},I}\rightarrow \mathbb{Z}$ by taking the degree of a
$\operatorname{deg}:\operatorname{Gr}_{\mathbb{G}_{m},I}\rightarrow \mathbb{Z}$ by taking the degree of a  $\mathbb{G}_{m}$-bundle. We have the composition of morphisms
$\mathbb{G}_{m}$-bundle. We have the composition of morphisms
 $$\begin{eqnarray}\operatorname{Gr}_{M,I}\rightarrow \operatorname{Gr}_{\mathbb{G}_{m},I}\xrightarrow[{}]{\operatorname{deg}}\mathbb{Z}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Gr}_{M,I}\rightarrow \operatorname{Gr}_{\mathbb{G}_{m},I}\xrightarrow[{}]{\operatorname{deg}}\mathbb{Z}.\end{eqnarray}$$ We define  $\operatorname{Gr}_{M,I}^{n}$ as the inverse image of
$\operatorname{Gr}_{M,I}^{n}$ as the inverse image of  $n\in \mathbb{Z}$. It is open and closed in
$n\in \mathbb{Z}$. It is open and closed in  $\operatorname{Gr}_{M,I}$. We define
$\operatorname{Gr}_{M,I}$. We define  $\operatorname{Gr}_{P,I}^{n}:=(\unicode[STIX]{x1D70B}^{0})^{-1}\operatorname{Gr}_{M,I}^{n}$. Morphism (1.5) induces a morphism
$\operatorname{Gr}_{P,I}^{n}:=(\unicode[STIX]{x1D70B}^{0})^{-1}\operatorname{Gr}_{M,I}^{n}$. Morphism (1.5) induces a morphism
 $$\begin{eqnarray}\operatorname{Gr}_{G,I}\xleftarrow[{}]{i_{n}^{0}}\operatorname{Gr}_{P,I}^{n}\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{n}^{0}}\operatorname{Gr}_{M,I}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Gr}_{G,I}\xleftarrow[{}]{i_{n}^{0}}\operatorname{Gr}_{P,I}^{n}\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{n}^{0}}\operatorname{Gr}_{M,I}^{n}.\end{eqnarray}$$3.2.2
Recall that we have defined  $\widehat{\unicode[STIX]{x1D6EC}}_{G,P}$ in 1.4.2. As in [Reference SchiederSch15, 2.1.2], we define
$\widehat{\unicode[STIX]{x1D6EC}}_{G,P}$ in 1.4.2. As in [Reference SchiederSch15, 2.1.2], we define  $\unicode[STIX]{x1D6EC}_{G,P}:=\{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{G}|\langle \check{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D706}\rangle =0\text{ for all }\check{\unicode[STIX]{x1D6FC}}\in \widehat{\unicode[STIX]{x1D6E4}}_{M}\}$. The pairing
$\unicode[STIX]{x1D6EC}_{G,P}:=\{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}_{G}|\langle \check{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D706}\rangle =0\text{ for all }\check{\unicode[STIX]{x1D6FC}}\in \widehat{\unicode[STIX]{x1D6E4}}_{M}\}$. The pairing  $\langle ~,~\rangle$ in 1.4.1 induces a pairing
$\langle ~,~\rangle$ in 1.4.1 induces a pairing  $\langle ~,~\rangle :\widehat{\unicode[STIX]{x1D6EC}}_{G,P}\times \unicode[STIX]{x1D6EC}_{G,P}\rightarrow \mathbb{Z}$.
$\langle ~,~\rangle :\widehat{\unicode[STIX]{x1D6EC}}_{G,P}\times \unicode[STIX]{x1D6EC}_{G,P}\rightarrow \mathbb{Z}$.
3.2.3
We denote by  $\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})$ the category of finite-dimensional
$\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})$ the category of finite-dimensional  $\mathbb{Q}_{\ell }$-linear representations of
$\mathbb{Q}_{\ell }$-linear representations of  $\widehat{M}^{I}$. Let
$\widehat{M}^{I}$. Let  $W\in \operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})$. Then
$W\in \operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})$. Then  $Z_{\widehat{M}}$ acts on
$Z_{\widehat{M}}$ acts on  $W$ via
$W$ via  $Z_{\widehat{M}}{\hookrightarrow}\widehat{M}^{I}$ diagonally. We have the decomposition as
$Z_{\widehat{M}}{\hookrightarrow}\widehat{M}^{I}$ diagonally. We have the decomposition as  $Z_{\widehat{M}}$ representation:
$Z_{\widehat{M}}$ representation:  $W=\bigoplus _{\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6EC}_{Z_{\widehat{M}}}}W^{\unicode[STIX]{x1D703}}$.
$W=\bigoplus _{\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6EC}_{Z_{\widehat{M}}}}W^{\unicode[STIX]{x1D703}}$.
Since  $\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6EC}_{Z_{\widehat{M}}}=\widehat{\unicode[STIX]{x1D6EC}}_{G,P}$ and
$\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6EC}_{Z_{\widehat{M}}}=\widehat{\unicode[STIX]{x1D6EC}}_{G,P}$ and  $2(\unicode[STIX]{x1D70C}_{G}-\unicode[STIX]{x1D70C}_{M})\in \unicode[STIX]{x1D6EC}_{G,P}$, we can consider
$2(\unicode[STIX]{x1D70C}_{G}-\unicode[STIX]{x1D70C}_{M})\in \unicode[STIX]{x1D6EC}_{G,P}$, we can consider  $\langle \unicode[STIX]{x1D703},2(\unicode[STIX]{x1D70C}_{G}-\unicode[STIX]{x1D70C}_{M})\rangle$. Let
$\langle \unicode[STIX]{x1D703},2(\unicode[STIX]{x1D70C}_{G}-\unicode[STIX]{x1D70C}_{M})\rangle$. Let  $W_{n}=\bigoplus _{\langle \unicode[STIX]{x1D703},2(\unicode[STIX]{x1D70C}_{G}-\unicode[STIX]{x1D70C}_{M})\rangle =n}W^{\unicode[STIX]{x1D703}}$. We have
$W_{n}=\bigoplus _{\langle \unicode[STIX]{x1D703},2(\unicode[STIX]{x1D70C}_{G}-\unicode[STIX]{x1D70C}_{M})\rangle =n}W^{\unicode[STIX]{x1D703}}$. We have  $W=\bigoplus _{n\in \mathbb{Z}}W_{n}$.
$W=\bigoplus _{n\in \mathbb{Z}}W_{n}$.
Let  $\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})^{\unicode[STIX]{x1D703}}$ be the category of finite-dimensional
$\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})^{\unicode[STIX]{x1D703}}$ be the category of finite-dimensional  $\mathbb{Q}_{\ell }$-linear representations of
$\mathbb{Q}_{\ell }$-linear representations of  $\widehat{M}^{I}$ such that
$\widehat{M}^{I}$ such that  $Z_{\widehat{M}}$ acts by
$Z_{\widehat{M}}$ acts by  $\unicode[STIX]{x1D703}$. We have
$\unicode[STIX]{x1D703}$. We have  $\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})=\bigoplus _{\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6EC}_{Z_{\widehat{M}}}}\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})^{\unicode[STIX]{x1D703}}$. Let
$\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})=\bigoplus _{\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6EC}_{Z_{\widehat{M}}}}\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})^{\unicode[STIX]{x1D703}}$. Let
 $$\begin{eqnarray}\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})_{n}=\bigoplus _{\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6EC}_{Z_{\widehat{M}}},\,\langle \unicode[STIX]{x1D703},2(\unicode[STIX]{x1D70C}_{G}-\unicode[STIX]{x1D70C}_{M})\rangle =n}\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})^{\unicode[STIX]{x1D703}}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})_{n}=\bigoplus _{\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6EC}_{Z_{\widehat{M}}},\,\langle \unicode[STIX]{x1D703},2(\unicode[STIX]{x1D70C}_{G}-\unicode[STIX]{x1D70C}_{M})\rangle =n}\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})^{\unicode[STIX]{x1D703}}.\end{eqnarray}$$We have
 $$\begin{eqnarray}\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})=\bigoplus _{n\in \mathbb{Z}}\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})=\bigoplus _{n\in \mathbb{Z}}\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})_{n}.\end{eqnarray}$$ We define  $(\operatorname{Res}_{\widehat{M}^{I}}^{\widehat{G}^{I}})_{n}$ to be the composition of morphisms
$(\operatorname{Res}_{\widehat{M}^{I}}^{\widehat{G}^{I}})_{n}$ to be the composition of morphisms  $\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{G}^{I})\xrightarrow[{}]{\operatorname{Res}_{\widehat{M}^{I}}^{\widehat{G}^{I}}}\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I}){\twoheadrightarrow}\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})_{n}$.
$\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{G}^{I})\xrightarrow[{}]{\operatorname{Res}_{\widehat{M}^{I}}^{\widehat{G}^{I}}}\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I}){\twoheadrightarrow}\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})_{n}$.
3.2.4
In morphism (3.13),  $\operatorname{Gr}_{M,I,W^{\unicode[STIX]{x1D703}}}$ is sent to
$\operatorname{Gr}_{M,I,W^{\unicode[STIX]{x1D703}}}$ is sent to  $\langle \unicode[STIX]{x1D703},2(\unicode[STIX]{x1D70C}_{G}-\unicode[STIX]{x1D70C}_{M})\rangle$. We deduce that
$\langle \unicode[STIX]{x1D703},2(\unicode[STIX]{x1D70C}_{G}-\unicode[STIX]{x1D70C}_{M})\rangle$. We deduce that  $\operatorname{Gr}_{M,I}^{n}\cap \operatorname{Gr}_{M,I,W}=\operatorname{Gr}_{M,I,W_{n}}$.
$\operatorname{Gr}_{M,I}^{n}\cap \operatorname{Gr}_{M,I,W}=\operatorname{Gr}_{M,I,W_{n}}$.
3.2.5
In Corollary 2.1.7, we defined a fully faithful functor
 $$\begin{eqnarray}\text{Sat}_{G,I}:\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{G}^{I})\rightarrow \operatorname{Perv}_{G_{I,\infty }}(\operatorname{Gr}_{G,I},\mathbb{Q}_{\ell })\end{eqnarray}$$
$$\begin{eqnarray}\text{Sat}_{G,I}:\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{G}^{I})\rightarrow \operatorname{Perv}_{G_{I,\infty }}(\operatorname{Gr}_{G,I},\mathbb{Q}_{\ell })\end{eqnarray}$$ which sends  $W$ to
$W$ to  ${\mathcal{S}}_{G,I,W}$. We denote by
${\mathcal{S}}_{G,I,W}$. We denote by  $\operatorname{Perv}_{G_{I,\infty }}(\operatorname{Gr}_{G,I},\mathbb{Q}_{\ell })^{\operatorname{MV}}$ the subcategory of essential image of this functor. Similarly, we define
$\operatorname{Perv}_{G_{I,\infty }}(\operatorname{Gr}_{G,I},\mathbb{Q}_{\ell })^{\operatorname{MV}}$ the subcategory of essential image of this functor. Similarly, we define
 $$\begin{eqnarray}\text{Sat}_{M,I}:\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})\rightarrow \operatorname{Perv}_{M_{I,\infty }}(\operatorname{Gr}_{M,I},\mathbb{Q}_{\ell })^{\operatorname{MV}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Sat}_{M,I}:\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})\rightarrow \operatorname{Perv}_{M_{I,\infty }}(\operatorname{Gr}_{M,I},\mathbb{Q}_{\ell })^{\operatorname{MV}}.\end{eqnarray}$$ Let  $\text{Sat}_{M,I,n}$ be the restriction of
$\text{Sat}_{M,I,n}$ be the restriction of  $\text{Sat}_{M,I}$ to
$\text{Sat}_{M,I}$ to  $\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})_{n}$.
$\operatorname{Rep}_{\mathbb{Q}_{\ell }}(\widehat{M}^{I})_{n}$.
Theorem 3.2.6 ([Reference Beilinson and DrinfeldBD99, 5.3.29], [Reference Braverman and GaitsgoryBG02, Theorem 4.3.4], [Reference Mirkovic and VilonenMV07, Theorem 3.6] (for  $M=T$), [Reference Baumann and RicheBR18, Proposition 15.2]).
$M=T$), [Reference Baumann and RicheBR18, Proposition 15.2]).
(a) For any
 $n\in \mathbb{Z}$, the complex is in
$n\in \mathbb{Z}$, the complex is in $$\begin{eqnarray}(\unicode[STIX]{x1D70B}_{n}^{0})_{!}(i_{n}^{0})^{\ast }{\mathcal{S}}_{G,I,W}\otimes \big(\mathbb{Q}_{\ell }[1]({\textstyle \frac{1}{2}})\big)^{\otimes n}\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70B}_{n}^{0})_{!}(i_{n}^{0})^{\ast }{\mathcal{S}}_{G,I,W}\otimes \big(\mathbb{Q}_{\ell }[1]({\textstyle \frac{1}{2}})\big)^{\otimes n}\end{eqnarray}$$ $\operatorname{Perv}_{M_{I,\infty }}(\operatorname{Gr}_{M,I}^{n},\mathbb{Q}_{\ell })^{\operatorname{MV}}$.
$\operatorname{Perv}_{M_{I,\infty }}(\operatorname{Gr}_{M,I}^{n},\mathbb{Q}_{\ell })^{\operatorname{MV}}$.(b) We denote by
 $((\unicode[STIX]{x1D70B}_{n}^{0})_{!}(i_{n}^{0})^{\ast })^{{\sim}}$ the shifted functor
$((\unicode[STIX]{x1D70B}_{n}^{0})_{!}(i_{n}^{0})^{\ast })^{{\sim}}$ the shifted functor  $(\unicode[STIX]{x1D70B}_{n}^{0})_{!}(i_{n}^{0})^{\ast }\otimes (\mathbb{Q}_{\ell }[1]({\textstyle \frac{1}{2}}))^{\otimes n}$. Then there is a canonical isomorphism of fiber functors (3.15)
$(\unicode[STIX]{x1D70B}_{n}^{0})_{!}(i_{n}^{0})^{\ast }\otimes (\mathbb{Q}_{\ell }[1]({\textstyle \frac{1}{2}}))^{\otimes n}$. Then there is a canonical isomorphism of fiber functors (3.15) $$\begin{eqnarray}\text{Sat}_{M,I,n}\circ (\operatorname{Res}_{\widehat{M}^{I}}^{\widehat{G}^{I}})_{n}=((\unicode[STIX]{x1D70B}_{n}^{0})_{!}(i_{n}^{0})^{\ast })^{{\sim}}\circ \text{Sat}_{G,I}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Sat}_{M,I,n}\circ (\operatorname{Res}_{\widehat{M}^{I}}^{\widehat{G}^{I}})_{n}=((\unicode[STIX]{x1D70B}_{n}^{0})_{!}(i_{n}^{0})^{\ast })^{{\sim}}\circ \text{Sat}_{G,I}.\end{eqnarray}$$
In other words, the following diagram of categories canonically commutes.

Remark 3.2.7. The references cited above in Theorem 3.2.6 are for the case of affine grassmannians (i.e.  $I$ is a singleton). The general case (i.e.
$I$ is a singleton). The general case (i.e.  $I$ is arbitrary) can be deduced from the case of affine grassmannians using the fact that the constant term functor commutes with fusion (i.e. convolution). The proof for
$I$ is arbitrary) can be deduced from the case of affine grassmannians using the fact that the constant term functor commutes with fusion (i.e. convolution). The proof for  $I=\{1,2\}$ is already included in the proof of [Reference Baumann and RicheBR18, Proposition 15.2]. For general
$I=\{1,2\}$ is already included in the proof of [Reference Baumann and RicheBR18, Proposition 15.2]. For general  $I$ the proof is similar.
$I$ the proof is similar.
Corollary 3.2.8. There is a canonical isomorphism
 $$\begin{eqnarray}{\mathcal{S}}_{M,I,W_{n}}\simeq (\unicode[STIX]{x1D70B}_{n}^{0})_{!}(i_{n}^{0})^{\ast }{\mathcal{S}}_{G,I,W}[n](n/2).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{S}}_{M,I,W_{n}}\simeq (\unicode[STIX]{x1D70B}_{n}^{0})_{!}(i_{n}^{0})^{\ast }{\mathcal{S}}_{G,I,W}[n](n/2).\end{eqnarray}$$3.2.9
For any  $n$, denote by
$n$, denote by  $\operatorname{Gr}_{P,I,W}^{n}=\operatorname{Gr}_{P,I}^{n}\cap \operatorname{Gr}_{P,I,W}$. We have a commutative diagram, where the first line is induced by (3.6).
$\operatorname{Gr}_{P,I,W}^{n}=\operatorname{Gr}_{P,I}^{n}\cap \operatorname{Gr}_{P,I,W}$. We have a commutative diagram, where the first line is induced by (3.6).

The morphism
 $$\begin{eqnarray}\operatorname{Gr}_{P,I,W}^{n}\rightarrow [P_{I,d}\backslash \operatorname{Gr}_{P,I,W}^{n}]\underset{[M_{I,d}\backslash \operatorname{Gr}_{M,I,W_{n}}]}{\times }\operatorname{Gr}_{M,I,W_{n}}=[U_{I,d}\backslash \operatorname{Gr}_{P,I,W}^{n}]\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Gr}_{P,I,W}^{n}\rightarrow [P_{I,d}\backslash \operatorname{Gr}_{P,I,W}^{n}]\underset{[M_{I,d}\backslash \operatorname{Gr}_{M,I,W_{n}}]}{\times }\operatorname{Gr}_{M,I,W_{n}}=[U_{I,d}\backslash \operatorname{Gr}_{P,I,W}^{n}]\end{eqnarray}$$ is a  $U_{I,d}$-torsor. Since the group scheme
$U_{I,d}$-torsor. Since the group scheme  $U_{I,d}$ is unipotent over
$U_{I,d}$ is unipotent over  $X^{I}$, we deduce that
$X^{I}$, we deduce that
 $$\begin{eqnarray}(\unicode[STIX]{x1D70B}_{n}^{0})_{!}(\unicode[STIX]{x1D709}_{P,d})^{\ast }\simeq (\unicode[STIX]{x1D709}_{M,d})^{\ast }(\overline{\unicode[STIX]{x1D70B}_{d,n}^{0}})_{!}[-2m](-m),\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70B}_{n}^{0})_{!}(\unicode[STIX]{x1D709}_{P,d})^{\ast }\simeq (\unicode[STIX]{x1D709}_{M,d})^{\ast }(\overline{\unicode[STIX]{x1D70B}_{d,n}^{0}})_{!}[-2m](-m),\end{eqnarray}$$ where  $m=\dim \unicode[STIX]{x1D709}_{P,d}-\dim \unicode[STIX]{x1D709}_{M,d}=\dim _{X^{I}}U_{I,d}$.
$m=\dim \unicode[STIX]{x1D709}_{P,d}-\dim \unicode[STIX]{x1D709}_{M,d}=\dim _{X^{I}}U_{I,d}$.
Corollary 3.2.8 implies
 $$\begin{eqnarray}{\mathcal{S}}_{M,I,W_{n}}^{d}\overset{{\sim}}{\rightarrow }(\overline{\unicode[STIX]{x1D70B}_{d,n}^{0}})_{!}(\overline{i_{d,n}^{0}})^{\ast }{\mathcal{S}}_{G,I,W}^{d}[n-2m](n/2-m).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{S}}_{M,I,W_{n}}^{d}\overset{{\sim}}{\rightarrow }(\overline{\unicode[STIX]{x1D70B}_{d,n}^{0}})_{!}(\overline{i_{d,n}^{0}})^{\ast }{\mathcal{S}}_{G,I,W}^{d}[n-2m](n/2-m).\end{eqnarray}$$3.2.10
Let  $(\unicode[STIX]{x1D714}_{i})_{i\in I}\in (\widehat{\unicode[STIX]{x1D6EC}}_{M}^{+})^{I}$. Let
$(\unicode[STIX]{x1D714}_{i})_{i\in I}\in (\widehat{\unicode[STIX]{x1D6EC}}_{M}^{+})^{I}$. Let  $V^{\unicode[STIX]{x1D714}_{i}}$ be the irreducible representation of
$V^{\unicode[STIX]{x1D714}_{i}}$ be the irreducible representation of  $\widehat{M}$ of highest weight
$\widehat{M}$ of highest weight  $\unicode[STIX]{x1D714}_{i}$. Note that
$\unicode[STIX]{x1D714}_{i}$. Note that  $\widehat{\unicode[STIX]{x1D6EC}}_{G,P}=\widehat{\unicode[STIX]{x1D6EC}}_{M,M}$ (defined in 1.4.2). By definition, it coincides with
$\widehat{\unicode[STIX]{x1D6EC}}_{G,P}=\widehat{\unicode[STIX]{x1D6EC}}_{M,M}$ (defined in 1.4.2). By definition, it coincides with  $\unicode[STIX]{x1D70B}_{1}(M)$ defined in [Reference VarshavskyVar04, Lemma 2.2]. We denote by
$\unicode[STIX]{x1D70B}_{1}(M)$ defined in [Reference VarshavskyVar04, Lemma 2.2]. We denote by  $[\sum _{i\in I}\unicode[STIX]{x1D714}_{i}]$ the image of
$[\sum _{i\in I}\unicode[STIX]{x1D714}_{i}]$ the image of  $\sum _{i\in I}\unicode[STIX]{x1D714}_{i}$ by the projection
$\sum _{i\in I}\unicode[STIX]{x1D714}_{i}$ by the projection  $\widehat{\unicode[STIX]{x1D6EC}}_{M}{\twoheadrightarrow}\widehat{\unicode[STIX]{x1D6EC}}_{M,M}$.
$\widehat{\unicode[STIX]{x1D6EC}}_{M}{\twoheadrightarrow}\widehat{\unicode[STIX]{x1D6EC}}_{M,M}$.
Lemma 3.2.11 [Reference VarshavskyVar04, Proposition 2.16(d)].
The stack  $\operatorname{Cht}_{M,N,I,\boxtimes _{i\in I}V^{\unicode[STIX]{x1D714}_{i}}}$ is non-empty if and only if
$\operatorname{Cht}_{M,N,I,\boxtimes _{i\in I}V^{\unicode[STIX]{x1D714}_{i}}}$ is non-empty if and only if  $[\sum _{i\in I}\unicode[STIX]{x1D714}_{i}]$ is zero.
$[\sum _{i\in I}\unicode[STIX]{x1D714}_{i}]$ is zero.
3.2.12
Let  $W$ and
$W$ and  $W^{\unicode[STIX]{x1D703}}$ as in 3.2.3. Then
$W^{\unicode[STIX]{x1D703}}$ as in 3.2.3. Then  $W$ has a unique decomposition of the form
$W$ has a unique decomposition of the form
 $$\begin{eqnarray}W=\bigoplus _{(\unicode[STIX]{x1D714}_{i})_{i\in I}\in (\widehat{\unicode[STIX]{x1D6EC}}_{M}^{+})^{I}}(\boxtimes _{i\in I}V^{\unicode[STIX]{x1D714}_{i}})\otimes _{\mathbb{Q}_{\ell }}\mathfrak{M}_{(\unicode[STIX]{x1D714}_{i})_{i\in I}},\end{eqnarray}$$
$$\begin{eqnarray}W=\bigoplus _{(\unicode[STIX]{x1D714}_{i})_{i\in I}\in (\widehat{\unicode[STIX]{x1D6EC}}_{M}^{+})^{I}}(\boxtimes _{i\in I}V^{\unicode[STIX]{x1D714}_{i}})\otimes _{\mathbb{Q}_{\ell }}\mathfrak{M}_{(\unicode[STIX]{x1D714}_{i})_{i\in I}},\end{eqnarray}$$ where  $\mathfrak{M}_{(\unicode[STIX]{x1D714}_{i})_{i\in I}}$ are finite-dimensional
$\mathfrak{M}_{(\unicode[STIX]{x1D714}_{i})_{i\in I}}$ are finite-dimensional  $\mathbb{Q}_{\ell }$-vector spaces, all but a finite number of them are zero. We have
$\mathbb{Q}_{\ell }$-vector spaces, all but a finite number of them are zero. We have
 $$\begin{eqnarray}W^{\unicode[STIX]{x1D703}}=\bigoplus _{(\unicode[STIX]{x1D714}_{i})_{i\in I}\in (\widehat{\unicode[STIX]{x1D6EC}}_{M}^{+})^{I},\,[\mathop{\sum }_{i\in I}\unicode[STIX]{x1D714}_{i}]=\unicode[STIX]{x1D703}}(\boxtimes _{i\in I}V^{\unicode[STIX]{x1D714}_{i}})\otimes _{\mathbb{Q}_{\ell }}\mathfrak{M}_{(\unicode[STIX]{x1D714}_{i})_{i\in I}}.\end{eqnarray}$$
$$\begin{eqnarray}W^{\unicode[STIX]{x1D703}}=\bigoplus _{(\unicode[STIX]{x1D714}_{i})_{i\in I}\in (\widehat{\unicode[STIX]{x1D6EC}}_{M}^{+})^{I},\,[\mathop{\sum }_{i\in I}\unicode[STIX]{x1D714}_{i}]=\unicode[STIX]{x1D703}}(\boxtimes _{i\in I}V^{\unicode[STIX]{x1D714}_{i}})\otimes _{\mathbb{Q}_{\ell }}\mathfrak{M}_{(\unicode[STIX]{x1D714}_{i})_{i\in I}}.\end{eqnarray}$$ Lemma 3.2.11 implies that  $\operatorname{Cht}_{M,N,I,W^{\unicode[STIX]{x1D703}}}$ is non-empty if and only if
$\operatorname{Cht}_{M,N,I,W^{\unicode[STIX]{x1D703}}}$ is non-empty if and only if  $\unicode[STIX]{x1D703}$ is zero. For such
$\unicode[STIX]{x1D703}$ is zero. For such  $\unicode[STIX]{x1D703}$, we have
$\unicode[STIX]{x1D703}$, we have  $\langle \unicode[STIX]{x1D703},2(\unicode[STIX]{x1D70C}_{G}-\unicode[STIX]{x1D70C}_{M})\rangle =0$. We deduce that
$\langle \unicode[STIX]{x1D703},2(\unicode[STIX]{x1D70C}_{G}-\unicode[STIX]{x1D70C}_{M})\rangle =0$. We deduce that  $\operatorname{Cht}_{M,N,I,W}=\bigcup _{n\in \mathbb{Z}}\operatorname{Cht}_{M,N,I,W_{n}}=\operatorname{Cht}_{M,N,I,W_{0}}$. So the image of
$\operatorname{Cht}_{M,N,I,W}=\bigcup _{n\in \mathbb{Z}}\operatorname{Cht}_{M,N,I,W_{n}}=\operatorname{Cht}_{M,N,I,W_{0}}$. So the image of
 $$\begin{eqnarray}\unicode[STIX]{x1D716}_{M,d}:\operatorname{Cht}_{M,N,I,W}\rightarrow [M_{I,d}\backslash \operatorname{Gr}_{M,I,W}]\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}_{M,d}:\operatorname{Cht}_{M,N,I,W}\rightarrow [M_{I,d}\backslash \operatorname{Gr}_{M,I,W}]\end{eqnarray}$$ is in  $[M_{I,d}\backslash \operatorname{Gr}_{M,I,W_{0}}]$.
$[M_{I,d}\backslash \operatorname{Gr}_{M,I,W_{0}}]$.
3.2.13
With the notations of diagram (3.8), we have
 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D716}_{M,d})^{\ast }{\mathcal{S}}_{M,I,W}^{d} & = & \displaystyle (\unicode[STIX]{x1D716}_{M,d})^{\ast }{\mathcal{S}}_{M,I,W_{0}}^{d}\nonumber\\ \displaystyle & \overset{{\sim}}{\rightarrow } & \displaystyle (\unicode[STIX]{x1D716}_{M,d})^{\ast }(\overline{\unicode[STIX]{x1D70B}_{d,0}^{0}})_{!}(\overline{i_{d,0}^{0}})^{\ast }{\mathcal{S}}_{G,I,W}^{d}[-2m](-m)\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D716}_{M,d})^{\ast }(\overline{\unicode[STIX]{x1D70B}_{d}^{0}})_{!}(\overline{i_{d}^{0}})^{\ast }{\mathcal{S}}_{G,I,W}^{d}[-2m](-m).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D716}_{M,d})^{\ast }{\mathcal{S}}_{M,I,W}^{d} & = & \displaystyle (\unicode[STIX]{x1D716}_{M,d})^{\ast }{\mathcal{S}}_{M,I,W_{0}}^{d}\nonumber\\ \displaystyle & \overset{{\sim}}{\rightarrow } & \displaystyle (\unicode[STIX]{x1D716}_{M,d})^{\ast }(\overline{\unicode[STIX]{x1D70B}_{d,0}^{0}})_{!}(\overline{i_{d,0}^{0}})^{\ast }{\mathcal{S}}_{G,I,W}^{d}[-2m](-m)\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D716}_{M,d})^{\ast }(\overline{\unicode[STIX]{x1D70B}_{d}^{0}})_{!}(\overline{i_{d}^{0}})^{\ast }{\mathcal{S}}_{G,I,W}^{d}[-2m](-m).\end{eqnarray}$$ The first and third equality follows from 3.2.12. The second isomorphism follows from (3.19) applied to  $n=0$.
$n=0$.
3.3 Construction of the morphism (3.2)
3.3.1
Consider diagrams (3.8) and (3.9). Let  $m=\dim _{X^{I}}U_{I,d}$ as in 3.2.9. By Lemma 3.1.8,
$m=\dim _{X^{I}}U_{I,d}$ as in 3.2.9. By Lemma 3.1.8,  $m=\dim \unicode[STIX]{x1D70B}_{d}$. We construct a canonical map of functors from
$m=\dim \unicode[STIX]{x1D70B}_{d}$. We construct a canonical map of functors from  $D_{c}^{b}([P_{I,d}\backslash \operatorname{Gr}_{P,I,W}],\mathbb{Q}_{\ell })$ to
$D_{c}^{b}([P_{I,d}\backslash \operatorname{Gr}_{P,I,W}],\mathbb{Q}_{\ell })$ to  $D_{c}^{b}(\operatorname{Cht}_{M,N,I,W},\mathbb{Q}_{\ell })$,
$D_{c}^{b}(\operatorname{Cht}_{M,N,I,W},\mathbb{Q}_{\ell })$,
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{!}(\unicode[STIX]{x1D716}_{P,d})^{\ast }\rightarrow (\unicode[STIX]{x1D716}_{M,d})^{\ast }(\overline{\unicode[STIX]{x1D70B}_{d}^{0}})_{!}[-2m](-m),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{!}(\unicode[STIX]{x1D716}_{P,d})^{\ast }\rightarrow (\unicode[STIX]{x1D716}_{M,d})^{\ast }(\overline{\unicode[STIX]{x1D70B}_{d}^{0}})_{!}[-2m](-m),\end{eqnarray}$$as the composition
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{!}(\unicode[STIX]{x1D716}_{P,d})^{\ast } & \simeq & \displaystyle (\widetilde{\unicode[STIX]{x1D70B}_{d}^{0}})_{!}(\unicode[STIX]{x1D70B}_{d})_{!}(\unicode[STIX]{x1D70B}_{d})^{\ast }(\widetilde{\unicode[STIX]{x1D716}_{M,d}})^{\ast }\nonumber\\ \displaystyle & \rightarrow & \displaystyle (\widetilde{\unicode[STIX]{x1D70B}_{d}^{0}})_{!}(\widetilde{\unicode[STIX]{x1D716}_{M,d}})^{\ast }[-2m](-m)\overset{{\sim}}{\leftarrow }(\unicode[STIX]{x1D716}_{M,d})^{\ast }(\overline{\unicode[STIX]{x1D70B}_{d}^{0}})_{!}[-2m](-m).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{!}(\unicode[STIX]{x1D716}_{P,d})^{\ast } & \simeq & \displaystyle (\widetilde{\unicode[STIX]{x1D70B}_{d}^{0}})_{!}(\unicode[STIX]{x1D70B}_{d})_{!}(\unicode[STIX]{x1D70B}_{d})^{\ast }(\widetilde{\unicode[STIX]{x1D716}_{M,d}})^{\ast }\nonumber\\ \displaystyle & \rightarrow & \displaystyle (\widetilde{\unicode[STIX]{x1D70B}_{d}^{0}})_{!}(\widetilde{\unicode[STIX]{x1D716}_{M,d}})^{\ast }[-2m](-m)\overset{{\sim}}{\leftarrow }(\unicode[STIX]{x1D716}_{M,d})^{\ast }(\overline{\unicode[STIX]{x1D70B}_{d}^{0}})_{!}[-2m](-m).\end{eqnarray}$$ The second morphism in (3.22) is induced by the isomorphism  $(\unicode[STIX]{x1D70B}_{d})^{\ast }[2m](m)\simeq (\unicode[STIX]{x1D70B}_{d})^{!}$ (because
$(\unicode[STIX]{x1D70B}_{d})^{\ast }[2m](m)\simeq (\unicode[STIX]{x1D70B}_{d})^{!}$ (because  $\unicode[STIX]{x1D70B}_{d}$ is smooth) and the counit map
$\unicode[STIX]{x1D70B}_{d}$ is smooth) and the counit map  $\operatorname{Co}:(\unicode[STIX]{x1D70B}_{d})_{!}(\unicode[STIX]{x1D70B}_{d})^{!}\rightarrow \operatorname{Id}$. (The composition
$\operatorname{Co}:(\unicode[STIX]{x1D70B}_{d})_{!}(\unicode[STIX]{x1D70B}_{d})^{!}\rightarrow \operatorname{Id}$. (The composition  $(\unicode[STIX]{x1D70B}_{d})_{!}(\unicode[STIX]{x1D70B}_{d})^{\ast }[2m](m)\overset{{\sim}}{\rightarrow }(\unicode[STIX]{x1D70B}_{d})_{!}(\unicode[STIX]{x1D70B}_{d})^{!}\rightarrow \operatorname{Id}$ is the trace map in [Reference Grothendieck, Artin and VerdierSGA4, XVIII 2].)
$(\unicode[STIX]{x1D70B}_{d})_{!}(\unicode[STIX]{x1D70B}_{d})^{\ast }[2m](m)\overset{{\sim}}{\rightarrow }(\unicode[STIX]{x1D70B}_{d})_{!}(\unicode[STIX]{x1D70B}_{d})^{!}\rightarrow \operatorname{Id}$ is the trace map in [Reference Grothendieck, Artin and VerdierSGA4, XVIII 2].)
The third morphism is the proper base change ([Reference Grothendieck, Artin and VerdierSGA4, XVII 5], [Reference Laszlo and OlssonLO08, § 12]).
3.3.2
Now we construct a morphism of complexes in  $D_{c}^{b}(\operatorname{Cht}_{M,N,I,W},\mathbb{Q}_{\ell })$:
$D_{c}^{b}(\operatorname{Cht}_{M,N,I,W},\mathbb{Q}_{\ell })$:

where (a) is induced by the commutativity of diagram (3.8), (b) is induced by morphism (3.21), and (c) is (3.20).
3.3.3
All the constructions in 3.1–3.3 are compatible with the quotient by  $\unicode[STIX]{x1D6EF}$. In particular, just as in 3.1.4, diagram (1.10) induces a commutative diagram.
$\unicode[STIX]{x1D6EF}$. In particular, just as in 3.1.4, diagram (1.10) induces a commutative diagram.

Construction 3.3.4. Just as in 3.3.2 (using (3.24) instead of (3.8)), we construct a canonical morphism of complexes in  $D_{c}^{b}(\operatorname{Cht}_{M,N,I,W}/\unicode[STIX]{x1D6EF},\mathbb{Q}_{\ell })$:
$D_{c}^{b}(\operatorname{Cht}_{M,N,I,W}/\unicode[STIX]{x1D6EF},\mathbb{Q}_{\ell })$:
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{!}i^{\ast }{\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}\rightarrow {\mathcal{F}}_{M,N,I,W}^{\unicode[STIX]{x1D6EF}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{!}i^{\ast }{\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}\rightarrow {\mathcal{F}}_{M,N,I,W}^{\unicode[STIX]{x1D6EF}}.\end{eqnarray}$$3.4 More on cohomology groups
When the level structure  $N$ is non-empty, to construct the constant term morphism of cohomology groups, we need a variant of
$N$ is non-empty, to construct the constant term morphism of cohomology groups, we need a variant of  $H_{M,N,I,W}^{j}$.
$H_{M,N,I,W}^{j}$.
3.4.1
Let  ${\mathcal{O}}_{N}$ be the ring of functions on
${\mathcal{O}}_{N}$ be the ring of functions on  $N$ as in 0.0.8. The finite group
$N$ as in 0.0.8. The finite group  $G({\mathcal{O}}_{N})$ (respectively
$G({\mathcal{O}}_{N})$ (respectively  $P({\mathcal{O}}_{N})$ and
$P({\mathcal{O}}_{N})$ and  $M({\mathcal{O}}_{N})$) acts on
$M({\mathcal{O}}_{N})$) acts on  $\operatorname{Cht}_{G,N,I,W}$ (respectively
$\operatorname{Cht}_{G,N,I,W}$ (respectively  $\operatorname{Cht}_{P,N,I,W}$ and
$\operatorname{Cht}_{P,N,I,W}$ and  $\operatorname{Cht}_{M,N,I,W}$) by changing the level structure on
$\operatorname{Cht}_{M,N,I,W}$) by changing the level structure on  $N$:
$N$:  $g\in G({\mathcal{O}}_{N})$ sends a level structure
$g\in G({\mathcal{O}}_{N})$ sends a level structure  $\unicode[STIX]{x1D713}_{G}$ to
$\unicode[STIX]{x1D713}_{G}$ to  $g^{-1}\circ \unicode[STIX]{x1D713}_{G}$.
$g^{-1}\circ \unicode[STIX]{x1D713}_{G}$.
By [Reference VarshavskyVar04, Proposition 2.16(b)],  $\operatorname{Cht}_{G,N,I,W}$ (respectively
$\operatorname{Cht}_{G,N,I,W}$ (respectively  $\operatorname{Cht}_{P,N,I,W}$ and
$\operatorname{Cht}_{P,N,I,W}$ and  $\operatorname{Cht}_{M,N,I,W}$) is a finite étale Galois cover of
$\operatorname{Cht}_{M,N,I,W}$) is a finite étale Galois cover of  $\left.\operatorname{Cht}_{G,I,W}\!\vphantom{\big|}\right|_{(X\smallsetminus N)^{I}}$ (respectively
$\left.\operatorname{Cht}_{G,I,W}\!\vphantom{\big|}\right|_{(X\smallsetminus N)^{I}}$ (respectively  $\left.\operatorname{Cht}_{P,I,W}\!\vphantom{\big|}\right|_{(X\smallsetminus N)^{I}}$ and
$\left.\operatorname{Cht}_{P,I,W}\!\vphantom{\big|}\right|_{(X\smallsetminus N)^{I}}$ and  $\left.\operatorname{Cht}_{M,I,W}\!\vphantom{\big|}\right|_{(X\smallsetminus N)^{I}}$) with Galois group
$\left.\operatorname{Cht}_{M,I,W}\!\vphantom{\big|}\right|_{(X\smallsetminus N)^{I}}$) with Galois group  $G({\mathcal{O}}_{N})$ (respectively
$G({\mathcal{O}}_{N})$ (respectively  $P({\mathcal{O}}_{N})$ and
$P({\mathcal{O}}_{N})$ and  $M({\mathcal{O}}_{N})$).
$M({\mathcal{O}}_{N})$).
Definition 3.4.2. We define
 $$\begin{eqnarray}\operatorname{Cht}_{P,N,I,W}^{\prime }:=\operatorname{Cht}_{P,N,I,W}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N}),\quad \operatorname{Cht}_{M,N,I,W}^{\prime }:=\operatorname{Cht}_{M,N,I,W}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{P,N,I,W}^{\prime }:=\operatorname{Cht}_{P,N,I,W}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N}),\quad \operatorname{Cht}_{M,N,I,W}^{\prime }:=\operatorname{Cht}_{M,N,I,W}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N}),\end{eqnarray}$$ where  $P({\mathcal{O}}_{N})$ acts on
$P({\mathcal{O}}_{N})$ acts on  $G({\mathcal{O}}_{N})$ by left action (by left multiplication) and
$G({\mathcal{O}}_{N})$ by left action (by left multiplication) and  $P({\mathcal{O}}_{N})$ acts on
$P({\mathcal{O}}_{N})$ acts on  $\operatorname{Cht}_{M,N,I,W}$ via the quotient
$\operatorname{Cht}_{M,N,I,W}$ via the quotient  $P({\mathcal{O}}_{N}){\twoheadrightarrow}M({\mathcal{O}}_{N})$.
$P({\mathcal{O}}_{N}){\twoheadrightarrow}M({\mathcal{O}}_{N})$.
3.4.3
Morphisms (3.7) induce morphisms
 $$\begin{eqnarray}\operatorname{Cht}_{G,N,I,W}\xleftarrow[{}]{i^{\prime }}\operatorname{Cht}_{P,N,I,W}^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\prime }}\operatorname{Cht}_{M,N,I,W}^{\prime }\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{G,N,I,W}\xleftarrow[{}]{i^{\prime }}\operatorname{Cht}_{P,N,I,W}^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\prime }}\operatorname{Cht}_{M,N,I,W}^{\prime }\!.\end{eqnarray}$$ Indeed, the morphism  $i^{\prime }$ is giving by
$i^{\prime }$ is giving by
 $$\begin{eqnarray}(({\mathcal{P}},\unicode[STIX]{x1D713}_{P})\rightarrow (\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{P}},^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}_{P}),g\in G({\mathcal{O}}_{N}))\mapsto (({\mathcal{G}},g^{-1}\circ \unicode[STIX]{x1D713}_{G})\rightarrow (\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}},{g^{-1}\circ }^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}_{G})),\end{eqnarray}$$
$$\begin{eqnarray}(({\mathcal{P}},\unicode[STIX]{x1D713}_{P})\rightarrow (\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{P}},^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}_{P}),g\in G({\mathcal{O}}_{N}))\mapsto (({\mathcal{G}},g^{-1}\circ \unicode[STIX]{x1D713}_{G})\rightarrow (\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}},{g^{-1}\circ }^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}_{G})),\end{eqnarray}$$ where  ${\mathcal{G}}={\mathcal{P}}\overset{P}{\times }G$ and
${\mathcal{G}}={\mathcal{P}}\overset{P}{\times }G$ and  $\unicode[STIX]{x1D713}_{G}=\unicode[STIX]{x1D713}_{P}\overset{P}{\times }G$. The morphism
$\unicode[STIX]{x1D713}_{G}=\unicode[STIX]{x1D713}_{P}\overset{P}{\times }G$. The morphism  $\unicode[STIX]{x1D70B}^{\prime }$ is induced by
$\unicode[STIX]{x1D70B}^{\prime }$ is induced by  $\unicode[STIX]{x1D70B}$, which is
$\unicode[STIX]{x1D70B}$, which is  $P({\mathcal{O}}_{N})$-equivariant (because
$P({\mathcal{O}}_{N})$-equivariant (because  $P({\mathcal{O}}_{N})$ acts on
$P({\mathcal{O}}_{N})$ acts on  $\operatorname{Cht}_{P,N,I,W}$ and
$\operatorname{Cht}_{P,N,I,W}$ and  $\operatorname{Cht}_{M,N,I,W}$ by changing the level structure on
$\operatorname{Cht}_{M,N,I,W}$ by changing the level structure on  $N$).
$N$).
Remark 3.4.4. The morphism  $\operatorname{Cht}_{P,N,I,W}^{\prime }\rightarrow \operatorname{Cht}_{P,I,W}\underset{\operatorname{Cht}_{G,I,W}}{\times }\operatorname{Cht}_{G,N,I,W}$ is a
$\operatorname{Cht}_{P,N,I,W}^{\prime }\rightarrow \operatorname{Cht}_{P,I,W}\underset{\operatorname{Cht}_{G,I,W}}{\times }\operatorname{Cht}_{G,N,I,W}$ is a  $G({\mathcal{O}}_{N})$-equivariant morphism of
$G({\mathcal{O}}_{N})$-equivariant morphism of  $G({\mathcal{O}}_{N})$-torsors over
$G({\mathcal{O}}_{N})$-torsors over  $\operatorname{Cht}_{P,I,W}$, and thus it is an isomorphism. In [Reference VarshavskyVar04, 2.28], the stack
$\operatorname{Cht}_{P,I,W}$, and thus it is an isomorphism. In [Reference VarshavskyVar04, 2.28], the stack  $\operatorname{Cht}_{P,N,I,W}^{\prime }$ is denoted by
$\operatorname{Cht}_{P,N,I,W}^{\prime }$ is denoted by  $FBun_{P,D,n,\bar{\unicode[STIX]{x1D714}}}$. The reason why we will need
$FBun_{P,D,n,\bar{\unicode[STIX]{x1D714}}}$. The reason why we will need  $\operatorname{Cht}_{P,N,I,W}^{\prime }$ instead of
$\operatorname{Cht}_{P,N,I,W}^{\prime }$ instead of  $\operatorname{Cht}_{P,N,I,W}$ is justified in Example 3.5.15 and Theorem 4.2.1.
$\operatorname{Cht}_{P,N,I,W}$ is justified in Example 3.5.15 and Theorem 4.2.1.
Definition 3.4.5. We define
 $$\begin{eqnarray}\displaystyle & \operatorname{Cht}_{P,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707}}:=\operatorname{Cht}_{P,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N}), & \displaystyle \nonumber\\ \displaystyle & \operatorname{Cht}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707}}:=\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N}),\quad \operatorname{Cht}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}:=\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N}). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \operatorname{Cht}_{P,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707}}:=\operatorname{Cht}_{P,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N}), & \displaystyle \nonumber\\ \displaystyle & \operatorname{Cht}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707}}:=\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N}),\quad \operatorname{Cht}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}:=\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N}). & \displaystyle \nonumber\end{eqnarray}$$3.4.6
We have a commutative diagram of algebraic stacks.

We deduce that  $\operatorname{Cht}_{P,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707}}$ is also the inverse image of
$\operatorname{Cht}_{P,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707}}$ is also the inverse image of  $\operatorname{Bun}_{P}^{{\leqslant}\unicode[STIX]{x1D707}}$ by
$\operatorname{Bun}_{P}^{{\leqslant}\unicode[STIX]{x1D707}}$ by  $\operatorname{Cht}_{P,N,I,W}^{\prime }\rightarrow \operatorname{Bun}_{P}$ and
$\operatorname{Cht}_{P,N,I,W}^{\prime }\rightarrow \operatorname{Bun}_{P}$ and  $\operatorname{Cht}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707}}$ (respectively
$\operatorname{Cht}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707}}$ (respectively  $\operatorname{Cht}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$) is also the inverse image of
$\operatorname{Cht}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$) is also the inverse image of  $\operatorname{Bun}_{M}^{{\leqslant}\unicode[STIX]{x1D707}}$ (respectively
$\operatorname{Bun}_{M}^{{\leqslant}\unicode[STIX]{x1D707}}$ (respectively  $\operatorname{Bun}_{M}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$) by
$\operatorname{Bun}_{M}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$) by  $\operatorname{Cht}_{M,N,I,W}^{\prime }\rightarrow \operatorname{Bun}_{M}$.
$\operatorname{Cht}_{M,N,I,W}^{\prime }\rightarrow \operatorname{Bun}_{M}$.
Definition 3.4.7. Just as in §2.6, we construct a morphism  $\unicode[STIX]{x1D716}_{M,d}^{\unicode[STIX]{x1D6EF}\,^{\prime }}:\operatorname{Cht}_{M,N,I,W}^{\prime }/\unicode[STIX]{x1D6EF}\rightarrow [\overline{M}_{I,d}\backslash \operatorname{Gr}_{M,I,W}]$ and we define
$\unicode[STIX]{x1D716}_{M,d}^{\unicode[STIX]{x1D6EF}\,^{\prime }}:\operatorname{Cht}_{M,N,I,W}^{\prime }/\unicode[STIX]{x1D6EF}\rightarrow [\overline{M}_{I,d}\backslash \operatorname{Gr}_{M,I,W}]$ and we define  ${\mathcal{F}}_{M,N,I,W}^{\;^{\prime }\;\unicode[STIX]{x1D6EF}}$ to be the inverse image of
${\mathcal{F}}_{M,N,I,W}^{\;^{\prime }\;\unicode[STIX]{x1D6EF}}$ to be the inverse image of  ${\mathcal{S}}_{M,I,W}^{\operatorname{ad},d}$. We define
${\mathcal{S}}_{M,I,W}^{\operatorname{ad},d}$. We define  ${\mathcal{H}}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}:=R(\mathfrak{p}_{M})_{!}(\left.{\mathcal{F}}_{M,I,N,W}^{\;^{\prime }\,\unicode[STIX]{x1D6EF}}\vphantom{\big|}\right|_{\operatorname{Cht}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}})$,
${\mathcal{H}}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}:=R(\mathfrak{p}_{M})_{!}(\left.{\mathcal{F}}_{M,I,N,W}^{\;^{\prime }\,\unicode[STIX]{x1D6EF}}\vphantom{\big|}\right|_{\operatorname{Cht}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}})$,  ${\mathcal{H}}_{M,N,I,W}^{\prime \,j,\;\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}:=H^{j}({\mathcal{H}}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}})$ and
${\mathcal{H}}_{M,N,I,W}^{\prime \,j,\;\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}:=H^{j}({\mathcal{H}}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}})$ and  $H_{M,N,I,W}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}:=\left.{\mathcal{H}}_{M,N,I,W}^{\prime \;j,\;\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}\vphantom{\big|}\right|_{\overline{\unicode[STIX]{x1D702}^{I}}}$.
$H_{M,N,I,W}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}:=\left.{\mathcal{H}}_{M,N,I,W}^{\prime \;j,\;\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}\vphantom{\big|}\right|_{\overline{\unicode[STIX]{x1D702}^{I}}}$.
3.4.8
Just as in 2.6.5, if  $\unicode[STIX]{x1D708}\notin \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}$ (defined in 1.5.20), then
$\unicode[STIX]{x1D708}\notin \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}$ (defined in 1.5.20), then  $\operatorname{Cht}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$ is empty and
$\operatorname{Cht}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$ is empty and  $H_{M,N,I,W}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}=0$.
$H_{M,N,I,W}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}=0$.
Definition 3.4.10. For any  $\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$, we define
$\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$, we define  $H_{M,N,I,W}^{\prime \,j,\,\unicode[STIX]{x1D708}}:=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}}H_{M,N,I,W}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$.
$H_{M,N,I,W}^{\prime \,j,\,\unicode[STIX]{x1D708}}:=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}}H_{M,N,I,W}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$.
3.5 Constant term morphism for cohomology groups
3.5.2
For any  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and any
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and any  $\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$, the first line of morphisms (3.28) induces morphisms over
$\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$, the first line of morphisms (3.28) induces morphisms over  $(X\smallsetminus N)^{I}$:
$(X\smallsetminus N)^{I}$:
 $$\begin{eqnarray}\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\xleftarrow[{}]{i^{\prime }}\operatorname{Cht}_{P,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\prime }}\operatorname{Cht}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\xleftarrow[{}]{i^{\prime }}\operatorname{Cht}_{P,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\prime }}\operatorname{Cht}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}.\end{eqnarray}$$The proof of [Reference VarshavskyVar04, Proposition 5.7] in fact proves the following.
Proposition 3.5.3 [Reference VarshavskyVar04, Proposition 5.7].
For any  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and any
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and any  $\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}$ (defined in 1.5.20), there exists an open dense subscheme
$\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}$ (defined in 1.5.20), there exists an open dense subscheme  $\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$ of
$\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$ of  $(X\smallsetminus N)^{I}$ such that the restriction of the morphism
$(X\smallsetminus N)^{I}$ such that the restriction of the morphism  $i^{\prime }$ on
$i^{\prime }$ on  $\left.\operatorname{Cht}_{P,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}}$ is proper. In particular, the restriction of the morphism
$\left.\operatorname{Cht}_{P,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}}$ is proper. In particular, the restriction of the morphism  $i^{\prime }$ on
$i^{\prime }$ on  $\left.\operatorname{Cht}_{P,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}\vphantom{\big|}\right|_{\unicode[STIX]{x1D702}^{I}}$ is proper.
$\left.\operatorname{Cht}_{P,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}\vphantom{\big|}\right|_{\unicode[STIX]{x1D702}^{I}}$ is proper.
Remark 3.5.4. In [Reference VarshavskyVar04, Proposition 5.7], the level is denoted by  $D$, the paws are indexed by
$D$, the paws are indexed by  $n$, the index
$n$, the index  $d$ is related to our
$d$ is related to our  $\unicode[STIX]{x1D708}$, the index
$\unicode[STIX]{x1D708}$, the index  $\overline{k}$ is related to our
$\overline{k}$ is related to our  $W$, and the index
$W$, and the index  $[g]$ is in
$[g]$ is in  $G({\mathcal{O}}_{N})/P({\mathcal{O}}_{N})$. The open subscheme
$G({\mathcal{O}}_{N})/P({\mathcal{O}}_{N})$. The open subscheme  $\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$ is of the form
$\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}}$ is of the form
 $$\begin{eqnarray}\unicode[STIX]{x1D6FA}(m)=\{(x_{i})_{i\in I}\in (X\smallsetminus N)^{I},\;x_{i}\neq ^{\unicode[STIX]{x1D70F}^{r}}x_{j}\text{ for all }i,j\text{ and }r=1,2,\ldots ,m\},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}(m)=\{(x_{i})_{i\in I}\in (X\smallsetminus N)^{I},\;x_{i}\neq ^{\unicode[STIX]{x1D70F}^{r}}x_{j}\text{ for all }i,j\text{ and }r=1,2,\ldots ,m\},\end{eqnarray}$$ where  $^{\unicode[STIX]{x1D70F}^{r}}x$ is the image of
$^{\unicode[STIX]{x1D70F}^{r}}x$ is the image of  $x$ by
$x$ by  $\operatorname{Frob}^{r}:X\rightarrow X$ and
$\operatorname{Frob}^{r}:X\rightarrow X$ and  $m$ is some positive integer.
$m$ is some positive integer.
In the proof of [Reference VarshavskyVar04, Proposition 5.7],  $\operatorname{Bun}_{G}^{{\leqslant}\unicode[STIX]{x1D707}}$ is denoted by
$\operatorname{Bun}_{G}^{{\leqslant}\unicode[STIX]{x1D707}}$ is denoted by  $V$ and
$V$ and  $\unicode[STIX]{x1D6FA}(m)$ is denoted by
$\unicode[STIX]{x1D6FA}(m)$ is denoted by  $U$. Varshavsky shows that for fixed
$U$. Varshavsky shows that for fixed  $\unicode[STIX]{x1D707}$ and
$\unicode[STIX]{x1D707}$ and  $\unicode[STIX]{x1D708}$, there exists a level
$\unicode[STIX]{x1D708}$, there exists a level  $D$ large enough and an integer
$D$ large enough and an integer  $m$ large enough (both depending on
$m$ large enough (both depending on  $\unicode[STIX]{x1D707}$ and
$\unicode[STIX]{x1D707}$ and  $\unicode[STIX]{x1D708}$), such that over
$\unicode[STIX]{x1D708}$), such that over  $\operatorname{Bun}_{G}^{{\leqslant}\unicode[STIX]{x1D707}}\times \,\unicode[STIX]{x1D6FA}(m)\subset \operatorname{Bun}_{G}\times \,(X\smallsetminus N)^{I}$, the morphism However,
$\operatorname{Bun}_{G}^{{\leqslant}\unicode[STIX]{x1D707}}\times \,\unicode[STIX]{x1D6FA}(m)\subset \operatorname{Bun}_{G}\times \,(X\smallsetminus N)^{I}$, the morphism However,
 $$\begin{eqnarray}\left.\operatorname{Cht}_{P,D,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}\!\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}(m)}\rightarrow \left.\operatorname{Cht}_{G,D,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}\!\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}(m)}\end{eqnarray}$$
$$\begin{eqnarray}\left.\operatorname{Cht}_{P,D,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}\!\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}(m)}\rightarrow \left.\operatorname{Cht}_{G,D,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}\!\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}(m)}\end{eqnarray}$$ is a closed embedding. In particular, it is proper. Then we descend to level  $N$.
$N$.
Note that  $i^{\prime }$ is schematic (i.e. representable). This is implied by the well-known fact that
$i^{\prime }$ is schematic (i.e. representable). This is implied by the well-known fact that  $\operatorname{Bun}_{P}\rightarrow \operatorname{Bun}_{G}$ is schematic (a
$\operatorname{Bun}_{P}\rightarrow \operatorname{Bun}_{G}$ is schematic (a  $P$-structure of a
$P$-structure of a  $G$-bundle
$G$-bundle  ${\mathcal{G}}$ over
${\mathcal{G}}$ over  $X\times S$ is a section of the fibration
$X\times S$ is a section of the fibration  ${\mathcal{G}}/P\rightarrow X\times S$).
${\mathcal{G}}/P\rightarrow X\times S$).
3.5.5
Now consider the following commutative diagram.

To simplify the notations, we denote by  ${\mathcal{F}}_{G,N,\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}},W}^{\;\unicode[STIX]{x1D6EF}}$ the restriction of
${\mathcal{F}}_{G,N,\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}},W}^{\;\unicode[STIX]{x1D6EF}}$ the restriction of  ${\mathcal{F}}_{G,I,N,W}^{\;\unicode[STIX]{x1D6EF}}$ to
${\mathcal{F}}_{G,I,N,W}^{\;\unicode[STIX]{x1D6EF}}$ to  $\left.\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}}$ and by
$\left.\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}}$ and by  ${\mathcal{F}}_{M,N,\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}},W}^{\prime \;\unicode[STIX]{x1D6EF},\,\unicode[STIX]{x1D708}}$ the restriction of
${\mathcal{F}}_{M,N,\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}},W}^{\prime \;\unicode[STIX]{x1D6EF},\,\unicode[STIX]{x1D708}}$ the restriction of  ${\mathcal{F}}_{M,I,N,W}^{\prime \;\unicode[STIX]{x1D6EF}}$ to
${\mathcal{F}}_{M,I,N,W}^{\prime \;\unicode[STIX]{x1D6EF}}$ to  $\left.\operatorname{Cht}_{M,N,I,W}^{\prime \;\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}}$.
$\left.\operatorname{Cht}_{M,N,I,W}^{\prime \;\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}}$.
The commutative diagram (3.28) is compatible with the Harder–Narasimhan stratification. Just as in Construction 3.3.4, we construct a canonical morphism of complexes
 $$\begin{eqnarray}(\unicode[STIX]{x1D70B}^{\prime })_{!}(i^{\prime })^{\ast }{\mathcal{F}}_{G,N,\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}},W}^{\;\unicode[STIX]{x1D6EF}}\rightarrow {\mathcal{F}}_{M,N,\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}},W}^{\prime \;\unicode[STIX]{x1D6EF},\,\unicode[STIX]{x1D708}}\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70B}^{\prime })_{!}(i^{\prime })^{\ast }{\mathcal{F}}_{G,N,\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}},W}^{\;\unicode[STIX]{x1D6EF}}\rightarrow {\mathcal{F}}_{M,N,\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}},W}^{\prime \;\unicode[STIX]{x1D6EF},\,\unicode[STIX]{x1D708}}\end{eqnarray}$$ in  $D_{c}^{b}(\left.\operatorname{Cht}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}},\mathbb{Q}_{\ell })$.
$D_{c}^{b}(\left.\operatorname{Cht}_{M,N,I,W}^{\prime \,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}},\mathbb{Q}_{\ell })$.
3.5.6
Thanks to Proposition 3.5.3, we can apply [Reference GrothendieckSGA5, III 3] to diagram (3.30) and the cohomological correspondence (3.31).
Concretely, first we have morphisms of functors from  $D_{c}^{b}(\left.\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}},\mathbb{Q}_{\ell })$ to
$D_{c}^{b}(\left.\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}},\mathbb{Q}_{\ell })$ to  $D_{c}^{b}(\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}},\mathbb{Q}_{\ell })$ (all functors are considered as derived functors):
$D_{c}^{b}(\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}},\mathbb{Q}_{\ell })$ (all functors are considered as derived functors):
 $$\begin{eqnarray}(\mathfrak{p}_{G})_{!}\overset{(a)}{\rightarrow }(\mathfrak{p}_{G})_{!}(i^{\prime })_{\ast }(i^{\prime })^{\ast }\overset{(b)}{\simeq }(\mathfrak{p}_{G})_{!}(i^{\prime })_{!}(i^{\prime })^{\ast }\overset{(c)}{\simeq }(\mathfrak{p}_{M})_{!}(\unicode[STIX]{x1D70B}^{\prime })_{!}(i^{\prime })^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}(\mathfrak{p}_{G})_{!}\overset{(a)}{\rightarrow }(\mathfrak{p}_{G})_{!}(i^{\prime })_{\ast }(i^{\prime })^{\ast }\overset{(b)}{\simeq }(\mathfrak{p}_{G})_{!}(i^{\prime })_{!}(i^{\prime })^{\ast }\overset{(c)}{\simeq }(\mathfrak{p}_{M})_{!}(\unicode[STIX]{x1D70B}^{\prime })_{!}(i^{\prime })^{\ast },\end{eqnarray}$$ where (a) is the adjunction morphism, (b) is induced by  $i_{!}^{\prime }\overset{{\sim}}{\rightarrow }i_{\ast }^{\prime }$ which is because that
$i_{!}^{\prime }\overset{{\sim}}{\rightarrow }i_{\ast }^{\prime }$ which is because that  $i^{\prime }$ is schematic and proper (Proposition 3.5.3), and (c) is induced by the commutativity of diagram (3.30).
$i^{\prime }$ is schematic and proper (Proposition 3.5.3), and (c) is induced by the commutativity of diagram (3.30).
Second we combine (3.32) with (3.31). We obtain a composition of morphisms of complexes in  $D_{c}^{b}(\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}},\mathbb{Q}_{\ell })$.
$D_{c}^{b}(\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}},\mathbb{Q}_{\ell })$.

By Definition 2.5.1 and Definition 3.4.7, (
3.33) is also written as
 $$\begin{eqnarray}{\mathcal{C}}_{G}^{P,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}:\left.{\mathcal{H}}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}}\rightarrow \left.{{\mathcal{H}}^{\prime }}_{\!\!\!M,N,I,W}^{\;\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}_{G}^{P,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}:\left.{\mathcal{H}}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}}\rightarrow \left.{{\mathcal{H}}^{\prime }}_{\!\!\!M,N,I,W}^{\;\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6FA}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}}.\end{eqnarray}$$3.5.7
From now on, we restrict everything to the geometric generic point  $\overline{\unicode[STIX]{x1D702}^{I}}$ of
$\overline{\unicode[STIX]{x1D702}^{I}}$ of  $X^{I}$ fixed in 2.5.4. Recall that we have defined
$X^{I}$ fixed in 2.5.4. Recall that we have defined  $H_{G,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}}=\left.{\mathcal{H}}_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}}\vphantom{\big|}\right|_{\overline{\unicode[STIX]{x1D702}^{I}}}$ in Definition 2.5.5 and
$H_{G,N,I,W}^{j,\,\leqslant \unicode[STIX]{x1D707}}=\left.{\mathcal{H}}_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}}\vphantom{\big|}\right|_{\overline{\unicode[STIX]{x1D702}^{I}}}$ in Definition 2.5.5 and  $H_{M,N,I,W}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}=\left.{\mathcal{H}}_{M,N,I,W}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}\vphantom{\big|}\right|_{\overline{\unicode[STIX]{x1D702}^{I}}}$ in Definition 3.4.7.
$H_{M,N,I,W}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}=\left.{\mathcal{H}}_{M,N,I,W}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}\vphantom{\big|}\right|_{\overline{\unicode[STIX]{x1D702}^{I}}}$ in Definition 3.4.7.
For any  $j\in \mathbb{Z}$, morphism (3.34) induces a morphism of cohomology groups
$j\in \mathbb{Z}$, morphism (3.34) induces a morphism of cohomology groups
 $$\begin{eqnarray}C_{G}^{P,\,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}:H_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}}\rightarrow {H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}.\end{eqnarray}$$
$$\begin{eqnarray}C_{G}^{P,\,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}:H_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}}\rightarrow {H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}.\end{eqnarray}$$ By 3.4.8, for  $\unicode[STIX]{x1D708}\notin \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}$, the morphism
$\unicode[STIX]{x1D708}\notin \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}$, the morphism  $C_{G}^{P,\,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$ is the zero morphism.
$C_{G}^{P,\,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$ is the zero morphism.
3.5.8
We define a morphism:
 $$\begin{eqnarray}C_{G}^{P,\,j,\,\leqslant \unicode[STIX]{x1D707}}=\mathop{\prod }_{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}}C_{G}^{P,\,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}:H_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}}\rightarrow {H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\leqslant \unicode[STIX]{x1D707}}\end{eqnarray}$$
$$\begin{eqnarray}C_{G}^{P,\,j,\,\leqslant \unicode[STIX]{x1D707}}=\mathop{\prod }_{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}}C_{G}^{P,\,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}:H_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}}\rightarrow {H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\leqslant \unicode[STIX]{x1D707}}\end{eqnarray}$$ where  ${H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\leqslant \unicode[STIX]{x1D707}}$ is defined in Definition 3.4.9.
${H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\leqslant \unicode[STIX]{x1D707}}$ is defined in Definition 3.4.9.
3.5.9
Let  $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ with
$\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ with  $\unicode[STIX]{x1D707}_{1}\leqslant \unicode[STIX]{x1D707}_{2}$. By Lemma A.0.8, the commutative diagram of stacks
$\unicode[STIX]{x1D707}_{1}\leqslant \unicode[STIX]{x1D707}_{2}$. By Lemma A.0.8, the commutative diagram of stacks

induces a commutative diagram of cohomology groups.

We have defined  $H_{G,N,I,W}^{j}=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}}H_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}}$ in Definition 2.5.5 and
$H_{G,N,I,W}^{j}=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}}H_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}}$ in Definition 2.5.5 and  ${H^{\prime }}_{\!\!\!M,N,I,W}^{\;j}=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}}{H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\leqslant \unicode[STIX]{x1D707}}$ in Definition 3.4.9. The commutative diagram (3.38) induces a morphism between inductive limits.
${H^{\prime }}_{\!\!\!M,N,I,W}^{\;j}=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}}{H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\leqslant \unicode[STIX]{x1D707}}$ in Definition 3.4.9. The commutative diagram (3.38) induces a morphism between inductive limits.
Definition 3.5.10. For all parabolic subgroups  $P$, for all degrees
$P$, for all degrees  $j\in \mathbb{Z}$, we define the constant term morphism of cohomology groups:
$j\in \mathbb{Z}$, we define the constant term morphism of cohomology groups:
 $$\begin{eqnarray}C_{G,N}^{P,\,j}:H_{G,N,I,W}^{j}\rightarrow {H^{\prime }}_{\!\!\!M,N,I,W}^{\;j}.\end{eqnarray}$$
$$\begin{eqnarray}C_{G,N}^{P,\,j}:H_{G,N,I,W}^{j}\rightarrow {H^{\prime }}_{\!\!\!M,N,I,W}^{\;j}.\end{eqnarray}$$Remark 3.5.11. The morphisms  ${H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}\rightarrow \mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}^{\prime }}{H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\leqslant \unicode[STIX]{x1D707}^{\prime },\;\unicode[STIX]{x1D708}}$ for each
${H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\leqslant \unicode[STIX]{x1D707},\;\unicode[STIX]{x1D708}}\rightarrow \mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}^{\prime }}{H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\leqslant \unicode[STIX]{x1D707}^{\prime },\;\unicode[STIX]{x1D708}}$ for each  $\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$ induce a morphism
$\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$ induce a morphism

With the notations in Definitions 3.4.9 and 3.4.10, morphism (
3.40) is the natural map
 $$\begin{eqnarray}H_{M,N,I,W}^{\prime \,j}\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}}{H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\unicode[STIX]{x1D708}}.\end{eqnarray}$$
$$\begin{eqnarray}H_{M,N,I,W}^{\prime \,j}\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}}{H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\unicode[STIX]{x1D708}}.\end{eqnarray}$$ For each  $\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$, taking inductive limit over
$\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$, taking inductive limit over  $\unicode[STIX]{x1D707}$ of (3.35), we define
$\unicode[STIX]{x1D707}$ of (3.35), we define  $C_{G,N}^{P,\,j,\,\unicode[STIX]{x1D708}}:H_{G,N,I,W}^{j}\rightarrow {H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\unicode[STIX]{x1D708}}$. We form a morphism
$C_{G,N}^{P,\,j,\,\unicode[STIX]{x1D708}}:H_{G,N,I,W}^{j}\rightarrow {H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\unicode[STIX]{x1D708}}$. We form a morphism
 $$\begin{eqnarray}\mathop{\prod }_{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}}C_{G,N}^{P,\,j,\,\unicode[STIX]{x1D708}}:H_{G,N,I,W}^{j}\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}}{H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\unicode[STIX]{x1D708}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}}C_{G,N}^{P,\,j,\,\unicode[STIX]{x1D708}}:H_{G,N,I,W}^{j}\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}}{H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\unicode[STIX]{x1D708}}.\end{eqnarray}$$It is equal to the composition of (3.39) and (3.41).
In Lemma 5.3.4 below, we will prove that, for  $\unicode[STIX]{x1D707}$ large enough,
$\unicode[STIX]{x1D707}$ large enough,
 $$\begin{eqnarray}H_{M,N,I,W}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707}}\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}}\!\!{H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\unicode[STIX]{x1D708}}\end{eqnarray}$$
$$\begin{eqnarray}H_{M,N,I,W}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707}}\rightarrow \mathop{\prod }_{\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}}\!\!{H^{\prime }}_{\!\!\!M,N,I,W}^{\;j,\;\unicode[STIX]{x1D708}}\end{eqnarray}$$is injective. This implies that (3.41) is injective. Thus the kernel of (3.42) is the same as the kernel of (3.39).
Remark 3.5.12. Now consider all parabolic subgroups (not only the standard ones). If  $P_{1}$ and
$P_{1}$ and  $P_{2}$ are conjugated, then the conjugation induces an isomorphism
$P_{2}$ are conjugated, then the conjugation induces an isomorphism  $M_{1}\simeq M_{2}$. This induces for any
$M_{1}\simeq M_{2}$. This induces for any  $j$ an isomorphism
$j$ an isomorphism  ${H^{\prime }}_{\!\!\!M_{1},N,I,W}^{\;j}\simeq {H^{\prime }}_{\!\!\!M_{2},N,I,W}^{\;j}$. The following diagram commutes
${H^{\prime }}_{\!\!\!M_{1},N,I,W}^{\;j}\simeq {H^{\prime }}_{\!\!\!M_{2},N,I,W}^{\;j}$. The following diagram commutes

and thus we have  $\operatorname{Ker}C_{G,N}^{P_{1},\,j}=\operatorname{Ker}C_{G,N}^{P_{2},\,j}$ in
$\operatorname{Ker}C_{G,N}^{P_{1},\,j}=\operatorname{Ker}C_{G,N}^{P_{2},\,j}$ in  $H_{G,N,I,W}^{j}$.
$H_{G,N,I,W}^{j}$.
However, we do not know how to compare the constant term morphism along different parabolic subgroups which have a common Levi subgroup. It is perhaps possible to do that, but quite difficult because it would be a generalization of the functional equation for Eisenstein series.
Definition 3.5.13. For any degree  $j\in \mathbb{Z}$, we define the cuspidal cohomology group:
$j\in \mathbb{Z}$, we define the cuspidal cohomology group:
 $$\begin{eqnarray}H_{G,N,I,W}^{j,\;\operatorname{cusp}}:=\underset{P\subsetneq G}{\bigcap }\operatorname{Ker}\mathop{C}_{G,N}^{P,\,j}.\end{eqnarray}$$
$$\begin{eqnarray}H_{G,N,I,W}^{j,\;\operatorname{cusp}}:=\underset{P\subsetneq G}{\bigcap }\operatorname{Ker}\mathop{C}_{G,N}^{P,\,j}.\end{eqnarray}$$ This is a  $\mathbb{Q}_{\ell }$-vector subspace of
$\mathbb{Q}_{\ell }$-vector subspace of  $H_{G,N,I,W}^{j}$.
$H_{G,N,I,W}^{j}$.
Remark 3.5.14. For

we have  $C_{M_{2},N}^{P_{1,2},\,j}\circ C_{G,N}^{P_{2},\,j}=C_{G,N}^{P_{1},\,j}$. Thus we have an equivalent definition:
$C_{M_{2},N}^{P_{1,2},\,j}\circ C_{G,N}^{P_{2},\,j}=C_{G,N}^{P_{1},\,j}$. Thus we have an equivalent definition:
 $$\begin{eqnarray}H_{G,N,I,W}^{j,\;\operatorname{cusp}}=\underset{P\text{ maximal parabolic}}{\bigcap }\operatorname{Ker}\mathop{C}_{G,N}^{P,\,j}.\end{eqnarray}$$
$$\begin{eqnarray}H_{G,N,I,W}^{j,\;\operatorname{cusp}}=\underset{P\text{ maximal parabolic}}{\bigcap }\operatorname{Ker}\mathop{C}_{G,N}^{P,\,j}.\end{eqnarray}$$Example 3.5.15 (Shtukas without paws).
When  $I=\emptyset$ and
$I=\emptyset$ and  $W=\mathbf{1}$, we have
$W=\mathbf{1}$, we have  $\operatorname{Cht}_{G,N,\emptyset ,\mathbf{1}}=G(F)\backslash G(\mathbb{A})/K_{G,N}$. (Note that
$\operatorname{Cht}_{G,N,\emptyset ,\mathbf{1}}=G(F)\backslash G(\mathbb{A})/K_{G,N}$. (Note that  $G$ is split. See [Reference LafforgueLaf18, (0.5) and Remarque 8.21] for more details.) Moreover, let
$G$ is split. See [Reference LafforgueLaf18, (0.5) and Remarque 8.21] for more details.) Moreover, let  $K_{P,N}:=K_{G,N}\cap P(\mathbb{O})$,
$K_{P,N}:=K_{G,N}\cap P(\mathbb{O})$,  $K_{U,N}:=K_{G,N}\cap U(\mathbb{O})$ and
$K_{U,N}:=K_{G,N}\cap U(\mathbb{O})$ and  $K_{M,N}:=K_{P,N}/K_{U,N}$. We write
$K_{M,N}:=K_{P,N}/K_{U,N}$. We write  $\overset{\operatorname{set}}{=}$ for equalities of sets which are not equalities of groupoids. We have
$\overset{\operatorname{set}}{=}$ for equalities of sets which are not equalities of groupoids. We have
 $$\begin{eqnarray}\displaystyle \operatorname{Cht}_{P,N,\emptyset ,\mathbf{1}}^{\prime } & = & \displaystyle (P(F)\backslash P(\mathbb{A})/K_{P,N})\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N})=P(F)\backslash (P(\mathbb{A})\overset{P(\mathbb{O})}{\times }G(\mathbb{O}))/K_{G,N}\nonumber\\ \displaystyle & = & \displaystyle P(F)\backslash G(\mathbb{A})/K_{G,N},\nonumber\\ \displaystyle \operatorname{Cht}_{M,N,\emptyset ,\mathbf{1}}^{\prime } & = & \displaystyle (M(F)\backslash M(\mathbb{A})/K_{M,N})\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N})\nonumber\\ \displaystyle & = & \displaystyle M(F)\backslash (M(\mathbb{A})\overset{P(\mathbb{O})/K_{U,N}}{\times }G(\mathbb{O})/K_{G,N})\overset{\operatorname{set}}{=}M(F)\backslash (M(\mathbb{A})\overset{P(\mathbb{O})}{\times }G(\mathbb{O}))/K_{G,N}\nonumber\\ \displaystyle & = & \displaystyle M(F)U(\mathbb{A})\backslash (P(\mathbb{A})\overset{P(\mathbb{O})}{\times }G(\mathbb{O}))/K_{G,N}=M(F)U(\mathbb{A})\backslash G(\mathbb{A})/K_{G,N}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Cht}_{P,N,\emptyset ,\mathbf{1}}^{\prime } & = & \displaystyle (P(F)\backslash P(\mathbb{A})/K_{P,N})\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N})=P(F)\backslash (P(\mathbb{A})\overset{P(\mathbb{O})}{\times }G(\mathbb{O}))/K_{G,N}\nonumber\\ \displaystyle & = & \displaystyle P(F)\backslash G(\mathbb{A})/K_{G,N},\nonumber\\ \displaystyle \operatorname{Cht}_{M,N,\emptyset ,\mathbf{1}}^{\prime } & = & \displaystyle (M(F)\backslash M(\mathbb{A})/K_{M,N})\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N})\nonumber\\ \displaystyle & = & \displaystyle M(F)\backslash (M(\mathbb{A})\overset{P(\mathbb{O})/K_{U,N}}{\times }G(\mathbb{O})/K_{G,N})\overset{\operatorname{set}}{=}M(F)\backslash (M(\mathbb{A})\overset{P(\mathbb{O})}{\times }G(\mathbb{O}))/K_{G,N}\nonumber\\ \displaystyle & = & \displaystyle M(F)U(\mathbb{A})\backslash (P(\mathbb{A})\overset{P(\mathbb{O})}{\times }G(\mathbb{O}))/K_{G,N}=M(F)U(\mathbb{A})\backslash G(\mathbb{A})/K_{G,N}.\nonumber\end{eqnarray}$$ In this case,  $\operatorname{Gr}_{P,\emptyset ,\mathbf{1}}=\operatorname{Gr}_{M,\emptyset ,\mathbf{1}}=\operatorname{Spec}\overline{\mathbb{F}_{q}}$. We can choose
$\operatorname{Gr}_{P,\emptyset ,\mathbf{1}}=\operatorname{Gr}_{M,\emptyset ,\mathbf{1}}=\operatorname{Spec}\overline{\mathbb{F}_{q}}$. We can choose  $d=0$ in (3.9). Thus
$d=0$ in (3.9). Thus  $\widetilde{\operatorname{Cht}}_{M,N,\emptyset ,1}^{\prime }=\operatorname{Cht}_{M,N,\emptyset ,1}^{\prime }$. The constant term morphism
$\widetilde{\operatorname{Cht}}_{M,N,\emptyset ,1}^{\prime }=\operatorname{Cht}_{M,N,\emptyset ,1}^{\prime }$. The constant term morphism  $C_{G,N}^{P,\,j}$ in Definition 3.5.10 coincides (up to constants depending on
$C_{G,N}^{P,\,j}$ in Definition 3.5.10 coincides (up to constants depending on  $\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$ component by component) with the classical constant term morphism:
$\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$ component by component) with the classical constant term morphism:

Therefore  $H_{G,N,\emptyset ,\mathbf{1}}^{0,\,\operatorname{cusp}}=C_{c}^{\operatorname{cusp}}(G(F)\backslash G(\mathbb{A})/K_{G,N}\unicode[STIX]{x1D6EF},\mathbb{Q}_{\ell })$.
$H_{G,N,\emptyset ,\mathbf{1}}^{0,\,\operatorname{cusp}}=C_{c}^{\operatorname{cusp}}(G(F)\backslash G(\mathbb{A})/K_{G,N}\unicode[STIX]{x1D6EF},\mathbb{Q}_{\ell })$.
Remark 3.5.16. When  $I=\emptyset$,
$I=\emptyset$,  $W=\mathbf{1}$ and
$W=\mathbf{1}$ and  $N=\emptyset$ (without level), for any
$N=\emptyset$ (without level), for any  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$,
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$,  $H_{M,N,I,W}^{\prime \,0,\,\leqslant \unicode[STIX]{x1D707}}$ is included in the subspace of
$H_{M,N,I,W}^{\prime \,0,\,\leqslant \unicode[STIX]{x1D707}}$ is included in the subspace of  $C(U(\mathbb{A})M(F)\backslash G(\mathbb{A})/G(\mathbb{O})\unicode[STIX]{x1D6EF},\mathbb{Q}_{\ell })$ of functions supported on the components of
$C(U(\mathbb{A})M(F)\backslash G(\mathbb{A})/G(\mathbb{O})\unicode[STIX]{x1D6EF},\mathbb{Q}_{\ell })$ of functions supported on the components of  $U(\mathbb{A})M(F)\backslash G(\mathbb{A})/G(\mathbb{O})\unicode[STIX]{x1D6EF}$ indexed by a translated cone
$U(\mathbb{A})M(F)\backslash G(\mathbb{A})/G(\mathbb{O})\unicode[STIX]{x1D6EF}$ indexed by a translated cone  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}$ in
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}$ in  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$. The image of the constant term morphism is included in
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$. The image of the constant term morphism is included in  $H_{M,N,I,W}^{\prime \,0}=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}}H_{M,N,I,W}^{\prime \,0,\,\leqslant \unicode[STIX]{x1D707}}$. This space is already defined independently by Wang in [Reference WangWan18, §5.1] and is denoted by
$H_{M,N,I,W}^{\prime \,0}=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}}H_{M,N,I,W}^{\prime \,0,\,\leqslant \unicode[STIX]{x1D707}}$. This space is already defined independently by Wang in [Reference WangWan18, §5.1] and is denoted by  ${\mathcal{C}}_{P,\,-}$ in [Reference WangWan18].
${\mathcal{C}}_{P,\,-}$ in [Reference WangWan18].
4 Contractibility of deep enough horospheres
In this section, let  $P$ be a parabolic subgroup of
$P$ be a parabolic subgroup of  $G$ and
$G$ and  $M$ its Levi quotient. The goal is to prove Proposition 4.6.4, which will be a consequence of Theorems 4.2.1 and 4.2.4.
$M$ its Levi quotient. The goal is to prove Proposition 4.6.4, which will be a consequence of Theorems 4.2.1 and 4.2.4.
4.1 More on Harder–Narasimhan stratification
To state Theorems 4.2.1 and 4.2.4, we need to introduce some locally closed substacks of  $\operatorname{Cht}_{G,N,I,W}$.
$\operatorname{Cht}_{G,N,I,W}$.
Definition 4.1.1. Let  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. We define a set
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. We define a set

where the second equality follows from 1.5.16 (taking into account Notation 1.7.1). The set  $S_{M}(\unicode[STIX]{x1D707})$ is bounded.
$S_{M}(\unicode[STIX]{x1D707})$ is bounded.
Remark 4.1.2. The set  $S_{M}(\unicode[STIX]{x1D707})$ is the same as the one (modulo
$S_{M}(\unicode[STIX]{x1D707})$ is the same as the one (modulo  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{G}}^{\mathbb{Q}}$) used in [Reference Drinfeld and GaitsgoryDG15, §§8 and 9].
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{G}}^{\mathbb{Q}}$) used in [Reference Drinfeld and GaitsgoryDG15, §§8 and 9].
Definition 4.1.3. We define
 $$\begin{eqnarray}\operatorname{Bun}_{G}^{=\unicode[STIX]{x1D707}}:=\underset{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}},\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D707}}{\bigcup }\mathop{\operatorname{Bun}}_{G}^{(\unicode[STIX]{x1D706})},\quad \operatorname{Bun}_{M}^{=\unicode[STIX]{x1D707}}:=\underset{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}},\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D707}}{\bigcup }\mathop{\operatorname{Bun}}_{M}^{(\unicode[STIX]{x1D706})},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{G}^{=\unicode[STIX]{x1D707}}:=\underset{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{G}^{+,\mathbb{Q}},\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D707}}{\bigcup }\mathop{\operatorname{Bun}}_{G}^{(\unicode[STIX]{x1D706})},\quad \operatorname{Bun}_{M}^{=\unicode[STIX]{x1D707}}:=\underset{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{M}^{+,\mathbb{Q}},\;\unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D707}}{\bigcup }\mathop{\operatorname{Bun}}_{M}^{(\unicode[STIX]{x1D706})},\end{eqnarray}$$ where  $\operatorname{Bun}_{G}^{(\unicode[STIX]{x1D706})}$ (respectively
$\operatorname{Bun}_{G}^{(\unicode[STIX]{x1D706})}$ (respectively  $\operatorname{Bun}_{M}^{(\unicode[STIX]{x1D706})}$) is defined in Definition 1.4.9 (respectively Definition 1.5.3).
$\operatorname{Bun}_{M}^{(\unicode[STIX]{x1D706})}$) is defined in Definition 1.4.9 (respectively Definition 1.5.3).
Definition 4.1.4. We define
 $$\begin{eqnarray}\operatorname{Bun}_{G}^{S_{M}(\unicode[STIX]{x1D707})}:=\underset{\unicode[STIX]{x1D706}\in S_{M}(\unicode[STIX]{x1D707})}{\bigcup }\mathop{\operatorname{Bun}}_{G}^{=\unicode[STIX]{x1D706}};\quad \operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}:=\underset{\unicode[STIX]{x1D706}\in S_{M}(\unicode[STIX]{x1D707})}{\bigcup }\mathop{\operatorname{Bun}}_{M}^{=\unicode[STIX]{x1D706}}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{G}^{S_{M}(\unicode[STIX]{x1D707})}:=\underset{\unicode[STIX]{x1D706}\in S_{M}(\unicode[STIX]{x1D707})}{\bigcup }\mathop{\operatorname{Bun}}_{G}^{=\unicode[STIX]{x1D706}};\quad \operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}:=\underset{\unicode[STIX]{x1D706}\in S_{M}(\unicode[STIX]{x1D707})}{\bigcup }\mathop{\operatorname{Bun}}_{M}^{=\unicode[STIX]{x1D706}}\!.\end{eqnarray}$$4.1.5
If  $\unicode[STIX]{x1D706}\in S_{M}(\unicode[STIX]{x1D707})$,
$\unicode[STIX]{x1D706}\in S_{M}(\unicode[STIX]{x1D707})$,  $\unicode[STIX]{x1D706}^{\prime }\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and
$\unicode[STIX]{x1D706}^{\prime }\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and  $\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D706}^{\prime }\leqslant \unicode[STIX]{x1D707}$, then
$\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D706}^{\prime }\leqslant \unicode[STIX]{x1D707}$, then  $\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D706})=\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D706}^{\prime })=\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})$. This implies that
$\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D706})=\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D706}^{\prime })=\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})$. This implies that  $\unicode[STIX]{x1D706}^{\prime }\in S_{M}(\unicode[STIX]{x1D707})$. Using [Reference Drinfeld and GaitsgoryDG15, Corollary 7.4.11], we deduce the following.
$\unicode[STIX]{x1D706}^{\prime }\in S_{M}(\unicode[STIX]{x1D707})$. Using [Reference Drinfeld and GaitsgoryDG15, Corollary 7.4.11], we deduce the following.
Lemma 4.1.6. The substack  $\operatorname{Bun}_{G}^{S_{M}(\unicode[STIX]{x1D707})}$ is closed in
$\operatorname{Bun}_{G}^{S_{M}(\unicode[STIX]{x1D707})}$ is closed in  $\operatorname{Bun}_{G}^{{\leqslant}\unicode[STIX]{x1D707}}$.
$\operatorname{Bun}_{G}^{{\leqslant}\unicode[STIX]{x1D707}}$.
4.1.7
We deduce from the definition of  $S_{M}(\unicode[STIX]{x1D707})$ and 1.5.12 that
$S_{M}(\unicode[STIX]{x1D707})$ and 1.5.12 that
 $$\begin{eqnarray}\operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}=\operatorname{Bun}_{M}^{{\leqslant}\unicode[STIX]{x1D707},\;\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})}\!\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}=\operatorname{Bun}_{M}^{{\leqslant}\unicode[STIX]{x1D707},\;\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})}\!\!.\end{eqnarray}$$ Recall that  $\operatorname{Bun}_{M}^{{\leqslant}\unicode[STIX]{x1D707}}$ is open in
$\operatorname{Bun}_{M}^{{\leqslant}\unicode[STIX]{x1D707}}$ is open in  $\operatorname{Bun}_{M}$ (see Lemma 1.5.5) and
$\operatorname{Bun}_{M}$ (see Lemma 1.5.5) and  $\operatorname{Bun}_{M}^{\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})}$ is open and closed in
$\operatorname{Bun}_{M}^{\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})}$ is open and closed in  $\operatorname{Bun}_{M}$ (see 1.5.7).
$\operatorname{Bun}_{M}$ (see 1.5.7).
Lemma 4.1.8 [Reference Drinfeld and GaitsgoryDG15, Corollary 7.4.11, Lemma 8.2.6].
The substack  $\operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}$ is open and closed in
$\operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}$ is open and closed in  $\operatorname{Bun}_{M}^{{\leqslant}\unicode[STIX]{x1D707}}$, and is open in
$\operatorname{Bun}_{M}^{{\leqslant}\unicode[STIX]{x1D707}}$, and is open in  $\operatorname{Bun}_{M}^{\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})}$ and in
$\operatorname{Bun}_{M}^{\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})}$ and in  $\operatorname{Bun}_{M}$.
$\operatorname{Bun}_{M}$.
We define  $\operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}:=\operatorname{Bun}_{P}^{{\leqslant}\unicode[STIX]{x1D707}}\cap \;\unicode[STIX]{x1D70B}^{-1}(\operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})})$. By Lemma 4.1.8, it is open and closed in
$\operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}:=\operatorname{Bun}_{P}^{{\leqslant}\unicode[STIX]{x1D707}}\cap \;\unicode[STIX]{x1D70B}^{-1}(\operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})})$. By Lemma 4.1.8, it is open and closed in  $\operatorname{Bun}_{P}^{{\leqslant}\unicode[STIX]{x1D707}}$, and is open in
$\operatorname{Bun}_{P}^{{\leqslant}\unicode[STIX]{x1D707}}$, and is open in  $\operatorname{Bun}_{P}$. So it is reduced.
$\operatorname{Bun}_{P}$. So it is reduced.
Lemma 4.1.9. Morphisms (1.25) induce morphisms
 $$\begin{eqnarray}\operatorname{Bun}_{G}^{S_{M}(\unicode[STIX]{x1D707})}\leftarrow \operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}\!\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{G}^{S_{M}(\unicode[STIX]{x1D707})}\leftarrow \operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}\!\!.\end{eqnarray}$$Proof. We need to verify that the image of  $\operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{G}^{{\leqslant}\unicode[STIX]{x1D707}}$ is in the closed substack
$\operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{G}^{{\leqslant}\unicode[STIX]{x1D707}}$ is in the closed substack  $\operatorname{Bun}_{G}^{S_{M}(\unicode[STIX]{x1D707})}$. Since
$\operatorname{Bun}_{G}^{S_{M}(\unicode[STIX]{x1D707})}$. Since  $\operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}$ is reduced, it is enough to consider geometric points. Let
$\operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}$ is reduced, it is enough to consider geometric points. Let  ${\mathcal{P}}\in \operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}$ be a geometric point. Let
${\mathcal{P}}\in \operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}$ be a geometric point. Let  ${\mathcal{M}}$ be its image in
${\mathcal{M}}$ be its image in  $\operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}$. By definition of
$\operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}$. By definition of  $\operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}$, there exists
$\operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}$, there exists  $\unicode[STIX]{x1D706}\in S_{M}(\unicode[STIX]{x1D707})$ such that
$\unicode[STIX]{x1D706}\in S_{M}(\unicode[STIX]{x1D707})$ such that  ${\mathcal{M}}\in \operatorname{Bun}_{M}^{=\unicode[STIX]{x1D706}}$.
${\mathcal{M}}\in \operatorname{Bun}_{M}^{=\unicode[STIX]{x1D706}}$.
Let  ${\mathcal{G}}$ be the image of
${\mathcal{G}}$ be the image of  ${\mathcal{P}}$ in
${\mathcal{P}}$ in  $\operatorname{Bun}_{G}^{{\leqslant}\unicode[STIX]{x1D707}}$. By 1.4.14, there exists
$\operatorname{Bun}_{G}^{{\leqslant}\unicode[STIX]{x1D707}}$. By 1.4.14, there exists  $\unicode[STIX]{x1D706}^{\prime }\leqslant \unicode[STIX]{x1D707}$ such that
$\unicode[STIX]{x1D706}^{\prime }\leqslant \unicode[STIX]{x1D707}$ such that  ${\mathcal{G}}\in \operatorname{Bun}_{G}^{=\unicode[STIX]{x1D706}^{\prime }}$. Taking into account that
${\mathcal{G}}\in \operatorname{Bun}_{G}^{=\unicode[STIX]{x1D706}^{\prime }}$. Taking into account that  $\operatorname{Bun}_{G}^{=\unicode[STIX]{x1D706}^{\prime }}\subset \operatorname{Bun}_{G}^{{\leqslant}\unicode[STIX]{x1D706}^{\prime }}$, by Lemma 1.6.2, we deduce that
$\operatorname{Bun}_{G}^{=\unicode[STIX]{x1D706}^{\prime }}\subset \operatorname{Bun}_{G}^{{\leqslant}\unicode[STIX]{x1D706}^{\prime }}$, by Lemma 1.6.2, we deduce that  ${\mathcal{M}}\in \operatorname{Bun}_{M}^{{\leqslant}\unicode[STIX]{x1D706}^{\prime }}$. Hence
${\mathcal{M}}\in \operatorname{Bun}_{M}^{{\leqslant}\unicode[STIX]{x1D706}^{\prime }}$. Hence  $\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D706}^{\prime }$. By 4.1.5, this implies that
$\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D706}^{\prime }$. By 4.1.5, this implies that  $\unicode[STIX]{x1D706}^{\prime }\in S_{M}(\unicode[STIX]{x1D707})$. Thus
$\unicode[STIX]{x1D706}^{\prime }\in S_{M}(\unicode[STIX]{x1D707})$. Thus  ${\mathcal{G}}\in \operatorname{Bun}_{G}^{S_{M}(\unicode[STIX]{x1D707})}$.◻
${\mathcal{G}}\in \operatorname{Bun}_{G}^{S_{M}(\unicode[STIX]{x1D707})}$.◻
Definition 4.1.10. We define  $\operatorname{Cht}_{G,N,I,W}^{=\unicode[STIX]{x1D707}}$ (respectively
$\operatorname{Cht}_{G,N,I,W}^{=\unicode[STIX]{x1D707}}$ (respectively  $\operatorname{Cht}_{G,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}$) as the inverse image of
$\operatorname{Cht}_{G,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}$) as the inverse image of  $\operatorname{Bun}_{G}^{=\,\unicode[STIX]{x1D707}}$ (respectively
$\operatorname{Bun}_{G}^{=\,\unicode[STIX]{x1D707}}$ (respectively  $\operatorname{Bun}_{G}^{S_{M}(\unicode[STIX]{x1D707})}$) by the morphism
$\operatorname{Bun}_{G}^{S_{M}(\unicode[STIX]{x1D707})}$) by the morphism
 $$\begin{eqnarray}\operatorname{Cht}_{G,N,I,W}\rightarrow \operatorname{Bun}_{G},\quad ((x_{i})_{i\in I},({\mathcal{G}},\unicode[STIX]{x1D713})\xrightarrow[{}]{\unicode[STIX]{x1D719}}(\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}},^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}))\mapsto {\mathcal{G}}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{G,N,I,W}\rightarrow \operatorname{Bun}_{G},\quad ((x_{i})_{i\in I},({\mathcal{G}},\unicode[STIX]{x1D713})\xrightarrow[{}]{\unicode[STIX]{x1D719}}(\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}},^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}))\mapsto {\mathcal{G}}.\end{eqnarray}$$ Similarly, we define  $\operatorname{Cht}_{P,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}$,
$\operatorname{Cht}_{P,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}$,  $\operatorname{Cht}_{M,N,I,W}^{=\unicode[STIX]{x1D707}}$ and
$\operatorname{Cht}_{M,N,I,W}^{=\unicode[STIX]{x1D707}}$ and  $\operatorname{Cht}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}$.
$\operatorname{Cht}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}$.
4.1.11
We deduce from Lemma 4.1.6 that  $\operatorname{Cht}_{G,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}$ is closed in
$\operatorname{Cht}_{G,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}$ is closed in  $\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}$. We deduce from Lemma 4.1.8 that
$\operatorname{Cht}_{G,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}$. We deduce from Lemma 4.1.8 that  $\operatorname{Cht}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}$ is open and closed in
$\operatorname{Cht}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}$ is open and closed in  $\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}$, and is open in
$\operatorname{Cht}_{M,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}$, and is open in  $\operatorname{Cht}_{M,N,I,W}^{\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})}$ and in
$\operatorname{Cht}_{M,N,I,W}^{\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})}$ and in  $\operatorname{Cht}_{M,N,I,W}$.
$\operatorname{Cht}_{M,N,I,W}$.
4.1.12
The commutativity of diagram (1.28) and Lemma 4.1.9 imply that  $\operatorname{Cht}_{P,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}=\operatorname{Cht}_{P,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}\cap \;\unicode[STIX]{x1D70B}^{-1}(\operatorname{Cht}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}).$ Morphisms (1.29) induce morphisms:
$\operatorname{Cht}_{P,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}=\operatorname{Cht}_{P,N,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}\cap \;\unicode[STIX]{x1D70B}^{-1}(\operatorname{Cht}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}).$ Morphisms (1.29) induce morphisms:
 $$\begin{eqnarray}\operatorname{Cht}_{G,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\xleftarrow[{}]{i^{S_{M}(\unicode[STIX]{x1D707})}}\operatorname{Cht}_{P,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{S_{M}(\unicode[STIX]{x1D707})}}\operatorname{Cht}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{G,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\xleftarrow[{}]{i^{S_{M}(\unicode[STIX]{x1D707})}}\operatorname{Cht}_{P,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{S_{M}(\unicode[STIX]{x1D707})}}\operatorname{Cht}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\!.\end{eqnarray}$$4.1.13
As in Definition 3.4.2, we define
 $$\begin{eqnarray}\operatorname{Cht}_{P,N,I,W}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}:=\operatorname{Cht}_{P,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N}),\quad \operatorname{Cht}_{M,N,I,W}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}:=\operatorname{Cht}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{P,N,I,W}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}:=\operatorname{Cht}_{P,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N}),\quad \operatorname{Cht}_{M,N,I,W}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}:=\operatorname{Cht}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N}).\end{eqnarray}$$Morphisms (3.26) induce morphisms
 $$\begin{eqnarray}\operatorname{Cht}_{G,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\xleftarrow[{}]{i^{\prime \,S_{M}(\unicode[STIX]{x1D707})}}\operatorname{Cht}_{P,N,I,W}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}}\operatorname{Cht}_{M,N,I,W}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{G,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\xleftarrow[{}]{i^{\prime \,S_{M}(\unicode[STIX]{x1D707})}}\operatorname{Cht}_{P,N,I,W}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}}\operatorname{Cht}_{M,N,I,W}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}\!.\end{eqnarray}$$4.2 Geometric statements
First consider the morphism  $i^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$.
$i^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$.
Theorem 4.2.1 ([Reference VarshavskyVar04, Theorem 2.25 and Proposition 5.7], [Reference Drinfeld and GaitsgoryDG15, Proposition 9.2.2]).
There exists a constant  $C^{\prime }(G,X,N,W)$, such that if
$C^{\prime }(G,X,N,W)$, such that if  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and  $\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >C^{\prime }(G,X,N,W)$ for all
$\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >C^{\prime }(G,X,N,W)$ for all  $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then the morphism
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then the morphism  $i^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ is a schematic finite universal homeomorphism.
$i^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ is a schematic finite universal homeomorphism.
Proof. (1) Schematic and finite follows from [Reference VarshavskyVar04, Proposition 5.7] (recalled in Proposition 3.5.3 and Remark 3.5.4).
(2) Surjectivity is implied by [Reference VarshavskyVar04, Theorem 2.25].
(3) Universally injectivity is implied by the fact that  $\operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{G}^{S_{M}(\unicode[STIX]{x1D707})}$ is an isomorphism for
$\operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{G}^{S_{M}(\unicode[STIX]{x1D707})}$ is an isomorphism for  $\unicode[STIX]{x1D707}$ satisfying the assumption of Theorem 4.2.1 (see [Reference Drinfeld and GaitsgoryDG15, Proposition 9.2.2]) and the well-known fact that
$\unicode[STIX]{x1D707}$ satisfying the assumption of Theorem 4.2.1 (see [Reference Drinfeld and GaitsgoryDG15, Proposition 9.2.2]) and the well-known fact that  $\operatorname{Gr}_{P,I,W}\rightarrow \operatorname{Gr}_{G,I,W}$ is bijective. (More concretely, it is enough to prove that for any algebraically closed field
$\operatorname{Gr}_{P,I,W}\rightarrow \operatorname{Gr}_{G,I,W}$ is bijective. (More concretely, it is enough to prove that for any algebraically closed field  $k$ containing
$k$ containing  $\overline{\mathbb{F}_{q}}$, the map
$\overline{\mathbb{F}_{q}}$, the map  $\operatorname{Cht}_{P,I,W}^{S_{M}(\unicode[STIX]{x1D707})}(k)\rightarrow \operatorname{Cht}_{G,I,W}^{S_{M}(\unicode[STIX]{x1D707})}(k)$ is injective. Let
$\operatorname{Cht}_{P,I,W}^{S_{M}(\unicode[STIX]{x1D707})}(k)\rightarrow \operatorname{Cht}_{G,I,W}^{S_{M}(\unicode[STIX]{x1D707})}(k)$ is injective. Let  $((x_{i}),{\mathcal{G}}\xrightarrow[{}]{\unicode[STIX]{x1D719}_{G}}\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}})\in \operatorname{Cht}_{G,I,W}^{S_{M}(\unicode[STIX]{x1D707})}(k)$. By (3), there exists
$((x_{i}),{\mathcal{G}}\xrightarrow[{}]{\unicode[STIX]{x1D719}_{G}}\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}})\in \operatorname{Cht}_{G,I,W}^{S_{M}(\unicode[STIX]{x1D707})}(k)$. By (3), there exists  $((x_{i}),{\mathcal{P}}\xrightarrow[{}]{\unicode[STIX]{x1D719}_{P}}\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{P}})\in \operatorname{Cht}_{P,I,W}^{S_{M}(\unicode[STIX]{x1D707})}(k)$ such that
$((x_{i}),{\mathcal{P}}\xrightarrow[{}]{\unicode[STIX]{x1D719}_{P}}\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{P}})\in \operatorname{Cht}_{P,I,W}^{S_{M}(\unicode[STIX]{x1D707})}(k)$ such that  ${\mathcal{P}}\overset{P}{\times }G\simeq {\mathcal{G}}$ and
${\mathcal{P}}\overset{P}{\times }G\simeq {\mathcal{G}}$ and  $\unicode[STIX]{x1D719}_{P}\overset{P}{\times }G\simeq \unicode[STIX]{x1D719}_{G}$. Since
$\unicode[STIX]{x1D719}_{P}\overset{P}{\times }G\simeq \unicode[STIX]{x1D719}_{G}$. Since  $\operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}(k)\rightarrow \operatorname{Bun}_{G}^{S_{M}(\unicode[STIX]{x1D707})}(k)$ is injective,
$\operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}(k)\rightarrow \operatorname{Bun}_{G}^{S_{M}(\unicode[STIX]{x1D707})}(k)$ is injective,  ${\mathcal{P}}$ is unique. Choosing a trivialization of
${\mathcal{P}}$ is unique. Choosing a trivialization of  ${\mathcal{P}}$ over
${\mathcal{P}}$ over  $\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}$, we deduce from the injectivity of
$\unicode[STIX]{x1D6E4}_{\sum \infty x_{i}}$, we deduce from the injectivity of  $\operatorname{Gr}_{P,I,W}(k)\rightarrow \operatorname{Gr}_{G,I,W}(k)$ that
$\operatorname{Gr}_{P,I,W}(k)\rightarrow \operatorname{Gr}_{G,I,W}(k)$ that  $\unicode[STIX]{x1D719}_{P}$ is unique.)◻
$\unicode[STIX]{x1D719}_{P}$ is unique.)◻
4.2.2
Now we consider the morphism  $\unicode[STIX]{x1D70B}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$. For all
$\unicode[STIX]{x1D70B}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$. For all  $d$ large enough, similar to diagram (3.9), we have a commutative diagram
$d$ large enough, similar to diagram (3.9), we have a commutative diagram

where  $\widetilde{\operatorname{Cht}}_{M,N,I,W}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ is the fiber product, which depends on
$\widetilde{\operatorname{Cht}}_{M,N,I,W}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ is the fiber product, which depends on  $d$. By 4.1.11,
$d$. By 4.1.11,  $\operatorname{Cht}_{M,N,I,W}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ is open in
$\operatorname{Cht}_{M,N,I,W}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ is open in  $\operatorname{Cht}_{M,N,I,W}^{\prime }$ and
$\operatorname{Cht}_{M,N,I,W}^{\prime }$ and  $\operatorname{Cht}_{P,N,I,W}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ is open in
$\operatorname{Cht}_{P,N,I,W}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ is open in  $\operatorname{Cht}_{P,N,I,W}^{\prime }$. By Lemma 3.1.8, the morphism
$\operatorname{Cht}_{P,N,I,W}^{\prime }$. By Lemma 3.1.8, the morphism  $\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ is smooth of relative dimension
$\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ is smooth of relative dimension  $\dim _{X^{I}}U_{I,d}$.
$\dim _{X^{I}}U_{I,d}$.
We now introduce a notion of unipotent group scheme (which should rather be called ‘elementary unipotent group scheme’).
Definition 4.2.3. (a) Let  $H$ be a group scheme of finite dimension over a scheme
$H$ be a group scheme of finite dimension over a scheme  $S$. We say that
$S$. We say that  $H$ is a unipotent group scheme if
$H$ is a unipotent group scheme if  $H$ admits a filtration
$H$ admits a filtration  $H=H^{(0)}\supset H^{(1)}\supset \cdots \supset H^{(m)}\supset H^{(m+1)}=0$ such that for every
$H=H^{(0)}\supset H^{(1)}\supset \cdots \supset H^{(m)}\supset H^{(m+1)}=0$ such that for every  $j$, the quotient
$j$, the quotient  $H^{(j)}/H^{(j+1)}$ is an additive group scheme (i.e. isomorphic to
$H^{(j)}/H^{(j+1)}$ is an additive group scheme (i.e. isomorphic to  $\mathbb{G}_{a,S}^{n}$ for some
$\mathbb{G}_{a,S}^{n}$ for some  $n$ locally for the étale topology) over
$n$ locally for the étale topology) over  $S$.
$S$.
(b) A morphism of algebraic stacks  $f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ is called unipotent if for any scheme
$f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$ is called unipotent if for any scheme  $S$ and any morphism
$S$ and any morphism  $S\rightarrow {\mathcal{Y}}$, the fiber product
$S\rightarrow {\mathcal{Y}}$, the fiber product  $S\underset{{\mathcal{Y}}}{\times }{\mathcal{X}}$ is locally for the smooth topology on
$S\underset{{\mathcal{Y}}}{\times }{\mathcal{X}}$ is locally for the smooth topology on  $S$ isomorphic to a quotient stack
$S$ isomorphic to a quotient stack  $[H_{1}/H_{2}]$, where
$[H_{1}/H_{2}]$, where  $H_{1}$ and
$H_{1}$ and  $H_{2}$ are unipotent group schemes over
$H_{2}$ are unipotent group schemes over  $S$ and
$S$ and  $H_{2}$ acts on
$H_{2}$ acts on  $H_{1}$ as a group scheme over S acting on a scheme over S.
$H_{1}$ as a group scheme over S acting on a scheme over S.
Theorem 4.2.4. There exists a constant  $C(G,X,N,I,d)$, such that if
$C(G,X,N,I,d)$, such that if  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and  $\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >C(G,X,N,I,d)$ for all
$\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >C(G,X,N,I,d)$ for all  $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then the morphism
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then the morphism  $\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ is unipotent in the sense of Definition 4.2.3.
$\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ is unipotent in the sense of Definition 4.2.3.
The proof will be given in §§4.3–4.5.
Remark 4.2.5. Theorem 4.2.4 will be used to prove Proposition 4.6.4, where only the statement for the geometric fibers of  $\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ is needed. Since the proof is the same for a geometric fiber or a fiber over a general base, we prove it over a general base.
$\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ is needed. Since the proof is the same for a geometric fiber or a fiber over a general base, we prove it over a general base.
4.3 Proof of Theorem 4.2.4: step 1
4.3.1
We have a similar diagram as (4.4) without index  $^{\prime }$. The morphism
$^{\prime }$. The morphism
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{d}^{S_{M}(\unicode[STIX]{x1D707})}:\operatorname{Cht}_{P,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \widetilde{\operatorname{Cht}}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{d}^{S_{M}(\unicode[STIX]{x1D707})}:\operatorname{Cht}_{P,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \widetilde{\operatorname{Cht}}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\end{eqnarray}$$ is  $P({\mathcal{O}}_{N})$-equivariant and the morphism
$P({\mathcal{O}}_{N})$-equivariant and the morphism  $\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ is induced by
$\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ is induced by  $\unicode[STIX]{x1D70B}_{d}^{S_{M}(\unicode[STIX]{x1D707})}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N})$. So to prove Theorem 4.2.4, it is enough to prove the statement for
$\unicode[STIX]{x1D70B}_{d}^{S_{M}(\unicode[STIX]{x1D707})}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N})$. So to prove Theorem 4.2.4, it is enough to prove the statement for  $\unicode[STIX]{x1D70B}_{d}^{S_{M}(\unicode[STIX]{x1D707})}$ instead of
$\unicode[STIX]{x1D70B}_{d}^{S_{M}(\unicode[STIX]{x1D707})}$ instead of  $\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$.
$\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$.
The problem is local for the smooth topology. So it is enough to prove the statement for the base change by  $\operatorname{Gr}_{P,I,W}\rightarrow [P_{I,d}\backslash \operatorname{Gr}_{P,I,W}]$:
$\operatorname{Gr}_{P,I,W}\rightarrow [P_{I,d}\backslash \operatorname{Gr}_{P,I,W}]$:
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{d}^{\times ,\,S_{M}(\unicode[STIX]{x1D707})}:\operatorname{Cht}_{P,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\underset{[P_{I,d}\backslash \operatorname{Gr}_{P,I,W}]}{\times }\operatorname{Gr}_{P,I,W}\rightarrow \widetilde{\operatorname{Cht}}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\underset{[P_{I,d}\backslash \operatorname{Gr}_{P,I,W}]}{\times }\operatorname{Gr}_{P,I,W}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{d}^{\times ,\,S_{M}(\unicode[STIX]{x1D707})}:\operatorname{Cht}_{P,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\underset{[P_{I,d}\backslash \operatorname{Gr}_{P,I,W}]}{\times }\operatorname{Gr}_{P,I,W}\rightarrow \widetilde{\operatorname{Cht}}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\underset{[P_{I,d}\backslash \operatorname{Gr}_{P,I,W}]}{\times }\operatorname{Gr}_{P,I,W}.\end{eqnarray}$$4.3.2
Note that  $\widetilde{\operatorname{Cht}}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\underset{[P_{I,d}\backslash \operatorname{Gr}_{P,I,W}]}{\times }\operatorname{Gr}_{P,I,W}\simeq \operatorname{Cht}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\underset{[M_{I,d}\backslash \operatorname{Gr}_{M,I,W}]}{\times }\operatorname{Gr}_{P,I,W}$. We have the following commutative diagram, where the front and back Cartesian squares are defined in the proof of [Reference LafforgueLaf18, Proposition 2.8] (replace
$\widetilde{\operatorname{Cht}}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\underset{[P_{I,d}\backslash \operatorname{Gr}_{P,I,W}]}{\times }\operatorname{Gr}_{P,I,W}\simeq \operatorname{Cht}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\underset{[M_{I,d}\backslash \operatorname{Gr}_{M,I,W}]}{\times }\operatorname{Gr}_{P,I,W}$. We have the following commutative diagram, where the front and back Cartesian squares are defined in the proof of [Reference LafforgueLaf18, Proposition 2.8] (replace  $G$ by
$G$ by  $P$ and
$P$ and  $M$, respectively). We have already used these Cartesian squares in (3.11) and (3.12).
$M$, respectively). We have already used these Cartesian squares in (3.11) and (3.12).

4.3.3
Now let  $S$ be an affine scheme over
$S$ be an affine scheme over  $\overline{\mathbb{F}_{q}}$ and let
$\overline{\mathbb{F}_{q}}$ and let
 $$\begin{eqnarray}((x_{i}),({\mathcal{M}},\unicode[STIX]{x1D713})\xrightarrow[{}]{\unicode[STIX]{x1D719}}(\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{M}},^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}),s):S\rightarrow \widetilde{\operatorname{Cht}}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\underset{[P_{I,d}\backslash \operatorname{Gr}_{P,I,W}]}{\times }\operatorname{Gr}_{P,I,W}\end{eqnarray}$$
$$\begin{eqnarray}((x_{i}),({\mathcal{M}},\unicode[STIX]{x1D713})\xrightarrow[{}]{\unicode[STIX]{x1D719}}(\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{M}},^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}),s):S\rightarrow \widetilde{\operatorname{Cht}}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\underset{[P_{I,d}\backslash \operatorname{Gr}_{P,I,W}]}{\times }\operatorname{Gr}_{P,I,W}\end{eqnarray}$$ be an  $S$-point. Consider
$S$-point. Consider
 $$\begin{eqnarray}S\rightarrow \widetilde{\operatorname{Cht}}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\underset{[P_{I,d}\backslash \operatorname{Gr}_{P,I,W}]}{\times }\operatorname{Gr}_{P,I,W}\rightarrow \underset{(X\smallsetminus N)^{I}}{\operatorname{Bun}_{M,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}\times \operatorname{Gr}_{P,I,W}}\end{eqnarray}$$
$$\begin{eqnarray}S\rightarrow \widetilde{\operatorname{Cht}}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\underset{[P_{I,d}\backslash \operatorname{Gr}_{P,I,W}]}{\times }\operatorname{Gr}_{P,I,W}\rightarrow \underset{(X\smallsetminus N)^{I}}{\operatorname{Bun}_{M,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}\times \operatorname{Gr}_{P,I,W}}\end{eqnarray}$$and
 $$\begin{eqnarray}S\rightarrow \widetilde{\operatorname{Cht}}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\underset{[P_{I,d}\backslash \operatorname{Gr}_{P,I,W}]}{\times }\operatorname{Gr}_{P,I,W}\rightarrow \operatorname{Bun}_{M,N}^{S_{M}(\unicode[STIX]{x1D707})}.\end{eqnarray}$$
$$\begin{eqnarray}S\rightarrow \widetilde{\operatorname{Cht}}_{M,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}\underset{[P_{I,d}\backslash \operatorname{Gr}_{P,I,W}]}{\times }\operatorname{Gr}_{P,I,W}\rightarrow \operatorname{Bun}_{M,N}^{S_{M}(\unicode[STIX]{x1D707})}.\end{eqnarray}$$ We define  $\mathscr{Z}$,
$\mathscr{Z}$,  $\mathscr{Y}_{N,d}$ and
$\mathscr{Y}_{N,d}$ and  $\mathscr{Y}_{N}$ to be the following fiber products.
$\mathscr{Y}_{N}$ to be the following fiber products.

Applying Lemma B.0.1 to the diagram in 4.3.2, we deduce a Cartesian square

where  $b_{1}$ (respectively
$b_{1}$ (respectively  $b_{2}$) is induced by
$b_{2}$) is induced by  $b_{1}^{P}$ (respectively
$b_{1}^{P}$ (respectively  $b_{2}^{P}$).
$b_{2}^{P}$).
Remark 4.3.4. By the proof of [Reference LafforgueLaf18, Proposition 2.8],  $b_{1}^{P}$ (respectively
$b_{1}^{P}$ (respectively  $b_{1}^{M}$) is the forgetful morphism of the level structure on
$b_{1}^{M}$) is the forgetful morphism of the level structure on  $I$ (thus smooth) and
$I$ (thus smooth) and  $b_{2}^{P}$ (respectively
$b_{2}^{P}$ (respectively  $b_{2}^{M}$) is the composition of the Frobenius morphism with some other morphism. We deduce that
$b_{2}^{M}$) is the composition of the Frobenius morphism with some other morphism. We deduce that  $b_{1}$ is smooth and
$b_{1}$ is smooth and  $b_{2}$ has zero differential. Moreover, the morphism
$b_{2}$ has zero differential. Moreover, the morphism 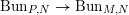 $\operatorname{Bun}_{P,N}\rightarrow \operatorname{Bun}_{M,N}$ is smooth, and thus
$\operatorname{Bun}_{P,N}\rightarrow \operatorname{Bun}_{M,N}$ is smooth, and thus 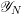 $\mathscr{Y}_{N}$ is smooth over
$\mathscr{Y}_{N}$ is smooth over  $S$. Similarly
$S$. Similarly  $\mathscr{Y}_{N,d}$ is smooth over
$\mathscr{Y}_{N,d}$ is smooth over  $S$. We deduce that
$S$. We deduce that  $\mathscr{Z}$ is smooth over
$\mathscr{Z}$ is smooth over  $S$. Note that the same argument without
$S$. Note that the same argument without  $S_{M}(\unicode[STIX]{x1D707})$ would give another proof of Lemma 3.1.8.
$S_{M}(\unicode[STIX]{x1D707})$ would give another proof of Lemma 3.1.8.
4.4 Proof of Theorem 4.2.4: step 2
The goal of this subsection is to describe  $\mathscr{Y}_{N}$ and
$\mathscr{Y}_{N}$ and  $\mathscr{Y}_{N,d}$.
$\mathscr{Y}_{N,d}$.
(1) First we describe the fiber of  $\operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}$ in Proposition 4.4.4.
$\operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}$ in Proposition 4.4.4.
4.4.1
We fix a maximal torus  $T\subset B$. This allows us to view the Levi quotient
$T\subset B$. This allows us to view the Levi quotient  $M$ of a standard parabolic subgroup
$M$ of a standard parabolic subgroup  $P$ as a subgroup
$P$ as a subgroup  $M\subset P$ (the unique splitting that contains
$M\subset P$ (the unique splitting that contains  $T$). Then
$T$). Then  $P=M\rtimes U$, where
$P=M\rtimes U$, where  $M$ acts on
$M$ acts on  $U$ via the embedding
$U$ via the embedding  $M\subset P$ and
$M\subset P$ and  $P$ acts on
$P$ acts on  $U$ by the adjoint action.
$U$ by the adjoint action.
4.4.2
Let  $S\rightarrow \operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}$ be a morphism and
$S\rightarrow \operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}$ be a morphism and  ${\mathcal{M}}$ the corresponding
${\mathcal{M}}$ the corresponding  $M$-bundle over
$M$-bundle over  $X\times S$. We define the fiber space
$X\times S$. We define the fiber space  $U_{{\mathcal{M}}}:=(U\times {\mathcal{M}})/M$. It is easy to check that it is a group scheme over
$U_{{\mathcal{M}}}:=(U\times {\mathcal{M}})/M$. It is easy to check that it is a group scheme over  $X\times S$ (see [Reference XueXue17, C.2] for more details).
$X\times S$ (see [Reference XueXue17, C.2] for more details).
Definition 4.4.3. Let  $S$ be an affine scheme over
$S$ be an affine scheme over  $\overline{\mathbb{F}_{q}}$. Let
$\overline{\mathbb{F}_{q}}$. Let  $A$ be a sheaf of groups on
$A$ be a sheaf of groups on  $X\times S$. We denote by
$X\times S$. We denote by  $\operatorname{pr}_{S}:X\times S\rightarrow S$ the second projection.
$\operatorname{pr}_{S}:X\times S\rightarrow S$ the second projection.
(a) We define
 $R^{0}(\operatorname{pr}_{S})_{\ast }A$ as the sheaf of groups on
$R^{0}(\operatorname{pr}_{S})_{\ast }A$ as the sheaf of groups on  $S$: where
$S$: where $$\begin{eqnarray}(S^{\prime }\rightarrow S)\mapsto \operatorname{Hom}_{X\times S}(X\times S^{\prime },A^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}(S^{\prime }\rightarrow S)\mapsto \operatorname{Hom}_{X\times S}(X\times S^{\prime },A^{\prime }),\end{eqnarray}$$ $A^{\prime }$ is the inverse image of
$A^{\prime }$ is the inverse image of  $A$ by
$A$ by  $X\times S^{\prime }\rightarrow X\times S$.
$X\times S^{\prime }\rightarrow X\times S$.(b) [Reference GiraudGir71, V.2.1] We define
 $R^{1}(\operatorname{pr}_{S})_{\ast }A$ as the sheaf of sets on
$R^{1}(\operatorname{pr}_{S})_{\ast }A$ as the sheaf of sets on  $S$ associated to the presheaf: Indeed
$S$ associated to the presheaf: Indeed $$\begin{eqnarray}(S^{\prime }\rightarrow S)\mapsto H^{1}(X\times S^{\prime },A^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}(S^{\prime }\rightarrow S)\mapsto H^{1}(X\times S^{\prime },A^{\prime }).\end{eqnarray}$$ $R^{1}(\operatorname{pr}_{S})_{\ast }A$ is a sheaf of pointed sets with a canonical section which corresponds to the trivial
$R^{1}(\operatorname{pr}_{S})_{\ast }A$ is a sheaf of pointed sets with a canonical section which corresponds to the trivial  $A$-torsor.
$A$-torsor.
Proposition 4.4.4. There exists a constant  $C(G,X)\in \mathbb{Q}_{{\geqslant}0}$, such that if
$C(G,X)\in \mathbb{Q}_{{\geqslant}0}$, such that if  $\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >C(G,X)$ for all
$\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >C(G,X)$ for all  $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then  $R^{0}(\operatorname{pr}_{S})_{\ast }U_{{\mathcal{M}}}$ is a unipotent group scheme over
$R^{0}(\operatorname{pr}_{S})_{\ast }U_{{\mathcal{M}}}$ is a unipotent group scheme over  $S$ and the fiber of
$S$ and the fiber of  $\operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}$ over
$\operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}$ over  $S$ is the classifying stack
$S$ is the classifying stack  $[S/R^{0}(\operatorname{pr}_{S})_{\ast }U_{{\mathcal{M}}}]$.
$[S/R^{0}(\operatorname{pr}_{S})_{\ast }U_{{\mathcal{M}}}]$.
Proof. We denote by  $\mathscr{Y}$ the fiber of
$\mathscr{Y}$ the fiber of  $\operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}$ over
$\operatorname{Bun}_{P}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}$ over  $S$. For any scheme
$S$. For any scheme  $S^{\prime }\rightarrow S$, the groupoid
$S^{\prime }\rightarrow S$, the groupoid  $\mathscr{Y}(S^{\prime })$ classifies the
$\mathscr{Y}(S^{\prime })$ classifies the  $\left.U_{{\mathcal{M}}}\vphantom{\big|}\right|_{X\times S^{\prime }}$-bundle over
$\left.U_{{\mathcal{M}}}\vphantom{\big|}\right|_{X\times S^{\prime }}$-bundle over  $X\times S^{\prime }$ (see [Reference XueXue17, Lemme C.3.2] for more details).
$X\times S^{\prime }$ (see [Reference XueXue17, Lemme C.3.2] for more details).
By Lemma 4.4.5(b) below, all  $U_{{\mathcal{M}}}$-bundles are trivial. Taking into account that
$U_{{\mathcal{M}}}$-bundles are trivial. Taking into account that  $R^{0}(\text{pr}_{S})_{\ast }U_{{\mathcal{M}}}(S^{\prime })$ is the group of automorphisms of the trivial
$R^{0}(\text{pr}_{S})_{\ast }U_{{\mathcal{M}}}(S^{\prime })$ is the group of automorphisms of the trivial  $\left.U_{{\mathcal{M}}}\vphantom{\big|}\right|_{X\times S^{\prime }}$-bundle on
$\left.U_{{\mathcal{M}}}\vphantom{\big|}\right|_{X\times S^{\prime }}$-bundle on  $X\times S^{\prime }$ and Lemma 4.4.5(a), we deduce the proposition.◻
$X\times S^{\prime }$ and Lemma 4.4.5(a), we deduce the proposition.◻
Lemma 4.4.5. There exists a constant  $C(G,X)\in \mathbb{Q}_{{\geqslant}0}$, such that if
$C(G,X)\in \mathbb{Q}_{{\geqslant}0}$, such that if  $\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >C(G,X)$ for all
$\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >C(G,X)$ for all  $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then we have the following.
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then we have the following.
(a) The sheaf of groups
 $R^{0}(\text{pr}_{S})_{\ast }U_{{\mathcal{M}}}$ is a unipotent group scheme.
$R^{0}(\text{pr}_{S})_{\ast }U_{{\mathcal{M}}}$ is a unipotent group scheme.(b) The sheaf of pointed sets
 $R^{1}(\text{pr}_{S})_{\ast }U_{{\mathcal{M}}}$ is trivial.
$R^{1}(\text{pr}_{S})_{\ast }U_{{\mathcal{M}}}$ is trivial.
Remark 4.4.6. If  $U$ is commutative, then
$U$ is commutative, then  $U_{{\mathcal{M}}}$ is an additive group scheme over
$U_{{\mathcal{M}}}$ is an additive group scheme over  $X\times S$ (in the sense of Definition 4.2.3). Part (a) of Lemma 4.4.5 is automatic and part (b) follows directly from [Reference Drinfeld and GaitsgoryDG15, Proposition 10.4.5].
$X\times S$ (in the sense of Definition 4.2.3). Part (a) of Lemma 4.4.5 is automatic and part (b) follows directly from [Reference Drinfeld and GaitsgoryDG15, Proposition 10.4.5].
The difficulty is that in general,  $U$ is not commutative. To prove Lemma 4.4.5, we will need to use a filtration of
$U$ is not commutative. To prove Lemma 4.4.5, we will need to use a filtration of  $U$ where the graded are commutative groups.
$U$ where the graded are commutative groups.
4.4.7
We have a canonical filtration of  $U$ (see the proof of [Reference Drinfeld and GaitsgoryDG15, Proposition 11.1.4(c)] for more details):
$U$ (see the proof of [Reference Drinfeld and GaitsgoryDG15, Proposition 11.1.4(c)] for more details):
 $$\begin{eqnarray}U=U^{(0)}\supset U^{(1)}\supset \cdots \supset U^{(m)}\supset U^{(m+1)}=0,\end{eqnarray}$$
$$\begin{eqnarray}U=U^{(0)}\supset U^{(1)}\supset \cdots \supset U^{(m)}\supset U^{(m+1)}=0,\end{eqnarray}$$ where  $U^{(j)}$ is the subgroup generated by the root subgroups corresponding to the positive roots
$U^{(j)}$ is the subgroup generated by the root subgroups corresponding to the positive roots  $\unicode[STIX]{x1D6FC}$ of
$\unicode[STIX]{x1D6FC}$ of  $G$, such that
$G$, such that
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}}\operatorname{coeff}_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6FC})\geqslant j+1.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}}\operatorname{coeff}_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6FC})\geqslant j+1.\end{eqnarray}$$ (Here  $\operatorname{coeff}_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6FC})$ denotes the coefficient of
$\operatorname{coeff}_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6FC})$ denotes the coefficient of  $\unicode[STIX]{x1D6FC}$ in simple root
$\unicode[STIX]{x1D6FC}$ in simple root  $\unicode[STIX]{x1D6FD}$.) For each
$\unicode[STIX]{x1D6FD}$.) For each  $j$, the subgroup
$j$, the subgroup  $U^{(j+1)}$ of
$U^{(j+1)}$ of  $U^{(j)}$ is normal and the quotient is equipped with an isomorphism
$U^{(j)}$ is normal and the quotient is equipped with an isomorphism  $\unicode[STIX]{x1D717}^{(j)}:\mathbb{G}_{a}^{n_{j}}\overset{{\sim}}{\rightarrow }U^{(j)}/U^{(j+1)}$ for some
$\unicode[STIX]{x1D717}^{(j)}:\mathbb{G}_{a}^{n_{j}}\overset{{\sim}}{\rightarrow }U^{(j)}/U^{(j+1)}$ for some  $n_{j}\in \mathbb{N}$.
$n_{j}\in \mathbb{N}$.
4.4.8
The filtration (4.6) induces for every  $j\in \{1,\ldots ,m+1\}$ an exact sequence of groups:
$j\in \{1,\ldots ,m+1\}$ an exact sequence of groups:
 $$\begin{eqnarray}0\rightarrow U^{(j-1)}/U^{(j)}\rightarrow U/U^{(j)}\rightarrow U/U^{(j-1)}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow U^{(j-1)}/U^{(j)}\rightarrow U/U^{(j)}\rightarrow U/U^{(j-1)}\rightarrow 0.\end{eqnarray}$$ For every  $j$, the subgroup
$j$, the subgroup  $U^{(j)}$ of
$U^{(j)}$ of  $P$ is normal. Then
$P$ is normal. Then  $P$ acts on
$P$ acts on  $U^{(j)}$ by the adjoint action and
$U^{(j)}$ by the adjoint action and  $M$ acts on
$M$ acts on  $U^{(j)}$ via
$U^{(j)}$ via  $M{\hookrightarrow}P$. We deduce that
$M{\hookrightarrow}P$. We deduce that  $M$ acts on
$M$ acts on  $U^{(j)}/U^{(j+1)}$ and
$U^{(j)}/U^{(j+1)}$ and  $U/U^{(j)}$.
$U/U^{(j)}$.
We define the fiber spaces  $(U^{(j)}/U^{(j+1)})_{{\mathcal{M}}}:=({\mathcal{M}}\times U^{(j)}/U^{(j+1)})/M$, it is an additive group scheme over
$(U^{(j)}/U^{(j+1)})_{{\mathcal{M}}}:=({\mathcal{M}}\times U^{(j)}/U^{(j+1)})/M$, it is an additive group scheme over  $X\times S$. We define the fiber space
$X\times S$. We define the fiber space  $(U/U^{(j)})_{{\mathcal{M}}}:=({\mathcal{M}}\times U/U^{(j)})/M$, it is a group scheme over
$(U/U^{(j)})_{{\mathcal{M}}}:=({\mathcal{M}}\times U/U^{(j)})/M$, it is a group scheme over  $X\times S$ (see [Reference XueXue17, C.2] for more details).
$X\times S$ (see [Reference XueXue17, C.2] for more details).
Proposition 4.4.9. There exists a constant  $C(G,X)$ such that for
$C(G,X)$ such that for  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, if
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, if  $\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >C(G,X)$ for all
$\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >C(G,X)$ for all  $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then for any
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then for any  ${\mathcal{M}}\in \operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}(S)$ and any
${\mathcal{M}}\in \operatorname{Bun}_{M}^{S_{M}(\unicode[STIX]{x1D707})}(S)$ and any  $j$, the sheaf
$j$, the sheaf  $R^{1}(\text{pr}_{S})_{\ast }((U^{(j)}/U^{(j+1)})_{{\mathcal{M}}})$ is trivial.
$R^{1}(\text{pr}_{S})_{\ast }((U^{(j)}/U^{(j+1)})_{{\mathcal{M}}})$ is trivial.
Proof. This is [Reference Drinfeld and GaitsgoryDG15, Proposition 10.4.5(a)]. We take  $C(G,X):=\operatorname{max}_{i}\{c_{i}^{\prime }\}$, where
$C(G,X):=\operatorname{max}_{i}\{c_{i}^{\prime }\}$, where  $c_{i}^{\prime }$ are the constants in [Reference Drinfeld and GaitsgoryDG15, Proposition 10.4.5(a)].◻
$c_{i}^{\prime }$ are the constants in [Reference Drinfeld and GaitsgoryDG15, Proposition 10.4.5(a)].◻
Lemma 4.4.10. Let  $0\rightarrow A\rightarrow B\rightarrow C\rightarrow 0$ be an exact sequence of sheaves of groups on
$0\rightarrow A\rightarrow B\rightarrow C\rightarrow 0$ be an exact sequence of sheaves of groups on  $X\times S$.
$X\times S$.
(a) If the sheaf of pointed sets
 $R^{1}(\text{pr}_{S})_{\ast }A$ is trivial, then we have an exact sequence of sheaves of groups:
$R^{1}(\text{pr}_{S})_{\ast }A$ is trivial, then we have an exact sequence of sheaves of groups:  $$\begin{eqnarray}0\rightarrow R^{0}(\text{pr}_{S})_{\ast }A\rightarrow R^{0}(\text{pr}_{S})_{\ast }B\rightarrow R^{0}(\text{pr}_{S})_{\ast }C\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow R^{0}(\text{pr}_{S})_{\ast }A\rightarrow R^{0}(\text{pr}_{S})_{\ast }B\rightarrow R^{0}(\text{pr}_{S})_{\ast }C\rightarrow 0.\end{eqnarray}$$(b) If moreover the sheaf of pointed sets
 $R^{1}(\text{pr}_{S})_{\ast }C$ is also trivial, then the sheaf of pointed sets
$R^{1}(\text{pr}_{S})_{\ast }C$ is also trivial, then the sheaf of pointed sets  $R^{1}(\text{pr}_{S})_{\ast }B$ is trivial.
$R^{1}(\text{pr}_{S})_{\ast }B$ is trivial.
Proof. By [Reference GiraudGir71, V Proposition 2.3], the exact sequence  $0\rightarrow A\rightarrow B\rightarrow C\rightarrow 0$ induces an exact sequence of sheaves of pointed sets on
$0\rightarrow A\rightarrow B\rightarrow C\rightarrow 0$ induces an exact sequence of sheaves of pointed sets on  $S$:
$S$:

We deduce the lemma. ◻
Proof of Lemma 4.4.5.
For each  $j$, the exact sequence (4.7) induces an exact sequence of group schemes over
$j$, the exact sequence (4.7) induces an exact sequence of group schemes over  $X\times S$:
$X\times S$:
 $$\begin{eqnarray}0\rightarrow (U^{(j-1)}/U^{(j)})_{{\mathcal{M}}}\rightarrow (U/U^{(j)})_{{\mathcal{M}}}\rightarrow (U/U^{(j-1)})_{{\mathcal{M}}}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow (U^{(j-1)}/U^{(j)})_{{\mathcal{M}}}\rightarrow (U/U^{(j)})_{{\mathcal{M}}}\rightarrow (U/U^{(j-1)})_{{\mathcal{M}}}\rightarrow 0.\end{eqnarray}$$ We apply Lemma 4.4.10 to (4.8) successively for  $j=1,j=2,\ldots ,$ until
$j=1,j=2,\ldots ,$ until  $j=m+1$. Taking into account the fact that
$j=m+1$. Taking into account the fact that  $R^{1}(\text{pr}_{S})_{\ast }((U^{(j)}/U^{(j+1)})_{{\mathcal{M}}})$ is trivial (by Proposition 4.4.9) and
$R^{1}(\text{pr}_{S})_{\ast }((U^{(j)}/U^{(j+1)})_{{\mathcal{M}}})$ is trivial (by Proposition 4.4.9) and  $R^{0}(\text{pr}_{S})_{\ast }(U^{(j)}/U^{(j+1)})_{{\mathcal{M}}}$ is additive in the sense of Definition 4.2.3 (because
$R^{0}(\text{pr}_{S})_{\ast }(U^{(j)}/U^{(j+1)})_{{\mathcal{M}}}$ is additive in the sense of Definition 4.2.3 (because  $U^{(j)}/U^{(j+1)}\overset{{\sim}}{\rightarrow }\mathbb{G}_{a}^{n_{j}}$), we deduce Lemma 4.4.5. ◻
$U^{(j)}/U^{(j+1)}\overset{{\sim}}{\rightarrow }\mathbb{G}_{a}^{n_{j}}$), we deduce Lemma 4.4.5. ◻
(2) Now we add level structure on  $N\times S+\unicode[STIX]{x1D6E4}_{\sum dx_{i}}$ to the argument in (1), i.e. we describe the fiber of
$N\times S+\unicode[STIX]{x1D6E4}_{\sum dx_{i}}$ to the argument in (1), i.e. we describe the fiber of  $\operatorname{Bun}_{P,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{M,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}$ in Proposition 4.4.13.
$\operatorname{Bun}_{P,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{M,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}$ in Proposition 4.4.13.
4.4.11
Let  $V$ be a group scheme on
$V$ be a group scheme on  $X\times S$. For any divisor
$X\times S$. For any divisor  $i_{D}:D{\hookrightarrow}X\times S$, we denote by
$i_{D}:D{\hookrightarrow}X\times S$, we denote by  $\left.V\vphantom{\big|}\right|_{D}$ the fiber product
$\left.V\vphantom{\big|}\right|_{D}$ the fiber product  $D\underset{X\times S}{\times }V$. We denote by
$D\underset{X\times S}{\times }V$. We denote by  ${\mathcal{V}}$ and
${\mathcal{V}}$ and  $\left.{\mathcal{V}}\vphantom{\big|}\right|_{D}$ the associated sheaves of groups. We define the sheaf of groups
$\left.{\mathcal{V}}\vphantom{\big|}\right|_{D}$ the associated sheaves of groups. We define the sheaf of groups  ${\mathcal{K}}er_{V,D}$ on
${\mathcal{K}}er_{V,D}$ on  $X\times S$ as the kernel of the morphism
$X\times S$ as the kernel of the morphism  ${\mathcal{V}}\rightarrow (i_{D})_{\ast }(\left.{\mathcal{V}}\vphantom{\big|}\right|_{D}).$ If
${\mathcal{V}}\rightarrow (i_{D})_{\ast }(\left.{\mathcal{V}}\vphantom{\big|}\right|_{D}).$ If  $V$ is smooth, the morphism
$V$ is smooth, the morphism  ${\mathcal{V}}\rightarrow (i_{D})_{\ast }(\left.{\mathcal{V}}\vphantom{\big|}\right|_{D})$ is surjective.
${\mathcal{V}}\rightarrow (i_{D})_{\ast }(\left.{\mathcal{V}}\vphantom{\big|}\right|_{D})$ is surjective.
4.4.12
Let  $S$ be an affine scheme over
$S$ be an affine scheme over  $\overline{\mathbb{F}_{q}}$. Let
$\overline{\mathbb{F}_{q}}$. Let  $((x_{i})_{i\in I},{\mathcal{M}},\unicode[STIX]{x1D713}_{M})$ be an
$((x_{i})_{i\in I},{\mathcal{M}},\unicode[STIX]{x1D713}_{M})$ be an  $S$-point of
$S$-point of  $\operatorname{Bun}_{M,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}$. Let
$\operatorname{Bun}_{M,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}$. Let  $D:=N\times S+\unicode[STIX]{x1D6E4}_{\sum dx_{i}}$. Applying 4.4.11 to the group scheme
$D:=N\times S+\unicode[STIX]{x1D6E4}_{\sum dx_{i}}$. Applying 4.4.11 to the group scheme  $U_{{\mathcal{M}}}$ on
$U_{{\mathcal{M}}}$ on  $X\times S$, we obtain an exact sequence of sheaves of groups:
$X\times S$, we obtain an exact sequence of sheaves of groups:
 $$\begin{eqnarray}0\rightarrow {\mathcal{K}}er_{U_{{\mathcal{M}}},D}\rightarrow {\mathcal{U}}_{{\mathcal{M}}}\rightarrow (i_{D})_{\ast }\left.{\mathcal{U}}_{{\mathcal{M}}}\vphantom{\big|}\right|_{D}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{K}}er_{U_{{\mathcal{M}}},D}\rightarrow {\mathcal{U}}_{{\mathcal{M}}}\rightarrow (i_{D})_{\ast }\left.{\mathcal{U}}_{{\mathcal{M}}}\vphantom{\big|}\right|_{D}\rightarrow 0.\end{eqnarray}$$Proposition 4.4.13. There exists a constant  $C(G,X,N,I,d)\in \mathbb{Q}_{{\geqslant}0}$, such that if
$C(G,X,N,I,d)\in \mathbb{Q}_{{\geqslant}0}$, such that if  $\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >C(G,X,N,I,d)$ for all
$\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >C(G,X,N,I,d)$ for all  $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then  $R^{0}(\text{pr}_{S})_{\ast }{\mathcal{K}}er_{U_{{\mathcal{M}}},D}$ is a unipotent group scheme over
$R^{0}(\text{pr}_{S})_{\ast }{\mathcal{K}}er_{U_{{\mathcal{M}}},D}$ is a unipotent group scheme over  $S$ and the fiber of
$S$ and the fiber of  $\operatorname{Bun}_{P,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{M,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}$ over
$\operatorname{Bun}_{P,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{M,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}$ over  $S$ is the classifying stack
$S$ is the classifying stack  $[S/R^{0}(\text{pr}_{S})_{\ast }{\mathcal{K}}er_{U_{{\mathcal{M}}},D}]$.
$[S/R^{0}(\text{pr}_{S})_{\ast }{\mathcal{K}}er_{U_{{\mathcal{M}}},D}]$.
Proof. We recall that  $\mathscr{Y}_{N,d}$ denotes the fiber of
$\mathscr{Y}_{N,d}$ denotes the fiber of  $\operatorname{Bun}_{P,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{M,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}$ over
$\operatorname{Bun}_{P,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Bun}_{M,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}$ over  $S$. For any scheme
$S$. For any scheme  $S^{\prime }\rightarrow S$, the groupoid
$S^{\prime }\rightarrow S$, the groupoid  $\mathscr{Y}_{N,d}(S^{\prime })$ classifies the data of
$\mathscr{Y}_{N,d}(S^{\prime })$ classifies the data of  $({\mathcal{F}},\unicode[STIX]{x1D6FD})$, where
$({\mathcal{F}},\unicode[STIX]{x1D6FD})$, where  ${\mathcal{F}}$ is a
${\mathcal{F}}$ is a  ${\mathcal{U}}_{{\mathcal{M}}}$-bundle on
${\mathcal{U}}_{{\mathcal{M}}}$-bundle on  $X\times S^{\prime }$ and
$X\times S^{\prime }$ and  $\unicode[STIX]{x1D6FD}$ is an isomorphism of
$\unicode[STIX]{x1D6FD}$ is an isomorphism of  ${\mathcal{U}}_{{\mathcal{M}}}$-bundles
${\mathcal{U}}_{{\mathcal{M}}}$-bundles  $\left.{\mathcal{F}}\vphantom{\big|}\right|_{D}\overset{{\sim}}{\rightarrow }\left.{\mathcal{U}}_{{\mathcal{M}}}\vphantom{\big|}\right|_{D}$. By (4.9), this groupoid is equivalent to the groupoid of
$\left.{\mathcal{F}}\vphantom{\big|}\right|_{D}\overset{{\sim}}{\rightarrow }\left.{\mathcal{U}}_{{\mathcal{M}}}\vphantom{\big|}\right|_{D}$. By (4.9), this groupoid is equivalent to the groupoid of  ${\mathcal{K}}er_{U_{{\mathcal{M}}},D}$-bundles on
${\mathcal{K}}er_{U_{{\mathcal{M}}},D}$-bundles on  $X\times S^{\prime }$.
$X\times S^{\prime }$.
Similarly to the case without level, Proposition 4.4.13 follows from Lemma 4.4.14 below. ◻
Lemma 4.4.14. There exists a constant  $C(G,X,N,I,d)\in \mathbb{Q}_{{\geqslant}0}$, such that if
$C(G,X,N,I,d)\in \mathbb{Q}_{{\geqslant}0}$, such that if  $\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >C(G,X,N,I,d)$ for all
$\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >C(G,X,N,I,d)$ for all  $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then we have the following.
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then we have the following.
(a) The sheaf of groups
 $R^{0}(\text{pr}_{S})_{\ast }{\mathcal{K}}er_{U_{{\mathcal{M}}},D}$ is a unipotent group scheme.
$R^{0}(\text{pr}_{S})_{\ast }{\mathcal{K}}er_{U_{{\mathcal{M}}},D}$ is a unipotent group scheme.(b) The sheaf of pointed sets
 $R^{1}(\text{pr}_{S})_{\ast }{\mathcal{K}}er_{U_{{\mathcal{M}}},D}$ is trivial.
$R^{1}(\text{pr}_{S})_{\ast }{\mathcal{K}}er_{U_{{\mathcal{M}}},D}$ is trivial.
Proof. The proof is the same as Lemma 4.4.5, except that we replace  $(U^{(j-1)}/U^{(j)})_{{\mathcal{M}}}$ by
$(U^{(j-1)}/U^{(j)})_{{\mathcal{M}}}$ by  ${\mathcal{K}}er_{(U^{(j-1)}/U^{(j)})_{{\mathcal{M}}},D}$, and that we use Lemma 4.4.15 below instead of Proposition 4.4.9.◻
${\mathcal{K}}er_{(U^{(j-1)}/U^{(j)})_{{\mathcal{M}}},D}$, and that we use Lemma 4.4.15 below instead of Proposition 4.4.9.◻
Lemma 4.4.15. There exists a constant  $C(G,X,N,I,d)\in \mathbb{Q}_{{\geqslant}0}$ such that for
$C(G,X,N,I,d)\in \mathbb{Q}_{{\geqslant}0}$ such that for  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, if
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, if  $\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >C(G,X,N,I,d),\text{ for all }\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then for any
$\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >C(G,X,N,I,d),\text{ for all }\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then for any  $((x_{i}),{\mathcal{M}},\unicode[STIX]{x1D713})\in \operatorname{Bun}_{M,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}(S)$ and any
$((x_{i}),{\mathcal{M}},\unicode[STIX]{x1D713})\in \operatorname{Bun}_{M,N,I,d}^{S_{M}(\unicode[STIX]{x1D707})}(S)$ and any  $j$, the sheaf
$j$, the sheaf  $R^{1}(\text{pr}_{S})_{\ast }((U^{(j)}/U^{(j+1)})_{{\mathcal{M}}}(-N\times S-\unicode[STIX]{x1D6E4}_{\sum dx_{i}}))$ is trivial.
$R^{1}(\text{pr}_{S})_{\ast }((U^{(j)}/U^{(j+1)})_{{\mathcal{M}}}(-N\times S-\unicode[STIX]{x1D6E4}_{\sum dx_{i}}))$ is trivial.
Proof. Let  $C(G,X,N,I,d):=C(G,X)+\deg N+|I|\cdot d$, where
$C(G,X,N,I,d):=C(G,X)+\deg N+|I|\cdot d$, where  $C(G,X)$ is the constant in Proposition 4.4.9. We repeat the argument in [Reference Drinfeld and GaitsgoryDG15, Proposition 10.4.5], except that in [Reference Drinfeld and GaitsgoryDG15, Remark 10.3.5] we replace the reductive group
$C(G,X)$ is the constant in Proposition 4.4.9. We repeat the argument in [Reference Drinfeld and GaitsgoryDG15, Proposition 10.4.5], except that in [Reference Drinfeld and GaitsgoryDG15, Remark 10.3.5] we replace the reductive group  $\widetilde{G}$ by
$\widetilde{G}$ by  $\widetilde{G}\times \mathbb{G}_{m}$ and the
$\widetilde{G}\times \mathbb{G}_{m}$ and the  $\widetilde{G}$-bundle
$\widetilde{G}$-bundle  ${\mathcal{F}}_{\widetilde{G}}$ by the
${\mathcal{F}}_{\widetilde{G}}$ by the  $\widetilde{G}\times \mathbb{G}_{m}$-bundle
$\widetilde{G}\times \mathbb{G}_{m}$-bundle  ${\mathcal{F}}_{\widetilde{G}}\times {\mathcal{O}}(-N\times S-\unicode[STIX]{x1D6E4}_{\sum dx_{i}})$.◻
${\mathcal{F}}_{\widetilde{G}}\times {\mathcal{O}}(-N\times S-\unicode[STIX]{x1D6E4}_{\sum dx_{i}})$.◻
4.5 Proof of Theorem 4.2.4: step 3
4.5.1
Let  $S$ be a scheme over
$S$ be a scheme over  $\mathbb{F}_{q}$. Let
$\mathbb{F}_{q}$. Let  $H_{S}$ and
$H_{S}$ and  $H_{S}^{\prime }$ be two group schemes over
$H_{S}^{\prime }$ be two group schemes over  $S$. Let
$S$. Let  $f:H_{S}^{\prime }\rightarrow H_{S}$ be a morphism of group schemes over
$f:H_{S}^{\prime }\rightarrow H_{S}$ be a morphism of group schemes over  $S$. We denote by
$S$. We denote by  $[S/H_{S}^{\prime }]$ the classifying stack of
$[S/H_{S}^{\prime }]$ the classifying stack of  $H_{S}^{\prime }$ on
$H_{S}^{\prime }$ on  $S$. Similarly for
$S$. Similarly for  $[S/H_{S}]$. Then
$[S/H_{S}]$. Then  $f$ induces a morphism of stacks:
$f$ induces a morphism of stacks:  $\overline{f}:[S/H_{S}^{\prime }]\rightarrow [S/H_{S}]$.
$\overline{f}:[S/H_{S}^{\prime }]\rightarrow [S/H_{S}]$.
Lemma 4.5.2. Let  $f,g:H_{S}^{\prime }\rightarrow H_{S}$ be two morphisms of connected group schemes. Let
$f,g:H_{S}^{\prime }\rightarrow H_{S}$ be two morphisms of connected group schemes. Let  $[H_{S}/H_{S}^{\prime }]$ be the quotient stack where
$[H_{S}/H_{S}^{\prime }]$ be the quotient stack where  $H_{S}^{\prime }$ acts on
$H_{S}^{\prime }$ acts on  $H_{S}$ by
$H_{S}$ by  $h^{\prime }\cdot h=f(h^{\prime })hg(h^{\prime })^{-1}$. Then the following diagram is Cartesian
$h^{\prime }\cdot h=f(h^{\prime })hg(h^{\prime })^{-1}$. Then the following diagram is Cartesian

where the morphism  $[H_{S}/H_{S}^{\prime }]\rightarrow [S/H_{S}]$ is induced by
$[H_{S}/H_{S}^{\prime }]\rightarrow [S/H_{S}]$ is induced by  $H_{S}\rightarrow S$ and
$H_{S}\rightarrow S$ and  $H_{S}^{\prime }\xrightarrow[{}]{g}H_{S}$.
$H_{S}^{\prime }\xrightarrow[{}]{g}H_{S}$.
Proof. The fiber product is  $[H_{S}\times _{S}H_{S}/H_{S}^{\prime }\times _{S}H_{S}]$, where
$[H_{S}\times _{S}H_{S}/H_{S}^{\prime }\times _{S}H_{S}]$, where  $H_{S}^{\prime }$ acts on
$H_{S}^{\prime }$ acts on  $H_{S}\times _{S}H_{S}$ by
$H_{S}\times _{S}H_{S}$ by  $(f,g)$ (from the left) and
$(f,g)$ (from the left) and  $H_{S}$ acts on
$H_{S}$ acts on  $H_{S}\times _{S}H_{S}$ by diagonal action (from the right). The morphism
$H_{S}\times _{S}H_{S}$ by diagonal action (from the right). The morphism  $\unicode[STIX]{x1D6FC}:[H_{S}\times _{S}H_{S}/H_{S}^{\prime }\times _{S}H_{S}]\rightarrow [S/H_{S}]$ (respectively
$\unicode[STIX]{x1D6FC}:[H_{S}\times _{S}H_{S}/H_{S}^{\prime }\times _{S}H_{S}]\rightarrow [S/H_{S}]$ (respectively  $\unicode[STIX]{x1D6FD}:[H_{S}\times _{S}H_{S}/H_{S}^{\prime }\times _{S}H_{S}]\rightarrow [S/H_{S}^{\prime }]$) is given by
$\unicode[STIX]{x1D6FD}:[H_{S}\times _{S}H_{S}/H_{S}^{\prime }\times _{S}H_{S}]\rightarrow [S/H_{S}^{\prime }]$) is given by  $H_{S}\times _{S}H_{S}\rightarrow S$ and the second projection
$H_{S}\times _{S}H_{S}\rightarrow S$ and the second projection  $H_{S}^{\prime }\times _{S}H_{S}\rightarrow H_{S}$ (respectively the first projection
$H_{S}^{\prime }\times _{S}H_{S}\rightarrow H_{S}$ (respectively the first projection  $H_{S}^{\prime }\times _{S}H_{S}\rightarrow H_{S}^{\prime }$).
$H_{S}^{\prime }\times _{S}H_{S}\rightarrow H_{S}^{\prime }$).
The morphism of group schemes over  $S$
$S$
 $$\begin{eqnarray}H_{S}\times _{S}H_{S}\rightarrow H_{S}\times _{S}H_{S},\quad (x,y)\mapsto (xy^{-1},y)\end{eqnarray}$$
$$\begin{eqnarray}H_{S}\times _{S}H_{S}\rightarrow H_{S}\times _{S}H_{S},\quad (x,y)\mapsto (xy^{-1},y)\end{eqnarray}$$ is an isomorphism. Moreover, it is  $H_{S}^{\prime }\times _{S}H_{S}$-equivariant for the action of
$H_{S}^{\prime }\times _{S}H_{S}$-equivariant for the action of  $H_{S}^{\prime }\times _{S}H_{S}$ on the left-hand side as above and the action of
$H_{S}^{\prime }\times _{S}H_{S}$ on the left-hand side as above and the action of  $H_{S}^{\prime }\times _{S}H_{S}$ on the right-hand side given by
$H_{S}^{\prime }\times _{S}H_{S}$ on the right-hand side given by  $(h^{\prime },h)(z,t)=(f(h^{\prime })zg(h^{\prime })^{-1},g(h^{\prime })th^{-1})$. The isomorphism (4.11) induces an isomorphism of quotient stacks
$(h^{\prime },h)(z,t)=(f(h^{\prime })zg(h^{\prime })^{-1},g(h^{\prime })th^{-1})$. The isomorphism (4.11) induces an isomorphism of quotient stacks

where  $H_{S}^{\prime }$ acts on
$H_{S}^{\prime }$ acts on  $H_{S}$ by
$H_{S}$ by  $h^{\prime }\cdot x=f(h^{\prime })xg(h^{\prime })^{-1}$. The morphism
$h^{\prime }\cdot x=f(h^{\prime })xg(h^{\prime })^{-1}$. The morphism  $[H_{S}/H_{S}^{\prime }]\rightarrow [S/H_{S}]$ is the composition of the inverse of (
$[H_{S}/H_{S}^{\prime }]\rightarrow [S/H_{S}]$ is the composition of the inverse of (
) and  $\unicode[STIX]{x1D6FC}$.◻
$\unicode[STIX]{x1D6FC}$.◻
Lemma 4.5.3. Let  $S$ be an affine scheme. Let
$S$ be an affine scheme. Let  $H_{1}$ and
$H_{1}$ and  $H_{2}$ be two unipotent group schemes over
$H_{2}$ be two unipotent group schemes over  $S$. Let
$S$. Let  $\unicode[STIX]{x1D711}:[S/H_{1}]\rightarrow [S/H_{2}]$ be a morphism of stacks. Then there exists
$\unicode[STIX]{x1D711}:[S/H_{1}]\rightarrow [S/H_{2}]$ be a morphism of stacks. Then there exists  $f:H_{1}\rightarrow H_{2}$ a morphism of group schemes over
$f:H_{1}\rightarrow H_{2}$ a morphism of group schemes over  $S$ such that
$S$ such that  $\unicode[STIX]{x1D711}=\overline{f}$.
$\unicode[STIX]{x1D711}=\overline{f}$.
Proof. Since  $S$ is affine and
$S$ is affine and  $H_{2}$ is unipotent, all
$H_{2}$ is unipotent, all  $H_{2}$-torsors on
$H_{2}$-torsors on  $S$ are trivial. The morphism
$S$ are trivial. The morphism  $\unicode[STIX]{x1D711}$ is given by a
$\unicode[STIX]{x1D711}$ is given by a  $H_{2}$-torsor
$H_{2}$-torsor  $\mathscr{H}$ on
$\mathscr{H}$ on  $S$ which is
$S$ which is  $H_{1}$-equivariant. We trivialize
$H_{1}$-equivariant. We trivialize  $\mathscr{H}$ as a
$\mathscr{H}$ as a  $H_{2}$-torsor. Then the action of
$H_{2}$-torsor. Then the action of  $H_{1}$ on
$H_{1}$ on  $\mathscr{H}$ gives the morphism
$\mathscr{H}$ gives the morphism  $f$.◻
$f$.◻
End of the proof of Theorem 4.2.4.
Let  $\unicode[STIX]{x1D707}$ satisfy the hypothesis in Proposition 4.4.13; then
$\unicode[STIX]{x1D707}$ satisfy the hypothesis in Proposition 4.4.13; then  $\mathscr{Y}_{N,d}=[S/H_{N,d}]$ (respectively
$\mathscr{Y}_{N,d}=[S/H_{N,d}]$ (respectively  $\mathscr{Y}_{N}=[S/H_{N}]$), where
$\mathscr{Y}_{N}=[S/H_{N}]$), where  $H_{N,d}:=R^{0}(\text{pr}_{S})_{\ast }{\mathcal{K}}er_{U_{{\mathcal{M}}},N\times S+\unicode[STIX]{x1D6E4}_{\sum dx_{i}}}$ (respectively
$H_{N,d}:=R^{0}(\text{pr}_{S})_{\ast }{\mathcal{K}}er_{U_{{\mathcal{M}}},N\times S+\unicode[STIX]{x1D6E4}_{\sum dx_{i}}}$ (respectively  $H_{N}:=R^{0}(\text{pr}_{S})_{\ast }{\mathcal{K}}er_{U_{{\mathcal{M}}},N\times S}$) is a unipotent group scheme over
$H_{N}:=R^{0}(\text{pr}_{S})_{\ast }{\mathcal{K}}er_{U_{{\mathcal{M}}},N\times S}$) is a unipotent group scheme over  $S$.
$S$.
By Lemma 4.5.3, the two morphisms  $b_{1}$ and
$b_{1}$ and  $b_{2}$ in diagram (4.5) are induced by two morphisms of group schemes
$b_{2}$ in diagram (4.5) are induced by two morphisms of group schemes  $f_{1},f_{2}:H_{N,d}\rightarrow H_{N}$. By Lemma 4.5.2,
$f_{1},f_{2}:H_{N,d}\rightarrow H_{N}$. By Lemma 4.5.2,  $\mathscr{Z}$ is isomorphic to
$\mathscr{Z}$ is isomorphic to  $[H_{N}/H_{N,d}],$ where
$[H_{N}/H_{N,d}],$ where  $H_{N,d}$ acts on
$H_{N,d}$ acts on  $H_{N}$ by
$H_{N}$ by  $h^{\prime }\cdot h=f_{1}(h^{\prime })hf_{2}(h^{\prime })^{-1}$.◻
$h^{\prime }\cdot h=f_{1}(h^{\prime })hf_{2}(h^{\prime })^{-1}$.◻
4.6 Cohomological statements
Definition 4.6.1. Let  $d_{W}$ be the smallest integer in Proposition 2.2.1 such that the action of
$d_{W}$ be the smallest integer in Proposition 2.2.1 such that the action of  $G_{I,\infty }$ on
$G_{I,\infty }$ on  $\operatorname{Gr}_{G,I,W}$ factors through
$\operatorname{Gr}_{G,I,W}$ factors through  $G_{I,d_{W}}$. We have defined the constants
$G_{I,d_{W}}$. We have defined the constants  $C^{\prime }(G,X,N,W)$ and
$C^{\prime }(G,X,N,W)$ and  $C(G,X,N,I,d_{W})$ in Theorems 4.2.1 and 4.2.4 respectively. We take
$C(G,X,N,I,d_{W})$ in Theorems 4.2.1 and 4.2.4 respectively. We take
 $$\begin{eqnarray}\widetilde{C}(G,X,N,W):=\text{Max}\{C^{\prime }(G,X,N,W),\;C(G,X,N,I,d_{W})\}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{C}(G,X,N,W):=\text{Max}\{C^{\prime }(G,X,N,W),\;C(G,X,N,I,d_{W})\}.\end{eqnarray}$$Definition 4.6.2. Let  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. For any
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. For any  $j\in \mathbb{Z}$, we define degree
$j\in \mathbb{Z}$, we define degree  $j$ cohomology sheaves
$j$ cohomology sheaves
 $$\begin{eqnarray}\displaystyle & {\mathcal{H}}_{G,N,I,W}^{j,\,S_{M}(\unicode[STIX]{x1D707})}=R^{j}(\mathfrak{p}_{G})_{!}(\left.{\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}\vphantom{\big|}\right|_{\operatorname{Cht}_{G,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}/\unicode[STIX]{x1D6EF}}), & \displaystyle \nonumber\\ \displaystyle & {\mathcal{H}}_{M,N,I,W}^{\prime \,j,\,S_{M}(\unicode[STIX]{x1D707})}=R^{j}(\mathfrak{p}_{M}^{\prime })_{!}(\left.{\mathcal{F}}_{M,N,I,W}^{^{\prime }\,\unicode[STIX]{x1D6EF}}\vphantom{\big|}\right|_{\operatorname{Cht}_{M,N,I,W}^{\prime S_{M}(\unicode[STIX]{x1D707})}/\unicode[STIX]{x1D6EF}}). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\mathcal{H}}_{G,N,I,W}^{j,\,S_{M}(\unicode[STIX]{x1D707})}=R^{j}(\mathfrak{p}_{G})_{!}(\left.{\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}\vphantom{\big|}\right|_{\operatorname{Cht}_{G,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}/\unicode[STIX]{x1D6EF}}), & \displaystyle \nonumber\\ \displaystyle & {\mathcal{H}}_{M,N,I,W}^{\prime \,j,\,S_{M}(\unicode[STIX]{x1D707})}=R^{j}(\mathfrak{p}_{M}^{\prime })_{!}(\left.{\mathcal{F}}_{M,N,I,W}^{^{\prime }\,\unicode[STIX]{x1D6EF}}\vphantom{\big|}\right|_{\operatorname{Cht}_{M,N,I,W}^{\prime S_{M}(\unicode[STIX]{x1D707})}/\unicode[STIX]{x1D6EF}}). & \displaystyle \nonumber\end{eqnarray}$$4.6.3
If  $\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >\widetilde{C}(G,X,N,W)\text{ for all }\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then by Theorem 4.2.1, the morphism
$\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >\widetilde{C}(G,X,N,W)\text{ for all }\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then by Theorem 4.2.1, the morphism  $i^{\prime \,S_{M}(\unicode[STIX]{x1D707})}:\operatorname{Cht}_{P,N,I,W}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Cht}_{G,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}$ is proper and schematic. Applying the construction in §3 to the truncation
$i^{\prime \,S_{M}(\unicode[STIX]{x1D707})}:\operatorname{Cht}_{P,N,I,W}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}\rightarrow \operatorname{Cht}_{G,N,I,W}^{S_{M}(\unicode[STIX]{x1D707})}$ is proper and schematic. Applying the construction in §3 to the truncation  $S_{M}(\unicode[STIX]{x1D707})$, we obtain a constant term morphism (in
$S_{M}(\unicode[STIX]{x1D707})$, we obtain a constant term morphism (in  $D_{c}^{b}((X\smallsetminus N)^{I},\mathbb{Q}_{\ell })$):
$D_{c}^{b}((X\smallsetminus N)^{I},\mathbb{Q}_{\ell })$):
 $$\begin{eqnarray}{\mathcal{C}}_{G,N}^{P,\,j,\,S_{M}(\unicode[STIX]{x1D707})}:{\mathcal{H}}_{G,N,I,W}^{j,\,S_{M}(\unicode[STIX]{x1D707})}\rightarrow {\mathcal{H}}_{M,N,I,W}^{\prime \,j,\,S_{M}(\unicode[STIX]{x1D707})}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}_{G,N}^{P,\,j,\,S_{M}(\unicode[STIX]{x1D707})}:{\mathcal{H}}_{G,N,I,W}^{j,\,S_{M}(\unicode[STIX]{x1D707})}\rightarrow {\mathcal{H}}_{M,N,I,W}^{\prime \,j,\,S_{M}(\unicode[STIX]{x1D707})}.\end{eqnarray}$$Here is the main result of §4.
Proposition 4.6.4. Let  $P$ be a parabolic subgroup of
$P$ be a parabolic subgroup of  $G$ and
$G$ and  $M$ its Levi quotient. For
$M$ its Levi quotient. For  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, if
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, if  $\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >\widetilde{C}(G,X,N,W)\text{ for all }\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then for any
$\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle >\widetilde{C}(G,X,N,W)\text{ for all }\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}$, then for any  $j$, morphism (4.13) is an isomorphism.
$j$, morphism (4.13) is an isomorphism.
Proof. By (3.33),  ${\mathcal{C}}_{G,N}^{P,\,j,\,S_{M}(\unicode[STIX]{x1D707})}$ is the composition of two morphisms:
${\mathcal{C}}_{G,N}^{P,\,j,\,S_{M}(\unicode[STIX]{x1D707})}$ is the composition of two morphisms:

The morphism (1) is induced by the composition of functors

defined in (3.32). By Theorem 4.2.1 and Lemma 4.6.5 below applied to  $i^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$, the morphism (1) is an isomorphism.
$i^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$, the morphism (1) is an isomorphism.
The morphism (2) is induced by the morphism
 $$\begin{eqnarray}(\unicode[STIX]{x1D70B}^{\prime \,S_{M}(\unicode[STIX]{x1D707})})_{!}(i^{\prime \,S_{M}(\unicode[STIX]{x1D707})})^{\ast }{\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}\rightarrow {\mathcal{F}}_{M,N,I,W}^{\prime \,\unicode[STIX]{x1D6EF}}\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70B}^{\prime \,S_{M}(\unicode[STIX]{x1D707})})_{!}(i^{\prime \,S_{M}(\unicode[STIX]{x1D707})})^{\ast }{\mathcal{F}}_{G,N,I,W}^{\unicode[STIX]{x1D6EF}}\rightarrow {\mathcal{F}}_{M,N,I,W}^{\prime \,\unicode[STIX]{x1D6EF}}\end{eqnarray}$$defined in (3.23), which is a composition of the counit map
 $$\begin{eqnarray}\text{Co}:(\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})})_{!}(\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})})^{!}\rightarrow \operatorname{Id}\end{eqnarray}$$
$$\begin{eqnarray}\text{Co}:(\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})})_{!}(\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})})^{!}\rightarrow \operatorname{Id}\end{eqnarray}$$ and some isomorphisms. By Theorem 4.2.4 and Lemma 4.6.6 below applied to  $\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$, the morphism (2) is an isomorphism.◻
$\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$, the morphism (2) is an isomorphism.◻
Lemma 4.6.5. Let  $f:\mathscr{X}\rightarrow \mathscr{Y}$ be a schematic finite universal homeomorphism of algebraic stacks; then the unit map
$f:\mathscr{X}\rightarrow \mathscr{Y}$ be a schematic finite universal homeomorphism of algebraic stacks; then the unit map  $\operatorname{Id}\rightarrow f_{\ast }f^{\ast }$ is an isomorphism.
$\operatorname{Id}\rightarrow f_{\ast }f^{\ast }$ is an isomorphism.
Lemma 4.6.6. Let  $f:\mathscr{X}\rightarrow \mathscr{Y}$ be an unipotent morphism of algebraic stacks (see Definition 4.2.3); then the counit map
$f:\mathscr{X}\rightarrow \mathscr{Y}$ be an unipotent morphism of algebraic stacks (see Definition 4.2.3); then the counit map  $f_{!}f^{!}\rightarrow \operatorname{Id}$ is an isomorphism.
$f_{!}f^{!}\rightarrow \operatorname{Id}$ is an isomorphism.
Proof. The proof consists of four steps.
(i) Using proper base change and the fact that  $f$ is smooth, we reduce to the case when
$f$ is smooth, we reduce to the case when  $\mathscr{Y}=\operatorname{Spec}k$ is a point, and thus
$\mathscr{Y}=\operatorname{Spec}k$ is a point, and thus  $\mathscr{X}=U_{1}/U_{2}$ is a quotient of unipotent group schemes
$\mathscr{X}=U_{1}/U_{2}$ is a quotient of unipotent group schemes  $U_{1}$ and
$U_{1}$ and  $U_{2}$ over
$U_{2}$ over  $k$.
$k$.
Indeed, to prove the lemma, it is enough to prove that for any geometric point  $i_{y}:y\rightarrow \mathscr{Y}$, the morphism
$i_{y}:y\rightarrow \mathscr{Y}$, the morphism  $(i_{y})^{\ast }f_{!}f^{!}\rightarrow (i_{y})^{\ast }$ is an isomorphism. Form the following Cartesian square.
$(i_{y})^{\ast }f_{!}f^{!}\rightarrow (i_{y})^{\ast }$ is an isomorphism. Form the following Cartesian square.

Since  $f$ is smooth, we have
$f$ is smooth, we have  $f^{!}\simeq f^{\ast }[2n](n)$ and
$f^{!}\simeq f^{\ast }[2n](n)$ and  $(\widetilde{f})^{!}\simeq (\widetilde{f})^{\ast }[2n](n)$, where
$(\widetilde{f})^{!}\simeq (\widetilde{f})^{\ast }[2n](n)$, where  $n$ is the dimension of
$n$ is the dimension of  $f$. We deduce that
$f$. We deduce that
 $$\begin{eqnarray}(i_{y})^{\ast }f_{!}f^{!}\simeq (\widetilde{f})_{!}(\widetilde{i}_{y})^{\ast }f^{!}\simeq (\widetilde{f})_{!}(\widetilde{i}_{y})^{\ast }(f)^{\ast }[2n](n)\simeq (\widetilde{f})_{!}(\widetilde{f})^{\ast }(i_{y})^{\ast }[2n](n)\simeq (\widetilde{f})_{!}(\widetilde{f})^{!}(i_{y})^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}(i_{y})^{\ast }f_{!}f^{!}\simeq (\widetilde{f})_{!}(\widetilde{i}_{y})^{\ast }f^{!}\simeq (\widetilde{f})_{!}(\widetilde{i}_{y})^{\ast }(f)^{\ast }[2n](n)\simeq (\widetilde{f})_{!}(\widetilde{f})^{\ast }(i_{y})^{\ast }[2n](n)\simeq (\widetilde{f})_{!}(\widetilde{f})^{!}(i_{y})^{\ast },\end{eqnarray}$$ where the first isomorphism is the proper base change [Reference Laszlo and OlssonLO08, § 12]. Thus it is enough to prove that  $(\widetilde{f})_{!}(\widetilde{f})^{!}(i_{y})^{\ast }\rightarrow (i_{y})^{\ast }$ is an isomorphism.
$(\widetilde{f})_{!}(\widetilde{f})^{!}(i_{y})^{\ast }\rightarrow (i_{y})^{\ast }$ is an isomorphism.
(ii) We denote by  $BU_{2}$ the classifying stack of
$BU_{2}$ the classifying stack of  $U_{2}$ over
$U_{2}$ over  $k$. Let
$k$. Let  $f_{1}:U_{1}/U_{2}\rightarrow BU_{2}$ and
$f_{1}:U_{1}/U_{2}\rightarrow BU_{2}$ and  $f_{2}:BU_{2}\rightarrow \operatorname{Spec}k$ be the canonical morphisms. Then
$f_{2}:BU_{2}\rightarrow \operatorname{Spec}k$ be the canonical morphisms. Then  $f=f_{2}\circ f_{1}$. We have a commutative diagram of functors.
$f=f_{2}\circ f_{1}$. We have a commutative diagram of functors.

Thus it is enough to prove that the counit maps  $(f_{1})_{!}(f_{1})^{!}\rightarrow \operatorname{Id}$ and
$(f_{1})_{!}(f_{1})^{!}\rightarrow \operatorname{Id}$ and  $(f_{2})_{!}(f_{2})^{!}\rightarrow \operatorname{Id}$ are isomorphisms.
$(f_{2})_{!}(f_{2})^{!}\rightarrow \operatorname{Id}$ are isomorphisms.
(iii) Note that  $f_{1}$ is a
$f_{1}$ is a  $U_{1}$-torsor over
$U_{1}$-torsor over  $BU_{2}$. By Definition 4.2.3, we reduce to the case of
$BU_{2}$. By Definition 4.2.3, we reduce to the case of  $\mathbb{A}^{1}$-torsor. Using (i) again, we reduce to the case when
$\mathbb{A}^{1}$-torsor. Using (i) again, we reduce to the case when  $f_{1}$ is the map
$f_{1}$ is the map  $\mathbb{A}^{1}\rightarrow \operatorname{Spec}k$, where it is clear that
$\mathbb{A}^{1}\rightarrow \operatorname{Spec}k$, where it is clear that  $(f_{1})_{!}(f_{1})^{!}\rightarrow \operatorname{Id}$ is an isomorphism.
$(f_{1})_{!}(f_{1})^{!}\rightarrow \operatorname{Id}$ is an isomorphism.
(iv) Let  $g_{2}:\operatorname{Spec}k\rightarrow BU_{2}$ be the canonical morphism. Then
$g_{2}:\operatorname{Spec}k\rightarrow BU_{2}$ be the canonical morphism. Then  $f_{2}\circ g_{2}\simeq \operatorname{Id}$. We have a commutative diagram of functors.
$f_{2}\circ g_{2}\simeq \operatorname{Id}$. We have a commutative diagram of functors.

We deduce that to prove that  $(f_{2})_{!}(f_{2})^{!}\rightarrow \operatorname{Id}$ is an isomorphism, it is enough to prove that
$(f_{2})_{!}(f_{2})^{!}\rightarrow \operatorname{Id}$ is an isomorphism, it is enough to prove that  $(g_{2})_{!}(g_{2})^{!}\rightarrow \operatorname{Id}$ is an isomorphism. Note that
$(g_{2})_{!}(g_{2})^{!}\rightarrow \operatorname{Id}$ is an isomorphism. Note that  $g_{2}$ is a
$g_{2}$ is a  $U_{2}$-torsor over
$U_{2}$-torsor over  $BU_{2}$. Just like in (iii), we prove that
$BU_{2}$. Just like in (iii), we prove that  $(g_{2})_{!}(g_{2})^{!}\rightarrow \operatorname{Id}$ is an isomorphism.◻
$(g_{2})_{!}(g_{2})^{!}\rightarrow \operatorname{Id}$ is an isomorphism.◻
Remark 4.6.7. In fact, to prove that the morphism (2) in Proposition 4.6.4 is an isomorphism, it is enough to write  $\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ as the tower
$\unicode[STIX]{x1D70B}_{d}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$ as the tower
 $$\begin{eqnarray}\operatorname{Cht}_{P}^{S_{M}(\unicode[STIX]{x1D707})}\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{d,m}}\cdots \rightarrow \widetilde{\operatorname{Cht}}_{P/U^{(j+1)}}\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{d,j}}\widetilde{\operatorname{Cht}}_{P/U^{(j)}}\rightarrow \cdots \xrightarrow[{}]{\unicode[STIX]{x1D70B}_{d,0}}\widetilde{\operatorname{Cht}}_{M}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{P}^{S_{M}(\unicode[STIX]{x1D707})}\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{d,m}}\cdots \rightarrow \widetilde{\operatorname{Cht}}_{P/U^{(j+1)}}\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{d,j}}\widetilde{\operatorname{Cht}}_{P/U^{(j)}}\rightarrow \cdots \xrightarrow[{}]{\unicode[STIX]{x1D70B}_{d,0}}\widetilde{\operatorname{Cht}}_{M}\end{eqnarray}$$ and prove that for each  $j$, the morphism
$j$, the morphism  $\operatorname{Co}:(\unicode[STIX]{x1D70B}_{d,j})_{!}(\unicode[STIX]{x1D70B}_{d,j})^{!}\rightarrow \operatorname{Id}$ is an isomorphism. For this, we only need the statement of Theorem 4.2.4 for each
$\operatorname{Co}:(\unicode[STIX]{x1D70B}_{d,j})_{!}(\unicode[STIX]{x1D70B}_{d,j})^{!}\rightarrow \operatorname{Id}$ is an isomorphism. For this, we only need the statement of Theorem 4.2.4 for each  $\unicode[STIX]{x1D70B}_{d,j}$ (and replace unipotent group scheme by additive group scheme). The proof of such a statement still uses the three steps, but in step 2 Remark 4.4.6 we only need to consider the case of commutative groups.
$\unicode[STIX]{x1D70B}_{d,j}$ (and replace unipotent group scheme by additive group scheme). The proof of such a statement still uses the three steps, but in step 2 Remark 4.4.6 we only need to consider the case of commutative groups.
5 Finiteness of the cuspidal cohomology
The goal of this section is to prove the following.
Theorem 5.0.1. The  $\mathbb{Q}_{\ell }$-vector space
$\mathbb{Q}_{\ell }$-vector space  $H_{G,N,I,W}^{j,\;\operatorname{cusp}}$ (defined in Definition 3.5.13) has finite dimension.
$H_{G,N,I,W}^{j,\;\operatorname{cusp}}$ (defined in Definition 3.5.13) has finite dimension.
Theorem 5.0.1 will be a direct consequence of the following proposition.
Proposition 5.0.2. Let  $G,X,N,I,W$ as before. There exists
$G,X,N,I,W$ as before. There exists  $\unicode[STIX]{x1D707}_{0}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ (depending on
$\unicode[STIX]{x1D707}_{0}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ (depending on  $G$,
$G$,  $X$,
$X$,  $N$,
$N$,  $W$ and
$W$ and  $j$) such that
$j$) such that
 $$\begin{eqnarray}H_{G,N,I,W}^{j,\;\operatorname{cusp}}\subset \text{Im}(H_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}_{0}}\rightarrow H_{G,N,I,W}^{j}).\end{eqnarray}$$
$$\begin{eqnarray}H_{G,N,I,W}^{j,\;\operatorname{cusp}}\subset \text{Im}(H_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}_{0}}\rightarrow H_{G,N,I,W}^{j}).\end{eqnarray}$$ The proof of this proposition is essentially based on Proposition 4.6.4 and an induction argument on the semisimple rank of the group  $G$. We will present our strategy in §5.1 and give the proof in §§5.2–5.4.
$G$. We will present our strategy in §5.1 and give the proof in §§5.2–5.4.
Notation 5.0.3. In the remaining part of this section, to simplify the notations, we will omit the indices  $N,I,W$.
$N,I,W$.
5.1 Strategy of the proof
5.1.1
We denote by  $\widehat{R}_{G^{\text{ad}}}$ the coroot lattice of
$\widehat{R}_{G^{\text{ad}}}$ the coroot lattice of  $G^{\text{ad}}$. We have
$G^{\text{ad}}$. We have  $\widehat{R}_{G^{\text{ad}}}\subset \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}$. Let
$\widehat{R}_{G^{\text{ad}}}\subset \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}$. Let  $\widehat{R}_{G^{\text{ad}}}^{+}:=\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+}\cap \widehat{R}_{G^{\text{ad}}}$. For any
$\widehat{R}_{G^{\text{ad}}}^{+}:=\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+}\cap \widehat{R}_{G^{\text{ad}}}$. For any  $r\in \mathbb{N}$, we have
$r\in \mathbb{N}$, we have  $(1/r)\widehat{R}_{G^{\text{ad}}}^{+}\subset \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and
$(1/r)\widehat{R}_{G^{\text{ad}}}^{+}\subset \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ and

Let  $\unicode[STIX]{x1D704}:\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}\subset \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}$ be the inclusion. We fix
$\unicode[STIX]{x1D704}:\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}\subset \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}$ be the inclusion. We fix  $r$ such that
$r$ such that  $\bigcup _{P\subsetneq G}\unicode[STIX]{x1D704}\circ \operatorname{pr}_{P}^{\text{ad}}(\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+})\subset (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$, where
$\bigcup _{P\subsetneq G}\unicode[STIX]{x1D704}\circ \operatorname{pr}_{P}^{\text{ad}}(\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+})\subset (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$, where  $\operatorname{pr}_{P}^{\text{ad}}:\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$ is defined in (1.18).
$\operatorname{pr}_{P}^{\text{ad}}:\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$ is defined in (1.18).
5.1.2
For any  $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}$, we denote by
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}$, we denote by  $\check{\unicode[STIX]{x1D6FC}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}$ the corresponding coroot, and vice versa. Let
$\check{\unicode[STIX]{x1D6FC}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}$ the corresponding coroot, and vice versa. Let  $P_{\unicode[STIX]{x1D6FC}}$ be the maximal parabolic subgroup with Levi quotient
$P_{\unicode[STIX]{x1D6FC}}$ be the maximal parabolic subgroup with Levi quotient  $M_{\unicode[STIX]{x1D6FC}}$ such that
$M_{\unicode[STIX]{x1D6FC}}$ such that  $\unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M_{\unicode[STIX]{x1D6FC}}}=\{\unicode[STIX]{x1D6FC}\}$.
$\unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M_{\unicode[STIX]{x1D6FC}}}=\{\unicode[STIX]{x1D6FC}\}$.
In this section, for  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, we will write
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, we will write  $\unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}$ instead of
$\unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}$ instead of  $\unicode[STIX]{x1D707}-(1/r)\unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FC}})$, where
$\unicode[STIX]{x1D707}-(1/r)\unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FC}})$, where  $\unicode[STIX]{x1D6F6}_{G}:\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}$ is defined in 1.15.
$\unicode[STIX]{x1D6F6}_{G}:\widehat{\unicode[STIX]{x1D6EC}}_{G}^{\mathbb{Q}}\rightarrow \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{\mathbb{Q}}$ is defined in 1.15.
5.1.3
We have defined the inductive limits  $H_{G}^{j}$ in Definition 2.5.5 and
$H_{G}^{j}$ in Definition 2.5.5 and  $H_{M_{\unicode[STIX]{x1D6FC}}}^{\prime \,j}$ in Definition 3.4.9. For any
$H_{M_{\unicode[STIX]{x1D6FC}}}^{\prime \,j}$ in Definition 3.4.9. For any  $\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$, let
$\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$, let  ${\mathcal{I}}_{\unicode[STIX]{x1D706}}:H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}}\rightarrow H_{G}^{j}$ be the morphism to the inductive limit. Let
${\mathcal{I}}_{\unicode[STIX]{x1D706}}:H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}}\rightarrow H_{G}^{j}$ be the morphism to the inductive limit. Let  $H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}}\rightarrow H_{M_{\unicode[STIX]{x1D6FC}}}^{\prime \,j}$ be the composition of morphisms
$H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}}\rightarrow H_{M_{\unicode[STIX]{x1D6FC}}}^{\prime \,j}$ be the composition of morphisms  $H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}}\xrightarrow[{}]{{\mathcal{I}}_{\unicode[STIX]{x1D706}}}H_{G}^{j}\xrightarrow[{}]{C_{G}^{P_{\unicode[STIX]{x1D6FC}},\,j}}H_{M_{\unicode[STIX]{x1D6FC}}}^{\prime \,j}$, where the second morphism is defined in Definition 3.5.10.
$H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}}\xrightarrow[{}]{{\mathcal{I}}_{\unicode[STIX]{x1D706}}}H_{G}^{j}\xrightarrow[{}]{C_{G}^{P_{\unicode[STIX]{x1D6FC}},\,j}}H_{M_{\unicode[STIX]{x1D6FC}}}^{\prime \,j}$, where the second morphism is defined in Definition 3.5.10.
5.1.4
Since for every  $c\in H_{G}^{j}$, there exists
$c\in H_{G}^{j}$, there exists  $\unicode[STIX]{x1D706}\in \widehat{R}_{G^{\text{ad}}}^{+}$ large enough such that
$\unicode[STIX]{x1D706}\in \widehat{R}_{G^{\text{ad}}}^{+}$ large enough such that  $c\in \text{Im}(H_{G}^{j,\;\leqslant \unicode[STIX]{x1D706}}\rightarrow H_{G}^{j})$, Proposition 5.0.2 will be a direct consequence of part (b) in the following proposition.
$c\in \text{Im}(H_{G}^{j,\;\leqslant \unicode[STIX]{x1D706}}\rightarrow H_{G}^{j})$, Proposition 5.0.2 will be a direct consequence of part (b) in the following proposition.
Proposition 5.1.5. Let  $G$ be a connected split reductive group. There exists a constant
$G$ be a connected split reductive group. There exists a constant  $C_{G}^{0}\in \mathbb{Q}^{{\geqslant}0}$ (depending on
$C_{G}^{0}\in \mathbb{Q}^{{\geqslant}0}$ (depending on  $G,X,N,W,j$), such that the following properties hold.
$G,X,N,W,j$), such that the following properties hold.
(a) Let
 $\unicode[STIX]{x1D707}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ such that
$\unicode[STIX]{x1D707}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ such that  $\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FE}\rangle \geqslant C_{G}^{0}$ for all
$\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FE}\rangle \geqslant C_{G}^{0}$ for all  $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{G}$. Then for any
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{G}$. Then for any  $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}$ such that
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}$ such that  $\unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ (which is automatic if
$\unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ (which is automatic if  $C_{G}^{0}>2/r$), the morphism is surjective.
$C_{G}^{0}>2/r$), the morphism is surjective. $$\begin{eqnarray}\operatorname{Ker}(H_{G}^{j,\,\leqslant \unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}}\rightarrow H_{M_{\unicode[STIX]{x1D6FC}}}^{\prime \,j})\rightarrow \operatorname{Ker}(H_{G}^{j,\,\leqslant \unicode[STIX]{x1D707}}\rightarrow H_{M_{\unicode[STIX]{x1D6FC}}}^{\prime \,j})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ker}(H_{G}^{j,\,\leqslant \unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}}\rightarrow H_{M_{\unicode[STIX]{x1D6FC}}}^{\prime \,j})\rightarrow \operatorname{Ker}(H_{G}^{j,\,\leqslant \unicode[STIX]{x1D707}}\rightarrow H_{M_{\unicode[STIX]{x1D6FC}}}^{\prime \,j})\end{eqnarray}$$(b) There exists
 $\unicode[STIX]{x1D707}_{0}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ (depending on
$\unicode[STIX]{x1D707}_{0}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ (depending on  $C_{G}^{0}$), such that for any
$C_{G}^{0}$), such that for any  $\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ satisfying
$\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ satisfying  $\unicode[STIX]{x1D706}\geqslant \unicode[STIX]{x1D707}_{0}$ and
$\unicode[STIX]{x1D706}\geqslant \unicode[STIX]{x1D707}_{0}$ and  $\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D6FE}\rangle \geqslant C_{G}^{0}$ for all
$\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D6FE}\rangle \geqslant C_{G}^{0}$ for all  $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{G}$, the morphism is surjective.
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{G}$, the morphism is surjective. $$\begin{eqnarray}\operatorname{Ker}\biggl(H_{G}^{j,\,\leqslant \unicode[STIX]{x1D707}_{0}}\rightarrow \mathop{\prod }_{P\subsetneq G}H_{M}^{\prime \,j}\biggr)\rightarrow \operatorname{Ker}\biggl(H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}}\rightarrow \mathop{\prod }_{P\subsetneq G}H_{M}^{\prime \,j}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ker}\biggl(H_{G}^{j,\,\leqslant \unicode[STIX]{x1D707}_{0}}\rightarrow \mathop{\prod }_{P\subsetneq G}H_{M}^{\prime \,j}\biggr)\rightarrow \operatorname{Ker}\biggl(H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}}\rightarrow \mathop{\prod }_{P\subsetneq G}H_{M}^{\prime \,j}\biggr)\end{eqnarray}$$(c) There exists a constant
 $C_{G}\geqslant C_{G}^{0}$, such that for any
$C_{G}\geqslant C_{G}^{0}$, such that for any  $\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ satisfying
$\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ satisfying  $\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D6FE}\rangle \geqslant C_{G}$ for all
$\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D6FE}\rangle \geqslant C_{G}$ for all  $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{G}$, the morphism
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{G}$, the morphism  ${\mathcal{I}}_{\unicode[STIX]{x1D706}}:H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}}\rightarrow H_{G}^{j}$ is injective.
${\mathcal{I}}_{\unicode[STIX]{x1D706}}:H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}}\rightarrow H_{G}^{j}$ is injective.
5.1.6
The proof of Proposition 5.1.5 uses an induction argument on the semisimple rank of the group  $G$: first we prove the statements (a), (b) and (c) for every Levi subgroup of
$G$: first we prove the statements (a), (b) and (c) for every Levi subgroup of  $G$ of rank
$G$ of rank  $0$. Second we prove the key step: for
$0$. Second we prove the key step: for  $n\geqslant 1$, if (c) is true for all Levi subgroups of rank
$n\geqslant 1$, if (c) is true for all Levi subgroups of rank  $n-1$, then (a) is true for all Levi subgroups of rank
$n-1$, then (a) is true for all Levi subgroups of rank  $n$. Then we deduce easily (a)
$n$. Then we deduce easily (a)  $\Rightarrow$ (b) and (b)
$\Rightarrow$ (b) and (b)  $\Rightarrow$ (c) for all Levi subgroups of rank
$\Rightarrow$ (c) for all Levi subgroups of rank  $n$.
$n$.
5.1.7
As in 4.4.1, we fix a maximal torus  $T\subset B$ and view the Levi quotient
$T\subset B$ and view the Levi quotient  $M$ of a (standard) parabolic
$M$ of a (standard) parabolic  $P$ as a subgroup
$P$ as a subgroup  $M\subset P$.
$M\subset P$.
Recall that we have fixed  $\unicode[STIX]{x1D6EF}=\unicode[STIX]{x1D6EF}_{G}\subset Z_{G}(\mathbb{A})$ in 0.0.4. Applying 0.0.4 to each Levi subgroup
$\unicode[STIX]{x1D6EF}=\unicode[STIX]{x1D6EF}_{G}\subset Z_{G}(\mathbb{A})$ in 0.0.4. Applying 0.0.4 to each Levi subgroup  $M$ of
$M$ of  $G$, we fix
$G$, we fix  $\unicode[STIX]{x1D6EF}_{M}\subset Z_{M}(\mathbb{A})$. Moreover, we choose
$\unicode[STIX]{x1D6EF}_{M}\subset Z_{M}(\mathbb{A})$. Moreover, we choose  $\unicode[STIX]{x1D6EF}_{M}$ for different Levi subgroups in a compatible way: if
$\unicode[STIX]{x1D6EF}_{M}$ for different Levi subgroups in a compatible way: if  $M_{2}$ is a Levi subgroup of
$M_{2}$ is a Levi subgroup of  $M_{1}$, then we have
$M_{1}$, then we have  $\unicode[STIX]{x1D6EF}_{G}\subset \unicode[STIX]{x1D6EF}_{M_{1}}\subset \unicode[STIX]{x1D6EF}_{M_{2}}\subset T(\mathbb{A})$.
$\unicode[STIX]{x1D6EF}_{G}\subset \unicode[STIX]{x1D6EF}_{M_{1}}\subset \unicode[STIX]{x1D6EF}_{M_{2}}\subset T(\mathbb{A})$.
5.2 Beginning of the induction: semisimple rank  $0$
$0$
5.2.1
The only Levi subgroup of semisimple rank  $0$ is the maximal torus
$0$ is the maximal torus  $T$. Then
$T$. Then  $T^{\text{ad}}$ is trivial and
$T^{\text{ad}}$ is trivial and  $\widehat{\unicode[STIX]{x1D6EC}}_{T^{\text{ad}}}^{+}=\widehat{\unicode[STIX]{x1D6EC}}_{T^{\text{ad}}}$ has only one element:
$\widehat{\unicode[STIX]{x1D6EC}}_{T^{\text{ad}}}^{+}=\widehat{\unicode[STIX]{x1D6EC}}_{T^{\text{ad}}}$ has only one element:  $0$.
$0$.
The algebraic stack  $\operatorname{Cht}_{T}/\unicode[STIX]{x1D6EF}_{T}$ is of finite type. There is only one term in the inductive limit
$\operatorname{Cht}_{T}/\unicode[STIX]{x1D6EF}_{T}$ is of finite type. There is only one term in the inductive limit  $H_{T}^{j}$, which is of finite dimension.
$H_{T}^{j}$, which is of finite dimension.
There is no constant term morphism for  $T$. So we have
$T$. So we have  $H_{T}^{j,\,\operatorname{cusp}}=H_{T}^{j}$.
$H_{T}^{j,\,\operatorname{cusp}}=H_{T}^{j}$.
Lemma 5.2.2. Take  $C_{T}^{0}=C_{T}=0$ and
$C_{T}^{0}=C_{T}=0$ and  $\unicode[STIX]{x1D707}_{0}=0$. Proposition 5.1.5 is true for
$\unicode[STIX]{x1D707}_{0}=0$. Proposition 5.1.5 is true for  $T$.
$T$.
5.3 From semisimple rank  $n-1$ to
$n-1$ to  $n$
$n$
Lemma 5.3.1. Let  $G$ be a connected split reductive group of semisimple rank
$G$ be a connected split reductive group of semisimple rank  $n$. Suppose that Proposition 5.1.5(c) is true for every Levi quotient
$n$. Suppose that Proposition 5.1.5(c) is true for every Levi quotient  $M$ of
$M$ of  $G$ of semisimple rank
$G$ of semisimple rank  $n-1$, with a constant
$n-1$, with a constant  $C_{M}$. We take
$C_{M}$. We take
 $$\begin{eqnarray}C_{G}^{0}:=\text{Max}\{\{C_{M}\;|\;M\text{ Levi quotient of semisimple rank }n-1\text{ of }G\},\;\widetilde{C}(G,X,N,W)\},\end{eqnarray}$$
$$\begin{eqnarray}C_{G}^{0}:=\text{Max}\{\{C_{M}\;|\;M\text{ Levi quotient of semisimple rank }n-1\text{ of }G\},\;\widetilde{C}(G,X,N,W)\},\end{eqnarray}$$ where  $\widetilde{C}(G,X,N,W)$ is the constant defined in Definition 4.6.1. Then for this constant
$\widetilde{C}(G,X,N,W)$ is the constant defined in Definition 4.6.1. Then for this constant  $C_{G}^{0}$ Proposition 5.1.5(a) is true for
$C_{G}^{0}$ Proposition 5.1.5(a) is true for  $G$.
$G$.
We need some preparations before the proof of Lemma 5.3.1.
5.3.2
Let  $\unicode[STIX]{x1D707}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ such that
$\unicode[STIX]{x1D707}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ such that  $\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FE}\rangle \geqslant C_{G}^{0}$ for all
$\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FE}\rangle \geqslant C_{G}^{0}$ for all  $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{G}$. Let
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{G}$. Let  $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}$ such that
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E4}_{G}$ such that  $\unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$. Let
$\unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$. Let  $P:=P_{\unicode[STIX]{x1D6FC}}$ and
$P:=P_{\unicode[STIX]{x1D6FC}}$ and  $M:=M_{\unicode[STIX]{x1D6FC}}$ as in 5.1.2. Note that
$M:=M_{\unicode[STIX]{x1D6FC}}$ as in 5.1.2. Note that  $\unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}=\{\unicode[STIX]{x1D6FC}\}$.
$\unicode[STIX]{x1D6E4}_{G}-\unicode[STIX]{x1D6E4}_{M}=\{\unicode[STIX]{x1D6FC}\}$.
Lemma 5.3.3. Let  $S_{1}=\{\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}|\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}\}$ and
$S_{1}=\{\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}|\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}\}$ and  $S_{2}=\{\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}|\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D707}\}$. Then
$S_{2}=\{\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}|\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D707}\}$. Then
 $$\begin{eqnarray}S_{2}-S_{1}=S_{M}(\unicode[STIX]{x1D707})\cap \biggl(\frac{1}{r}\widehat{R}_{G^{\text{ad}}}^{+}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}S_{2}-S_{1}=S_{M}(\unicode[STIX]{x1D707})\cap \biggl(\frac{1}{r}\widehat{R}_{G^{\text{ad}}}^{+}\biggr),\end{eqnarray}$$ where  $S_{M}(\unicode[STIX]{x1D707})$ is defined in Definition 4.1.1.
$S_{M}(\unicode[STIX]{x1D707})$ is defined in Definition 4.1.1.
Proof. For any  $\unicode[STIX]{x1D706}\in S_{2}$, we have
$\unicode[STIX]{x1D706}\in S_{2}$, we have  $\unicode[STIX]{x1D707}-\unicode[STIX]{x1D706}=\sum _{\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}}(c_{\unicode[STIX]{x1D6FE}}/r)\check{\unicode[STIX]{x1D6FE}}$ for some
$\unicode[STIX]{x1D707}-\unicode[STIX]{x1D706}=\sum _{\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}}(c_{\unicode[STIX]{x1D6FE}}/r)\check{\unicode[STIX]{x1D6FE}}$ for some  $c_{\unicode[STIX]{x1D6FE}}\in \mathbb{Z}_{{\geqslant}0}$. Thus
$c_{\unicode[STIX]{x1D6FE}}\in \mathbb{Z}_{{\geqslant}0}$. Thus
 $$\begin{eqnarray}\biggl(\unicode[STIX]{x1D707}-\frac{1}{r}\check{\unicode[STIX]{x1D6FC}}\biggr)-\unicode[STIX]{x1D706}=\biggl(\frac{c_{\unicode[STIX]{x1D6FC}}}{r}-\frac{1}{r}\biggr)\check{\unicode[STIX]{x1D6FC}}+\mathop{\sum }_{\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G},\,\check{\unicode[STIX]{x1D6FE}}\neq \check{\unicode[STIX]{x1D6FC}}}\frac{c_{\unicode[STIX]{x1D6FE}}}{r}\check{\unicode[STIX]{x1D6FE}},\quad c_{\unicode[STIX]{x1D6FE}}\in \mathbb{Z}_{{\geqslant}0}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\unicode[STIX]{x1D707}-\frac{1}{r}\check{\unicode[STIX]{x1D6FC}}\biggr)-\unicode[STIX]{x1D706}=\biggl(\frac{c_{\unicode[STIX]{x1D6FC}}}{r}-\frac{1}{r}\biggr)\check{\unicode[STIX]{x1D6FC}}+\mathop{\sum }_{\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G},\,\check{\unicode[STIX]{x1D6FE}}\neq \check{\unicode[STIX]{x1D6FC}}}\frac{c_{\unicode[STIX]{x1D6FE}}}{r}\check{\unicode[STIX]{x1D6FE}},\quad c_{\unicode[STIX]{x1D6FE}}\in \mathbb{Z}_{{\geqslant}0}.\end{eqnarray}$$ If moreover  $\unicode[STIX]{x1D706}\notin S_{1}$, then in (5.2), there should be at least one coefficient strictly negative. So we must have
$\unicode[STIX]{x1D706}\notin S_{1}$, then in (5.2), there should be at least one coefficient strictly negative. So we must have  $c_{\unicode[STIX]{x1D6FC}}-1<0$. Since
$c_{\unicode[STIX]{x1D6FC}}-1<0$. Since  $c_{\unicode[STIX]{x1D6FC}}\in \mathbb{Z}_{{\geqslant}0}$, we must have
$c_{\unicode[STIX]{x1D6FC}}\in \mathbb{Z}_{{\geqslant}0}$, we must have  $c_{\unicode[STIX]{x1D6FC}}=0$. We deduce that
$c_{\unicode[STIX]{x1D6FC}}=0$. We deduce that
 $$\begin{eqnarray}\unicode[STIX]{x1D707}-\unicode[STIX]{x1D706}=\mathop{\sum }_{\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G},\,\check{\unicode[STIX]{x1D6FE}}\neq \check{\unicode[STIX]{x1D6FC}}}\frac{c_{\unicode[STIX]{x1D6FE}}}{r}\check{\unicode[STIX]{x1D6FE}}=\mathop{\sum }_{\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{M}}\frac{c_{\unicode[STIX]{x1D6FE}}}{r}\check{\unicode[STIX]{x1D6FE}},\quad c_{\unicode[STIX]{x1D6FE}}\in \mathbb{Z}_{{\geqslant}0}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}-\unicode[STIX]{x1D706}=\mathop{\sum }_{\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G},\,\check{\unicode[STIX]{x1D6FE}}\neq \check{\unicode[STIX]{x1D6FC}}}\frac{c_{\unicode[STIX]{x1D6FE}}}{r}\check{\unicode[STIX]{x1D6FE}}=\mathop{\sum }_{\check{\unicode[STIX]{x1D6FE}}\in \widehat{\unicode[STIX]{x1D6E4}}_{M}}\frac{c_{\unicode[STIX]{x1D6FE}}}{r}\check{\unicode[STIX]{x1D6FE}},\quad c_{\unicode[STIX]{x1D6FE}}\in \mathbb{Z}_{{\geqslant}0}.\end{eqnarray}$$ By Definition 4.1.1, we have  $\unicode[STIX]{x1D706}\in S_{M}(\unicode[STIX]{x1D707})$.◻
$\unicode[STIX]{x1D706}\in S_{M}(\unicode[STIX]{x1D707})$.◻
Lemma 5.3.4. Let  $\unicode[STIX]{x1D707}$ and
$\unicode[STIX]{x1D707}$ and  $M$ as in 5.3.2. Suppose that Proposition 5.1.5(c) is true for
$M$ as in 5.3.2. Suppose that Proposition 5.1.5(c) is true for  $M$. Then for any
$M$. Then for any  $j\in \mathbb{Z}$, the morphism
$j\in \mathbb{Z}$, the morphism  $H_{M}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707}}\rightarrow H_{M}^{\prime \,j}$ is injective.
$H_{M}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707}}\rightarrow H_{M}^{\prime \,j}$ is injective.
The point of the proof of this lemma is to replace the quotient by  $\unicode[STIX]{x1D6EF}_{M}$ in (5.3) by the quotient by
$\unicode[STIX]{x1D6EF}_{M}$ in (5.3) by the quotient by  $\unicode[STIX]{x1D6EF}_{G}$ in (5.5).
$\unicode[STIX]{x1D6EF}_{G}$ in (5.5).
Proof. By Proposition 5.1.5(c) for  $M$, for any
$M$, for any  $\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{M^{\text{ad}}}^{+}$ satisfying
$\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{M^{\text{ad}}}^{+}$ satisfying  $\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D6FE}\rangle >C_{M}$ for all
$\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D6FE}\rangle >C_{M}$ for all  $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{M}$, the morphism
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{M}$, the morphism
 $$\begin{eqnarray}H_{c}^{j}(\operatorname{Cht}_{M,\overline{\unicode[STIX]{x1D702}^{I}}}^{{\leqslant}\text{}^{M^{\text{ad}}}\unicode[STIX]{x1D706}}/\unicode[STIX]{x1D6EF}_{M},{\mathcal{F}}_{M})\rightarrow H_{c}^{j}(\operatorname{Cht}_{M,\overline{\unicode[STIX]{x1D702}^{I}}}/\unicode[STIX]{x1D6EF}_{M},{\mathcal{F}}_{M})\end{eqnarray}$$
$$\begin{eqnarray}H_{c}^{j}(\operatorname{Cht}_{M,\overline{\unicode[STIX]{x1D702}^{I}}}^{{\leqslant}\text{}^{M^{\text{ad}}}\unicode[STIX]{x1D706}}/\unicode[STIX]{x1D6EF}_{M},{\mathcal{F}}_{M})\rightarrow H_{c}^{j}(\operatorname{Cht}_{M,\overline{\unicode[STIX]{x1D702}^{I}}}/\unicode[STIX]{x1D6EF}_{M},{\mathcal{F}}_{M})\end{eqnarray}$$ is injective, where everything is defined as in §2.5 by replacing  $G$ by
$G$ by  $M$.
$M$.
We can assume that  $\unicode[STIX]{x1D6EF}_{M}$ in 5.1.7 is small enough (containing
$\unicode[STIX]{x1D6EF}_{M}$ in 5.1.7 is small enough (containing  $\unicode[STIX]{x1D6EF}_{G}$). Then for any
$\unicode[STIX]{x1D6EF}_{G}$). Then for any  $\unicode[STIX]{x1D708}\in A_{M}$ (defined in 1.5.7), the composition of morphisms
$\unicode[STIX]{x1D708}\in A_{M}$ (defined in 1.5.7), the composition of morphisms
 $$\begin{eqnarray}\operatorname{Cht}_{M}^{\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}_{G}\rightarrow \operatorname{Cht}_{M}/\unicode[STIX]{x1D6EF}_{G}\rightarrow \operatorname{Cht}_{M}/\unicode[STIX]{x1D6EF}_{M}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{M}^{\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}_{G}\rightarrow \operatorname{Cht}_{M}/\unicode[STIX]{x1D6EF}_{G}\rightarrow \operatorname{Cht}_{M}/\unicode[STIX]{x1D6EF}_{M}\end{eqnarray}$$is an open and closed immersion.
(For the following discussion, see [Reference XueXue17, Illustration 7.4.4] for an example for  $G=\text{GL}_{3}$.) Let
$G=\text{GL}_{3}$.) Let  $\unicode[STIX]{x1D708}\leqslant \operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})$. We use a special case of 1.5.17. By 1.5.13, we have
$\unicode[STIX]{x1D708}\leqslant \operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})$. We use a special case of 1.5.17. By 1.5.13, we have  $\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FC}})>0$. Let
$\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FC}})>0$. Let  $c_{\unicode[STIX]{x1D6FC}}\in \mathbb{Q}_{{\geqslant}0}$ such that
$c_{\unicode[STIX]{x1D6FC}}\in \mathbb{Q}_{{\geqslant}0}$ such that  $\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})-c_{\unicode[STIX]{x1D6FC}}\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FC}})=\unicode[STIX]{x1D708}$. Let
$\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})-c_{\unicode[STIX]{x1D6FC}}\operatorname{pr}_{P}^{\text{ad}}\circ \unicode[STIX]{x1D6F6}_{G}(\check{\unicode[STIX]{x1D6FC}})=\unicode[STIX]{x1D708}$. Let  $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}}:=\unicode[STIX]{x1D707}-c_{\unicode[STIX]{x1D6FC}}\check{\unicode[STIX]{x1D6FC}}$. For any
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}}:=\unicode[STIX]{x1D707}-c_{\unicode[STIX]{x1D6FC}}\check{\unicode[STIX]{x1D6FC}}$. For any  $\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}$, the condition
$\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}$, the condition  $\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D707}$ and
$\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D707}$ and  $\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D708}$ is equivalent to
$\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D708}$ is equivalent to  $\unicode[STIX]{x1D706}\leqslant \text{}^{\overline{M}}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}}$. We deduce that
$\unicode[STIX]{x1D706}\leqslant \text{}^{\overline{M}}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}}$. We deduce that  $\operatorname{Cht}_{M}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}=\operatorname{Cht}_{M}^{{\leqslant}\text{}^{\overline{M}}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}}}$.
$\operatorname{Cht}_{M}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}=\operatorname{Cht}_{M}^{{\leqslant}\text{}^{\overline{M}}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}}}$.
Let  $\unicode[STIX]{x1D6F9}:\overline{M}{\twoheadrightarrow}M^{\text{ad}}$. If
$\unicode[STIX]{x1D6F9}:\overline{M}{\twoheadrightarrow}M^{\text{ad}}$. If  $\unicode[STIX]{x1D707}_{1}\leqslant \unicode[STIX]{x1D707}_{2}$, then
$\unicode[STIX]{x1D707}_{1}\leqslant \unicode[STIX]{x1D707}_{2}$, then  $\unicode[STIX]{x1D707}_{1,\unicode[STIX]{x1D708}}\leqslant \text{}^{\overline{M}}\unicode[STIX]{x1D707}_{2,\unicode[STIX]{x1D708}}$ and
$\unicode[STIX]{x1D707}_{1,\unicode[STIX]{x1D708}}\leqslant \text{}^{\overline{M}}\unicode[STIX]{x1D707}_{2,\unicode[STIX]{x1D708}}$ and  $\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{1,\unicode[STIX]{x1D708}})\leqslant \text{}^{M^{\text{ad}}}\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{2,\unicode[STIX]{x1D708}})$. For all
$\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{1,\unicode[STIX]{x1D708}})\leqslant \text{}^{M^{\text{ad}}}\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{2,\unicode[STIX]{x1D708}})$. For all  $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{M}$, since
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{M}$, since  $\langle \check{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FE}\rangle \leqslant 0$, we have
$\langle \check{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FE}\rangle \leqslant 0$, we have  $\langle \unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D6FE}\rangle \geqslant \langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FE}\rangle$. By hypothesis
$\langle \unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D6FE}\rangle \geqslant \langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FE}\rangle$. By hypothesis  $\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FE}\rangle \geqslant C_{G}^{0}\geqslant C_{M}$, so
$\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FE}\rangle \geqslant C_{G}^{0}\geqslant C_{M}$, so  $\langle \unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D6FE}\rangle \geqslant C_{M}$. Then the injectivity of (5.3) with
$\langle \unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D6FE}\rangle \geqslant C_{M}$. Then the injectivity of (5.3) with  $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}})$ implies that the morphism
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D708}})$ implies that the morphism
 $$\begin{eqnarray}H_{c}^{j}(\operatorname{Cht}_{M,\overline{\unicode[STIX]{x1D702}^{I}}}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}_{G},{\mathcal{F}}_{M})\rightarrow H_{c}^{j}(\operatorname{Cht}_{M,\overline{\unicode[STIX]{x1D702}^{I}}}^{\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}_{G},{\mathcal{F}}_{M})\end{eqnarray}$$
$$\begin{eqnarray}H_{c}^{j}(\operatorname{Cht}_{M,\overline{\unicode[STIX]{x1D702}^{I}}}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}_{G},{\mathcal{F}}_{M})\rightarrow H_{c}^{j}(\operatorname{Cht}_{M,\overline{\unicode[STIX]{x1D702}^{I}}}^{\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}_{G},{\mathcal{F}}_{M})\end{eqnarray}$$ is injective. Note that we have defined  $H_{M}^{j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}=H_{c}^{j}(\operatorname{Cht}_{M,\overline{\unicode[STIX]{x1D702}^{I}}}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}_{G},{\mathcal{F}}_{M})$ in Definition 2.6.6 and
$H_{M}^{j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}=H_{c}^{j}(\operatorname{Cht}_{M,\overline{\unicode[STIX]{x1D702}^{I}}}^{{\leqslant}\unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}_{G},{\mathcal{F}}_{M})$ in Definition 2.6.6 and  $H_{M}^{j,\,\unicode[STIX]{x1D708}}=H_{c}^{j}(\operatorname{Cht}_{M,\overline{\unicode[STIX]{x1D702}^{I}}}^{\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}_{G},{\mathcal{F}}_{M})$ in Definition 2.6.9.
$H_{M}^{j,\,\unicode[STIX]{x1D708}}=H_{c}^{j}(\operatorname{Cht}_{M,\overline{\unicode[STIX]{x1D702}^{I}}}^{\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}_{G},{\mathcal{F}}_{M})$ in Definition 2.6.9.
Moreover, since  $\operatorname{Cht}_{M}^{\prime }=\operatorname{Cht}_{M}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N})$ is a disjoint union of copies of
$\operatorname{Cht}_{M}^{\prime }=\operatorname{Cht}_{M}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N})$ is a disjoint union of copies of  $\operatorname{Cht}_{M}$, we deduce that the morphism
$\operatorname{Cht}_{M}$, we deduce that the morphism  $H_{M}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}\rightarrow H_{M}^{\prime \,j,\,\unicode[STIX]{x1D708}}$ is also injective, where
$H_{M}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}\rightarrow H_{M}^{\prime \,j,\,\unicode[STIX]{x1D708}}$ is also injective, where  $H_{M}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$ is defined in Definition 3.4.7 and
$H_{M}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}$ is defined in Definition 3.4.7 and  $H_{M}^{\prime \,j,\,\unicode[STIX]{x1D708}}$ is defined in Definition 3.4.10.
$H_{M}^{\prime \,j,\,\unicode[STIX]{x1D708}}$ is defined in Definition 3.4.10.
Note that by Lemma 1.5.14, for  $\unicode[STIX]{x1D708}\notin A_{M}$ or
$\unicode[STIX]{x1D708}\notin A_{M}$ or  $\unicode[STIX]{x1D708}\nleq \operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})$, the cohomology group
$\unicode[STIX]{x1D708}\nleq \operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})$, the cohomology group  $H_{M}^{\prime \;j,\;\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}=0$. By Remark 3.5.11, we have a commutative diagram,
$H_{M}^{\prime \;j,\;\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}=0$. By Remark 3.5.11, we have a commutative diagram,

where  $f$ is (3.41) and
$f$ is (3.41) and  $h$ is induced component by component by
$h$ is induced component by component by  $H_{M}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}\rightarrow H_{M}^{\prime \,j,\,\unicode[STIX]{x1D708}}$. By the above discussion,
$H_{M}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}\rightarrow H_{M}^{\prime \,j,\,\unicode[STIX]{x1D708}}$. By the above discussion,  $h$ is injective. We deduce that the morphism
$h$ is injective. We deduce that the morphism  $g$ is injective.◻
$g$ is injective.◻
Proof of Lemma 5.3.1.
The proof consists of four steps.
(1) Let  $S_{1}$ and
$S_{1}$ and  $S_{2}$ as in Lemma 5.3.3. We define
$S_{2}$ as in Lemma 5.3.3. We define  $\operatorname{Cht}_{G}^{S_{2}}$ and
$\operatorname{Cht}_{G}^{S_{2}}$ and  $\operatorname{Cht}_{G}^{S_{1}}$ as in A.0.2 (taking into account A.0.1). We deduce from Lemma 5.3.3 that
$\operatorname{Cht}_{G}^{S_{1}}$ as in A.0.2 (taking into account A.0.1). We deduce from Lemma 5.3.3 that  $\operatorname{Cht}_{G}^{S_{2}}-\operatorname{Cht}_{G}^{S_{1}}=\operatorname{Cht}_{G}^{S_{M}(\unicode[STIX]{x1D707})}$ and
$\operatorname{Cht}_{G}^{S_{2}}-\operatorname{Cht}_{G}^{S_{1}}=\operatorname{Cht}_{G}^{S_{M}(\unicode[STIX]{x1D707})}$ and  $\operatorname{Cht}_{M}^{\prime \,S_{2}}-\operatorname{Cht}_{M}^{\prime \,S_{1}}=\operatorname{Cht}_{M}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$.
$\operatorname{Cht}_{M}^{\prime \,S_{2}}-\operatorname{Cht}_{M}^{\prime \,S_{1}}=\operatorname{Cht}_{M}^{\prime \,S_{M}(\unicode[STIX]{x1D707})}$.
We deduce from 1.4.10 that
 $$\begin{eqnarray}\operatorname{Bun}_{G}^{=\unicode[STIX]{x1D706}}\neq \emptyset \Rightarrow \unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\in \mathop{\bigcup }_{P\subsetneq G}\unicode[STIX]{x1D704}\circ \operatorname{pr}_{P}^{\text{ad}}(\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+})\subset \frac{1}{r}\widehat{R}_{G^{\text{ad}}}^{+},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{G}^{=\unicode[STIX]{x1D706}}\neq \emptyset \Rightarrow \unicode[STIX]{x1D6F6}_{G}(\unicode[STIX]{x1D706})\in \mathop{\bigcup }_{P\subsetneq G}\unicode[STIX]{x1D704}\circ \operatorname{pr}_{P}^{\text{ad}}(\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+})\subset \frac{1}{r}\widehat{R}_{G^{\text{ad}}}^{+},\end{eqnarray}$$ where the last inclusion follows from the choice of  $r$ in 5.1.1. We deduce that
$r$ in 5.1.1. We deduce that  $\operatorname{Cht}_{G}^{=\unicode[STIX]{x1D706}}=\emptyset$ if
$\operatorname{Cht}_{G}^{=\unicode[STIX]{x1D706}}=\emptyset$ if  $\unicode[STIX]{x1D706}\notin (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$. Thus
$\unicode[STIX]{x1D706}\notin (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$. Thus  $\operatorname{Cht}_{G}^{S_{2}}=\operatorname{Cht}_{G}^{{\leqslant}\unicode[STIX]{x1D707}}$,
$\operatorname{Cht}_{G}^{S_{2}}=\operatorname{Cht}_{G}^{{\leqslant}\unicode[STIX]{x1D707}}$,  $\operatorname{Cht}_{G}^{S_{1}}=\operatorname{Cht}_{G}^{{\leqslant}\unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}}$,
$\operatorname{Cht}_{G}^{S_{1}}=\operatorname{Cht}_{G}^{{\leqslant}\unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}}$,  $\operatorname{Cht}_{M}^{\prime \,S_{2}}=\operatorname{Cht}_{M}^{\prime \,\leqslant \unicode[STIX]{x1D707}}$ and
$\operatorname{Cht}_{M}^{\prime \,S_{2}}=\operatorname{Cht}_{M}^{\prime \,\leqslant \unicode[STIX]{x1D707}}$ and  $\operatorname{Cht}_{M}^{\prime \,S_{1}}=\operatorname{Cht}_{M}^{\prime \,\leqslant \unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}}$.
$\operatorname{Cht}_{M}^{\prime \,S_{1}}=\operatorname{Cht}_{M}^{\prime \,\leqslant \unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}}$.
Applying Lemma A.0.8 to  $S_{1}$ and
$S_{1}$ and  $S_{2}$, we obtain a commutative diagram of cohomology groups, where the upper and lower lines are part of the long exact sequences in (A.2).
$S_{2}$, we obtain a commutative diagram of cohomology groups, where the upper and lower lines are part of the long exact sequences in (A.2).

Note that if  $\operatorname{Cht}_{G}^{S_{M}(\unicode[STIX]{x1D707})}=\emptyset$, then the proof is finished.
$\operatorname{Cht}_{G}^{S_{M}(\unicode[STIX]{x1D707})}=\emptyset$, then the proof is finished.
(2) By the hypothesis of Lemma 5.3.1,  $\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle \geqslant C_{G}^{0}\geqslant \widetilde{C}(G,X,N,W)$. By Proposition 4.6.4, for any
$\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FC}\rangle \geqslant C_{G}^{0}\geqslant \widetilde{C}(G,X,N,W)$. By Proposition 4.6.4, for any  $j$, the morphism
$j$, the morphism  $C_{G}^{P,\,j,\,S_{M}(\unicode[STIX]{x1D707})}:H_{G}^{j,\,S_{M}(\unicode[STIX]{x1D707})}\rightarrow H_{M}^{\prime \,j,\,S_{M}(\unicode[STIX]{x1D707})}$ is an isomorphism.
$C_{G}^{P,\,j,\,S_{M}(\unicode[STIX]{x1D707})}:H_{G}^{j,\,S_{M}(\unicode[STIX]{x1D707})}\rightarrow H_{M}^{\prime \,j,\,S_{M}(\unicode[STIX]{x1D707})}$ is an isomorphism.
(3) We deduce from (3.38) a commutative diagram.

By Lemma 5.3.4, the morphism  ${\mathcal{I}}_{M}$ in (
${\mathcal{I}}_{M}$ in (
) is injective.
(4) Let  $a\in \operatorname{Ker}(H_{G}^{j,\leqslant \unicode[STIX]{x1D707}}\rightarrow H_{M}^{\prime \,j})$. By the commutativity of (5.7),
$a\in \operatorname{Ker}(H_{G}^{j,\leqslant \unicode[STIX]{x1D707}}\rightarrow H_{M}^{\prime \,j})$. By the commutativity of (5.7),  ${\mathcal{I}}_{M}\circ C_{G}^{P,\,j,\,\leqslant \unicode[STIX]{x1D707}}(a)=C_{G}^{P,\,j}\circ {\mathcal{I}}_{G}(a)=0$. By step (3),
${\mathcal{I}}_{M}\circ C_{G}^{P,\,j,\,\leqslant \unicode[STIX]{x1D707}}(a)=C_{G}^{P,\,j}\circ {\mathcal{I}}_{G}(a)=0$. By step (3),  ${\mathcal{I}}_{M}$ is injective. So
${\mathcal{I}}_{M}$ is injective. So  $C_{G}^{P,\,j,\,\leqslant \unicode[STIX]{x1D707}}(a)=0$.
$C_{G}^{P,\,j,\,\leqslant \unicode[STIX]{x1D707}}(a)=0$.
By the commutativity of (5.6) and the isomorphism in step (2), we deduce that the image of  $a$ in
$a$ in  $H_{G}^{j,\,S_{M}(\unicode[STIX]{x1D707})}$ is zero. So there exists
$H_{G}^{j,\,S_{M}(\unicode[STIX]{x1D707})}$ is zero. So there exists  $a^{\prime }\in H_{G}^{j,\leqslant \unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}}$ whose image in
$a^{\prime }\in H_{G}^{j,\leqslant \unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}}$ whose image in  $H_{G}^{j,\leqslant \unicode[STIX]{x1D707}}$ is
$H_{G}^{j,\leqslant \unicode[STIX]{x1D707}}$ is  $a$.◻
$a$.◻
Remark 5.3.5. In fact, we have
 $$\begin{eqnarray}H_{M}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707}}=\biggl(\mathop{\prod }_{\unicode[STIX]{x1D708}<\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})}H_{M}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}\biggr)\oplus H_{M}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\,\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})}=H_{M}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}}\oplus H_{M}^{\prime \,j,\,S_{M}(\unicode[STIX]{x1D707})}.\end{eqnarray}$$
$$\begin{eqnarray}H_{M}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707}}=\biggl(\mathop{\prod }_{\unicode[STIX]{x1D708}<\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})}H_{M}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\,\unicode[STIX]{x1D708}}\biggr)\oplus H_{M}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707},\,\operatorname{pr}_{P}^{\text{ad}}(\unicode[STIX]{x1D707})}=H_{M}^{\prime \,j,\,\leqslant \unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}}\oplus H_{M}^{\prime \,j,\,S_{M}(\unicode[STIX]{x1D707})}.\end{eqnarray}$$Thus the bottom line of (5.6) was canonically split.
Lemma 5.3.6. If the property (a) of Proposition 5.1.5 is true for  $G$, then the property (b) of Proposition 5.1.5 is true for
$G$, then the property (b) of Proposition 5.1.5 is true for  $G$.
$G$.
Proof. Let  $\unicode[STIX]{x1D6FB}(C_{G}^{0})$ be the set of
$\unicode[STIX]{x1D6FB}(C_{G}^{0})$ be the set of  $\unicode[STIX]{x1D707}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ such that
$\unicode[STIX]{x1D707}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ such that  $\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FE}\rangle >C_{G}^{0}$ for all
$\langle \unicode[STIX]{x1D707},\unicode[STIX]{x1D6FE}\rangle >C_{G}^{0}$ for all  $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{G}$. Let
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{G}$. Let  $\unicode[STIX]{x1D6FA}(C_{G}^{0})$ be the set of
$\unicode[STIX]{x1D6FA}(C_{G}^{0})$ be the set of  $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6FB}(C_{G}^{0})$ such that
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6FB}(C_{G}^{0})$ such that  $\unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}\notin \unicode[STIX]{x1D6FB}(C_{G}^{0})$ for all
$\unicode[STIX]{x1D707}-(1/r)\check{\unicode[STIX]{x1D6FC}}\notin \unicode[STIX]{x1D6FB}(C_{G}^{0})$ for all  $\check{\unicode[STIX]{x1D6FC}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}$. The set
$\check{\unicode[STIX]{x1D6FC}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}$. The set  $\unicode[STIX]{x1D6FA}(C_{G}^{0})$ is bounded, and thus is finite. Let
$\unicode[STIX]{x1D6FA}(C_{G}^{0})$ is bounded, and thus is finite. Let  $\unicode[STIX]{x1D707}_{0}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ such that
$\unicode[STIX]{x1D707}_{0}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ such that  $\unicode[STIX]{x1D707}_{0}>\unicode[STIX]{x1D707}$ for all
$\unicode[STIX]{x1D707}_{0}>\unicode[STIX]{x1D707}$ for all  $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6FA}(C_{G}^{0})$.
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6FA}(C_{G}^{0})$.
For any  $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6FB}(C_{G}^{0})$, there exists a (zigzag) chain
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6FB}(C_{G}^{0})$, there exists a (zigzag) chain  $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}^{(0)}>\unicode[STIX]{x1D706}^{(1)}>\cdots >\unicode[STIX]{x1D706}^{(m-1)}>\unicode[STIX]{x1D706}^{(m)}$ in
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}^{(0)}>\unicode[STIX]{x1D706}^{(1)}>\cdots >\unicode[STIX]{x1D706}^{(m-1)}>\unicode[STIX]{x1D706}^{(m)}$ in  $(1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ for some
$(1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ for some  $m\in \mathbb{Z}_{{\geqslant}0}$ such that:
$m\in \mathbb{Z}_{{\geqslant}0}$ such that:
(i) for any
 $j$, we have
$j$, we have  $\unicode[STIX]{x1D706}^{(j)}\in \unicode[STIX]{x1D6FB}(C_{G}^{0})$;
$\unicode[STIX]{x1D706}^{(j)}\in \unicode[STIX]{x1D6FB}(C_{G}^{0})$;(ii) for any
 $j$, we have
$j$, we have  $\unicode[STIX]{x1D706}^{(j)}-\unicode[STIX]{x1D706}^{(j+1)}=(1/r)\check{\unicode[STIX]{x1D6FC}}$ for some simple coroot
$\unicode[STIX]{x1D706}^{(j)}-\unicode[STIX]{x1D706}^{(j+1)}=(1/r)\check{\unicode[STIX]{x1D6FC}}$ for some simple coroot  $\check{\unicode[STIX]{x1D6FC}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}$;
$\check{\unicode[STIX]{x1D6FC}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}$;(iii)
 $\unicode[STIX]{x1D706}^{(m)}\in \unicode[STIX]{x1D6FA}(C_{G}^{0})$.
$\unicode[STIX]{x1D706}^{(m)}\in \unicode[STIX]{x1D6FA}(C_{G}^{0})$.
(Indeed,  $\unicode[STIX]{x1D706}^{(0)}$ satisfies (i). Suppose that we have already constructed a chain until
$\unicode[STIX]{x1D706}^{(0)}$ satisfies (i). Suppose that we have already constructed a chain until  $\unicode[STIX]{x1D706}^{(j)}$ which satisfies (i) and (ii). If
$\unicode[STIX]{x1D706}^{(j)}$ which satisfies (i) and (ii). If  $\unicode[STIX]{x1D706}^{(j)}$ satisfies (iii), we are done. If not, then there exists some
$\unicode[STIX]{x1D706}^{(j)}$ satisfies (iii), we are done. If not, then there exists some  $\check{\unicode[STIX]{x1D6FC}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}$ such that
$\check{\unicode[STIX]{x1D6FC}}\in \widehat{\unicode[STIX]{x1D6E4}}_{G}$ such that  $\unicode[STIX]{x1D706}^{(j)}-(1/r)\check{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D6FB}(C_{G}^{0})$. We define
$\unicode[STIX]{x1D706}^{(j)}-(1/r)\check{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D6FB}(C_{G}^{0})$. We define  $\unicode[STIX]{x1D706}^{(j+1)}:=\unicode[STIX]{x1D706}^{(j)}-(1/r)\check{\unicode[STIX]{x1D6FC}}$ and continue the process.)
$\unicode[STIX]{x1D706}^{(j+1)}:=\unicode[STIX]{x1D706}^{(j)}-(1/r)\check{\unicode[STIX]{x1D6FC}}$ and continue the process.)
Applying successively the property (a) of Proposition 5.1.5 to  $\unicode[STIX]{x1D706}^{(0)}$,
$\unicode[STIX]{x1D706}^{(0)}$,  $\unicode[STIX]{x1D706}^{(1)},\ldots$ , until
$\unicode[STIX]{x1D706}^{(1)},\ldots$ , until  $\unicode[STIX]{x1D706}^{(m)}$, we deduce that the morphism
$\unicode[STIX]{x1D706}^{(m)}$, we deduce that the morphism
 $$\begin{eqnarray}\operatorname{Ker}\biggl(H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}^{(m)}}\rightarrow \mathop{\prod }_{P\subsetneq G}H_{M}^{\prime \,j}\biggr)\rightarrow \operatorname{Ker}\biggl(H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}}\rightarrow \mathop{\prod }_{P\subsetneq G}H_{M}^{\prime \,j}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ker}\biggl(H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}^{(m)}}\rightarrow \mathop{\prod }_{P\subsetneq G}H_{M}^{\prime \,j}\biggr)\rightarrow \operatorname{Ker}\biggl(H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}}\rightarrow \mathop{\prod }_{P\subsetneq G}H_{M}^{\prime \,j}\biggr)\end{eqnarray}$$ is surjective. Assume in addition that  $\unicode[STIX]{x1D706}\geqslant \unicode[STIX]{x1D707}_{0}$; then the morphism
$\unicode[STIX]{x1D706}\geqslant \unicode[STIX]{x1D707}_{0}$; then the morphism  $H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}^{(m)}}\rightarrow H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}}$ factors through
$H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}^{(m)}}\rightarrow H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}}$ factors through  $H_{G}^{j,\,\leqslant \unicode[STIX]{x1D707}_{0}}$. We deduce the lemma.◻
$H_{G}^{j,\,\leqslant \unicode[STIX]{x1D707}_{0}}$. We deduce the lemma.◻
5.4 Injectivity
Lemma 5.4.1. If the property (b) of Proposition 5.1.5 is true for  $G$, then the property (c) of Proposition 5.1.5 is true for
$G$, then the property (c) of Proposition 5.1.5 is true for  $G$.
$G$.
We need some preparations before the proof of Lemma 5.4.1.
5.4.2
For  $\unicode[STIX]{x1D707}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$, let
$\unicode[STIX]{x1D707}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$, let  ${\mathcal{I}}_{\unicode[STIX]{x1D707}}:H_{G}^{j,\,\leqslant \unicode[STIX]{x1D707}}\rightarrow H_{G}^{j}$ be the morphism to the inductive limit as in 5.1.3. For
${\mathcal{I}}_{\unicode[STIX]{x1D707}}:H_{G}^{j,\,\leqslant \unicode[STIX]{x1D707}}\rightarrow H_{G}^{j}$ be the morphism to the inductive limit as in 5.1.3. For  $\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ such that
$\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ such that  $\unicode[STIX]{x1D706}\geqslant \unicode[STIX]{x1D707}$, we denote by
$\unicode[STIX]{x1D706}\geqslant \unicode[STIX]{x1D707}$, we denote by  ${\mathcal{I}}_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}:H_{G}^{j,\leqslant \unicode[STIX]{x1D707}}\rightarrow H_{G}^{j,\leqslant \unicode[STIX]{x1D706}}$ the morphism defined in 2.5.2. We have
${\mathcal{I}}_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}:H_{G}^{j,\leqslant \unicode[STIX]{x1D707}}\rightarrow H_{G}^{j,\leqslant \unicode[STIX]{x1D706}}$ the morphism defined in 2.5.2. We have  $\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}})\subset \operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}})\subset H_{G}^{j,\leqslant \unicode[STIX]{x1D707}}$.
$\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}})\subset \operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}})\subset H_{G}^{j,\leqslant \unicode[STIX]{x1D707}}$.
For  $\unicode[STIX]{x1D706}_{2}\geqslant \unicode[STIX]{x1D706}_{1}\geqslant \unicode[STIX]{x1D707}$, we have
$\unicode[STIX]{x1D706}_{2}\geqslant \unicode[STIX]{x1D706}_{1}\geqslant \unicode[STIX]{x1D707}$, we have  $\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}_{1}})\subset \operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}_{2}})$.
$\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}_{1}})\subset \operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}_{2}})$.
Lemma 5.4.3. Let  $\unicode[STIX]{x1D707}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$. There exists
$\unicode[STIX]{x1D707}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$. There exists  $\unicode[STIX]{x1D707}^{\sharp }\in \widehat{R}_{G^{\text{ad}}}^{+}$ such that
$\unicode[STIX]{x1D707}^{\sharp }\in \widehat{R}_{G^{\text{ad}}}^{+}$ such that  $\unicode[STIX]{x1D707}^{\sharp }\geqslant \unicode[STIX]{x1D707}$ and
$\unicode[STIX]{x1D707}^{\sharp }\geqslant \unicode[STIX]{x1D707}$ and  $\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D707}^{\sharp }})=\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}})$.
$\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D707}^{\sharp }})=\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}})$.
Proof. We have the filtered system  $\{\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}})\;|\;\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+},\unicode[STIX]{x1D706}\geqslant \unicode[STIX]{x1D707}\}$ in
$\{\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}})\;|\;\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+},\unicode[STIX]{x1D706}\geqslant \unicode[STIX]{x1D707}\}$ in  $\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}})$ and
$\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}})$ and  $\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}})=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D706}}\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}})$. Since
$\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}})=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D706}}\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}})$. Since  $\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}})$ is of finite dimension, the result is clear.◻
$\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}})$ is of finite dimension, the result is clear.◻
Construction 5.4.4. Let  $\unicode[STIX]{x1D707}_{0}$ be the one in the property (b) of Proposition 5.1.5. Choose
$\unicode[STIX]{x1D707}_{0}$ be the one in the property (b) of Proposition 5.1.5. Choose  $\unicode[STIX]{x1D707}_{0}^{\sharp }\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ which satisfies Lemma 5.4.3 for
$\unicode[STIX]{x1D707}_{0}^{\sharp }\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ which satisfies Lemma 5.4.3 for  $\unicode[STIX]{x1D707}_{0}$. Let
$\unicode[STIX]{x1D707}_{0}$. Let  $C_{G}=\operatorname{max}\{C_{G}^{0},\operatorname{max}_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{G}}\{\langle \unicode[STIX]{x1D707}_{0}^{\sharp },\unicode[STIX]{x1D6FE}\rangle \}\}$.
$C_{G}=\operatorname{max}\{C_{G}^{0},\operatorname{max}_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{G}}\{\langle \unicode[STIX]{x1D707}_{0}^{\sharp },\unicode[STIX]{x1D6FE}\rangle \}\}$.
Proof of Lemma 5.4.1.
Let  $\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ such that
$\unicode[STIX]{x1D706}\in (1/r)\widehat{R}_{G^{\text{ad}}}^{+}$ such that  $\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D6FE}\rangle \geqslant C_{G}$ for all
$\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D6FE}\rangle \geqslant C_{G}$ for all  $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{G}$. By Construction 5.4.4,
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{G}$. By Construction 5.4.4,  $\langle \unicode[STIX]{x1D706}-\unicode[STIX]{x1D707}_{0}^{\sharp },\unicode[STIX]{x1D6FE}\rangle =\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D6FE}\rangle -\langle \unicode[STIX]{x1D707}_{0}^{\sharp },\unicode[STIX]{x1D6FE}\rangle \geqslant C_{G}-\langle \unicode[STIX]{x1D707}_{0}^{\sharp },\unicode[STIX]{x1D6FE}\rangle \geqslant 0$ for all
$\langle \unicode[STIX]{x1D706}-\unicode[STIX]{x1D707}_{0}^{\sharp },\unicode[STIX]{x1D6FE}\rangle =\langle \unicode[STIX]{x1D706},\unicode[STIX]{x1D6FE}\rangle -\langle \unicode[STIX]{x1D707}_{0}^{\sharp },\unicode[STIX]{x1D6FE}\rangle \geqslant C_{G}-\langle \unicode[STIX]{x1D707}_{0}^{\sharp },\unicode[STIX]{x1D6FE}\rangle \geqslant 0$ for all  $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{G}$. Thus
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{G}$. Thus  $\unicode[STIX]{x1D707}_{0}^{\sharp }\leqslant \unicode[STIX]{x1D706}$. Consider the morphisms
$\unicode[STIX]{x1D707}_{0}^{\sharp }\leqslant \unicode[STIX]{x1D706}$. Consider the morphisms
 $$\begin{eqnarray}H_{G}^{j,\,\leqslant \unicode[STIX]{x1D707}_{0}}\rightarrow H_{G}^{j,\,\leqslant \unicode[STIX]{x1D707}_{0}^{\sharp }}\rightarrow H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}}\rightarrow H_{G}^{j}.\end{eqnarray}$$
$$\begin{eqnarray}H_{G}^{j,\,\leqslant \unicode[STIX]{x1D707}_{0}}\rightarrow H_{G}^{j,\,\leqslant \unicode[STIX]{x1D707}_{0}^{\sharp }}\rightarrow H_{G}^{j,\,\leqslant \unicode[STIX]{x1D706}}\rightarrow H_{G}^{j}.\end{eqnarray}$$ We have  $\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}}^{\unicode[STIX]{x1D707}_{0}^{\sharp }})\subset \operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}}^{\unicode[STIX]{x1D706}})\subset \operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}})$. By Lemma 5.4.3,
$\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}}^{\unicode[STIX]{x1D707}_{0}^{\sharp }})\subset \operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}}^{\unicode[STIX]{x1D706}})\subset \operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}})$. By Lemma 5.4.3,  $\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}}^{\unicode[STIX]{x1D707}_{0}^{\sharp }})=\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}})$, and hence
$\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}}^{\unicode[STIX]{x1D707}_{0}^{\sharp }})=\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}})$, and hence  $\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}}^{\unicode[STIX]{x1D706}})=\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}})$.
$\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}}^{\unicode[STIX]{x1D706}})=\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}})$.
For any element  $b\in \operatorname{Ker}(H_{G}^{j,\leqslant \unicode[STIX]{x1D706}}\rightarrow H_{G}^{j})$, we have
$b\in \operatorname{Ker}(H_{G}^{j,\leqslant \unicode[STIX]{x1D706}}\rightarrow H_{G}^{j})$, we have  $b\in \operatorname{Ker}(H_{G}^{j,\leqslant \unicode[STIX]{x1D706}}\rightarrow \prod H_{M}^{\prime \,j})$. By the property (b) of Proposition 5.1.5,
$b\in \operatorname{Ker}(H_{G}^{j,\leqslant \unicode[STIX]{x1D706}}\rightarrow \prod H_{M}^{\prime \,j})$. By the property (b) of Proposition 5.1.5,  $b$ is the image of an element
$b$ is the image of an element  $b_{0}\in \operatorname{Ker}(H_{G}^{j,\leqslant \unicode[STIX]{x1D707}_{0}}\rightarrow \prod H_{M}^{\prime \,j})$. We have
$b_{0}\in \operatorname{Ker}(H_{G}^{j,\leqslant \unicode[STIX]{x1D707}_{0}}\rightarrow \prod H_{M}^{\prime \,j})$. We have  $b_{0}\in \operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}})=\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}}^{\unicode[STIX]{x1D706}})$, so its image
$b_{0}\in \operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}})=\operatorname{Ker}({\mathcal{I}}_{\unicode[STIX]{x1D707}_{0}}^{\unicode[STIX]{x1D706}})$, so its image  $b$ in
$b$ in  $H_{G}^{j,\leqslant \unicode[STIX]{x1D706}}$ is zero. This implies that the morphism
$H_{G}^{j,\leqslant \unicode[STIX]{x1D706}}$ is zero. This implies that the morphism  $H_{G}^{j,\leqslant \unicode[STIX]{x1D706}}\rightarrow H_{G}^{j}$ is injective.◻
$H_{G}^{j,\leqslant \unicode[STIX]{x1D706}}\rightarrow H_{G}^{j}$ is injective.◻
6 Rational Hecke-finite cohomology
In this section, we will define a subspace  $H_{G,N,I,W}^{j,\;\operatorname{Hf-rat}}$ of
$H_{G,N,I,W}^{j,\;\operatorname{Hf-rat}}$ of  $H_{G,N,I,W}^{j}$ and prove the following.
$H_{G,N,I,W}^{j}$ and prove the following.
Proposition 6.0.1. The two  $\mathbb{Q}_{\ell }$-vector subspaces
$\mathbb{Q}_{\ell }$-vector subspaces  $H_{G,N,I,W}^{j,\;\operatorname{cusp}}$ and
$H_{G,N,I,W}^{j,\;\operatorname{cusp}}$ and  $H_{G,N,I,W}^{j,\;\operatorname{Hf-rat}}$ of
$H_{G,N,I,W}^{j,\;\operatorname{Hf-rat}}$ of  $H_{G,N,I,W}^{j}$ are equal.
$H_{G,N,I,W}^{j}$ are equal.
In §6.1 we give some preparations. In §6.2 we show that the constant term morphisms commute with the action of the Hecke algebra. Using this, in §6.3 we prove Proposition 6.0.1.
In §6, all the stacks are restricted to  $\overline{\unicode[STIX]{x1D702}^{I}}$.
$\overline{\unicode[STIX]{x1D702}^{I}}$.
6.1 Compatibility of constant term morphisms and level change
6.1.1
Let  $K$ be a compact open subgroup of
$K$ be a compact open subgroup of  $G(\mathbb{O})$. Let
$G(\mathbb{O})$. Let  $N$ be a level such that
$N$ be a level such that  $K_{N}\subset K$. We define
$K_{N}\subset K$. We define
 $$\begin{eqnarray}\operatorname{Cht}_{G,K,I,W}:=\operatorname{Cht}_{G,N,I,W}/(K/K_{N}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{G,K,I,W}:=\operatorname{Cht}_{G,N,I,W}/(K/K_{N}).\end{eqnarray}$$ It is independent of the choice of  $N$.
$N$.
Let  $d\in \mathbb{N}$ be large enough as in Proposition 2.2.1; we define
$d\in \mathbb{N}$ be large enough as in Proposition 2.2.1; we define  ${\mathcal{F}}_{G,K,I,W}$ to be the inverse image of
${\mathcal{F}}_{G,K,I,W}$ to be the inverse image of  ${\mathcal{S}}_{G,I,W}^{d}$ by
${\mathcal{S}}_{G,I,W}^{d}$ by  $\unicode[STIX]{x1D716}_{K,d}:\operatorname{Cht}_{G,K,I,W}\rightarrow [G_{I,d}\backslash \operatorname{Gr}_{G,I,W}]$. Just as in Remark 2.4.6,
$\unicode[STIX]{x1D716}_{K,d}:\operatorname{Cht}_{G,K,I,W}\rightarrow [G_{I,d}\backslash \operatorname{Gr}_{G,I,W}]$. Just as in Remark 2.4.6,  ${\mathcal{F}}_{G,K,I,W}$ is independent of
${\mathcal{F}}_{G,K,I,W}$ is independent of  $d$. Similarly we define
$d$. Similarly we define  ${\mathcal{F}}_{G,K,I,W}^{\unicode[STIX]{x1D6EF}}$ over
${\mathcal{F}}_{G,K,I,W}^{\unicode[STIX]{x1D6EF}}$ over  $\operatorname{Cht}_{G,K,I,W}/\unicode[STIX]{x1D6EF}$. We define
$\operatorname{Cht}_{G,K,I,W}/\unicode[STIX]{x1D6EF}$. We define  $H_{G,K,I,W}^{j}:=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}}H_{c}^{j}(\operatorname{Cht}_{G,K,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF},{\mathcal{F}}_{G,K,I,W}^{\unicode[STIX]{x1D6EF}})$.
$H_{G,K,I,W}^{j}:=\mathop{\varinjlim }\nolimits_{\unicode[STIX]{x1D707}}H_{c}^{j}(\operatorname{Cht}_{G,K,I,W}^{{\leqslant}\unicode[STIX]{x1D707}}/\unicode[STIX]{x1D6EF},{\mathcal{F}}_{G,K,I,W}^{\unicode[STIX]{x1D6EF}})$.
6.1.2
Let  $K^{\prime }\subset K$ be two compact open subgroups of
$K^{\prime }\subset K$ be two compact open subgroups of  $G(\mathbb{O})$. The inclusion
$G(\mathbb{O})$. The inclusion  $K^{\prime }/K_{N}{\hookrightarrow}K/K_{N}$ induces a morphism
$K^{\prime }/K_{N}{\hookrightarrow}K/K_{N}$ induces a morphism  $\operatorname{pr}_{K^{\prime },K}^{G}:\operatorname{Cht}_{G,K^{\prime },I,W}\rightarrow \operatorname{Cht}_{G,K,I,W}$. Note that all the stacks are restricted to
$\operatorname{pr}_{K^{\prime },K}^{G}:\operatorname{Cht}_{G,K^{\prime },I,W}\rightarrow \operatorname{Cht}_{G,K,I,W}$. Note that all the stacks are restricted to  $\overline{\unicode[STIX]{x1D702}^{I}}$. Morphism
$\overline{\unicode[STIX]{x1D702}^{I}}$. Morphism  $\operatorname{pr}_{K^{\prime },K}^{G}$ is finite étale of degree the cardinality of
$\operatorname{pr}_{K^{\prime },K}^{G}$ is finite étale of degree the cardinality of  $K/K^{\prime }$. The following diagram is commutative.
$K/K^{\prime }$. The following diagram is commutative.

Note that  $(\operatorname{pr}_{K^{\prime },K}^{G})_{\ast }=(\operatorname{pr}_{K^{\prime },K}^{G})_{!}$ and
$(\operatorname{pr}_{K^{\prime },K}^{G})_{\ast }=(\operatorname{pr}_{K^{\prime },K}^{G})_{!}$ and
 $$\begin{eqnarray}(\operatorname{pr}_{K^{\prime },K}^{G})^{\ast }{\mathcal{F}}_{G,K,I,W}=(\operatorname{pr}_{K^{\prime },K}^{G})^{\ast }(\unicode[STIX]{x1D716}_{K,d})^{\ast }{\mathcal{S}}_{G,I,W}^{d}=(\unicode[STIX]{x1D716}_{K^{\prime },d})^{\ast }{\mathcal{S}}_{G,I,W}^{d}={\mathcal{F}}_{G,K^{\prime },I,W}.\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{pr}_{K^{\prime },K}^{G})^{\ast }{\mathcal{F}}_{G,K,I,W}=(\operatorname{pr}_{K^{\prime },K}^{G})^{\ast }(\unicode[STIX]{x1D716}_{K,d})^{\ast }{\mathcal{S}}_{G,I,W}^{d}=(\unicode[STIX]{x1D716}_{K^{\prime },d})^{\ast }{\mathcal{S}}_{G,I,W}^{d}={\mathcal{F}}_{G,K^{\prime },I,W}.\end{eqnarray}$$ The adjunction morphism  $\operatorname{adj}(\operatorname{pr}_{K^{\prime },K}^{G}):\operatorname{Id}\rightarrow (\operatorname{pr}_{K^{\prime },K}^{G})_{\ast }(\operatorname{pr}_{K^{\prime },K}^{G})^{\ast }$ induces an (injective) morphism of cohomology groups, which we still denote by
$\operatorname{adj}(\operatorname{pr}_{K^{\prime },K}^{G}):\operatorname{Id}\rightarrow (\operatorname{pr}_{K^{\prime },K}^{G})_{\ast }(\operatorname{pr}_{K^{\prime },K}^{G})^{\ast }$ induces an (injective) morphism of cohomology groups, which we still denote by
 $$\begin{eqnarray}\operatorname{adj}(\operatorname{pr}_{K^{\prime },K}^{G}):H_{G,K,I,W}^{j}\rightarrow H_{G,K^{\prime },I,W}^{j}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{adj}(\operatorname{pr}_{K^{\prime },K}^{G}):H_{G,K,I,W}^{j}\rightarrow H_{G,K^{\prime },I,W}^{j}.\end{eqnarray}$$ Note that  $(\operatorname{pr}_{K^{\prime },K}^{G})^{!}=(\operatorname{pr}_{K^{\prime },K}^{G})^{\ast }$. The counit morphism (in this case equal to the trace map)
$(\operatorname{pr}_{K^{\prime },K}^{G})^{!}=(\operatorname{pr}_{K^{\prime },K}^{G})^{\ast }$. The counit morphism (in this case equal to the trace map)  $\operatorname{Co}(\operatorname{pr}_{K^{\prime },K}^{G}):(\operatorname{pr}_{K^{\prime },K}^{G})_{!}(\operatorname{pr}_{K^{\prime },K}^{G})^{!}\rightarrow \operatorname{Id}$ induces a (surjective) morphism of cohomology groups, which we still denote by
$\operatorname{Co}(\operatorname{pr}_{K^{\prime },K}^{G}):(\operatorname{pr}_{K^{\prime },K}^{G})_{!}(\operatorname{pr}_{K^{\prime },K}^{G})^{!}\rightarrow \operatorname{Id}$ induces a (surjective) morphism of cohomology groups, which we still denote by
 $$\begin{eqnarray}\operatorname{Co}(\operatorname{pr}_{K^{\prime },K}^{G}):H_{G,K^{\prime },I,W}^{j}\rightarrow H_{G,K,I,W}^{j}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Co}(\operatorname{pr}_{K^{\prime },K}^{G}):H_{G,K^{\prime },I,W}^{j}\rightarrow H_{G,K,I,W}^{j}.\end{eqnarray}$$6.1.3
Let  $v$ be a place in
$v$ be a place in  $X$. Let
$X$. Let  $N=N^{v}+nv$. Taking projective limit over
$N=N^{v}+nv$. Taking projective limit over  $n$, we define
$n$, we define

Let  $g\in G(F_{v})$. The right action of
$g\in G(F_{v})$. The right action of  $g$ (by left multiplication by
$g$ (by left multiplication by  $g^{-1}$) induces an isomorphism
$g^{-1}$) induces an isomorphism

where  $\unicode[STIX]{x1D713}^{v}$ (respectively
$\unicode[STIX]{x1D713}^{v}$ (respectively  $\unicode[STIX]{x1D713}_{v}$) is the level structure outside
$\unicode[STIX]{x1D713}_{v}$) is the level structure outside  $v$ (respectively on
$v$ (respectively on  $v$). The
$v$). The  $G$-bundle
$G$-bundle  ${\mathcal{G}}^{\prime }$ is defined by gluing
${\mathcal{G}}^{\prime }$ is defined by gluing  $\left.G\vphantom{\big|}\right|_{\unicode[STIX]{x1D6E4}_{\infty v}}$ and
$\left.G\vphantom{\big|}\right|_{\unicode[STIX]{x1D6E4}_{\infty v}}$ and  $\left.{\mathcal{G}}\vphantom{\big|}\right|_{X-v}$ by
$\left.{\mathcal{G}}\vphantom{\big|}\right|_{X-v}$ by  $\left.G\vphantom{\big|}\right|_{\unicode[STIX]{x1D6E4}_{\infty v}-v}\xrightarrow[{}]{g}\left.G\vphantom{\big|}\right|_{\unicode[STIX]{x1D6E4}_{\infty v}-v}\underset{{\sim}}{\xleftarrow[{}]{\unicode[STIX]{x1D713}_{v}}}\left.{\mathcal{G}}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6E4}_{\infty v}-v}$. We have
$\left.G\vphantom{\big|}\right|_{\unicode[STIX]{x1D6E4}_{\infty v}-v}\xrightarrow[{}]{g}\left.G\vphantom{\big|}\right|_{\unicode[STIX]{x1D6E4}_{\infty v}-v}\underset{{\sim}}{\xleftarrow[{}]{\unicode[STIX]{x1D713}_{v}}}\left.{\mathcal{G}}\vphantom{\big|}\right|_{\unicode[STIX]{x1D6E4}_{\infty v}-v}$. We have  $\unicode[STIX]{x1D713}_{v}^{\prime }=g^{-1}\circ \unicode[STIX]{x1D713}_{v}$.
$\unicode[STIX]{x1D713}_{v}^{\prime }=g^{-1}\circ \unicode[STIX]{x1D713}_{v}$.
Let

Similarly,  $\operatorname{Cht}_{G,\infty ,I,W}$ is equipped with an action of
$\operatorname{Cht}_{G,\infty ,I,W}$ is equipped with an action of  $G(\mathbb{A})$.
$G(\mathbb{A})$.
6.1.4
Let  $P$ be a parabolic subgroup of
$P$ be a parabolic subgroup of  $G$ and
$G$ and  $M$ its Levi quotient. We define
$M$ its Levi quotient. We define

Just as in 6.1.3,  $\operatorname{Cht}_{P,\infty ,I,W}$ is equipped with an action of
$\operatorname{Cht}_{P,\infty ,I,W}$ is equipped with an action of  $P(\mathbb{A})$. For any compact open subgroup
$P(\mathbb{A})$. For any compact open subgroup  $K\subset G(\mathbb{O})$, we define
$K\subset G(\mathbb{O})$, we define
 $$\begin{eqnarray}\operatorname{Cht}_{P,K,I,W}^{\prime }:=\operatorname{Cht}_{P,\infty ,I,W}\overset{P(\mathbb{O})}{\times }G(\mathbb{O})/K.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{P,K,I,W}^{\prime }:=\operatorname{Cht}_{P,\infty ,I,W}\overset{P(\mathbb{O})}{\times }G(\mathbb{O})/K.\end{eqnarray}$$We have a morphism
 $$\begin{eqnarray}\operatorname{Cht}_{P,\infty ,I,W}\overset{P(\mathbb{O})}{\times }G(\mathbb{O})\rightarrow \operatorname{Cht}_{G,\infty ,I,W}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{P,\infty ,I,W}\overset{P(\mathbb{O})}{\times }G(\mathbb{O})\rightarrow \operatorname{Cht}_{G,\infty ,I,W}\end{eqnarray}$$ by sending  $(({\mathcal{P}},\unicode[STIX]{x1D713}_{P})\rightarrow (\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{P}},^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}_{P}),g\in G(\mathbb{O}))$ to
$(({\mathcal{P}},\unicode[STIX]{x1D713}_{P})\rightarrow (\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{P}},^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}_{P}),g\in G(\mathbb{O}))$ to  $(({\mathcal{G}},g^{-1}\circ \unicode[STIX]{x1D713}_{G})\rightarrow (\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}},{g^{-1}\circ }^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}_{G}))$, where
$(({\mathcal{G}},g^{-1}\circ \unicode[STIX]{x1D713}_{G})\rightarrow (\text{}^{\unicode[STIX]{x1D70F}}{\mathcal{G}},{g^{-1}\circ }^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D713}_{G}))$, where  ${\mathcal{G}}={\mathcal{P}}\,\overset{P}{\times }\,G$ and
${\mathcal{G}}={\mathcal{P}}\,\overset{P}{\times }\,G$ and  $\unicode[STIX]{x1D713}_{G}=\unicode[STIX]{x1D713}_{P}\overset{P}{\times }G$. It induces a morphism
$\unicode[STIX]{x1D713}_{G}=\unicode[STIX]{x1D713}_{P}\overset{P}{\times }G$. It induces a morphism
 $$\begin{eqnarray}\operatorname{Cht}_{P,\infty ,I,W}\overset{P(\mathbb{O})}{\times }G(\mathbb{O})\rightarrow \operatorname{Cht}_{P,I,W}\underset{\operatorname{Cht}_{G,I,W}}{\times }\operatorname{Cht}_{G,\infty ,I,W}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{P,\infty ,I,W}\overset{P(\mathbb{O})}{\times }G(\mathbb{O})\rightarrow \operatorname{Cht}_{P,I,W}\underset{\operatorname{Cht}_{G,I,W}}{\times }\operatorname{Cht}_{G,\infty ,I,W}\!.\end{eqnarray}$$ This is a  $G(\mathbb{O})$-equivariant morphism of
$G(\mathbb{O})$-equivariant morphism of  $G(\mathbb{O})$-torsors over
$G(\mathbb{O})$-torsors over  $\operatorname{Cht}_{P,I,W}$, where
$\operatorname{Cht}_{P,I,W}$, where  $G(\mathbb{O})$ acts on the left-hand side of (6.3) by right action (right multiplication) on
$G(\mathbb{O})$ acts on the left-hand side of (6.3) by right action (right multiplication) on  $G(\mathbb{O})$ and acts on the right-hand side of (6.3) by the right action on
$G(\mathbb{O})$ and acts on the right-hand side of (6.3) by the right action on  $\operatorname{Cht}_{G,\infty ,I,W}$ defined in 6.1.3. Thus (6.3) is an isomorphism. We have
$\operatorname{Cht}_{G,\infty ,I,W}$ defined in 6.1.3. Thus (6.3) is an isomorphism. We have
 $$\begin{eqnarray}\operatorname{Cht}_{P,\infty ,I,W}\overset{P(\mathbb{O})}{\times }G(\mathbb{O})/K\overset{{\sim}}{\rightarrow }\operatorname{Cht}_{P,I,W}\underset{\operatorname{Cht}_{G,I,W}}{\times }\operatorname{Cht}_{G,\infty ,I,W\!}/K,\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{P,\infty ,I,W}\overset{P(\mathbb{O})}{\times }G(\mathbb{O})/K\overset{{\sim}}{\rightarrow }\operatorname{Cht}_{P,I,W}\underset{\operatorname{Cht}_{G,I,W}}{\times }\operatorname{Cht}_{G,\infty ,I,W\!}/K,\end{eqnarray}$$i.e.
 $$\begin{eqnarray}\operatorname{Cht}_{P,K,I,W}^{\prime }=\operatorname{Cht}_{P,I,W}\underset{\operatorname{Cht}_{G,I,W}}{\times }\operatorname{Cht}_{G,K,I,W}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{P,K,I,W}^{\prime }=\operatorname{Cht}_{P,I,W}\underset{\operatorname{Cht}_{G,I,W}}{\times }\operatorname{Cht}_{G,K,I,W}\!.\end{eqnarray}$$ When  $K=K_{N}$ for some level
$K=K_{N}$ for some level  $N$, we have
$N$, we have  $\operatorname{Cht}_{P,N,I,W}=\operatorname{Cht}_{P,\infty ,I,W}/K_{P,N}$, where
$\operatorname{Cht}_{P,N,I,W}=\operatorname{Cht}_{P,\infty ,I,W}/K_{P,N}$, where  $K_{P,N}:=K_{N}\cap P(\mathbb{O})$. We deduce that
$K_{P,N}:=K_{N}\cap P(\mathbb{O})$. We deduce that  $\operatorname{Cht}_{P,K_{N},I,W}^{\prime }$ defined in (6.1) coincides with
$\operatorname{Cht}_{P,K_{N},I,W}^{\prime }$ defined in (6.1) coincides with  $\operatorname{Cht}_{P,N,I,W}^{\prime }$ defined in Definition 3.4.2.
$\operatorname{Cht}_{P,N,I,W}^{\prime }$ defined in Definition 3.4.2.
6.1.5
We define

Just as in 6.1.3,  $\operatorname{Cht}_{M,\infty ,I,W}$ is equipped with an action of
$\operatorname{Cht}_{M,\infty ,I,W}$ is equipped with an action of  $M(\mathbb{A})$. Recall that for any level
$M(\mathbb{A})$. Recall that for any level  $N$, in Definition 3.4.2, we defined
$N$, in Definition 3.4.2, we defined  $\operatorname{Cht}_{M,N,I,W}^{\prime }=\operatorname{Cht}_{M,N,I,W}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N})$. Let
$\operatorname{Cht}_{M,N,I,W}^{\prime }=\operatorname{Cht}_{M,N,I,W}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N})$. Let  $K_{U,N}:=K_{N}\,\cap \,U(\mathbb{O})$ and
$K_{U,N}:=K_{N}\,\cap \,U(\mathbb{O})$ and  $K_{M,N}:=K_{P,N}/K_{U,N}$. Taking into account that
$K_{M,N}:=K_{P,N}/K_{U,N}$. Taking into account that  $\operatorname{Cht}_{M,N,I,W}=\operatorname{Cht}_{M,\infty ,I,W}/K_{M,N}$, we deduce
$\operatorname{Cht}_{M,N,I,W}=\operatorname{Cht}_{M,\infty ,I,W}/K_{M,N}$, we deduce
 $$\begin{eqnarray}\operatorname{Cht}_{M,N,I,W}^{\prime }=\operatorname{Cht}_{M,\infty ,I,W}\overset{P(\mathbb{O})/K_{U,N}}{\times }G(\mathbb{O})/K_{N}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{M,N,I,W}^{\prime }=\operatorname{Cht}_{M,\infty ,I,W}\overset{P(\mathbb{O})/K_{U,N}}{\times }G(\mathbb{O})/K_{N}.\end{eqnarray}$$ When we consider the action of the Hecke algebras in 6.2.4 in the next section, we will need some functoriality on  $K_{N}$. For this reason, we rewrite (6.5) in the following way. Note that
$K_{N}$. For this reason, we rewrite (6.5) in the following way. Note that  $K_{N}$ is normal in
$K_{N}$ is normal in  $G(\mathbb{O})$. The stabilizer of any
$G(\mathbb{O})$. The stabilizer of any  $P(\mathbb{O})$-orbit in
$P(\mathbb{O})$-orbit in  $G(\mathbb{O})/K_{N}$ is
$G(\mathbb{O})/K_{N}$ is  $K_{P,N}$. We deduce from (6.5) that
$K_{P,N}$. We deduce from (6.5) that

The second equation is because that  $P(\mathbb{O})\backslash G(\mathbb{O})=P(\mathbb{A})\backslash G(\mathbb{A})$, and that in each
$P(\mathbb{O})\backslash G(\mathbb{O})=P(\mathbb{A})\backslash G(\mathbb{A})$, and that in each  $P(\mathbb{A})$-orbit in
$P(\mathbb{A})$-orbit in  $G(\mathbb{A})/K_{N}$, we can choose a representative in
$G(\mathbb{A})/K_{N}$, we can choose a representative in  $G(\mathbb{O})/K_{N}$.
$G(\mathbb{O})/K_{N}$.
In the following, we want to generalize (6.6) for any compact open subgroup  $K\subset G(\mathbb{O})$ (which may not be normal in
$K\subset G(\mathbb{O})$ (which may not be normal in  $G(\mathbb{O})$).
$G(\mathbb{O})$).
6.1.6
Let  ${\mathcal{D}}$ be the category of discrete sets
${\mathcal{D}}$ be the category of discrete sets  $S$ equipped with a continuous action of
$S$ equipped with a continuous action of  $P(\mathbb{A})$ with finitely many orbits such that the stabilizer of any point is conjugated to some open subgroup of finite index in
$P(\mathbb{A})$ with finitely many orbits such that the stabilizer of any point is conjugated to some open subgroup of finite index in  $P(\mathbb{O})$. In particular, for any compact open subgroup
$P(\mathbb{O})$. In particular, for any compact open subgroup  $K\subset G(\mathbb{O})$, the set
$K\subset G(\mathbb{O})$, the set  $S=G(\mathbb{A})/K$ is an object in
$S=G(\mathbb{A})/K$ is an object in  ${\mathcal{D}}$.
${\mathcal{D}}$.
For any  $S\in {\mathcal{D}}$, we define functorially the cohomology group
$S\in {\mathcal{D}}$, we define functorially the cohomology group  $H_{M,S,I,W}^{\prime }$ in the following way.
$H_{M,S,I,W}^{\prime }$ in the following way.
When  $S$ has only one orbit, choose a point
$S$ has only one orbit, choose a point  $s\in S$, and let
$s\in S$, and let  $H$ be the stabilizer of
$H$ be the stabilizer of  $s$. Then
$s$. Then  $H$ is a subgroup of
$H$ is a subgroup of  $P(\mathbb{A})$ conjugated to some open subgroup of finite index in
$P(\mathbb{A})$ conjugated to some open subgroup of finite index in  $P(\mathbb{O})$. We have
$P(\mathbb{O})$. We have  $S=P(\mathbb{A})/H$. Let
$S=P(\mathbb{A})/H$. Let  $R$ be a subgroup of finite index in
$R$ be a subgroup of finite index in  $H\cap U(\mathbb{A})$ and normal in
$H\cap U(\mathbb{A})$ and normal in  $H$. By 6.1.5,
$H$. By 6.1.5,  $\operatorname{Cht}_{M,\infty ,I,W}$ is equipped with an action of
$\operatorname{Cht}_{M,\infty ,I,W}$ is equipped with an action of  $M(\mathbb{A})$, thus an action of
$M(\mathbb{A})$, thus an action of  $P(\mathbb{A})$ by the projection
$P(\mathbb{A})$ by the projection  $P(\mathbb{A}){\twoheadrightarrow}M(\mathbb{A})$. Note that
$P(\mathbb{A}){\twoheadrightarrow}M(\mathbb{A})$. Note that  $R\subset U(\mathbb{A})$ acts trivially on
$R\subset U(\mathbb{A})$ acts trivially on  $\operatorname{Cht}_{M,\infty ,I,W}$. We define a Deligne–Mumford stack
$\operatorname{Cht}_{M,\infty ,I,W}$. We define a Deligne–Mumford stack
 $$\begin{eqnarray}\operatorname{Cht}_{M,\infty ,I,W}/(H/R).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{M,\infty ,I,W}/(H/R).\end{eqnarray}$$ We define the cohomology group  $H_{M,S,R,I,W}^{\prime }$ as in Definition 2.6.8 for
$H_{M,S,R,I,W}^{\prime }$ as in Definition 2.6.8 for  $\operatorname{Cht}_{M,\infty ,I,W}/(H/R)$ (instead of
$\operatorname{Cht}_{M,\infty ,I,W}/(H/R)$ (instead of  $\operatorname{Cht}_{M,N,I,W}$). Concretely, we have a morphism
$\operatorname{Cht}_{M,N,I,W}$). Concretely, we have a morphism  $\operatorname{Cht}_{M,\infty ,I,W}/(H/R)\unicode[STIX]{x1D6EF}\rightarrow \operatorname{Cht}_{M,I,W}/\unicode[STIX]{x1D6EF}$, where
$\operatorname{Cht}_{M,\infty ,I,W}/(H/R)\unicode[STIX]{x1D6EF}\rightarrow \operatorname{Cht}_{M,I,W}/\unicode[STIX]{x1D6EF}$, where  $\operatorname{Cht}_{M,I,W}$ is the stack of
$\operatorname{Cht}_{M,I,W}$ is the stack of  $M$-shtukas without level structure. Let
$M$-shtukas without level structure. Let  ${\mathcal{F}}_{M,\infty ,I,W}^{\unicode[STIX]{x1D6EF}}$ be the inverse image of
${\mathcal{F}}_{M,\infty ,I,W}^{\unicode[STIX]{x1D6EF}}$ be the inverse image of  ${\mathcal{F}}_{M,I,W}^{\unicode[STIX]{x1D6EF}}$. We define
${\mathcal{F}}_{M,I,W}^{\unicode[STIX]{x1D6EF}}$. We define

Let  $R_{1}\subset R_{2}$ be two subgroups of finite index in
$R_{1}\subset R_{2}$ be two subgroups of finite index in  $H\cap U(\mathbb{A})$ and normal in
$H\cap U(\mathbb{A})$ and normal in  $H$. The projection
$H$. The projection  $H/R_{1}{\twoheadrightarrow}H/R_{2}$ induces a morphism
$H/R_{1}{\twoheadrightarrow}H/R_{2}$ induces a morphism
 $$\begin{eqnarray}\mathfrak{q}_{R_{1},R_{2}}:\operatorname{Cht}_{M,\infty ,I,W}/(H/R_{1})\rightarrow \operatorname{Cht}_{M,\infty ,I,W}/(H/R_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{q}_{R_{1},R_{2}}:\operatorname{Cht}_{M,\infty ,I,W}/(H/R_{1})\rightarrow \operatorname{Cht}_{M,\infty ,I,W}/(H/R_{2}).\end{eqnarray}$$ It is a gerbe for the finite  $q$-group
$q$-group  $R_{2}/R_{1}$. The counit morphism (which is equal to the trace map because
$R_{2}/R_{1}$. The counit morphism (which is equal to the trace map because  $\mathfrak{q}_{R_{1},R_{2}}$ is smooth of dimension
$\mathfrak{q}_{R_{1},R_{2}}$ is smooth of dimension  $0$)
$0$)  $\operatorname{Co}(\mathfrak{q}_{R_{1},R_{2}}):(\mathfrak{q}_{R_{1},R_{2}})_{!}(\mathfrak{q}_{R_{1},R_{2}})^{!}\rightarrow \operatorname{Id}$ is an isomorphism. Indeed, just as in the proof (i) of Lemma 4.6.6, by proper base change and the fact that
$\operatorname{Co}(\mathfrak{q}_{R_{1},R_{2}}):(\mathfrak{q}_{R_{1},R_{2}})_{!}(\mathfrak{q}_{R_{1},R_{2}})^{!}\rightarrow \operatorname{Id}$ is an isomorphism. Indeed, just as in the proof (i) of Lemma 4.6.6, by proper base change and the fact that  $\mathfrak{q}_{R_{1},R_{2}}$ is smooth, we reduce to the case of Lemma 6.1.7 below with
$\mathfrak{q}_{R_{1},R_{2}}$ is smooth, we reduce to the case of Lemma 6.1.7 below with  $\unicode[STIX]{x1D6E4}=R_{2}/R_{1}$. The morphism
$\unicode[STIX]{x1D6E4}=R_{2}/R_{1}$. The morphism  $\operatorname{Co}(\mathfrak{q}_{R_{1},R_{2}})$ induces an isomorphism of cohomology groups
$\operatorname{Co}(\mathfrak{q}_{R_{1},R_{2}})$ induces an isomorphism of cohomology groups
 $$\begin{eqnarray}H_{M,S,R_{1},I,W}^{\prime }\overset{{\sim}}{\rightarrow }H_{M,S,R_{2},I,W}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}H_{M,S,R_{1},I,W}^{\prime }\overset{{\sim}}{\rightarrow }H_{M,S,R_{2},I,W}^{\prime }.\end{eqnarray}$$ We define  $H_{M,S,I,W}^{\prime }$ to be any
$H_{M,S,I,W}^{\prime }$ to be any  $H_{M,S,R,I,W}^{\prime }$, where we identify
$H_{M,S,R,I,W}^{\prime }$, where we identify  $H_{M,S,R_{1},I,W}^{\prime }$ and
$H_{M,S,R_{1},I,W}^{\prime }$ and  $H_{M,S,R_{2},I,W}^{\prime }$ by (6.7).
$H_{M,S,R_{2},I,W}^{\prime }$ by (6.7).
Recall that  $S$ has only one orbit.
$S$ has only one orbit.  $H_{M,S,I,W}^{\prime }$ is independent of the choice of the point
$H_{M,S,I,W}^{\prime }$ is independent of the choice of the point  $s$ in
$s$ in  $S$. In fact, let
$S$. In fact, let  $s_{1},s_{2}$ be two points of
$s_{1},s_{2}$ be two points of  $S$, and let
$S$, and let  $H_{1}$ (respectively
$H_{1}$ (respectively  $H_{2}$) be the stabilizer of
$H_{2}$) be the stabilizer of  $s_{1}$ (respectively
$s_{1}$ (respectively  $s_{2}$); then
$s_{2}$); then  $H_{2}=p^{-1}H_{1}p$ for some
$H_{2}=p^{-1}H_{1}p$ for some  $p\in P(\mathbb{A})$. The action of
$p\in P(\mathbb{A})$. The action of  $p$ induces an isomorphism
$p$ induces an isomorphism  $\operatorname{Cht}_{M,\infty ,I,W}/(H_{1}/R)\overset{{\sim}}{\rightarrow }\operatorname{Cht}_{M,\infty ,I,W}/(p^{-1}H_{1}p/p^{-1}Rp)$. We deduce an isomorphism of cohomology groups by the adjunction morphism.
$\operatorname{Cht}_{M,\infty ,I,W}/(H_{1}/R)\overset{{\sim}}{\rightarrow }\operatorname{Cht}_{M,\infty ,I,W}/(p^{-1}H_{1}p/p^{-1}Rp)$. We deduce an isomorphism of cohomology groups by the adjunction morphism.
In general,  $S=\bigsqcup _{\unicode[STIX]{x1D6FC}\in A}\unicode[STIX]{x1D6FC}$ is a finite union of orbits, and we define
$S=\bigsqcup _{\unicode[STIX]{x1D6FC}\in A}\unicode[STIX]{x1D6FC}$ is a finite union of orbits, and we define
 $$\begin{eqnarray}H_{M,S,I,W}^{\prime }:=\bigoplus _{\unicode[STIX]{x1D6FC}\in A}H_{M,\unicode[STIX]{x1D6FC},I,W}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}H_{M,S,I,W}^{\prime }:=\bigoplus _{\unicode[STIX]{x1D6FC}\in A}H_{M,\unicode[STIX]{x1D6FC},I,W}^{\prime }.\end{eqnarray}$$ When  $S=G(\mathbb{A})/K$ for some compact open subgroup
$S=G(\mathbb{A})/K$ for some compact open subgroup  $K$ in
$K$ in  $G(\mathbb{O})$, we write
$G(\mathbb{O})$, we write
 $$\begin{eqnarray}H_{M,K,I,W}^{\prime }:=H_{M,S,I,W}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}H_{M,K,I,W}^{\prime }:=H_{M,S,I,W}^{\prime }.\end{eqnarray}$$Lemma 6.1.7. Let  $\unicode[STIX]{x1D6E4}$ be a finite group over an algebraically closed field
$\unicode[STIX]{x1D6E4}$ be a finite group over an algebraically closed field  $k$ over
$k$ over  $\mathbb{F}_{q}$. We denote by
$\mathbb{F}_{q}$. We denote by  $B\unicode[STIX]{x1D6E4}$ the classifying stack of
$B\unicode[STIX]{x1D6E4}$ the classifying stack of  $\unicode[STIX]{x1D6E4}$ over
$\unicode[STIX]{x1D6E4}$ over  $k$. Let
$k$. Let  $\mathfrak{q}:B\unicode[STIX]{x1D6E4}\rightarrow \operatorname{Spec}k$ be the structure morphism. Then the counit morphism (equal to the trace map)
$\mathfrak{q}:B\unicode[STIX]{x1D6E4}\rightarrow \operatorname{Spec}k$ be the structure morphism. Then the counit morphism (equal to the trace map)  $\operatorname{Co}(\mathfrak{q}):\mathfrak{q}_{!}\mathfrak{q}^{!}\rightarrow \operatorname{Id}$ of functors on
$\operatorname{Co}(\mathfrak{q}):\mathfrak{q}_{!}\mathfrak{q}^{!}\rightarrow \operatorname{Id}$ of functors on  $D_{c}(\operatorname{Spec}k,\mathbb{Q}_{\ell })$ is an isomorphism.
$D_{c}(\operatorname{Spec}k,\mathbb{Q}_{\ell })$ is an isomorphism.
Proof. The counit morphism  $\operatorname{Co}(\mathfrak{q})$ is the dual of the adjunction morphism
$\operatorname{Co}(\mathfrak{q})$ is the dual of the adjunction morphism  $\operatorname{adj}(\mathfrak{q}):\operatorname{Id}\rightarrow \mathfrak{q}_{\ast }\mathfrak{q}^{\ast }$. For any
$\operatorname{adj}(\mathfrak{q}):\operatorname{Id}\rightarrow \mathfrak{q}_{\ast }\mathfrak{q}^{\ast }$. For any  ${\mathcal{F}}\in D_{c}(\operatorname{Spec}k,\mathbb{Q}_{\ell })$,
${\mathcal{F}}\in D_{c}(\operatorname{Spec}k,\mathbb{Q}_{\ell })$,  $\mathfrak{q}^{\ast }{\mathcal{F}}$ is a complex
$\mathfrak{q}^{\ast }{\mathcal{F}}$ is a complex  $F$ of
$F$ of  $\unicode[STIX]{x1D6E4}$-modules with trivial action of
$\unicode[STIX]{x1D6E4}$-modules with trivial action of  $\unicode[STIX]{x1D6E4}$. Since
$\unicode[STIX]{x1D6E4}$. Since  $H^{j}(B\unicode[STIX]{x1D6E4},\mathfrak{q}^{\ast }{\mathcal{F}})=H^{j}(\unicode[STIX]{x1D6E4},F)$ (group cohomology), we have
$H^{j}(B\unicode[STIX]{x1D6E4},\mathfrak{q}^{\ast }{\mathcal{F}})=H^{j}(\unicode[STIX]{x1D6E4},F)$ (group cohomology), we have  $H^{0}(B\unicode[STIX]{x1D6E4},\mathfrak{q}^{\ast }{\mathcal{F}})=F^{\unicode[STIX]{x1D6E4}}=F$ and
$H^{0}(B\unicode[STIX]{x1D6E4},\mathfrak{q}^{\ast }{\mathcal{F}})=F^{\unicode[STIX]{x1D6E4}}=F$ and  $H^{j}(B\unicode[STIX]{x1D6E4},\mathfrak{q}^{\ast }{\mathcal{F}})=0$ for
$H^{j}(B\unicode[STIX]{x1D6E4},\mathfrak{q}^{\ast }{\mathcal{F}})=0$ for  $j>0$. So
$j>0$. So  $\operatorname{adj}(\mathfrak{q})$ is an isomorphism. By duality, we deduce the lemma.◻
$\operatorname{adj}(\mathfrak{q})$ is an isomorphism. By duality, we deduce the lemma.◻
6.1.8
Let  $S\in {\mathcal{D}}$. We define
$S\in {\mathcal{D}}$. We define
 $$\begin{eqnarray}\operatorname{Cht}_{P,S,I,W}^{\prime }:=\operatorname{Cht}_{P,\infty ,I,W}\overset{P(\mathbb{A})}{\times }S.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{P,S,I,W}^{\prime }:=\operatorname{Cht}_{P,\infty ,I,W}\overset{P(\mathbb{A})}{\times }S.\end{eqnarray}$$ For each orbit  $\unicode[STIX]{x1D6FC}$ in
$\unicode[STIX]{x1D6FC}$ in  $S$, choose a representative, and let
$S$, choose a representative, and let  $H^{\unicode[STIX]{x1D6FC}}$ be the stabilizer (well defined up to conjugation). Then
$H^{\unicode[STIX]{x1D6FC}}$ be the stabilizer (well defined up to conjugation). Then
 $$\begin{eqnarray}\operatorname{Cht}_{P,S,I,W}^{\prime }=\bigsqcup _{\unicode[STIX]{x1D6FC}\in \{P(\mathbb{A})\text{-orbits in }S\}}\operatorname{Cht}_{P,\infty ,I,W}/H^{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{P,S,I,W}^{\prime }=\bigsqcup _{\unicode[STIX]{x1D6FC}\in \{P(\mathbb{A})\text{-orbits in }S\}}\operatorname{Cht}_{P,\infty ,I,W}/H^{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$ For each  $\unicode[STIX]{x1D6FC}$, let
$\unicode[STIX]{x1D6FC}$, let  $R^{\unicode[STIX]{x1D6FC}}$ be a subgroup of finite index in
$R^{\unicode[STIX]{x1D6FC}}$ be a subgroup of finite index in  $H^{\unicode[STIX]{x1D6FC}}\cap U(\mathbb{A})$ and normal in
$H^{\unicode[STIX]{x1D6FC}}\cap U(\mathbb{A})$ and normal in  $H^{\unicode[STIX]{x1D6FC}}$. Let
$H^{\unicode[STIX]{x1D6FC}}$. Let  $R=(R^{\unicode[STIX]{x1D6FC}})_{\unicode[STIX]{x1D6FC}\in \{P(\mathbb{A})\text{-orbits in }S\}}$. We define
$R=(R^{\unicode[STIX]{x1D6FC}})_{\unicode[STIX]{x1D6FC}\in \{P(\mathbb{A})\text{-orbits in }S\}}$. We define
 $$\begin{eqnarray}\operatorname{Cht}_{M,S,R,I,W}^{\prime }:=\bigsqcup _{\unicode[STIX]{x1D6FC}\in \{P(\mathbb{A})\text{-orbits in }S\}}\operatorname{Cht}_{M,\infty ,I,W}/(H^{\unicode[STIX]{x1D6FC}}/R^{\unicode[STIX]{x1D6FC}}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{M,S,R,I,W}^{\prime }:=\bigsqcup _{\unicode[STIX]{x1D6FC}\in \{P(\mathbb{A})\text{-orbits in }S\}}\operatorname{Cht}_{M,\infty ,I,W}/(H^{\unicode[STIX]{x1D6FC}}/R^{\unicode[STIX]{x1D6FC}}).\end{eqnarray}$$ For each  $\unicode[STIX]{x1D6FC}$, we have morphisms of prestacks
$\unicode[STIX]{x1D6FC}$, we have morphisms of prestacks
 $$\begin{eqnarray}\operatorname{Cht}_{P,\infty ,I,W}/H^{\unicode[STIX]{x1D6FC}}\rightarrow \operatorname{Cht}_{M,\infty ,I,W}/H^{\unicode[STIX]{x1D6FC}}\rightarrow \operatorname{Cht}_{M,\infty ,I,W}/(H^{\unicode[STIX]{x1D6FC}}/R^{\unicode[STIX]{x1D6FC}}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{P,\infty ,I,W}/H^{\unicode[STIX]{x1D6FC}}\rightarrow \operatorname{Cht}_{M,\infty ,I,W}/H^{\unicode[STIX]{x1D6FC}}\rightarrow \operatorname{Cht}_{M,\infty ,I,W}/(H^{\unicode[STIX]{x1D6FC}}/R^{\unicode[STIX]{x1D6FC}}),\end{eqnarray}$$where the first and third prestacks are Deligne–Mumford stacks, while the second is only a prestack. Taking union over all the orbits, we deduce from (6.11) a morphism
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{S,R}:\operatorname{Cht}_{P,S,I,W}^{\prime }\rightarrow \operatorname{Cht}_{M,S,R,I,W}^{\prime }\!.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{S,R}:\operatorname{Cht}_{P,S,I,W}^{\prime }\rightarrow \operatorname{Cht}_{M,S,R,I,W}^{\prime }\!.\end{eqnarray}$$ In particular, when  $S=G(\mathbb{A})/K_{N}$, the stack
$S=G(\mathbb{A})/K_{N}$, the stack  $\operatorname{Cht}_{P,S,I,W}^{\prime }$ coincides with
$\operatorname{Cht}_{P,S,I,W}^{\prime }$ coincides with  $\operatorname{Cht}_{P,N,I,W}^{\prime }$. For every orbit
$\operatorname{Cht}_{P,N,I,W}^{\prime }$. For every orbit  $\unicode[STIX]{x1D6FC}$, we can choose a representative in
$\unicode[STIX]{x1D6FC}$, we can choose a representative in  $G(\mathbb{O})/K_{N}$ (so that
$G(\mathbb{O})/K_{N}$ (so that  $H^{\unicode[STIX]{x1D6FC}}=K_{P,N}$) and choose
$H^{\unicode[STIX]{x1D6FC}}=K_{P,N}$) and choose  $R^{\unicode[STIX]{x1D6FC}}=K_{U,N}$. Then
$R^{\unicode[STIX]{x1D6FC}}=K_{U,N}$. Then  $\operatorname{Cht}_{M,S,R,I,W}^{\prime }$ coincides with
$\operatorname{Cht}_{M,S,R,I,W}^{\prime }$ coincides with  $\operatorname{Cht}_{M,N,I,W}^{\prime }$,
$\operatorname{Cht}_{M,N,I,W}^{\prime }$,  $H_{M,S,R,I,W}^{\prime }$ coincides with
$H_{M,S,R,I,W}^{\prime }$ coincides with  $H_{M,N,I,W}^{\prime }$ defined in Definition 3.4.9, and (6.12) coincides with
$H_{M,N,I,W}^{\prime }$ defined in Definition 3.4.9, and (6.12) coincides with  $\unicode[STIX]{x1D70B}^{\prime }$ defined in (3.26).
$\unicode[STIX]{x1D70B}^{\prime }$ defined in (3.26).
6.1.9
For any compact open subgroup  $K\subset G(\mathbb{O})$, let
$K\subset G(\mathbb{O})$, let  $S=G(\mathbb{A})/K$. Note that in this case we have
$S=G(\mathbb{A})/K$. Note that in this case we have  $\operatorname{Cht}_{P,K,I,W}^{\prime }=\operatorname{Cht}_{P,S,I,W}^{\prime }$. For any
$\operatorname{Cht}_{P,K,I,W}^{\prime }=\operatorname{Cht}_{P,S,I,W}^{\prime }$. For any  $R$ as in 6.1.8, we have the following morphisms.
$R$ as in 6.1.8, we have the following morphisms.

Just as in Proposition 3.5.3 and Remark 3.5.4, the morphism  $i_{K}$ is schematic and proper. Apply the construction in §3 to (
$i_{K}$ is schematic and proper. Apply the construction in §3 to (
). Similarly to (3.9), we have

where  $\unicode[STIX]{x1D70B}_{S,R,d}$ is smooth. Let
$\unicode[STIX]{x1D70B}_{S,R,d}$ is smooth. Let  ${\mathcal{F}}_{G}$ be the canonical Satake sheaf on
${\mathcal{F}}_{G}$ be the canonical Satake sheaf on  $\operatorname{Cht}_{G,K,I,W}$ and
$\operatorname{Cht}_{G,K,I,W}$ and  ${\mathcal{F}}_{M}$ be the canonical Satake sheaf on
${\mathcal{F}}_{M}$ be the canonical Satake sheaf on  $\operatorname{Cht}_{M,S,R,I,W}^{\prime }$. We construct a morphism
$\operatorname{Cht}_{M,S,R,I,W}^{\prime }$. We construct a morphism  $c_{G,K}^{P}:(\unicode[STIX]{x1D70B}_{S,R})_{!}(i_{K})^{\ast }{\mathcal{F}}_{G}\rightarrow {\mathcal{F}}_{M}$ similar to (3.22) and (3.23). Namely,
$c_{G,K}^{P}:(\unicode[STIX]{x1D70B}_{S,R})_{!}(i_{K})^{\ast }{\mathcal{F}}_{G}\rightarrow {\mathcal{F}}_{M}$ similar to (3.22) and (3.23). Namely,  $c_{G,K}^{P}$ is the composition of some isomorphisms and the counit morphism
$c_{G,K}^{P}$ is the composition of some isomorphisms and the counit morphism  $(\unicode[STIX]{x1D70B}_{S,R,d})_{!}(\unicode[STIX]{x1D70B}_{S,R,d})^{!}\rightarrow \operatorname{Id}$. Note that since
$(\unicode[STIX]{x1D70B}_{S,R,d})_{!}(\unicode[STIX]{x1D70B}_{S,R,d})^{!}\rightarrow \operatorname{Id}$. Note that since  $\unicode[STIX]{x1D70B}_{S,R,d}$ is smooth, the composition
$\unicode[STIX]{x1D70B}_{S,R,d}$ is smooth, the composition  $(\unicode[STIX]{x1D70B}_{S,R,d})_{!}(\unicode[STIX]{x1D70B}_{S,R,d})^{\ast }[2m](m)\overset{{\sim}}{\rightarrow }(\unicode[STIX]{x1D70B}_{d})_{!}(\unicode[STIX]{x1D70B}_{d})^{!}\rightarrow \operatorname{Id}$ is the trace map in [Reference Grothendieck, Artin and VerdierSGA4, XVIII 2], where
$(\unicode[STIX]{x1D70B}_{S,R,d})_{!}(\unicode[STIX]{x1D70B}_{S,R,d})^{\ast }[2m](m)\overset{{\sim}}{\rightarrow }(\unicode[STIX]{x1D70B}_{d})_{!}(\unicode[STIX]{x1D70B}_{d})^{!}\rightarrow \operatorname{Id}$ is the trace map in [Reference Grothendieck, Artin and VerdierSGA4, XVIII 2], where  $m$ is the dimension of
$m$ is the dimension of  $\unicode[STIX]{x1D70B}_{S,R,d}$.
$\unicode[STIX]{x1D70B}_{S,R,d}$.
Similar to (3.33), we have a composition of morphisms of functors in  $D_{c}^{b}(\overline{\unicode[STIX]{x1D702}^{I}},\mathbb{Q}_{\ell })$:
$D_{c}^{b}(\overline{\unicode[STIX]{x1D702}^{I}},\mathbb{Q}_{\ell })$:
 $$\begin{eqnarray}(\mathfrak{p}_{G})_{!}{\mathcal{F}}_{G}\xrightarrow[{}]{\operatorname{adj}(i_{K})}(\mathfrak{p}_{G})_{!}(i_{K})_{\ast }(i_{K})^{\ast }{\mathcal{F}}_{G}\simeq (\mathfrak{p}_{M})_{!}(\unicode[STIX]{x1D70B}_{S,R})_{!}(i_{K})^{\ast }{\mathcal{F}}_{G}\xrightarrow[{}]{c_{G,K}^{P}}(\mathfrak{p}_{M})_{!}{\mathcal{F}}_{M}.\end{eqnarray}$$
$$\begin{eqnarray}(\mathfrak{p}_{G})_{!}{\mathcal{F}}_{G}\xrightarrow[{}]{\operatorname{adj}(i_{K})}(\mathfrak{p}_{G})_{!}(i_{K})_{\ast }(i_{K})^{\ast }{\mathcal{F}}_{G}\simeq (\mathfrak{p}_{M})_{!}(\unicode[STIX]{x1D70B}_{S,R})_{!}(i_{K})^{\ast }{\mathcal{F}}_{G}\xrightarrow[{}]{c_{G,K}^{P}}(\mathfrak{p}_{M})_{!}{\mathcal{F}}_{M}.\end{eqnarray}$$We define
 $$\begin{eqnarray}H_{P,K,I,W}^{\prime }:=H_{P,S,I,W}^{\prime }:=(\mathfrak{p}_{P})_{!}(i_{K})^{\ast }{\mathcal{F}}_{G}.\end{eqnarray}$$
$$\begin{eqnarray}H_{P,K,I,W}^{\prime }:=H_{P,S,I,W}^{\prime }:=(\mathfrak{p}_{P})_{!}(i_{K})^{\ast }{\mathcal{F}}_{G}.\end{eqnarray}$$ The morphism  $(\mathfrak{p}_{G})_{!}{\mathcal{F}}_{G}\xrightarrow[{}]{\operatorname{adj}(i_{K})}(\mathfrak{p}_{G})_{!}(i_{K})_{\ast }(i_{K})^{\ast }{\mathcal{F}}_{G}$ induces a morphism
$(\mathfrak{p}_{G})_{!}{\mathcal{F}}_{G}\xrightarrow[{}]{\operatorname{adj}(i_{K})}(\mathfrak{p}_{G})_{!}(i_{K})_{\ast }(i_{K})^{\ast }{\mathcal{F}}_{G}$ induces a morphism
 $$\begin{eqnarray}H_{G,K,I,W}^{j}\rightarrow H_{P,S,I,W}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}H_{G,K,I,W}^{j}\rightarrow H_{P,S,I,W}^{\prime }.\end{eqnarray}$$ The morphism  $(\mathfrak{p}_{M})_{!}(\unicode[STIX]{x1D70B}_{S,R})_{!}(i_{K})^{\ast }{\mathcal{F}}_{G}\xrightarrow[{}]{c_{G,K}^{P}}(\mathfrak{p}_{M})_{!}{\mathcal{F}}_{M}$ induces a morphism
$(\mathfrak{p}_{M})_{!}(\unicode[STIX]{x1D70B}_{S,R})_{!}(i_{K})^{\ast }{\mathcal{F}}_{G}\xrightarrow[{}]{c_{G,K}^{P}}(\mathfrak{p}_{M})_{!}{\mathcal{F}}_{M}$ induces a morphism
 $$\begin{eqnarray}H_{P,S,I,W}^{\prime }\rightarrow H_{M,S,R,I,W}^{\prime \,j}.\end{eqnarray}$$
$$\begin{eqnarray}H_{P,S,I,W}^{\prime }\rightarrow H_{M,S,R,I,W}^{\prime \,j}.\end{eqnarray}$$We define the constant term morphism to be the composition of (6.15) and (6.16)
 $$\begin{eqnarray}C_{G,S,R}^{P,\,j}:H_{G,K,I,W}^{j}\rightarrow H_{M,S,R,I,W}^{\prime \,j}.\end{eqnarray}$$
$$\begin{eqnarray}C_{G,S,R}^{P,\,j}:H_{G,K,I,W}^{j}\rightarrow H_{M,S,R,I,W}^{\prime \,j}.\end{eqnarray}$$ For  $R_{1}\subset R_{2}$ as in 6.1.6, the following diagram is commutative
$R_{1}\subset R_{2}$ as in 6.1.6, the following diagram is commutative

because  $C_{G,S,R_{1}}^{P,\,j}$,
$C_{G,S,R_{1}}^{P,\,j}$,  $C_{G,S,R_{2}}^{P,\,j}$ and (6.7) are defined by counit morphisms (which in these cases are equal to trace maps), and by [Reference Grothendieck, Artin and VerdierSGA4, XVIII Théorème 2.9], the trace morphism is compatible with composition.
$C_{G,S,R_{2}}^{P,\,j}$ and (6.7) are defined by counit morphisms (which in these cases are equal to trace maps), and by [Reference Grothendieck, Artin and VerdierSGA4, XVIII Théorème 2.9], the trace morphism is compatible with composition.
In 6.1.6 we defined  $H_{M,K,I,W}^{\prime \,j}$. We deduce from (6.18) a morphism
$H_{M,K,I,W}^{\prime \,j}$. We deduce from (6.18) a morphism
 $$\begin{eqnarray}C_{G,K}^{P,\,j}:H_{G,K,I,W}^{j}\rightarrow H_{M,K,I,W}^{\prime \,j},\end{eqnarray}$$
$$\begin{eqnarray}C_{G,K}^{P,\,j}:H_{G,K,I,W}^{j}\rightarrow H_{M,K,I,W}^{\prime \,j},\end{eqnarray}$$ which is the composition  $H_{G,K,I,W}^{j}\rightarrow H_{P,K,I,W}^{\prime \,j}\rightarrow H_{M,K,I,W}^{\prime \,j}$.
$H_{G,K,I,W}^{j}\rightarrow H_{P,K,I,W}^{\prime \,j}\rightarrow H_{M,K,I,W}^{\prime \,j}$.
6.1.10
Let  $S_{1},S_{2}\in {\mathcal{D}}$ and
$S_{1},S_{2}\in {\mathcal{D}}$ and  $f:S_{1}\rightarrow S_{2}$ be a morphism in
$f:S_{1}\rightarrow S_{2}$ be a morphism in  ${\mathcal{D}}$. Note that
${\mathcal{D}}$. Note that  $f$ is
$f$ is  $P(\mathbb{A})$-equivariant and it sends orbit to orbit. For each
$P(\mathbb{A})$-equivariant and it sends orbit to orbit. For each  $P(\mathbb{A})$-orbit
$P(\mathbb{A})$-orbit  $\unicode[STIX]{x1D6FD}$ in
$\unicode[STIX]{x1D6FD}$ in  $S_{2}$, choose a representative
$S_{2}$, choose a representative  $s^{\unicode[STIX]{x1D6FD}}\in \unicode[STIX]{x1D6FD}$ with stabilizer
$s^{\unicode[STIX]{x1D6FD}}\in \unicode[STIX]{x1D6FD}$ with stabilizer  $H^{\unicode[STIX]{x1D6FD}}$. If
$H^{\unicode[STIX]{x1D6FD}}$. If  $f^{-1}(\unicode[STIX]{x1D6FD})$ is empty, take any
$f^{-1}(\unicode[STIX]{x1D6FD})$ is empty, take any  $R^{\unicode[STIX]{x1D6FD}}$ subgroup of finite index in
$R^{\unicode[STIX]{x1D6FD}}$ subgroup of finite index in  $H_{2}^{\unicode[STIX]{x1D6FD}}\cap U(\mathbb{A})$ and normal in
$H_{2}^{\unicode[STIX]{x1D6FD}}\cap U(\mathbb{A})$ and normal in  $H_{2}^{\unicode[STIX]{x1D6FD}}$. If
$H_{2}^{\unicode[STIX]{x1D6FD}}$. If  $f^{-1}(\unicode[STIX]{x1D6FD})$ is non-empty, for every
$f^{-1}(\unicode[STIX]{x1D6FD})$ is non-empty, for every  $P(\mathbb{A})$-orbit
$P(\mathbb{A})$-orbit  $\unicode[STIX]{x1D6FC}\in f^{-1}(\unicode[STIX]{x1D6FD})$, choose a representative
$\unicode[STIX]{x1D6FC}\in f^{-1}(\unicode[STIX]{x1D6FD})$, choose a representative  $s^{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D6FC}$ such that
$s^{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D6FC}$ such that  $f(s^{\unicode[STIX]{x1D6FC}})=s^{\unicode[STIX]{x1D6FD}}$. Let
$f(s^{\unicode[STIX]{x1D6FC}})=s^{\unicode[STIX]{x1D6FD}}$. Let  $H_{1}^{\unicode[STIX]{x1D6FC}}$ be the stabilizer of
$H_{1}^{\unicode[STIX]{x1D6FC}}$ be the stabilizer of  $s^{\unicode[STIX]{x1D6FC}}$. Then
$s^{\unicode[STIX]{x1D6FC}}$. Then  $H_{1}^{\unicode[STIX]{x1D6FC}}\subset H_{2}^{\unicode[STIX]{x1D6FC}}$. Let
$H_{1}^{\unicode[STIX]{x1D6FC}}\subset H_{2}^{\unicode[STIX]{x1D6FC}}$. Let  $R^{\unicode[STIX]{x1D6FD}}$ be a subgroup of finite index in
$R^{\unicode[STIX]{x1D6FD}}$ be a subgroup of finite index in  $(\bigcap _{\unicode[STIX]{x1D6FC}\in f^{-1}(\unicode[STIX]{x1D6FD})}H_{1}^{\unicode[STIX]{x1D6FC}})\cap U(\mathbb{A})\subset H_{2}^{\unicode[STIX]{x1D6FD}}\cap U(\mathbb{A})$ and normal in
$(\bigcap _{\unicode[STIX]{x1D6FC}\in f^{-1}(\unicode[STIX]{x1D6FD})}H_{1}^{\unicode[STIX]{x1D6FC}})\cap U(\mathbb{A})\subset H_{2}^{\unicode[STIX]{x1D6FD}}\cap U(\mathbb{A})$ and normal in  $H_{2}^{\unicode[STIX]{x1D6FD}}$.
$H_{2}^{\unicode[STIX]{x1D6FD}}$.
The morphism  $H_{1}^{\unicode[STIX]{x1D6FC}}/R^{\unicode[STIX]{x1D6FD}}{\hookrightarrow}H_{2}^{\unicode[STIX]{x1D6FD}}/R^{\unicode[STIX]{x1D6FD}}$ for
$H_{1}^{\unicode[STIX]{x1D6FC}}/R^{\unicode[STIX]{x1D6FD}}{\hookrightarrow}H_{2}^{\unicode[STIX]{x1D6FD}}/R^{\unicode[STIX]{x1D6FD}}$ for  $\unicode[STIX]{x1D6FD}=f(\unicode[STIX]{x1D6FC})$ induces a morphism
$\unicode[STIX]{x1D6FD}=f(\unicode[STIX]{x1D6FC})$ induces a morphism
 $$\begin{eqnarray}\mathfrak{q}_{\unicode[STIX]{x1D6FC}}^{M}:\operatorname{Cht}_{M,\infty ,I,W}/(H_{1}^{\unicode[STIX]{x1D6FC}}/R^{\unicode[STIX]{x1D6FD}})\rightarrow \operatorname{Cht}_{M,\infty ,I,W}/(H_{2}^{\unicode[STIX]{x1D6FD}}/R^{\unicode[STIX]{x1D6FD}}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{q}_{\unicode[STIX]{x1D6FC}}^{M}:\operatorname{Cht}_{M,\infty ,I,W}/(H_{1}^{\unicode[STIX]{x1D6FC}}/R^{\unicode[STIX]{x1D6FD}})\rightarrow \operatorname{Cht}_{M,\infty ,I,W}/(H_{2}^{\unicode[STIX]{x1D6FD}}/R^{\unicode[STIX]{x1D6FD}}).\end{eqnarray}$$ Let  $R=((R^{\unicode[STIX]{x1D6FD}})_{\unicode[STIX]{x1D6FD}\in \{P(\mathbb{A})\text{-orbits in }S_{2}\}})$. Similarly to (6.10), we define
$R=((R^{\unicode[STIX]{x1D6FD}})_{\unicode[STIX]{x1D6FD}\in \{P(\mathbb{A})\text{-orbits in }S_{2}\}})$. Similarly to (6.10), we define  $\operatorname{Cht}_{M,S_{1},R,I,W}^{\prime }$ and
$\operatorname{Cht}_{M,S_{1},R,I,W}^{\prime }$ and  $\operatorname{Cht}_{M,S_{2},R,I,W}^{\prime }$. Then (6.20) for every orbit
$\operatorname{Cht}_{M,S_{2},R,I,W}^{\prime }$. Then (6.20) for every orbit  $\unicode[STIX]{x1D6FC}$ induces a morphism
$\unicode[STIX]{x1D6FC}$ induces a morphism
 $$\begin{eqnarray}\mathfrak{q}_{f}^{M}:\operatorname{Cht}_{M,S_{1},R,I,W}^{\prime }\rightarrow \operatorname{Cht}_{M,S_{2},R,I,W}^{\prime }\!.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{q}_{f}^{M}:\operatorname{Cht}_{M,S_{1},R,I,W}^{\prime }\rightarrow \operatorname{Cht}_{M,S_{2},R,I,W}^{\prime }\!.\end{eqnarray}$$ Similarly to 6.1.2, the adjunction morphism  $\operatorname{Id}\rightarrow (\mathfrak{q}_{f}^{M})_{\ast }(\mathfrak{q}_{f}^{M})^{\ast }$ induces a morphism
$\operatorname{Id}\rightarrow (\mathfrak{q}_{f}^{M})_{\ast }(\mathfrak{q}_{f}^{M})^{\ast }$ induces a morphism
 $$\begin{eqnarray}\operatorname{adj}(\mathfrak{q}_{f}^{M}):H_{M,S_{2},I,W}^{\prime }\rightarrow H_{M,S_{1},I,W}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{adj}(\mathfrak{q}_{f}^{M}):H_{M,S_{2},I,W}^{\prime }\rightarrow H_{M,S_{1},I,W}^{\prime }.\end{eqnarray}$$ The counit morphism  $(\mathfrak{q}_{f}^{M})_{!}(\mathfrak{q}_{f}^{M})^{!}\rightarrow \operatorname{Id}$ induces a morphism
$(\mathfrak{q}_{f}^{M})_{!}(\mathfrak{q}_{f}^{M})^{!}\rightarrow \operatorname{Id}$ induces a morphism
 $$\begin{eqnarray}\operatorname{Co}(\mathfrak{q}_{f}^{M}):H_{M,S_{1},I,W}^{\prime }\rightarrow H_{M,S_{2},I,W}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Co}(\mathfrak{q}_{f}^{M}):H_{M,S_{1},I,W}^{\prime }\rightarrow H_{M,S_{2},I,W}^{\prime }.\end{eqnarray}$$In the following, we will apply the functoriality to the cases:
–
 $K^{\prime }\subset K$,
$K^{\prime }\subset K$,  $S_{1}=G(\mathbb{A})/K^{\prime }$,
$S_{1}=G(\mathbb{A})/K^{\prime }$,  $S_{2}=G(\mathbb{A})/K$ and
$S_{2}=G(\mathbb{A})/K$ and  $f$ is the projection
$f$ is the projection  $G(\mathbb{A})/K^{\prime }{\twoheadrightarrow}G(\mathbb{A})/K$;
$G(\mathbb{A})/K^{\prime }{\twoheadrightarrow}G(\mathbb{A})/K$;–
 $S_{1}=G(\mathbb{A})/\widetilde{K}$,
$S_{1}=G(\mathbb{A})/\widetilde{K}$,  $S_{2}=G(\mathbb{A})/g^{-1}\widetilde{K}g$ and
$S_{2}=G(\mathbb{A})/g^{-1}\widetilde{K}g$ and  $f$ is the isomorphism induced by the right multiplication by
$f$ is the isomorphism induced by the right multiplication by  $g$:
$g$:  $G(\mathbb{A})/\widetilde{K}\overset{{\sim}}{\rightarrow }G(\mathbb{A})/g^{-1}\widetilde{K}g$.
$G(\mathbb{A})/\widetilde{K}\overset{{\sim}}{\rightarrow }G(\mathbb{A})/g^{-1}\widetilde{K}g$.
Remark 6.1.11. In 6.1.10, we can also first define morphisms of cohomology groups for each orbit  $\unicode[STIX]{x1D6FC}$: the adjunction morphism
$\unicode[STIX]{x1D6FC}$: the adjunction morphism  $\operatorname{Id}\rightarrow (\mathfrak{q}_{\unicode[STIX]{x1D6FC}}^{M})_{\ast }(\mathfrak{q}_{\unicode[STIX]{x1D6FC}}^{M})^{\ast }$ induces a morphism
$\operatorname{Id}\rightarrow (\mathfrak{q}_{\unicode[STIX]{x1D6FC}}^{M})_{\ast }(\mathfrak{q}_{\unicode[STIX]{x1D6FC}}^{M})^{\ast }$ induces a morphism
 $$\begin{eqnarray}\operatorname{adj}(\mathfrak{q}_{\unicode[STIX]{x1D6FC}}^{M}):H_{M,f(\unicode[STIX]{x1D6FC}),I,W}^{\prime }\rightarrow H_{M,\unicode[STIX]{x1D6FC},I,W}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{adj}(\mathfrak{q}_{\unicode[STIX]{x1D6FC}}^{M}):H_{M,f(\unicode[STIX]{x1D6FC}),I,W}^{\prime }\rightarrow H_{M,\unicode[STIX]{x1D6FC},I,W}^{\prime },\end{eqnarray}$$ where the orbit  $\unicode[STIX]{x1D6FC}$ (respectively
$\unicode[STIX]{x1D6FC}$ (respectively  $f(\unicode[STIX]{x1D6FC})$) is considered as subset of
$f(\unicode[STIX]{x1D6FC})$) is considered as subset of  $S_{1}$ (respectively
$S_{1}$ (respectively  $S_{2}$). The counit morphism
$S_{2}$). The counit morphism  $(\mathfrak{q}_{\unicode[STIX]{x1D6FC}}^{M})_{!}(\mathfrak{q}_{\unicode[STIX]{x1D6FC}}^{M})^{!}\rightarrow \operatorname{Id}$ induces a morphism
$(\mathfrak{q}_{\unicode[STIX]{x1D6FC}}^{M})_{!}(\mathfrak{q}_{\unicode[STIX]{x1D6FC}}^{M})^{!}\rightarrow \operatorname{Id}$ induces a morphism
 $$\begin{eqnarray}\operatorname{Co}(\mathfrak{q}_{\unicode[STIX]{x1D6FC}}^{M}):H_{M,\unicode[STIX]{x1D6FC},I,W}^{\prime }\rightarrow H_{M,f(\unicode[STIX]{x1D6FC}),I,W}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Co}(\mathfrak{q}_{\unicode[STIX]{x1D6FC}}^{M}):H_{M,\unicode[STIX]{x1D6FC},I,W}^{\prime }\rightarrow H_{M,f(\unicode[STIX]{x1D6FC}),I,W}^{\prime }.\end{eqnarray}$$Then taking sum over all the orbits, we obtain (6.22) and (6.23).
Similarly, in 6.1.12 below, we can first prove the statement for cohomology groups orbit by orbit, and then take the sum over all the orbits. But the notations would be more complicated.
6.1.12
Any  $S_{1},S_{2}\in {\mathcal{D}}$ and
$S_{1},S_{2}\in {\mathcal{D}}$ and  $f:S_{1}\rightarrow S_{2}$ morphism in
$f:S_{1}\rightarrow S_{2}$ morphism in  ${\mathcal{D}}$ induce a morphism
${\mathcal{D}}$ induce a morphism
 $$\begin{eqnarray}\mathfrak{q}_{f}^{P}:\operatorname{Cht}_{P,S_{1},I,W}^{\prime }\rightarrow \operatorname{Cht}_{P,S_{2},I,W}^{\prime }\!.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{q}_{f}^{P}:\operatorname{Cht}_{P,S_{1},I,W}^{\prime }\rightarrow \operatorname{Cht}_{P,S_{2},I,W}^{\prime }\!.\end{eqnarray}$$ The adjunction morphism  $\operatorname{Id}\rightarrow (\mathfrak{q}_{f}^{P})_{\ast }(\mathfrak{q}_{f}^{P})^{\ast }$ induces a morphism
$\operatorname{Id}\rightarrow (\mathfrak{q}_{f}^{P})_{\ast }(\mathfrak{q}_{f}^{P})^{\ast }$ induces a morphism
 $$\begin{eqnarray}\operatorname{adj}(\mathfrak{q}_{f}^{P}):H_{P,S_{2},I,W}^{\prime }\rightarrow H_{P,S_{1},I,W}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{adj}(\mathfrak{q}_{f}^{P}):H_{P,S_{2},I,W}^{\prime }\rightarrow H_{P,S_{1},I,W}^{\prime }.\end{eqnarray}$$ The counit morphism  $(\mathfrak{q}_{f}^{P})_{!}(\mathfrak{q}_{f}^{P})^{!}\rightarrow \operatorname{Id}$ induces a morphism
$(\mathfrak{q}_{f}^{P})_{!}(\mathfrak{q}_{f}^{P})^{!}\rightarrow \operatorname{Id}$ induces a morphism
 $$\begin{eqnarray}\operatorname{Co}(\mathfrak{q}_{f}^{P}):H_{P,S_{1},I,W}^{\prime }\rightarrow H_{P,S_{2},I,W}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Co}(\mathfrak{q}_{f}^{P}):H_{P,S_{1},I,W}^{\prime }\rightarrow H_{P,S_{2},I,W}^{\prime }.\end{eqnarray}$$ For each orbit  $\unicode[STIX]{x1D6FC}$ in
$\unicode[STIX]{x1D6FC}$ in  $S_{1}$ with
$S_{1}$ with  $\unicode[STIX]{x1D6FD}=f(\unicode[STIX]{x1D6FC})$, let
$\unicode[STIX]{x1D6FD}=f(\unicode[STIX]{x1D6FC})$, let  $H_{1}^{\unicode[STIX]{x1D6FC}}$,
$H_{1}^{\unicode[STIX]{x1D6FC}}$,  $H_{2}^{\unicode[STIX]{x1D6FD}}$ and
$H_{2}^{\unicode[STIX]{x1D6FD}}$ and  $R^{\unicode[STIX]{x1D6FD}}$ as in 6.1.10. We have a Cartesian square.
$R^{\unicode[STIX]{x1D6FD}}$ as in 6.1.10. We have a Cartesian square.

Taking union over all the orbits, with the notations in 6.1.8 and 6.1.10, we deduce a Cartesian square.

Diagram (6.27) induces a commutative diagram of cohomology groups

because (6.27) is Cartesian, (6.16) is given by a counit morphism (equal to the trace morphism), and by [Reference Grothendieck, Artin and VerdierSGA4, XVIII Théorème 2.9], the trace morphism commutes with base change.
Diagram (6.27) induces a commutative diagram of cohomology groups

because by [Reference Grothendieck, Artin and VerdierSGA4, XVIII Théorème 2.9], the trace morphism is compatible with composition.
Remark 6.1.13. When  $S_{1}=G(\mathbb{A})/K_{N_{1}}$ and
$S_{1}=G(\mathbb{A})/K_{N_{1}}$ and  $S_{2}=G(\mathbb{A})/K_{N_{2}}$ with
$S_{2}=G(\mathbb{A})/K_{N_{2}}$ with  $N_{1}\supset N_{2}$, we have the projection
$N_{1}\supset N_{2}$, we have the projection  $f:G(\mathbb{A})/K_{N_{1}}{\twoheadrightarrow}G(\mathbb{A})/K_{N_{2}}$. We have
$f:G(\mathbb{A})/K_{N_{1}}{\twoheadrightarrow}G(\mathbb{A})/K_{N_{2}}$. We have  $\operatorname{Cht}_{M,N_{1},I,W}^{\prime }=\operatorname{Cht}_{M,S_{1},R_{1},I,W}^{\prime }$ with
$\operatorname{Cht}_{M,N_{1},I,W}^{\prime }=\operatorname{Cht}_{M,S_{1},R_{1},I,W}^{\prime }$ with  $R_{1}^{\unicode[STIX]{x1D6FC}}=K_{U,N_{1}}$ for each
$R_{1}^{\unicode[STIX]{x1D6FC}}=K_{U,N_{1}}$ for each  $P(\mathbb{A})$-orbit
$P(\mathbb{A})$-orbit  $\unicode[STIX]{x1D6FC}$ in
$\unicode[STIX]{x1D6FC}$ in  $S_{1}$ and
$S_{1}$ and  $\operatorname{Cht}_{M,N_{2},I,W}^{\prime }=\operatorname{Cht}_{M,S_{2},R_{2},I,W}^{\prime }$ with
$\operatorname{Cht}_{M,N_{2},I,W}^{\prime }=\operatorname{Cht}_{M,S_{2},R_{2},I,W}^{\prime }$ with  $R_{2}^{\unicode[STIX]{x1D6FD}}=K_{U,N_{2}}$ for each
$R_{2}^{\unicode[STIX]{x1D6FD}}=K_{U,N_{2}}$ for each  $P(\mathbb{A})$-orbit
$P(\mathbb{A})$-orbit  $\unicode[STIX]{x1D6FD}$ in
$\unicode[STIX]{x1D6FD}$ in  $S_{2}$. Note that
$S_{2}$. Note that  $R_{1}^{\unicode[STIX]{x1D6FC}}\neq R_{2}^{f(\unicode[STIX]{x1D6FC})}$, and thus the commutative diagram
$R_{1}^{\unicode[STIX]{x1D6FC}}\neq R_{2}^{f(\unicode[STIX]{x1D6FC})}$, and thus the commutative diagram

does NOT coincide with diagram (6.27). In particular, diagram (
6.30) is not Cartesian (the morphism from  $\operatorname{Cht}_{P,N_{1},I,W}^{\prime }$ to the fiber product is finite étale of degree
$\operatorname{Cht}_{P,N_{1},I,W}^{\prime }$ to the fiber product is finite étale of degree  $\sharp (K_{U,N_{2}}/K_{U,N_{1}})$ which is a power of
$\sharp (K_{U,N_{2}}/K_{U,N_{1}})$ which is a power of  $q$).
$q$).
6.1.14
Let  $K^{\prime }\subset K$ be two compact open subgroups of
$K^{\prime }\subset K$ be two compact open subgroups of  $G(\mathbb{O})$. Applying 6.1.10 to
$G(\mathbb{O})$. Applying 6.1.10 to  $S_{1}=G(\mathbb{A})/K^{\prime }$,
$S_{1}=G(\mathbb{A})/K^{\prime }$,  $S_{2}=G(\mathbb{A})/K$ and the projection
$S_{2}=G(\mathbb{A})/K$ and the projection  $f:G(\mathbb{A})/K^{\prime }{\twoheadrightarrow}G(\mathbb{A})/K$, we deduce a finite étale morphism (denoted by
$f:G(\mathbb{A})/K^{\prime }{\twoheadrightarrow}G(\mathbb{A})/K$, we deduce a finite étale morphism (denoted by  $\mathfrak{q}_{f}^{M}$ in 6.1.10)
$\mathfrak{q}_{f}^{M}$ in 6.1.10)
 $$\begin{eqnarray}\operatorname{pr}_{K^{\prime },K}^{M}:\operatorname{Cht}_{M,S_{1},R,I,W}^{\prime }\rightarrow \operatorname{Cht}_{M,S_{2},R,I,W}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{pr}_{K^{\prime },K}^{M}:\operatorname{Cht}_{M,S_{1},R,I,W}^{\prime }\rightarrow \operatorname{Cht}_{M,S_{2},R,I,W}^{\prime },\end{eqnarray}$$ where  $R$ is defined in 6.1.10. The adjunction morphism
$R$ is defined in 6.1.10. The adjunction morphism  $\operatorname{adj}(\operatorname{pr}_{K^{\prime },K}^{M}):\operatorname{Id}\rightarrow (\operatorname{pr}_{K^{\prime },K}^{M})_{\ast }(\operatorname{pr}_{K^{\prime },K}^{M})^{\ast }$ induces
$\operatorname{adj}(\operatorname{pr}_{K^{\prime },K}^{M}):\operatorname{Id}\rightarrow (\operatorname{pr}_{K^{\prime },K}^{M})_{\ast }(\operatorname{pr}_{K^{\prime },K}^{M})^{\ast }$ induces
 $$\begin{eqnarray}\operatorname{adj}(\operatorname{pr}_{K^{\prime },K}^{M}):H_{M,K,I,W}^{\prime \,j}\rightarrow H_{M,K^{\prime },I,W}^{\prime \,j}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{adj}(\operatorname{pr}_{K^{\prime },K}^{M}):H_{M,K,I,W}^{\prime \,j}\rightarrow H_{M,K^{\prime },I,W}^{\prime \,j}.\end{eqnarray}$$ The counit morphism  $\operatorname{Co}(\operatorname{pr}_{K^{\prime },K}^{M}):(\operatorname{pr}_{K^{\prime },K}^{M})_{!}(\operatorname{pr}_{K^{\prime },K}^{M})^{!}\rightarrow \operatorname{Id}$ induces
$\operatorname{Co}(\operatorname{pr}_{K^{\prime },K}^{M}):(\operatorname{pr}_{K^{\prime },K}^{M})_{!}(\operatorname{pr}_{K^{\prime },K}^{M})^{!}\rightarrow \operatorname{Id}$ induces
 $$\begin{eqnarray}\operatorname{Co}(\operatorname{pr}_{K^{\prime },K}^{M}):H_{M,K^{\prime },I,W}^{\prime \,j}\rightarrow H_{M,K,I,W}^{\prime \,j}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Co}(\operatorname{pr}_{K^{\prime },K}^{M}):H_{M,K^{\prime },I,W}^{\prime \,j}\rightarrow H_{M,K,I,W}^{\prime \,j}.\end{eqnarray}$$Lemma 6.1.15. For  $K^{\prime }\subset K$ as in 6.1.14, the following diagram of cohomology groups commutes.
$K^{\prime }\subset K$ as in 6.1.14, the following diagram of cohomology groups commutes.

Proof. (1) By (6.4), we have a Cartesian square.

Since adjunction morphism is compatible with composition, we deduce that the following diagram is commutative.

(2) Applying 6.1.12 to  $S_{1}=G(\mathbb{A})/K^{\prime }$,
$S_{1}=G(\mathbb{A})/K^{\prime }$,  $S_{2}=G(\mathbb{A})/K$ and the projection
$S_{2}=G(\mathbb{A})/K$ and the projection  $f:G(\mathbb{A})/K^{\prime }{\twoheadrightarrow}G(\mathbb{A})/K$, we deduce from (6.28) that the following diagram is commutative.
$f:G(\mathbb{A})/K^{\prime }{\twoheadrightarrow}G(\mathbb{A})/K$, we deduce from (6.28) that the following diagram is commutative.

◻
Lemma 6.1.16. For  $K^{\prime }\subset K$ as in 6.1.14, the following diagram of cohomology groups commutes.
$K^{\prime }\subset K$ as in 6.1.14, the following diagram of cohomology groups commutes.

Proof. (1) By [Reference Grothendieck, Artin and VerdierSGA4, XVIII Théorème 2.9], the trace morphism commutes with base change. Since (6.32) is Cartesian, we deduce that the following diagram is commutative.

(2) Applying 6.1.12 to  $S_{1}=G(\mathbb{A})/K^{\prime }$,
$S_{1}=G(\mathbb{A})/K^{\prime }$,  $S_{2}=G(\mathbb{A})/K$ and the projection
$S_{2}=G(\mathbb{A})/K$ and the projection  $f:G(\mathbb{A})/K^{\prime }{\twoheadrightarrow}G(\mathbb{A})/K$, we deduce from (6.29) that the following diagram is commutative.
$f:G(\mathbb{A})/K^{\prime }{\twoheadrightarrow}G(\mathbb{A})/K$, we deduce from (6.29) that the following diagram is commutative.

◻
6.2 Compatibility of constant term morphisms and actions of Hecke algebras
We first recall the action of the local Hecke algebras. The goal of this subsection is Lemmas 6.2.6 and 6.2.12.
6.2.1
Let  $v$ be a place in
$v$ be a place in  $X$. Let
$X$. Let  $g\in G(F_{v})$. By 6.1.3, the right action of
$g\in G(F_{v})$. By 6.1.3, the right action of  $g$ induces an isomorphism
$g$ induces an isomorphism
 $$\begin{eqnarray}\operatorname{Cht}_{G,\infty ,I,W}\overset{{\sim}}{\rightarrow }\operatorname{Cht}_{G,\infty ,I,W}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{G,\infty ,I,W}\overset{{\sim}}{\rightarrow }\operatorname{Cht}_{G,\infty ,I,W}\!.\end{eqnarray}$$ Let  $\widetilde{K}\subset G(\mathbb{O})$ be a compact open subgroup such that
$\widetilde{K}\subset G(\mathbb{O})$ be a compact open subgroup such that  $g^{-1}\widetilde{K}g\subset G(\mathbb{O})$. The isomorphism (6.33) is
$g^{-1}\widetilde{K}g\subset G(\mathbb{O})$. The isomorphism (6.33) is  $\widetilde{K}$-equivariant, where
$\widetilde{K}$-equivariant, where  $k\in \widetilde{K}$ acts on the second stack by
$k\in \widetilde{K}$ acts on the second stack by  $g^{-1}kg$. It induces an isomorphism
$g^{-1}kg$. It induces an isomorphism
 $$\begin{eqnarray}\operatorname{Cht}_{G,\infty ,I,W}/\widetilde{K}\overset{{\sim}}{\rightarrow }\operatorname{Cht}_{G,\infty ,I,W}/g^{-1}\widetilde{K}g,\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cht}_{G,\infty ,I,W}/\widetilde{K}\overset{{\sim}}{\rightarrow }\operatorname{Cht}_{G,\infty ,I,W}/g^{-1}\widetilde{K}g,\end{eqnarray}$$ i.e.  $\operatorname{Cht}_{G,\widetilde{K},I,W}\overset{{\sim}}{\rightarrow }\operatorname{Cht}_{G,g^{-1}\widetilde{K}g,I,W}$. It induces (by adjunction) an isomorphism of cohomology groups
$\operatorname{Cht}_{G,\widetilde{K},I,W}\overset{{\sim}}{\rightarrow }\operatorname{Cht}_{G,g^{-1}\widetilde{K}g,I,W}$. It induces (by adjunction) an isomorphism of cohomology groups
 $$\begin{eqnarray}\operatorname{adj}(g):H_{G,g^{-1}\widetilde{K}g,I,W}^{j}\overset{{\sim}}{\rightarrow }H_{G,\widetilde{K},I,W}^{j}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{adj}(g):H_{G,g^{-1}\widetilde{K}g,I,W}^{j}\overset{{\sim}}{\rightarrow }H_{G,\widetilde{K},I,W}^{j}.\end{eqnarray}$$6.2.2
We denote by  $\mathbb{O}^{v}$ the ring of integral adèles outside
$\mathbb{O}^{v}$ the ring of integral adèles outside  $v$. Let
$v$. Let  $K=K^{v}K_{v}\subset G(\mathbb{O}^{v})G({\mathcal{O}}_{v})=G(\mathbb{O})$ be an open compact subgroup. Let
$K=K^{v}K_{v}\subset G(\mathbb{O}^{v})G({\mathcal{O}}_{v})=G(\mathbb{O})$ be an open compact subgroup. Let  $h=\mathbf{1}_{K_{v}gK_{v}}\in C_{c}(K_{v}\backslash G(F_{v})/K_{v},\mathbb{Q}_{\ell })$ be the characteristic function of
$h=\mathbf{1}_{K_{v}gK_{v}}\in C_{c}(K_{v}\backslash G(F_{v})/K_{v},\mathbb{Q}_{\ell })$ be the characteristic function of  $K_{v}gK_{v}$ for some
$K_{v}gK_{v}$ for some  $g\in G(F_{v})$. The action of
$g\in G(F_{v})$. The action of  $h$ on
$h$ on  $H_{G,K,I,W}^{j}$ is given by the following composition of morphisms
$H_{G,K,I,W}^{j}$ is given by the following composition of morphisms
 $$\begin{eqnarray}T(h):H_{G,K,I,W}^{j}\xrightarrow[{}]{\operatorname{adj}}H_{G,K\cap g^{-1}Kg,I,W}^{j}\underset{{\sim}}{\xrightarrow[{}]{\operatorname{adj}(g)}}H_{G,gKg^{-1}\cap K,I,W}^{j}\xrightarrow[{}]{\operatorname{Co}}H_{G,K,I,W}^{j},\end{eqnarray}$$
$$\begin{eqnarray}T(h):H_{G,K,I,W}^{j}\xrightarrow[{}]{\operatorname{adj}}H_{G,K\cap g^{-1}Kg,I,W}^{j}\underset{{\sim}}{\xrightarrow[{}]{\operatorname{adj}(g)}}H_{G,gKg^{-1}\cap K,I,W}^{j}\xrightarrow[{}]{\operatorname{Co}}H_{G,K,I,W}^{j},\end{eqnarray}$$ where  $\operatorname{adj}=\operatorname{adj}(\operatorname{pr}_{K\cap g^{-1}Kg,K}^{G})$ and
$\operatorname{adj}=\operatorname{adj}(\operatorname{pr}_{K\cap g^{-1}Kg,K}^{G})$ and  $\operatorname{Co}=\operatorname{Co}(\operatorname{pr}_{gKg^{-1}\cap K,K}^{G})$, the isomorphism
$\operatorname{Co}=\operatorname{Co}(\operatorname{pr}_{gKg^{-1}\cap K,K}^{G})$, the isomorphism  $\operatorname{adj}(g)$ is induced by (6.34) applied to
$\operatorname{adj}(g)$ is induced by (6.34) applied to  $\widetilde{K}=gKg^{-1}\cap K$. Note that (6.35) depends only on the class
$\widetilde{K}=gKg^{-1}\cap K$. Note that (6.35) depends only on the class  $K_{v}gK_{v}$ of
$K_{v}gK_{v}$ of  $g$ in
$g$ in  $G(F_{v})$. The action of
$G(F_{v})$. The action of  $T(h)$ is equivalent to the one constructed by Hecke correspondence (see [Reference LafforgueLaf18, 2.20 and 4.4]).
$T(h)$ is equivalent to the one constructed by Hecke correspondence (see [Reference LafforgueLaf18, 2.20 and 4.4]).
6.2.3
Let  $\widetilde{K}$ and
$\widetilde{K}$ and  $g$ as in 6.2.1. The right action of
$g$ as in 6.2.1. The right action of  $g$ (by right multiplication by
$g$ (by right multiplication by  $g$) on
$g$) on  $G(\mathbb{A})$ induces an isomorphism
$G(\mathbb{A})$ induces an isomorphism
 $$\begin{eqnarray}G(\mathbb{A})/\widetilde{K}\overset{{\sim}}{\rightarrow }G(\mathbb{A})/g^{-1}\widetilde{K}g.\end{eqnarray}$$
$$\begin{eqnarray}G(\mathbb{A})/\widetilde{K}\overset{{\sim}}{\rightarrow }G(\mathbb{A})/g^{-1}\widetilde{K}g.\end{eqnarray}$$ Applying 6.1.10 to  $S_{1}=G(\mathbb{A})/\widetilde{K}$,
$S_{1}=G(\mathbb{A})/\widetilde{K}$,  $S_{2}=G(\mathbb{A})/g^{-1}\widetilde{K}g$ and the isomorphism (6.36), we deduce an isomorphism of cohomology groups
$S_{2}=G(\mathbb{A})/g^{-1}\widetilde{K}g$ and the isomorphism (6.36), we deduce an isomorphism of cohomology groups
 $$\begin{eqnarray}\operatorname{adj}(g):H_{M,g^{-1}\widetilde{K}g,I,W}^{\prime \,j}\overset{{\sim}}{\rightarrow }H_{M,\widetilde{K},I,W}^{\prime \,j}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{adj}(g):H_{M,g^{-1}\widetilde{K}g,I,W}^{\prime \,j}\overset{{\sim}}{\rightarrow }H_{M,\widetilde{K},I,W}^{\prime \,j}.\end{eqnarray}$$6.2.4
Let  $K$ and
$K$ and  $h$ as in 6.2.2. The action of
$h$ as in 6.2.2. The action of  $h$ on
$h$ on  $H_{M,K,I,W}^{\prime \,j}$ is given by the following composition of morphisms
$H_{M,K,I,W}^{\prime \,j}$ is given by the following composition of morphisms
 $$\begin{eqnarray}T(h):H_{M,K,I,W}^{\prime \,j}\xrightarrow[{}]{\operatorname{adj}}H_{M,K\cap g^{-1}Kg,I,W}^{\prime \,j}\underset{{\sim}}{\xrightarrow[{}]{\operatorname{adj}(g)}}H_{M,gKg^{-1}\cap K,I,W}^{\prime \,j}\xrightarrow[{}]{\operatorname{Co}}H_{M,K,I,W}^{\prime \,j},\end{eqnarray}$$
$$\begin{eqnarray}T(h):H_{M,K,I,W}^{\prime \,j}\xrightarrow[{}]{\operatorname{adj}}H_{M,K\cap g^{-1}Kg,I,W}^{\prime \,j}\underset{{\sim}}{\xrightarrow[{}]{\operatorname{adj}(g)}}H_{M,gKg^{-1}\cap K,I,W}^{\prime \,j}\xrightarrow[{}]{\operatorname{Co}}H_{M,K,I,W}^{\prime \,j},\end{eqnarray}$$ where  $\operatorname{adj}=\operatorname{adj}(\operatorname{pr}_{K\cap g^{-1}Kg,K}^{M})$ and
$\operatorname{adj}=\operatorname{adj}(\operatorname{pr}_{K\cap g^{-1}Kg,K}^{M})$ and  $\operatorname{Co}=\operatorname{Co}(\operatorname{pr}_{gKg^{-1}\cap K,K}^{M})$, the isomorphism
$\operatorname{Co}=\operatorname{Co}(\operatorname{pr}_{gKg^{-1}\cap K,K}^{M})$, the isomorphism  $\operatorname{adj}(g)$ is induced by (6.37) applied to
$\operatorname{adj}(g)$ is induced by (6.37) applied to  $\widetilde{K}=gKg^{-1}\cap K$. Note that
$\widetilde{K}=gKg^{-1}\cap K$. Note that  $\widetilde{K}$ may not be normal in
$\widetilde{K}$ may not be normal in  $G(\mathbb{O})$. Note that (6.38) depends only on the class
$G(\mathbb{O})$. Note that (6.38) depends only on the class  $K_{v}gK_{v}$ of
$K_{v}gK_{v}$ of  $g$ in
$g$ in  $G(F_{v})$.
$G(F_{v})$.
Lemma 6.2.5. Let  $\widetilde{K}$ and
$\widetilde{K}$ and  $g$ as in 6.2.1. The following diagram of cohomology groups commutes.
$g$ as in 6.2.1. The following diagram of cohomology groups commutes.

Proof. (1) Since the isomorphism (6.3) is  $G(\mathbb{O})$-equivariant, we deduce a Cartesian square.
$G(\mathbb{O})$-equivariant, we deduce a Cartesian square.

We deduce a Cartesian square.

It induces a commutative diagram.

(2) Applying 6.1.12 to  $S_{1}=G(\mathbb{A})/\widetilde{K}$,
$S_{1}=G(\mathbb{A})/\widetilde{K}$,  $S_{2}=G(\mathbb{A})/g^{-1}\widetilde{K}g$ and
$S_{2}=G(\mathbb{A})/g^{-1}\widetilde{K}g$ and  $f$ the isomorphism (6.36), we deduce from (6.29) a commutative diagram.
$f$ the isomorphism (6.36), we deduce from (6.29) a commutative diagram.

Lemma 6.2.6. For any place  $v$ of
$v$ of  $X$, any
$X$, any  $K$ and
$K$ and  $h\in C_{c}(K_{v}\backslash G(F_{v})/K_{v},\mathbb{Q}_{\ell })$ as in 6.2.2, the following diagram of cohomology groups commutes
$h\in C_{c}(K_{v}\backslash G(F_{v})/K_{v},\mathbb{Q}_{\ell })$ as in 6.2.2, the following diagram of cohomology groups commutes

where the horizontal morphisms are defined in 6.2.2 and 6.2.4, the vertical morphisms are the constant term morphism defined in (6.19).
6.2.7
From now on let  $N\subset X$ be a closed subscheme and
$N\subset X$ be a closed subscheme and  $v$ be a place in
$v$ be a place in  $X\smallsetminus N$. We have the (unnormalized) Satake transform:
$X\smallsetminus N$. We have the (unnormalized) Satake transform:
 $$\begin{eqnarray}\displaystyle C_{c}(G({\mathcal{O}}_{v})\backslash G(F_{v})/G({\mathcal{O}}_{v}),\mathbb{Q}_{\ell }) & \displaystyle {\hookrightarrow}C_{c}(M({\mathcal{O}}_{v})\backslash M(F_{v})/M({\mathcal{O}}_{v}),\mathbb{Q}_{\ell }) & \displaystyle \\ \displaystyle h\quad & \displaystyle \mapsto \quad h^{M}:m\mapsto \mathop{\sum }_{u\in U(F_{v})/U({\mathcal{O}}_{v})}h(mu).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C_{c}(G({\mathcal{O}}_{v})\backslash G(F_{v})/G({\mathcal{O}}_{v}),\mathbb{Q}_{\ell }) & \displaystyle {\hookrightarrow}C_{c}(M({\mathcal{O}}_{v})\backslash M(F_{v})/M({\mathcal{O}}_{v}),\mathbb{Q}_{\ell }) & \displaystyle \\ \displaystyle h\quad & \displaystyle \mapsto \quad h^{M}:m\mapsto \mathop{\sum }_{u\in U(F_{v})/U({\mathcal{O}}_{v})}h(mu).\end{eqnarray}$$6.2.8
We have  $K_{M,N}=K_{M,N}^{v}K_{M,N,v}\subset M(\mathbb{O}^{v})M({\mathcal{O}}_{v})$. For any
$K_{M,N}=K_{M,N}^{v}K_{M,N,v}\subset M(\mathbb{O}^{v})M({\mathcal{O}}_{v})$. For any  $K_{M,v}\subset M({\mathcal{O}}_{v})$ open compact subgroup, we have
$K_{M,v}\subset M({\mathcal{O}}_{v})$ open compact subgroup, we have  $K_{M,N}^{v}K_{M,v}\subset M(\mathbb{O}^{v})M({\mathcal{O}}_{v})$. We define
$K_{M,N}^{v}K_{M,v}\subset M(\mathbb{O}^{v})M({\mathcal{O}}_{v})$. We define  $H_{M,K_{M,N}^{v}K_{M,v},I,W}^{j}$ as in Definition 2.6.8 (replacing
$H_{M,K_{M,N}^{v}K_{M,v},I,W}^{j}$ as in Definition 2.6.8 (replacing  $\operatorname{Cht}_{M,N,I,W}$ by
$\operatorname{Cht}_{M,N,I,W}$ by  $\operatorname{Cht}_{M,K_{M,N}^{v}K_{M,v},I,W}$). We define
$\operatorname{Cht}_{M,K_{M,N}^{v}K_{M,v},I,W}$). We define

As in 6.2.1 (by replacing  $G$ by
$G$ by  $M$), for any
$M$), for any  $m\in M(F_{v})$ and
$m\in M(F_{v})$ and  $K_{M,v}$ such that
$K_{M,v}$ such that  $m^{-1}K_{M,v}m\subset M({\mathcal{O}}_{v})$, we have an isomorphism
$m^{-1}K_{M,v}m\subset M({\mathcal{O}}_{v})$, we have an isomorphism  $H_{M,m^{-1}K_{M,N}^{v}K_{M,v}m,I,W}^{j}\overset{{\sim}}{\rightarrow }H_{M,K_{M,N}^{v}K_{M,v},I,W}^{j}$. Taking limit on
$H_{M,m^{-1}K_{M,N}^{v}K_{M,v}m,I,W}^{j}\overset{{\sim}}{\rightarrow }H_{M,K_{M,N}^{v}K_{M,v},I,W}^{j}$. Taking limit on  $K_{M,v}$, we deduce an action of
$K_{M,v}$, we deduce an action of  $M(F_{v})$ on
$M(F_{v})$ on  $\mathop{\varinjlim }\nolimits_{K_{M,v}}H_{M,K_{M,N}^{v}K_{M,v},I,W}^{j}.$
$\mathop{\varinjlim }\nolimits_{K_{M,v}}H_{M,K_{M,N}^{v}K_{M,v},I,W}^{j}.$
We have  $K_{N}=K_{N}^{v}K_{N,v}\subset G(\mathbb{O}^{v})G({\mathcal{O}}_{v})$. For any
$K_{N}=K_{N}^{v}K_{N,v}\subset G(\mathbb{O}^{v})G({\mathcal{O}}_{v})$. For any  $K_{v}\subset G({\mathcal{O}}_{v})$ open compact subgroup, we have
$K_{v}\subset G({\mathcal{O}}_{v})$ open compact subgroup, we have  $K_{N}^{v}K_{v}\subset G(\mathbb{O}^{v})G({\mathcal{O}}_{v})$. Applying 6.1.6 to
$K_{N}^{v}K_{v}\subset G(\mathbb{O}^{v})G({\mathcal{O}}_{v})$. Applying 6.1.6 to  $S=G(\mathbb{A})/K_{N}^{v}K_{v}$, we define
$S=G(\mathbb{A})/K_{N}^{v}K_{v}$, we define  $H_{M,K_{N}^{v}K_{v},I,W}^{\prime \,j}$. We define
$H_{M,K_{N}^{v}K_{v},I,W}^{\prime \,j}$. We define

Note that  $v$ is a place in
$v$ is a place in  $X\smallsetminus N$, so
$X\smallsetminus N$, so  $K_{N,v}=G({\mathcal{O}}_{v})$ and
$K_{N,v}=G({\mathcal{O}}_{v})$ and  $K_{M,N,v}=M({\mathcal{O}}_{v})$. We have
$K_{M,N,v}=M({\mathcal{O}}_{v})$. We have
 $$\begin{eqnarray}H_{M,K_{N}^{v}G({\mathcal{O}}_{v}),I,W}^{\prime \,j}=H_{M,N,I,W}^{\prime \,j}=H_{M,N,I,W}^{j}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N})=H_{M,K_{M,N}^{v}M({\mathcal{O}}_{v}),I,W}^{j}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N}),\end{eqnarray}$$
$$\begin{eqnarray}H_{M,K_{N}^{v}G({\mathcal{O}}_{v}),I,W}^{\prime \,j}=H_{M,N,I,W}^{\prime \,j}=H_{M,N,I,W}^{j}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N})=H_{M,K_{M,N}^{v}M({\mathcal{O}}_{v}),I,W}^{j}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N}),\end{eqnarray}$$ where  $H_{M,N,I,W}^{\prime \,j}$ is defined in Definition 3.4.9. We deduce
$H_{M,N,I,W}^{\prime \,j}$ is defined in Definition 3.4.9. We deduce

where  $\operatorname{Ind}_{P(F_{v})}^{G(F_{v})}$ is the (unnormalized) parabolic induction.
$\operatorname{Ind}_{P(F_{v})}^{G(F_{v})}$ is the (unnormalized) parabolic induction.
6.2.9
Let  $V$ be a
$V$ be a  $\mathbb{Q}_{\ell }$-vector space equipped with a continuous action of
$\mathbb{Q}_{\ell }$-vector space equipped with a continuous action of  $M(F_{v})$, denoted by
$M(F_{v})$, denoted by  $\unicode[STIX]{x1D70E}:M(F_{v})\rightarrow \text{GL}(V)$. We recall that
$\unicode[STIX]{x1D70E}:M(F_{v})\rightarrow \text{GL}(V)$. We recall that
 $$\begin{eqnarray}\operatorname{Ind}_{P(F_{v})}^{G(F_{v})}V=\{f:G(F_{v})\rightarrow V\text{ continuous},f(pg)=\unicode[STIX]{x1D70E}(p)f(g),p\in P(F_{v}),g\in G(F_{v})\}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ind}_{P(F_{v})}^{G(F_{v})}V=\{f:G(F_{v})\rightarrow V\text{ continuous},f(pg)=\unicode[STIX]{x1D70E}(p)f(g),p\in P(F_{v}),g\in G(F_{v})\}.\end{eqnarray}$$We have a morphism
 $$\begin{eqnarray}(\operatorname{Ind}_{P(F_{v})}^{G(F_{v})}V)^{G({\mathcal{O}}_{v})}\rightarrow V^{M({\mathcal{O}}_{v})}:\quad f\mapsto f(1).\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{Ind}_{P(F_{v})}^{G(F_{v})}V)^{G({\mathcal{O}}_{v})}\rightarrow V^{M({\mathcal{O}}_{v})}:\quad f\mapsto f(1).\end{eqnarray}$$Lemma 6.2.10. Morphism (6.43) is an isomorphism. Moreover, for  $h\in C_{c}(G({\mathcal{O}}_{v})\backslash G(F_{v})/G({\mathcal{O}}_{v}),\mathbb{Q}_{\ell })$, the action of
$h\in C_{c}(G({\mathcal{O}}_{v})\backslash G(F_{v})/G({\mathcal{O}}_{v}),\mathbb{Q}_{\ell })$, the action of  $T(h)$ on
$T(h)$ on  $(\operatorname{Ind}_{P(F_{v})}^{G(F_{v})}V)^{G({\mathcal{O}}_{v})}$ coincides with the action of
$(\operatorname{Ind}_{P(F_{v})}^{G(F_{v})}V)^{G({\mathcal{O}}_{v})}$ coincides with the action of  $T(h^{M})$ on
$T(h^{M})$ on  $V^{M({\mathcal{O}}_{v})}$.
$V^{M({\mathcal{O}}_{v})}$.
Proof. Morphism (6.43) admits an inverse  $f(1)\mapsto f$ given by
$f(1)\mapsto f$ given by
 $$\begin{eqnarray}f(x)=f(x_{P}x_{K})=\unicode[STIX]{x1D70E}(x_{P})f(x_{K})=\unicode[STIX]{x1D70E}(x_{P})f(1),\end{eqnarray}$$
$$\begin{eqnarray}f(x)=f(x_{P}x_{K})=\unicode[STIX]{x1D70E}(x_{P})f(x_{K})=\unicode[STIX]{x1D70E}(x_{P})f(1),\end{eqnarray}$$ where  $x=x_{P}x_{K}\in G(F_{v})=P(F_{v})G({\mathcal{O}}_{v})$. Thus
$x=x_{P}x_{K}\in G(F_{v})=P(F_{v})G({\mathcal{O}}_{v})$. Thus  $(\operatorname{Ind}_{P(F_{v})}^{G(F_{v})}V)^{G({\mathcal{O}}_{v})}=V^{M({\mathcal{O}}_{v})}$.
$(\operatorname{Ind}_{P(F_{v})}^{G(F_{v})}V)^{G({\mathcal{O}}_{v})}=V^{M({\mathcal{O}}_{v})}$.
Moreover, for  $g=g_{P}g_{K}\in G(F_{v})$ and
$g=g_{P}g_{K}\in G(F_{v})$ and  $f\in (\operatorname{Ind}_{P(F_{v})}^{G(F_{v})}V)^{G({\mathcal{O}}_{v})}$, we have
$f\in (\operatorname{Ind}_{P(F_{v})}^{G(F_{v})}V)^{G({\mathcal{O}}_{v})}$, we have
 $$\begin{eqnarray}gf(1)=f(g_{P}g_{K})=\unicode[STIX]{x1D70E}(g_{P})f(g_{K})=\unicode[STIX]{x1D70E}(g_{P})f(1).\end{eqnarray}$$
$$\begin{eqnarray}gf(1)=f(g_{P}g_{K})=\unicode[STIX]{x1D70E}(g_{P})f(g_{K})=\unicode[STIX]{x1D70E}(g_{P})f(1).\end{eqnarray}$$ Note that  $G(F_{v})=M(F_{v})U(F_{v})G({\mathcal{O}}_{v})$. Denote by
$G(F_{v})=M(F_{v})U(F_{v})G({\mathcal{O}}_{v})$. Denote by  $dg$ (respectively
$dg$ (respectively  $dm,du,dk$) the Haar measure on
$dm,du,dk$) the Haar measure on  $G(F_{v})$ (respectively
$G(F_{v})$ (respectively  $M(F_{v}),U(F_{v}),G({\mathcal{O}}_{v})$) such that the volume of
$M(F_{v}),U(F_{v}),G({\mathcal{O}}_{v})$) such that the volume of  $G(O_{v})$ (respectively
$G(O_{v})$ (respectively  $M({\mathcal{O}}_{v}),U({\mathcal{O}}_{v}),G({\mathcal{O}}_{v})$) is
$M({\mathcal{O}}_{v}),U({\mathcal{O}}_{v}),G({\mathcal{O}}_{v})$) is  $1$. We have
$1$. We have  $dg=dm\,du\,dk$. Taking the integral over
$dg=dm\,du\,dk$. Taking the integral over  $G(F_{v})$ of the product by
$G(F_{v})$ of the product by  $h(g)$ of (6.44), we deduce that the action of
$h(g)$ of (6.44), we deduce that the action of  $T(h)$ on
$T(h)$ on  $(\operatorname{Ind}_{P(F_{v})}^{G(F_{v})}V)^{G({\mathcal{O}}_{v})}$ coincides with the action of
$(\operatorname{Ind}_{P(F_{v})}^{G(F_{v})}V)^{G({\mathcal{O}}_{v})}$ coincides with the action of  $T(h^{M})$ on
$T(h^{M})$ on  $V^{M({\mathcal{O}}_{v})}$.◻
$V^{M({\mathcal{O}}_{v})}$.◻
6.2.11
Let  $V=(\mathop{\varinjlim }\nolimits_{K_{M,v}}H_{M,K_{M,N}^{v}K_{M,v},I,W}^{j})\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N})$. We have:
$V=(\mathop{\varinjlim }\nolimits_{K_{M,v}}H_{M,K_{M,N}^{v}K_{M,v},I,W}^{j})\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N})$. We have:
 $$\begin{eqnarray}V^{M({\mathcal{O}}_{v})}=H_{M,K_{M,N}^{v}M({\mathcal{O}}_{v}),I,W}^{j}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N})=H_{M,N,I,W}^{\prime \,j};\end{eqnarray}$$
$$\begin{eqnarray}V^{M({\mathcal{O}}_{v})}=H_{M,K_{M,N}^{v}M({\mathcal{O}}_{v}),I,W}^{j}\overset{P({\mathcal{O}}_{N})}{\times }G({\mathcal{O}}_{N})=H_{M,N,I,W}^{\prime \,j};\end{eqnarray}$$
By Lemma 6.2.10, the action of  $T(h)$ on
$T(h)$ on  $H_{M,N,I,W}^{\prime \,j}$ (defined in (6.38)) coincides with the action of
$H_{M,N,I,W}^{\prime \,j}$ (defined in (6.38)) coincides with the action of  $T(h^{M})$ on
$T(h^{M})$ on  $H_{M,N,I,W}^{\prime \,j}$ (induced by the action of
$H_{M,N,I,W}^{\prime \,j}$ (induced by the action of  $T(h^{M})$ on
$T(h^{M})$ on  $H_{M,N,I,W}^{j}$). Combining this fact and Lemma 6.2.6, we deduce the following.
$H_{M,N,I,W}^{j}$). Combining this fact and Lemma 6.2.6, we deduce the following.
Lemma 6.2.12. For any place  $v$ of
$v$ of  $X\smallsetminus N$ and any
$X\smallsetminus N$ and any  $h\in C_{c}(G({\mathcal{O}}_{v})\backslash G(F_{v})/G({\mathcal{O}}_{v}),\mathbb{Q}_{\ell })$, the following diagram of cohomology groups is commutative
$h\in C_{c}(G({\mathcal{O}}_{v})\backslash G(F_{v})/G({\mathcal{O}}_{v}),\mathbb{Q}_{\ell })$, the following diagram of cohomology groups is commutative

where the vertical morphisms are the constant term morphism defined in Definition 3.5.10.
Remark 6.2.13. For a direct proof of Lemma 6.2.12, see [Reference XueXue17, Lemme 8.1.1].
Remark 6.2.14. We could normalize the constant term morphism  $C_{G,N}^{P,\,j}$ and the Satake transform (6.41) by
$C_{G,N}^{P,\,j}$ and the Satake transform (6.41) by  $\unicode[STIX]{x1D6FF}^{1/2}$ as usual, where
$\unicode[STIX]{x1D6FF}^{1/2}$ as usual, where  $\unicode[STIX]{x1D6FF}$ is the modular function of
$\unicode[STIX]{x1D6FF}$ is the modular function of  $P(F_{v})$. But we do not need this normalization in this paper.
$P(F_{v})$. But we do not need this normalization in this paper.
Remark 6.2.15. When  $I=\emptyset$ and
$I=\emptyset$ and  $W=\mathbf{1}$,
$W=\mathbf{1}$,  $S=G(\mathbb{A})/K$, we have
$S=G(\mathbb{A})/K$, we have  $H_{M,S,R,I,W}^{\prime \,0}$ included in
$H_{M,S,R,I,W}^{\prime \,0}$ included in  $C(M(F)U(\mathbb{A})\backslash G(\mathbb{A})/K\unicode[STIX]{x1D6EF},\mathbb{Q}_{\ell })$. In (6.17), we defined
$C(M(F)U(\mathbb{A})\backslash G(\mathbb{A})/K\unicode[STIX]{x1D6EF},\mathbb{Q}_{\ell })$. In (6.17), we defined  $C_{G,S,R,I,W}^{P,\,0}$. Commutative diagram (6.18) implies that for a given Haar measure
$C_{G,S,R,I,W}^{P,\,0}$. Commutative diagram (6.18) implies that for a given Haar measure  $du$ on
$du$ on  $U(\mathbb{A})$,
$U(\mathbb{A})$,  $(\int _{R}\,du)\cdot C_{G,S,R,I,W}^{P,\,0}$ is independent on
$(\int _{R}\,du)\cdot C_{G,S,R,I,W}^{P,\,0}$ is independent on  $R$. This identifies
$R$. This identifies  $C_{G,S,I,W}^{P,\,0}$ with the classical constant term morphism (3.44) associated to
$C_{G,S,I,W}^{P,\,0}$ with the classical constant term morphism (3.44) associated to  $du$.
$du$.
6.3 Cuspidal cohomology and rational Hecke-finite cohomology
Definition 6.3.1. We define
 $$\begin{eqnarray}H_{G,N,I,W}^{j,\;\operatorname{Hf-rat}}:=\{c\in H_{G,N,I,W}^{j},\;\dim _{\mathbb{ Q}_{\ell }}C_{c}(K_{N}\backslash G(\mathbb{A})/K_{N},\mathbb{Q}_{\ell })\cdot c<+\infty \}.\end{eqnarray}$$
$$\begin{eqnarray}H_{G,N,I,W}^{j,\;\operatorname{Hf-rat}}:=\{c\in H_{G,N,I,W}^{j},\;\dim _{\mathbb{ Q}_{\ell }}C_{c}(K_{N}\backslash G(\mathbb{A})/K_{N},\mathbb{Q}_{\ell })\cdot c<+\infty \}.\end{eqnarray}$$Proposition 6.0.1 will follow from Lemmas 6.3.2 and 6.3.3 below.
Lemma 6.3.2. We have an inclusion
 $$\begin{eqnarray}H_{G,N,I,W}^{j,\;\operatorname{cusp}}\subset H_{G,N,I,W}^{j,\;\text{Hf-rat}}.\end{eqnarray}$$
$$\begin{eqnarray}H_{G,N,I,W}^{j,\;\operatorname{cusp}}\subset H_{G,N,I,W}^{j,\;\text{Hf-rat}}.\end{eqnarray}$$Proof. By Theorem 5.0.1, the  $\mathbb{Q}_{\ell }$-vector space
$\mathbb{Q}_{\ell }$-vector space  $H_{G,N,I,W}^{j,\,\operatorname{cusp}}$ has finite dimension. By Lemma 6.2.6, it is stable under the action of the Hecke algebra
$H_{G,N,I,W}^{j,\,\operatorname{cusp}}$ has finite dimension. By Lemma 6.2.6, it is stable under the action of the Hecke algebra  $C_{c}(K_{N}\backslash G(\mathbb{A})/K_{N},\mathbb{Q}_{\ell })$. We complete the proof by Definition 6.3.1.◻
$C_{c}(K_{N}\backslash G(\mathbb{A})/K_{N},\mathbb{Q}_{\ell })$. We complete the proof by Definition 6.3.1.◻
Lemma 6.3.3. We have an inclusion
 $$\begin{eqnarray}H_{G,N,I,W}^{j,\;\operatorname{cusp}}\supset H_{G,N,I,W}^{j,\;\text{Hf-rat}}.\end{eqnarray}$$
$$\begin{eqnarray}H_{G,N,I,W}^{j,\;\operatorname{cusp}}\supset H_{G,N,I,W}^{j,\;\text{Hf-rat}}.\end{eqnarray}$$ The proof of Lemma 6.3.3 will use the fact that any non-zero image of a constant term morphism  $C_{P}^{G,j}$ is supported on the components
$C_{P}^{G,j}$ is supported on the components  $H_{M}^{\prime \,j,\,\unicode[STIX]{x1D708}}$ indexed by
$H_{M}^{\prime \,j,\,\unicode[STIX]{x1D708}}$ indexed by  $\unicode[STIX]{x1D708}$ in a translated cone in
$\unicode[STIX]{x1D708}$ in a translated cone in  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{G}/Z_{M}}^{+,\mathbb{Q}}$. The proof will also need the following lemma, which is for example a consequence of the Satake isomorphism.
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{G}/Z_{M}}^{+,\mathbb{Q}}$. The proof will also need the following lemma, which is for example a consequence of the Satake isomorphism.
Lemma 6.3.4. Under the Satake transformation (6.41), the algebra  $C_{c}(M(O_{v})\backslash M(F_{v})/M(O_{v}),\mathbb{Q}_{\ell })$ is finite over
$C_{c}(M(O_{v})\backslash M(F_{v})/M(O_{v}),\mathbb{Q}_{\ell })$ is finite over  $C_{c}(G(O_{v})\backslash G(F_{v})/G(O_{v}),\mathbb{Q}_{\ell })$.
$C_{c}(G(O_{v})\backslash G(F_{v})/G(O_{v}),\mathbb{Q}_{\ell })$.
Proof of Lemma 6.3.3.
Let  $a\in H_{G,N,I,W}^{\text{Hf-rat}}$. We argue by contradiction. Suppose that
$a\in H_{G,N,I,W}^{\text{Hf-rat}}$. We argue by contradiction. Suppose that  $a\notin H_{G,N,I,W}^{j,\;\operatorname{cusp}}$. Then there exists a maximal parabolic subgroup
$a\notin H_{G,N,I,W}^{j,\;\operatorname{cusp}}$. Then there exists a maximal parabolic subgroup  $P$ such that
$P$ such that  $C_{G}^{P,\;j}(a)\neq 0$. We denote by
$C_{G}^{P,\;j}(a)\neq 0$. We denote by  $M$ the Levi quotient of
$M$ the Levi quotient of  $P$. Let
$P$. Let  $v$ be a place in
$v$ be a place in  $X\smallsetminus N$.
$X\smallsetminus N$.
(1) On the one hand, by Definition 6.3.1, the  $\mathbb{Q}_{\ell }$-vector subspace
$\mathbb{Q}_{\ell }$-vector subspace  $C_{c}(G(O_{v})\backslash G(F_{v})/G(O_{v}),\mathbb{Q}_{\ell })\cdot a$ has finite dimension. Then Lemma 6.2.12 applied to
$C_{c}(G(O_{v})\backslash G(F_{v})/G(O_{v}),\mathbb{Q}_{\ell })\cdot a$ has finite dimension. Then Lemma 6.2.12 applied to  $K=K_{N}$ and Lemma 6.3.4 imply that the
$K=K_{N}$ and Lemma 6.3.4 imply that the  $\mathbb{Q}_{\ell }$-vector space
$\mathbb{Q}_{\ell }$-vector space  $C_{c}(M(O_{v})\backslash M(F_{v})/M(O_{v}),\mathbb{Q}_{\ell })\cdot C_{G}^{P,\;j}(a)$ has finite dimension.
$C_{c}(M(O_{v})\backslash M(F_{v})/M(O_{v}),\mathbb{Q}_{\ell })\cdot C_{G}^{P,\;j}(a)$ has finite dimension.
(2) On the other hand, since  $a\in H_{G,N,I,W}^{j}$, there exists
$a\in H_{G,N,I,W}^{j}$, there exists  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ such that
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ such that  $a\in \operatorname{Im}(H_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}}\rightarrow H_{G,N,I,W}^{j})$. We deduce from (3.38) that
$a\in \operatorname{Im}(H_{G,N,I,W}^{j,\;\leqslant \unicode[STIX]{x1D707}}\rightarrow H_{G,N,I,W}^{j})$. We deduce from (3.38) that  $C_{G}^{P,\;j}(a)$ is the image of an element
$C_{G}^{P,\;j}(a)$ is the image of an element  $a^{0}\in H_{M,N,I,W}^{\prime \;j,\;\leqslant \unicode[STIX]{x1D707}}$ in
$a^{0}\in H_{M,N,I,W}^{\prime \;j,\;\leqslant \unicode[STIX]{x1D707}}$ in  $H_{M,N,I,W}^{\prime \;j}$. By 3.4.8,
$H_{M,N,I,W}^{\prime \;j}$. By 3.4.8,  $a^{0}$ is supported on the components
$a^{0}$ is supported on the components  $H_{M,N,I,W}^{\prime \;j,\,\unicode[STIX]{x1D708}}$ of
$H_{M,N,I,W}^{\prime \;j,\,\unicode[STIX]{x1D708}}$ of  $H_{M,N,I,W}^{\prime \;j}$ indexed by
$H_{M,N,I,W}^{\prime \;j}$ indexed by  $\unicode[STIX]{x1D708}$ in the translated cone
$\unicode[STIX]{x1D708}$ in the translated cone  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}\subset \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$. So is
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}\subset \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$. So is  $C_{G}^{P,\;j}(a)$.
$C_{G}^{P,\;j}(a)$.
Let  $g\in Z_{M}(F_{v})$ such that
$g\in Z_{M}(F_{v})$ such that  $g\notin Z_{M}(O_{v})Z_{G}(F_{v})$. We denote by
$g\notin Z_{M}(O_{v})Z_{G}(F_{v})$. We denote by  $\unicode[STIX]{x1D709}(g)$ the image of
$\unicode[STIX]{x1D709}(g)$ the image of  $g$ by the composition of morphisms
$g$ by the composition of morphisms

The choice of  $g$ implies that
$g$ implies that  $\unicode[STIX]{x1D709}(g)\neq 0$. Note that
$\unicode[STIX]{x1D709}(g)\neq 0$. Note that  $P$ is maximal, so
$P$ is maximal, so  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}\simeq \mathbb{Q}$. For all
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}\simeq \mathbb{Q}$. For all  $\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$, the action of
$\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$, the action of  $g$ on
$g$ on  $\operatorname{Cht}_{M}/\unicode[STIX]{x1D6EF}$ induces an isomorphism
$\operatorname{Cht}_{M}/\unicode[STIX]{x1D6EF}$ induces an isomorphism  $g:\operatorname{Cht}_{M}^{\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}\overset{{\sim}}{\rightarrow }\operatorname{Cht}_{M}^{\unicode[STIX]{x1D708}+\unicode[STIX]{x1D709}(g)}/\unicode[STIX]{x1D6EF}$ (the inverse is induced by
$g:\operatorname{Cht}_{M}^{\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}\overset{{\sim}}{\rightarrow }\operatorname{Cht}_{M}^{\unicode[STIX]{x1D708}+\unicode[STIX]{x1D709}(g)}/\unicode[STIX]{x1D6EF}$ (the inverse is induced by  $g^{-1}$). We denote by
$g^{-1}$). We denote by  $T(g)\in C_{c}(M(O_{v})\backslash M(F_{v})/M({\mathcal{O}}_{v}),\mathbb{Q}_{\ell })$ the Hecke operator associated to
$T(g)\in C_{c}(M(O_{v})\backslash M(F_{v})/M({\mathcal{O}}_{v}),\mathbb{Q}_{\ell })$ the Hecke operator associated to  $g$. Then
$g$. Then  $T(g)$ induces an isomorphism
$T(g)$ induces an isomorphism  $H_{M,N,I,W}^{\prime \,j,\,\unicode[STIX]{x1D708}}\overset{{\sim}}{\rightarrow }H_{M,N,I,W}^{\prime \,j,\,\unicode[STIX]{x1D708}+\unicode[STIX]{x1D709}(g)}$.
$H_{M,N,I,W}^{\prime \,j,\,\unicode[STIX]{x1D708}}\overset{{\sim}}{\rightarrow }H_{M,N,I,W}^{\prime \,j,\,\unicode[STIX]{x1D708}+\unicode[STIX]{x1D709}(g)}$.
Suppose that  $\unicode[STIX]{x1D709}(g)>0$ (if not, we take
$\unicode[STIX]{x1D709}(g)>0$ (if not, we take  $g^{-1}$ in place of
$g^{-1}$ in place of  $g$). Since
$g$). Since  $C_{G}^{P,\;j}(a)\neq 0$, there exists
$C_{G}^{P,\;j}(a)\neq 0$, there exists  $m\in \mathbb{Z}_{{>}0}$ such that
$m\in \mathbb{Z}_{{>}0}$ such that  $T(g)^{m}\cdot C_{G}^{P,\;j}(a)$ is supported on the cone
$T(g)^{m}\cdot C_{G}^{P,\;j}(a)$ is supported on the cone  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}+m\unicode[STIX]{x1D709}(g)}\supset \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}$, but not supported on
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}+m\unicode[STIX]{x1D709}(g)}\supset \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}$, but not supported on  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}$. Therefore
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}}$. Therefore  $T(g)^{2m}\cdot C_{G}^{P,\;j}(a)$ is supported on the cone
$T(g)^{2m}\cdot C_{G}^{P,\;j}(a)$ is supported on the cone  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}+2m\unicode[STIX]{x1D709}(g)}$, but not supported on
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}+2m\unicode[STIX]{x1D709}(g)}$, but not supported on  $\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}+m\unicode[STIX]{x1D709}(g)}$, etc. We deduce that
$\widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\unicode[STIX]{x1D707}+m\unicode[STIX]{x1D709}(g)}$, etc. We deduce that
 $$\begin{eqnarray}C_{G}^{P,\;j}(a),T(g)^{m}\cdot C_{G}^{P,\;j}(a),T(g)^{2m}\cdot C_{G}^{P,\;j}(a),T(g)^{3m}\cdot C_{G}^{P,\;j}(a),\ldots\end{eqnarray}$$
$$\begin{eqnarray}C_{G}^{P,\;j}(a),T(g)^{m}\cdot C_{G}^{P,\;j}(a),T(g)^{2m}\cdot C_{G}^{P,\;j}(a),T(g)^{3m}\cdot C_{G}^{P,\;j}(a),\ldots\end{eqnarray}$$ are linearly independent. So the  $\mathbb{Q}_{\ell }$-vector space generated by
$\mathbb{Q}_{\ell }$-vector space generated by  $T(g)^{\mathbb{Z}}\cdot C_{G}^{P,\;j}(a)$ has infinite dimension. Hence
$T(g)^{\mathbb{Z}}\cdot C_{G}^{P,\;j}(a)$ has infinite dimension. Hence  $C_{c}(M(O_{v})\backslash M(F_{v})/M(O_{v}),\mathbb{Q}_{\ell })\cdot C_{G}^{P,\;j}(a)$ has infinite dimension.
$C_{c}(M(O_{v})\backslash M(F_{v})/M(O_{v}),\mathbb{Q}_{\ell })\cdot C_{G}^{P,\;j}(a)$ has infinite dimension.
(3) We deduce from (1) and (2) a contradiction. So  $a\in H_{G,N,I,W}^{j\;\operatorname{cusp}}$.◻
$a\in H_{G,N,I,W}^{j\;\operatorname{cusp}}$.◻
Definition 6.3.5 [Reference LafforgueLaf18, Définition 8.19].
We define
 $$\begin{eqnarray}H_{G,N,I,W}^{j,\;\operatorname{Hf}}:=\{c\in H_{G,N,I,W}^{j},\;C_{c}(K_{N}\backslash G(\mathbb{A})/K_{N},\mathbb{Z}_{\ell })\cdot c\text{ is a finitely generated }\mathbb{Z}_{\ell }\text{-submodule}\}.\end{eqnarray}$$
$$\begin{eqnarray}H_{G,N,I,W}^{j,\;\operatorname{Hf}}:=\{c\in H_{G,N,I,W}^{j},\;C_{c}(K_{N}\backslash G(\mathbb{A})/K_{N},\mathbb{Z}_{\ell })\cdot c\text{ is a finitely generated }\mathbb{Z}_{\ell }\text{-submodule}\}.\end{eqnarray}$$ By definition,  $H_{G,N,I,W}^{j,\;\text{Hf}}\subset H_{G,N,I,W}^{j,\;\text{Hf-rat}}$. Thus Proposition 6.0.1 has the following corollary.
$H_{G,N,I,W}^{j,\;\text{Hf}}\subset H_{G,N,I,W}^{j,\;\text{Hf-rat}}$. Thus Proposition 6.0.1 has the following corollary.
 $$\begin{eqnarray}H_{G,N,I,W}^{j,\;\text{Hf}}\subset H_{G,N,I,W}^{j,\;\text{Hf-rat}}=H_{G,N,I,W}^{j,\;\operatorname{cusp}}.\end{eqnarray}$$
$$\begin{eqnarray}H_{G,N,I,W}^{j,\;\text{Hf}}\subset H_{G,N,I,W}^{j,\;\text{Hf-rat}}=H_{G,N,I,W}^{j,\;\operatorname{cusp}}.\end{eqnarray}$$ In particular,  $H_{G,N,I,W}^{j,\;\text{Hf}}$ has finite dimension.
$H_{G,N,I,W}^{j,\;\text{Hf}}$ has finite dimension.
Acknowledgements
This paper is based on my PhD thesis [Reference XueXue17], which I wrote at Université Paris-Sud. I thank my advisors, Vincent Lafforgue and Gérard Laumon, for suggesting this project and for the support during the writing of my thesis. I thank Jack Thorne for his helpful comments on a draft of this paper. I thank the referees for their suggestions for improving this paper.
Appendix A Exact sequences associated to an open and a closed substack of the stack of shtukas
For simplicity of the notation, we do not write the indices  $N$,
$N$,  $I$ and
$I$ and  $W$.
$W$.
A.0.1
In the following, we use  $\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. But everything remains true if we replace it by
$\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. But everything remains true if we replace it by  $(1/r)\widehat{R}_{G^{\text{ad}}}^{+}$.
$(1/r)\widehat{R}_{G^{\text{ad}}}^{+}$.
A.0.2
As in [Reference Drinfeld and GaitsgoryDG15, 7.4.10], we equip the set  $\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ with the order topology, i.e. the one where a base of open subsets is formed by subsets of the form
$\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ with the order topology, i.e. the one where a base of open subsets is formed by subsets of the form  $\{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}|\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D706}_{0}\}$ for
$\{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}|\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D706}_{0}\}$ for  $\unicode[STIX]{x1D706}_{0}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. Let
$\unicode[STIX]{x1D706}_{0}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. Let  $S$ be a subset of
$S$ be a subset of  $\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. We define
$\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. We define
 $$\begin{eqnarray}\operatorname{Bun}_{G}^{S}:=\underset{\unicode[STIX]{x1D706}\in S}{\bigcup }\mathop{\operatorname{Bun}}_{G}^{=\unicode[STIX]{x1D706}},\quad \operatorname{Cht}_{G}^{S}:=\underset{\unicode[STIX]{x1D706}\in S}{\bigcup }\mathop{\operatorname{Cht}}_{G}^{=\unicode[STIX]{x1D706}},\quad \operatorname{Cht}_{M}^{\prime \,S}:=\underset{\unicode[STIX]{x1D706}\in S}{\bigcup }\mathop{\operatorname{Cht}}_{M}^{\prime \,=\unicode[STIX]{x1D706}},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Bun}_{G}^{S}:=\underset{\unicode[STIX]{x1D706}\in S}{\bigcup }\mathop{\operatorname{Bun}}_{G}^{=\unicode[STIX]{x1D706}},\quad \operatorname{Cht}_{G}^{S}:=\underset{\unicode[STIX]{x1D706}\in S}{\bigcup }\mathop{\operatorname{Cht}}_{G}^{=\unicode[STIX]{x1D706}},\quad \operatorname{Cht}_{M}^{\prime \,S}:=\underset{\unicode[STIX]{x1D706}\in S}{\bigcup }\mathop{\operatorname{Cht}}_{M}^{\prime \,=\unicode[STIX]{x1D706}},\end{eqnarray}$$ where  $\operatorname{Cht}_{G}^{=\unicode[STIX]{x1D706}}$ and
$\operatorname{Cht}_{G}^{=\unicode[STIX]{x1D706}}$ and  $\operatorname{Cht}_{M}^{\prime \,=\unicode[STIX]{x1D706}}$ are defined in Definition 4.1.10. If the subset
$\operatorname{Cht}_{M}^{\prime \,=\unicode[STIX]{x1D706}}$ are defined in Definition 4.1.10. If the subset  $S$ is open (respectively closed) in
$S$ is open (respectively closed) in  $\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, then
$\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, then  $\operatorname{Bun}_{G}^{S}$ is open (respectively closed) in
$\operatorname{Bun}_{G}^{S}$ is open (respectively closed) in  $\operatorname{Bun}_{G}$. So
$\operatorname{Bun}_{G}$. So  $\operatorname{Cht}_{G}^{S}$ is open (respectively closed) in
$\operatorname{Cht}_{G}^{S}$ is open (respectively closed) in  $\operatorname{Cht}_{G}$ and
$\operatorname{Cht}_{G}$ and  $\operatorname{Cht}_{M}^{\prime \,S}$ is open (respectively closed) in
$\operatorname{Cht}_{M}^{\prime \,S}$ is open (respectively closed) in  $\operatorname{Cht}_{M}^{\prime }$.
$\operatorname{Cht}_{M}^{\prime }$.
If  $S$ is a bounded locally closed subset of
$S$ is a bounded locally closed subset of  $\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, then
$\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, then  $\operatorname{Cht}_{G}^{S}$ and
$\operatorname{Cht}_{G}^{S}$ and  $\operatorname{Cht}_{M}^{\prime \,S}$ are Deligne–Mumford stacks of finite type.
$\operatorname{Cht}_{M}^{\prime \,S}$ are Deligne–Mumford stacks of finite type.
A.0.3
Let  $\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. Let
$\unicode[STIX]{x1D707}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$. Let  $S_{2}=\{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}\mid \unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D707}\}$. By definition it is an open subset of
$S_{2}=\{\unicode[STIX]{x1D706}\in \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}\mid \unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D707}\}$. By definition it is an open subset of  $\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ for the order topology of
$\widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$ for the order topology of  $G^{\text{ad}}$. It is also open in
$G^{\text{ad}}$. It is also open in  $\widehat{\unicode[STIX]{x1D6EC}}_{\overline{M}}^{+,\mathbb{Q}}$ for the order topology of
$\widehat{\unicode[STIX]{x1D6EC}}_{\overline{M}}^{+,\mathbb{Q}}$ for the order topology of  $\overline{M}=M/Z_{G}$ (because
$\overline{M}=M/Z_{G}$ (because  $\unicode[STIX]{x1D706}\leqslant \text{}^{\overline{M}}\unicode[STIX]{x1D707}$ implies
$\unicode[STIX]{x1D706}\leqslant \text{}^{\overline{M}}\unicode[STIX]{x1D707}$ implies  $\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D707}$).
$\unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D707}$).
Let  $S_{1}$ be an open subset of
$S_{1}$ be an open subset of  $S_{2}$ for the order topology of
$S_{2}$ for the order topology of  $G^{\text{ad}}$. Thus the morphism of stacks
$G^{\text{ad}}$. Thus the morphism of stacks  $\operatorname{Cht}_{G}^{S_{1}}\xrightarrow[{}]{j_{G}}\operatorname{Cht}_{G}^{S_{2}}$ (respectively
$\operatorname{Cht}_{G}^{S_{1}}\xrightarrow[{}]{j_{G}}\operatorname{Cht}_{G}^{S_{2}}$ (respectively  $\operatorname{Cht}_{M}^{\prime \,S_{1}}\xrightarrow[{}]{j_{M}}\operatorname{Cht}_{M}^{\prime \,S_{2}}$) is an open immersion. By definition,
$\operatorname{Cht}_{M}^{\prime \,S_{1}}\xrightarrow[{}]{j_{M}}\operatorname{Cht}_{M}^{\prime \,S_{2}}$) is an open immersion. By definition,  $\operatorname{Cht}_{G}^{S_{2}-S_{1}}$ (respectively
$\operatorname{Cht}_{G}^{S_{2}-S_{1}}$ (respectively  $\operatorname{Cht}_{M}^{\prime \,S_{2}-S_{1}}$) is the closed substack in
$\operatorname{Cht}_{M}^{\prime \,S_{2}-S_{1}}$) is the closed substack in  $\operatorname{Cht}_{G}^{S_{2}}$ (respectively
$\operatorname{Cht}_{G}^{S_{2}}$ (respectively  $\operatorname{Cht}_{M}^{\prime \,S_{2}}$) which is the complement of
$\operatorname{Cht}_{M}^{\prime \,S_{2}}$) which is the complement of  $\operatorname{Cht}_{G}^{S_{1}}$ (respectively
$\operatorname{Cht}_{G}^{S_{1}}$ (respectively  $\operatorname{Cht}_{M}^{\prime \,S_{1}}$).
$\operatorname{Cht}_{M}^{\prime \,S_{1}}$).
We define  $\operatorname{Cht}_{P}^{\prime \,S_{2}}$ (respectively
$\operatorname{Cht}_{P}^{\prime \,S_{2}}$ (respectively  $\operatorname{Cht}_{P}^{\prime \,S_{1}}$) to be the inverse image of
$\operatorname{Cht}_{P}^{\prime \,S_{1}}$) to be the inverse image of  $\operatorname{Cht}_{G}^{S_{2}}$ (respectively
$\operatorname{Cht}_{G}^{S_{2}}$ (respectively  $\operatorname{Cht}_{G}^{S_{1}}$) in
$\operatorname{Cht}_{G}^{S_{1}}$) in  $\operatorname{Cht}_{P}^{\prime }$. Just as in Lemma 1.7.4, we have
$\operatorname{Cht}_{P}^{\prime }$. Just as in Lemma 1.7.4, we have  $\unicode[STIX]{x1D70B}_{2}:\operatorname{Cht}_{P}^{\prime \,S_{2}}\rightarrow \operatorname{Cht}_{M}^{\prime \,S_{2}}$ (respectively
$\unicode[STIX]{x1D70B}_{2}:\operatorname{Cht}_{P}^{\prime \,S_{2}}\rightarrow \operatorname{Cht}_{M}^{\prime \,S_{2}}$ (respectively  $\unicode[STIX]{x1D70B}_{1}:\operatorname{Cht}_{P}^{\prime \,S_{1}}\rightarrow \operatorname{Cht}_{M}^{\prime \,S_{1}}$). We have
$\unicode[STIX]{x1D70B}_{1}:\operatorname{Cht}_{P}^{\prime \,S_{1}}\rightarrow \operatorname{Cht}_{M}^{\prime \,S_{1}}$). We have  $\operatorname{Cht}_{P}^{\prime \,S_{1}}\xrightarrow[{}]{j_{P}}\operatorname{Cht}_{P}^{\prime \,S_{2}}$, which is an open immersion. We define
$\operatorname{Cht}_{P}^{\prime \,S_{1}}\xrightarrow[{}]{j_{P}}\operatorname{Cht}_{P}^{\prime \,S_{2}}$, which is an open immersion. We define  $\operatorname{Cht}_{P}^{\prime \,S_{2}-S_{1}}:=\operatorname{Cht}_{P}^{\prime \,S_{2}}\,\cap \,\unicode[STIX]{x1D70B}^{-1}(\operatorname{Cht}_{M}^{\prime \,S_{2}-S_{1}})$. It is a closed substack in the complement of
$\operatorname{Cht}_{P}^{\prime \,S_{2}-S_{1}}:=\operatorname{Cht}_{P}^{\prime \,S_{2}}\,\cap \,\unicode[STIX]{x1D70B}^{-1}(\operatorname{Cht}_{M}^{\prime \,S_{2}-S_{1}})$. It is a closed substack in the complement of  $\operatorname{Cht}_{P}^{\prime \,S_{1}}$ in
$\operatorname{Cht}_{P}^{\prime \,S_{1}}$ in  $\operatorname{Cht}_{P}^{\prime \,S_{2}}$, but may not be equal to it.
$\operatorname{Cht}_{P}^{\prime \,S_{2}}$, but may not be equal to it.
Lemma A.0.4. The following diagram of algebraic stacks is commutative.

Moreover, the left bottom square and the right top square are Cartesian.
A.0.5
For any  $j$, any
$j$, any  $\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$ and any bounded locally closed subset
$\unicode[STIX]{x1D708}\in \widehat{\unicode[STIX]{x1D6EC}}_{Z_{M}/Z_{G}}^{\mathbb{Q}}$ and any bounded locally closed subset  $S\subset \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, we define
$S\subset \widehat{\unicode[STIX]{x1D6EC}}_{G^{\text{ad}}}^{+,\mathbb{Q}}$, we define
 $$\begin{eqnarray}H_{G}^{j,\,S}:=H_{c}^{j}(\operatorname{Cht}_{G,\overline{\unicode[STIX]{x1D702}^{I}}}^{S}/\unicode[STIX]{x1D6EF}_{G},{\mathcal{F}}_{G});\quad H_{M}^{\prime \,j,\,S,\,\unicode[STIX]{x1D708}}:=H_{c}^{j}(\operatorname{Cht}_{M,\overline{\unicode[STIX]{x1D702}^{I}}}^{^{\prime }\,S,\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}_{G},{\mathcal{F}}_{M}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}H_{G}^{j,\,S}:=H_{c}^{j}(\operatorname{Cht}_{G,\overline{\unicode[STIX]{x1D702}^{I}}}^{S}/\unicode[STIX]{x1D6EF}_{G},{\mathcal{F}}_{G});\quad H_{M}^{\prime \,j,\,S,\,\unicode[STIX]{x1D708}}:=H_{c}^{j}(\operatorname{Cht}_{M,\overline{\unicode[STIX]{x1D702}^{I}}}^{^{\prime }\,S,\,\unicode[STIX]{x1D708}}/\unicode[STIX]{x1D6EF}_{G},{\mathcal{F}}_{M}^{\prime }).\end{eqnarray}$$A.0.6
By Proposition 3.5.3, the restriction of morphism  $i_{1}$ (respectively
$i_{1}$ (respectively  $i_{2}$) to
$i_{2}$) to  $\overline{\unicode[STIX]{x1D702}^{I}}$ is proper. The restriction of morphism
$\overline{\unicode[STIX]{x1D702}^{I}}$ is proper. The restriction of morphism  $i_{12}$ to
$i_{12}$ to  $\overline{\unicode[STIX]{x1D702}^{I}}$ is also proper because
$\overline{\unicode[STIX]{x1D702}^{I}}$ is also proper because  $\operatorname{Cht}_{P}^{\prime \,S_{2}-S_{1}}\rightarrow \operatorname{Cht}_{G}^{S_{2}-S_{1}}\underset{\operatorname{Cht}_{G}^{S_{2}}}{\times }\operatorname{Cht}_{P}^{\prime \,S_{2}}$ is a closed immersion. Moreover
$\operatorname{Cht}_{P}^{\prime \,S_{2}-S_{1}}\rightarrow \operatorname{Cht}_{G}^{S_{2}-S_{1}}\underset{\operatorname{Cht}_{G}^{S_{2}}}{\times }\operatorname{Cht}_{P}^{\prime \,S_{2}}$ is a closed immersion. Moreover  $i_{1}$,
$i_{1}$,  $i_{2}$ and
$i_{2}$ and  $i_{12}$ are schematic. Applying the construction in §3 to each line in diagram (A.1), respectively, we obtain the constant term morphism
$i_{12}$ are schematic. Applying the construction in §3 to each line in diagram (A.1), respectively, we obtain the constant term morphism  $C_{G}^{P,\,j,\,S_{1}}:H_{G}^{j,\,S_{1}}\rightarrow H_{M}^{\prime \,j,\,S_{1}}$,
$C_{G}^{P,\,j,\,S_{1}}:H_{G}^{j,\,S_{1}}\rightarrow H_{M}^{\prime \,j,\,S_{1}}$,  $C_{G}^{P,\,j,\,S_{2}}$ and
$C_{G}^{P,\,j,\,S_{2}}$ and  $C_{G}^{P,\,j,\,S_{2}-S_{1}}$ (note that the morphism
$C_{G}^{P,\,j,\,S_{2}-S_{1}}$ (note that the morphism  $\unicode[STIX]{x1D70B}_{12,d}:\operatorname{Cht}_{P}^{\prime \,S_{2}-S_{1}}\rightarrow \widetilde{\operatorname{Cht}}_{M}^{\prime \,S_{2}-S_{1}}$ is smooth because the right top square of diagram (A.1) is Cartesian).
$\unicode[STIX]{x1D70B}_{12,d}:\operatorname{Cht}_{P}^{\prime \,S_{2}-S_{1}}\rightarrow \widetilde{\operatorname{Cht}}_{M}^{\prime \,S_{2}-S_{1}}$ is smooth because the right top square of diagram (A.1) is Cartesian).
A.0.7
Diagram (A.1) induces a diagram of cohomology groups with compact support for which we will study the commutativity.

The horizontal maps are the long exact sequences associated to an open substack and the complementary closed substack. The vertical maps are the constant term morphisms.
Lemma A.0.8. For any  $j$, the following diagram is commutative.
$j$, the following diagram is commutative.

Proof. We denote the morphisms of paws by  $p_{G}:\operatorname{Cht}_{G}^{S_{2}}\rightarrow \unicode[STIX]{x1D702}^{I}$ and
$p_{G}:\operatorname{Cht}_{G}^{S_{2}}\rightarrow \unicode[STIX]{x1D702}^{I}$ and  $p_{M}:\operatorname{Cht}_{M}^{\prime \,S_{2}}\rightarrow \unicode[STIX]{x1D702}^{I}$. For
$p_{M}:\operatorname{Cht}_{M}^{\prime \,S_{2}}\rightarrow \unicode[STIX]{x1D702}^{I}$. For  $S=S_{1}$ or
$S=S_{1}$ or  $S_{2}$ or
$S_{2}$ or  $S_{2}-S_{1}$, denote
$S_{2}-S_{1}$, denote  ${\mathcal{F}}_{G}^{S}:=\left.{\mathcal{F}}_{G}\vphantom{\big|}\right|_{\operatorname{Cht}_{G}^{S}}$ and
${\mathcal{F}}_{G}^{S}:=\left.{\mathcal{F}}_{G}\vphantom{\big|}\right|_{\operatorname{Cht}_{G}^{S}}$ and  ${\mathcal{F}}_{M}^{S}:=\left.{\mathcal{F}}_{M}^{\prime }\vphantom{\big|}\right|_{\operatorname{Cht}_{M}^{\prime \,S}}$. Note that
${\mathcal{F}}_{M}^{S}:=\left.{\mathcal{F}}_{M}^{\prime }\vphantom{\big|}\right|_{\operatorname{Cht}_{M}^{\prime \,S}}$. Note that  ${\mathcal{F}}_{G}^{S_{1}}=(j_{G})^{\ast }{\mathcal{F}}_{G}^{S_{2}}$ and
${\mathcal{F}}_{G}^{S_{1}}=(j_{G})^{\ast }{\mathcal{F}}_{G}^{S_{2}}$ and  ${\mathcal{F}}_{G}^{S_{2}-S_{1}}=(i_{G})^{\ast }{\mathcal{F}}_{G}^{S_{2}}$. Similarly
${\mathcal{F}}_{G}^{S_{2}-S_{1}}=(i_{G})^{\ast }{\mathcal{F}}_{G}^{S_{2}}$. Similarly  ${\mathcal{F}}_{M}^{S_{1}}=(j_{M})^{\ast }{\mathcal{F}}_{M}^{S_{2}}$ and
${\mathcal{F}}_{M}^{S_{1}}=(j_{M})^{\ast }{\mathcal{F}}_{M}^{S_{2}}$ and  ${\mathcal{F}}_{M}^{S_{2}-S_{1}}=(i_{M})^{\ast }{\mathcal{F}}_{M}^{S_{2}}$. Lemma A.0.8 will follow from the commutativity of the following diagram of complexes in
${\mathcal{F}}_{M}^{S_{2}-S_{1}}=(i_{M})^{\ast }{\mathcal{F}}_{M}^{S_{2}}$. Lemma A.0.8 will follow from the commutativity of the following diagram of complexes in  $D_{c}^{b}(\unicode[STIX]{x1D702}^{I},\mathbb{Q}_{\ell })$.
$D_{c}^{b}(\unicode[STIX]{x1D702}^{I},\mathbb{Q}_{\ell })$.

The commutativity of the left square is induced by (1) and (2) below. The commutativity of the right square is induced by (3) and (4) below.
We consider the left square of (A.3)

where (1) and (2) are detailed below.
(1) The following diagram of functors is commutative

where  $(\ast )$ is given by
$(\ast )$ is given by  $(j_{G})_{!}(i_{1})_{!}(i_{1})^{\ast }\simeq (i_{2})_{!}(j_{P})_{!}(i_{1})^{\ast }\simeq (i_{2})_{!}(i_{2})^{\ast }(j_{G})_{!}$, the last isomorphism is the proper base change for the left bottom square of diagram (A.1). The commutativity of (1) follows from the fact that the adjunction morphism commutes with base change and the trace morphism commutes with base change [Reference Grothendieck, Artin and VerdierSGA4, XVIII Théorème 2.9].
$(j_{G})_{!}(i_{1})_{!}(i_{1})^{\ast }\simeq (i_{2})_{!}(j_{P})_{!}(i_{1})^{\ast }\simeq (i_{2})_{!}(i_{2})^{\ast }(j_{G})_{!}$, the last isomorphism is the proper base change for the left bottom square of diagram (A.1). The commutativity of (1) follows from the fact that the adjunction morphism commutes with base change and the trace morphism commutes with base change [Reference Grothendieck, Artin and VerdierSGA4, XVIII Théorème 2.9].
(2) Taking (3.9) into account, we have a commutative diagram, where  $\unicode[STIX]{x1D70B}_{2}$ (respectively
$\unicode[STIX]{x1D70B}_{2}$ (respectively  $\unicode[STIX]{x1D70B}_{1}$) is the composition
$\unicode[STIX]{x1D70B}_{1}$) is the composition  $\widetilde{\unicode[STIX]{x1D70B}_{2,\text{}\underline{d}}^{0}}\circ \unicode[STIX]{x1D70B}_{2,\text{}\underline{d}}$ (respectively
$\widetilde{\unicode[STIX]{x1D70B}_{2,\text{}\underline{d}}^{0}}\circ \unicode[STIX]{x1D70B}_{2,\text{}\underline{d}}$ (respectively  $\widetilde{\unicode[STIX]{x1D70B}_{1,\text{}\underline{d}}^{0}}\circ \unicode[STIX]{x1D70B}_{1,\text{}\underline{d}}$) for some
$\widetilde{\unicode[STIX]{x1D70B}_{1,\text{}\underline{d}}^{0}}\circ \unicode[STIX]{x1D70B}_{1,\text{}\underline{d}}$) for some  $d$ large enough as in Proposition 2.2.1.
$d$ large enough as in Proposition 2.2.1.

The square (c) is Cartesian. The square (b) may not be Cartesian. As in Lemma 3.1.8,  $\unicode[STIX]{x1D70B}_{1,d}$ and
$\unicode[STIX]{x1D70B}_{1,d}$ and  $\unicode[STIX]{x1D70B}_{2,d}$ are smooth. We have
$\unicode[STIX]{x1D70B}_{2,d}$ are smooth. We have  $\dim (\unicode[STIX]{x1D70B}_{1,d})=\dim (\unicode[STIX]{x1D70B}_{2,d})=d\cdot |I|\dim U$. We denote this dimension by
$\dim (\unicode[STIX]{x1D70B}_{1,d})=\dim (\unicode[STIX]{x1D70B}_{2,d})=d\cdot |I|\dim U$. We denote this dimension by  $m$.
$m$.
By (3.22) and (3.23), the morphism  $f_{1}$ (respectively
$f_{1}$ (respectively  $f_{2}$) defined in diagram (A.4) is the composition of
$f_{2}$) defined in diagram (A.4) is the composition of  $\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{1,d}}:(\unicode[STIX]{x1D70B}_{1,d})_{!}(\unicode[STIX]{x1D70B}_{1,d})^{\ast }\rightarrow \operatorname{Id}[-2m](-m)$ (respectively
$\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{1,d}}:(\unicode[STIX]{x1D70B}_{1,d})_{!}(\unicode[STIX]{x1D70B}_{1,d})^{\ast }\rightarrow \operatorname{Id}[-2m](-m)$ (respectively  $\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{2,d}}:(\unicode[STIX]{x1D70B}_{2,d})_{!}(\unicode[STIX]{x1D70B}_{2,d})^{\ast }\rightarrow \operatorname{Id}[-2m](-m)$) with some isomorphisms. By [Reference Grothendieck, Artin and VerdierSGA4, XVIII Théorème 2.9], the trace morphism is compatible with composition, and thus
$\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{2,d}}:(\unicode[STIX]{x1D70B}_{2,d})_{!}(\unicode[STIX]{x1D70B}_{2,d})^{\ast }\rightarrow \operatorname{Id}[-2m](-m)$) with some isomorphisms. By [Reference Grothendieck, Artin and VerdierSGA4, XVIII Théorème 2.9], the trace morphism is compatible with composition, and thus
 $$\begin{eqnarray}\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{2,d}}\circ \operatorname{Tr}_{j_{P}}\simeq \operatorname{Tr}_{\unicode[STIX]{x1D70B}_{2,d}\circ j_{P}}\simeq \operatorname{Tr}_{\widetilde{j_{M}}\circ \unicode[STIX]{x1D70B}_{1,d}}\simeq \operatorname{Tr}_{\widetilde{j_{M}}}\circ \operatorname{Tr}_{\unicode[STIX]{x1D70B}_{1,d}},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{2,d}}\circ \operatorname{Tr}_{j_{P}}\simeq \operatorname{Tr}_{\unicode[STIX]{x1D70B}_{2,d}\circ j_{P}}\simeq \operatorname{Tr}_{\widetilde{j_{M}}\circ \unicode[STIX]{x1D70B}_{1,d}}\simeq \operatorname{Tr}_{\widetilde{j_{M}}}\circ \operatorname{Tr}_{\unicode[STIX]{x1D70B}_{1,d}},\end{eqnarray}$$where the middle isomorphism is due to the commutativity of square (b). Moreover, by [Reference Grothendieck, Artin and VerdierSGA4] the trace morphism is compatible with base change, and thus
 $$\begin{eqnarray}\operatorname{Tr}_{\widetilde{j_{M}}}=(\widetilde{\unicode[STIX]{x1D70B}_{1,d}^{0}})^{\ast }\operatorname{Tr}_{j_{M}}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Tr}_{\widetilde{j_{M}}}=(\widetilde{\unicode[STIX]{x1D70B}_{1,d}^{0}})^{\ast }\operatorname{Tr}_{j_{M}}\!.\end{eqnarray}$$We deduce that (2) is commutative.
Now we consider the right square of (A.3)

where (3) and (4) are detailed below.
(3) The following diagram of functors is commutative.

(4) Taking (3.9) into account, we have a commutative diagram, where  $\unicode[STIX]{x1D70B}_{12}$ is the composition
$\unicode[STIX]{x1D70B}_{12}$ is the composition  $\widetilde{\unicode[STIX]{x1D70B}_{12,\text{}\underline{d}}^{0}}\circ \unicode[STIX]{x1D70B}_{12,\text{}\underline{d}}$.
$\widetilde{\unicode[STIX]{x1D70B}_{12,\text{}\underline{d}}^{0}}\circ \unicode[STIX]{x1D70B}_{12,\text{}\underline{d}}$.

The squares (e) and (f) are Cartesian.
By (3.22) and (3.23),  $f_{12}$ defined in diagram (A.6) is the composition of
$f_{12}$ defined in diagram (A.6) is the composition of  $\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{12,d}}:(\unicode[STIX]{x1D70B}_{12,d})_{!}(\unicode[STIX]{x1D70B}_{12,d})^{\ast }\rightarrow \operatorname{Id}[-2(\dim \unicode[STIX]{x1D70B}_{12,d})](-\text{dim}\unicode[STIX]{x1D70B}_{12,d})$ with some isomorphisms. By [Reference Grothendieck, Artin and VerdierSGA4, XVIII Théorème 2.9], the trace morphism is compatible with base change, and thus
$\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{12,d}}:(\unicode[STIX]{x1D70B}_{12,d})_{!}(\unicode[STIX]{x1D70B}_{12,d})^{\ast }\rightarrow \operatorname{Id}[-2(\dim \unicode[STIX]{x1D70B}_{12,d})](-\text{dim}\unicode[STIX]{x1D70B}_{12,d})$ with some isomorphisms. By [Reference Grothendieck, Artin and VerdierSGA4, XVIII Théorème 2.9], the trace morphism is compatible with base change, and thus
 $$\begin{eqnarray}\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{12,d}}=(\widetilde{i_{M}})^{\ast }\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{2,d}}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{12,d}}=(\widetilde{i_{M}})^{\ast }\operatorname{Tr}_{\unicode[STIX]{x1D70B}_{2,d}}\!.\end{eqnarray}$$We deduce that (4) is commutative. ◻
Remark A.0.9. We do not know if the complete diagram (A.2) is commutative.
Appendix B Lemma of the cubic commutative diagram
Lemma B.0.1. Let  $\mathscr{X},\mathscr{Y},\mathscr{Z},\mathscr{W},\mathscr{X}^{\prime },\mathscr{Y}^{\prime },\mathscr{Z}^{\prime },\mathscr{W}^{\prime }$ be algebraic stacks. Suppose that we have two Cartesian squares.
$\mathscr{X},\mathscr{Y},\mathscr{Z},\mathscr{W},\mathscr{X}^{\prime },\mathscr{Y}^{\prime },\mathscr{Z}^{\prime },\mathscr{W}^{\prime }$ be algebraic stacks. Suppose that we have two Cartesian squares.

If these two squares are the front and back faces of a commutative diagram

then the fibers  $f_{\mathscr{Z}}$,
$f_{\mathscr{Z}}$,  $f_{\mathscr{X}}$,
$f_{\mathscr{X}}$,  $f_{\mathscr{Y}}$ and
$f_{\mathscr{Y}}$ and  $f_{\mathscr{W}}$ form a Cartesian square.
$f_{\mathscr{W}}$ form a Cartesian square.
Concretely, let  $T$ be a scheme. For any morphism
$T$ be a scheme. For any morphism  $T\rightarrow \mathscr{Z}$, we have the compositions of morphisms
$T\rightarrow \mathscr{Z}$, we have the compositions of morphisms  $T\rightarrow \mathscr{Z}\rightarrow \mathscr{X}$,
$T\rightarrow \mathscr{Z}\rightarrow \mathscr{X}$,  $T\rightarrow \mathscr{Z}\rightarrow \mathscr{Y}$ and
$T\rightarrow \mathscr{Z}\rightarrow \mathscr{Y}$ and  $T\rightarrow \mathscr{Z}\rightarrow \mathscr{W}$. We denote by
$T\rightarrow \mathscr{Z}\rightarrow \mathscr{W}$. We denote by  $\mathscr{Z}_{T}$ (respectively
$\mathscr{Z}_{T}$ (respectively  $\mathscr{X}_{T}$,
$\mathscr{X}_{T}$,  $\mathscr{Y}_{T}$,
$\mathscr{Y}_{T}$,  $\mathscr{W}_{T}$) the fiber of
$\mathscr{W}_{T}$) the fiber of  $f_{\mathscr{Z}}$ (respectively
$f_{\mathscr{Z}}$ (respectively  $f_{\mathscr{X}}$,
$f_{\mathscr{X}}$,  $f_{\mathscr{Y}}$,
$f_{\mathscr{Y}}$,  $f_{\mathscr{W}}$) over
$f_{\mathscr{W}}$) over  $T$. The lemma says that
$T$. The lemma says that  $\mathscr{Z}_{T}$ is equivalent to
$\mathscr{Z}_{T}$ is equivalent to  $\mathscr{X}_{T}\underset{\mathscr{W}_{T}}{\times }\mathscr{Y}_{T}$.
$\mathscr{X}_{T}\underset{\mathscr{W}_{T}}{\times }\mathscr{Y}_{T}$.
Proof. We will prove a more general statement. Suppose that we have another Cartesian square

and a commutative diagram.

Then we have a canonical isomorphism:
 $$\begin{eqnarray}\mathscr{Z}^{\prime }\times _{\mathscr{ Z}}\mathscr{Z}^{\prime \prime }\overset{{\sim}}{\rightarrow }(\mathscr{X}^{\prime }\times _{\mathscr{ X}}\mathscr{X}^{\prime \prime })\underset{\mathscr{W}^{\prime }\times _{\mathscr{ W}}\mathscr{W}^{\prime \prime }}{\times }(\mathscr{Y}^{\prime }\times _{\mathscr{ Y}}\mathscr{Y}^{\prime \prime }).\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{Z}^{\prime }\times _{\mathscr{ Z}}\mathscr{Z}^{\prime \prime }\overset{{\sim}}{\rightarrow }(\mathscr{X}^{\prime }\times _{\mathscr{ X}}\mathscr{X}^{\prime \prime })\underset{\mathscr{W}^{\prime }\times _{\mathscr{ W}}\mathscr{W}^{\prime \prime }}{\times }(\mathscr{Y}^{\prime }\times _{\mathscr{ Y}}\mathscr{Y}^{\prime \prime }).\end{eqnarray}$$In fact, by definition, we have
 $$\begin{eqnarray}\mathscr{Z}^{\prime }\times _{\mathscr{ Z}}\mathscr{Z}^{\prime \prime }\simeq (\mathscr{X}^{\prime }\times _{\mathscr{ W}^{\prime }}\mathscr{Y}^{\prime })\underset{\mathscr{X}\times _{\mathscr{ W}}\mathscr{Y}}{\times }(\mathscr{X}^{\prime \prime }\times _{\mathscr{ W}^{\prime \prime }}\mathscr{Y}^{\prime \prime }).\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{Z}^{\prime }\times _{\mathscr{ Z}}\mathscr{Z}^{\prime \prime }\simeq (\mathscr{X}^{\prime }\times _{\mathscr{ W}^{\prime }}\mathscr{Y}^{\prime })\underset{\mathscr{X}\times _{\mathscr{ W}}\mathscr{Y}}{\times }(\mathscr{X}^{\prime \prime }\times _{\mathscr{ W}^{\prime \prime }}\mathscr{Y}^{\prime \prime }).\end{eqnarray}$$ For any scheme  $S$, the
$S$, the  $S$-points of both sides of (B.3) classify the data of
$S$-points of both sides of (B.3) classify the data of  $S$-points
$S$-points  $x^{\prime }$ in
$x^{\prime }$ in  $\mathscr{X}^{\prime }$,
$\mathscr{X}^{\prime }$,  $x^{\prime \prime }$ in
$x^{\prime \prime }$ in  $\mathscr{X}^{\prime \prime }$,
$\mathscr{X}^{\prime \prime }$,  $y^{\prime }$ in
$y^{\prime }$ in  $\mathscr{Y}^{\prime }$,
$\mathscr{Y}^{\prime }$,  $y^{\prime \prime }$ in
$y^{\prime \prime }$ in  $\mathscr{Y}^{\prime \prime }$, an isomorphism between the images of
$\mathscr{Y}^{\prime \prime }$, an isomorphism between the images of  $x^{\prime }$ and
$x^{\prime }$ and  $x^{\prime \prime }$ in
$x^{\prime \prime }$ in  $\mathscr{X}$, an isomorphism between the images of
$\mathscr{X}$, an isomorphism between the images of  $y^{\prime }$ and
$y^{\prime }$ and  $y^{\prime \prime }$ in
$y^{\prime \prime }$ in  $\mathscr{Y}$, an isomorphism between the images of
$\mathscr{Y}$, an isomorphism between the images of  $x^{\prime }$ and
$x^{\prime }$ and  $y^{\prime }$ in
$y^{\prime }$ in  $\mathscr{W}^{\prime }$, an isomorphism between the images of
$\mathscr{W}^{\prime }$, an isomorphism between the images of  $x^{\prime \prime }$ and
$x^{\prime \prime }$ and  $y^{\prime \prime }$ in
$y^{\prime \prime }$ in  $\mathscr{W}^{\prime \prime }$, such that the diagram deduced from these four isomorphisms between the images of
$\mathscr{W}^{\prime \prime }$, such that the diagram deduced from these four isomorphisms between the images of  $x^{\prime }$,
$x^{\prime }$,  $x^{\prime \prime }$,
$x^{\prime \prime }$,  $y^{\prime }$,
$y^{\prime }$,  $y^{\prime \prime }$ in
$y^{\prime \prime }$ in  $\mathscr{W}$ is commutative. We deduce (B.3).
$\mathscr{W}$ is commutative. We deduce (B.3).
The lemma is the special case when  $\mathscr{X}^{\prime \prime }=\mathscr{Y}^{\prime \prime }=\mathscr{W}^{\prime \prime }=\mathscr{Z}^{\prime \prime }=T$.◻
$\mathscr{X}^{\prime \prime }=\mathscr{Y}^{\prime \prime }=\mathscr{W}^{\prime \prime }=\mathscr{Z}^{\prime \prime }=T$.◻