Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-29T06:20:37.532Z Has data issue: false hasContentIssue false
  • English
  • Français

Decomposition of degenerate Gromov–Witten invariants

Part of: Families, fibrations Projective and enumerative geometry

Published online by Cambridge University Press:  19 November 2020

Dan Abramovich ,
Qile Chen ,
Mark Gross  and
Bernd Siebert
Dan Abramovich
Affiliation:
Department of Mathematics, Brown University, Box 1917, Providence, RI02912, USAdan_abramovich@brown.edu
Qile Chen
Affiliation:
Department of Mathematics, Boston College, Chestnut Hill, MA02467-3806, USAqile.chen@bc.edu
Mark Gross
Affiliation:
DPMMS, Centre for Mathematical Sciences, Wilberforce Road, CambridgeCB3 0WB, UKmgross@dpmms.cam.ac.uk
Bernd Siebert
Affiliation:
Department of Mathematics, The University of Texas at Austin, 2515 Speedway, Austin, TX78712, USAsiebert@math.utexas.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a decomposition formula of logarithmic Gromov–Witten invariants in a degeneration setting. A one-parameter log smooth family 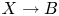$X \longrightarrow B$ with singular fibre over 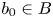$b_0\in B$ yields a family 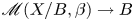$\mathscr {M}(X/B,\beta ) \longrightarrow B$ of moduli stacks of stable logarithmic maps. We give a virtual decomposition of the fibre of this family over 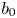$b_0$ in terms of rigid tropical maps to the tropicalization of 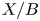$X/B$. This generalizes one aspect of known results in the case that the fibre 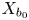$X_{b_0}$ is a normal crossings union of two divisors. We exhibit our formulas in explicit examples.

Keywords

logarithmic Gromov–Witten invariantmoduli stacklogarithmic stable mapdegenerationdecompositiontropical curvetropical maprigid tropical curveArtin fan

MSC classification

Primary: 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants
Secondary: 14D23: Stacks and moduli problems
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 10 , October 2020 , pp. 2020 - 2075
Check for updates
Copyright
© The Author(s) 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research by D.A. was supported in part by NSF grants DMS-1162367, DMS-1500525 and DMS-1759514. Research by Q.C. was supported in part by NSF grant DMS-1403271 and DMS-1560830. M.G. was supported by NSF grant DMS-1262531, EPSRC grant EP/N03189X/1 and a Royal Society Wolfson Research Merit Award. Research by B.S. was partially supported by NSF grant DMS-1903437.

References

Abramovich, D., Caporaso, L. and Payne, S., The tropicalization of the moduli space of curves, Ann. Sci. Éc. Norm. Supér. (4) 48 (2015), 765–809.CrossRefGoogle Scholar
Abramovich, D. and Chen, Q., Stable logarithmic maps to Deligne-Faltings pairs II, Asian J. Math. 18 (2014), 465–488.CrossRefGoogle Scholar
Abramovich, D., Chen, Q., Gross, M. and Siebert, B., Punctured logarithmic maps, Preprint (2020), arXiv:2009.07720.Google Scholar
Abramovich, D., Chen, Q., Marcus, S. and Wise, J., Boundedness of the space of stable logarithmic maps, J. Eur. Math. Soc. (JEMS) 19 (2017), 2783–2809.CrossRefGoogle Scholar
Abramovich, D. and Karu, K., Weak semistable reduction in characteristic 0, Invent. Math. 139 (2000), 241–273.CrossRefGoogle Scholar
Abramovich, D. and Wise, J., Birational invariance in logarithmic Gromov–Witten theory, Compos. Math. 154 (2018), 595–620.CrossRefGoogle Scholar
Arbarello, E., Cornalba, M. and Griffiths, P., Geometry of algebraic curves, Volume II (Springer, 2011).CrossRefGoogle Scholar
Behrend, K., Gromov–Witten invariants in algebraic geometry, Invent. Math. 127 (1997), 601–617.CrossRefGoogle Scholar
Behrend, K. and Fantechi, B., The intrinsic normal cone, Invent. Math. 128 (1997), 45–88.CrossRefGoogle Scholar
Behrend, K. and Manin, Y., Stacks of stable maps and Gromov–Witten invariants, Duke Math. J. 85 (1996), 1–60.CrossRefGoogle Scholar
Bryan, J. and Leung, N. C., The enumerative geometry of $K3$ surfaces and modular forms, J. Amer. Math. Soc. 13 (2000), 371–410.CrossRefGoogle Scholar
Burgos Gil, J. and Sombra, M., When do the recession cones of a polyhedral complex form a fan? Discrete Comput. Geom. 46 (2011), 789–798.CrossRefGoogle Scholar
Cadman, C., Using stacks to impose tangency conditions on curves, Amer. J. Math. 129 (2007), 405–427.CrossRefGoogle Scholar
Cavalieri, R., Chan, M., Ulirsch, M. and Wise, J., A moduli stack of tropical curves, Forum Math. Sigma 8 (2020), e23.Google Scholar
Chen, Q., Stable logarithmic maps to Deligne–Faltings pairs I, Ann. of Math. (2) 180 (2014), 455–521.CrossRefGoogle Scholar
Costello, K., Higher genus Gromov–Witten invariants as genus zero invariants of symmetric products, Ann. of Math. (2) 164 (2006), 561–601.CrossRefGoogle Scholar
Gross, M. and Siebert, B., Logarithmic Gromov–Witten invariants, J. Amer. Math. Soc. 26 (2013), 451–510.CrossRefGoogle Scholar
Gross, M. and Siebert, B., Intrinsic mirror symmetry, Preprint (2019), arXiv:1909.07649.Google Scholar
Kato, K., Logarithmic structures of Fontaine–Illusie, in Algebraic analysis, geometry, and number theory, Baltimore, MD, 1988 (Johns Hopkins University Press, 1989), 191–224.Google Scholar
Kato, F., Exactness, integrality, and log modifications, Preprint (1999), arXiv:math/9907124.Google Scholar
Kato, F., Log smooth deformation and moduli of log smooth curves, Internat. J. Math. 11 (2000), 215–232.CrossRefGoogle Scholar
Kempf, G., Knudsen, F., Mumford, D. and Saint-Donat, B., Toroidal embeddings I, Lecture Notes in Mathematics, vol. 339 (Springer, 1973).CrossRefGoogle Scholar
Kim, B., Lho, H. and Ruddat, H., The degeneration formula for stable log maps, Preprint (2018), arXiv:1803.04210.Google Scholar
Knudsen, F., The projectivity of the moduli space of stable curves. II. The stacks $M_{g,n}$, Math. Scand. 52 (1983), 161–199.CrossRefGoogle Scholar
Kresch, A., Cycle groups for Artin stacks, Invent. Math. 138 (1999), 495–536.CrossRefGoogle Scholar
Li, J., A degeneration formula of GW-invariants, J. Differential Geom. 60 (2002), 199–293.CrossRefGoogle Scholar
Mandel, T. and Ruddat, H., Descendant log Gromov–Witten invariants for toric varieties and tropical curves, Trans. Amer. Math. Soc. 373 (2020), 1109–1152.CrossRefGoogle Scholar
Manolache, C., Virtual pull-backs, J. Algebraic Geom. 21 (2012), 201–245.CrossRefGoogle Scholar
Mikhalkin, G., Enumerative tropical algebraic geometry in $\mathbb {R}^2$, J. Amer. Math. Soc. 18 (2005), 313–377.CrossRefGoogle Scholar
Mochizuki, S., The geometry of the compactification of the Hurwitz scheme, Publ. Res. Inst. Math. Sci. 31 (1995), 355–441.CrossRefGoogle Scholar
Nishinou, T. and Siebert, B., Toric degenerations of toric varieties and tropical curves, Duke Math. J. 135 (2006), 1–51.CrossRefGoogle Scholar
Ogus, A., Lectures on logarithmic algebraic geometry (Cambridge University Press, 2018).CrossRefGoogle Scholar
Olsson, M., Logarithmic geometry and algebraic stacks, Ann. Sci. École Norm. Sup. (4) 36 (2003), 747–791.CrossRefGoogle Scholar
Parker, B., Holomorphic curves in exploded manifolds: compactness, Adv. Math. 283 (2015), 377–457.CrossRefGoogle Scholar
Parker, B., Tropical gluing formulae for Gromov–Witten invariants, Preprint (2017), arXiv:1703.05433.Google Scholar
Parker, B., Holomorphic curves in exploded manifolds: regularity, Geom. Topol. 23 (2019), 1621–1690.CrossRefGoogle Scholar
Parker, B., Holomorphic curves in exploded manifolds: Kuranishi structure, Preprint (2019), arXiv:1301.4748.Google Scholar
Parker, B., Holomorphic curves in exploded manifolds: virtual fundamental class, Geom. Topol. 23 (2019), 1877–1960.CrossRefGoogle Scholar
Ranganathan, D., Logarithmic Gromov–Witten theory with expansions, Preprint (2020), arXiv:1903.09006.Google Scholar
The Stacks Project Authors, Stacks Project, http://stacks.math.columbia.edu (2017).Google Scholar
Ulirsch, M., Tropical geometry of logarithmic schemes, PhD thesis, Brown University (2015).Google Scholar
Ulirsch, M., Functorial tropicalization of logarithmic schemes: the case of constant coefficients, Proc. Lond. Math. Soc. (3) 114 (2017), 1081–1113.Google Scholar
Ulirsch, M., A non-Archimedean analogue of Teichmüller space and its tropicalization, Preprint (2020), arXiv:2004.07508.Google Scholar
Wise, J., Moduli of morphisms of logarithmic schemes, Algebra Number Theory 10 (2016), 695–735.CrossRefGoogle Scholar
Wise, J., Uniqueness of minimal morphisms of logarithmic schemes, Algebr. Geom. 6 (2019), 50–63.CrossRefGoogle Scholar
Yu, T. Y., Enumeration of holomorphic cylinders in log Calabi-Yau surfaces. II. Positivity, integrality and the gluing formula, Geom. Topol., to appear. Preprint (2020), arXiv:1608.07651.Google Scholar