Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T14:07:45.133Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometric Manin’s conjecture and rational curves

Part of: Curves

Published online by Cambridge University Press:  10 April 2019

Brian Lehmann  and
Sho Tanimoto
Brian Lehmann
Affiliation:
Department of Mathematics, Boston College, 1400 Commonwealth Ave., Chestnut Hill, MA, 02467, USA email lehmannb@bc.edu
Sho Tanimoto
Affiliation:
Department of Mathematics, Faculty of Science, Kumamoto University, Kurokami 2-39-1, Kumamoto 860-8555, Japan email stanimoto@kumamoto-u.ac.jp Priority Organization for Innovation and Excellence, Kumamoto University, Japan
Get access Rights & Permissions [Opens in a new window]

Abstract

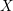Let $X$ be a smooth projective Fano variety over the complex numbers. We study the moduli space of rational curves on 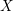$X$ using the perspective of Manin’s conjecture. In particular, we bound the dimension and number of components of spaces of rational curves on 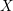$X$. We propose a geometric Manin’s conjecture predicting the growth rate of a counting function associated to the irreducible components of these moduli spaces.

Keywords

rational curvesManin’s conjectureFujita invariant

MSC classification

Primary: 14H10: Families, moduli (algebraic)
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 5 , May 2019 , pp. 833 - 862
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Lehmann is supported by NSF grant 1600875. Tanimoto is partially supported by Lars Hesselholt’s Niels Bohr professorship, and MEXT Japan, Leading Initiative for Excellent Young Researchers (LEADER).

References

Andreatta, M., Minimal model program with scaling and adjunction theory , Internat. J. Math. 24 (2013), 1350007.Google Scholar
Boucksom, S., Demailly, J.-P., Paun, M. and Peternell, T., The pseudo-effective cone of a compact Kähler manifold and varieties of negative Kodaira dimension , J. Algebraic Geom. 22 (2013), 201–248.Google Scholar
Birch, B. J., Forms in many variables , Proc. Roy. Soc. Edinburgh Sect. A 265 (1961/1962), 245–263.Google Scholar
Birkar, C., Singularities of linear systems and boundedness of Fano varieties, Preprint (2016), arXiv:1609.05543 [math.AG].10.1515/crelle-2014-0033Google Scholar
Beheshti, R. and Mohan Kumar, N., Spaces of rational curves on complete intersections , Compos. Math. 149 (2013), 1041–1060.Google Scholar
Browning, T. D. and Loughran, D., Varieties with too many rational points , Math. Z. 285 (2017), 1249–1267.Google Scholar
Batyrev, V. V. and Manin, Yu. I., Sur le nombre des points rationnels de hauteur borné des variétés algébriques , Math. Ann. 286 (1990), 27–43.Google Scholar
Behrend, K. and Manin, Yu., Stacks of stable maps and Gromov-Witten invariants , Duke Math. J. 85 (1996), 1–60.Google Scholar
Bourqui, D., Asymptotic behaviour of rational curves, Preprint (2011), arXiv:1107.3824.Google Scholar
Bourqui, D., Moduli spaces of curves and Cox rings , Michigan Math. J. 61 (2012), 593–613.Google Scholar
Bourqui, D., Exemples de comptages de courbes sur les surfaces , Math. Ann. 357 (2013), 1291–1327.Google Scholar
Bourqui, D., Algebraic points, non-anticanonical heights and the Severi problem on toric varieties , Proc. Lond. Math. Soc. (3) 113 (2016), 474–514.Google Scholar
Batyrev, V. V. and Tschinkel, Y., Rational points on some Fano cubic bundles , C. R. Acad. Sci. Paris Sér. I Math. 323 (1996), 41–46.Google Scholar
Browning, T. and Vishe, P., Rational curves on hypersurfaces of low degree , Algebra Number Theory 11 (2017), 1657–1675.Google Scholar
Campana, F., Connexité rationnelle des variétés de Fano , Ann. Sci. Éc. Norm. Supér. (4) 25 (1992), 539–545.Google Scholar
Castravet, A.-M., Rational families of vector bundles on curves , Internat. J. Math. 15 (2004), 13–45.Google Scholar
Cheltsov, I., Park, J. and Won, J., Cylinders in del Pezzo surfaces , Int. Math. Res. Not. IMRN 2017 (2017), 1179–1230.Google Scholar
Coskun, I. and Starr, J., Rational curves on smooth cubic hypersurfaces , Int. Math. Res. Not. IMRN 2009 (2009), 4626–4641.Google Scholar
Ellenberg, J. S. and Venkatesh, A., Counting extensions of function fields with bounded discriminant and specified Galois group , in Geometric methods in algebra and number theory, Progress in Mathematics, vol. 235 (Birkhäuser, Boston, 2005), 151–168.Google Scholar
Fujita, T., Remarks on quasi-polarized varieties , Nagoya Math. J. 115 (1989), 105–123.Google Scholar
Grothendieck, A., Techniques de construction et théorèmes d’existence en géométrie algébrique. IV. Les schémas de Hilbert , in Séminaire Bourbaki, Vol. 6, Exp. No. 221 (Société Mathématique de France, Paris, 1995), 249–276.Google Scholar
Guerra, L., Complexity of Chow varieties and number of morphisms on surfaces of general type , Manuscripta Math. 98 (1999), 1–8.Google Scholar
Höring, A., The sectional genus of quasi-polarised varieties , Arch. Math. (Basel) 95 (2010), 125–133.Google Scholar
Hacon, C. and Jiang, C., On Fujita invariants of subvarieties of a uniruled variety , Algebr. Geom. 4 (2017), 304–310.Google Scholar
Harris, J., Roth, M. and Starr, J., Rational curves on hypersurfaces of low degree , J. Reine Angew. Math. 571 (2004), 73–106.Google Scholar
Hassett, B., Tanimoto, S. and Tschinkel, Y., Balanced line bundles and equivariant compactifications of homogeneous spaces , Int. Math. Res. Not. IMRN 2015 (2015), 6375–6410.Google Scholar
Hwang, J.-M., A bound on the number of curves of a given degree through a general point of a projective variety , Compos. Math. 141 (2005), 703–712.Google Scholar
Iskovskih, V. A., Anticanonical models of three-dimensional algebraic varieties , in Current problems in mathematics, Vol. 12 (Russian) (VINITI, Moscow, 1979), 59–157; 239 (loose errata).Google Scholar
Iskovskikh, V. A. and Prokhorov, Yu. G., Fano varieties , in Algebraic geometry, V, Encyclopaedia of Mathematical Sciences, vol. 47 (Springer, Berlin, 1999), 1–247.Google Scholar
Keel, S. and McKernan, J., Rational curves on quasi-projective surfaces , Mem. Amer. Math. Soc. 140 (1999).Google Scholar
Kollár, J., Miyaoka, Y. and Mori, S., Rational connectedness and boundedness of Fano manifolds , J. Differential Geom. 36 (1992), 765–779.Google Scholar
Kollár, J., Rational curves on algebraic varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, vol. 32 (Springer, Berlin, 1996).Google Scholar
Kollár, J., The Lefschetz property for families of curves , in Rational points, rational curves, and entire holomorphic curves on projective varieties, Contemporary Mathematics, vol. 654 (American Mathematical Society, Providence, RI, 2015), 143–154.Google Scholar
Kim, B. and Pandharipande, R., The connectedness of the moduli space of maps to homogeneous spaces , in Symplectic geometry and mirror symmetry (Seoul, 2000) (World Scientific, River Edge, NJ, 2001), 187–201.10.1142/9789812799821_0006Google Scholar
Lehmann, B. and Tanimoto, S., On the geometry of thin exceptional sets in Manin’s conjecture , Duke Math. J. 166 (2017), 2815–2869.Google Scholar
Lehmann, B. and Tanimoto, S., On exceptional sets in Manin’s Conjecture , Res. Math. Sci. 6(1) (2019), paper No. 12.Google Scholar
Lehmann, B., Tanimoto, S. and Tschinkel, Y., Balanced line bundles on Fano varieties , J. Reine Angew. Math. 743 (2018), 91–131.Google Scholar
Manin, Yu. I., Problems on rational points and rational curves on algebraic varieties , in Surveys in differential geometry, Vol. II (Cambridge, MA, 1993) (International Press, Cambridge, MA, 1995), 214–245.Google Scholar
Mori, S., Cone of curves, and Fano 3-folds , in Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Warsaw, 1983) (PWN, Warsaw, 1984).Google Scholar
Miyanishi, M. and Zhang, D.-Q., Gorenstein log del Pezzo surfaces of rank one , J. Algebra 118 (1988), 63–84.Google Scholar
Peyre, E., Points de hauteur bornée, topologie adélique et mesures de Tamagawa , J. Théor. Nombres Bordeaux 15 (2003), 319–349.Google Scholar
Rudulier, C. L., Points algébriques de hauteur bornée sur une surface, 2014,http://cecile.lerudulier.fr/Articles/surfaces.pdf.Google Scholar
Riedl, E. and Yang, D., Kontsevich spaces of rational curves on Fano hypersurfaces , J. Reine Agnew. Math. 748 (2019), 207–225.Google Scholar
Sanna, G., Rational curves and instantons on the Fano threefold  $Y_{5}$ . PhD thesis, Scuola Internazionale di Studi Superiori Avanzati (2013/2014).Google Scholar
Testa, D., The Severi problem for rational curves on del Pezzo surfaces. PhD thesis, Massachusetts Institute of Technology (2005), https://arxiv.org/abs/math/0609355.Google Scholar
Testa, D., The irreducibility of the spaces of rational curves on del Pezzo surfaces , J. Algebraic Geom. 18 (2009), 37–61.Google Scholar
Thomsen, J. F., Irreducibility of M 0, n (G/P, 𝛽) , Internat. J. Math. 9 (1998), 367–376.Google Scholar
Tschinkel, Y., Algebraic varieties with many rational points , in Arithmetic geometry, Clay Mathematics Proceedings, vol. 8 (American Mathematical Society, Providence, RI, 2009), 243–334.Google Scholar
Tian, Z. and Zong, H. R., One-cycles on rationally connected varieties , Compos. Math. 150 (2014), 396–408.Google Scholar