Hostname: page-component-7dd5485656-gs9qr Total loading time: 0 Render date: 2025-10-30T02:44:48.632Z Has data issue: false hasContentIssue false
  • English
  • Français

The geometry of Hida families II: 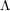$\unicode[STIX]{x1D6EC}$ -adic 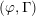$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$ -modules and 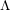$\unicode[STIX]{x1D6EC}$ -adic Hodge theory

Part of: Discontinuous groups and automorphic forms Arithmetic algebraic geometry Algebraic number theory: global fields

Published online by Cambridge University Press:  08 March 2018

Bryden Cais
Bryden Cais*
Affiliation:
Department of Mathematics, The University of Arizona, 617 N. Santa Rita Ave., Tucson, AZ 85721, USA email cais@math.arizona.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct the 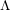$\unicode[STIX]{x1D6EC}$ -adic crystalline and Dieudonné analogues of Hida’s ordinary 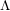$\unicode[STIX]{x1D6EC}$ -adic étale cohomology, and employ integral 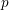$p$ -adic Hodge theory to prove 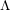$\unicode[STIX]{x1D6EC}$ -adic comparison isomorphisms between these cohomologies and the 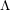$\unicode[STIX]{x1D6EC}$ -adic de Rham cohomology studied in Cais [The geometry of Hida families I: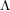$\unicode[STIX]{x1D6EC}$ -adic de Rham cohomology, Math. Ann. (2017), doi:10.1007/s00208-017-1608-1] as well as Hida’s 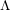$\unicode[STIX]{x1D6EC}$ -adic étale cohomology. As applications of our work, we provide a ‘cohomological’ construction of the family of 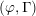$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$ -modules attached to Hida’s ordinary 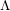$\unicode[STIX]{x1D6EC}$ -adic étale cohomology by Dee [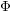$\unicode[STIX]{x1D6F7}$ –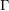$\unicode[STIX]{x1D6E4}$ modules for families of Galois representations, J. Algebra 235 (2001), 636–664], and we give a new and purely geometric proof of Hida’s finiteness and control theorems. We also prove suitable 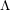$\unicode[STIX]{x1D6EC}$ -adic duality theorems for each of the cohomologies we construct.

Keywords

Hida familiesintegral p-adic Hodge theoryde Rham cohomologycrystalline cohomology

MSC classification

Primary: 11F33: Congruences for modular and $p$-adic modular forms
Secondary: 11F67: Special values of automorphic $L$-series, periods of modular forms, cohomology, modular symbols 11G18: Arithmetic aspects of modular and Shimura varieties 11R23: Iwasawa theory

Information

Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 4 , April 2018 , pp. 719 - 760
Copyright
© The Author 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Berger, L., Représentations p-adiques et équations différentielles , Invent. Math. 148 (2002), 219–284.Google Scholar
Berger, L., Limites de représentations cristallines , Compositio Math. 140 (2004), 1473–1498.CrossRefGoogle Scholar
Berger, L. and Breuil, C., Sur quelques représentations potentiellement cristallines de GL2(Q p ) , Astérisque 330 (2010), 155–211.Google Scholar
Berthelot, P., Cohomologie cristalline des schémas de caractéristique p > 0, Lecture Notes in Mathematics, vol. 407 (Springer, Berlin, 1974).Google Scholar
Berthelot, P. and Messing, W., Théorie de Dieudonné cristalline. I , in Journées de Géométrie Algébrique de Rennes (Rennes, 1978), Vol. I, Astérisque, vol. 63 (Société Mathématique de France, Paris, 1979), 17–37.Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 21 (Springer, Berlin, 1990).Google Scholar
Cais, B., Canonical integral structures on the de Rham cohomology of curves , Ann. Inst. Fourier (Grenoble) 59 (2009), 2255–2300.Google Scholar
Cais, B., Canonical extensions of Néron models of Jacobians , Algebra Number Theory 4 (2010), 111–150.CrossRefGoogle Scholar
Cais, B., The geometry of Hida families I: 𝛬-adic de Rham cohomology , Math. Ann. (2017), doi:10.1007/s00208-017-1608-1.Google Scholar
Cais, B. and Lau, E., Dieudonné crystals and Wach modules for p-divisible groups , Proc. Lond. Math. Soc. (3) 114 (2017), 733–763.Google Scholar
Carayol, H., Sur les représentations l-adiques associées aux formes modulaires de Hilbert , Ann. Sci. Éc. Norm. Supér. (4) 19 (1986), 409–468.Google Scholar
Colmez, P., Espaces vectoriels de dimension finie et représentations de de Rham , Astérisque 319 (2008), 117–186. Représentations $p$ -adiques de groupes $p$ -adiques. I. Représentations galoisiennes et $(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6E4})$ -modules.Google Scholar
Dee, J., 𝛷–𝛤 modules for families of Galois representations , J. Algebra 235 (2001), 636–664.Google Scholar
Deligne, P., Formes modulaires et représentations ℓ-adiques , in Séminaire Bourbaki. Vol. 1968/69: Exposés 347–363, Lecture Notes in Mathematics, vol. 175 (Springer, Berlin, 1971), Exp. No. 355, 139–172.Google Scholar
Deligne, P. and Serre, J.-P., Formes modulaires de poids 1 , Ann. Sci. Éc. Norm. Supér. (4) 7 (1974), 507–530.Google Scholar
Fontaine, J.-M., Représentations p-adiques des corps locaux. I , in The Grothendieck Festschrift, Vol. II, Progress in Mathematics, vol. 87 (Birkhäuser, Boston, MA, 1990), 249–309.Google Scholar
Fukaya, T. and Kato, K., On conjectures of Sharifi, Preprint (2012),http://math.ucla.edu/∼sharifi/sharificonj.pdf.Google Scholar
Grothendieck, A., Modèles de Néron et monodromie, SGA 7, Exposé IX, Lecture Notes in Mathematics, vol. 288 (Springer, 1972), 313–523.Google Scholar
Hida, H., Galois representations into GL2(Z p [[X]]) attached to ordinary cusp forms , Invent. Math. 85 (1986), 545–613.Google Scholar
Hida, H., Iwasawa modules attached to congruences of cusp forms , Ann. Sci. Éc. Norm. Supér. (4) 19 (1986), 231–273.Google Scholar
Hida, H., $\unicode[STIX]{x1D6EC}$ -adic $p$ -divisible groups, I, Unpublished notes from a talk at the Centre de Recherches Mathématiques, Montréal (2005), http://www.math.ucla.edu/∼hida/CRM1.pdf.Google Scholar
Hida, H., $\unicode[STIX]{x1D6EC}$ -adic $p$ -divisible groups, II, Unpublished notes from a talk at the Centre de Recherches Mathématiques, Montréal (2005), http://www.math.ucla.edu/∼hida/CRM2.pdf.Google Scholar
Hida, H., 𝛬-adic Barsotti–Tate groups , Pacific J. Math. 268 (2014), 283–312.Google Scholar
Illusie, L., Complexe de de Rham–Witt et cohomologie cristalline , Ann. Sci. Éc. Norm. Supér. (4) 12 (1979), 501–661.Google Scholar
Kato, K., Logarithmic degeneration and Dieudonné theory, Unpublished notes (1989).Google Scholar
Katz, N., Serre–Tate local moduli , in Algebraic surfaces (Orsay, 1976–78), Lecture Notes in Mathematics, vol. 868 (Springer, Berlin, 1981), 138–202.Google Scholar
Katz, N. M. and Mazur, B., Arithmetic moduli of elliptic curves, Annals of Mathematics Studies, vol. 108 (Princeton University Press, Princeton, NJ, 1985).Google Scholar
Kisin, M. and Ren, W., Galois representations and Lubin–Tate groups , Doc. Math. 14 (2009), 441–461.Google Scholar
Kitagawa, K., On standard p-adic L-functions of families of elliptic cusp forms , in p-adic monodromy and the Birch and Swinnerton-Dyer conjecture (Boston, MA, 1991), Contemporary Mathematics, vol. 165 (American Mathematical Society, Providence, RI, 1994), 81–110.CrossRefGoogle Scholar
Mazur, B. and Messing, W., Universal extensions and one dimensional crystalline cohomology, Lecture Notes in Mathematics, vol. 370 (Springer, Berlin, 1974).CrossRefGoogle Scholar
Mazur, B. and Wiles, A., Analogies between function fields and number fields , Amer. J. Math. 105 (1983), 507–521.Google Scholar
Mazur, B. and Wiles, A., Class fields of abelian extensions of Q , Invent. Math. 76 (1984), 179–330.Google Scholar
Mazur, B. and Wiles, A., On p-adic analytic families of Galois representations , Compos. Math. 59 (1986), 231–264.Google Scholar
Oda, T., The first de Rham cohomology group and Dieudonné modules , Ann. Sci. Éc. Norm. Supér. (4) 2 (1969), 63–135.Google Scholar
Ohta, M., On the p-adic Eichler–Shimura isomorphism for 𝛬-adic cusp forms , J. reine angew. Math. 463 (1995), 49–98.Google Scholar
Ohta, M., Ordinary p-adic étale cohomology groups attached to towers of elliptic modular curves , Compos. Math. 115 (1999), 241–301.Google Scholar
Ohta, M., Ordinary p-adic étale cohomology groups attached to towers of elliptic modular curves. II , Math. Ann. 318 (2000), 557–583.Google Scholar
Sharifi, R., Iwasawa theory and the Eisenstein ideal , Duke Math. J. 137 (2007), 63–101.CrossRefGoogle Scholar
Sharifi, R., A reciprocity map and the two-variable p-adic L-function , Ann. of Math. (2) 173 (2011), 251–300.CrossRefGoogle Scholar
Tate, J. T., p-divisible groups , in Proc. Conf. Local Fields, Driebergen, 1966 (Springer, Berlin, 1967), 158–183.Google Scholar
Tilouine, J., Un sous-groupe p-divisible de la jacobienne de X 1(Np r ) comme module sur l’algèbre de Hecke , Bull. Soc. Math. France 115 (1987), 329–360.Google Scholar
Wach, N., Représentations p-adiques potentiellement cristallines , Bull. Soc. Math. France 124 (1996), 375–400.Google Scholar
Wake, P., The $\unicode[STIX]{x1D6EC}$ -adic Eichler–Shimura isomorphism and $p$ -adic etale cohomology, Unpublished note (2013), arXiv:1303.0406.Google Scholar
Wiles, A., The Iwasawa conjecture for totally real fields , Ann. of Math. (2) 131 (1990), 493–540.Google Scholar