Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-06-07T23:06:28.648Z Has data issue: false hasContentIssue false
  • English
  • Français

The homological projective dual of 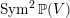$\operatorname{Sym}^{2}\mathbb{P}(V)$

Part of: Symplectic geometry, contact geometry Homological methods (Co)homology theory

Published online by Cambridge University Press:  17 January 2020

Jørgen Vold Rennemo
Jørgen Vold Rennemo*
Affiliation:
Department of Mathematics, Imperial College London, LondonSW7 2AZ, UK email jvrennemo@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the derived category of a complete intersection $X$ of bilinear divisors in the orbifold 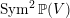$\operatorname{Sym}^{2}\mathbb{P}(V)$. Our results are in the spirit of Kuznetsov’s theory of homological projective duality, and we describe a homological projective duality relation between 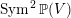$\operatorname{Sym}^{2}\mathbb{P}(V)$ and a category of modules over a sheaf of Clifford algebras on 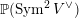$\mathbb{P}(\operatorname{Sym}^{2}V^{\vee })$. The proof follows a recently developed strategy combining variation of geometric invariant theory (VGIT) stability and categories of global matrix factorisations. We begin by translating 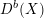$D^{b}(X)$ into a derived category of factorisations on a Landau–Ginzburg (LG) model, and then apply VGIT to obtain a birational LG model. Finally, we interpret the derived factorisation category of the new LG model as a Clifford module category. In some cases we can compute this Clifford module category as the derived category of a variety. As a corollary we get a new proof of a result of Hosono and Takagi, which says that a certain pair of non-birational Calabi–Yau 3-folds have equivalent derived categories.

Keywords

derived category of coherent sheaveshomological projective dualitymatrix factorisations

MSC classification

Primary: 14F05: Sheaves, derived categories of sheaves and related constructions 16E35: Derived categories 53D37: Mirror symmetry, symplectic aspects; homological mirror symmetry; Fukaya category
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 3 , March 2020 , pp. 476 - 525
Copyright
© The Author 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Current address: Departmet of Mathematics, University of Oslo, P.O. Box 1053 Blindern, 0316 Oslo, Norway

References

Addington, N., Spinor sheaves and complete intersections of quadrics, PhD thesis, University of Wisconsin–Madison (2009).Google Scholar
Addington, N., Donovan, W. and Segal, E., The Pfaffian–Grassmannian equivalence revisited, Algebr. Geom. 2 (2015), 332–364.CrossRefGoogle Scholar
Addington, N. M., Segal, E. P. and Sharpe, E. R., D-brane probes, branched double covers, and noncommutative resolutions, Adv. Theor. Math. Phys. 18 (2014), 1369–1436.CrossRefGoogle Scholar
Ballard, M., Deliu, D., Favero, D., Isik, M. U. and Katzarkov, L., Resolutions in factorization categories, Adv. Math. 295 (2016), 195–249.CrossRefGoogle Scholar
Ballard, M., Deliu, D., Favero, D., Isik, M. U. and Katzarkov, L., Homological projective duality via variation of geometric invariant theory quotients, J. Eur. Math. Soc. (JEMS) 19 (2017), 1127–1158.CrossRefGoogle Scholar
Ballard, M., Deliu, D., Favero, D., Isik, M. U. and Katzarkov, L., On the derived categories of degree d hypersurface fibrations, Math. Ann. 371 (2018), 337–370.CrossRefGoogle Scholar
Ballard, M., Favero, D. and Katzarkov, L., A category of kernels for equivariant factorizations and its implications for Hodge theory, Publ. Math. Inst. Hautes Études Sci. 120 (2014), 1–111.CrossRefGoogle Scholar
Ballard, M., Favero, D. and Katzarkov, L., Variation of geometric invariant theory quotients and derived categories, J. Reine Angew. Math. 746 (2019), 235–303.CrossRefGoogle Scholar
Bernstein, J. and Lunts, V., Equivariant sheaves and functors, Lecture Notes in Mathematics, vol. 1578 (Springer, Berlin, 1994).CrossRefGoogle Scholar
Bondal, A. and Orlov, D., Semiorthogonal decomposition for algebraic varieties, Preprint (1995), arXiv:alg-geom/9506012v1.Google Scholar
Bondal, A. I., Representations of associative algebras and coherent sheaves, Izv. Akad. Nauk SSSR Ser. Mat. 53 (1989), 25–44.Google Scholar
Borisov, L. and Căldăraru, A., The Pfaffian–Grassmannian derived equivalence, J. Algebraic Geom. 18 (2009), 201–222.CrossRefGoogle Scholar
Dyckerhoff, T., Compact generators in categories of matrix factorizations, Duke Math. J. 159 (2011), 223–274.CrossRefGoogle Scholar
Efimov, A. I. and Positselski, L., Coherent analogues of matrix factorizations and relative singularity categories, Algebra Number Theory 9 (2015), 1159–1292.CrossRefGoogle Scholar
Favero, D. and Kelly, T. L., Proof of a conjecture of Batyrev and Nill, Amer. J. Math. 139 (2017), 1493–1520.CrossRefGoogle Scholar
Grayson, D. R. and Stillman, M. E., Macaulay2, a software system for research in algebraic geometry. Available at http://www.math.uiuc.edu/Macaulay2/.Google Scholar
Halpern-Leistner, D., The derived category of a GIT quotient, J. Amer. Math. Soc. 28 (2015), 871–912.CrossRefGoogle Scholar
Herbst, M., Hori, K. and Page, D., Phases of $N=2$theories in $1+1$dimensions with boundary, Preprint (2008), arXiv:0803.2045v1 [hep-th].Google Scholar
Hori, K., Duality in two-dimensional (2, 2) supersymmetric non-abelian gauge theories, J. High Energy Phys. 2013(10) (2013), 121.CrossRefGoogle Scholar
Hori, K. and Knapp, J., Linear sigma models with strongly coupled phases – one parameter models, J. High Energy Phys. 2013(11) (2013), 70.CrossRefGoogle Scholar
Hosono, S. and Takagi, H., Double quintic symmetroids, Reye congruences, and their derived equivalence, J. Differential Geom. 104 (2016), 443–497.CrossRefGoogle Scholar
Ingalls, C. and Kuznetsov, A., On nodal Enriques surfaces and quartic double solids, Math. Ann. 361 (2015), 107–133.CrossRefGoogle Scholar
Isik, M. U., Equivalence of the derived category of a variety with a singularity category, Int. Math. Res. Not. IMRN 2013 (2013), 2787–2808.CrossRefGoogle Scholar
Kuznetsov, A., Homological projective duality for Grassmannians of lines, Preprint (2006),arXiv:math/0610957v1.CrossRefGoogle Scholar
Kuznetsov, A., Homological projective duality, Publ. Math. Inst. Hautes Études Sci. 105 (2007), 157–220.CrossRefGoogle Scholar
Kuznetsov, A., Derived categories of quadric fibrations and intersections of quadrics, Adv. Math. 218 (2008), 1340–1369.CrossRefGoogle Scholar
Laumon, G. and Moret-Bailly, L., Champs algébriques, Ergebnisse der Mathematik und ihrer Grenzgebiete, 3. Folge, vol. 39 (Springer, Berlin, 2000).CrossRefGoogle Scholar
Mac Lane, S., Categories for the working mathematician, Graduate Texts in Mathematics, vol. 5, second edition (Springer, New York, 1998).Google Scholar
Masuda, M., Moser-Jauslin, L. and Petrie, T., The equivariant Serre problem for abelian groups, Topology 35 (1996), 329–334.CrossRefGoogle Scholar
Mirković, I. and Riche, S., Linear Koszul duality, Compos. Math. 146 (2010), 233–258.CrossRefGoogle Scholar
Orlov, D., Matrix factorizations for nonaffine LG-models, Math. Ann. 353 (2012), 95–108.CrossRefGoogle Scholar
Positselski, L., Two kinds of derived categories, Koszul duality, and comodule-contramodule correspondence, Mem. Amer. Math. Soc. 212 (2011).Google Scholar
Rennemo, J. V., The fundamental theorem of homological projective duality via variation of GIT stability, Preprint (2017), arXiv:1705.01437 [math].Google Scholar
Riche, S., Koszul duality and modular representations of semisimple Lie algebras, Duke Math. J. 154 (2010), 31–134.CrossRefGoogle Scholar
Segal, E., Equivalence between GIT quotients of Landau–Ginzburg B-models, Comm. Math. Phys. 304 (2011), 411–432.CrossRefGoogle Scholar
Grothendieck, A., Cohomologie locale des faisceaux cohérents et théorèmes de Lefschetz locaux et globaux (SGA 2), Documents Mathématiques (Paris), vol. 4 (Société Mathématique de France, Paris, 2005).Google Scholar
M., Artin, Grothendieck, A. and Verdier, J.-L., Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 – Théorie des topos et cohomologie étale des schémas (SGA 4), tome 3, Lecture Notes in Mathematics, vol. 305 (Springer, Berlin, 1972).Google Scholar
Shipman, I., A geometric approach to Orlov’s theorem, Compos. Math. 148 (2012), 1365–1389.CrossRefGoogle Scholar
Spaltenstein, N., Resolutions of unbounded complexes, Compos. Math. 65 (1988), 121–154.Google Scholar
Segal, E. and Thomas, R. P., Quintic threefolds and Fano elevenfolds, J. Reine Angew. Math. 743 (2018), 245–259.CrossRefGoogle Scholar
Stacks Project Authors, Stacks Project. https://stacks.math.columbia.edu(2019).Google Scholar
Thomason, R. W., Equivariant resolution, linearization, and Hilbert’s fourteenth problem over arbitrary base schemes, Adv. Math. 65 (1987), 16–34.CrossRefGoogle Scholar