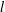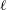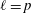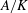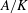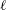Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
ČESNAVIČIUS, KĘSTUTIS
2018.
The ℓ-parity conjecture over the constant quadratic extension.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 165,
Issue. 3,
p.
385.
Yuan, Xinyi
2021.
Positivity of Hodge bundles of abelian varieties over some function fields.
Compositio Mathematica,
Vol. 157,
Issue. 9,
p.
1964.
Lai, King-Fai
Longhi, Ignazio
Suzuki, Takashi
Tan, Ki-Seng
and
Trihan, Fabien
2021.
On the μ-invariants of abelian varieties over function fields of positive characteristic.
Algebra & Number Theory,
Vol. 15,
Issue. 4,
p.
863.