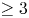1. Introduction
Throughout we fix a base field ![]() $k$ and all constructions are linear over
$k$ and all constructions are linear over ![]() $k$. In 1997, Orlov proved the following result.
$k$. In 1997, Orlov proved the following result.
Theorem 1.1 [Reference OrlovOrl97, Theorem 2.2]
Let ![]() $X/k, Y/k$ be smooth projective schemes. Then every fully faithful exact functor
$X/k, Y/k$ be smooth projective schemes. Then every fully faithful exact functor ![]() $\Psi :D^b(\mathop {\text {coh}}(X)) \rightarrow D^b(\mathop {\text {coh}}(Y))$ is isomorphic to a Fourier–Mukai functor associated with an object of
$\Psi :D^b(\mathop {\text {coh}}(X)) \rightarrow D^b(\mathop {\text {coh}}(Y))$ is isomorphic to a Fourier–Mukai functor associated with an object of ![]() $D^b(\mathop {\text {coh}}(X \times _k Y))$, the Fourier–Mukai kernel.
$D^b(\mathop {\text {coh}}(X \times _k Y))$, the Fourier–Mukai kernel.
This result is of seminal importance because it allows for such a functor ![]() $\Psi$ to be analysed by means of a geometric study of the kernel.
$\Psi$ to be analysed by means of a geometric study of the kernel.
1.1 Non-Fourier–Mukai functors
The first example of a non-Fourier–Mukai functor between bounded derived categories of smooth projective schemes was given by the second and third authors, and can be found in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19] together with an appendix by Amnon Neeman improving on one of the key results. The functor is of the form
where ![]() $Q$ is a three-dimensional smooth quadric and
$Q$ is a three-dimensional smooth quadric and ![]() ${\mathbb {P}}^4$ is its ambient projective space. The construction proceeds in two steps.
${\mathbb {P}}^4$ is its ambient projective space. The construction proceeds in two steps.
(i) First a prototypical non-Fourier–Mukai functor is constructed between certain non-geometric DG-categories.
(ii) Then, using a quite involved argument, this functor is turned into a geometric one.
In step (i), for a smooth projective variety ![]() $X$, and given a Hochschild cohomology class
$X$, and given a Hochschild cohomology class ![]() $0 \neq \eta \in {\rm HH}^{2\dim _k(X)}(X,\omega _X^{\otimes 2})$, a functor
$0 \neq \eta \in {\rm HH}^{2\dim _k(X)}(X,\omega _X^{\otimes 2})$, a functor
is constructed, where ![]() $D_{\infty }(\mathcal {X}_\eta )$ is the derived category of an
$D_{\infty }(\mathcal {X}_\eta )$ is the derived category of an ![]() $A_{\infty }$-category
$A_{\infty }$-category ![]() $\mathcal {X}_\eta$ which can be thought of as a generalized deformation of
$\mathcal {X}_\eta$ which can be thought of as a generalized deformation of ![]() $X$ in the
$X$ in the ![]() $\eta$-direction (see § 5 for more details). This functor is not Fourier–Mukai in a generalized sense, see Definition 2.2.
$\eta$-direction (see § 5 for more details). This functor is not Fourier–Mukai in a generalized sense, see Definition 2.2.
In step (ii), one needs to move from the non-geometric category ![]() $D_{\infty }(\mathcal {X}_\eta )$ to an honest derived category of coherent sheaves. In [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, § 11] this is achieved by showing that the inclusion
$D_{\infty }(\mathcal {X}_\eta )$ to an honest derived category of coherent sheaves. In [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, § 11] this is achieved by showing that the inclusion ![]() $f:X \rightarrow Y$ of a smooth quadric
$f:X \rightarrow Y$ of a smooth quadric ![]() $X=Q$ of maximal isotropy index in
$X=Q$ of maximal isotropy index in ![]() $Y={\mathbb {P}}^4$ annihilates
$Y={\mathbb {P}}^4$ annihilates ![]() $\eta$ (in the sense that
$\eta$ (in the sense that ![]() $f_*\eta =0$), which allows for the construction of the functor
$f_*\eta =0$), which allows for the construction of the functor ![]() $\Psi$ as a composition of
$\Psi$ as a composition of ![]() $L$ with a pushforward to
$L$ with a pushforward to ![]() $D^b(\mathop {\text {coh}}({\mathbb {P}}^4))$, back to the geometric world. The composition with the pushforward yields the required functor
$D^b(\mathop {\text {coh}}({\mathbb {P}}^4))$, back to the geometric world. The composition with the pushforward yields the required functor
but the drawback is the need to again check that the composition is non-Fourier–Mukai. This is achieved using an obstruction theory that quickly gets hard to control as the dimension of ![]() $X$ grows, and indeed the original paper [Reference Rizzardo, Van den Bergh and NeemanRVdBN19] only gave one concrete example of a non-Fourier–Mukai functor despite the very general initial setup.
$X$ grows, and indeed the original paper [Reference Rizzardo, Van den Bergh and NeemanRVdBN19] only gave one concrete example of a non-Fourier–Mukai functor despite the very general initial setup.
In this paper we show that, as long as one is not worried about keeping ![]() $\dim _k(Y)$ small, it is possible to bypass this intricate analysis and construct non-Fourier–Mukai functors starting from
$\dim _k(Y)$ small, it is possible to bypass this intricate analysis and construct non-Fourier–Mukai functors starting from ![]() $L$ in a different way.
$L$ in a different way.
Remark 1.2 In a short note [Reference VologodskyVol19], Vologodsky shows that over a field of positive characteristic non-Fourier–Mukai functors arise quite naturally. Given a smooth projective scheme ![]() $X$ over
$X$ over ![]() ${\mathbb{Z}}_p$, one considers the embedding
${\mathbb{Z}}_p$, one considers the embedding ![]() $i:X \hookrightarrow Z$ of the special fiber. The main result is a criterion for the endofunctor
$i:X \hookrightarrow Z$ of the special fiber. The main result is a criterion for the endofunctor ![]() $Li^* \circ i_*$ of
$Li^* \circ i_*$ of ![]() $D^b(\mathop {\text {coh}}(X))$ not to be of Fourier–Mukai type. This criterion is satisfied, in particular, for
$D^b(\mathop {\text {coh}}(X))$ not to be of Fourier–Mukai type. This criterion is satisfied, in particular, for ![]() $X$ the flag variety of
$X$ the flag variety of ![]() $\operatorname {GL}_n$, for
$\operatorname {GL}_n$, for ![]() $n>2$. However, the functors obtained in this way do admit a
$n>2$. However, the functors obtained in this way do admit a ![]() ${\mathbb{Z}}$-linear DG-lift.
${\mathbb{Z}}$-linear DG-lift.
1.2 New examples
In this paper we show that if one is not interested in ‘small’ examples the second part of the construction can be simplified, giving rise to many more examples of non-Fourier–Mukai functors.
Recall that if ![]() $X$ is a scheme, then a tilting bundle
$X$ is a scheme, then a tilting bundle ![]() $T$ on
$T$ on ![]() $X$ is a vector bundle on
$X$ is a vector bundle on ![]() $X$ such that
$X$ such that ![]() $\operatorname {Ext}^{>0}_X(T,T)=0$ and such that
$\operatorname {Ext}^{>0}_X(T,T)=0$ and such that ![]() $T$ generates
$T$ generates ![]() $D_{\operatorname {Qch}}(\mathcal {O}_X)$. The following is our main result.
$D_{\operatorname {Qch}}(\mathcal {O}_X)$. The following is our main result.
Theorem 1.3 (see § 5)
Let ![]() $X$ be a smooth projective scheme of dimension
$X$ be a smooth projective scheme of dimension ![]() $m\ge 3$ which has a tilting bundle. Then there is a non-Fourier–Mukai functor
$m\ge 3$ which has a tilting bundle. Then there is a non-Fourier–Mukai functor
where ![]() $Y$ is a smooth projective scheme.
$Y$ is a smooth projective scheme.
As a concrete example, we may for instance take ![]() $X={\mathbb {P}}^m$,
$X={\mathbb {P}}^m$, ![]() $m\ge 3$, which has the Beilinson tilting bundle
$m\ge 3$, which has the Beilinson tilting bundle ![]() $T=\bigoplus _{i=0}^m \mathcal {O}_X(i)$.
$T=\bigoplus _{i=0}^m \mathcal {O}_X(i)$.
1.3 Geometric realizations
To prove Theorem 1.3, we combine results from [Reference OrlovOrl16] with ideas from [Reference OrlovOrl20]. There are again two main steps involved.
(i) In a first step, we construct a fully faithful functor
 $\mathrm {Aus}$
from (the thick envelope of) the essential image
$\mathrm {Aus}$
from (the thick envelope of) the essential image
 $\mathcal {A}$ of
$\mathcal {A}$ of  $L$ to a triangulated category
$L$ to a triangulated category  $\mathcal {T}$ with a full exceptional collection. This construction is based on a version of the Auslander(–Dlab–Ringel) algebra for filtered
$\mathcal {T}$ with a full exceptional collection. This construction is based on a version of the Auslander(–Dlab–Ringel) algebra for filtered  $A_{\infty }$-algebras, which is explained in § 3.
$A_{\infty }$-algebras, which is explained in § 3.(ii) We then invoke Orlov's gluing result [Reference OrlovOrl16, Theorem 4.15], which implies the existence of a fully faithful functor
for some smooth and projective scheme
 $Y$ (this is often referred to as a geometric realization, not to be confused with the geometric realization of a simplicial set).
$Y$ (this is often referred to as a geometric realization, not to be confused with the geometric realization of a simplicial set).
One can then show that the composed functor
is still non-Fourier–Mukai, thus proving Theorem 1.3.
2. Preliminaries on  $A_\infty$-categories
$A_\infty$-categories
Fix an arbitrary base field ![]() $k$.Footnote 1 Our general reference for
$k$.Footnote 1 Our general reference for ![]() $A_\infty$-algebras and
$A_\infty$-algebras and ![]() $A_\infty$-categories will be [Reference Lefèvre-HasegawaLef03]. For a good reference in English, consult [Reference Efimov, Lunts and OrlovELO10]. Sometimes we silently use notions for categories which are only introduced for algebras (i.e. categories with one object) in [Reference Efimov, Lunts and OrlovELO10]. We assume that all
$A_\infty$-categories will be [Reference Lefèvre-HasegawaLef03]. For a good reference in English, consult [Reference Efimov, Lunts and OrlovELO10]. Sometimes we silently use notions for categories which are only introduced for algebras (i.e. categories with one object) in [Reference Efimov, Lunts and OrlovELO10]. We assume that all ![]() $A_\infty$-notions are strictly unital. Unless otherwise specified we use cohomological grading.
$A_\infty$-notions are strictly unital. Unless otherwise specified we use cohomological grading.
Remark 2.1 We rely throughout on the fact that the homotopy categories of ![]() $A_\infty$-categories and DG-categories are equivalent. See [Reference Canonaco, Ornaghi and StellariCOS19]. This implies, in particular, that we can freely use Orlov's gluing results in [Reference OrlovOrl16] in the
$A_\infty$-categories and DG-categories are equivalent. See [Reference Canonaco, Ornaghi and StellariCOS19]. This implies, in particular, that we can freely use Orlov's gluing results in [Reference OrlovOrl16] in the ![]() $A_\infty$-context.
$A_\infty$-context.
Definition 2.2 Let ![]() $\mathfrak {a}$,
$\mathfrak {a}$, ![]() $\mathfrak {b}$ be pretriangulated
$\mathfrak {b}$ be pretriangulated ![]() $A_\infty$-categories [Reference Bespalov, Lyubashenko and ManzyukBLM17] and put
$A_\infty$-categories [Reference Bespalov, Lyubashenko and ManzyukBLM17] and put ![]() $\mathcal {A}=H^0(\mathfrak {a})$,
$\mathcal {A}=H^0(\mathfrak {a})$, ![]() $\mathcal {B}=H^0(\mathfrak {b})$. We say that an exact functor
$\mathcal {B}=H^0(\mathfrak {b})$. We say that an exact functor ![]() $F:\mathcal {A}\rightarrow \mathcal {B}$ is Fourier–Mukai if there is an
$F:\mathcal {A}\rightarrow \mathcal {B}$ is Fourier–Mukai if there is an ![]() $A_\infty$-functor
$A_\infty$-functor ![]() $f:\mathfrak {a}\rightarrow \mathfrak {b}$ such that
$f:\mathfrak {a}\rightarrow \mathfrak {b}$ such that ![]() $F\cong H^0(f)$ as graded functors.
$F\cong H^0(f)$ as graded functors.
Often ![]() $\mathfrak {a}$,
$\mathfrak {a}$, ![]() $\mathfrak {b}$ are uniquely determined by
$\mathfrak {b}$ are uniquely determined by ![]() $\mathcal {A}$,
$\mathcal {A}$, ![]() $\mathcal {B}$ (see [Reference Canonaco and StellariCS18, Reference Lunts and OrlovLO10]) or else implicit from the context, and then we do not specify them.
$\mathcal {B}$ (see [Reference Canonaco and StellariCS18, Reference Lunts and OrlovLO10]) or else implicit from the context, and then we do not specify them.
Remark 2.3 If ![]() $X$,
$X$, ![]() $Y$ are smooth projective varieties and
$Y$ are smooth projective varieties and ![]() $F:D^b(\mathop {\text {coh}}(X))\rightarrow D^b(\mathop {\text {coh}}(Y))$ is a traditional Fourier–Mukai functor which means that it can be written as
$F:D^b(\mathop {\text {coh}}(X))\rightarrow D^b(\mathop {\text {coh}}(Y))$ is a traditional Fourier–Mukai functor which means that it can be written as ![]() $R\mathop {\text {pr}}\nolimits _{2\ast }(\mathcal {K}\overset {L}{\otimes }_{X\times Y}L\mathop {\text {pr}}\nolimits _1^\ast (-))$ for
$R\mathop {\text {pr}}\nolimits _{2\ast }(\mathcal {K}\overset {L}{\otimes }_{X\times Y}L\mathop {\text {pr}}\nolimits _1^\ast (-))$ for ![]() $\mathcal {K}\in D^b(\mathop {\text {coh}}(X\times Y))$, then it is Fourier–Mukai in our sense. This follows from the easy part of [Reference ToënToë07, Theorem 8.15] combined with Remark 2.1.
$\mathcal {K}\in D^b(\mathop {\text {coh}}(X\times Y))$, then it is Fourier–Mukai in our sense. This follows from the easy part of [Reference ToënToë07, Theorem 8.15] combined with Remark 2.1.
For an ![]() $A_\infty$-category
$A_\infty$-category ![]() $\mathfrak {a}$ we denote byFootnote 2
$\mathfrak {a}$ we denote byFootnote 2 ![]() $\mathcal {D}_\infty (\mathfrak {a})$ the DG-category of left
$\mathcal {D}_\infty (\mathfrak {a})$ the DG-category of left ![]() $A_\infty$-modules. The
$A_\infty$-modules. The ![]() $A_\infty$-Yoneda functor
$A_\infty$-Yoneda functor
is quasi-fully faithful [Reference Lefèvre-HasegawaLef03, Lemma 7.4.0.1]. The corresponding homotopy category ![]() $D_{\infty }(\mathfrak {a}):= H^0(\mathcal {D}_\infty (\mathfrak {a}))$ is a compactly generated triangulated category [Reference KellerKel06, § 4.9] with compact generators
$D_{\infty }(\mathfrak {a}):= H^0(\mathcal {D}_\infty (\mathfrak {a}))$ is a compactly generated triangulated category [Reference KellerKel06, § 4.9] with compact generators ![]() $\mathfrak {a}(X,-)$ for
$\mathfrak {a}(X,-)$ for ![]() $X\in \operatorname {Ob}(\mathfrak {a})$. We write
$X\in \operatorname {Ob}(\mathfrak {a})$. We write ![]() $\mathcal {P}\mathrm {erf}(\mathfrak {a})$ for the full DG-subcategory of
$\mathcal {P}\mathrm {erf}(\mathfrak {a})$ for the full DG-subcategory of ![]() $\mathcal {D}_\infty (\mathfrak {a})$ spanned by the compact objects in
$\mathcal {D}_\infty (\mathfrak {a})$ spanned by the compact objects in ![]() $D_{\infty }(\mathfrak {a})$ and we also put
$D_{\infty }(\mathfrak {a})$ and we also put ![]() $\operatorname {Perf}(\mathfrak {a})=H^0(\mathcal {P}\mathrm {erf}(\mathfrak {a}))$.
$\operatorname {Perf}(\mathfrak {a})=H^0(\mathcal {P}\mathrm {erf}(\mathfrak {a}))$.
If ![]() $\mathcal {A}$ is a triangulated category and
$\mathcal {A}$ is a triangulated category and ![]() $S\subset \operatorname {Ob}(\mathcal {A})$, then the category classically generated by
$S\subset \operatorname {Ob}(\mathcal {A})$, then the category classically generated by ![]() $S$ [Reference Bondal and Van den BerghBVdB03, § 1] is the smallest thick subcategory of
$S$ [Reference Bondal and Van den BerghBVdB03, § 1] is the smallest thick subcategory of ![]() $\mathcal {A}$ containing
$\mathcal {A}$ containing ![]() $S$. It is denoted by
$S$. It is denoted by ![]() $\langle S\rangle$. By [Reference KellerKel94, § 5.3],[Reference NeemanNee92, Lemma 2.2]
$\langle S\rangle$. By [Reference KellerKel94, § 5.3],[Reference NeemanNee92, Lemma 2.2] ![]() $\operatorname {Perf}(\mathfrak {a})$ is classically generated by the objects
$\operatorname {Perf}(\mathfrak {a})$ is classically generated by the objects ![]() $\mathfrak {a}(X,-)$.
$\mathfrak {a}(X,-)$.
If ![]() $f:\mathfrak {a}\rightarrow \mathfrak {b}$ is an
$f:\mathfrak {a}\rightarrow \mathfrak {b}$ is an ![]() $A_\infty$-functor, then we may view
$A_\infty$-functor, then we may view ![]() $\mathfrak {b}$ as an
$\mathfrak {b}$ as an ![]() $A_\infty$-
$A_\infty$-![]() $\mathfrak {b}$-
$\mathfrak {b}$-![]() $\mathfrak {a}$-bimodule. Hence, we have a ‘standard’ DG-functor
$\mathfrak {a}$-bimodule. Hence, we have a ‘standard’ DG-functor
which (for algebras) is introduced in [Reference Lefèvre-HasegawaLef03, § 4.1.1]. We recall the following basic result.
Lemma 2.4 For ![]() $A_{\infty }$-categories
$A_{\infty }$-categories ![]() $\mathfrak {a}, \mathfrak {b}$ and a quasi-fully faithful
$\mathfrak {a}, \mathfrak {b}$ and a quasi-fully faithful ![]() $A_{\infty }$-functor
$A_{\infty }$-functor ![]() $f:\mathfrak {a} \to \mathfrak {b}$, the induced functor
$f:\mathfrak {a} \to \mathfrak {b}$, the induced functor ![]() $\mathfrak {b}\overset {\infty }{\otimes }_{\mathfrak {a}}-:D_{\infty }(\mathfrak {a})\rightarrow D_{\infty }(\mathfrak {b})$ is fully faithful. Moreover, this functor restricts to a fully faithful Fourier–Mukai functor
$\mathfrak {b}\overset {\infty }{\otimes }_{\mathfrak {a}}-:D_{\infty }(\mathfrak {a})\rightarrow D_{\infty }(\mathfrak {b})$ is fully faithful. Moreover, this functor restricts to a fully faithful Fourier–Mukai functor ![]() $\operatorname {Perf}(\mathfrak {a})\rightarrow \operatorname {Perf}(\mathfrak {b})$.
$\operatorname {Perf}(\mathfrak {a})\rightarrow \operatorname {Perf}(\mathfrak {b})$.
Proof. By the same argument as in the proof of [Reference Lefèvre-HasegawaLef03, Lemme 4.1.1.6] there is a quasi-isomorphism
for ![]() $X \in \operatorname {Ob}(\mathfrak {a})$, functorial in
$X \in \operatorname {Ob}(\mathfrak {a})$, functorial in ![]() $X$. In other words there is a pseudo-commutative diagram
$X$. In other words there is a pseudo-commutative diagram

where the vertical arrows are the Yoneda embeddings ![]() $X\mapsto \mathfrak {a}(X,-)$,
$X\mapsto \mathfrak {a}(X,-)$, ![]() $Y\mapsto \mathfrak {b}(Y,-)$. The full faithfulness of the lower arrow follows by dévissage. The claim about
$Y\mapsto \mathfrak {b}(Y,-)$. The full faithfulness of the lower arrow follows by dévissage. The claim about ![]() $\operatorname {Perf}$ follows immediately from (3).
$\operatorname {Perf}$ follows immediately from (3).
The following lemma is a variant on Lemma 2.4 and could have been deduced from it.
Lemma 2.5 Assume that ![]() $\mathfrak {a}$ is a pre-triangulated
$\mathfrak {a}$ is a pre-triangulated ![]() $A_\infty$-category [Reference Bespalov, Lyubashenko and ManzyukBLM17] such that
$A_\infty$-category [Reference Bespalov, Lyubashenko and ManzyukBLM17] such that ![]() $H^0(\mathfrak {a})$ is Karoubian and classically generated by
$H^0(\mathfrak {a})$ is Karoubian and classically generated by ![]() $T\in \operatorname {Ob}(\mathfrak {a})$. Put
$T\in \operatorname {Ob}(\mathfrak {a})$. Put ![]() $\mathsf {R}=\mathfrak {a}(T,T)$. The
$\mathsf {R}=\mathfrak {a}(T,T)$. The ![]() $A_\infty$-functor
$A_\infty$-functor
defines a quasi-equivalence
or, equivalently, an equivalence of triangulated categories
Proof. We must prove (4). We have ![]() $H^0(f)(T)=\mathsf {R}$. By hypothesis
$H^0(f)(T)=\mathsf {R}$. By hypothesis ![]() $H^0(\mathfrak {a})$ is classically generated by
$H^0(\mathfrak {a})$ is classically generated by ![]() $T$ and by the previous discussion
$T$ and by the previous discussion ![]() $\operatorname {Perf}(\mathsf {R}^\circ )$ is classically generated by
$\operatorname {Perf}(\mathsf {R}^\circ )$ is classically generated by ![]() $\mathsf {R}$. Moreover, because the Yoneda functor is quasi-fully faithful,
$\mathsf {R}$. Moreover, because the Yoneda functor is quasi-fully faithful, ![]() $H^0(f)$ is fully faithful when restricted to
$H^0(f)$ is fully faithful when restricted to ![]() $T$. The rest follows by dévissage.
$T$. The rest follows by dévissage.
3. Geometric realization of a filtered  $A_{\infty }$-algebra
$A_{\infty }$-algebra
Let ![]() $(\mathsf {R},m_*)$ denote a finite-dimensional
$(\mathsf {R},m_*)$ denote a finite-dimensional ![]() $A_{\infty }$-algebra equipped with a (decreasing) filtration
$A_{\infty }$-algebra equipped with a (decreasing) filtration ![]() $F^*:= \{F^p\mathsf {R}\}_{p \geq 0}$. This means that
$F^*:= \{F^p\mathsf {R}\}_{p \geq 0}$. This means that ![]() $\{F^p\mathsf {R}\}_{p \geq 0}$ is a decreasing filtration of the underlying (finite-dimensional) graded vector space of
$\{F^p\mathsf {R}\}_{p \geq 0}$ is a decreasing filtration of the underlying (finite-dimensional) graded vector space of ![]() $\mathsf {R}$ satisfying the compatibility conditions
$\mathsf {R}$ satisfying the compatibility conditions
for all ![]() $p$ and all
$p$ and all ![]() $i_1,\ldots,i_p$.
$i_1,\ldots,i_p$.
Assume ![]() $F^n\mathsf {R}=F^n=0$ for some
$F^n\mathsf {R}=F^n=0$ for some ![]() $n\ge 0$. In this case we may define the (modified) Auslander
$n\ge 0$. In this case we may define the (modified) Auslander ![]() $A_{\infty }$-category
$A_{\infty }$-category ![]() $\mathsf {\Gamma }=\mathsf {\Gamma }_{\mathsf {R},F^*}$ of
$\mathsf {\Gamma }=\mathsf {\Gamma }_{\mathsf {R},F^*}$ of ![]() $(\mathsf {R},F^*)$. The objects of
$(\mathsf {R},F^*)$. The objects of ![]() $\mathsf {\Gamma }$ are the integers
$\mathsf {\Gamma }$ are the integers ![]() $0,\ldots,n-1$ and we set
$0,\ldots,n-1$ and we set
By setting ![]() $\mathsf {\Gamma }_{i,j}=\mathsf {\Gamma }(j,i)$, we can represent
$\mathsf {\Gamma }_{i,j}=\mathsf {\Gamma }(j,i)$, we can represent ![]() $\mathsf {\Gamma }$ schematically via the matrix
$\mathsf {\Gamma }$ schematically via the matrix
 \begin{equation} (\mathsf {\Gamma }_{i,j})= \begin{pmatrix} \mathsf{R} & F^1 & F^2 & \cdots & F^{n-1} \\ \mathsf{R}/F^{n-1} & \mathsf{R}/F^{n-1} & F^1/F^{n-1} & \cdots & F^{n-2}/F^{n-1} \\ \mathsf{R}/F^{n-2} & \mathsf{R}/F^{n-2} & \mathsf{R}/F^{n-2} & \cdots & F^{n-3}/F^{n-2} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \mathsf{R}/F^1 & \mathsf{R}/F^1 & \mathsf{R}/F^1 & \mathsf{R}/F^1 & \mathsf{R}/F^1 \end{pmatrix} \end{equation}
\begin{equation} (\mathsf {\Gamma }_{i,j})= \begin{pmatrix} \mathsf{R} & F^1 & F^2 & \cdots & F^{n-1} \\ \mathsf{R}/F^{n-1} & \mathsf{R}/F^{n-1} & F^1/F^{n-1} & \cdots & F^{n-2}/F^{n-1} \\ \mathsf{R}/F^{n-2} & \mathsf{R}/F^{n-2} & \mathsf{R}/F^{n-2} & \cdots & F^{n-3}/F^{n-2} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \mathsf{R}/F^1 & \mathsf{R}/F^1 & \mathsf{R}/F^1 & \mathsf{R}/F^1 & \mathsf{R}/F^1 \end{pmatrix} \end{equation}so that composition is given by matrix multiplication.
The grading on ![]() $\mathsf {R}$ induces a grading on
$\mathsf {R}$ induces a grading on ![]() $\mathsf {\Gamma }$. Because of condition (5), the higher multiplications on
$\mathsf {\Gamma }$. Because of condition (5), the higher multiplications on ![]() $\mathsf {R}$ also induce higher multiplications on
$\mathsf {R}$ also induce higher multiplications on ![]() $\mathsf {\Gamma }$. Indeed,
$\mathsf {\Gamma }$. Indeed,
so
In addition,
 \begin{align} &\max(i_2-i_1,0)+\cdots+\max(i_k -i_{k-1})+(n-i_k)\nonumber\\ &\qquad +\max(i_{k+2}-i_{k+1},0) + \cdots + \max(i_{p+1}-i_p,0) \nonumber\\ &\qquad \geq \max(i_2-i_1,0)+\cdots+\max(i_{k-1} -i_{k-2})+(n-i_{k-1}) \geq n -i_1, \end{align}
\begin{align} &\max(i_2-i_1,0)+\cdots+\max(i_k -i_{k-1})+(n-i_k)\nonumber\\ &\qquad +\max(i_{k+2}-i_{k+1},0) + \cdots + \max(i_{p+1}-i_p,0) \nonumber\\ &\qquad \geq \max(i_2-i_1,0)+\cdots+\max(i_{k-1} -i_{k-2})+(n-i_{k-1}) \geq n -i_1, \end{align}
so ![]() $m_p$ passes to the quotients
$m_p$ passes to the quotients
making ![]() $\mathsf {\Gamma }$ into an
$\mathsf {\Gamma }$ into an ![]() $A_{\infty }$-category.
$A_{\infty }$-category.
Remark 3.1 The same construction also yields the ![]() $A_\infty$-algebra
$A_\infty$-algebra ![]() $\bigoplus _{i,j} \mathsf {\Gamma }_{i,j}$, which encodes the same data as
$\bigoplus _{i,j} \mathsf {\Gamma }_{i,j}$, which encodes the same data as ![]() $\mathsf {\Gamma }$. The above construction is similar in spirit to [Reference Kuznetsov and LuntsKL15, § 5]. If
$\mathsf {\Gamma }$. The above construction is similar in spirit to [Reference Kuznetsov and LuntsKL15, § 5]. If ![]() $\mathsf {R}$ is concentrated in degree
$\mathsf {R}$ is concentrated in degree ![]() $0$ and
$0$ and ![]() $F$ is the radical filtration, we obtain a subalgebra of Auslander's original algebra [Reference AuslanderAus99], which is nowadays often referred to as the Auslander–Dlab–Ringel algebra (see, for example, [Reference Conde and ErdmannCE18]).
$F$ is the radical filtration, we obtain a subalgebra of Auslander's original algebra [Reference AuslanderAus99], which is nowadays often referred to as the Auslander–Dlab–Ringel algebra (see, for example, [Reference Conde and ErdmannCE18]).
As ![]() $\mathsf {\Gamma }_{0,0}=\mathsf {R}$, by thinking of
$\mathsf {\Gamma }_{0,0}=\mathsf {R}$, by thinking of ![]() $\mathsf {R}$ as an
$\mathsf {R}$ as an ![]() $A_\infty$-category with one object we have a fully faithful strict
$A_\infty$-category with one object we have a fully faithful strict ![]() $A_\infty$-functor
$A_\infty$-functor
whence we obtain the following result by Lemma 2.4.
Corollary 3.2 There is a fully faithful functor
Proposition 3.3 Let ![]() $\bar {\mathsf {R}}=R/F^1$. There are
$\bar {\mathsf {R}}=R/F^1$. There are ![]() $n$ quasi-fully-faithful
$n$ quasi-fully-faithful ![]() $A_\infty$-functors
$A_\infty$-functors
giving rise to a semi-orthogonal decomposition
Proof. For ![]() $i=0,\ldots,n-1$ let
$i=0,\ldots,n-1$ let
and ![]() $P_n=0$. For
$P_n=0$. For ![]() $i=0,\ldots,n-1$ the element
$i=0,\ldots,n-1$ the element ![]() $P_i \in D_{\infty }(\mathsf {\Gamma })$ corresponds to the
$P_i \in D_{\infty }(\mathsf {\Gamma })$ corresponds to the ![]() $(i+1)$th column in (7) and we have obvious inclusion maps
$(i+1)$th column in (7) and we have obvious inclusion maps
Put
 \begin{equation} S_i:=\operatorname{cone} \psi_i=\begin{pmatrix} F^i/F^{i+1}\\ F^{i-1}/F^{i}\\\vdots\\ \mathsf{R}/F^1\\ 0\\\vdots\\0 \end{pmatrix} \end{equation}
\begin{equation} S_i:=\operatorname{cone} \psi_i=\begin{pmatrix} F^i/F^{i+1}\\ F^{i-1}/F^{i}\\\vdots\\ \mathsf{R}/F^1\\ 0\\\vdots\\0 \end{pmatrix} \end{equation}
(in particular, ![]() $S_{n-1}=P_{n-1}$). By the Yoneda lemma we see that
$S_{n-1}=P_{n-1}$). By the Yoneda lemma we see that
 \begin{equation} \operatorname{Hom}^\ast_{D_{\infty}(\mathsf {\Gamma })}(P_j,S_i)=H^*(S_i(j))= \begin{cases} 0, & \text{if}\ j>i,\\ H^\ast(\bar{\mathsf{R}}), & \text{if }j=i. \end{cases} \end{equation}
\begin{equation} \operatorname{Hom}^\ast_{D_{\infty}(\mathsf {\Gamma })}(P_j,S_i)=H^*(S_i(j))= \begin{cases} 0, & \text{if}\ j>i,\\ H^\ast(\bar{\mathsf{R}}), & \text{if }j=i. \end{cases} \end{equation}We also find using the long exact sequence for the distinguished triangle
that
We now have by (13) semi-orthogonal decompositions
which, by induction, yield a semi-orthogonal decomposition
Using (12) and the compatibility conditions (5) for the filtration ![]() $F^*$, we check that the
$F^*$, we check that the ![]() $S_i$ are, in fact,
$S_i$ are, in fact, ![]() $A_\infty -\mathsf {\Gamma }-\bar {\mathsf {R}}$-bimodules. Thus, we have DG functors
$A_\infty -\mathsf {\Gamma }-\bar {\mathsf {R}}$-bimodules. Thus, we have DG functors
and the corresponding exact functors
which send ![]() $\bar {\mathsf {R}}$ to
$\bar {\mathsf {R}}$ to ![]() $S_i$ and therefore are fully faithful by (14) and Lemma 2.4. Thus, they establish equivalences
$S_i$ and therefore are fully faithful by (14) and Lemma 2.4. Thus, they establish equivalences
finishing the proof.
Let us call an ![]() $A_\infty$-algebra
$A_\infty$-algebra ![]() $A$ geometric if there is a fully faithful Fourier–Mukai functor (in the sense of Definition 2.2)
$A$ geometric if there is a fully faithful Fourier–Mukai functor (in the sense of Definition 2.2) ![]() $f:\operatorname {Perf} A\hookrightarrow D^b(\mathop {\text {coh}}(X))$ for
$f:\operatorname {Perf} A\hookrightarrow D^b(\mathop {\text {coh}}(X))$ for ![]() $X$ a smooth and projective
$X$ a smooth and projective ![]() $k$-scheme, such that in addition
$k$-scheme, such that in addition ![]() $f$ has a left and a right adjoint.
$f$ has a left and a right adjoint.
In the following corollary, we make use of Orlov's powerful gluing result, which in our setting may be formulated as follows (see also Remark 2.1).
Theorem 3.4 [Reference OrlovOrl16, Theorem 4.15]
Given ![]() $A_{\infty }$-algebras
$A_{\infty }$-algebras ![]() $A, B, C$ with
$A, B, C$ with ![]() $C$ proper and a semi-orthogonal decomposition
$C$ proper and a semi-orthogonal decomposition
If ![]() $A$ and
$A$ and ![]() $B$ are geometric, then so is
$B$ are geometric, then so is ![]() $C$.
$C$.
Corollary 3.5 (Geometric realization)
Let ![]() $\mathsf {R}$ be a finite-dimensional
$\mathsf {R}$ be a finite-dimensional ![]() $A_\infty$-algebra equipped with a finite descending filtration such that
$A_\infty$-algebra equipped with a finite descending filtration such that ![]() $\bar {\mathsf {R}}=\mathsf {R}/F^1\mathsf {R}$ is geometric. Then there exists a fully faithful Fourier–Mukai functor
$\bar {\mathsf {R}}=\mathsf {R}/F^1\mathsf {R}$ is geometric. Then there exists a fully faithful Fourier–Mukai functor ![]() $\operatorname {Perf}{\mathsf {R}}\hookrightarrow D^b(\mathop {\text {coh}}(X))$ where
$\operatorname {Perf}{\mathsf {R}}\hookrightarrow D^b(\mathop {\text {coh}}(X))$ where ![]() $X$ is a smooth projective
$X$ is a smooth projective ![]() $k$-scheme.
$k$-scheme.
Proof. Combining Proposition 3.3 with Theorem 3.4 we obtain that there exists a fully faithful Fourier–Mukai functor
where ![]() $X$ is a smooth projective
$X$ is a smooth projective ![]() $k$-scheme. Then we pre-compose this functor with the fully faithful Fourier–Mukai functor
$k$-scheme. Then we pre-compose this functor with the fully faithful Fourier–Mukai functor
of Corollary 3.2.
Corollary 3.6 Assume ![]() $\mathsf {R}$ is an
$\mathsf {R}$ is an ![]() $A_\infty$-algebra such that
$A_\infty$-algebra such that ![]() $H^\ast (\mathsf {R})$ is finite dimensional and concentrated in degrees
$H^\ast (\mathsf {R})$ is finite dimensional and concentrated in degrees ![]() $\le 0$, and moreover
$\le 0$, and moreover ![]() $H^0(\mathsf {R})$ is geometric. Then there exists a fully faithful Fourier–Mukai functor
$H^0(\mathsf {R})$ is geometric. Then there exists a fully faithful Fourier–Mukai functor ![]() $\operatorname {Perf}{\mathsf {R}}\hookrightarrow D^b(\mathop {\text {coh}}(X))$, where
$\operatorname {Perf}{\mathsf {R}}\hookrightarrow D^b(\mathop {\text {coh}}(X))$, where ![]() $X$ is a smooth projective
$X$ is a smooth projective ![]() $k$-scheme.
$k$-scheme.
Proof. Without loss of generality we may assume that ![]() $\mathsf {R}$ is minimal. We now apply Corollary 3.5 with the filtration
$\mathsf {R}$ is minimal. We now apply Corollary 3.5 with the filtration ![]() $F^p\mathsf {R}=\bigoplus _{i\ge p} \mathsf {R}^{-i}$.
$F^p\mathsf {R}=\bigoplus _{i\ge p} \mathsf {R}^{-i}$.
Remark 3.7 As ![]() $H^0(\mathsf {R})$ is assumed to be a finite-dimensional algebra, the following lemma may be helpful for checking geometricity of
$H^0(\mathsf {R})$ is assumed to be a finite-dimensional algebra, the following lemma may be helpful for checking geometricity of ![]() $H^0(\mathsf {R})$ in order to apply Corollary 3.6:
$H^0(\mathsf {R})$ in order to apply Corollary 3.6:
Lemma 3.8 Assume that ![]() $A$ is a finite-dimensional
$A$ is a finite-dimensional ![]() $k$-algebra. The following are equivalent:
$k$-algebra. The following are equivalent:
(i)
 $A$ is geometric;
$A$ is geometric;(ii)
 $A$ is smooth (i.e.
$A$ is smooth (i.e.  $\operatorname {p\,dim}_{A^e}A<\infty$);
$\operatorname {p\,dim}_{A^e}A<\infty$);(iii)
 $A/\operatorname {rad} A$ is separable over
$A/\operatorname {rad} A$ is separable over  $k$ and
$k$ and  $\operatorname {gl\,dim} A<\infty$.
$\operatorname {gl\,dim} A<\infty$.
Proof.
(i)⇒(ii) This is [Reference OrlovOrl16, Theorem 3.25].
(ii)⇒(iii) The fact that
 $A/\operatorname {rad} A$ is separable over
$A/\operatorname {rad} A$ is separable over  $k$ is [Reference Reyes and RogalskiRR22, Theorem 3.6], which in turn comes from a MathOverflow answer by Rickard [Reference RickardRic16]. Finite global dimension is classical.
$k$ is [Reference Reyes and RogalskiRR22, Theorem 3.6], which in turn comes from a MathOverflow answer by Rickard [Reference RickardRic16]. Finite global dimension is classical.(iii)⇒(i) This is [Reference OrlovOrl16, Corollary 5.4].
Remark 3.9 If ![]() $k$ is algebraically closed, one can even assume that the scheme
$k$ is algebraically closed, one can even assume that the scheme ![]() $X$ in Corollary 3.6 has a full exceptional collection. Indeed, using the radical filtration
$X$ in Corollary 3.6 has a full exceptional collection. Indeed, using the radical filtration ![]() $F^pH^0(\mathsf {R})=\operatorname {rad}^p H^0(\mathsf {R})$ for the finite-dimensional algebra
$F^pH^0(\mathsf {R})=\operatorname {rad}^p H^0(\mathsf {R})$ for the finite-dimensional algebra ![]() $H^0(\mathsf {R})$, we see that there is a fully faithful functor
$H^0(\mathsf {R})$, we see that there is a fully faithful functor
and a semi-orthogonal decomposition
In particular, each copy ![]() $\mathcal {A}_i=\operatorname {Perf} (H^0(\mathsf {R}))$ in the semi-orthogonal decomposition
$\mathcal {A}_i=\operatorname {Perf} (H^0(\mathsf {R}))$ in the semi-orthogonal decomposition
admits a fully faithful functor ![]() $\mathcal {A}_i \to \mathsf {C}_i$ for some category
$\mathcal {A}_i \to \mathsf {C}_i$ for some category ![]() $\mathsf {C}_i$ with a full exceptional collection. We claim this implies there is also a fully faithful functor
$\mathsf {C}_i$ with a full exceptional collection. We claim this implies there is also a fully faithful functor
for some category ![]() $\mathsf {C}$ with a full exceptional collection. Indeed, first assume
$\mathsf {C}$ with a full exceptional collection. Indeed, first assume ![]() $n=2$, then we can base change the (perfect) gluing
$n=2$, then we can base change the (perfect) gluing ![]() $\mathcal {A}_1$–
$\mathcal {A}_1$–![]() $\mathcal {A}_2$-bimodule
$\mathcal {A}_2$-bimodule ![]() $M$ (responsible for (17)) to a perfect
$M$ (responsible for (17)) to a perfect ![]() $\mathsf {C}_1$–
$\mathsf {C}_1$–![]() $\mathsf {C}_2$-bimodule, say
$\mathsf {C}_2$-bimodule, say ![]() $M'$. The corresponding gluing
$M'$. The corresponding gluing ![]() $\mathsf {C}$ of
$\mathsf {C}$ of ![]() $\mathsf {C}_1$ and
$\mathsf {C}_1$ and ![]() $\mathsf {C}_2$ along
$\mathsf {C}_2$ along ![]() $M'$ then has a semi-orthogonal decomposition
$M'$ then has a semi-orthogonal decomposition
and, by construction, ![]() $\mathsf {C}$ has a full exceptional collection. Moreover, one can check that the induced functor
$\mathsf {C}$ has a full exceptional collection. Moreover, one can check that the induced functor
is still fully faithful. For ![]() $n>2$, we proceed by induction.
$n>2$, we proceed by induction.
Finally, by applying [Reference OrlovOrl16, Theorem 5.8], there exists a fully faithful Fourier–Mukai functor
for some smooth projective ![]() $k$-scheme
$k$-scheme ![]() $X$ with a full exceptional collection.
$X$ with a full exceptional collection.
4.  $A_\infty$-deformations of schemes and objects
$A_\infty$-deformations of schemes and objects
In this section we review some material on ![]() $A_\infty$-deformations of schemes and the corresponding results for deformations of objects. For the benefit of the reader, we collect the results we need in the rest of the paper, in the generality that we need in this situation. A more general treatment of this can be found in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, §§ 6 and 8].
$A_\infty$-deformations of schemes and the corresponding results for deformations of objects. For the benefit of the reader, we collect the results we need in the rest of the paper, in the generality that we need in this situation. A more general treatment of this can be found in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, §§ 6 and 8].
Definition 4.1 Let ![]() $\mathcal {X}$ be a
$\mathcal {X}$ be a ![]() $k$-linear category and
$k$-linear category and ![]() $\mathcal {M}$ be a
$\mathcal {M}$ be a ![]() $k$-central
$k$-central ![]() $\mathcal {X}$-bimodule. The Hochschild complex
$\mathcal {X}$-bimodule. The Hochschild complex ![]() $\mathbf {C}^\bullet (\mathcal {X}, \mathcal {M})$ is defined as
$\mathbf {C}^\bullet (\mathcal {X}, \mathcal {M})$ is defined as
with the usual differential (see [Reference MitchellMit72]).
The Hochschild cohomology ![]() ${\rm HH}^\bullet (\mathcal {X}, \mathcal {M})$ is the cohomology of the Hochschild complex
${\rm HH}^\bullet (\mathcal {X}, \mathcal {M})$ is the cohomology of the Hochschild complex ![]() $\mathbf {C}^\bullet (\mathcal {X}, \mathcal {M})$.
$\mathbf {C}^\bullet (\mathcal {X}, \mathcal {M})$.
Remark 4.2 Let ![]() $\mathcal {X}$ be a
$\mathcal {X}$ be a ![]() $k$-linear category,
$k$-linear category, ![]() $A$ be a
$A$ be a ![]() $k$-algebra, and
$k$-algebra, and ![]() $\mathcal {M}$ be a
$\mathcal {M}$ be a ![]() $k$-central
$k$-central ![]() $\mathcal {X}$-bimodule. There is a morphism
$\mathcal {X}$-bimodule. There is a morphism
where ![]() $\eta \cup 1$ is defined by
$\eta \cup 1$ is defined by
for suitable composable arrows ![]() $x_1,\ldots,x_n$ in
$x_1,\ldots,x_n$ in ![]() $\mathcal {X}$, where the sign is given by the Koszul convention.
$\mathcal {X}$, where the sign is given by the Koszul convention.
Definition 4.3 Let ![]() $\mathcal {X}$ be a
$\mathcal {X}$ be a ![]() $k$-linear
$k$-linear ![]() $A_\infty$-category and
$A_\infty$-category and ![]() $A$ be a
$A$ be a ![]() $k$-algebra. The tensor product
$k$-algebra. The tensor product ![]() $\mathcal {X}\otimes A$ is the
$\mathcal {X}\otimes A$ is the ![]() $A_\infty$-category with the same objects as
$A_\infty$-category with the same objects as ![]() $\mathcal {X}$ and morphisms
$\mathcal {X}$ and morphisms ![]() $\mathcal {X}(-,-)\otimes _k A$. The codifferential
$\mathcal {X}(-,-)\otimes _k A$. The codifferential ![]() $b_{\mathcal {X}\otimes _k A}$ is given by the Taylor coefficients
$b_{\mathcal {X}\otimes _k A}$ is given by the Taylor coefficients
 \begin{align*} &b^1_{\mathcal{X}\otimes_k A}(s(x\otimes a))=b^1_\mathcal{X} (sx)\otimes a,\\ &b^n_{\mathcal{X}\otimes_k A}(s(x_1\otimes a_1),\ldots, s(x_n\otimes a_n))= \pm b^n_\mathcal{X} (sx_1,\ldots, sx_n)\otimes a_1\cdots a_n \end{align*}
\begin{align*} &b^1_{\mathcal{X}\otimes_k A}(s(x\otimes a))=b^1_\mathcal{X} (sx)\otimes a,\\ &b^n_{\mathcal{X}\otimes_k A}(s(x_1\otimes a_1),\ldots, s(x_n\otimes a_n))= \pm b^n_\mathcal{X} (sx_1,\ldots, sx_n)\otimes a_1\cdots a_n \end{align*}for suitable composable arrows, where the sign is given by the Koszul convention.
For the rest of this section, unless specified otherwise, ![]() $X$ denotes a quasi-compact separated
$X$ denotes a quasi-compact separated ![]() $k$-scheme.
$k$-scheme.
Definition 4.4 If ![]() $M\in D(\mathcal {O}_X)$, then the Hochschild cohomology of
$M\in D(\mathcal {O}_X)$, then the Hochschild cohomology of ![]() $M$ is defined as
$M$ is defined as
where ![]() $i_\Delta :X\rightarrow X\times X$ is the diagonal map.
$i_\Delta :X\rightarrow X\times X$ is the diagonal map.
Definition 4.5 Let ![]() $X=\bigcup _{i=1}^n U_i$ be an affine covering. For
$X=\bigcup _{i=1}^n U_i$ be an affine covering. For ![]() $I\subset \{1,\ldots,n\}$ let
$I\subset \{1,\ldots,n\}$ let ![]() $U_I=\bigcap _{i\in I} U_i$. Let
$U_I=\bigcap _{i\in I} U_i$. Let ![]() $\mathcal {I}$ be the set
$\mathcal {I}$ be the set ![]() $\{I\subset \{1,\ldots,n\}\mid I\neq \emptyset \}$. Then
$\{I\subset \{1,\ldots,n\}\mid I\neq \emptyset \}$. Then ![]() $\mathcal {X}$ is defined to be the category with objects
$\mathcal {X}$ is defined to be the category with objects ![]() $\mathcal {I}$ and
$\mathcal {I}$ and ![]() $\operatorname {Hom}$-sets
$\operatorname {Hom}$-sets
 \begin{equation} \mathcal{X}(I,J)= \begin{cases} \mathcal{O}_X(U_J), & I\subset J,\\ 0, & \text{otherwise}. \end{cases} \end{equation}
\begin{equation} \mathcal{X}(I,J)= \begin{cases} \mathcal{O}_X(U_J), & I\subset J,\\ 0, & \text{otherwise}. \end{cases} \end{equation} Roughly this allows us to think of ![]() $\operatorname {Mod}(\mathcal {X})$ as the category of presheaves associated with an affine covering of
$\operatorname {Mod}(\mathcal {X})$ as the category of presheaves associated with an affine covering of ![]() $X$. This construction has many good properties, some of which are summarized in the following.
$X$. This construction has many good properties, some of which are summarized in the following.
Lemma 4.6 There is a fully faithful embedding
and a corresponding fully faithful embedding for bimodules
where ![]() $D^{\delta }(\operatorname {Qch}(X))=i_{\Delta,*}D(\operatorname {Qch}(X))$ is the category with the same objects as
$D^{\delta }(\operatorname {Qch}(X))=i_{\Delta,*}D(\operatorname {Qch}(X))$ is the category with the same objects as ![]() $D(\operatorname {Qch}(X))$ and morphisms
$D(\operatorname {Qch}(X))$ and morphisms
Moreover, for a quasi-coherent sheaf ![]() $M$ on
$M$ on ![]() $X$ we have
$X$ we have
For ![]() $A$ a (not necessarily commutative)
$A$ a (not necessarily commutative) ![]() $k$-algebra, there exists an
$k$-algebra, there exists an ![]() $A$-equivariant version of
$A$-equivariant version of ![]() $w$:
$w$:
which is also a fully faithful embedding.
Proof. For the construction of the embeddings ![]() $w$ and
$w$ and ![]() $W$ see [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, § 8.3]. The proof of the equivalence (23) is also sketched in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, § 8.3], for a full proof see [Reference Lowen and Van den BerghLVdB05]. The
$W$ see [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, § 8.3]. The proof of the equivalence (23) is also sketched in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, § 8.3], for a full proof see [Reference Lowen and Van den BerghLVdB05]. The ![]() $A$-equivariant version is constructed in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, § 8.5].
$A$-equivariant version is constructed in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, § 8.5].
We also need a deformed version of ![]() $\mathcal {X}$. We give the definition in this case, but the general construction can be found in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, § 6].
$\mathcal {X}$. We give the definition in this case, but the general construction can be found in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, § 6].
Definition 4.7 Let ![]() $\mathcal {M}$ be a
$\mathcal {M}$ be a ![]() $k$-central
$k$-central ![]() $\mathcal {X}$-bimodule and
$\mathcal {X}$-bimodule and ![]() $\eta \in {\rm HH}^n(\mathcal {X},\mathcal {M})$. Let
$\eta \in {\rm HH}^n(\mathcal {X},\mathcal {M})$. Let ![]() $\tilde {\mathcal {X}}$ be the DG-category
$\tilde {\mathcal {X}}$ be the DG-category ![]() $\mathcal {X}\oplus \Sigma ^{n-2}\mathcal {M}$: its objects are the objects of
$\mathcal {X}\oplus \Sigma ^{n-2}\mathcal {M}$: its objects are the objects of ![]() $\mathcal {X}$, morphisms are given by
$\mathcal {X}$, morphisms are given by ![]() $\mathcal {X}(-,-)\oplus \Sigma ^{n-2}\mathcal {M}(-,-)$, and composition is coming from the composition in
$\mathcal {X}(-,-)\oplus \Sigma ^{n-2}\mathcal {M}(-,-)$, and composition is coming from the composition in ![]() $\mathcal {X}$ and the action of
$\mathcal {X}$ and the action of ![]() $\mathcal {X}$ on
$\mathcal {X}$ on ![]() $\mathcal {M}$.
$\mathcal {M}$.
Lift ![]() $\eta \in {\rm HH}^n(\mathcal {X},\mathcal {M})$ to a Hochschild cocycle, which we also denote by
$\eta \in {\rm HH}^n(\mathcal {X},\mathcal {M})$ to a Hochschild cocycle, which we also denote by ![]() $\eta$. We can think of
$\eta$. We can think of ![]() $\eta$ as a map
$\eta$ as a map ![]() $(\Sigma \mathcal {X})^{\otimes n}\to \Sigma (\Sigma ^{n-2}\mathcal {M})$ of degree one.
$(\Sigma \mathcal {X})^{\otimes n}\to \Sigma (\Sigma ^{n-2}\mathcal {M})$ of degree one.
We define as ![]() $\mathcal {X}_{\eta }$ the
$\mathcal {X}_{\eta }$ the ![]() $A_{\infty }$-category
$A_{\infty }$-category ![]() $\tilde {\mathcal {X}}$ with deformed
$\tilde {\mathcal {X}}$ with deformed ![]() $A_{\infty }$-structure given by
$A_{\infty }$-structure given by
where ![]() $b_{(-)}$ denotes the codifferential on the corresponding bar construction giving the
$b_{(-)}$ denotes the codifferential on the corresponding bar construction giving the ![]() $A_{\infty }$-structure, and where we view
$A_{\infty }$-structure, and where we view ![]() $\eta$ as a map of degree one
$\eta$ as a map of degree one ![]() $(\Sigma \mathcal {X})^{\otimes n}\to \Sigma (\Sigma ^{n-2}\mathcal {M})$ and extend it to a map
$(\Sigma \mathcal {X})^{\otimes n}\to \Sigma (\Sigma ^{n-2}\mathcal {M})$ and extend it to a map ![]() $\eta :(\Sigma \mathcal {X}_{\eta })^{\otimes n}\to \Sigma \mathcal {X}_\eta$ by making the unspecified component zero. Clearly we have
$\eta :(\Sigma \mathcal {X}_{\eta })^{\otimes n}\to \Sigma \mathcal {X}_\eta$ by making the unspecified component zero. Clearly we have ![]() $H^*(\mathcal {X}_\eta )=\tilde {\mathcal {X}}$; the only nontrivial Taylor coefficients of the codifferential
$H^*(\mathcal {X}_\eta )=\tilde {\mathcal {X}}$; the only nontrivial Taylor coefficients of the codifferential ![]() $b_{\mathcal {X}_{\eta }}$ are
$b_{\mathcal {X}_{\eta }}$ are ![]() $b_{\mathcal {X}_{\eta },2}$ and
$b_{\mathcal {X}_{\eta },2}$ and ![]() $b_{\mathcal {X}_{\eta },n}$.
$b_{\mathcal {X}_{\eta },n}$.
Remark 4.8 For ![]() $\eta$ a cocycle in
$\eta$ a cocycle in ![]() $\mathbf {C}^\bullet (\mathcal {X}, \mathcal {M})$ and
$\mathbf {C}^\bullet (\mathcal {X}, \mathcal {M})$ and ![]() $\eta \cup 1$ the corresponding cocycle in
$\eta \cup 1$ the corresponding cocycle in ![]() $\mathbf {C}^\bullet (\mathcal {X}\otimes _k A, \mathcal {M}\otimes _k A)$ we have that
$\mathbf {C}^\bullet (\mathcal {X}\otimes _k A, \mathcal {M}\otimes _k A)$ we have that ![]() $(\mathcal {X}\otimes _k A)_{\eta \cup 1}=\mathcal {X}_\eta \otimes _k A$.
$(\mathcal {X}\otimes _k A)_{\eta \cup 1}=\mathcal {X}_\eta \otimes _k A$.
Definition 4.9 Let ![]() $\mathcal {U}\in \operatorname {Mod}(\mathcal {X})$. A colift of
$\mathcal {U}\in \operatorname {Mod}(\mathcal {X})$. A colift of ![]() $\mathcal {U}$ to
$\mathcal {U}$ to ![]() $\mathcal {X}_\eta$ is a pair
$\mathcal {X}_\eta$ is a pair ![]() $(\mathcal {V}, \phi )$, where
$(\mathcal {V}, \phi )$, where ![]() $\mathcal {V}\in D_{\infty }(\mathcal {X}_\eta )$ and
$\mathcal {V}\in D_{\infty }(\mathcal {X}_\eta )$ and ![]() $\phi$ is an isomorphism of graded
$\phi$ is an isomorphism of graded ![]() $H^*(\mathcal {X}_\eta )$-modules
$H^*(\mathcal {X}_\eta )$-modules ![]() $H^*(\mathcal {V})\cong \operatorname {Hom}_\mathcal {X}(H^*(\mathcal {X}_\eta ), \mathcal {U})$.
$H^*(\mathcal {V})\cong \operatorname {Hom}_\mathcal {X}(H^*(\mathcal {X}_\eta ), \mathcal {U})$.
Proposition 4.10 Assume that ![]() $\mathcal {M}$ is an invertible
$\mathcal {M}$ is an invertible ![]() $\mathcal {X}$-bimodule and
$\mathcal {X}$-bimodule and ![]() $\mathcal {X}_\eta$ is as in Definition 4.7. The object
$\mathcal {X}_\eta$ is as in Definition 4.7. The object ![]() $\mathcal {U}\in \operatorname {Mod}(\mathcal {X})$ has a colift to
$\mathcal {U}\in \operatorname {Mod}(\mathcal {X})$ has a colift to ![]() $\mathcal {X}_\eta$ if and only if
$\mathcal {X}_\eta$ if and only if ![]() $c_\mathcal {U}(\eta )=0$, where
$c_\mathcal {U}(\eta )=0$, where ![]() $c_\mathcal {U}$ is the characteristic morphism
$c_\mathcal {U}$ is the characteristic morphism
obtained by interpreting ![]() $\eta \in {\rm HH}^{n}(\mathcal {X},\mathcal {M})$ as a map
$\eta \in {\rm HH}^{n}(\mathcal {X},\mathcal {M})$ as a map ![]() $\mathcal {X}\to \Sigma ^{n}\mathcal {M}$ in
$\mathcal {X}\to \Sigma ^{n}\mathcal {M}$ in ![]() $D(\mathcal {X}\otimes _k \mathcal {X}^\circ )$ and then applying the functor
$D(\mathcal {X}\otimes _k \mathcal {X}^\circ )$ and then applying the functor ![]() $-\otimes _\mathcal {X} \mathcal {U}$ to get a map
$-\otimes _\mathcal {X} \mathcal {U}$ to get a map ![]() $U\to \Sigma ^{n}\mathcal {M}\otimes _\mathcal {X} \mathcal {U}$.
$U\to \Sigma ^{n}\mathcal {M}\otimes _\mathcal {X} \mathcal {U}$.
Proof. This is a combination of [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, Lemma 6.4.1] and [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, Lemma 6.3.1].
5. Proof of Theorem 1.3
We now proceed to give a construction of an exact functor ![]() $L:D^b(\mathop {\text {coh}}(X))\to D_{\infty }(\mathcal {X}_\eta )$, originally given in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19]. We summarize the construction in this particular case for the benefit of the reader. More details in the general setting are in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, § 10].
$L:D^b(\mathop {\text {coh}}(X))\to D_{\infty }(\mathcal {X}_\eta )$, originally given in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19]. We summarize the construction in this particular case for the benefit of the reader. More details in the general setting are in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, § 10].
Construction 5.1 Let ![]() $X$ be a smooth projective scheme of dimension
$X$ be a smooth projective scheme of dimension ![]() $m\ge 3$, which has a tilting bundle. Let
$m\ge 3$, which has a tilting bundle. Let ![]() $M=\omega _X^{\otimes 2}$; by [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, Lemma 9.6.1] we have
$M=\omega _X^{\otimes 2}$; by [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, Lemma 9.6.1] we have ![]() ${\rm HH}^{2m}(X,M)\cong k$, so that we can pick
${\rm HH}^{2m}(X,M)\cong k$, so that we can pick ![]() $0\neq \eta \in {\rm HH}^{2m}(X,M)$. View
$0\neq \eta \in {\rm HH}^{2m}(X,M)$. View ![]() $\eta$ as an element of
$\eta$ as an element of ![]() ${\rm HH}^*(\mathcal {X},\mathcal {M})$, for
${\rm HH}^*(\mathcal {X},\mathcal {M})$, for ![]() $\mathcal {M}=W(M)$, via (23). Construct the
$\mathcal {M}=W(M)$, via (23). Construct the ![]() $A_\infty$-category
$A_\infty$-category ![]() $\mathcal {X}_\eta$ as in Definition 4.7.
$\mathcal {X}_\eta$ as in Definition 4.7.
We are now in the situation of [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, § 10.1] and we can define an exact functor
as in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, (10.3)], where ![]() $\mathcal {X}^{\operatorname {dg}}_\eta$ is the unital DG-hull of
$\mathcal {X}^{\operatorname {dg}}_\eta$ is the unital DG-hull of ![]() $\mathcal {X}_\eta$. Then we obtain our exact functor (also denoted by
$\mathcal {X}_\eta$. Then we obtain our exact functor (also denoted by ![]() $L$) as the composition
$L$) as the composition
where ![]() $D_{\infty }(\mathcal {X}_\eta )\cong D_{\infty }(\mathcal {X}_\eta ^{\mathrm {dg}}) \cong D(\mathcal {X}_\eta ^{\mathrm {dg}})$ by [Reference Lefèvre-HasegawaLef03, Lemme 4.1.3.8] (cf. also Remark 2.1).
$D_{\infty }(\mathcal {X}_\eta )\cong D_{\infty }(\mathcal {X}_\eta ^{\mathrm {dg}}) \cong D(\mathcal {X}_\eta ^{\mathrm {dg}})$ by [Reference Lefèvre-HasegawaLef03, Lemme 4.1.3.8] (cf. also Remark 2.1).
Lemma 5.2 Let ![]() $T\in D^b(\mathop {\text {coh}}(X))$ and
$T\in D^b(\mathop {\text {coh}}(X))$ and ![]() $\mathcal {T}=w(T)$. Let
$\mathcal {T}=w(T)$. Let ![]() $L$ be the functor constructed in Construction 5.1. The following is a distinguished triangle in
$L$ be the functor constructed in Construction 5.1. The following is a distinguished triangle in ![]() $D_{\infty }(\mathcal {X}_\eta )$:
$D_{\infty }(\mathcal {X}_\eta )$:
Proof. This is the distinguished triangle in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, Lemma 10.3] under the equivalence of categories ![]() $D(\mathcal {X}^{\operatorname {dg}}_\eta ) \cong D_{\infty }(\mathcal {X}_\eta )$.
$D(\mathcal {X}^{\operatorname {dg}}_\eta ) \cong D_{\infty }(\mathcal {X}_\eta )$.
Lemma 5.3 Let ![]() $X$ be a smooth projective scheme of dimension
$X$ be a smooth projective scheme of dimension ![]() $m\ge 3$ that has a tilting bundle. Then the exact functor
$m\ge 3$ that has a tilting bundle. Then the exact functor
of Construction 5.1 is non-Fourier–Mukai (see Definition 2.2).
Proof. This proof follows the proof of [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, Lemma 11.4] (the argument is written there for the case ![]() $m=3$, but the proof is the same for a general
$m=3$, but the proof is the same for a general ![]() $m\geq 3$). We repeat it here for the benefit of the reader.
$m\geq 3$). We repeat it here for the benefit of the reader.
Let ![]() $T$ be a tilting bundle for
$T$ be a tilting bundle for ![]() $X$,
$X$, ![]() $A=\operatorname {End}_X(T)$ and
$A=\operatorname {End}_X(T)$ and ![]() $\mathcal {T}=w(T)$. We can think of
$\mathcal {T}=w(T)$. We can think of ![]() $\mathcal {T}$ as an element in
$\mathcal {T}$ as an element in ![]() $\operatorname {Mod}(\mathcal {X}\otimes _k A)$. If
$\operatorname {Mod}(\mathcal {X}\otimes _k A)$. If ![]() $L$ were a Fourier–Mukai functor with an
$L$ were a Fourier–Mukai functor with an ![]() $A_\infty$-lift
$A_\infty$-lift ![]() $\ell$ such that
$\ell$ such that ![]() $H^0(\ell )\cong L$, then by
$H^0(\ell )\cong L$, then by ![]() $A_\infty$-functoriality
$A_\infty$-functoriality ![]() $\ell (T)$ could be viewed as an object in
$\ell (T)$ could be viewed as an object in ![]() $\mathcal {D}_\infty (\mathcal {X}_\eta \otimes _k A)$ and, consequently,
$\mathcal {D}_\infty (\mathcal {X}_\eta \otimes _k A)$ and, consequently, ![]() $L(T)$ would be an element in
$L(T)$ would be an element in ![]() $D_{\infty }(\mathcal {X}_\eta \otimes _k A)$.
$D_{\infty }(\mathcal {X}_\eta \otimes _k A)$.
On the other hand, thanks to the distinguished triangle (24) we have
By construction, this isomorphism is compatible with the ![]() $H^\ast (\mathcal {X}_\eta )$- and
$H^\ast (\mathcal {X}_\eta )$- and ![]() $A$-actions. Using Remark 4.8 we obtain that
$A$-actions. Using Remark 4.8 we obtain that ![]() $L(T)$ is a colift of
$L(T)$ is a colift of ![]() $\mathcal {T}\in \operatorname {Mod}(\mathcal {X}\otimes _k A)$ to
$\mathcal {T}\in \operatorname {Mod}(\mathcal {X}\otimes _k A)$ to ![]() $D_{\infty }((\mathcal {X}\otimes _k A)_{\eta \cup 1})=D_{\infty }(\mathcal {X}_\eta \otimes _k A)$.
$D_{\infty }((\mathcal {X}\otimes _k A)_{\eta \cup 1})=D_{\infty }(\mathcal {X}_\eta \otimes _k A)$.
By Proposition 4.10 the obstruction against the existence of such a colift is the image of ![]() $\eta \cup 1$ under the characteristic morphism
$\eta \cup 1$ under the characteristic morphism
Let ![]() $c_{\mathcal {T},A}$ be the composition
$c_{\mathcal {T},A}$ be the composition
By the ![]() $A$-equivariant version of [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, (8.14)] we have a commutative diagram
$A$-equivariant version of [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, (8.14)] we have a commutative diagram

of ![]() $A$-equivariant characteristic maps. The rightmost map is an isomorphism by [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, (8.13)] and the fact that the
$A$-equivariant characteristic maps. The rightmost map is an isomorphism by [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, (8.13)] and the fact that the ![]() $A$-equivariant version of
$A$-equivariant version of ![]() $w$ is fully faithful (Lemma 4.6). The leftmost map is an isomorphism by (23). By [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, Proposition 8.9.2], the upper horizontal map is also an isomorphism. It follows that, because we chose
$w$ is fully faithful (Lemma 4.6). The leftmost map is an isomorphism by (23). By [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, Proposition 8.9.2], the upper horizontal map is also an isomorphism. It follows that, because we chose ![]() $\eta \neq 0$, its image
$\eta \neq 0$, its image ![]() $c_{\mathcal {T},A}(\eta )$ is also nonzero and provides an obstruction to the existence of a colift. Thus,
$c_{\mathcal {T},A}(\eta )$ is also nonzero and provides an obstruction to the existence of a colift. Thus, ![]() $L$ cannot be a Fourier–Mukai functor.
$L$ cannot be a Fourier–Mukai functor.
Proof of Theorem 1.3 Let ![]() $\mathcal {A}$ be the smallest thick subcategory of
$\mathcal {A}$ be the smallest thick subcategory of ![]() $D_{\infty }(\mathcal {X}_\eta )$ containing the essential image of
$D_{\infty }(\mathcal {X}_\eta )$ containing the essential image of ![]() $D^b(\mathop {\text {coh}}(X))$ under
$D^b(\mathop {\text {coh}}(X))$ under ![]() $L$. It is clear that the corestricted functor
$L$. It is clear that the corestricted functor
is still non-Fourier–Mukai.
Let ![]() $\mathfrak {a}$ be the full sub-DG-category of
$\mathfrak {a}$ be the full sub-DG-category of ![]() $\mathcal {D}_\infty (\mathcal {X}_\eta )$ spanned by
$\mathcal {D}_\infty (\mathcal {X}_\eta )$ spanned by ![]() $\operatorname {Ob}(\mathcal {A})$ and let
$\operatorname {Ob}(\mathcal {A})$ and let ![]() $T$ be a tilting bundle for
$T$ be a tilting bundle for ![]() $X$. Then we have
$X$. Then we have ![]() $H^0(\mathfrak {a})=\mathcal {A}$. Let
$H^0(\mathfrak {a})=\mathcal {A}$. Let ![]() $\mathsf {R}=\mathfrak {a}(L(T),L(T))$. By Lemma 2.5 we have a quasi-equivalence
$\mathsf {R}=\mathfrak {a}(L(T),L(T))$. By Lemma 2.5 we have a quasi-equivalence ![]() $\mathfrak {a}\rightarrow \mathcal {P}\mathrm {erf}(\mathsf {R}^\circ )$. The composed functor
$\mathfrak {a}\rightarrow \mathcal {P}\mathrm {erf}(\mathsf {R}^\circ )$. The composed functor
is still non-Fourier–Mukai because quasi-equivalences are invertible up to homotopy [Reference Lefèvre-HasegawaLef03, Théorème 9.2.0.4].
Let ![]() $\mathcal {T}=w(T)$ be the left
$\mathcal {T}=w(T)$ be the left ![]() $\mathcal {X}$-module associated with
$\mathcal {X}$-module associated with ![]() $T$ and let
$T$ and let ![]() $\mathcal {M}=W(M)$ be the
$\mathcal {M}=W(M)$ be the ![]() $\mathcal {X}$-bimodule associated with
$\mathcal {X}$-bimodule associated with ![]() $M$. By the discussion before [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, (11.5)] we have a distinguished triangle of complexes of vector spaces (taking into account that in the current setting the quantity
$M$. By the discussion before [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, (11.5)] we have a distinguished triangle of complexes of vector spaces (taking into account that in the current setting the quantity ![]() $n$ in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, (11.5)] is equal to
$n$ in [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, (11.5)] is equal to ![]() $2m$)
$2m$)
Using [Reference Rizzardo, Van den Bergh and NeemanRVdBN19, Lemma 9.4.1] this becomes
which is equivalent to
The cohomology of ![]() $\operatorname {RHom}_{X}( T, M\otimes _X T)$ is concentrated in degrees
$\operatorname {RHom}_{X}( T, M\otimes _X T)$ is concentrated in degrees ![]() $\le m$. Whence the cohomology of
$\le m$. Whence the cohomology of ![]() $\Sigma ^{2m-2}\operatorname {RHom}_{X}( T, M\otimes _X T)$ is concentrated in degrees
$\Sigma ^{2m-2}\operatorname {RHom}_{X}( T, M\otimes _X T)$ is concentrated in degrees ![]() $\le m-(2m-2)<0$ (as
$\le m-(2m-2)<0$ (as ![]() $m\ge 3$). It now follows from (26) that
$m\ge 3$). It now follows from (26) that ![]() $\mathsf {R}$ is an
$\mathsf {R}$ is an ![]() $A_\infty$-algebra such that
$A_\infty$-algebra such that ![]() $H^\ast (\mathsf {R})$ is finite dimensional and concentrated in degrees
$H^\ast (\mathsf {R})$ is finite dimensional and concentrated in degrees ![]() $\le 0$ and moreover
$\le 0$ and moreover ![]() $H^0(\mathsf {R})=\operatorname {End}_X(T)$. As
$H^0(\mathsf {R})=\operatorname {End}_X(T)$. As ![]() $\operatorname {End}_X(T)^\circ$ is tautologically geometric we obtain by Corollary 3.6 a fully faithful Fourier–Mukai functor
$\operatorname {End}_X(T)^\circ$ is tautologically geometric we obtain by Corollary 3.6 a fully faithful Fourier–Mukai functor
The functor (1) is now the composition of (25) and (27). To see that is non-Fourier–Mukai we factor it as
where ![]() $\operatorname {Perf}(\mathsf {R}^\circ )\,\tilde {}$ is the essential image of (27). Note that because
$\operatorname {Perf}(\mathsf {R}^\circ )\,\tilde {}$ is the essential image of (27). Note that because ![]() $A_\infty$-quasi-equivalences may be inverted up to homotopy by [Reference Lefèvre-HasegawaLef03, Théorème 9.2.0.4], the inverse of
$A_\infty$-quasi-equivalences may be inverted up to homotopy by [Reference Lefèvre-HasegawaLef03, Théorème 9.2.0.4], the inverse of ![]() $\operatorname {Perf}(\mathsf {R}^\circ )\cong \operatorname {Perf}(\mathsf {R}^\circ )\,\tilde {}$ is also a Fourier–Mukai functor. Now if the composition (28) were Fourier–Mukai, then so would be the corestricted functor
$\operatorname {Perf}(\mathsf {R}^\circ )\cong \operatorname {Perf}(\mathsf {R}^\circ )\,\tilde {}$ is also a Fourier–Mukai functor. Now if the composition (28) were Fourier–Mukai, then so would be the corestricted functor ![]() $D^b(\mathop {\text {coh}}(X))\rightarrow \operatorname {Perf}(\mathsf {R}^\circ )\,\tilde {}$. Hence, the composition
$D^b(\mathop {\text {coh}}(X))\rightarrow \operatorname {Perf}(\mathsf {R}^\circ )\,\tilde {}$. Hence, the composition
would also be a Fourier–Mukai functor; but this composition is equivalent to (25). This is a contradiction.
Remark 5.4 With a little bit more work one may show that the fact that (25) is non-Fourier–Mukai is also true without the hypothesis that ![]() $X$ has a tilting bundle. However the tilting bundle is anyway needed for the rest of the construction.
$X$ has a tilting bundle. However the tilting bundle is anyway needed for the rest of the construction.
Remark 5.5 If ![]() $k$ is algebraically closed, then using Remark 3.9, one may show that
$k$ is algebraically closed, then using Remark 3.9, one may show that ![]() $Y$ can be chosen to have a full exceptional collection.
$Y$ can be chosen to have a full exceptional collection.