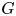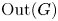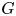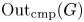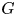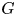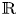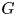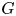1. Introduction
It was first shown by Dehn in 1922 that mapping class groups of closed surfaces are generated by finitely many Dehn twists around simple closed curves [Reference DehnDeh38]. Many decades later, one of the successes of Rips–Sela theory was the extension of this result to outer automorphism groups of all Gromov-hyperbolic groups [Reference Rips and SelaRS94].
More precisely, whenever a group 
$G$ splits as an amalgamated product 
$G=A\ast _CB$, we can construct an automorphism 
$\varphi \in \operatorname {Aut}(G)$ by defining 
$\varphi |_A$ as the identity and 
$\varphi |_B$ as the conjugation by an element of the centre of 
$C$. A similar construction can be applied to HNN splittings 
$G=A\ast _C$. We refer to group automorphisms obtained in this way as algebraic Dehn twists. Indeed, when 
$G=\pi _1\Sigma$ for a closed surface 
$\Sigma$ and 
$C\simeq \mathbb {Z}$, algebraic Dehn twists are precisely the action on 
$\pi _1\Sigma$ of the usual homeomorphisms of 
$\Sigma$ known as Dehn twists.
When 
$G$ is a one-ended Gromov-hyperbolic group (without torsion), Rips and Sela showed that a finite index subgroup of 
$\operatorname {Out}(G)$ is generated by finitely many algebraic Dehn twists arising from cyclic splittings of 
$G$ [Reference Rips and SelaRS94]. An analogous result was obtained by Groves for toral relatively hyperbolic groups 
$G$, where one must consider more generally all abelian splittings of 
$G$ [Reference GrovesGro09].
Both results are proved by first constructing an isometric 
$G$-action on an 
$\mathbb {R}$-tree and then applying the Rips machine. However, the trees involved have a very specific structure, they are superstable and small (i.e. with abelian arc-stabilisers), and thus they do not require the full power of Rips’ techniques, which can handle stable 
$G$-trees with arbitrary arc-stabilisers [Reference Bestvina and FeighnBF95].
For this reason, it is natural to expect that the class of groups 
$G$ for which 
$\operatorname {Out}(G)$ can be understood through Rips–Sela theory should be broader. The difficulty to overcome is that, when 
$G$ lacks strong hyperbolic features (mostly Gromov-hyperbolicity or relative hyperbolicity), it is generally hard to construct 
$G$-trees that simultaneously capture many significant features of the geometry of 
$G$. Nevertheless, in certain contexts, acylindrical hyperbolicity has been shown to suffice when addressing related questions, such as equational Noetherianity [Reference Groves and HullGH19, Reference Groves, Hull and LiangGHL21] and the existence of (higher-rank) Makanin–Razborov diagrams [Reference SelaSel22].
It is worth remarking that the above results are no exception and, in fact, all classical applications of the Rips machine only require its most ‘basic’ form for small superstable 
$G$-trees: from acylindrical accessibility [Reference SelaSel97a] and JSJ decompositions for finitely presented groups [Reference Rips and SelaRS97], to the Hopf property [Reference SelaSel99] and the isomorphism problem for hyperbolic groups [Reference SelaSel95, Reference Dahmani and GuirardelDG11], to the elementary theory of free groups [Reference SelaSel01, Reference SelaSel06].
In this paper, we seek to obtain an analogous relationship between the structure of 
$\operatorname {Out}(G)$ and the splittings of 
$G$ when 
$G$ is not relatively hyperbolic.
We choose to focus on special groups 
$G$, in the sense of Haglund and Wise [Reference Haglund and WiseHW08]. This is the remarkably broad class of subgroups of right-angled Artin groups that are quasi-convex in the standard word metric. Little seems to be known on 
$\operatorname {Out}(G)$ in this context, other than the fact that it is always a residually finite group [Reference Antolín, Minasyan and SistoAMS16].
Special groups are best known for their Gromov-hyperbolic examples: hyperbolic 
$3$-manifold groups [Reference Kahn and MarkovicKM12, Reference Bergeron and WiseBW12, Reference AgolAgo13], hyperbolic free-by-cyclic groups [Reference Hagen and WiseHW16, Reference Hagen and WiseHW15], finitely presented small cancellation groups [Reference WiseWis04] among many others. Hyperbolic special groups also played a central role in Agol and Wise's resolution of Thurston's virtual fibering and virtual Haken conjectures [Reference AgolAgo14, Reference WiseWis14].
However, special groups also admit many non-relatively-hyperbolic examples: for instance, finite-index subgroups of right-angled Artin and Coxeter groups, most non-geometric 
$3$-manifold groups [Reference Przytycki and WisePW14, Reference Hagen and PrzytyckiHP15, Reference Przytycki and WisePW18], graph braid groups [Reference Crisp and WiestCW04], cocompact diagram groups [Reference Guba and SapirGS97, Reference GenevoisGen18, Reference GenevoisGen17], and the examples from [Reference Kropholler and VigoloKV21]. Various other non-hyperbolic groups are expected to be special (for instance, among free-by-cyclic groups), but for the moment this runs into the general difficulty of cocompactly cubulating groups without relying on Sageev's criterion [Reference SageevSag97, Reference SageevSag95].
The case when 
$G$ is a right-angled Artin group 
$\mathcal {A}_{\Gamma }$ already demonstrates that 
$\operatorname {Out}(G)$ can well be infinite even when 
$G$ does not split over an abelian subgroup [Reference Groves and HullGH17], suggesting that we will have to deal with non-small 
$G$-trees and automorphisms of 
$G$ that are more general than the algebraic Dehn twists defined above.
A particularly simple generating set for 
$\operatorname {Out}(\mathcal {A}_{\Gamma })$ was given by Laurence and Servatius [Reference LaurenceLau95, Reference ServatiusSer89]. With this in mind, it is natural to consider the following generalisation of algebraic Dehn twists which provides a unified perspective on automorphisms of hyperbolic groups and right-angled Artin groups. If 
$G$ is a group, 
$H\leq G$ is a subgroup and 
$K\subseteq G$ is a subset, we denote by 
$Z_H(K)$ the centraliser of 
$K$ in 
$H$.
Definition (DLS automorphisms)
Let 
$G$ be a group. A Dehn–Laurence–Servatius (DLS) automorphism of 
$G$ is any of the following two kinds of automorphisms of 
$G$.
• Suppose that
$G$ splits as an amalgamated product $A\ast _CB$. Each element $z\in Z_A(C)$ defines an automorphism $\sigma \in \operatorname {Aut}(G)$ with $\sigma (a)=a$ for all $a\in A$ and $\sigma (b)=zbz^{-1}$ for all $b\in B$. We refer to $\sigma$ as a partial conjugation.• Suppose that
$G$ splits as an HNN extension $A\ast _C=\langle A,t \mid t^{-1}ct=\alpha (c),\ \forall c\in C\rangle$. Each $z\in Z_A(C)$ defines an automorphism $\tau \in \operatorname {Aut}(G)$ with $\tau (a)=a$ for all $a\in A$ and $\tau (t)=zt$. We refer to $\tau$ as a transvection.
DLS automorphisms generate a finite index subgroup of 
$\operatorname {Out}(G)$ both when 
$G$ is hyperbolic (or toral relatively hyperbolic) and when 
$G$ is a right-angled Artin or Coxeter group.
DLS automorphisms were previously introduced by Levitt [Reference LevittLev05] and they appear in even earlier work of Bass and Jiang [Reference Bass and JiangBJ96]. DLS automorphisms are often simply called ‘twists’ in the literature, but this terminology would be rather confusing in the present paper since, in the context of right-angled Artin groups, the word ‘twist’ has come to refer only to a very specific type of DLS automorphism [Reference Charney, Stambaugh and VogtmannCSV17]. We will stick to the latter convention and reserve the term ‘twist’ for transvections induced by elements of the centre of 
$C$ (see below).
When 
$G$ is a special group with a fixed embedding in a right-angled Artin group 
$G\hookrightarrow \mathcal {A}_{\Gamma }$, we can endow 
$G$ with a natural coarse median structure 
$[\mu ]$ [Reference BowditchBow13]. This provides us with a notion of quasi-convexity for subgroups 
$H\leq G$. In fact, a subgroup 
$H\leq G$ is quasi-convex with respect to 
$[\mu ]$ if and only if its action on the universal cover of the Salvetti complex of 
$\mathcal {A}_{\Gamma }$ is convex-cocompact: 
$H$ stabilises a convex subcomplex, acting cocompactly on it. For this reason, we will speak interchangeably of ‘quasi-convex’ and ‘convex-cocompact’ subgroups of 
$G$.
The coarse median structure on 
$G$ also gives us a notion of orthogonality between subgroups (denoted 
$\perp$, see Definition 2.23). Because of this, it is convenient to differentiate between two types of transvections that always display quite different behaviours. This distinction was first introduced for automorphisms of right-angled Artin groups in [Reference Charney, Stambaugh and VogtmannCSV17].
Definition (Twists and folds)
Let 
$(G,[\mu ])$ be a coarse median group. Suppose that 
$G$ splits as an HNN extension 
$A\ast _C$, where 
$C$ is quasi-convex with respect to 
$[\mu ]$. Let 
$\tau \in \operatorname {Aut}(G)$ be the transvection determined by an element 
$z\in Z_A(C)$.
• If
$z$ lies in the centre of $C$, we say that $\tau$ is a twist.• If instead
$\langle z\rangle \perp C$, we say that $\tau$ is a fold.
Fixing an embedding of 
$G$ in 
$\mathcal {A}_{\Gamma }$ and the corresponding coarse median structure 
$[\mu ]$, it is also interesting to study the subgroup 
$\operatorname {Out}_{\rm cmp}(G)\leq \operatorname {Out}(G)$ of coarse-median preserving automorphisms. This was introduced in previous work of the author [Reference FioravantiFio22] and often makes up a significant portion of the whole automorphism group. For instance, 
$\operatorname {Out}_{\rm cmp}(G)=\operatorname {Out}(G)$ when 
$G$ is either Gromov-hyperbolic or a right-angled Coxeter group, while 
$\operatorname {Out}_{\rm cmp}(G)$ is the group of untwisted automorphisms when 
$G$ is a right-angled Artin group (which was studied e.g. in [Reference Charney, Stambaugh and VogtmannCSV17, Reference Hensel and KielakHK18]).
The results of [Reference FioravantiFio22] show that, in various respects, 
$\operatorname {Out}_{\rm cmp}(G)$ displays a much closer similarity to automorphisms of hyperbolic groups than the whole 
$\operatorname {Out}(G)$. This pattern is confirmed in the present paper (compare Theorems A and B).
We are now ready to state our two main theorems. Previous results of this type for hyperbolic and relatively hyperbolic groups include [Reference PaulinPau91, Reference LevittLev05, Reference Druţu and SapirDS08, Reference Guirardel and LevittGL15], among many others. The correct extension to general special groups seems to require replacing abelian subgroups with centralisers.
Theorem 1 Let 
$G$ be a special group. Then 
$\operatorname {Out}_{\rm cmp}(G)$ is infinite if and only if 
$\operatorname {Out}_{\rm cmp}(G)$ contains an infinite-order DLS automorphism 
$\varphi$ of one of the following forms:
(1)
$G$ splits as $A\ast _CB$ or $A\ast _C$, where $C$ is the centraliser of a finite subset of $G$, and $\varphi$ is a partial conjugation or fold associated to this splitting;(2)
$G$ splits as $A\ast _C$, where $C=Z_G(g)$ for an element $g\in G$ such that $\langle g\rangle$ is convex-cocompact, and $\varphi$ is the twist determined by this splitting and the element $g$.
Theorem 2 Let 
$G$ be a special group. Then 
$\operatorname {Out}(G)$ is infinite if and only if 
$\operatorname {Out}(G)$ contains an infinite-order DLS automorphism 
$\varphi$ either as in types (1) and (2) of Theorem A, or of the following form:
(3)
$\varphi$ is a twist associated to an HNN splitting $G=A\ast _C$, where $C$ is the kernel of a non-trivial homomorphism $Z_G(x)\rightarrow \mathbb {Z}$ for some $x\in G$. In addition, the stable letter of the HNN splitting can be chosen within $Z_G(x)$.
Thinking of right-angled Artin groups 
$\mathcal {A}_{\Gamma }$, most of the Laurence–Servatius generators for 
$\operatorname {Out}(\mathcal {A}_{\Gamma })$ fall into types (1) and (3) of the previous theorems (for the experts, we are only excluding graph automorphisms and inversions, which have finite order). Automorphisms of type (2) never occur for 
$\mathcal {A}_{\Gamma }$, but many algebraic Dehn twists of hyperbolic groups are of this form.
We emphasise that, in many cases, a general DLS automorphism can turn out to be an inner automorphism of 
$G$, or to have an inner power. By contrast, Theorems A and B do provide DLS automorphisms with infinite order in 
$\operatorname {Out}(G)$. In particular, this shows that 
$\operatorname {Out}(G)$ and 
$\operatorname {Out}_{\rm cmp}(G)$ can never be infinite torsion groups.
An immediate consequence of the above two theorems is the following.
Corollary 3 Let 
$G$ be a special group.
(1) If
$\operatorname {Out}_{\rm cmp}(G)$ is infinite, then $G$ splits over the centraliser of a finite subset of $G$.(2) If
$\operatorname {Out}(G)$ is infinite, then $G$ splits over the centraliser of a finite subset of $G$, or over the kernel of a homomorphism $Z_G(x)\rightarrow \mathbb {Z}$ for some $x\in G$.
Note that all special groups split over ‘some’ convex-cocompact subgroup, simply because they act properly on Salvetti complexes, hence on the associated products of trees. Such a splitting does not tell us anything about 
$\operatorname {Out}(G)$ in general, so it is important that the splittings provided by Corollary C are over centralisers, or subgroups thereof.
It seems that Corollary C(2) and part of Theorem B can also be deduced from the work of Casals-Ruiz and Kazachkov [Reference Casals-Ruiz and KazachkovCRK11, Reference Casals-Ruiz and KazachkovCRK15]. Indeed, if 
$\operatorname {Out}(G)$ is infinite, the Bestvina–Paulin construction yields a nice 
$G$-action on an asymptotic cone of a right-angled Artin group. By [Reference Casals-Ruiz and KazachkovCRK15, Theorem 9.33], it follows that 
$G$ can be embedded in a graph tower, in the sense of [Reference Casals-Ruiz and KazachkovCRK15, § 5]. Every graph tower 
$T$ admits particular splittings over centralisers of subsets of 
$T$. With significant additional work, these splittings can be translated into splittings of 
$G$ over the required subgroups of centralisers of subsets of 
$G$ (the main difficulty is passing from centralisers of subsets of 
$T$ to centralisers of subsets of 
$G$).
We emphasise that Corollary C(1) can fail if 
$\operatorname {Out}(G)$ is infinite, but 
$\operatorname {Out}_{\rm cmp}(G)$ is finite. The simplest example is provided by the right-angled Artin group 
$\mathcal {A}_{\Gamma }$ with 
$\Gamma$ as in Figure 1. Note that 
$G=\mathcal {A}_{\Gamma }$ does not split over any centraliser of a subset, but it does split as an HNN extension over the subgroup 
$\langle b,c,f\rangle$, which is the kernel of a homomorphism 
$Z_G(a)\rightarrow \mathbb {Z}$.
Figure 1. A graph 
$\Gamma$ such that 
${\rm Out}(\mathcal{A}_{\Gamma})$ is infinite, but 
$\mathcal{A}_{\Gamma}$ does not split over any centralisers.
With a bit more work, it is also possible to deduce from Theorems A and B the following result, which I found rather unexpected.
Corollary 4 Let 
$G$ be a special group. Suppose that 
$\operatorname {Out}(G)$ is infinite, but 
$\operatorname {Out}_{\rm cmp}(G)$ is finite. Then there exists 
$x\in G$ such that the 
$G$-conjugacy class of the subgroup 
$Z_G(x)$ is preserved by a finite-index subgroup of 
$\operatorname {Out}(G)$.
Theorems A and B (and their proof) provide significant evidence for the following conjecture, which has so far resisted all our attempts at a proof. We briefly illustrate the issue at the end of the introduction: it involves shortening the 
$G$-action on an 
$\mathbb {R}$-tree (which we were able to do), while not lengthening finitely many other 
$G$-trees (which appears to be quite delicate).
Conjecture Let 
$G$ be a special group.
(1) The DLS automorphisms appearing in Theorem A generate a finite-index subgroup of
$\operatorname {Out}_{\rm cmp}(G)$. Moreover, finitely many such automorphisms suffice.(2) The DLS automorphisms appearing in Theorems A and B generate a finite-index subgroup of
$\operatorname {Out}(G)$. Moreover, finitely many such automorphisms suffice.
In particular, 
$\operatorname {Out}(G)$ and 
$\operatorname {Out}_{\rm cmp}(G)$ are finitely generated.
For one-ended hyperbolic groups 
$G$, one can give a much more precise description of 
$\operatorname {Out}(G)$: up to passing to finite index, it has a free abelian normal subgroup whose quotient is a finite product of mapping class groups [Reference SelaSel97b, Reference LevittLev05]. A similar description also holds in the toral relatively hyperbolic case [Reference Guirardel and LevittGL15].
The usual approach to these results relies heavily on the existence of JSJ decompositions. For general special groups 
$G$, it appears that one would need to consider splittings over a class of groups that is not closed under taking subgroups, so JSJ techniques seem rather hard to apply.
Finally, we would like to highlight the following result, which is required in the proof of Theorem A. It characterises which DLS automorphisms of a special group preserve the coarse median structure, provided that they originate from splittings over convex-cocompact subgroups. For a more general statement on (possibly non-special) cocompactly cubulated groups, see Theorem 7.1.
Theorem 5 Let 
$G$ be a special group with a splitting 
$G=A\ast _CB$ or 
$G=A\ast _C$. Suppose that 
$C$ is convex-cocompact in 
$G$. Then we have the following.
(1) All partial conjugations and folds determined by this splitting are coarse-median preserving.
(2) If
$G=A\ast _C$ and $z\in Z_C(C)$ is such that $\langle z\rangle$ is convex-cocompact in $G$ and $Z_G(z)$ is contained in a conjugate of $A$, then the twist determined by $z$ is coarse-median preserving.(3) More generally, if for every
$c\in Z_C(C)\setminus \{1\}$ the centraliser $Z_G(c)$ is contained in a conjugate of $A$, then all transvections determined by $G=A\ast _C$ are coarse-median preserving.
For instance, all DLS automorphisms determined by acylindrical splittings of 
$G$ (over convex-cocompact subgroups) are coarse-median preserving. By contrast, the reader can easily check that the twist of 
$\mathbb {Z}^2=\langle a,b\rangle$ fixing 
$a$ and mapping 
$b\mapsto ab$ is not coarse-median preserving (here 
$A=C=\langle a\rangle$).
Theorem E greatly expands the class of automorphisms to which the techniques of [Reference FioravantiFio22] can be applied. In particular, if 
$\varphi$ is a product of DLS automorphisms as in Theorem E, then the subgroup 
$\operatorname {Fix}\varphi \leq G$ is finitely generated, undistorted, and cocompactly cubulated (see [Reference FioravantiFio22, Theorem B]).
On the proof of Theorems A and B. Let 
$G$ be a special group with an infinite sequence of automorphisms 
$\phi _n\in \operatorname {Out}(G)$. The core of the proof lies in the construction of a non-elliptic, stable 
$G$-tree 
$T_{\omega }$ with ‘nice’ arc-stabilisers. From there, the conclusion is technical, but relatively straightforward given the work of Bestvina–Feighn [Reference Bestvina and FeighnBF95] and Guirardel [Reference GuirardelGui98, Reference GuirardelGui08].
Arc-stabilisers of 
$T_{\omega }$ will be centralisers when the 
$\phi _n$ are coarse-median preserving, and kernels of homomorphisms from centralisers to 
$\mathbb {R}$ in the general case. Here the expression ‘centraliser’ always refers to centralisers of finite subsets of 
$G$. These properties ensure that 
$T_{\omega }$ is stable, even though arc-stabilisers can be infinitely generated in general. In addition, 
$T_{\omega }$ will not normally be superstable, and tripod-stabilisers can always be non-trivial centralisers.
The mere construction of the tree 
$T_{\omega }$ is straightforward (for instance, it already appears in [Reference GenevoisGen20]). What requires new ideas is analysing its arc-stabilisers, as we now discuss.
Fixing a convex-cocompact embedding in a right-angled Artin group 
$G\hookrightarrow \mathcal {A}_{\Gamma }$, we obtain a 
$G$-action on the universal cover 
$\mathcal {X}_{\Gamma }$ of the Salvetti complex. It is known that 
$\mathcal {X}_{\Gamma }$ equivariantly embeds in a finite product of simplicial trees 
$\prod _{v\in \Gamma }\mathcal {T}_v$, so we obtain a proper action of 
$G$ on this product. It follows that there exists 
$v\in \Gamma$ such that the twisted trees 
$\mathcal {T}_v^{\phi _n}$ diverge, and we can define 
$T_{\omega }$ as an ultralimit of these trees, suitably rescaled.
Arc-stabilisers for the actions 
$G\curvearrowright \mathcal {T}_v$ are quite nice: they are convex-cocompact in 
$G$, and they are the intersection between 
$G$ and the centraliser of a subset of 
$\mathcal {A}_{\Gamma }$. However, they are usually not centralisers of subsets of 
$G$. As a consequence, the moment we start twisting by automorphisms of 
$G$, we lose all control over their images, which can for instance stop being convex-cocompact in 
$G$. This compromises the study of arc-stabilisers of 
$T_{\omega }$, since we cannot control those of the trees 
$\mathcal {T}_v^{\phi _n}$.
The key observation (Theorem 4.2) is that sufficiently long arcs of 
$\mathcal {T}_v$ can be perturbed so that their 
$G$-stabiliser (and even their ‘almost-stabiliser’) becomes a centraliser in 
$G$. This rescues us, as automorphisms of 
$G$ will take centralisers to centralisers, and 
$\omega$-intersections of centralisers are again centralisers.
The main steps of the proof are taken in §§ 4–6. Section 4 proves Theorem 4.2 on perturbations of arcs of 
$\mathcal {T}_v$. Section 5 (and in particular § 5.4) uses this to obtain all necessary information on arc-stabilisers of 
$T_{\omega }$. Finally, § 6 considers geometric trees approximating 
$T_{\omega }$, applies the Rips machine (blackboxed), and draws the required conclusions.
On the conjecture. The classical Rips–Sela argument for hyperbolic groups is based on a well-known shortening argument [Reference Rips and SelaRS94, Reference Weidmann and ReinfeldtWR19]. We would like to emphasise that the tree 
$T_{\omega }$ mentioned above can indeed always be shortened by a DLS automorphism of the form described in the statement of the two theorems. This requires a significant amount of work, which we have chosen to omit from this article, as it can be circumvented for a more direct proof of our main results.
The reason why the Conjecture remains unproven is that shortening a single tree no longer suffices in this context. Recall that 
$G$ acts properly on the finite product of trees 
$\prod _{v\in \Gamma }\mathcal {T}_v$. Each 
$\mathcal {T}_v$ gives rise to a (possibly elliptic) tree 
$T_{\omega }(v)$ as above. When we shorten some 
$T_{\omega }(v)$ by a DLS automorphism, it is possible that some other 
$T_{\omega }(w)$ will ‘get longer’, which deals a serious blow to this kind of approach.
Excluding this eventuality would require some compatibility conditions between the trees 
$T_{\omega }(v)$. For instance, if 
$G$ is a surface group and the 
$\phi _n$ are powers of a pseudo-Anosov with stable and unstable trees 
$T_{\pm }$, it seems that we cannot hope to shorten 
$T_+$ without lengthening 
$T_-$.
Perhaps a more successful strategy would be based on a theory of cospecial actions on median spaces, the first promising steps of which were taken in [Reference Casals-Ruiz and KazachkovCRK15, § 9.4].
Structure of the paper. Section 2 contains basic information on 
${\rm CAT(0)}$ cube complexes, coarse median groups and ultralimits. Within it, § 2.3 proves a few new results on convex-cocompactness in cube complexes, though these will certainly not surprise experts. Section 3 studies centralisers in special groups and the kernels of their homomorphisms to abelian groups.
As discussed above, the proof of Theorems A and B is spread out over §§ 4–6. The final argument and the proof of Corollary D are given at the end of § 6.3.
Theorem E is proved in § 7. For the latter, an ingredient we find of particular interest is the discussion of Guirardel cores of products of cube complexes in § 7.3.
2. Preliminaries
2.1 ${\rm CAT(0)}$ cube complexes
We refer the reader to [Reference Caprace and SageevCS11, Reference SageevSag14, Reference Chatterji, Fernós and IozziCFI16, Reference FioravantiFio20] for basic facts on 
${\rm CAT(0)}$ cube complexes. Here we simply fix terminology and notation, and recall a few standard results. Some of these are relevant also in the one-dimensional case of simplicial trees.
Let 
$X$ be a 
${\rm CAT(0)}$ cube complex.
2.1.1 Halfspaces and hyperplanes
We denote by 
$\mathscr {W}(X)$ and 
$\mathscr {H}(X)$, respectively, the set of hyperplanes and halfspaces of 
$X$. If 
$\mathfrak {h}$ is a halfspace, 
$\mathfrak {h}^*$ denotes its complement. Two hyperplanes are transverse if they are distinct and meet. Halfspaces 
$\mathfrak {h},\mathfrak {k}$ are transverse if they are bounded by transverse hyperplanes; equivalently, all four intersections 
$\mathfrak {h}\cap \mathfrak {k}$, 
$\mathfrak {h}^*\cap \mathfrak {k}$, 
$\mathfrak {h}\cap \mathfrak {k}^*$, 
$\mathfrak {h}^*\cap \mathfrak {k}^*$ are non-empty. We also say that a hyperplane is transverse to a halfspace if it is transverse to the hyperplane bounding it. Subsets 
$\mathcal {U},\mathcal {V}\subseteq \mathscr {W}(X)$ are transverse if every element of 
$\mathcal {U}$ is transverse to every element of 
$\mathcal {V}$.
If 
$A$ and 
$B$ are sets of vertices, 
$\mathscr {H}(A|B)\subseteq \mathscr {H}(X)$ is the subset of halfspaces 
$\mathfrak {h}$ such that 
$A\subseteq \mathfrak {h}^*$ and 
$B\subseteq \mathfrak {h}$. Similarly, 
$\mathscr {W}(A|B)\subseteq \mathscr {W}(X)$ is the set of hyperplanes bounding the elements of 
$\mathscr {H}(A|B)$. We say that the elements of 
$\mathscr {W}(A|B)$ separate 
$A$ and 
$B$.
2.1.2 Metrics and geodesics
We always endow 
$X$ with its 
$\ell ^1$ metric (denoted by 
$d$), rather than the 
${\rm CAT(0)}$ metric. We will only be interested in distances between vertices of 
$X$ (possibly after passing to its cubical subdivision), in which case the 
$\ell ^1$ metric coincides with the intrinsic path metric of the 
$1$-skeleton. The latter is also known as the combinatorial metric. If 
$x$ and 
$y$ are vertices of 
$X$, we have 
$d(x,y)=\#\mathscr {W}(x|y)$.
All geodesics in 
$X$ are implicitly assumed to be combinatorial geodesics contained in the 
$1$-skeleton and with their endpoints at vertices. For such a geodesic 
$\alpha$, we denote by 
$\mathscr {W}(\alpha )\subseteq \mathscr {W}(X)$ the set of hyperplanes dual to the edges of 
$\alpha$. We say that these are the hyperplanes crossed by 
$\alpha$. We write 
$\ell (\alpha )$ for the length of 
$\alpha$, which coincides with the cardinality of 
$\mathscr {W}(\alpha )$.
2.1.3 Convexity
If 
$Y\subseteq X$ is a convex subcomplex, we do not distinguish between hyperplanes of 
$Y$ and hyperplanes of 
$X$ separating vertices of 
$Y$. The set of such hyperplanes is denoted 
$\mathscr {W}(Y)$. If 
$Y\subseteq X$ is a convex subcomplex, we denote its gate-projection by 
$\pi _Y\colon X\rightarrow Y$. For every vertex 
$x\in X$, the image 
$\pi _Y(x)$ is a vertex of 
$Y$ and it is the unique point of 
$Y$ that is closest to 
$x$. Gate-projections are 
$1$-Lipschitz and satisfy 
$\mathscr {W}(x|\pi _Y(x))=\mathscr {W}(x|Y)$.
If 
$Y,Z\subseteq X$ are convex subcomplexes, we say that 
$y\in Y$ and 
$z\in Z$ form a pair of gates if 
$d(y,z)=d(Y,Z)$. Equivalently, 
$\pi _Y(z)=y$ and 
$\pi _Z(y)=z$, or again 
$\mathscr {W}(y|z)=\mathscr {W}(Y|Z)$. The projections 
$\pi _Y(Z)$ and 
$\pi _Z(Y)$ are also convex subcomplexes.
Note that all hyperplanes 
$\mathfrak {w}\in \mathscr {W}(X)$ are convex subcomplexes of the cubical subdivision of 
$X$. For this reason, they have a cellular structure that makes them into lower-dimension 
${\rm CAT(0)}$ cube complexes. In addition, we can consider the gate-projections 
$\pi _{\mathfrak {w}}\colon X\rightarrow \mathfrak {w}$.
2.1.4 Isometries and actions
We denote by 
$\operatorname {Aut}(X)$ the group of automorphisms of 
$X$, i.e. isometries that take vertices to vertices. All actions on 
$X$ are assumed to be by automorphisms without explicit mention.
If 
$g\in \operatorname {Aut}(X)$, we denote its translation length by 
$\ell _X(g)=\inf _{x\in X}d(x,gx)$. The minimal set of 
$g$ is the subset 
$\mathrm {Min}(g,X)\subseteq X$ (or just 
$\mathrm {Min}(g)$) where 
$\ell _X(g)$ is realised. We write 
$\operatorname {Fix}(g,X)\subseteq X$ for the set of fixed points of 
$g$.
An action 
$G\curvearrowright X$ is without inversions if there do not exist 
$g\in G$ and 
$\mathfrak {h}\in \mathscr {H}(X)$ with 
$g\mathfrak {h}=\mathfrak {h}^*$. Note that 
$\operatorname {Aut}(X)$ acts on the cubical subdivision of 
$X$ without inversions. Given an action without inversions 
$G\curvearrowright X$, every 
$g\in G$ contains at least one vertex of 
$X$ in its minimal set. In particular, if 
$g$ does not have fixed vertices, then it admits an axis: a 
$\langle g\rangle$-invariant geodesic along which 
$g$ translates non-trivially [Reference HaglundHag07].
A hyperplane 
$\mathfrak {w}\in \mathscr {W}(X)$ is skewered by 
$g\in \operatorname {Aut}(X)$ if it bounds a halfspace 
$\mathfrak {h}$ with 
$g\mathfrak {h}\subsetneq \mathfrak {h}$. Given an action 
$G\curvearrowright X$, we keep the notation from [Reference FioravantiFio21] and write
\begin{align*} \mathcal{W}_1(G,X)&:=\{\mathfrak{w}\in\mathscr{W}(X) \mid \text{$\exists g\in G$ skewering $\mathfrak{w}$}\}, \\ \overline{\mathcal{W}}_0(G,X)&:=\{\mathfrak{w}\in\mathscr{W}(X) \mid \text{$\forall g\in G$, either $g\mathfrak{w}=\mathfrak{w}$, or $g\mathfrak{w}$ is transverse to $\mathfrak{w}$}\}. \end{align*}
We write 
$\mathcal {W}_1(G)$ and 
$\overline {\mathcal {W}}_0(G)$ when the ambient cube complex is clear, or 
$\mathcal {W}_1(g)$ and 
$\overline {\mathcal {W}}_0(g)$ if 
$G=\langle g\rangle$. Note that a hyperplane in 
$\mathcal {W}_1(g)$ might only be skewered by a power of 
$g$.
Consider an action 
$G\curvearrowright X$. We say that 
$X$ is 
$G$-essential if 
$\mathcal {W}_1(G)=\mathscr {W}(X)$. We say that 
$X$ is simply essential if no halfspace of 
$X$ is at finite Hausdorff distance from the hyperplane bounding it. When 
$G$ acts cocompactly on 
$X$, these two notions of essentiality coincide.
We say that 
$X$ is 
$G$-hyperplane-essential if every hyperplane 
$\mathfrak {w}\in \mathscr {W}(X)$ is 
$G_{\mathfrak {w}}$-essential with its induced cubical structure. Here 
$G_{\mathfrak {w}}$ denotes the subgroup of 
$G$ leaving 
$\mathfrak {w}$ invariant. Again, we say that 
$X$ is simply hyperplane-essential if every hyperplane of 
$X$ is an essential cube complex with its induced cubical structure. As before, 
$X$ is 
$G$-hyperplane-essential if and only if 
$X$ is hyperplane-essential, provided that 
$G$ acts cocompactly on 
$X$ (see e.g. [Reference Fioravanti and HagenFH21, Lemma 2.3]).
Given an action 
$G\curvearrowright X$ and a hyperplane 
$\mathfrak {w}$ lying neither in 
$\mathcal {W}_1(G)$ nor in 
$\overline {\mathcal {W}}_0(G)$, exactly one of the two halfspaces bounded by 
$\mathfrak {w}$ contains an entire 
$G$-orbit in 
$X$. Taking the intersection of all such halfspaces, we obtain a 
$G$-invariant convex subcomplex of 
$X$, which is non-empty as soon as 
$G$ satisfies weak assumptions. As a consequence, we obtain the following result (see [Reference FioravantiFio21, Remark 3.16, Theorem 3.17, Proposition 3.23(2) and Corollary 4.6] for more details).
Proposition 2.1 If 
$G\leq \operatorname {Aut}(X)$ is finitely generated and acts on 
$X$ without inversions, then there exists a non-empty, 
$G$-invariant, convex subcomplex 
$\overline {\mathcal {C}}(G,X)\subseteq X$ such that the following hold.
(1) There is a
$G$-invariant splitting $\overline {\mathcal {C}}(G,X)=\overline {\mathcal {C}}_0(G,X)\times \mathcal {C}_1(G,X)$, where the sets of hyperplanes dual to the two factors are precisely $\overline {\mathcal {W}}_0(G,X)$ and $\mathcal {W}_1(G,X)$.(2) The action
$G\curvearrowright \overline {\mathcal {C}}_0(G,X)$ has fixed vertices, whereas $\mathcal {C}_1(G,X)$ is $G$-essential.(3) If
$h\in \operatorname {Aut}(X)$ normalises $G$, then $h$ preserves $\overline {\mathcal {C}}(G,X)$ and leaves invariant its two factors.
Again, we simply write 
$\overline {\mathcal {C}}(G)$ when the cube complex 
$X$ is clear, and 
$\overline {\mathcal {C}}(g)$ if 
$G=\langle g\rangle$.
2.1.5 Median subalgebras and median morphisms
A median algebra is a set 
$M$ equipped with a ternary operation 
$m\colon M^3\rightarrow M$ invariant under permutations and satisfying:
•
$m(a,a,b)=a$ for $a,b\in M$;•
$m(m(a,x,b),x,c)=m(a,x,m(b,x,c))$ for $a,b,c,x\in M$.
A median subalgebra is a subset 
$N\subseteq M$ with 
$m(N\times N\times N)\subseteq N$. A subset 
$C\subseteq M$ is convex if 
$m(C\times C\times M)\subseteq C$. A subset 
$\mathfrak {h}\subseteq M$ is a halfspace if both 
$\mathfrak {h}$ and its complement 
$\mathfrak {h}^*:=M\setminus\mathfrak {h}$ are convex and non-empty. A wall of 
$M$ is an unordered pair 
$\{\mathfrak {h},\mathfrak {h}^*\}$, where 
$\mathfrak {h}$ is a halfspace. Let 
$\mathscr {W}(M)$ and 
$\mathscr {H}(M)$ denote, respectively, the sets of walls and halfspaces of 
$M$.
If 
$A\subseteq M$ is a subset, we denote by 
$\langle A\rangle \subseteq M$ the median subalgebra generated by 
$A$. This is the intersection of all median subalgebras of 
$M$ that contain 
$A$.
Every 
${\rm CAT(0)}$ cube complex 
$X$ has a natural structure of median algebra given by its median operator 
$m\colon X^3\rightarrow X$. If 
$x,y,z\in X$ are vertices, 
$m(x,y,z)$ is also a vertex and it is uniquely determined by the following property: a halfspace of 
$X$ contains 
$m(x,y,z)$ if and only if it contains at least two among 
$x,y,z$. The definitions of convexity, halfspaces and hyperplanes/walls coincide for a cube complex 
$X$ and the median-algebra structure on its 
$0$-skeleton. In addition, note that the map 
$m\colon X^3\rightarrow X$ is 
$1$-Lipschitz.
A map 
$f\colon M\rightarrow N$ between median algebras is a median morphism if, for all 
$x,y,z\in M$, we have 
$f(m(x,y,z))=m(f(x),f(y),f(z))$. If 
$f$ is a median morphism, then preimages of convex subsets are again convex. In particular, if 
$f$ is onto, preimages of halfspaces are halfspaces. When 
$f$ is onto, it also takes convex subsets to convex subsets.
If 
$X$ is a 
${\rm CAT(0)}$ cube complex and 
$C\subseteq X$ is a convex subcomplex, then the gate-projection to 
$C$ is a median morphism.
A median algebra is discrete if any two of its points are separated by only finitely many walls. It was shown by Chepoi [Reference ChepoiChe00] and later by Roller [Reference RollerRol98] that every discrete median algebra is canonically isomorphic to the 
$0$-skeleton of a unique 
${\rm CAT(0)}$ cube complex. We will rely on this fact repeatedly in § 7.3, referring to it as Chepoi–Roller duality.
2.1.6 Restriction quotients
Consider an action 
$G\curvearrowright X$ and a 
$G$-invariant set of hyperplanes 
$\mathcal {U}\subseteq \mathscr {W}(X)$. Then there exists a unique action on a 
${\rm CAT(0)}$ cube complex 
$G\curvearrowright X(\mathcal {U})$ satisfying the following properties.
• There is a
$G$-equivariant, surjective, median morphism $p\colon X\rightarrow X(\mathcal {U})$.• If
$\mathfrak {h}$ is a halfspace of $X(\mathcal {U})$, then $p^{-1}(\mathfrak {h})$ is a halfspace of $X$ bounded by a hyperplane in $\mathcal {U}$.• This establishes a
$G$-equivariant bijection between hyperplanes of $X(\mathcal {U})$ and elements of $\mathcal {U}$.
The cube complex 
$X(\mathcal {U})$ is known as the restriction quotient of 
$X$ associated to 
$\mathcal {U}$. Restriction quotients were introduced by Caprace and Sageev in [Reference Caprace and SageevCS11, p. 860].
2.2 Euclidean factors
The goal of this subsection is to prove the following result, which will only be required in § 7.4 in order to prove Theorem E.
Proposition 2.2 Consider a product of 
${\rm CAT(0)}$ cube complexes 
$X\times L$, where 
$L$ is a quasi-line. If 
$G$ acts properly, cocompactly and faithfully on 
$X\times L$ preserving the splitting, then 
$G$ has a finite-index subgroup of the form 
$H\times \mathbb {Z}$, where 
$H$ acts trivially on 
$L$ and the 
$\mathbb {Z}$-factor acts trivially on 
$X$.
This is similar to [Reference Nevo and SageevNS13, Corollary 2.8], whose proof however relies on [Reference Nevo and SageevNS13, Lemma 2.7], which appears to be false (if ‘flat’ is to be interpreted in the 
${\rm CAT(0)}$ sense). For instance, consider the quasi-line obtained by stringing together countably many squares diagonally to form a chain, whose automorphism group is not discrete (it contains a direct product of countably many copies of 
$\mathbb {Z}/2\mathbb {Z}$).
For this reason, we give an alternative proof here, based on the following two lemmas. Note that the first lemma can fail if we replace automorphisms of 
$X$ with isometries (e.g. for 
$X=\mathbb {R}^2$).
Lemma 2.3 Let 
$G\leq \operatorname {Aut}(X)$ act properly and cocompactly on the 
${\rm CAT(0)}$ cube complex 
$X$. Then 
$G$ has finite index in its normaliser within 
$\operatorname {Aut}(X)$.
Proof. Let 
$N$ be the normaliser of 
$G$ in 
$\operatorname {Aut}(X)$. Fix a vertex 
$p\in X$ and let 
$N_p$ be the subgroup of 
$N$ fixing it. Since 
$N$ permutes the finitely many 
$G$-orbits of vertices, 
$N$ has a finite index subgroup of the form 
$G\cdot N_p$. We will prove the lemma by showing that 
$N_p$ is finite.
If 
$g\in G$ and 
$n\in N_p$, then 
$d(ngn^{-1}p,p)=d(gp,p)$. Since 
$G$ acts properly on 
$X$, all orbits of the conjugation action of 
$N_p$ on 
$G$ must be finite. Hence, since 
$G$ is finitely generated by the Milnor–Schwarz lemma, a finite-index subgroup of 
$N_p$ commutes with 
$G$.
Now, let 
$F\subseteq X$ be a finite set of vertices meeting all 
$G$-orbits. Since 
$X$ is locally finite and 
$N_p$ takes vertices to vertices, a finite-index subgroup 
$N_0\leq N_p$ fixes 
$F$ pointwise. By the above paragraph, we can choose 
$N_0$ so that it commutes with 
$G$. Given 
$f\in F$, 
$g\in G$ and 
$n\in N_0$, we have 
$n\cdot gf=ngn^{-1}\cdot nf=gf$. This shows that 
$N_0$ fixes the 
$0$-skeleton of 
$X$ pointwise, so it is the trivial group. Since 
$N_0$ has finite index in 
$N_p$, this proves that 
$N_p$ is finite, as required.
Lemma 2.4 Consider a product of 
${\rm CAT(0)}$ cube complexes 
$X\times Y$. Let 
$G$ act properly, cocompactly and faithfully on 
$X\times Y$ preserving the factors. If the image of 
$G$ in 
$\operatorname {Aut}(Y)$ is discrete, then 
$G$ has a finite-index subgroup of the form 
$H\times K$, where 
$H$ acts trivially on 
$Y$ and 
$K$ acts trivially on 
$X$.
Proof. Let 
$\rho _X\colon G\rightarrow \operatorname {Aut}(X)$ and 
$\rho _Y\colon G\rightarrow \operatorname {Aut}(Y)$ be the homomorphisms corresponding to the actions on the two factors. Note that, since 
$X\times Y$ admits a proper cocompact action, it is locally finite; in particular, 
$Y$ is locally finite. Thus, since 
$\rho _Y(G)$ is discrete, it acts on 
$Y$ with finite vertex-stabilisers. This shows that 
$\ker \rho _Y$ is commensurable to the 
$G$-stabiliser of a vertex of 
$Y$, so 
$\ker \rho _Y$ acts cocompactly on 
$X$. By Lemma 2.3, 
$\rho _X(\ker \rho _Y)$ has finite index in 
$\rho _X(G)$. This shows that the subgroup 
$\rho _X^{-1}\rho _X(\ker \rho _Y)=\ker \rho _X\cdot \ker \rho _Y$ has finite index in 
$G$. Since both kernels are normal in 
$G$ and they have trivial intersection, this is a direct product.
The first paragraph of the following proof was suggested to me by Michah Sageev, as it has the advantage of only requiring basic 
${\rm CAT(0)}$ geometry. Alternatively, one can also use panel collapse [Reference Hagen and TouikanHT19, Theorem A] to find a subcomplex of 
$L$ isomorphic to 
$\mathbb {R}$.
Proof of Proposition 2.2 Let 
$P\subseteq L$ be the union of all geodesic lines in 
$L$ for the 
${\rm CAT(0)}$ metric. By [Reference Bridson and HaefligerBH99, Theorem II.2.14], we have a 
$G$-invariant splitting 
$P=P_0\times \mathbb {R}$, where 
$P_0$ is compact. Thus, since 
$G$ must fix a point of 
$P_0$, there exists a 
$G$-invariant 
${\rm CAT(0)}$-line 
$L_0\subseteq L$. Note that 
$G$ acts on 
$L_0$ with discrete orbits (e.g. because the projection to 
$L_0$ of the set of vertices of 
$L$ in a bounded neighbourhood of 
$L_0$ is 
$G$-invariant, and 
$L$ is locally finite).
Now, since 
$G$ acts discretely on 
$L_0\simeq \mathbb {R}$, we can apply Lemma 2.4 to the 
$G$-action on 
$X\times L_0$ (modulo its finite kernel). It follows that the image of 
$G$ in 
$\operatorname {Aut} X$ is discrete and so we can apply Lemma 2.4 again, this time to the whole product 
$X\times L$. This yields the required conclusion.
2.3 Convex-cocompactness
Fix a proper cocompact action without inversions on a 
${\rm CAT(0)}$ cube complex 
$G\curvearrowright X$ throughout this subsection.
Definition 2.5 A subgroup 
$H\leq G$ is convex-cocompact with respect to the action 
$G\curvearrowright X$ (or just in 
$X$) if there exists an 
$H$-invariant convex subcomplex 
$Y\subseteq X$ on which 
$H$ acts cocompactly.
As observed in [Reference FioravantiFio22, Lemma 3.2], 
$H$ is convex-cocompact if and only if the action on 
$\mathcal {C}_1(H)$ is cocompact and 
$H$ is finitely generated. Thus, we can always take 
$Y$ to be 
$H$-essential in Definition 2.5, using Proposition 2.1.
We will often need to quantify convex-cocompactness, hence the following definition.
Definition 2.6 A subgroup 
$H\leq G$ is 
$q$-convex-cocompact if there exists an 
$H$-invariant convex subcomplex 
$Y\subseteq X$ on which 
$H$ acts with exactly 
$q$ orbits of vertices.
Since the number of 
$H$-orbits is minimised by 
$H$-essential convex subcomplexes, we can always take 
$Y$ in Definition 2.6 to be 
$H$-essential.
Remark 2.7 Let 
$H\leq G$ be 
$q$-convex-cocompact and let 
$N$ be the maximum cardinality of the 
$G$-stabiliser of a vertex of 
$X$. Then 
$H$ has index 
$\leq qN$ in all its finite-index overgroups within 
$G$.
Indeed, suppose 
$H$ has finite index 
$d$ in a subgroup 
$H'\leq G$. Note that a hyperplane of 
$X$ is skewered by an element of 
$H$ if and only if it is skewered by an element of 
$H'$, so 
$\mathcal {C}_1(H)=\mathcal {C}_1(H')$. Since 
$\mathcal {C}_1(H')$ equivariantly embeds in 
$X$, the 
$H'$-stabiliser of any vertex of 
$\mathcal {C}_1(H')$ has cardinality 
$\leq N$. Now, if 
$H'$ acts on 
$\mathcal {C}_1(H')$ with 
$k$ orbits of vertices, then 
$H$ acts on 
$\mathcal {C}_1(H)$ with at least 
$kd/N$ orbits of vertices, hence 
$q\geq kd/N\geq d/N$.
Lemma 2.8 Let 
$H,K\leq G$ be subgroups that leave invariant convex subcomplexes 
$Y,Z\subseteq X$, respectively, and act cocompactly on them. Then 
$H\cap K$ acts cocompactly on 
$\pi _Y(Z)$.
Proof. We split the proof into the following three claims.
Claim 1 For every ball 
$B\subseteq X$, only finitely many distinct 
$G$-translates of 
$Y$ and 
$Z$ meet 
$B$.
Proof of Claim 1 Suppose this is not the case for a ball 
$B\subseteq X$. Then, since 
$B$ contains only finitely many vertices, there are infinitely many, pairwise distinct translates 
$g_nY$ all containing the same vertex 
$p\in B$. Since 
$H\curvearrowright Y$ is cocompact, there exists a compact subset 
$Q\subseteq Y$ and elements 
$h_n\in H$ with 
$h_ng_n^{-1}p\in Q$. Since 
$G\curvearrowright X$ is proper, the set 
$F=\{h_ng_n^{-1}\}$ is finite. Hence 
$g_n^{-1}\in h_n^{-1}F$ and 
$g_n\in F^{-1}\cdot H$, contradicting the fact that the set 
$\{g_nY\}$ is infinite.
Claim 2 For every ball 
$B\subseteq X$, only finitely many distinct 
$G$-translates of 
$\pi _Y(Z)$ meet 
$B$.
Proof of Claim 2 Consider 
$g\in G$ such that 
$g\cdot \pi _Y(Z)=\pi _{gY}(gZ)$ intersects 
$B$. Then 
$gY$ intersects 
$B$, while 
$gZ$ intersects the neighbourhood of 
$B$ of radius 
$d(Y,Z)$. By Claim 1, there are only finitely many possibilities for the sets 
$gY$ and 
$gZ$. It follows that only finitely many sets of the form 
$\pi _{gY}(gZ)$ intersect 
$B$.
Let 
$L\leq G$ be the 
$G$-stabiliser of 
$\pi _Y(Z)$. Claim 2 and [Reference Hagen and SusseHS20, Lemma 2.3] imply that 
$L\curvearrowright \pi _Y(Z)$ is cocompact.
Claim 3 A finite-index subgroup of 
$L$ leaves 
$Y$ and 
$Z$ invariant.
Proof of Claim 3 By Claim 1, only finitely many distinct 
$G$-translates of 
$Y$ contain 
$\pi _Y(Z)$. By the same argument, 
$Z$ is among the finitely many 
$G$-translates of 
$Z$ that contain 
$\pi _Y(Z)$ in their neighbourhood of radius 
$d(Y,Z)$. Observing that 
$L$ permutes these translates of 
$Y$ and 
$Z$, we conclude that a finite-index subgroup of 
$L$ must preserve both 
$Y$ and 
$Z$.
Let 
$G_Y,G_Z\leq G$ denote the 
$G$-stabilisers of 
$Y$ and 
$Z$. Since 
$H\curvearrowright Y$ is cocompact, 
$H$ has finite index in 
$G_Y$. Similarly, 
$K$ has finite index in 
$G_Z$. It follows that 
$H\cap K$ has finite index in 
$G_Y\cap G_Z$, which has finite index in 
$L$ by Claim 3. We have already observed that 
$L\curvearrowright \pi _Y(Z)$ is cocompact, so this implies that 
$H\cap K\curvearrowright \pi _Y(Z)$ is cocompact.
Given a subgroup 
$H\leq G$, we denote by 
$N_G(H)\leq G$ its normaliser.
Lemma 2.9 If 
$H,K\leq G$ are convex-cocompact in 
$X$, there exists a finite subset 
$F\subseteq G$ such that
\[ \{g\in G \mid gHg^{-1}\leq K\} = K\cdot F\cdot N_G(H). \]
Proof. Let 
$\mathscr {C}(q)$ be the collection of 
$q$-convex-cocompact subgroups of 
$G$.
Claim For each 
$q\geq 1$, only finitely many 
$K$-conjugacy classes of subgroups of 
$K$ lie in 
$\mathscr {C}(q)$.
Proof of Claim Let 
$Y\subseteq X$ be a 
$K$-invariant, 
$K$-cocompact, convex subcomplex. Let 
$Y_0\subseteq Y$ be a finite set of vertices meeting every 
$K$-orbit.
Consider a subgroup 
$L\leq K$ lying in 
$\mathscr {C}(q)$. Then there exists an 
$L$-invariant convex subcomplex 
$Z\subseteq X$ on which 
$L$ acts with 
$\leq q$ orbits of vertices. Replacing 
$Z$ with its gate-projection to 
$Y$, we can assume that 
$Z\subseteq Y$. Conjugating 
$L$ by an element of 
$K$, we can assume that 
$Z$ meets 
$Y_0$.
Now, the 
$q$-neighbourhood of 
$Y_0$ in 
$Y$ contains a set of vertices 
$Z_0\subseteq Z$ meeting every 
$L$-orbit in 
$Z$. By [Reference Bridson and HaefligerBH99, Theorem I.8.10], 
$L$ is generated by the elements 
$\{g\in L\mid d(gZ_0,Z_0)\leq 1\}$.
Summing up, every subgroup of 
$K$ lying in 
$\mathscr {C}(q)$ is 
$K$-conjugate to a subgroup generated by a subset of the finite set 
$\{g\in G\mid d(gY_0,Y_0)\leq 2q+1\}$. This proves the claim.
Choose 
$q'$ such that 
$H\in \mathscr {C}(q')$. Then, for every 
$g\in G$, we have 
$gHg^{-1}\in \mathscr {C}(q')$. The claim implies that 
$K$ contains only finitely many subgroups of this form up to 
$K$-conjugacy, and the lemma follows.
Definition 2.10 An action on a 
${\rm CAT(0)}$ cube complex 
$H\curvearrowright X$ is non-transverse if there do not exist a hyperplane 
$\mathfrak {w}\in \mathscr {W}(X)$ and an element 
$h\in H$ such that 
$\mathfrak {w}$ and 
$h\mathfrak {w}$ are transverse.
Recall from Proposition 2.1 that 
$N_G(H)$ leaves invariant the convex subcomplex 
$\overline {\mathcal {C}}(H)$ and its splitting 
$\overline {\mathcal {C}}_0(H)\times \mathcal {C}_1(H)$.
Lemma 2.11 Let 
$H\leq G$ be convex-cocompact in 
$X$. Suppose that 
$H$ acts non-transversely on 
$X$. Then the action 
$N_G(H)\curvearrowright \overline {\mathcal {C}}_0(H)$ is cocompact.
Proof. Let 
$\mathscr {T}(X)$ be the set of tuples 
$(\mathfrak {w}_1,\dots,\mathfrak {w}_k)$ of pairwise-transverse hyperplanes of 
$X$. Since 
$H$ acts non-transversely on 
$X$, each hyperplane of 
$\overline {\mathcal {C}}_0(H)$ is left invariant by 
$H$. Thus, maximal cubes of 
$\overline {\mathcal {C}}_0(H)$ are in one-to-one correspondence with maximal 
$H$-fixed tuples in 
$\mathscr {T}(X)$.
Let us show that 
$N_G(H)$ acts cofinitely on the set of fixed points of 
$H$ in 
$\mathscr {T}(X)$. By the previous paragraph, this implies the lemma.
For every tuple 
$(\mathfrak {w}_1,\dots,\mathfrak {w}_k)$ in 
$\mathscr {T}(X)$, its stabiliser 
$G_{\mathfrak {w}_1}\cap \dots \cap G_{\mathfrak {w}_k}$ acts cocompactly on the intersection 
$\mathfrak {w}_1\cap \dots \cap \mathfrak {w}_k$ (see e.g. [Reference Fioravanti and HagenFH21, Lemma 2.3]), so it is convex-cocompact in 
$X$. Lemma 2.9 implies that there exists a finite set 
$F\subseteq G$ such that
\[ \{g\in G\mid H\text{ preserves } g\mathfrak{w}_1,\dots,g\mathfrak{w}_k\}= N_G(H)\cdot F\cdot (G_{\mathfrak{w}_1}\cap\dots\cap G_{\mathfrak{w}_k}). \]
It follows that every 
$G$-orbit in 
$\mathscr {T}(X)$ contains only finitely many 
$N_G(H)$-orbits of elements fixed by 
$H$. Since the action 
$G\curvearrowright \mathscr {T}(X)$ is cofinite, this shows that there are only finitely many 
$N_G(H)$-orbits of fixed points of 
$H$ in 
$\mathscr {T}(X)$, as required.
Example 2.12 Lemma 2.11 (and Corollary 2.13) can fail if 
$H$ does not act non-transversely.
For instance, let 
$G=\mathbb {Z}^2\rtimes \langle h\rangle$ act on the standard cubulation of 
$\mathbb {R}^3$, with 
$\mathbb {Z}^2$ generated by unit translations in the 
$x$- and 
$y$-directions, respectively, and 
$h(x,y,z)=(y,x,z+1)$. Taking 
$H=\langle h\rangle$, the space 
$\overline {\mathcal {C}}_0(H)$ is naturally identified with the 
$xy$-plane, but 
$N_G(H)$ is generated by 
$h$ and 
$(x,y,z)\mapsto (x+1,y+1,z)$.
Corollary 2.13 Let 
$H\leq G$ be convex-cocompact in 
$X$. If 
$H\curvearrowright X$ is non-transverse, then the following hold:
(1)
$N_G(H)$ has a finite-index subgroup of the form $H\cdot K$, where $H$ and $K$ commute and $H\cap K$ is finite (thus, if $G$ is virtually torsion-free, $N_G(H)$ is virtually a product $H\times K$);(2) there exists a point
$p\in \overline {\mathcal {C}}(H)$ such that the fibre $\overline {\mathcal {C}}_0(H)\times \{\ast \}$ through $p$ is $K$-invariant and $K$-cocompact, while the fibre $\{\ast \}\times \mathcal {C}_1(H)$ through $p$ is $H$-invariant and $H$-cocompact;(3) the action
$N_G(H)\curvearrowright \overline {\mathcal {C}}(H)$ is cocompact, hence $N_G(H)$ is convex-cocompact in $X$.
Proof. Recall that both 
$\mathcal {C}(H)\subseteq X$ and its splitting 
$\overline {\mathcal {C}}_0(H)\times \mathcal {C}_1(H)$ are preserved by 
$N_G(H)$. The action 
$H\curvearrowright \overline {\mathcal {C}}_0(H)$ has a fixed point, so we have an 
$H$-invariant fibre 
$\{p_0\}\times \mathcal {C}_1(H)$. The 
$H$-action on this fibre is cocompact (see e.g. [Reference FioravantiFio22, Lemma 3.2(3)]) and proper, since it equivariantly embeds in 
$X$. Let 
$p=(p_0,p_1)$ be any point in this fibre.
Consider the proper cocompact action 
$H\curvearrowright \mathcal {C}_1(H)$. A finite index-subgroup 
$N\leq N_G(H)$ preserves the 
$H$-orbit of 
$p_1$. If 
$N_1\leq N$ is the subgroup fixing 
$p_1$, then 
$N=H\cdot N_1$, the intersection 
$H\cap N_1$ is finite, and a finite-index subgroup 
$K\leq N_1$ commutes with 
$H$. This can all be shown exactly as in the proof of Lemma 2.3. Hence, part (1) follows.
By Lemma 2.11, 
$N_G(H)$ acts cocompactly on 
$\overline {\mathcal {C}}_0(H)$. The same holds for the finite-index subgroup 
$K\cdot H$. Since 
$H$ is elliptic in 
$\overline {\mathcal {C}}_0(H)$, a 
$K$-orbit coincides with a 
$K\cdot H$-orbit and so it is coarsely dense in 
$\overline {\mathcal {C}}_0(H)$. Note that 
$\overline {\mathcal {C}}_0(H)$ is locally finite, since it embeds in 
$X$. Thus, 
$K$ acts cocompactly on 
$\overline {\mathcal {C}}_0(H)$, hence on the fibre 
$\overline {\mathcal {C}}_0(H)\times \{p_1\}$. This proves part (2), and part (3) follows immediately.
2.4 Coarse medians
Coarse medians were introduced by Bowditch in [Reference BowditchBow13]. We present the following equivalent definition from [Reference Niblo, Wright and ZhangNWZ19]. We write ‘
$x\approx _Cy$’ with the meaning of ‘
$d(x,y)\leq C$’.
Definition 2.14 Let 
$X$ be a metric space. A coarse median on 
$X$ is a permutation-invariant map 
$\mu \colon X^3\rightarrow X$ for which there exists a constant 
$C\geq 0$ such that, for all 
$a,b,c,x\in X$, we have:
(1)
$\mu (a,a,b)=a$;(2)
$\mu (\mu (a,x,b),x,c)\approx _C\mu (a,x,\mu (b,x,c))$;(3)
$d(\mu (a,b,c),\mu (x,b,c))\leq Cd(a,x)+C$.
In accordance with [Reference FioravantiFio22, § 2.6], we also introduce the following.
Definition 2.15 Two coarse medians 
$\mu _1,\mu _2$ are at bounded distance if 
$\mu _1(x,y,z)\approx _C\mu _2(x,y,z)$ for some 
$C\geq 0$ and all 
$x,y,z\in X$. A coarse median structure on 
$X$ is the equivalence class 
$[\mu ]$ of coarse medians at bounded distance from 
$\mu$. A coarse median space is a metric space with a coarse median structure.
Definition 2.16 Let 
$(X,[\mu ])$ be a coarse median space. A coarsely Lipschitz map 
$f\colon X\rightarrow X$ is coarse-median preserving if 
$f(\mu (x,y,z))\approx _C\mu (f(x),f(y),f(z))$ for some 
$C\geq 0$ and all 
$x,y,z\in X$.
Recall that 
${\rm CAT(0)}$ cube complexes have a natural structure of median algebra, hence one of coarse median space. The following is a simple observation.
Lemma 2.17 Let 
$(X,m)$ be a 
${\rm CAT(0)}$ cube complex. A map 
$\Phi \colon X^{(0)}\rightarrow X^{(0)}$ is coarse-median preserving if and only if there exists a constant 
$C\geq 0$ such that, whenever 
$x,y,p\in X$ are vertices with 
$p=m(x,y,p)$, the set 
$\mathscr {W}(\Phi (p)|\Phi (x),\Phi (y))$ contains at most 
$C$ hyperplanes.
Proof. Suppose that 
$\Phi$ is coarse-median preserving and 
$C$ is the constant in Definition 2.16. Then, if 
$p=m(x,y,p)$, we have 
$\Phi (p)\approx _C m(\Phi (p),\Phi (x),\Phi (y))$. Hyperplanes separating these two points are precisely those in the set 
$\mathscr {W}(\Phi (p)|\Phi (x),\Phi (y))$, which then has cardinality at most 
$C$.
Conversely, suppose that 
$\Phi$ is a map satisfying 
$\#\mathscr {W}(\Phi (p)|\Phi (x),\Phi (y))\leq C$ for all 
$x,y,p\in X$ with 
$p=m(x,y,p)$. Consider arbitrary points 
$x',y',z'\in X$ and their median 
$m'=m(x',y',z')$. Then the set 
$\mathscr {W}(\Phi (m') | m(\Phi (x'),\Phi (y'),\Phi (z')))$ is contained in the union
\[ \mathscr{W}(\Phi(m')| \Phi(x'),\Phi(y'))\cup\mathscr{W}(\Phi(m')|\Phi(y'),\Phi(z'))\cup\mathscr{W}(\Phi(m')|\Phi(z'),\Phi(x')), \]
where each of the three sets has cardinality at most 
$C$ by our assumption on 
$\Phi$. It follows that 
$\Phi (m')\approx _{3C}m(\Phi (x'),\Phi (y'),\Phi (z'))$, showing that 
$\Phi$ is coarse-median preserving.
Definition 2.18 A coarse median group is a pair 
$(G,[\mu ])$ where 
$G$ is a finitely generated group and 
$[\mu ]$ is a coarse median structure with respect to the word metrics on 
$G$. Contrary to [Reference BowditchBow13], we additionally require all left multiplications by elements of 
$G$ to be coarse-median preserving.
Let 
$(G,[\mu ])$ be a coarse median group. Note that all automorphisms of 
$G$ are quasi-isometries with respect to the word metrics on 
$G$. We denote the set of coarse-median preserving automorphisms by 
$\operatorname {Aut}(G,[\mu ])$, or simply 
$\operatorname {Aut}_{\rm cmp}(G)$ when the coarse median structure is clear.
Note that 
$\operatorname {Aut}_{\rm cmp}(G)\leq \operatorname {Aut}(G)$ is a subgroup containing all inner automorphisms, so it descends to a subgroup 
$\operatorname {Out}_{\rm cmp}(G)\leq \operatorname {Out}(G)$.
All hyperbolic groups and mapping class groups are coarse median groups [Reference BowditchBow13]. However, the main example of interest for this paper is provided by cocompactly cubulated groups, as this provides structures of coarse median group on all special groups.
Example 2.19 Every proper cocompact action on a 
${\rm CAT(0)}$ cube complex 
$G\curvearrowright X$ induces a canonical structure of coarse median group on 
$G$. It suffices to pull back to 
$G$ the median operator of 
$X$ via any 
$G$-equivariant quasi-isometry 
$G\rightarrow X$. The result is independent of all choices involved.
Note however that different actions on 
${\rm CAT(0)}$ cube complexes can induce different coarse median structures on 
$G$. This is particularly evident for free abelian groups 
$\mathbb {Z}^n$ with 
$n\geq 2$ (corresponding to changes of basis). An exception is provided by hyperbolic groups, as they always admit a unique coarse median structure (see e.g. [Reference Niblo, Wright and ZhangNWZ19, Theorem 4.2]).
Definition 2.20 Let 
$(X,[\mu ])$ be a coarse median space. A subset 
$A\subseteq X$ is quasi-convex if there exists 
$C\geq 0$ such that 
$\mu (A\times A\times X)$ is contained in the 
$C$-neighbourhood of 
$A$.
Remark 2.21 Let 
$G\curvearrowright X$ be a proper cocompact action on a 
${\rm CAT(0)}$ cube complex, and let 
$[\mu _X]$ be the induced coarse median structure on 
$G$. Then a subgroup 
$H\leq G$ is quasi-convex with respect to 
$[\mu _X]$ if and only if it is convex-cocompact in 
$X$. See for instance [Reference FioravantiFio22, Lemma 3.2].
Remark 2.22 Let 
$(G,[\mu ])$ be a coarse median group. If 
$H\leq G$ is quasi-convex and 
$\varphi$ is a coarse-median preserving automorphism of 
$G$, then 
$\varphi (H)$ is again quasi-convex.
In coarse median groups we also have the following notion of orthogonality of subgroups, which was referenced in the definition of twists and folds in the Introduction.
Definition 2.23 Let 
$(G,[\mu ])$ be a coarse median group. Two subgroups 
$H,K\leq G$ are orthogonal (written 
$H\perp K$ or 
$H\perp _{[\mu ]} K$) if the set 
$\{\mu (1,h,k) \mid h\in H,\ k\in K\}$ is finite.
Remark 2.24 Orthogonal subgroups have finite intersection. The converse holds for quasi-convex subgroups.
Lemma 2.25 Suppose that 
$G$ admits a proper cocompact action on a 
${\rm CAT(0)}$ cube complex 
$X$. Let 
$[\mu _X]$ be the induced coarse median structure.
(1) If
$H,K\leq G$ commute and $H\perp K$, then $\mathcal {W}_1(H)\subseteq \overline {\mathcal {W}}_0(K)$ and $\mathcal {W}_1(K)\subseteq \overline {\mathcal {W}}_0(H)$.(2) If
$H,K\leq G$ are as in Corollary 2.13, then $H\perp K$.
Proof. Part (2) is immediate from Corollary 2.13(2) and the definition of orthogonality. Regarding part (1), it suffices to show that, for every 
$h\in H$, we have 
$\mathcal {W}_1(h)\subseteq \overline {\mathcal {W}}_0(K)$.
Since 
$h$ and 
$K$ commute, we have 
$k\mathcal {W}_1(h)=\mathcal {W}_1(h)$ for every 
$k\in K$. In addition, for every 
$\mathfrak {w}\in \mathcal {W}_1(h)$, each 
$k\in K$ takes the side of 
$\mathfrak {w}$ containing a positive semi-axis of 
$h$ to the side of 
$k\mathfrak {w}$ containing a positive semi-axis of 
$h$. Thus, either 
$k\mathfrak {w}$ and 
$\mathfrak {w}$ intersect, or 
$k$ skewers 
$\mathfrak {w}$.
If no element of 
$K$ skewers an element of 
$\mathcal {W}_1(h)$, this shows that 
$\mathcal {W}_1(h)\subseteq \overline {\mathcal {W}}_0(K)$, as required. If instead some 
$k\in K$ skewers a hyperplane 
$\mathfrak {w}\in \mathcal {W}_1(h)$, then 
$\langle k\rangle \cdot \mathfrak {w}\subseteq \mathcal {W}_1(h)\cap \mathcal {W}_1(k)$. In this case, 
$\mathcal {W}_1(h)\cap \mathcal {W}_1(k)$ is infinite, so 
$\mu (1,h^n,k^n)$ diverges for 
$n\rightarrow +\infty$, violating the fact that 
$H\perp K$.
2.5 Ultralimits
For a detailed treatment of ultrafilters and ultralimits, the reader can consult [Reference Druţu and KapovichDK18, Ch. 10]. Here we briefly recall only one basic construction.
Fix a non-principal ultrafilter 
$\omega$ on 
$\mathbb {N}$. Consider a sequence 
$G\curvearrowright X_n$ of isometric actions on metric spaces, with a sequence of basepoints 
$o_n\in X_n$. Let 
$S\subseteq G$ be a finite generating set.
We say that the sequence 
$(G\curvearrowright X_n,o_n)$ 
$\omega$-converges if, for every generator 
$s\in S$, we have 
$\lim _{\omega }d(o_n,so_n)<+\infty$. In this case, the 
$\omega$-limit is the isometric action 
$G\curvearrowright X_{\omega }$ constructed as follows. Points of 
$X_{\omega }$ are sequences 
$(x_n)$ with 
$x_n\in X_n$ and 
$\lim _{\omega }d(x_n,o_n)<+\infty$, where we identify sequences 
$(x_n)$ and 
$(x_n')$ if 
$\lim _{\omega }d(x_n,x_n')=0$. The 
$G$-action on 
$X_{\omega }$ is defined by 
$g(x_n):=(gx_n)$.
If a sequence of actions on 
$\mathbb {R}$-trees 
$G\curvearrowright T_n$ 
$\omega$-converges to an action 
$G\curvearrowright T_{\omega }$ (for some choice of basepoints), then 
$T_{\omega }$ is a complete 
$\mathbb {R}$-tree. Note that the action 
$G\curvearrowright T_{\omega }$ will almost always fail to be minimal, even if all actions 
$G\curvearrowright T_n$ are.
3. Special groups and right-angled Artin groups
A group is usually said to be special if it is the fundamental group of a compact special cube complex [Reference Haglund and WiseHW08, Reference SageevSag14]. For our purposes, it is more convenient to use the following, entirely equivalent characterisation.
Definition 3.1 A group 
$G$ is special if and only if 
$G$ is a convex-cocompact subgroup of a right-angled Artin group 
$\mathcal {A}_{\Gamma }$ with respect to the action on the universal cover of the Salvetti complex.
Note that special groups are torsion-free.
3.1 Notation and basic properties
In the rest of the paper, we employ the following notation.
• We denote right-angled Artin groups by
$\mathcal {A}_{\Gamma }$ and universal covers of Salvetti complexes by $\mathcal {X}_{\Gamma }$. As customary, we identify the $0$-skeleton of $\mathcal {X}_{\Gamma }$ with $\mathcal {A}_{\Gamma }$.• We have a map
$\gamma \colon \mathscr {W}(\mathcal {X}_{\Gamma })\rightarrow \Gamma ^{(0)}$ that pairs each hyperplane of $\mathcal {X}_{\Gamma }$ with its label.• For each
$v\in \Gamma ^{(0)}$, we denote by $\pi _v\colon \mathcal {X}_{\Gamma }\rightarrow \mathcal {T}_v$ the restriction quotient associated to the set of hyperplanes $\gamma ^{-1}(v)\subseteq \mathscr {W}(\mathcal {X}_{\Gamma })$. This is a simplicial tree with an $\mathcal {A}_{\Gamma }$-action.• If
$g\in \mathcal {A}_{\Gamma }$, we denote by $\Gamma (g)\subseteq \Gamma$ the set of labels appearing on one (equivalently, all) axis of $g$ in $\mathcal {X}_{\Gamma }$. Equivalently, $\Gamma (g)$ is the set of $v\in \Gamma$ for which $g$ is loxodromic in the tree $\mathcal {T}_v$. Note that $\Gamma (g)\subseteq \gamma (\mathscr {W}(1|g))$, though this might not be an equality if $g$ is not cyclically reduced.• If
$K\leq \mathcal {A}_{\Gamma }$ is a subgroup, we also write $\Gamma (K):=\bigcup _{g\in K}\Gamma (g)$.• We do not distinguish between subgraphs
$\Delta \subseteq \Gamma$ and their $0$-skeleton. If $\Delta \subseteq \Gamma$, we write
\[ \Delta^{\perp}=\bigcap_{v\in\Delta}\operatorname{lk} v, \quad \Delta_{\perp}=\bigcap_{v\in\Delta}\operatorname{st} v. \]
Remark 3.2
(1) For every
$\Delta \subseteq \Gamma$, the centraliser of $\mathcal {A}_{\Delta }$ in $\mathcal {A}_{\Gamma }$ is $\mathcal {A}_{\Delta _{\perp }}$.(2) We have
$\Delta _{\perp }=\Delta ^{\perp }\sqcup \{c_1,\dots,c_k\}$, where the $c_i$ are those vertices of $\Delta$ such that $\Delta \subseteq \operatorname {st} c_i$.
We record here a few basic lemmas for later use.
Lemma 3.3 Consider 
$a,b\in \mathcal {A}_{\Gamma }$ such that 
$1,a,ab$ lie on a geodesic of 
$\mathcal {X}_{\Gamma }$ in this order. Then
\[ \gamma(\mathscr{W}(1|a))\cap\gamma(\mathscr{W}(1|b))\subseteq\Gamma(a)\cup\Gamma(b)\cup\Gamma(ab). \]
Proof. Consider 
$v\in \gamma (\mathscr {W}(1|a))\cap \gamma (\mathscr {W}(1|b))$ and suppose that 
$v\not \in \Gamma (a)\cup \Gamma (b)$. Write 
$a=xa'x^{-1}$ and 
$b=yb'y^{-1}$ as reduced words, with 
$a',b'$ cyclically reduced. Since 
$1,a,ab$ lie on a geodesic, the word 
$xa'x^{-1}yb'y^{-1}$ spells a geodesic in 
$\mathcal {X}_{\Gamma }$.
Since 
$v\not \in \Gamma (a)\cup \Gamma (b)$, we must have 
$v\in \gamma (\mathscr {W}(1|x))\cap \gamma (\mathscr {W}(1|y))$. Thus, there exist halfspaces:
\[ \mathfrak{h}_1\in\mathscr{H}(1|x), \quad \mathfrak{h}_2\in\mathscr{H}(xa'x^{-1}yb'|xa'x^{-1}yb'y^{-1}), \]
bounded by hyperplanes labelled by 
$v$. Since 
$xa'x^{-1}yb'y^{-1}$ spells a geodesic, we have 
$\mathfrak {h}_2\subsetneq \mathfrak {h}_1$. Note that 
$ab\cdot \mathfrak {h}_1$ lies in 
$\mathscr {H}(xa'x^{-1}yb'y^{-1}|xa'x^{-1}yb'y^{-1}x)$. In addition, since 
$x^{-1}y$ is a sub-path of a geodesic, it is itself a geodesic, hence 
$y^{-1}x$ also spells a geodesic. This shows that 
$ab\cdot \mathfrak {h}_1\subsetneq \mathfrak {h}_2\subsetneq \mathfrak {h}_1$. In conclusion, 
$ab$ skewers a hyperplane labelled by 
$v$, so 
$v\in \Gamma (ab)$.
Lemma 3.4 Consider 
$g,h\in \mathcal {A}_{\Gamma }$ and 
$x\in \mathcal {X}_{\Gamma }$. If 
$h$ fixes 
$\mathscr {W}(x|gx)$ pointwise, then 
$g$ and 
$h$ commute.
Proof. Recall that 
$\mathrm {Min}(g)\subseteq \mathcal {X}_{\Gamma }$ is convex. Replacing 
$x$ with its gate-projection to 
$\mathrm {Min}(g)$ can only shrink the set 
$\mathscr {W}(x|gx)$, so we can assume that 
$x$ is on an axis of 
$g$. Conjugating 
$g$ and 
$h$ by 
$x$, we can further assume that 
$x=1$, i.e. that 
$g$ is cyclically reduced. Now, the conclusion is straightforward.
Lemma 3.5 Consider 
$g,h\in \mathcal {A}_{\Gamma }$.
(1) There exists
$k\in \langle g,h\rangle$ with $\Gamma (g)\cup \Gamma (h)\subseteq \Gamma (k)$.(2) If
$g$ is cyclically reduced and $h\not \in \mathcal {A}_{\Gamma (g)}$, then there exists $k\in \langle g,h\rangle$ with $\Gamma (k)\not \subseteq \Gamma (g)$.
Proof. In order to prove part (1), note that an element 
$x\in \mathcal {A}_{\Gamma }$ is loxodromic in the tree 
$\mathcal {T}_v$ if and only if 
$v\in \Gamma (x)$. Thus 
$\langle g,h\rangle$ acts without a global fixed point on all trees 
$\mathcal {T}_v$ with 
$v\in \Gamma (g)\cup \Gamma (h)$. It follows (for instance, by [Reference Clay and UyanikCU18, Theorem 5.1]) that there exists 
$k\in \langle g,h\rangle$ that is loxodromic in all these trees, that is, 
$\Gamma (g)\cup \Gamma (h)\subseteq \Gamma (k)$.
We now prove part (2). We can assume that 
$\Gamma (h)\subseteq \Gamma (g)$, otherwise we can take 
$k=h$. Since 
$g$ is cyclically reduced, the vertex set of 
$\mathrm {Min}(g)\subseteq \mathcal {X}_{\Gamma }$ is contained in 
$\mathcal {A}_{\Gamma (g)}\times \mathcal {A}_{\Gamma (g)^{\perp }}$.
Observe that 
$\mathrm {Min}(h)$ and 
$\mathcal {A}_{\Gamma (g)}\times \mathcal {A}_{\Gamma (g)^{\perp }}$ are disjoint. Indeed, suppose that a vertex 
$x\in \mathcal {X}_{\Gamma }$ lies in their intersection. Since 
$x\in \mathrm {Min}(h)$, we have 
$x^{-1}hx\in \mathcal {A}_{\Gamma (h)}\leq \mathcal {A}_{\Gamma (g)}$. Hence 
$h$ lies in 
$\mathcal {A}_{\Gamma (g)}$, since 
$x\in \mathcal {A}_{\Gamma (g)}\times \mathcal {A}_{\Gamma (g)^{\perp }}$. This contradicts the assumption that 
$h\not \in \mathcal {A}_{\Gamma (g)}$.
Now, since 
$\mathrm {Min}(h)$ and 
$\mathcal {A}_{\Gamma (g)}\times \mathcal {A}_{\Gamma (g)^{\perp }}$ are disjoint and convex, there exists a hyperplane 
$\mathfrak {w}$ separating them. Choosing 
$\mathfrak {w}$ closest to 
$\mathcal {A}_{\Gamma (g)}\times \mathcal {A}_{\Gamma (g)^{\perp }}$, we can assume that 
$w:=\gamma (\mathfrak {w})$ does not lie in 
$\Gamma (g)$. It follows that, in the tree 
$\mathcal {T}_w$, the elements 
$g$ and 
$h$ are both elliptic, with disjoint sets of fixed points (which are just the projections to 
$\mathcal {T}_w$ of 
$\mathrm {Min}(g)$ and 
$\mathrm {Min}(h)$). Thus, 
$gh$ is loxodromic in 
$\mathcal {T}_w$, which implies that 
$w\in \Gamma (gh)$.
3.2 Label-irreducible elements
The following notion will play a fundamental role in the rest of the paper. We recall here a few observations from [Reference FioravantiFio22, § 3.2].
Definition 3.6 An element 
$g\in \mathcal {A}_{\Gamma }\setminus \{1\}$ is label-irreducible if the subgraph 
$\Gamma (g)\subseteq \Gamma$ does not split as a non-trivial join.
Recall that, if 
$\mathcal {G}_1$ and 
$\mathcal {G}_2$ are graphs, then their join 
$\mathcal {G}_1\ast \mathcal {G}_2$ is the graph obtained by adding to the disjoint union 
$\mathcal {G}_1\sqcup \mathcal {G}_2$ edges between every vertex of 
$\mathcal {G}_1$ and every vertex of 
$\mathcal {G}_2$.
Remark 3.7 The following are straightforward properties of label-irreducibles.
(1) An element
$g$ is label-irreducible if and only if the subgroup $\langle g\rangle$ is convex-cocompact in $\mathcal {X}_{\Gamma }$.(2) Every
$g\in \mathcal {A}_{\Gamma }$ can be written as $g=g_1\cdot \ldots \cdot g_k$, where $g_1,\dots,g_k$ are pairwise-commuting label-irreducibles with $\langle g_i\rangle \cap \langle g_j\rangle =\{1\}$ for $i\neq j$. This decomposition is unique up to permutation, so we refer to the $g_i$ as the label-irreducible components of $g$. Here $\Gamma (g)=\Gamma (g_1)\sqcup \dots \sqcup \Gamma (g_k)$ is precisely the maximal join-decomposition of $\Gamma (g)$.(3) Elements
$g,h\in \mathcal {A}_{\Gamma }$ commute if and only if every label-irreducible component of $g$ commutes with every label-irreducible component of $h$.(4) If two label-irreducible elements
$g,h\in \mathcal {A}_{\Gamma }$ commute, then either $\Gamma (g)\subseteq \Gamma (h)^{\perp }$ or $\langle g,h\rangle \simeq \mathbb {Z}$ (for instance, this follows from Remark 2.24 and Lemma 2.25(1)).(5) If
$g=g_1\cdot \ldots \cdot g_k$ is the decomposition of $g$ into label-irreducibles, then the centraliser of $g$ in $\mathcal {A}_{\Gamma }$ splits as
where\[ C_1\times\cdots\times C_k\times P, \]
$C_i\leq \mathcal {A}_{\Gamma }$ is the maximal cyclic subgroup containing $g_i$, and $P\leq \mathcal {A}_{\Gamma }$ is parabolic. If $g$ is cyclically reduced, then $P=\mathcal {A}_{\Gamma (g)^{\perp }}$.(6) Let
$G\leq \mathcal {A}_{\Gamma }$ be convex-cocompact in $\mathcal {X}_{\Gamma }$. Consider an element $g\in G$ and its decomposition into label-irreducibles $g=g_1\cdot \ldots \cdot g_k$, where $g_i\in \mathcal {A}_{\Gamma }$. Then $G\cap \langle g_i\rangle \neq \{1\}$ for each $1\leq i\leq k$ (see for instance [Reference FioravantiFio22, Lemma 3.16]). In fact, if $G$ is $q$-convex-cocompact, then $G$ contains a power of each $g_i$ with exponent $\leq q$ (see [Reference FioravantiFio22, Remark 3.17]).
Lemma 3.8 Consider 
$g,h\in \mathcal {A}_{\Gamma }$ and 
$v\in \Gamma$. Suppose that 
$g$ is loxodromic in 
$\mathcal {T}_v$ with axis 
$\alpha$. If 
$\mathrm {Min}(h,\mathcal {T}_v)$ intersects 
$\alpha$ in an arc of length 
$>4\dim \mathcal {X}_{\Gamma }\cdot \max \{\ell _{\mathcal {T}_v}(g),\ell _{\mathcal {T}_v}(h)\}$, then 
$h\alpha =\alpha$.
Proof. Note that exactly one of the label-irreducible components of 
$g$ is loxodromic in 
$\mathcal {T}_v$. In addition, this component has the same axis and the same translation length as 
$g$. Thus, we can assume that 
$g$ is label-irreducible. In this case, [Reference FioravantiFio22, Corollary 3.14] shows that 
$g$ and 
$h$ commute, so it is clear that 
$h$ preserves the axis of 
$g$.
Recall that, given a group 
$G$, a subgroup 
$H\leq G$ and a subset 
$K\subseteq G$, we denote by 
$Z_H(K)$ the centraliser of 
$K$ in 
$H$, i.e. the subgroup of elements of 
$H$ that commute with all elements of 
$K$.
Remark 3.9 Let 
$G\leq \mathcal {A}_{\Gamma }$ be convex-cocompact and let 
$g\in G$ be label-irreducible.
(1) If
$\varphi \in \operatorname {Aut}(G)$ is coarse-median preserving (for the coarse median structure induced by $\mathcal {A}_{\Gamma }$), then $\varphi (g)$ is again label-irreducible. This follows from Remarks 3.7(1) and 2.21.(2) We can define the straight projection
$\pi _g\colon Z_G(g)\rightarrow \mathbb {Z}$ as the only homomorphism that is surjective, with convex-cocompact kernel, and with $\pi _g(g)>0$.Recall that
$Z_{\mathcal {A}_{\Gamma }}(g)=C\times P$, where $P\leq \mathcal {A}_{\Gamma }$ is parabolic and $C\leq \mathcal {A}_{\Gamma }$ is the maximal cyclic subgroup containing $g$. The subgroup $Z_G(g)\leq Z_{\mathcal {A}_{\Gamma }}(g)$ is virtually $\langle g\rangle \times (G\cap P)$. Thus, $\pi _g$ is simply the restriction to $Z_G(g)$ of the coordinate projection $C\times P\rightarrow C$, suitably shrinking the codomain to ensure that $\pi _g$ is surjective. In particular, we have $\ker \pi _g=G\cap P$.If
$\varphi \in \operatorname {Aut}(G)$ is coarse-median preserving, note that $\pi _{\varphi (g)}=\pi _g\circ \varphi ^{-1}$.
We conclude this subsection with a couple of definitions that will be needed later on.
Definition 3.10 A subgroup 
$H\leq \mathcal {A}_{\Gamma }$ is full if it is closed under taking label-irreducible components.
Remark 3.11 If 
$H\leq \mathcal {A}_{\Gamma }$ is full, then 
$H$ is generated by the label-irreducibles that it contains.
Observe that, for every group 
$G$ and every subset 
$A\subseteq G$, we have 
$Z_GZ_GZ_G(A)=Z_G(A)$.
Definition 3.12 Let 
$G$ be a group. We say that a subgroup 
$H\leq G$ is a centraliser in 
$G$ if 
$H=Z_GZ_G(H)$. Equivalently, there exists a subset 
$A\subseteq G$ such that 
$H=Z_G(A)$.
Remark 3.13 Centralisers in 
$\mathcal {A}_{\Gamma }$ are full, by Remark 3.7(3).
3.3 Parabolic subgroups
Recall the following standard terminology.
Definition 3.14 A subgroup 
$P\leq \mathcal {A}_{\Gamma }$ is parabolic if 
$P=g\mathcal {A}_{\Lambda }g^{-1}$ for some 
$\Lambda \subseteq \Gamma$ and 
$g\in \mathcal {A}_{\Gamma }$.
The following alternative characterisation of parabolic subgroups will be needed in § 3.5.
Proposition 3.15 A subgroup 
$H\leq \mathcal {A}_{\Gamma }$ is parabolic if and only if it satisfies the following property. For every cyclically reduced element 
$a\in \mathcal {A}_{\Gamma }$, written as a reduced word 
$a_1\dots a_n$ with 
$a_i\in \Gamma ^{\pm }$, and for every 
$g\in \mathcal {A}_{\Gamma }$ with 
$gag^{-1}\in H$, we have 
$ga_ig^{-1}\in H$ for every 
$i$.
Proof. We first show that parabolics have this property. Since the property is invariant under conjugation, it suffices to verify it for subgroups of the form 
$\mathcal {A}_{\Lambda }$ with 
$\Lambda \subseteq \Gamma$. If 
$gag^{-1}\in \mathcal {A}_{\Lambda }$, then 
$\Gamma (a)=\Gamma (gag^{-1})\subseteq \Lambda$ and, since 
$a$ is cyclically reduced, each 
$a_i$ must lie in 
$\Lambda$. Observing that elements of 
$\mathcal {A}_{\Lambda }$ are 
$\mathcal {A}_{\Gamma }$-conjugate if and only if they are 
$\mathcal {A}_{\Lambda }$-conjugate, we see that 
$g\in \mathcal {A}_{\Lambda }\cdot Z_{\mathcal {A}_{\Gamma }}(a)$. Since 
$a$ is cyclically reduced, 
$Z_{\mathcal {A}_{\Gamma }}(a)=\bigcap _iZ_{\mathcal {A}_{\Gamma }}(a_i)$, hence 
$ga_ig^{-1}\in \mathcal {A}_{\Lambda }$ for every 
$i$.
Conversely, let 
$H\leq \mathcal {A}_{\Gamma }$ be a subgroup satisfying the property. By Lemma 3.5(1), there exists 
$x\in H$ with 
$\Gamma (x)=\Gamma (H)$. Up to conjugating 
$H$, we can assume that 
$x$ is cyclically reduced. Our property then yields 
$\mathcal {A}_{\Gamma (H)}\leq H$. If the reverse inclusion did not hold, Lemma 3.5(2) would yield an element 
$y\in H$ with 
$\Gamma (y)\not \subseteq \Gamma (H)$, which is impossible. Thus 
$H=\mathcal {A}_{\Gamma (H)}$.
Definition 3.16 A parabolic stratum is a subset of 
$\mathcal {X}_{\Gamma }$ of the form 
$g\mathcal {A}_{\Delta }$ for some 
$\Delta \subseteq \Gamma$ and 
$g\in \mathcal {A}_{\Gamma }$ (we identify as usual the 
$0$-skeleton of 
$\mathcal {X}_{\Gamma }$ with 
$\mathcal {A}_{\Gamma }$).
A parabolic stratum can equivalently be defined as the set of points of 
$\mathcal {X}_{\Gamma }$ that one can reach starting at a given vertex 
$g\in \mathcal {X}_{\Gamma }$ and only crossing edges with label in a given subgraph 
$\Delta \subseteq \Gamma$.
Remark 3.17 Here are a few straightforward properties of parabolic strata.
(1) Intersections of parabolic strata are parabolic strata. Gate-projections of parabolic strata to parabolic strata are parabolic strata.
(2) If
$\mathcal {P}$ is a parabolic stratum and $g\in \mathcal {A}_{\Gamma }$ is an element with $g\mathcal {P}\cap \mathcal {P}\neq \emptyset$, then $g\mathcal {P}=\mathcal {P}$.(3) Stabilisers of parabolic strata are parabolic subgroups of
$\mathcal {A}_{\Gamma }$.(4) For every
$g\in \mathcal {A}_{\Gamma }$, there exists a parabolic stratum $\mathcal {P}$ such that the hyperplanes of $\mathcal {P}$ are precisely the hyperplanes of $\mathcal {X}_{\Gamma }$ that are preserved by $g$, namely the elements of $\overline {\mathcal {W}}_0(g,\mathcal {X}_{\Gamma })$. It follows that, for every subgroup $H\leq \mathcal {A}_{\Gamma }$, there exists a parabolic stratum $\mathcal {P}$ whose hyperplanes are precisely those in $\overline {\mathcal {W}}_0(H,\mathcal {X}_{\Gamma })$.
Lemma 3.18 If 
$H\leq \mathcal {A}_{\Gamma }$ is convex-cocompact and 
$gHg^{-1}\leq H$ for some 
$g\in \mathcal {A}_{\Gamma }$, then 
$gHg^{-1}=H$.
Proof. Let 
$Z\subseteq \mathcal {X}_{\Gamma }$ be an 
$H$-essential convex subcomplex. Since 
$g^{-1}Z$ is 
$g^{-1}Hg$-invariant and 
$H\leq g^{-1}Hg$, the finite set 
$\mathscr {W}(Z|g^{-1}Z)$ is 
$H$-invariant, hence it is contained in 
$\overline {\mathcal {W}}_0(H,\mathcal {X}_{\Gamma })$.
By Remark 3.17(4), there exists a parabolic stratum 
$\mathcal {P}\subseteq \mathcal {X}_{\Gamma }$ such that the hyperplanes of 
$\mathcal {P}$ are precisely those preserved by 
$H$. By the previous paragraph, we can choose 
$\mathcal {P}$ so that it intersects both 
$Z$ and 
$g^{-1}Z$. Note that 
$\mathcal {P}$ is acted upon vertex-transitively by its stabiliser 
$P\leq \mathcal {A}_{\Gamma }$, so there exists 
$x\in P$ such that 
$xg^{-1}Z\cap Z\neq \emptyset$. By Lemma 3.4, 
$x$ commutes with 
$H$. Thus, replacing 
$g$ with 
$gx^{-1}$, we can assume that 
$g^{-1}Z\cap Z\neq \emptyset$ without altering 
$gHg^{-1}$. Since 
$g^{-1}Z\cap Z$ is 
$H$-invariant and 
$Z$ is 
$H$-essential, we deduce that 
$Z\subseteq g^{-1}Z$. Hence 
$gZ\subseteq Z$.
Now, pick a vertex 
$y\in Z$. Since 
$H$ is convex-cocompact, it acts cocompactly on 
$Z$, hence there exist integers 
$1\leq m< n$ such that 
$g^my$ and 
$g^ny$ are in the same 
$H$-orbit. Since 
$\mathcal {A}_{\Gamma }$ acts freely on 
$\mathcal {X}_{\Gamma }$, this implies that 
$g^{n-m}\in H$. In particular, 
$g^{n-m}$ normalises 
$H$, so we cannot have 
$gHg^{-1}\lneq H$.
Definition 3.19 Let 
$G\leq \mathcal {A}_{\Gamma }$ be convex-cocompact. A subgroup of 
$G$ is 
$G$-parabolic if it is of the form 
$G\cap P$ with 
$P\leq \mathcal {A}_{\Gamma }$ parabolic. To avoid confusion, the prefix 
$G$- will never be omitted.
Lemma 3.20 Let 
$G\leq \mathcal {A}_{\Gamma }$ act cocompactly on a convex subcomplex 
$Y\subseteq \mathcal {X}_{\Gamma }$. For every parabolic subgroup 
$P\leq \mathcal {A}_{\Gamma }$, there exists a parabolic stratum 
$\mathcal {P}'$ stabilised by a parabolic subgroup 
$P'\leq P$ such that 
$G\cap P'=G\cap P$ and 
$\mathcal {P}'\cap Y\neq \emptyset$.
Proof. Consider the gate-projection 
$\pi _Y\colon \mathcal {X}_{\Gamma }\rightarrow Y$. Let 
$\mathcal {P}$ be a parabolic stratum stabilised by 
$P$ and pick a point 
$p\in \pi _Y(\mathcal {P})$. Define 
$\mathcal {P}'$ as the parabolic stratum that contains 
$p$ and satisfies 
$\gamma (\mathscr {W}(\mathcal {P'}))=\gamma (\mathscr {W}(\mathcal {P}))\cap \gamma (\mathscr {W}(Y|\mathcal {P}))^{\perp }$. It is easy to see that 
$\pi _Y(\mathcal {P})=Y\cap \mathcal {P}'$.
Let 
$P'\leq \mathcal {A}_{\Gamma }$ be the parabolic subgroup associated to 
$\mathcal {P}'$. Since 
$\mathcal {P}'$ crosses the same hyperplanes as a sub-stratum of 
$\mathcal {P}$, we have 
$P'\leq P$, hence 
$G\cap P'\leq G\cap P$. By Lemma 2.8, 
$G\cap P'$ acts cocompactly on 
$\pi _Y(\mathcal {P}')=Y\cap \mathcal {P}'$. This set coincides with 
$\pi _Y(\mathcal {P})$, so it is preserved by 
$G\cap P$, hence 
$G\cap P'$ has finite index in 
$G\cap P$. In particular, every element of 
$G\cap P$ has a power that lies in 
$P'$. Since 
$P'$ is parabolic, this implies that 
$G\cap P\leq P'$, and hence 
$G\cap P'=G\cap P$.
Corollary 3.21 If 
$G\leq \mathcal {A}_{\Gamma }$ is convex-cocompact, there are only finitely many 
$G$-conjugacy classes of 
$G$-parabolic subgroups.
Proof. Let 
$Y\subseteq \mathcal {X}_{\Gamma }$ be a convex subcomplex on which 
$G$ acts cocompactly. By Lemma 3.20, every 
$G$-parabolic subgroup is of the form 
$G\cap P$ for a parabolic subgroup 
$P\leq \mathcal {A}_{\Gamma }$ whose parabolic stratum 
$\mathcal {P}$ intersects 
$Y$. There are only finitely many 
$G$-orbits of such parabolic strata, hence only finitely many 
$G$-conjugacy classes of such subgroups of 
$\mathcal {A}_{\Gamma }$.
Lemma 3.22 Let 
$G\leq \mathcal {A}_{\Gamma }$ be a 
$q$-convex-cocompact subgroup for 
$q\geq 1$. Let 
$H\leq G$ be an arbitrary convex-cocompact subgroup. Then:
(1)
$N_G(H)$ has a finite-index subgroup that splits as $H\times K$, where $K\leq G$ is $G$-parabolic;(2)
$Z_G(H)$ acts on the set $\mathcal {W}_1(G)\cap \overline {\mathcal {W}}_0(H)$ with at most $2q\cdot \#\Gamma ^{(0)}$ orbits;(3) every
$G$-parabolic subgroup of $G$ is $q$-convex-cocompact in $\mathcal {A}_{\Gamma }$.
Proof. Choose convex subcomplexes 
$Z\subseteq Y\subseteq \mathcal {X}_{\Gamma }$, where 
$Z$ is 
$H$-invariant and 
$H$-essential, while 
$Y$ is 
$G$-invariant and 
$G$-essential.
We prove part (3) first. Lemma 3.20 shows that 
$G$-parabolic subgroups of 
$G$ are always of the form 
$G\cap P$, where 
$P$ is the stabiliser of a stratum 
$\mathcal {P}$ that intersects 
$Y$. Observe that points of 
$\mathcal {P}\cap Y$ in the same 
$G$-orbit are also in the same 
$(G\cap P)$-orbit. Indeed, if 
$x$ and 
$gx$ lie in 
$\mathcal {P}\cap Y$ for some 
$g\in G$, then 
$g\mathcal {P}\cap \mathcal {P}\neq \emptyset$, hence 
$g\mathcal {P}=\mathcal {P}$ and 
$g\in G\cap P$. This proves part (3).
We now discuss the rest of the lemma. Remark 3.17(4) provides a parabolic stratum 
$\mathcal {P}\subseteq \mathcal {X}_{\Gamma }$ whose hyperplanes are precisely the elements of 
$\overline {\mathcal {W}}_0(H)$. We can choose 
$\mathcal {P}$ so that 
$\mathcal {P}\cap Z\neq \emptyset$. Then the elements of 
$\mathcal {W}_1(G)\cap \overline {\mathcal {W}}_0(H)$ are precisely the hyperplanes of the intersection 
$\mathcal {P}\cap Y$, so we have a splitting 
$\overline {\mathcal {C}}(H,Y)=Z\times (\mathcal {P}\cap Y)$. Recall that 
$N_G(H)$ preserves 
$\overline {\mathcal {C}}(H,Y)$ along with its two factors.
Let 
$P\leq \mathcal {A}_{\Gamma }$ be the stabiliser of 
$\mathcal {P}$. By part (3), the 
$G$-parabolic subgroup 
$G\cap P$ acts on 
$\mathcal {P}\cap Y$ with at most 
$q$ orbits of vertices. In particular, since vertices of 
$\mathcal {X}_{\Gamma }$ have degree 
$2\#\Gamma ^{(0)}$, there are at most 
$2q\cdot \#\Gamma ^{(0)}$ orbits of hyperplanes of 
$\mathcal {P}\cap Y$. By Lemma 3.4, 
$G\cap P$ is contained in 
$Z_G(H)$. This proves parts (1) and (2), taking 
$K=G\cap P$.
3.4 Semi-parabolic subgroups
Definition 3.23 A subgroup 
$H\leq \mathcal {A}_{\Gamma }$ is semi-parabolic if it is conjugate to a subgroup of the form 
$\langle a_1,\dots,a_k\rangle \times \mathcal {A}_{\Delta }$ and the following hold.
• The
$a_i$ are cyclically reduced, label-irreducible and not proper powers.• We have
$\Gamma (a_i)\subseteq \Delta ^{\perp }$ for all $i$, and $\Gamma (a_i)\subseteq \Gamma (a_j)^{\perp }$ for all $i\neq j$.
We can always assume that 
$\mathcal {A}_{\Delta }$ has trivial centre, as this can be added to the 
$a_i$.
We say that a subgroup 
$H\leq \mathcal {A}_{\Gamma }$ is closed under taking roots if, whenever 
$g^n\in H$ for some 
$g\in \mathcal {A}_{\Gamma }$ and 
$n\geq 1$, we actually have 
$g\in H$.
Semi-parabolic subgroups are always convex-cocompact, full and closed under taking roots.
Lemma 3.24 A subgroup 
$H\leq \mathcal {A}_{\Gamma }$ is semi-parabolic if and only if it splits as 
$H=A\times P$, where 
$P$ is parabolic and 
$A$ is abelian, full and closed under taking roots.
Proof. It is clear that semi-parabolic subgroups admit such a splitting. Conversely, suppose that 
$H\leq \mathcal {A}_{\Gamma }$ is an arbitrary subgroup with a splitting 
$A\times P$ as in the statement.
Since 
$A$ is full, it has a basis of label-irreducible elements 
$g_1,\dots,g_k$. The fact that 
$A$ is closed under taking roots implies that none of the 
$g_i$ can be a proper power. Since the 
$g_i$ commute, we must have 
$\Gamma (g_i)\subseteq \Gamma (g_j)^{\perp }$ for all 
$i\neq j$, by Remark 3.7(4). Since 
$P$ is parabolic, we can conjugate 
$H$ and assume that 
$H=\langle g_1,\dots,g_k\rangle \times \mathcal {A}_{\Delta }$ for some 
$\Delta \subseteq \Gamma$. Since 
$g_i$ is label-irreducible and commutes with 
$\mathcal {A}_{\Delta }$, we have 
$\Gamma (g_i)\subseteq \Delta ^{\perp }$, again by Remark 3.7(4).
It remains to further conjugate 
$H$ in order to ensure that the 
$g_i$ are all cyclically reduced. Write 
$g_i=x_ia_ix_i^{-1}$ as a reduced word with 
$a_i$ cyclically reduced. Since 
$g_i$ commutes with 
$\mathcal {A}_{\Delta }$, we have 
$g_i\in \mathcal {A}_{\Delta _{\perp }}$ (Remark 3.2(1)). In particular, 
$x_1\in \mathcal {A}_{\Delta _{\perp }}$ commutes with 
$\mathcal {A}_{\Delta }$ and, conjugating 
$H$ by 
$x_1$, we can assume that 
$g_1=a_1$.
Now, since 
$g_1$ is cyclically reduced and 
$g_2$ is a label-irreducible commuting with 
$g_1$, Remark 3.7(5) shows that 
$x_2$ commutes with 
$g_1$. Thus, conjugating 
$H$ by 
$x_2$, we can assume that 
$g_2=a_2$ without affecting 
$g_1=a_1$. Repeating this procedure, we can ensure that all 
$g_i$ are cyclically reduced.
Corollary 3.25 Intersections of semi-parabolic subgroups are again semi-parabolic.
Proof. Let 
$H_1,H_2\leq \mathcal {A}_{\Gamma }$ be two semi-parabolic subgroups. Write 
$H_i=A_i\times P_i$, with 
$P_i$ parabolic and 
$A_i$ abelian, full and closed under taking roots.
Every label-irreducible element in 
$H_i$ lies either in 
$A_i$ or in 
$P_i$. Note that 
$H_1$ and 
$H_2$ are full, so 
$H_1\cap H_2$ is full. Remark 3.11 implies that 
$H_1\cap H_2$ is generated by the label-irreducibles that it contains. Hence 
$H_1\cap H_2$ is generated by the four subgroups 
$A_1\cap A_2$, 
$A_1\cap P_2$, 
$A_2\cap P_1$ and 
$P_1\cap P_2$. The first three subgroups generate a full abelian subgroup 
$A\leq H_1\cap H_2$ closed under taking roots. Since 
$H_1\cap H_2$ splits as 
$A\times (P_1\cap P_2)$, Lemma 3.24 shows that 
$H_1\cap H_2$ is semi-parabolic.
There is no need to consider intersections of infinitely many semi-parabolic subgroups because of Remark 3.26 below.
Remark 3.26 There is a uniform bound (depending only on 
$\Gamma$) on the length of any chain of semi-parabolic subgroups of 
$\mathcal {A}_{\Gamma }$. Indeed, let 
$H_1\lneq H_2\leq \mathcal {A}_{\Gamma }$ be two semi-parabolic subgroups and write 
$H_i=A_i\times P_i$ so that the 
$P_i$ have trivial centre. Then 
$P_1\cap A_2=\{1\}$ and, since 
$P_1$ is full, we must have 
$P_1\leq P_2$. In conclusion, either 
$P_1\lneq P_2$, or 
$P_1=P_2$ and 
$A_1\lneq A_2$, since 
$A_1$ is full. In the latter case, we have 
$\operatorname {rk} A_1<\operatorname {rk} A_2$, since 
$A_1$ is closed under taking roots.
Remark 3.27 Consider a semi-parabolic subgroup 
$H\leq \mathcal {A}_{\Gamma }$ and a parabolic subgroup 
$P\leq \mathcal {A}_{\Gamma }$ that does not split as a product. If 
$H\leq P$ and 
$\Gamma (H)=\Gamma (P)$, then either 
$H$ is cyclic or 
$H=P$.
Lemma 3.28 Let 
$H\leq \mathcal {A}_{\Gamma }$ be semi-parabolic. Let 
$K\leq H$ be any subgroup with 
$\Gamma (K)=\Gamma (H)$.
(1) If
$gKg^{-1}\leq H$ for some $g\in \mathcal {A}_{\Gamma }$, then $gHg^{-1}=H$.(2) Suppose that some
$g\in \mathcal {A}_{\Gamma }$ commutes with $K$, but not with $H$. Then $H$ admits a splitting $A\times P_1\times P_2$, where $A$ is abelian, the $P_i$ are parabolics with trivial centre (possibly with $P_2=\{1\}$), and $K$ is contained in $A\times A'\times P_2$ for some abelian subgroup $A'\leq P_1$.
Proof. We begin with part (1). Consider a splitting 
$H=A\times P$ as in Lemma 3.24. Recall that 
$\Gamma (A)\cap \Gamma (P)=\emptyset$ and that every label-irreducible element of 
$H$ lies in 
$A\cup P$. If 
$g\in \mathcal {A}_{\Gamma }$, the intersection 
$H\cap g^{-1}Hg$ is full, so Remark 3.11 gives
\[ H\cap g^{-1}Hg=(A\cap g^{-1}Ag)\times (P\cap g^{-1}Pg). \]
Now, if 
$gKg^{-1}\leq H$, we have 
$K\leq H\cap g^{-1}Hg$. Hence
\[ \Gamma(H)=\Gamma(K)\subseteq\Gamma(H\cap g^{-1}Hg). \]
This implies that 
$\Gamma (A)\subseteq \Gamma (A\cap g^{-1}Ag)$ and 
$\Gamma (P)\subseteq \Gamma (P\cap g^{-1}Pg)$, thus 
$g$ must normalise both 
$A$ and 
$P$. It follows that 
$gHg^{-1}=H$, proving part (1).
We now prove part (2). Let 
$g\in \mathcal {A}_{\Gamma }$ be an element that commutes with 
$K$, but not with 
$H$. We can assume that the parabolic subgroup 
$P$, defined as above, has trivial centre.
By Lemma 3.5(1), 
$K$ contains an element 
$k$ with 
$\Gamma (k)=\Gamma (K)=\Gamma (H)$. We can write 
$k=ap$, where 
$a\in A$ and 
$p\in P$ satisfy 
$\Gamma (a)=\Gamma (A)$ and 
$\Gamma (p)=\Gamma (P)$. Let 
$p_1,\dots,p_n$ be the label-irreducible components of 
$p$. Since 
$g$ commutes with 
$k$, it must commute with 
$A$ and with all the 
$p_i$. The intersection of the centralisers of the 
$p_i$ is the subgroup 
$\langle p_1',\dots,p_n'\rangle \times Z_{\mathcal {A}_{\Gamma }}(P)$, where 
$\langle p_i'\rangle$ is the maximal cyclic subgroup containing 
$\langle p_i\rangle$.
Since 
$g$ commutes with 
$A$, but not with 
$H$, it cannot commute with 
$P$, and so it must have powers of some of the 
$p_i'$ among its label-irreducible components. Up to reordering, these are powers of 
$p_1',\dots,p_m'$ for some 
$1\leq m\leq n$. We have a splitting 
$P=P_1\times P_2$ where the 
$P_i$ are parabolic and 
$\Gamma (P_1)=\Gamma (p_1)\sqcup \dots \sqcup \Gamma (p_m)$. Since 
$P$ has trivial centre, so do the 
$P_i$. Finally, since 
$K$ commutes with 
$g$, it is contained in 
$A\times \langle p_1',\dots,p_m'\rangle \times P_2$, as required.
In the rest of the subsection, we fix a convex-cocompact subgroup 
$G\leq \mathcal {A}_{\Gamma }$. By analogy with Definition 3.19, we introduce the following.
Definition 3.29 A subgroup 
$Q\leq G$ is 
$G$-semi-parabolic if 
$Q=G\cap H$ for a semi-parabolic subgroup 
$H\leq \mathcal {A}_{\Gamma }$. In order to avoid confusion, the prefix 
$G$- will never be omitted.
Our interest in this notion is due to the following remark.
Remark 3.30 Centralisers in 
$G$ (in the sense of Definition 3.12) are 
$G$-semi-parabolic. This follows from Remark 3.7(5) and Corollary 3.25.
Lemma 3.31 If 
$Q\leq G$ is 
$G$-semi-parabolic, there exists a unique minimal semi-parabolic subgroup 
$H\leq \mathcal {A}_{\Gamma }$ such that 
$Q=G\cap H$. We can write 
$H=\langle a_1,\dots,a_k\rangle \times P$, where:
(1) the
$a_i$ are pairwise-commuting label-irreducibles with $\langle a_i\rangle \cap Q\neq \{1\}$;(2)
$P\leq \mathcal {A}_{\Gamma }$ is parabolic and both $P$ and $G\cap P$ have trivial centre;(3) we have
$\Gamma (Q)=\Gamma (H)$.
Proof. By Corollary 3.25, the intersection 
$H$ of all semi-parabolic subgroups of 
$\mathcal {A}_{\Gamma }$ containing 
$Q$ is the unique minimal semi-parabolic subgroup with 
$Q=G\cap H$.
We can write 
$H=\langle a_1,\dots,a_k\rangle \times P$, where the 
$a_i$ are pairwise-commuting label-irreducibles and 
$P\leq \mathcal {A}_{\Gamma }$ is parabolic. Remark 3.7(6) shows that 
$G$ (and hence 
$Q$) contains a power of each 
$a_i$. We can assume that 
$P$ has trivial centre, as this can be incorporated in the 
$a_i$.
Let us show that 
$\Gamma (Q)=\Gamma (H)$. By Remark 3.7(6), the sets 
$\Gamma (a_i)$ are all contained in 
$\Gamma (Q)$ and we have 
$\Gamma (Q\cap P)=\Gamma (Q)\cap \Gamma (P)$. By Lemma 3.5(1), there exists 
$g\in Q\cap P$ with 
$\Gamma (g)=\Gamma (Q\cap P)$. If this were a proper subset of 
$\Gamma (P)$, we would be able to find a parabolic subgroup 
$P'$ with 
$g\in P'\lneq P$ and 
$\Gamma (g)=\Gamma (P')$. Lemma 3.5(2) would then guarantee that 
$Q\cap P\leq P'$. Remark 3.7(6) and the fact that 
$P'$ is closed under taking roots would imply that 
$Q$ is contained in 
$\langle a_1,\dots,a_k\rangle \times P'$, violating minimality of 
$H$. We conclude that 
$\Gamma (Q\cap P)=\Gamma (P)$, which shows that 
$\Gamma (Q)=\Gamma (H)$.
Finally, if 
$G\cap P$ contained a non-trivial element 
$g$ in its centre, we would have 
$G\cap P\leq Z_P(g)$. As above, the subgroup 
$Q=G\cap H$ would then be contained in 
$\langle a_1,\dots,a_k\rangle \times Z_P(g)$. Since 
$Z_P(g)$ has non-trivial centre, it is a proper semi-parabolic subgroup of 
$P$, which violates minimality of 
$H$.
Remark 3.32 Consider a 
$G$-semi-parabolic subgroup 
$Q\leq G$ and a homomorphism 
$\rho \colon Q\rightarrow \mathbb {R}$ with 
$\Gamma (\ker \rho )=\Gamma (Q)$. Then there exists a finitely generated subgroup 
$K\leq \ker \rho$ such that any 
$G$-semi-parabolic subgroup containing 
$K$ will contain 
$Q$.
Indeed, write 
$Q=G\cap H$ with 
$H=\langle a_1,\dots,a_k\rangle \times P$ as in Lemma 3.31. Write 
$P=P_1\times \cdots \times P_m$, where each 
$P_i$ is a parabolic subgroup of 
$\mathcal {A}_{\Gamma }$ that does not split as a product. By Remark 3.7(6), we have 
$\Gamma (G\cap P_i)=\Gamma (P_i)$. In addition, since 
$G\cap P$ has trivial centre, the intersection 
$G\cap P_i$ is non-abelian. Define 
$K$ so that 
$\Gamma (K)=\Gamma (Q)$ and so that it contains a non-abelian subgroup of each 
$G\cap P_i$. Remark 3.27 applied to each 
$P_i$ implies that 
$K$ satisfies the required property.
In the rest of the subsection, we prove a couple of results aimed at classifying kernels of homomorphisms 
$Q\rightarrow \mathbb {R}$, where 
$Q\leq G$ is 
$G$-semi-parabolic.
Lemma 3.33 Let 
$Q\leq G$ be 
$G$-semi-parabolic. Let 
$H=\langle a_1,\dots,a_k\rangle \times P$ be as in Lemma 3.31. If 
$\rho \colon Q\rightarrow \mathbb {R}$ is a homomorphism, then 
$\ker \rho \subseteq G\cap H'$ for a subgroup 
$H'\leq H$ such that:
(1)
$H'=\langle a_1,\dots,a_s\rangle \times P$ for some $0\leq s\leq k$, up to reordering the $a_i$;(2)
$\Gamma (\ker \rho )=\Gamma (H')$ and $Z_G(\ker \rho )=Z_G(H')$.
Proof. Define 
$H'=\langle a_1,\dots,a_s\rangle \times P$, where 
$s$ is the smallest integer such that 
$H'$ contains 
$\ker \rho$ (up to reordering the 
$a_i$). Minimality of 
$s$ implies that 
$\Gamma (\ker \rho )$ contains 
$\Gamma (a_1),\dots,\Gamma (a_s)$. In order to complete the proof, we only need to show that 
$\Gamma (P)\subseteq \Gamma (\ker \rho )$ and 
$Z_G(\ker \rho )=Z_G(H')$.
Since 
$\Gamma (G\cap H)=\Gamma (H)$, Remark 3.7(6) implies that 
$\Gamma (G\cap P)=\Gamma (P)$. Thus, for every 
$v\in \Gamma (P)$, the action 
$G\cap P\curvearrowright \mathcal {T}_v$ is not elliptic. If 
$G\cap P\curvearrowright \mathcal {T}_v$ had a fixed point at infinity, then Lemma 3.8 would show that all loxodromics have the same axis in 
$\mathcal {T}_v$ and, by [Reference FioravantiFio22, Corollary 3.14], they would lie in the centre of 
$G\cap P$. However, 
$G\cap P$ has trivial centre by our choice of 
$H$.
We conclude that, for every 
$v\in \Gamma (P)$, the action 
$G\cap P\curvearrowright \mathcal {T}_v$ is nonelementary. Now, we can use [Reference Maher and TiozzoMT18, Theorem 1.4] and the argument in the proof of [Reference SistoSis18, Corollary 1.7(2)] to conclude that, for every 
$v\in \Gamma (P)$, the kernel of 
$\rho |_{G\cap P}$ contains an element acting loxodromically on 
$\mathcal {T}_v$ (random walks can be easily avoided when 
$\ker (\rho |_{G\cap P})$ is finitely generated). Hence 
$\Gamma (P)\subseteq \Gamma (\ker \rho )$.
Finally, let us show that the inclusion 
$Z_G(H')\leq Z_G(\ker \rho )$ cannot be strict. If it were, Lemma 3.28(2) would yield a splitting 
$P=P_1\times P_2$, where 
$P_1$ is a non-abelian parabolic and 
$\ker \rho |_{G\cap P_1}$ is abelian. Since 
$P$ is chosen as in Lemma 3.31, the intersection 
$G\cap P_1$ is a non-virtually-abelian special group (recall Lemma 2.8). However, the above shows that 
$G\cap P_1$ is abelian–by–abelian, which contradicts the flat torus theorem (see e.g. [Reference Bridson and HaefligerBH99, Theorem II.7.1(5)]).
Remark 3.34 Given a 
$G$-semi-parabolic subgroup 
$Q\leq G$ and a homomorphism 
$\rho \colon Q\rightarrow \mathbb {R}$, the centre of 
$\ker \rho$ is always contained in the centre of 
$Q$.
Indeed, let the subgroups 
$H,H'$ and the integers 
$s,k$ be as in Lemma 3.33. The lemma shows that the centre of 
$\ker \rho$ commutes with 
$H'$. Since 
$\ker \rho \leq H'$, it is also clear that 
$\ker \rho$ commutes with 
$a_{s+1},\dots,a_k$. Together with 
$H'$, these elements generate 
$H$, hence the centre of 
$\ker \rho$ commutes with 
$H$, as required.
When the homomorphism 
$\rho$ is discrete, we have the following dichotomy.
Proposition 3.35 Let 
$Q\leq G$ be 
$G$-semi-parabolic. Let 
$\rho \colon Q\rightarrow \mathbb {Z}$ be a homomorphism. Then:
• either
$\Gamma (\ker \rho )=\Gamma (Q)$, and $N_G(\ker \rho )$ is a finite-index subgroup of $N_G(Q)$;• or
$\ker \rho$ is $G$-semi-parabolic, and a finite-index subgroup of $Q$ splits as $\mathbb {Z}\times \ker \rho$.
Proof. Write 
$Q=G\cap H$ and 
$H=\langle a_1,\dots,a_k\rangle \times P$ as in Lemma 3.31. Let 
$H'=\langle a_1,\dots,a_s\rangle \times P$ be the subgroup with 
$\ker \rho \subseteq G\cap H'$ and 
$\Gamma (\ker \rho )=\Gamma (H')$ provided by Lemma 3.33.
Suppose first that 
$H=H'$. Then 
$\Gamma (\ker \rho )=\Gamma (H)=\Gamma (Q)$ and Lemma 3.28(1) implies that 
$N_{\mathcal {A}_{\Gamma }}(\ker \rho )\leq N_{\mathcal {A}_{\Gamma }}(H)$. In particular, 
$N_G(\ker \rho )\leq N_G(Q)$. In addition, 
$N_G(\ker \rho )$ contains the subgroup 
$\langle Q,Z_G(Q)\rangle$, which has finite index in 
$N_G(Q)$ by Lemma 3.22(1).
Suppose instead that 
$H'\lneq H$. Since 
$\rho$ takes values in 
$\mathbb {Z}$ and every homomorphism 
$\mathbb {Z}^2\rightarrow \mathbb {Z}$ has non-trivial kernel, we must have 
$s=k-1$. Let 
$\pi \colon H\rightarrow \mathbb {Z}$ be a homomorphism with 
$\ker \pi =H'$. Since 
$\Gamma (Q)=\Gamma (H)$, the restriction 
$\pi |_Q\colon Q\rightarrow \mathbb {Z}$ is non-trivial and has kernel 
$G\cap H'$. Since 
$\ker \rho \subseteq G\cap H'=\ker \pi |_Q$, the homomorphism 
$\pi |_Q$ factors through 
$\rho$ and, since 
$\mathbb {Z}$ is Hopfian, we must have 
$\ker \rho =G\cap H'$. This shows that 
$\ker \rho$ is 
$G$-semi-parabolic.
By Remark 3.7(6), the intersection 
$G\cap \langle a_k\rangle$ has finite index in 
$\langle a_k\rangle$. It follows that the subgroup 
$(G\cap H')\times (G\cap \langle a_k\rangle )=\ker \rho \times \mathbb {Z}$ has finite index in 
$G\cap H=Q$. This proves the proposition.
We will also need the following.
Lemma 3.36 Let 
$\mathcal {K}$ be the collection of all subgroups of 
$G$ that are the kernel of a homomorphism 
$Q\rightarrow \mathbb {R}$, where 
$Q$ varies among 
$G$-semi-parabolic subgroups. Then there exists a constant 
$N$, depending only on 
$G$, such that every chain of subgroups in 
$\mathcal {K}$ has length at most 
$N$.
Proof. Choose 
$q\geq 1$ such that 
$G\leq \mathcal {A}_{\Gamma }$ is 
$q$-convex-cocompact.
Claim 1 There exists 
$N_1$ such that every chain of 
$G$-semi-parabolics has length at most 
$N_1$.
Proof of Claim 1 Let 
$H_1,\dots,H_n$ be semi-parabolic subgroups of 
$\mathcal {A}_{\Gamma }$ such that 
$G\cap H_1\lneq \dots \lneq G\cap H_n$. If the 
$H_i$ are chosen as in Lemma 3.31, then 
$H_1\lneq \dots \lneq H_n$. By Remark 3.26, the latter chain has length bounded purely in terms of 
$\Gamma$, proving the claim.
Claim 2 There exists 
$N_2$ such that every 
$G$-semi-parabolic subgroup has a generating set with at most 
$N_2$ elements.
Proof of Claim 2 We begin by showing that, if 
$H=A\times P$ is a semi-parabolic subgroup of 
$\mathcal {A}_{\Gamma }$, then the subgroup 
$(G\cap A)\times (G\cap P)$ has index at most 
$q$ in 
$G\cap H$.
Let 
$p_P\colon H\rightarrow P$ be the factor projection. By Lemma 2.8, 
$G\cap H$ is a convex-cocompact subgroup of 
$A\times P$, so 
$G\cap P$ has finite index in 
$p_P(G\cap H)$ (e.g. by Lemma 2.4). By Lemma 3.22(3) and Remark 2.7, this index is at most 
$q$. Now, if 
$g,g'\in G\cap H$ are such that 
$p_P(g)$ and 
$p_P(g')$ are in the same coset of 
$G\cap P$, then 
$g$ and 
$g'$ are in the same coset of 
$(G\cap A)\times (G\cap P)$. It follows that 
$(G\cap A)\times (G\cap P)$ has index at most 
$q$ in 
$G\cap H$.
Now, by Lemma 3.22(3) and [Reference Bridson and HaefligerBH99, Theorem I.8.10], there exists an integer 
$N_3$ such that every 
$G$-parabolic subgroup has a generating set with at most 
$N_3$ elements. Abelian subgroups of 
$G$ have rank at most 
$\dim \mathcal {X}_{\Gamma }$. Along with the above observation, this shows that every 
$G$-semi-parabolic subgroup has a generating set with at most 
$q+\dim \mathcal {X}_{\Gamma }+N_3$ elements.
Now, consider a sequence of homomorphisms 
$\rho _i\colon Q_i\rightarrow \mathbb {R}$, where each 
$Q_i$ is 
$G$-semi-parabolic and we have 
$\ker \rho _i\lneq \ker \rho _{i+1}$ for each 
$i$. By Lemma 3.25, the group 
$Q_i\cap Q_{i+1}$ is again 
$G$-semi-parabolic and it contains 
$\ker \rho _i$. Thus, replacing 
$Q_i$ with 
$Q_i\cap Q_{i+1}$ and restricting 
$\rho _i$, we can assume that 
$Q_i\leq Q_{i+1}$. Repeating the procedure, we can ensure that the 
$Q_i$ form a chain without altering the kernels.
By Claim 1, there are at most 
$N_1$ distinct subgroups among the 
$Q_i$. So it suffices to consider the situation where all 
$Q_i$ are the same group 
$Q$. In this case, the 
$\rho _i$ descend to the abelianisation of 
$Q$, which has rank 
$\leq N_2$ by Claim 2. In conclusion, the chain of kernels has length at most 
$N_1(N_2+1)$.
3.5 $\omega$-intersections of subgroups
Let 
$\omega$ be a non-principal ultrafilter on 
$\mathbb {N}$. Given a set 
$A$ and a sequence of subsets 
$A_i\subseteq A$, we denote their 
$\omega$-intersection by
\[ \bigcap_{\omega}A_i=\{a\in A \mid a\in A_i \text{ for $\omega$-all $i$}\}=\bigcup_{\omega(J)=1}\ \bigcap_{i\in J} A_i. \]
Remark 3.37 Let 
$G$ be a group and let 
$H_i\leq G$ be a sequence of subgroups. If 
$\bigcap _{\omega }H_i$ is finitely generated, then there exists 
$J\subseteq \mathbb {N}$ with 
$\omega (J)=1$ such that 
$\bigcap _{\omega }H_i=\bigcap _{i\in J}H_i$.
Indeed, suppose that 
$\bigcap _{\omega }H_i$ is generated by elements 
$h_1,\dots,h_k$. There are subsets 
$J_s\subseteq \mathbb {N}$ with 
$\omega (J_s)=1$ such that 
$h_s\in H_i$ for all 
$i\in J_s$. Thus it suffices to take 
$J:=J_1\cap \dots \cap J_k$.
Proposition 3.38 Let 
$G\leq \mathcal {A}_{\Gamma }$ be convex-cocompact. Let 
$K_i\leq G$ be a sequence of subgroups.
(1) If all
$K_i$ are $G$-semi-parabolic, then so is $\bigcap _{\omega }K_i$.(2) If all
$K_i$ are centralisers in $G$, then so is $\bigcap _{\omega }K_i$.
Proof. We begin with part (1). Let 
$H_i\leq \mathcal {A}_{\Gamma }$ be semi-parabolic subgroups with 
$K_i=G\cap H_i$. Write 
$H_i=A_i\times P_i$ with 
$P_i$ parabolic and 
$A_i$ abelian. Since the 
$H_i$ are all full, 
$\bigcap _{\omega }H_i$ is full, hence generated by the label-irreducibles that it contains. If 
$h\in \bigcap _{\omega }H_i$ is label-irreducible, then either 
$h\in A_i$ for 
$\omega$-all 
$i$, or 
$h\in P_i$ for 
$\omega$-all 
$i$. This shows that 
$\bigcap _{\omega }H_i$ is generated by 
$\bigcap _{\omega }A_i$ and 
$\bigcap _{\omega }P_i$. The former is clearly abelian, while the latter is parabolic by the characterisation in Proposition 3.15.
We conclude that 
$\bigcap _{\omega }H_i$ is finitely generated. By Remark 3.37 and Lemma 3.25, this is a semi-parabolic subgroup of 
$\mathcal {A}_{\Gamma }$. Since 
$\bigcap _{\omega }K_i=G\cap \bigcap _{\omega }H_i$, this proves part (1).
Regarding part (2), recall that centralisers in 
$G$ are 
$G$-semi-parabolic by Remark 3.30. If the 
$K_i$ are centralisers in 
$G$, part (1) ensures that 
$\bigcap _{\omega }K_i$ is finitely generated and so we can appeal again to Remark 3.37. Intersections of centralisers are again centralisers, so this completes the proof.
4. Arc-stabilisers versus centralisers
Throughout this section, we fix the following setting.
Assumption 4.1 Let 
$G\leq \mathcal {A}_{\Gamma }$ be a 
$q$-convex-cocompact subgroup of a right-angled Artin group. We fix a 
$G$-invariant, 
$G$-essential convex subcomplex 
$Y\subseteq \mathcal {X}_{\Gamma }$ on which 
$G$ acts with 
$q$ orbits of vertices 
$\mathcal {O}_1,\dots,\mathcal {O}_q$.
Recall from the beginning of § 3.1 that 
$\mathcal {X}_{\Gamma }$ admits various trees as restriction quotients 
$\pi _v\colon \mathcal {X}_{\Gamma }\rightarrow \mathcal {T}_v$, one for every vertex 
$v\in \Gamma$. Note that 
$\pi _v(Y)\subseteq \mathcal {T}_v$ is either a single point fixed by 
$G$, or it is the unique 
$G$-minimal subtree of 
$\mathcal {T}_v$ (independently of the choice of 
$Y$).
As discussed in the introduction, we are interested in understanding limits of sequences of 
$G$-trees consisting of 
$\mathcal {T}_v$ suitably rescaled and twisted by an automorphism of 
$G$. In order to identify arc-stabilisers of the limit 
$\mathbb {R}$-tree, it is necessary to gain a good understanding of arc-(almost-)stabilisers for each of the simplicial trees in the sequence.
Arc-stabilisers of 
$G\curvearrowright \mathcal {T}_v$ are quite nice (they are 
$G$-parabolic) but this niceness will normally be lost when we twist 
$\mathcal {T}_v$ by an automorphism of 
$G$: the image of a 
$G$-parabolic subgroup under an automorphism of 
$G$ is not even convex-cocompact in general. By contrast, centralisers (as in Definition 3.12) are much better behaved subgroups of 
$G$: we know that all automorphisms of 
$G$ take centralisers to centralisers, and that centralisers are always convex-cocompact.
Luckily, arcs of 
$\mathcal {T}_v$ can be perturbed so that their 
$G$-(almost-)stabiliser becomes a centraliser in 
$G$. The proof of this result is the main aim of this section. The precise statement is Corollary 4.17, which we reproduce here as a theorem for the reader's convenience.
We emphasise that, without perturbing, it is still true that arc-stabilisers for 
$G\curvearrowright \mathcal {T}_v$ are the intersection between 
$G$ and the centraliser of a subset of 
$\mathcal {A}_{\Gamma }$ (see Remark 4.4). The point is that only centralisers of subsets of 
$G$ are well behaved with respect to automorphisms of 
$G$.
Theorem 4.2 There exists a constant 
$L$, depending on 
$q$ and 
$\Gamma$, with the following property. Every arc 
$\beta \subseteq \pi _v(Y)\subseteq \mathcal {T}_v$ with 
$\ell (\beta )>2L$ contains a sub-arc 
$\beta '\subseteq \beta$ with 
$\ell (\beta ')\geq \ell (\beta )-2L$ such that:
(1) either the stabiliser
$G_{\beta '}$ is a centraliser in $G$, i.e. $Z_GZ_G(G_{\beta '})=G_{\beta '}$;(2) or
$Z_GZ_G(G_{\beta '})=Z_G(g)$ for a label-irreducible element $g\in Z_G(G_{\beta '})$.
In the 2nd case, the element 
$g$ is loxodromic in 
$\mathcal {T}_v$ and its axis 
$\eta \subseteq \mathcal {T}_v$ satisfies 
$\ell (\eta \cap \beta ')\geq \ell (\beta ')-4q$. In addition, 
$\ell _Y(g)\leq q$ and 
$Z_G(g)$ contains 
$\langle g\rangle \times G_{\beta '}$ as a subgroup of index 
$\leq q$.
4.1 Decent pairs of hyperplanes
In this subsection, we introduce decent pairs of hyperplanes of 
$Y$. Proposition 4.6 shows that stabilisers of decent pairs are (close to) centralisers in 
$G$. In the following subsections, we will see how to reduce general pairs of hyperplanes of 
$Y$ to decent ones.
For the following discussion, it is convenient to introduce the following notation.
Definition 4.3 Given disjoint hyperplanes 
$\mathfrak {u},\mathfrak {w}\in \mathscr {W}(\mathcal {X}_{\Gamma })$, we write:
•
$\mathcal {W}(\mathfrak {u},\mathfrak {w})=\mathscr {W}(\mathfrak {u}|\mathfrak {w})\sqcup \{\mathfrak {u},\mathfrak {w}\}\subseteq \mathscr {W}(\mathcal {X}_{\Gamma })$;•
$\Delta (\mathfrak {u},\mathfrak {w})=\gamma (\mathcal {W}(\mathfrak {u},\mathfrak {w}))\subseteq \Gamma$.
Remark 4.4 Let 
$\mathfrak {u}$ and 
$\mathfrak {w}$ be disjoint hyperplanes of 
$\mathcal {X}_{\Gamma }$. If 
$\Delta =\Delta (\mathfrak {u},\mathfrak {w})$, then:
(1) the subgroup of
$\mathcal {A}_{\Gamma }$ that stabilises $\mathfrak {u}$ and $\mathfrak {w}$ is conjugate to $\mathcal {A}_{\Delta ^{\perp }}$;(2)
$\Delta$ does not split as a non-trivial join.
Recall that, if 
$\alpha \subseteq Y$ is a geodesic, 
$\mathscr {W}(\alpha )\subseteq \mathscr {W}(Y)$ is the set of hyperplanes that it crosses.
Definition 4.5
(1) A geodesic
$\alpha \subseteq Y$ is decent if, for every $v\in \gamma (\mathscr {W}(\alpha ))$, there exist an element $g_v\in G$ and a vertex $x_v\in \alpha$ such that $g_vx_v\in \alpha$ and $v\in \Gamma (g_v)$.(2) A pair of disjoint hyperplanes
$\mathfrak {u},\mathfrak {w}\in \mathscr {W}(Y)$ is decent if there exists a decent geodesic $\alpha \subseteq Y$ with $\mathscr {W}(\alpha )=\mathcal {W}(\mathfrak {u},\mathfrak {w})$.
Given a hyperplane 
$\mathfrak {w}\in \mathscr {W}(\mathcal {X}_{\Gamma })$, we denote its 
$G$-stabiliser by 
$G_{\mathfrak {w}}$.
Proposition 4.6 Let 
$\mathfrak {u},\mathfrak {w}\in \mathscr {W}(Y)$ be a decent pair of hyperplanes. Set 
$\Delta =\Delta (\mathfrak {u},\mathfrak {w})$. Then:
(1) either
$Z_GZ_G(G_{\mathfrak {u}}\cap G_{\mathfrak {w}})=G_{\mathfrak {u}}\cap G_{\mathfrak {w}}$;(2) or
$Z_GZ_G(G_{\mathfrak {u}}\cap G_{\mathfrak {w}})=Z_G(g)$ for a label-irreducible element $g\in Z_G(G_{\mathfrak {u}}\cap G_{\mathfrak {w}})$. In this case, $\Gamma (g)=\Delta$ and $g$ skewers all but at most $2q$ hyperplanes of $\mathcal {W}(\mathfrak {u},\mathfrak {w})$. In addition, $\ell _Y(g)\leq q$ and the subgroup $\langle g\rangle \times (G_{\mathfrak {u}}\cap G_{\mathfrak {w}})$ has index $\leq q$ in $Z_G(g)$.
Proof. Let 
$\alpha \subseteq Y$ be a decent geodesic with 
$\mathscr {W}(\alpha )=\mathcal {W}(\mathfrak {u},\mathfrak {w})$. Replacing 
$\alpha,\mathfrak {u},\mathfrak {w}$ with their translates by an element of 
$\mathcal {A}_{\Gamma }$ and conjugating 
$G\leq \mathcal {A}_{\Gamma }$ accordingly, we can assume that the initial vertex of 
$\alpha$ is 
$1\in \mathcal {A}_{\Gamma }$. In particular, 
$G_{\mathfrak {u}}\cap G_{\mathfrak {w}}=G\cap \mathcal {A}_{\Delta ^{\perp }}$ (see Remark 4.4).
For every 
$v\in \gamma (\mathscr {W}(\alpha ))=\Delta$, consider an element 
$g_v\in G$ and a point 
$x_v\in \alpha$ such that 
$g_vx_v\in \alpha$ and 
$v\in \Gamma (g_v)$, as in Definition 4.5.
Note that 
$\alpha \subseteq \mathcal {A}_{\Delta }\subseteq \mathcal {X}_{\Gamma }$, so both 
$x_v$ and 
$g_vx_v$ lie in 
$\mathcal {A}_{\Delta }$. It follows that 
$g_v\in \mathcal {A}_{\Delta }$, and we can write 
$g_v=a_vh_va_v^{-1}$ as a reduced word with 
$h_v$ cyclically reduced and 
$a_v,h_v\in \mathcal {A}_{\Delta }$. We further separate 
$h_v=h_v'h_v''$, where 
$h_v'$ is the label-irreducible component of 
$h_v$ with 
$v\in \Gamma (h_v')$, and 
$h_v''$ is the (possibly trivial) product of the remaining label-irreducible components of 
$h_v$. Let 
$C(h_v')$ be the maximal cyclic subgroup of 
$\mathcal {A}_{\Gamma }$ containing 
$h_v'$.
Now, since 
$G_{\mathfrak {u}}\cap G_{\mathfrak {w}}$ fixes the set 
$\mathscr {W}(\alpha )$ pointwise, Lemma 3.4 implies that 
$g_v\in Z_G(G_{\mathfrak {u}}\cap G_{\mathfrak {w}})$ for every 
$v\in \Delta$. Thus,
\begin{align*} Z_GZ_G(G_{\mathfrak{u}}\cap G_{\mathfrak{w}})&\leq\bigcap_{v\in\Delta}Z_{\mathcal{A}_{\Gamma}}(g_v)=\bigcap_{v\in\Delta} a_vZ_{\mathcal{A}_{\Gamma}}(h_v)a_v^{-1}\leq\bigcap_{v\in\Delta} a_vZ_{\mathcal{A}_{\Gamma}}(h_v')a_v^{-1} \\ &=\bigcap_{v\in\Delta}a_v(C(h_v')\times\mathcal{A}_{\Gamma(h_v')^{\perp}})a_v^{-1}=\bigcap_{v\in\Delta}a_vC(h_v')a_v^{-1}\times\bigcap_{v\in\Delta}a_v\mathcal{A}_{\Gamma(h_v')^{\perp}}a_v^{-1} \\ &\leq\bigcap_{v\in\Delta}a_vC(h_v')a_v^{-1}\times\bigcap_{v\in\Delta}a_v\mathcal{A}_{\operatorname{lk} v}a_v^{-1}. \end{align*}
Here, the second equality in the second line follows from Remark 3.11: indeed, Remark 4.4(2) guarantees that the two sides contain exactly the same label-irreducibles.
Observe that 
$\bigcap _{v\in \Delta }a_v\mathcal {A}_{\operatorname {lk} v}a_v^{-1}=\mathcal {A}_{\Delta ^{\perp }}$. Indeed, for every 
$v\in \Delta$, we have 
$\Delta ^{\perp }\subseteq \operatorname {lk} v$. Since 
$a_v$ lies in 
$\mathcal {A}_{\Delta }$, it commutes with 
$\mathcal {A}_{\Delta ^{\perp }}$. This shows that 
$\mathcal {A}_{\Delta ^{\perp }}$ is contained in 
$P:=\bigcap _{v\in \Delta }a_v\mathcal {A}_{\operatorname {lk} v}a_v^{-1}$. Observing that 
$P$ is parabolic and 
$\Gamma (P)\subseteq \bigcap _{v\in \Delta }\operatorname {lk} v=\Delta ^{\perp }$, we conclude that 
$P=\mathcal {A}_{\Delta ^{\perp }}$.
Summing up, we have shown that
\[ G\cap\mathcal{A}_{\Delta^{\perp}}=G_{\mathfrak{u}}\cap G_{\mathfrak{w}}\leq Z_GZ_G(G_{\mathfrak{u}}\cap G_{\mathfrak{w}})\leq \Big[\bigcap a_vC(h_v')a_v^{-1}\Big]\times\mathcal{A}_{\Delta^{\perp}}. \]
If 
$Z_GZ_G(G_{\mathfrak {u}}\cap G_{\mathfrak {w}})$ is contained in 
$\mathcal {A}_{\Delta ^{\perp }}$, then 
$G_{\mathfrak {u}}\cap G_{\mathfrak {w}}=Z_GZ_G(G_{\mathfrak {u}}\cap G_{\mathfrak {w}})$, and we are in the first case of the proposition.
Otherwise, 
$Z_GZ_G(G_{\mathfrak {u}}\cap G_{\mathfrak {w}})$ intersects 
$\bigcap a_vC(h_v')a_v^{-1}$ by Remark 3.7(6) (recall that centralisers are convex-cocompact). Let 
$h\in \mathcal {A}_{\Gamma }$ be an element with 
$\langle h\rangle =\bigcap a_vC(h_v')a_v^{-1}$, and let 
$g$ be the smallest power of 
$h$ that lies in 
$G$.
It is clear that 
$g$ is label-irreducible and commutes with 
$G_{\mathfrak {u}}\cap G_{\mathfrak {w}}\leq \mathcal {A}_{\Delta ^{\perp }}$. Since 
$v\in \Gamma (h_v')\subseteq \Delta$ for every 
$v\in \Delta$, we must have 
$\Gamma (g)=\Delta$. Remark 3.7(5) shows that 
$Z_G(g)=G\cap (\langle h\rangle \times \mathcal {A}_{\Delta ^{\perp }})$. Since 
$Z_GZ_G(G_{\mathfrak {u}}\cap G_{\mathfrak {w}})$ is convex-cocompact and closed under taking roots in 
$G$, we conclude that
\begin{align*} Z_G(g)=Z_GZ_G(G_{\mathfrak{u}}\cap G_{\mathfrak{w}}). \end{align*}
It remains to prove the additional statements in the second case of the proposition.
Since 
$g$ lies in 
$Z_GZ_G(G_{\mathfrak {u}}\cap G_{\mathfrak {w}})$, it commutes with every element of the set
\[ A=\{k\in G \mid \exists x\in\alpha, \text{ s.t.}\ kx\in\alpha\}\subseteq Z_G(G_{\mathfrak{u}}\cap G_{\mathfrak{w}}). \]
In addition, for every 
$k\in A$, we have 
$\Gamma (k)\subseteq \gamma (\mathscr {W}(\alpha ))=\Delta =\Gamma (g)$. Thus, since 
$g$ is label-irreducible, Remark 3.7(4) applied to the label-irreducible components of 
$k$ shows that all 
$k\in A$ satisfy 
$\langle g,k\rangle \simeq \mathbb {Z}$. Since 
$g$ is the smallest power of 
$h$ that lies in 
$G$, we conclude that 
$A\subseteq \langle g\rangle$.
If 
$\mathcal {O}$ is a 
$G$-orbit with 
$\#(\mathcal {O}\cap \alpha )\geq 3$, then, since 
$A\subseteq \langle g\rangle$, there exists an axis of 
$g$ containing 
$\mathcal {O}\cap \alpha$. Let 
$\alpha _0\subseteq \alpha$ be the smallest subsegment that contains all intersections 
$\mathcal {O}_i\cap \alpha$, where 
$\mathcal {O}_i$ varies among 
$G$-orbits with 
$\#(\mathcal {O}_i\cap \alpha )\geq 3$. Since the union of all axes of 
$g$ forms a convex subcomplex 
$\mathrm {Min}(g)\subseteq \mathcal {X}_{\Gamma }$, we have 
$\alpha _0\subseteq \mathrm {Min}(g)$. Since 
$\Gamma (g)=\gamma (\mathscr {W}(\alpha ))$, the geodesic 
$\alpha _0$ cannot cross any hyperplanes separating distinct axes of 
$g$ (whose label would lie in 
$\Gamma (g)^{\perp }$). Hence 
$\alpha _0$ is contained in the convex hull of a single axis of 
$g$, and every hyperplane crossed by 
$\alpha _0$ is skewered by 
$g$.
At most 
$2q$ vertices of 
$\alpha$ (and, therefore, at most 
$2q$ edges) can lie outside 
$\alpha _0$. It follows that 
$g$ skewers all but at most 
$2q$ hyperplanes in 
$\mathscr {W}(\alpha )=\mathcal {W}(\mathfrak {u},\mathfrak {w})$.
Finally, note that 
$A$ contains an element 
$k$ with 
$\ell _Y(k)\leq q$ (for instance, consider 
$q+1$ consecutive vertices on 
$\alpha$). This implies that 
$\ell _Y(g)\leq q$. Recall that
\[ \langle g\rangle\times(G_{\mathfrak{u}}\cap G_{\mathfrak{w}})\leq Z_G(g) =G\cap\big[\langle h\rangle\times\mathcal{A}_{\Delta^{\perp}}\big]. \]
Since 
$\ell _Y(g)\leq q$, we must have 
$g=h^n$ with 
$n\leq q$. Recalling that 
$G_{\mathfrak {u}}\cap G_{\mathfrak {w}}=G\cap \mathcal {A}_{\Delta ^{\perp }}$, this shows that 
$\langle g\rangle \times (G_{\mathfrak {u}}\cap G_{\mathfrak {w}})$ has index 
$\leq q$ in 
$G\cap [\langle h\rangle \times \mathcal {A}_{\Delta ^{\perp }}]$.
This completes the proof of the proposition.
4.2 Decomposing geodesics in $Y$
In this subsection, we describe a procedure to decompose geodesics 
$\alpha \subseteq Y$ into a controlled number of better-behaved subsegments. The end result to keep in mind is Corollary 4.13.
It is convenient to introduce the following (admittedly a bit heavy) terminology and notation. Luckily, this will not be required outside of this subsection.
Definition 4.7 Consider a geodesic 
$\alpha \subseteq Y$.
(1) We denote by
$0\leq o(\alpha )\leq q$ the number of orbits $\mathcal {O}_i$ with $\alpha \cap \mathcal {O}_i\neq \emptyset$.(2) For
$v\in \Gamma$ and $1\leq i\leq q$, look at the words (in the standard generators of $\mathcal {A}_{\Gamma }$ and their inverses) spelled by the subsegments of $\alpha$ between consecutive points of $\alpha \cap \mathcal {O}_i$. We denote by $\rho _{i,v}(\alpha )\geq 0$ the number of such segments spelling words containing the letters $v^{\pm }$.(3) Define
$n(\alpha ):=\sum _i \#\{v\in \Gamma \mid \rho _{i,v}(\alpha )\neq 0\}$.
Definition 4.8 Consider a geodesic 
$\alpha \subseteq Y$.
(1) We say that
$\alpha$ is almost $i$-excellent if the endpoints of $\alpha$ lie in the same $\mathcal {O}_i$ and $\#(\alpha \cap \mathcal {O}_i)\geq 3$. The geodesic $\alpha$ is $i$-excellent if, in addition, $\rho _{i,v}(\alpha )\neq 1$ for every $v\in \Gamma$. We simply speak of (almost) excellent geodesics when they are (almost) $i$-excellent for some $i$.(2) The geodesic
$\alpha$ is almost good if it is a union of almost excellent subsegments (possibly with large overlaps). Similarly, $\alpha$ is good if $\alpha$ is a union of excellent subsegments.
The following is the reason why we care about these properties.
Lemma 4.9 Good geodesics are decent.
Proof. Since good geodesics are unions of excellent subsegments, it is enough to show that excellent geodesics are decent. So, consider an excellent geodesic 
$\alpha \subseteq Y$ and 
$v\in \gamma (\mathscr {W}(\alpha ))$.
Let 
$\mathcal {O}$ be the 
$G$-orbit that contains the endpoints of 
$\alpha$. Then we can write the points of 
$\alpha \cap \mathcal {O}$, in the order in which they appear along 
$\alpha$, as
\[ x,\ g_1x,\ g_1g_2x,\ \ldots,\ g_1g_2\dots g_kx, \]
with all 
$g_i\in G$. Setting 
$a_i=x^{-1}g_ix\in \mathcal {A}_{\Gamma }$, the points 
$1,a_1,a_1a_2,\ldots,a_1a_2\dots a_k$ lie on the geodesic 
$x^{-1}\alpha \subseteq \mathcal {X}_{\Gamma }$. Note that 
$v\in \gamma (\mathscr {W}(\alpha ))=\gamma (\mathscr {W}(x^{-1}\alpha ))$, so 
$v\in \gamma (\mathscr {W}(1|a_i))$ for some 
$i$.
Since 
$\alpha$ is excellent, there exists 
$j\neq i$ such that 
$v\in \gamma (\mathscr {W}(1|a_j))$. Without loss of generality, we have 
$i< j\leq k$. Lemma 3.3 guarantees that
\[ v\in \Gamma(a_1\dots a_i)\cup\Gamma(a_1\dots a_j)\cup\Gamma(a_{i+1}\dots a_j). \]
If 
$v\in \Gamma (a_1\dots a_i)=\Gamma (g_1\dots g_i)$, we can take 
$g_v=g_1\dots g_i$ and 
$x_v=x$. If instead 
$v\in \Gamma (a_{i+1}\dots a_j)=\Gamma (g_{i+1}\dots g_j)$, we set 
$x_v=g_1\dots g_ix$ and 
$g_v=(g_1\dots g_i)(g_{i+1}\dots g_j)(g_1\dots g_i)^{-1}$.
In the rest of the subsection, we describe how to decompose general geodesics into good subsegments. To be precise, we say that 
$\alpha \subseteq Y$ is decomposed into subsegments 
$\mu _1,\dots,\mu _r$ if 
$\alpha =\mu _1\cup \dots \cup \mu _r$ and 
$\mu _i\cap \mu _j$ is non-empty if and only if 
$|i-j|=1$, in which case 
$\mu _i\cap \mu _j$ is a single vertex.
Lemma 4.10 If 
$\alpha \subseteq Y$ is not almost good, then 
$\alpha$ can be decomposed into at most 
$\max \{7,2o(\alpha )\}$ subsegments 
$\mu _j$ such that each satisfies one of the following:
•
$\mu _j$ is a single edge;•
$o(\mu _j)< o(\alpha )$.
Proof. Set for simplicity 
$k=o(\alpha )$ and order the orbits so that 
$\mathcal {O}_1,\dots,\mathcal {O}_k$ are precisely those that intersect 
$\alpha$ non-trivially.
First, suppose that 
$\#(\alpha \cap \mathcal {O}_i)\leq 2$ for some 
$i\leq k$. Then we can decompose 
$\alpha$ into the 
$\leq 4$ edges that intersect 
$\alpha \cap \mathcal {O}_i$, plus the remaining 
$\leq 3$ subsegments of 
$\alpha$. Each of the latter intersects 
$\leq k-1$ orbits. In this case, we have decomposed 
$\alpha$ into 
$\leq 7$ subsegments with the required properties.
Thus, we can assume that 
$\#(\alpha \cap \mathcal {O}_i)\geq 3$ for all 
$i\leq k$. Let 
$\alpha _i\subseteq \alpha$ be the subsegment between the first and last points of 
$\alpha \cap \mathcal {O}_i$. Note that 
$\alpha _i$ is almost 
$i$-excellent.
Let 
$\alpha '\subseteq \alpha$ be the union of all 
$\alpha _i$. If 
$\alpha '$ were connected, then we would have 
$\alpha =\alpha '$ and 
$\alpha$ would be almost good. Thus, 
$\alpha '$ has between two and 
$k$ connected components, with consecutive ones separated by a single open edge. Each component intersects 
$\leq k-1$ orbits. Then it suffices to decompose 
$\alpha$ into these components plus the remaining edges. These are 
$\leq 2k-1$ subsegments with the required properties.
Lemma 4.11 If 
$\alpha \subseteq Y$ is not good, then 
$\alpha$ can be decomposed into at most 
$\max \{7,2o(\alpha )\}$ subsegments 
$\mu _j$ such that each satisfies one of the following:
•
$\mu _j$ is a single edge;•
$o(\mu _j)< o(\alpha )$;•
$o(\mu _j)=o(\alpha )$ and $n(\mu _j)< n(\alpha )$.
Proof. Set again 
$k=o(\alpha )$ and let 
$\mathcal {O}_1,\dots,\mathcal {O}_k$ be the orbits that intersect 
$\alpha$ in at least three vertices. Let 
$\alpha _i\subseteq \alpha$ be the subsegment between the first and last points of 
$\alpha \cap \mathcal {O}_i$.
If 
$\alpha$ is not almost good, we simply apply Lemma 4.10. Suppose instead that 
$\alpha$ is almost good, so that 
$\alpha =\bigcup _i\alpha _i$. Since 
$\alpha$ is not good, one of the 
$\alpha _i$ is not excellent, hence there exist 
$1\leq j\leq q$ and 
$w\in \Gamma$ such that 
$\rho _{j,w}(\alpha _j)=1$.
Let 
$I\subseteq \alpha _j$ be the only subsegment between consecutive points of 
$\alpha _j\cap \mathcal {O}_j$ in which 
$w$ appears. If 
$I$ is a single edge, we decompose 
$\alpha$ as the union of 
$I$ and two segments 
$\alpha ^{\pm }$ . Otherwise, let 
$p$ be a vertex in the interior of 
$I$ and define 
$\alpha ^{\pm }\subseteq \alpha$ as the two subsegments meeting at 
$p$. Observe that 
$\rho _{i,v}(\alpha ^{\pm })\leq \rho _{i,v}(\alpha )$ for all 
$i$ and 
$v$, and 
$0=\rho _{j,w}(\alpha ^{\pm })<\rho _{j,w}(\alpha )=1$. Thus 
$n(\alpha ^{\pm })< n(\alpha )$.
Lemma 4.12 Every geodesic 
$\alpha \subseteq Y$ can be decomposed into at most 
$q\cdot (\max \{7,2o(\alpha )\})^{n(\alpha )}$ subsegments 
$\mu _j$ such that each satisfies one of the following:
•
$\mu _j$ is a single edge;•
$o(\mu _j)< o(\alpha )$;•
$\mu _j$ is good.
Proof. This follows from Lemma 4.11 proceeding by induction on 
$n(\alpha )$. Note that a geodesic 
$\mu$ with 
$n(\mu )=0$ meets each 
$\mathcal {O}_i$ at most once and thus contains at most 
$q-1$ edges.
Corollary 4.13 Setting 
$V:=\#\Gamma ^{(0)}$, every geodesic 
$\alpha \subseteq Y$ can be decomposed into at most 
$q^q\cdot (\max \{7,2q\})^{q^2V}$ subsegments 
$\mu _j$ such that each satisfies one of the following:
•
$\mu _j$ is a single edge;•
$\mu _j$ is decent (in fact, good).
4.3 Decomposing chains of hyperplanes
Let for simplicity 
$N_q=q^q\cdot (\max \{7,2q\})^{q^2V}$ be the constant in Corollary 4.13. We say that hyperplanes 
$\mathfrak {v}_1,\dots,\mathfrak {v}_k$ form a chain if, for each 
$i$, we can pick a halfspace 
$\mathfrak {h}_i$ bounded by 
$\mathfrak {v}_i$ so that 
$\mathfrak {h}_1\subsetneq \dots \subsetneq \mathfrak {h}_k$.
Recall Definition 4.3. It is convenient to introduce the following additional notation for a pair of disjoint hyperplanes 
$\mathfrak {u},\mathfrak {w}$ of 
$\mathcal {X}_{\Gamma }$:
•
$\delta (\mathfrak {u},\mathfrak {w})=\#\Delta (\mathfrak {u},\mathfrak {w})\in \mathbb {N}$;•
$d_v(\mathfrak {u},\mathfrak {w})=\#(\gamma ^{-1}(v)\cap \mathscr {W}(\mathfrak {u}|\mathfrak {w}))\in \mathbb {N}$, where $v\in \Gamma ^{(0)}$.
Recall that, for every vertex 
$v\in \Gamma$, we have a restriction quotient 
$\pi _v\colon \mathcal {X}_{\Gamma }\rightarrow \mathcal {T}_v$. The next lemma is saying that every geodesic in 
$\mathcal {T}_v$ can be decomposed into a bounded number of subpaths, which are alternately short and lower-complexity.
Lemma 4.14 Let 
$\mathfrak {u},\mathfrak {w}\in \mathscr {W}(Y)$ be distinct hyperplanes with 
$\gamma (\mathfrak {u})=\gamma (\mathfrak {w})=v$. Suppose that 
$\mathfrak {u},\mathfrak {w}$ are not a decent pair. Then there exists a chain of hyperplanes 
$\mathfrak {v}_0=\mathfrak {u},\mathfrak {v}_1,\dots,\mathfrak {v}_{2s+1}=\mathfrak {w}$, where:
•
$\gamma (\mathfrak {v}_i)=v$ for $0\leq i\leq 2s+1$;•
$\delta (\mathfrak {v}_{2j-1},\mathfrak {v}_{2j})<\delta (\mathfrak {u},\mathfrak {w})$ for $1\leq j\leq s$;•
$d_v(\mathfrak {v}_{2j},\mathfrak {v}_{2j+1})\leq N_q$ for $0\leq j\leq s$;•
$s\leq N_q$.
Proof. Let 
$\alpha \subseteq Y$ be a geodesic with 
$\mathscr {W}(\alpha )=\mathcal {W}(\mathfrak {u},\mathfrak {w})$. Since 
$\mathfrak {u},\mathfrak {w}$ are not a decent pair, 
$\alpha$ is not decent. By Corollary 4.13, we can decompose 
$\alpha$ into at most 
$N_q$ subsegments, each being either decent or a single edge. Among these, call 
$\mu _1,\dots,\mu _s$ the decent subsegments that cross at least two hyperplanes labelled by 
$v$, in the order in which they appear along 
$\alpha$. Note that we must have 
$\gamma (\mathscr {W}(\mu _j))\subsetneq \gamma (\mathscr {W}(\alpha ))$, otherwise 
$\alpha$ would be decent.
Define 
$\mathfrak {v}_{2j-1}$ (respectively 
$\mathfrak {v}_{2j}$) as the first (respectively last) hyperplane labelled by 
$v$ that is crossed by 
$\mu _j$. By the previous paragraph,
\[ \delta(\mathfrak{v}_{2j-1},\mathfrak{v}_{2j})\leq\#\gamma(\mathscr{W}(\mu_j))<\#\gamma(\mathscr{W}(\alpha))=\delta(\mathfrak{u},\mathfrak{w}). \]
Note that 
$\mu _j$ and 
$\mu _{j+1}$ are separated by 
$\leq N_q$ subsegments of 
$\alpha$, each crossing at most one hyperplane labelled by 
$v$. This shows that 
$d_v(\mathfrak {v}_{2j},\mathfrak {v}_{2j+1})\leq N_q$, concluding the proof.
Corollary 4.15 Let 
$\mathfrak {u},\mathfrak {w}\in \mathscr {W}(Y)$ be distinct hyperplanes with 
$\gamma (\mathfrak {u})=\gamma (\mathfrak {w})=v$. Set 
$V=\#\Gamma ^{(0)}$. Then there exists a chain of hyperplanes 
$\mathfrak {v}_0=\mathfrak {u},\mathfrak {v}_1,\dots,\mathfrak {v}_{2s+1}=\mathfrak {w}$, where
•
$\gamma (\mathfrak {v}_i)=v$ for $0\leq i\leq 2s+1$;•
$\mathfrak {v}_{2j-1}$ and $\mathfrak {v}_{2j}$ form a decent pair for $1\leq j\leq s$;•
$d_v(\mathfrak {v}_{2j},\mathfrak {v}_{2j+1})\leq 2N_qV$ for $0\leq j\leq s$;•
$s\leq N_q^V$.
Proof. This follows from Lemma 4.14 by induction on 
$1\leq \delta (\mathfrak {u},\mathfrak {w})\leq V$.
Corollary 4.15 immediately implies the following.
Corollary 4.16 There exists a constant 
$L$, depending only on 
$q$ and 
$\Gamma$, such that the following holds. Every arc 
$\beta \subseteq \pi _v(Y)\subseteq \mathcal {T}_v$ can be decomposed as a sequence of arcs 
$\mu _0\nu _1\mu _1\dots \nu _s\mu _s$ such that consecutive arcs share exactly one vertex and:
• the first and last edge of each arc
$\nu _i$ correspond to a decent pair of hyperplanes of $Y$;•
$\ell (\mu _i)\leq L$ and $\ell (\nu _i)>2q$ for every $i$;•
$s\leq L$.
Adding Proposition 4.6 to the above corollary, we obtain the desired result.
Corollary 4.17 Let 
$L$ be the constant in Corollary 4.16. Every arc 
$\beta \subseteq \pi _v(Y)\subseteq \mathcal {T}_v$ with 
$\ell (\beta )>2L$ contains a sub-arc 
$\beta '\subseteq \beta$ with 
$\ell (\beta ')\geq \ell (\beta )-2L$ such that:
(1) either
$G_{\beta '}$ is a centraliser, i.e. $Z_GZ_G(G_{\beta '})=G_{\beta '}$;(2) or
$Z_GZ_G(G_{\beta '})=Z_G(g)$ for a label-irreducible element $g\in Z_G(G_{\beta '})$. The element $g$ is loxodromic in $\mathcal {T}_v$ and its axis $\eta \subseteq \mathcal {T}_v$ satisfies $\ell (\eta \cap \beta ')\geq \ell (\beta ')-4q$. In addition, $\ell _Y(g)\leq q$, and the subgroup $\langle g\rangle \times G_{\beta '}$ has index $\leq q$ in $Z_G(g)$.
Proof. Decompose 
$\beta =\mu _0\nu _1\mu _1\dots \nu _s\mu _s$ as in Corollary 4.16. Define 
$\beta '$ as the sub-arc obtained by removing 
$\mu _0$ and 
$\mu _s$. It is clear that 
$\ell (\beta ')\geq \ell (\beta )-2L$.
Proposition 4.6 shows that, for 
$i\in \{1,s\}$, one of the following two cases occurs:
(1) either
$Z_GZ_G(G_{\nu _i})=G_{\nu _i}$;(2) or
$Z_GZ_G(G_{\nu _i})=Z_G(g_i)$ for a label-irreducible element $g_i\in Z_G(G_{\nu _i})$.The element $g_i$ is loxodromic in $\mathcal {T}_v$ with axis $\eta _i$ satisfying $\ell (\eta _i\cap \nu _i)\geq \ell (\nu _i)-2q>0$. In addition, $\ell _Y(g_i)\leq q$ and the subgroup $\langle g_i\rangle \times G_{\nu _i}$ has index $\leq q$ in $Z_G(g_i)$.
Based on this, there are three possibilities for 
$G_{\beta '}=G_{\nu _1}\cap G_{\nu _s}$.
(a) Both
$i=1$ and $i=s$ are of type (1). Then $G_{\beta '}=Z_G\big (Z_G(G_{\nu _1})\cup Z_G(G_{\nu _s})\big )$ is a centraliser.(b) Only one of them is of type (1). Without loss of generality,
where\[ Z_GZ_G(G_{\nu_1})=Z_G(g_1)=G\cap\big[\langle h_1\rangle\times P_1\big], \quad Z_GZ_G(G_{\nu_s})=G_{\nu_s}=G\cap P_s, \]
$P_1,P_s\leq \mathcal {A}_{\Gamma }$ are parabolic, $\langle h_1\rangle$ is the maximal cyclic subgroup of $\mathcal {A}_{\Gamma }$ containing $g_1$, and $G_{\nu _1}=G\cap P_1$. Since $g_1$ is loxodromic in $\mathcal {T}_v$, it does not lie in $G_{\nu _s}$, hence $h_1\not \in P_s$. It follows from Remark 3.11 that $\left [\langle h_1\rangle \times P_1\right ]\cap P_s=P_1\cap P_s$.
This shows that
$Z_G(g_1)\cap Z_GZ_G(G_{\nu _s})=G\cap P_1\cap P_s=G_{\nu _1}\cap G_{\nu _s}$, so $G_{\beta '}$ is again a centraliser.(c) Both
$i=1$ and $i=s$ are of type (2). Write again
As in case (b), we have\[ Z_GZ_G(G_{\nu_1})=Z_G(g_1)=G\cap\big[\langle h_1\rangle\times P_1\big], \quad Z_GZ_G(G_{\nu_s})=Z_G(g_s)=G\cap\big[\langle h_s\rangle\times P_s\big]. \]
$Z_G(g_1)\cap Z_G(g_s)=G\cap P_1\cap P_s=G_{\nu _1}\cap G_{\nu _s}$, except when $\langle h_1\rangle =\langle h_s\rangle$.
In this case, we can assume that
$g_1=g_s$ and simply call this element $g$. Note that $P_1=P_s$ and $G\cap P_i=G_{\nu _i}$. In particular, $G_{\beta '}=G_{\nu _1}=G_{\nu _s}$, hence $Z_GZ_G(G_{\beta '})=Z_G(g)$.Finally, if
$\eta \subseteq \mathcal {T}_v$ is the axis of $g$, we have seen that $\eta$ must intersect both $\nu _1$ and $\nu _s$ and that, in both cases, $\ell (\eta \cap \nu _i)\geq \ell (\nu _i)-2q$. This implies that $\ell (\eta \cap \beta ')\geq \ell (\beta ')-4q$.
This completes the proof.
4.4 Rotating actions
In this subsection, we record a consequence of Corollary 4.16 that will be needed in the proof of Proposition 6.17.
Definition 4.18 Consider a group 
$H$ and an action on a tree 
$H\curvearrowright T$.
(1) We denote by
$\mathfrak {T}(H,T)\subseteq T$ the subtree $\operatorname {Fix}(H,T)$ if this is non-empty, and the $H$-minimal subtree otherwise.(2) We say that the action
$H\curvearrowright T$ is $c$-rotating, for some $c\geq 0$, if no element of $H\setminus \{1\}$ fixes an arc $\beta \subseteq T$ that is disjoint from $\mathfrak {T}(H,T)$ and of length $>c$.
Recall that we are fixing a convex-cocompact subgroup 
$G\leq \mathcal {A}_{\Gamma }$.
Lemma 4.19 There exists a constant 
$c=c(G)$ such that the following holds. Consider 
$v\in \Gamma$ and a 
$G$-parabolic subgroup 
$P\leq G$ that is not elliptic in 
$\mathcal {T}_v$. Then, for every free factor 
$P_0\leq P$, the action 
$P_0\curvearrowright \mathfrak {T}(P,\mathcal {T}_v)$ is 
$c$-rotating.
Proof. By Corollary 3.21, there are only finitely many 
$G$-conjugacy classes of 
$G$-parabolic subgroups and they are all convex-cocompact in 
$\mathcal {A}_{\Gamma }$. Thus, it suffices to prove the lemma with 
$P=G$.
Let 
$L$ be the constant provided by Corollary 4.16. If 
$\beta \subseteq \mathfrak {T}(G,\mathcal {T}_v)$ is an arc with 
$\ell (\beta )>L$, then it contains edges 
$e,e'$ corresponding to a decent pair of hyperplanes 
$\mathfrak {w},\mathfrak {w}'\in \mathscr {W}(Y)$. This means that there exist an element 
$g_0\in G$ such that 
$v\in \Gamma (g_0)$, and a point 
$x\in Y$ such that 
$\mathscr {W}(x|g_0x)\subseteq \mathcal {W}(\mathfrak {w},\mathfrak {w}')$. By Lemma 3.4, this implies that 
$g_0$ commutes with the stabiliser 
$G_{\beta }\leq G$. Also note that 
$g_0$ is loxodromic in 
$\mathcal {T}_v$ and its axis shares at least one edge with 
$\beta$.
Now, consider a free factor 
$G_0\leq G$. If an element of 
$G_0\setminus \{1\}$ fixes 
$\beta$, then 
$g_0$ commutes with it and so we must have 
$g_0\in G_0$. Thus, the axis of 
$g_0$ is contained in 
$\mathfrak {T}(G_0,\mathcal {T}_v)$ and 
$\beta$ must share a non-trivial arc with 
$\mathfrak {T}(G_0,\mathcal {T}_v)$. This shows that the action 
$G_0\curvearrowright \mathfrak {T}(G,\mathcal {T}_v)$ is 
$L$-rotating.
Corollary 4.20 Let 
$c$ be as in Lemma 4.19. Let 
$H\leq G$ be a convex-cocompact subgroup. Consider 
$v\in \Gamma$ such that 
$H$ is elliptic in 
$\mathcal {T}_v$, but 
$N_G(H)$ is not. Then the action 
$N_G(H)\curvearrowright \mathfrak {T}(N_G(H),\mathcal {T}_v)$ factors through an action of 
$N_G(H)/H$ and, for every free factor 
$N_0\leq N_G(H)/H$, the action 
$N_0\curvearrowright \mathfrak {T}(N_G(H),\mathcal {T}_v)$ is 
$c$-rotating.
Proof. Since 
$H$ is elliptic, 
$\operatorname {Fix}(H,\mathcal {T}_v)$ is non-empty and 
$N_G(H)$-invariant, hence it must contain the 
$N_G(H)$-minimal subtree. Thus, the action 
$N_G(H)\curvearrowright \mathfrak {T}(N_G(H),\mathcal {T}_v)$ factors through 
$N_G(H)/H$.
By Lemma 3.22(1), 
$N_G(H)$ has a finite-index subgroup of the form 
$H\times P$, where 
$P$ is 
$G$-parabolic. Thus, 
$P$ projects injectively to a finite-index subgroup 
$\overline P\leq N_G(H)/H$. Note that
\begin{align*} \mathfrak{T}(N_G(H),\mathcal{T}_v)=\mathfrak{T}(H\times P,\mathcal{T}_v)=\mathfrak{T}(P,\mathcal{T}_v). \end{align*}
Let 
$N_0\leq N_G(H)/H$ be a free factor. Then 
$N_0\cap \overline P$ is a free factor of 
$\overline P$ and Lemma 4.19 shows that the action 
$N_0\cap \overline P\curvearrowright \mathfrak {T}(N_G(H),\mathcal {T}_v)$ is 
$c$-rotating.
Since 
$N_0\cap \overline P$ has finite index in 
$N_0$, we have 
$\mathfrak {T}(N_0,\mathcal {T}_v)=\mathfrak {T}(N_0\cap \overline P,\mathcal {T}_v)$. If 
$N_0$ is not elliptic, this is clear. If 
$N_0$ is elliptic, this is because edge-stabilisers of 
$\mathcal {T}_v$ are closed under taking roots.
Thus, if 
$\beta \subseteq \mathfrak {T}(N_G(H),\mathcal {T}_v)$ is an arc of length 
$>c$ disjoint from 
$\mathfrak {T}(N_0,\mathcal {T}_v)$, its 
$(N_0\cap \overline P)$-stabiliser is trivial, hence its 
$N_0$-stabiliser is finite. Again, since edge-stabilisers of 
$\mathcal {T}_v$ are closed under taking roots, this implies that the 
$N_0$-stabiliser of 
$\beta$ is trivial, showing that the action 
$N_0\curvearrowright \mathfrak {T}(N_G(H),\mathcal {T}_v)$ is 
$c$-rotating.
5. Passing to the limit
This section is devoted to studying the limit 
$\mathbb {R}$-tree for a sequence 
$G\curvearrowright \mathcal {T}_v^{\phi _n}$, where 
$G\leq \mathcal {A}_{\Gamma }$ is a convex-cocompact subgroup, 
$v\in \Gamma$, and 
$\phi _n\in \operatorname {Out}(G)$. This is carried out in § 5.4; in particular, see Propositions 5.12, 5.13 and 5.15.
Before that, in §§ 5.1 and 5.2, we consider a more general setting: 
$G$ is an arbitrary group and we study limits of ‘tame’ actions on simplicial trees (Definition 5.4).
5.1 Almost-stabilisers
Let 
$G$ be a group with an action 
$G\curvearrowright T$ on an 
$\mathbb {R}$-tree.
Definition 5.1 Consider an arc 
$\beta \subseteq T$ with endpoints 
$p,q$.
• For
$0\leq s<\ell (\beta )/2$, we define
We also consider the subgroup\[ D(\beta,s)=\{g\in G\mid \max\{d(p,gp),d(q,gq)\}\leq s\}. \]
$\mathfrak {D}(\beta,s):=\langle D(\beta,s)\rangle \leq G$. We write $D_G(\beta,s)$ and $\mathfrak {D}_G(\beta,s)$ when it is necessary to specify the group under consideration.• For
$0\leq t\leq \ell (\beta )$, we denote by $\beta [t]\subseteq \beta$ the middle sub-arc of length $t$. We also set $\beta ^t:=\beta [\ell (\beta )-t]$; this is the closed sub-arc obtained by removing the initial and terminal segments of length $t/2$.
If 
$\beta \subseteq T$ is an arc, recall that 
$G_{\beta }\leq G$ denotes its stabiliser.
Lemma 5.2 Given an arc 
$\beta \subseteq T$ and 
$0\leq s<\ell (\beta )/2$, the following hold.
(1) For every
$g\in D(\beta,s)$, we have $\beta ^s\subseteq \mathrm {Min}(g,T)$.(2) Either
$D(\beta,s)$ contains a loxodromic, or $D(\beta,s)=G_{\beta ^s}$.
Proof. We first prove part (1). Let 
$x,y$ be the endpoints of 
$\beta$. For every 
$g\in G$, the midpoints of the arcs 
$[x,gx]$ and 
$[y,gy]$ lie in 
$\mathrm {Min}(g)$. If 
$s<\ell (\beta )/2$ and 
$g\in D(\beta,s)$, these two arcs are separated by the midpoint of 
$\beta$, and so are their midpoints. Since 
$\mathrm {Min}(g)$ is convex, it must contain the midpoint of 
$\beta$. Hence 
$\mathrm {Min}(g)\cap \beta$ is a sub-arc of 
$\beta$. Observing that 
$d(x,gx)\geq 2d(x,\mathrm {Min}(g))$, we deduce that 
$x$ and 
$y$ are at distance 
$\leq s/2$ from 
$\mathrm {Min}(g)$. Hence 
$\beta ^s\subseteq \mathrm {Min}(g)$.
Regarding part (2), suppose that every element of 
$D(\beta,s)$ is elliptic. Then part (1) shows that 
$D(\beta,s)\leq G_{\beta ^s}$. The reverse inclusion is clear.
Remark 5.3 Consider points 
$x,y\in T$ and 
$g\in G$. Since the metric of 
$T$ is convex, we have 
$d(z,gz)\leq \max \{d(x,gx),d(y,gy)\}$ for every 
$z\in [x,y]$.
In particular, given 
$\delta >0$, an arc 
$\beta \subseteq T$ and 
$0< t_1\leq t_2\leq \ell (\beta )$, we have 
$D(\beta [t_2],\delta )\subseteq D(\beta [t_1],\delta )$ and 
$\mathfrak {D}(\beta [t_2],\delta )\leq \mathfrak {D}(\beta [t_1],\delta )$.
5.2 Tame actions
This subsection introduces the notion of tame action on a tree. For sequences of tame actions, Proposition 5.6 allows us to understand arc-stabilisers of the limit in terms of those of the converging actions. In the next subsection, Corollary 5.9 shows that tameness is satisfied by convex-cocompact subgroups of right-angled Artin groups acting on the simplicial trees 
$\mathcal {T}_v$.
Let 
$G$ be any group.
Definition 5.4 An action on an 
$\mathbb {R}$-tree 
$G\curvearrowright T$ is 
$(\epsilon,N)$-tame, for some 
$0<\epsilon <1/2$ and 
$N\geq 1$, if the following conditions are satisfied. Let 
$\mathcal {S}$ be the collection of subgroups of 
$G$ of the form 
$\mathfrak {D}(\beta,\delta )$, where 
$\beta \subseteq T$ varies among non-trivial arcs and 
$\delta$ varies in the closed interval 
$[0,\epsilon \cdot \ell (\beta )]$.
(1) Every chain in
$\mathcal {S}$ has length $\leq N$.(2) For every
$0\leq \delta \leq \epsilon \cdot \ell (\beta )$ and every non-trivial arc $\beta \subseteq T$:
• either
$\mathfrak {D}(\beta,\delta )=D(\beta,\delta )=G_{\beta ^{\delta }}$;• or
$D(\beta,\delta )$ contains a loxodromic whose axis is $\mathfrak {D}(\beta,\delta )$-invariant.
$\mathfrak {D}(\beta,\delta )$ being elliptic and non-elliptic, respectively.(3) If
$H_1,H_2\in \mathcal {S}$ and $H_1\lneq H_2$, then $H_1$ is elliptic.
Definition 5.5 Let 
$T$ be an 
$\mathbb {R}$-tree. We identify arcs in 
$T$ with points in 
$T\times T$ by taking endpoints.
(1) A collection of arcs
$\mathcal {P}\subseteq T\times T$ is $\delta$-dense for some $\delta >0$ if, for every $x,y\in T$ satisfying $d(x,y)>2\delta$, there exists $(x',y')\in \mathcal {P}$ with $[x',y']\subseteq [x,y]$ and $\max \{d(x,x'),d(y,y')\}\leq \delta$.(2) Let
$T_n$ be a sequence of $\mathbb {R}$-trees. A sequence of collections of arcs $\mathcal {P}_n\subseteq T_n\times T_n$ is eventually dense if there exist $\delta _n>0$ such that each $\mathcal {P}_n$ is $\delta _n$-dense and $\delta _n\rightarrow 0$.
Fix a non-principal ultrafilter 
$\omega$ on 
$\mathbb {N}$ and recall the terminology from § 2.5.
Proposition 5.6 Let 
$G\curvearrowright T_n$ be a sequence of 
$(\epsilon,N)$-tame actions 
$\omega$-converging to 
$G\curvearrowright T_{\omega }$.
(1) Let
$\beta \subseteq T_{\omega }$ be an arc. Then we can choose a sequence of arcs $\beta _n\subseteq T_n$ converging to $\beta$ so that the following dichotomy holds.
(a) Either there exists
$0<\delta <\epsilon \cdot \ell (\beta )$ such that $\mathfrak {D}(\beta _n,\delta )=G_{\beta _n}$ for $\omega$-all $n$, and we have $G_{\beta }=\bigcap _{\omega }G_{\beta _n}$.(b) Or, for every
$0<\delta <\epsilon \cdot \ell (\beta )$, the subgroup $\mathfrak {D}(\beta _n,\delta )$ is non-elliptic for $\omega$-all $n$.In this case,
$G_{\beta }$ leaves invariant a line $\alpha \subseteq T_{\omega }$ containing $\beta$. The $G$-stabiliser of $\alpha$ equals $\bigcap _{\omega }\mathfrak {D}(\beta _n,\delta )$ (independently of the choice of $\delta$), and $G_{\beta }$ is the kernel of the (possibly trivial) homomorphism $\bigcap _{\omega }\mathfrak {D}(\beta _n,\delta )\rightarrow \mathbb {R}$ given by translation lengths along $\alpha$.
(2) Let
$\gamma \subseteq T_{\omega }$ be a line. Then we can choose a sequence of arcs $\beta _n\subseteq T_n$ converging to $\gamma$ so that, for every sufficiently large $\delta >0$, the $G$-stabiliser of $\gamma$ equals $\bigcap _{\omega }\mathfrak {D}(\beta _n,\delta )$.
Moreover, if 
$\mathcal {P}_n\subseteq T_n\times T_n$ is an eventually dense sequence of collections of arcs, then the approximations 
$\beta _n$ in (1) and (2) can be chosen within 
$\mathcal {P}_n$.
Proof. We will initially deal with both parts of the proposition simultaneously: set 
$\eta :=\beta$ in part (1) and 
$\eta :=\gamma$ in part (2). Let 
$\eta _n\subseteq T_n$ be a sequence of arcs converging to 
$\eta$. Recall that 
$\eta _n[s]$ is the middle segment of 
$\eta _n$ of length 
$s$.
Consider 
$0<\delta <\epsilon \cdot \ell (\eta )$. If there exists 
$ {\delta }/{\epsilon }\leq s\leq \ell (\eta _n)$ such that 
$\mathfrak {D}(\eta _n[s],\delta )$ is non-elliptic, let 
${\delta }/{\epsilon }\leq t_{n,\delta }\leq \ell (\eta _n)$ be the largest such 
$s$ (the maximum exists e.g. by (3) in Definition 5.4 and Remark 5.3). Otherwise, set 
$t_{n,\delta }=0$. Let 
$t_{\delta }$ be the 
$\omega$-limit of 
$t_{n,\delta }$.
If 
$\delta _1<\delta _2$, we have 
$t_{n,\delta _1}\leq t_{n,\delta _2}$ for every 
$n$, hence 
$t_{\delta _1}\leq t_{\delta _2}$. We will need the following observation.
Claim Suppose that, for some 
$\delta$ and 
$n$, we have 
$t_{n,\delta }\neq 0$. Then there exists a subgroup 
$H_n\leq G$ such that 
$H_n=\mathfrak {D}(\eta _n[s],\delta ')$ for all 
$\delta \leq \delta '\leq \epsilon t_{n,\delta }$ and 
${\delta '}/{\epsilon }\leq s\leq t_{n,\delta }$. There is a unique 
$H_n$-invariant line 
$\alpha _n\subseteq T_n$ and it contains 
$\eta _n[t_{n,\delta }-\delta ]$.
Proof of Claim Fix for a moment 
$\delta '\geq \delta$ and recall that 
$t_{n,\delta '}\geq t_{n,\delta }$. By (3) in Definition 5.4 and Remark 5.3, the subgroup 
$\mathfrak {D}(\eta _n[s],\delta ')$ is non-elliptic and constant as 
$s$ varies in 
$[{\delta '}/{\epsilon },t_{n,\delta }]$. Let us call it 
$H_{n,\delta '}$ for short. By (2) in Definition 5.4, 
$H_{n,\delta '}$ leaves invariant a line 
$\alpha _{n,\delta '}\subseteq T_n$, which must contain the arc 
$\eta _n[t_{n,\delta }-\delta ']$ by Lemma 5.2.
Taking 
$s=t_{n,\delta }$, the fact that 
$\delta \leq \delta '$ implies that 
$H_{n,\delta }\leq H_{n,\delta '}$. Applying again (3) in Definition 5.4, we deduce that 
$H_{n,\delta }=H_{n,\delta '}$, so this subgroup is independent of the specific value of 
$\delta '$ and we can call it 
$H_n$. The lines 
$\alpha _{n,\delta '}$ are also independent of 
$\delta '$, since they are the axis of all loxodromics in 
$H_{n,\delta '}=H_n$. This proves the claim.
Now, we distinguish three cases.
Case A: 
$\eta =\gamma$ and there exists 
$\delta _0>0$ with 
$t_{\delta _0}=+\infty$. We must have 
$t_{n,\delta _0}>0$ for 
$\omega$-all 
$n$, so the claim provides subgroups 
$H_n\leq G$ and lines 
$\alpha _n\subseteq T_n$. Since 
$\alpha _n$ contains 
$\eta _n[t_{n,\delta _0}-\delta _0]$ and 
$t_{n,\delta _0}$ diverges, the lines 
$\alpha _n$ converge to 
$\gamma$. Since 
$\alpha _n$ is 
$H_n$-invariant, it is clear that the subgroup 
$H:=\bigcap _{\omega }H_n$ leaves 
$\gamma$ invariant.
Let us show that 
$H$ coincides with the 
$G$-stabiliser of 
$\gamma$. Consider 
$g\in G$ with 
$g\gamma =\gamma$. Let 
$\alpha _n[s]$ denote the sub-arc of 
$\alpha _n$ of length 
$s$ that has the same midpoint as 
$\eta _n$. Choosing 
$s$ so that 
$\ell _{T_{\omega }}(g)<\epsilon s$, we have 
$g\in \bigcap _{\omega }D(\alpha _n[s],\epsilon s)$. If 
$s$ is large enough, we have 
$\delta _0<\epsilon s$ and, since 
$D(\eta _n[t_{n,\delta _0}],\delta _0)$ leaves 
$\alpha _n$ invariant, it follows that 
$D(\alpha _n[s],\epsilon s)\supseteq D(\eta _n[t_{n,\delta _0}],\delta _0)$. Thus, by (3) in Definition 5.4, we have 
$\mathfrak {D}(\alpha _n[s],\epsilon s)=\mathfrak {D}(\eta _n[t_{n,\delta _0}],\delta _0)=H_n$. This shows that 
$g\in \bigcap _{\omega }H_n=H$, as required.
Taking for instance 
$\beta _n=\eta _n[t_{n,\delta _0}]$ (or slightly smaller arcs lying in 
$\mathcal {P}_n$), this proves part (2) of the proposition in this case. Note that the other possibility for part (2) is easier. If 
$t_{\delta }<+\infty$ for every 
$\delta >0$, then the stabiliser of 
$\gamma$ actually fixes 
$\gamma$ pointwise, and it is easy to see that it coincides with 
$\bigcap _{\omega }\mathfrak {D}(\beta _n,\delta )=\bigcap _{\omega }G_{\beta _n}$ for every 
$\delta >0$.
We continue with part (1) of the proposition.
Case B: 
$\eta =\beta$ and 
$t_{\delta }=\ell (\beta )$ for every 
$0<\delta <\epsilon \cdot \ell (\beta )$. As in the previous case, the claim provides subgroups 
$H_n\leq G$ and 
$H_n$-invariant lines 
$\alpha _n\subseteq T_n$. Set 
$H:=\bigcap _{\omega }H_n$. For every 
$\delta >0$, the line 
$\alpha _n$ contains the arc 
$\eta _n[t_{n,\delta }-\delta ]$ for 
$\omega$-all 
$n$. It follows that the 
$\alpha _n$ converge to an 
$H$-invariant line 
$\alpha \subseteq T_{\omega }$ containing 
$\beta$. Exactly as in the previous case, one shows that 
$H$ is actually the entire 
$G$-stabiliser of 
$\alpha$.
We can define 
$\beta _n:=\alpha _n[\ell (\beta )]$ (or take a slightly smaller arc lying in 
$\mathcal {P}_n$). It is clear that 
$\beta _n$ converges to 
$\beta$ and, for each choice of 
$\delta$, we have 
$\mathfrak {D}(\beta _n,\delta )=H_n$ for 
$\omega$-all 
$n$.
Since the 
$\beta _n$ approximate 
$\beta$ and 
$\delta >0$, we have 
$G_{\beta }\subseteq \bigcap _{\omega }D(\beta _n,\delta ) \subseteq H$. Let 
$\tau _n\colon H_n\rightarrow \mathbb {R}$ be the homomorphism given by translation lengths along 
$\alpha _n$. The limit 
$\tau _{\omega }\colon H=\bigcap _{\omega }H_n\rightarrow \mathbb {R}$ gives translation lengths along 
$\alpha \subseteq T_{\omega }$. Since 
$G_{\beta }\leq H$, it is clear that 
$G_{\beta }$ is the kernel of 
$\tau _{\omega }$.
Thus, this case corresponds to case (b) of part (1) of the proposition. It remains to consider one last situation.
Case C: 
$\eta =\beta$ and there exists 
$\delta _0>0$ such that 
$t_{\delta _0}<\ell (\beta )$. By Definition 5.4, for each 
$n$ there exist 
$k\leq N$ and values 
$\ell (\eta _n)=s_{0,n}>s_{1,n}>\dots >s_{k,n}>0$ such that the 
$G$-stabiliser of 
$\eta _n[s]$ is constant as 
$s$ varies in each interval 
$s\in (s_{i+1,n},s_{i,n}]$. As 
$n$ varies, 
$k$ is 
$\omega$-constant and the 
$s_{i,n}$ converge to a sequence 
$\ell (\beta )=s_0\geq s_1\geq \dots \geq s_k\geq 0$.
Let 
$j$ be the largest index with 
$s_j=\ell (\beta )$. Up to shrinking the approximation 
$\eta _n$, we can assume that 
$j=0$ (and that 
$\eta _n$ lies within 
$\mathcal {P}_n$). Then, for every 
$s_1< s\leq \ell (\beta )$, the 
$G$-stabilisers of 
$\eta _n[s]$ and 
$\eta _n$ coincide for 
$\omega$-all 
$n$.
Consider 
$\delta >0$ and 
$g\in G$ with 
$g\beta =\beta$. If 
$s\leq \ell (\beta )$, we have 
$g\in \bigcap _{\omega }D(\eta _n[s],\delta )\subseteq \bigcap _{\omega }\mathfrak {D}(\eta _n[s],\delta )$. If 
$\delta <\delta _0$ we have 
$t_{\delta }\leq t_{\delta _0}$. Thus, if 
$s>t_{\delta _0}$, the subgroup 
$\mathfrak {D}(\eta _n[s],\delta )$ is elliptic for 
$\omega$-all 
$n$, and so it coincides with the 
$G$-stabiliser of 
$\eta _n[s-\delta ]$ by (2) in Definition 5.4. If 
$s>\delta +s_1$, the latter equals 
$G_{\eta _n}$. In conclusion, when 
$\delta$ is small enough and 
$s$ is large enough, we have shown that the 
$G$-stabiliser of 
$\eta$ is contained in 
$\bigcap _{\omega }G_{\eta _n}$, hence it coincides with it.
Taking 
$\beta _n:=\eta _n$, this corresponds to case (a) of part (1). This completes the proof of the proposition.
5.3 Almost-stabilisers in special groups
Consider a right-angled Artin group 
$\mathcal {A}_{\Gamma }$ and set 
$r:=\dim \mathcal {X}_{\Gamma }$. Recall that, for every 
$v\in \Gamma$, we have an action 
$\mathcal {A}_{\Gamma }\curvearrowright \mathcal {T}_v$ coming from a restriction quotient of 
$\mathcal {X}_{\Gamma }$. As usual, the stabiliser of an arc 
$\beta \subseteq \mathcal {T}_v$ is denoted 
$(\mathcal {A}_{\Gamma })_{\beta }$.
Lemma 5.7 Consider an arc 
$\beta \subseteq \mathcal {T}_v$ and 
$0\leq \delta \leq {\ell (\beta )}/({4r+2})$. Then:
(1) either
$D_{\mathcal {A}_{\Gamma }}(\beta,\delta )=(\mathcal {A}_{\Gamma })_{\beta ^{\delta }}$;(2) or
$(\mathcal {A}_{\Gamma })_{\beta ^{\delta }}\subsetneq D_{\mathcal {A}_{\Gamma }}(\beta,\delta )\subseteq \langle h\rangle \times (\mathcal {A}_{\Gamma })_{\beta ^{\delta }}=Z_{\mathcal {A}_{\Gamma }}(h)$ for a label-irreducible element $h\in \mathcal {A}_{\Gamma }$ that is not a proper power. Moreover, $0<\ell _{\mathcal {T}_v}(h)\leq \delta$ and the axis of $h$ in $\mathcal {T}_v$ contains $\beta ^{\delta }$.
Proof. Let 
$p,q$ be the endpoints of 
$\beta$ and let 
$p',q'$ be those of 
$\beta ^{\delta }$. Set 
$D=D_{\mathcal {A}_{\Gamma }}(\beta,\delta )$ for simplicity. Let 
$D_0\subseteq D$ be the subset of elliptic elements. By Lemma 5.2, we have 
$D_0=(\mathcal {A}_{\Gamma })_{\beta ^{\delta }}$. Let 
$D_1\subseteq D$ be the subset of loxodromic elements that, in addition, are label-irreducible.
Claim 1 Every 
$g\in D$ can be decomposed as a product 
$h_1h_0$ with 
$h_1\in D_1\sqcup \{1\}$ and 
$h_0\in D_0$, where 
$h_0$ commutes with 
$h_1$. If 
$h_1\neq 1$, it has the same axis and translation length in 
$\mathcal {T}_v$ as 
$g$.
Proof of Claim 1 Consider 
$g\in D$. If 
$g$ is elliptic, we can take 
$h_1=1$ and 
$h_0=g$. Suppose instead that 
$g$ is loxodromic, and let 
$g=g_1\cdot \ldots \cdot g_k$ be its decomposition into label-irreducibles.
Since the 
$g_i$ commute pairwise, at least one of them must be loxodromic in 
$\mathcal {T}_v$, or 
$g$ would be elliptic. Since the sets 
$\Gamma (g_i)$ are pairwise disjoint, at most one 
$g_i$ is loxodromic in 
$\mathcal {T}_v$. Say 
$g_1$ is the loxodromic component. Then its axis is fixed pointwise by 
$g_2,\dots,g_k$, so 
$g$ has the same axis and the same translation length in 
$\mathcal {T}_v$ as 
$g_1$. We can then set 
$h_1=g_1$ and 
$h_2=g_2\cdot \ldots \cdot g_k$.
We are only left to check that 
$h_1,h_0$ lie in 
$D$. Since 
$h_1$ and 
$g$ have the same axis and translation length, they displace all points of 
$\mathcal {T}_v$ by the same amount. Hence 
$h_1\in D$. By Lemma 5.2, the axis of 
$g$ contains 
$\beta ^{\delta }$. This coincides with the axis of 
$h_1$, which is fixed pointwise by 
$h_0$. So 
$h_0$ fixes 
$\beta ^{\delta }$ pointwise, hence 
$h_0\in D$.
If 
$D_1=\emptyset$, then we are in the first case of the lemma and we are done.
Claim 2 If 
$D_1\neq \emptyset$, there exists 
$h\in D_1$ such that 
$h$ is not a proper power in 
$\mathcal {A}_{\Gamma }$ and 
$D_1\subseteq \langle h\rangle$.
Proof of Claim 2 Recall that 
$d(p',q')=\ell (\beta )-\delta$. If 
$h\in D_1$, the points 
$p'$ and 
$q'$ lie on the axis of 
$h$ by Lemma 5.2. Hence 
$d(p',hp')\leq d(p,hp)\leq \delta$. By our choice of 
$\delta$, we have
\[ d(p',h^{4r+1}p')\leq (4r+1)\delta\leq \ell(\beta)-\delta=d(p',q'), \]
so the point 
$h^{4r+1}p'$ lies between 
$p'$ and 
$q'$ (up to replacing 
$h$ with 
$h^{-1}$). In conjunction with [Reference FioravantiFio22, Lemma 3.13], this shows that the subgroup of 
$\mathcal {A}_{\Gamma }$ generated by any two elements of 
$D_1$ is cyclic. Finally, it is clear that 
$D_1$ is closed under taking roots. The claim follows.
In conclusion, we have shown that 
$D_{\mathcal {A}_{\Gamma }}(\beta,\delta )\subseteq \langle h\rangle \times (\mathcal {A}_{\Gamma })_{\beta ^{\delta }}\subseteq Z_{\mathcal {A}_{\Gamma }}(h)$. Since 
$h\in D$, it is clear that 
$\ell _{\mathcal {T}_v}(h)\leq \delta$ and the axis of 
$h$ in 
$\mathcal {T}_v$ contains 
$\beta ^{\delta }$. We are only left to prove that 
$Z_{\mathcal {A}_{\Gamma }}(h)\subseteq \langle h\rangle \times (\mathcal {A}_{\Gamma })_{\beta ^{\delta }}$.
Since 
$h$ is label-irreducible, Remark 3.7(5) shows that 
$Z_{\mathcal {A}_{\Gamma }}(h)=\langle h\rangle \times P$ for some parabolic subgroup 
$P$. For every 
$g\in P$, we have 
$\Gamma (g)\subseteq \Gamma (h)^{\perp }$, so 
$v\not \in \Gamma (g)$. It follows that 
$P$ is elliptic in 
$\mathcal {T}_v$. Since 
$P$ commutes with 
$h$, it must fix the axis of 
$h$, which, in turn, contains 
$\beta ^{\delta }$. Hence 
$P$ is contained in 
$(\mathcal {A}_{\Gamma })_{\beta ^{\delta }}$, which completes the proof.
Corollary 5.8 Let 
$\beta$ and 
$\delta$ be as in Lemma 5.7. Let 
$G\leq \mathcal {A}_{\Gamma }$ be 
$q$-convex-cocompact. Then:
(1) either
$\mathfrak {D}_G(\beta,\delta )=G_{\beta ^{\delta }}$;(2) or
$\mathfrak {D}_G(\beta,\delta )=Z_G(g)$, for a label-irreducible element $g\in G$. In this case, $0<\ell _{\mathcal {T}_v}(g)\leq \delta q$ and the axis of $g$ in $\mathcal {T}_v$ contains $\beta ^{\delta }$.
Proof. If we are in case (1) of Lemma 5.7, it is clear that 
$G\cap D_{\mathcal {A}_{\Gamma }}(\beta,\delta )\subseteq G_{\beta ^{\delta }}$, hence 
$\mathfrak {D}_G(\beta,\delta )=G_{\beta ^{\delta }}$. So, let us suppose that we are in case (2) of Lemma 5.7 and 
$D_{\mathcal {A}_{\Gamma }}(\beta,\delta )\subseteq \langle h\rangle \times (\mathcal {A}_{\Gamma })_{\beta ^{\delta }}=Z_{\mathcal {A}_{\Gamma }}(h)$ for a label-irreducible element 
$h\in \mathcal {A}_{\Gamma }$. If 
$G\cap D_{\mathcal {A}_{\Gamma }}(\beta,\delta )$ is contained in 
$\{1\}\times (\mathcal {A}_{\Gamma })_{\beta ^{\delta }}$, we again obtain 
$G\cap D_{\mathcal {A}_{\Gamma }}(\beta,\delta )\subseteq G_{\beta ^{\delta }}$ and 
$\mathfrak {D}_G(\beta,\delta )=G_{\beta ^{\delta }}$.
Otherwise, an element of 
$G\cap D_{\mathcal {A}_{\Gamma }}(\beta,\delta )$ has a label-irreducible component that is a power of 
$h$. Remark 3.7(6) shows that there exists 
$1\leq k\leq q$ such that 
$h^k\in G$. Let 
$g$ be the smallest such power of 
$h$. Note that 
$\ell _{\mathcal {T}_v}(g)\leq q\ell _{\mathcal {T}_v}(h)\leq \delta q$. The axis of 
$g$ in 
$\mathcal {T}_v$ coincides with that of 
$h$, so it contains 
$\beta ^{\delta }$. It is clear that
\[ \mathfrak{D}_G(\beta,\delta)=\langle G\cap D_{\mathcal{A}_{\Gamma}}(\beta,\delta)\rangle \leq G\cap Z_{\mathcal{A}_{\Gamma}}(h)= Z_G(g). \]
Finally, if this inclusion were strict, then 
$Z_G(g)\setminus \mathfrak {D}_G(\beta,\delta )$ would contain an element of 
$\langle h\rangle \times (\mathcal {A}_{\Gamma })_{\beta ^{\delta }}$ with the same axis as 
$g$ and strictly smaller translation length, which contradicts our supposition.
Corollary 5.9 If 
$G\leq \mathcal {A}_{\Gamma }$ is convex-cocompact, then 
$G\curvearrowright \mathcal {T}_v$ is 
$({1}/({4r+2}),N)$-tame for some 
$N\geq 1$.
Proof. We verify the three conditions in Definition 5.4. Condition (2) is immediate from Corollary 5.8 (note that the loxodromic required by the condition might not be the element 
$g$ from Corollary 5.8, but rather any shortest loxodromic in 
$G\cap D_{\mathcal {A}_{\Gamma }}(\beta,\delta )$). Condition (1) follows from (a special case of) Lemma 3.36, since stabilisers of arcs of 
$\mathcal {T}_v$ are 
$G$-parabolic and centralisers are 
$G$-semi-parabolic. Finally, let 
$g_1,g_2\in G$ be label-irreducibles with 
$Z_G(g_1)\lneq Z_G(g_2)$. Then 
$\langle g_1\rangle \neq \langle g_2\rangle$, hence 
$\Gamma (g_1)\subseteq \Gamma (g_2)^{\perp }$ by Remark 3.7(4). This shows that 
$g_1,g_2$ cannot both be loxodromic in 
$\mathcal {T}_v$, which implies condition (3).
5.4 Arc-stabilisers in the limit
Let 
$G\leq \mathcal {A}_{\Gamma }$ be convex-cocompact and let 
$Y\subseteq \mathcal {X}_{\Gamma }$ be a convex subcomplex on which 
$G$ acts essentially and cocompactly. Let 
$S\subseteq G$ be a finite generating set. For every vertex 
$v\in \Gamma$, consider the restriction quotient 
$\pi _v\colon \mathcal {X}_{\Gamma }\rightarrow \mathcal {T}_v$.
Let 
$\varphi _n\in \operatorname {Aut}(G)$ be a sequence of automorphisms projecting to an infinite sequence in 
$\operatorname {Out}(G)$. The standard Bestvina–Paulin argument [Reference BestvinaBes88, Reference PaulinPau88] (see in particular [Reference PaulinPau91, § 2, p. 338, Case 1]) guarantees that the quantity
\[ \tau_n:=\inf_{x\in\mathcal{X}_{\Gamma}}\max_{s\in S}d(x,\varphi_n(s)x) \]
diverges for 
$n\rightarrow +\infty$. Let 
$o_n\in Y\subseteq \mathcal {X}_{\Gamma }$ be points realising these infima. For any 
$G$-metric space 
$Z$, we let 
$Z^{\varphi _n}$ represent 
$Z$ with the twisted 
$G$-action 
$g\cdot x:=\varphi _n(g)x$.
Fix a non-principal ultrafilter 
$\omega$. Let 
$(G\curvearrowright \mathcal {X}_{\omega },o)$ be the 
$\omega$-limit of the sequence 
$(G\curvearrowright ({1}/{\tau _n})\mathcal {X}_{\Gamma }^{\varphi _n},o_n)$. Note that the action 
$G\curvearrowright \mathcal {X}_{\omega }$ does not have a global fixed point: because of our choice of 
$\tau _n$, every point of 
$\mathcal {X}_{\omega }$ is displaced by at least one element of 
$S$. It follows that the action 
$G\curvearrowright \mathcal {X}_{\omega }$ has unbounded orbits, for instance because 
$\mathcal {X}_{\omega }$ has a bi-Lipschitz equivalent 
$G$-invariant 
${\rm CAT(0)}$ metric (the limit of the 
${\rm CAT(0)}$ metric on 
$\mathcal {X}_{\Gamma }$).
Since 
$\mathcal {X}_{\Gamma }$ embeds isometrically and 
$\mathcal {A}_{\Gamma }$-equivariantly in the finite product 
$\prod _{v\in \Gamma }\mathcal {T}_v$, the limit 
$\mathcal {X}_{\omega }$ embeds isometrically and 
$G$-equivariantly in 
$\prod _{v\in \Gamma }\mathcal {T}_v^{\omega }$, where 
$T_v^{\omega }$ is the 
$\omega$-limit of the sequence 
$(G\curvearrowright ({1}/{\tau _n})T_v^{\varphi _n},\pi _v(o_n))$. Since 
$G\curvearrowright \mathcal {X}_{\omega }$ has unbounded orbits, there exists a vertex 
$v\in \Gamma$ such that the action 
$G\curvearrowright \mathcal {T}_v^{\omega }$ is not elliptic.
Remark 5.10 It is not hard to show that there exists a vertex 
$v\in \Gamma$ such that
\[ \inf_{x\in \mathcal{T}_v}\max_{s\in S}d(x,\varphi_n(s)x)\geq c(\Gamma)\cdot\tau_n, \]
where 
$c(\Gamma )$ is a constant depending only on 
$\Gamma$. Without this inequality, it might happen (a priori) that the non-elliptic limit tree 
$\mathcal {T}_v^{\omega }$ has a 
$G$-fixed point at infinity. Indeed, 
$\pi _v(o_n)$ might be far from the point realising 
$\inf _{x\in \mathcal {T}_v}\max _{s\in S}d(x,\varphi _n(s)x)$, as 
$Y$ is not convex in the product 
$\prod _{v\in \Gamma }\pi _v(Y)$. In any case, there is no need to rule out this possibility, as it is irrelevant to the following discussion.
In the rest of the subsection, we consider the following setting.
Assumption 5.11 Fix a vertex 
$v\in \Gamma$ such that 
$G\curvearrowright \mathcal {T}_v^{\omega }$ is not elliptic. For simplicity, we set 
$T_G:=\pi _v(Y)$, which is the 
$G$-minimal subtree of 
$\mathcal {T}_v$. Denote by 
$G\curvearrowright T_n$ the action on 
$T_G^{\varphi _n}$ with its metric rescaled by 
$\tau _n$. We also set 
$T_{\omega }:=\mathcal {T}_v^{\omega }$, which is the 
$\omega$-limit of 
$(T_n,\pi _v(o_n))$.
We emphasise that the 
$G$-action on 
$T_{\omega }$ will not be minimal in general (
$T_{\omega }$ is the universal 
$\mathbb {R}$-tree as soon as it is not a line).
The following characterises arc-stabilisers for the action 
$G\curvearrowright T_{\omega }$. Recall Definition 3.12.
Proposition 5.12 For every arc 
$\beta \subseteq T_{\omega }$, at least one of the following two options occurs:
(1)
$G_{\beta }$ is a centraliser in $G$ and $G_{\beta }$ is elliptic in $\omega$-all $T_n$;(2)
$G_{\beta }$ is the kernel of a (possibly trivial) homomorphism $\rho \colon Z\rightarrow \mathbb {R}$, where $Z\leq G$ is a centraliser. In addition, $Z$ is the $G$-stabiliser of a line $\alpha \subseteq T_{\omega }$ containing $\beta$, and $\rho$ gives translation lengths along $\alpha$. The $Z$-minimal subtree of $T_n$ is a line for $\omega$-all $n$ (hence $Z$ is non-elliptic in $T_n$) and we have $N_G(Z)=Z$.
Proof. Recall that the trees 
$T_n$ and 
$T_G=\pi _v(Y)$ coincide up to rescaling, but are endowed with different 
$G$-actions. It is therefore convenient to adopt the following convention: if 
$\eta$ is an arc in 
$T_n$, we denote by 
$\widetilde \eta$ the corresponding arc of 
$T_G$. We will always write either 
$\mathfrak {D}_{T_n}(\cdot,\cdot )$ or 
$\mathfrak {D}_{T_G}(\cdot,\cdot )$ in order to emphasise the 
$G$-action under consideration.
Since twisting and rescaling preserve tameness (and its parameters), Corollary 5.9 shows that the actions 
$G\curvearrowright T_n$ are all 
$(\epsilon,N)$-tame for 
$\epsilon = {1}/({4r+2})$ and some fixed 
$N$. It follows that we can approximate 
$\beta$ by a sequence of arcs 
$\beta _n\subseteq T_n$ as in Proposition 5.6(1).
In addition, we can assume that the arcs 
$\widetilde \beta _n\subseteq T_G$ satisfy the dichotomy in Corollary 4.17. Indeed, since 
$L/\tau _n \rightarrow 0$, Corollary 4.17 shows that such arcs form an eventually dense family.
Note that, for every 
$0\leq \delta <\ell (\beta )$, we have
\[ \mathfrak{D}_{T_n}(\beta_n,\delta)=\varphi_n^{-1}\big(\mathfrak{D}_{T_G}(\widetilde\beta_n,\delta\tau_n)\big), \quad G_{\beta_n}=\varphi_n^{-1}\big(G_{\widetilde\beta_n}\big). \]
We distinguish two cases, corresponding to cases (1a) and (1b) of Proposition 5.6.
Case A: There exists 
$0<\delta <\epsilon \cdot \ell (\beta )$ such that 
$\mathfrak {D}_{T_n}(\beta _n,\delta )=G_{\beta _n}$ for 
$\omega$-all 
$n$. In this case, 
$G_{\beta }=\bigcap _{\omega }G_{\beta _n}$. Thus, it suffices to show that 
$G_{\beta _n}$ is a centraliser for 
$\omega$-all 
$n$. Then Proposition 3.38(2) guarantees that 
$G_{\beta }$ is itself a centraliser. In particular 
$G_{\beta }$ is finitely generated, so 
$G_{\beta }\leq G_{\beta _n}$ for 
$\omega$-all 
$n$ and 
$G_{\beta }$ is elliptic in 
$\omega$-all 
$T_n$. This is case (1) of our proposition.
Since automorphisms of 
$G$ take centralisers to centralisers, it suffices to show that the subgroups 
$G_{\widetilde \beta _n}$ are centralisers. These must fall into one of the two cases of Corollary 4.17. In the first case, it is clear that 
$G_{\widetilde \beta _n}$ is a centraliser. The other case can be ruled out as follows.
There would exist elements 
$g_n\in G$ that are loxodromic in 
$T_G$ with 
$0<\ell _{T_G}(g_n)\leq \ell _Y(g_n)\leq q$, and whose axes 
$\eta _n\subseteq T_G$ satisfy 
$\ell (\eta _n\cap \widetilde \beta _n)\geq \ell (\widetilde \beta _n)-4q$. In particular, 
$g_n\in \mathfrak {D}_{T_G}(\widetilde \beta _n,9q)$ and, for large 
$n$, we have
\[ \varphi_n^{-1}(g_n)\in\varphi_n^{-1}\big(\mathfrak{D}_{T_G}(\widetilde\beta_n,9q)\big)=\mathfrak{D}_{T_n}(\beta_n,9q/\tau_n)\subseteq\mathfrak{D}_{T_n}(\beta_n,\delta)=G_{\beta_n}. \]
This contradicts the fact that the elements 
$\varphi _n^{-1}(g_n)$ are loxodromic in 
$T_n$.
Case B: for each 
$0<\delta <\epsilon \cdot \ell (\beta )$, the subgroup 
$\mathfrak {D}_{T_n}(\beta _n,\delta )$ is non-elliptic for 
$\omega$-all 
$n$. In this case, 
$G_{\beta }$ leaves invariant a line 
$\alpha \subseteq T_{\omega }$ containing 
$\beta$. The stabiliser of 
$\alpha$ is 
$\bigcap _{\omega }\mathfrak {D}_{T_n}(\beta _n,\delta )$ for some choice of 
$\delta$, and 
$G_{\beta }$ is the kernel of the homomorphism giving translation lengths along 
$\alpha$.
Since 
$\mathfrak {D}_{T_n}(\beta _n,\delta )$ is non-elliptic, Corollary 5.8 shows that 
$\mathfrak {D}_{T_G}(\widetilde \beta _n,\delta \tau _n)=Z_G(g_n)$ for a label-irreducible element 
$g_n\in G$ that is loxodromic in 
$T_G$. Again by Proposition 3.38, the subgroup
\[ Z:=\bigcap_{\omega}\mathfrak{D}_{T_n}(\beta_n,\delta)=\bigcap_{\omega}Z_G(\varphi_n^{-1}(g_n)) \]
is a centraliser. Summing up, 
$Z$ is the entire 
$G$-stabiliser of the line 
$\alpha$ and 
$G_{\beta }=\ker \rho$, where 
$\rho \colon Z\rightarrow \mathbb {R}$ gives translation lengths along 
$\alpha$.
Note that 
$Z_G(g_n)$ leaves invariant the axis 
$\widetilde \alpha _n\subseteq T_G$ of 
$g_n$, and translation lengths along it are given by a homomorphism 
$\eta _n\colon Z_G(g_n)\rightarrow \mathbb {R}$. The lines 
$\widetilde \alpha _n\subseteq T_G$ correspond to lines 
$\alpha _n\subseteq T_n$ converging to 
$\alpha$, and the homomorphism 
$\rho \colon Z\rightarrow \mathbb {R}$ is the 
$\omega$-limit of the restrictions to 
$Z$ of the compositions 
$\rho _n:=\eta _n\circ \varphi _n$ rescaled by 
$\tau _n$.
If 
$\rho _n$ vanishes on 
$Z$ for 
$\omega$-all 
$n$, then 
$\rho$ vanishes on 
$Z$, so 
$Z=G_{\beta }$ and 
$G_{\beta }$ is elliptic in 
$\omega$-all 
$T_n$. In this case, we fall again in case (1) of our proposition.
Otherwise 
$\rho _n$ is nonzero on 
$Z$ for 
$\omega$-all 
$n$, hence the 
$Z$-minimal subtree of 
$T_n$ is the line 
$\alpha _n$. If 
$g\in G$ normalises 
$Z$, then we have 
$g\alpha _n=\alpha _n$ for 
$\omega$-all 
$n$. Since 
$\alpha _n$ converge to 
$\alpha$, we then have 
$g\alpha =\alpha$ and, since 
$Z$ is the entire 
$G$-stabiliser of 
$\alpha$, we have 
$g\in Z$. In conclusion 
$N_G(Z)=Z$.
This yields case (2) of our proposition and completes the proof.
An infinite tripod in an 
$\mathbb {R}$-tree is the union of three rays pairwise intersecting at a single point.
Proposition 5.13 All line- and (infinite tripod)-stabilisers for 
$G\curvearrowright T_{\omega }$ are centralisers.
Proof. The stabiliser of an infinite tripod is the intersection of two line-stabilisers, so it suffices to show that line-stabilisers are centralisers. The latter follows from part (2) of Proposition 5.6, retracing the proof of Proposition 5.12.
Remark 5.14 Proposition 5.12 shows in particular that arc-stabilisers are closed under taking roots in 
$G$. Thus, the stabiliser of a line in 
$T_{\omega }$ can never swap its two ends.
The following expands on case (2) of Proposition 5.12.
Proposition 5.15 Let 
$\alpha \subseteq T_{\omega }$ be a line acted upon by its stabiliser 
$G_{\alpha }$ via a (possibly trivial) homomorphism 
$\rho \colon G_{\alpha }\rightarrow \mathbb {R}$. Suppose that 
$G_{\alpha }$ is non-elliptic in 
$T_n$ for 
$\omega$-all 
$n$.
(a) There exists
$x\in G$ such that $G_{\alpha }=Z_G(x)$ and we have $N_G(G_{\alpha })=G_{\alpha }$.(b) Assuming that
$\rho$ is discrete and $\ker \rho$ is finitely generated, the following hold.
• If
$\ker \rho$ is elliptic in $\omega$-all $T_n$, then $\ker \rho$ is $G$-semi-parabolic and $G_{\alpha }\lneq N_G(\ker \rho )$.• If
$\ker \rho$ is non-elliptic in $\omega$-all $T_n$, then the centre of $\ker \rho$ contains an element $h$ that is loxodromic in $\omega$-all $T_n$. If $\ker \rho =G_{\alpha }$, then $h$ can be chosen to be label-irreducible.
(c) Suppose that:
(c1) either the automorphisms
$\varphi _n$ are coarse-median preserving;(c2) or there does not exist an element
$x\in G$ such that $\varphi _n(Z_G(x))$ lies in a single $G$-conjugacy class of subgroups for $\omega$-all $n$.
Then
$\rho$ is discrete, $\ker \rho$ is a centraliser, and $G_{\alpha }$ is a proper subgroup of $G$. In addition, if $\ker \rho \neq G_{\alpha }$, then $\ker \rho$ is elliptic in $\omega$-all $T_n$.(d) Suppose that either
$\rho$ is not discrete, or $\ker \rho$ is not $G$-semi-parabolic. Then either the centre of $Z$ has rank $\geq 2$, or it is infinite cyclic and contained in $\ker \rho$.(e) If
$\rho$ is not discrete, then, for every arc $\beta \subseteq \alpha$, we have $G_{\beta }\leq G_{\alpha }$.
Proof. We begin with some preliminary remarks.
By Proposition 5.13, we know that 
$G_{\alpha }$ is a centraliser, so let us write 
$Z:=G_{\alpha }$ for short. Since 
$Z$ is finitely generated, and we are assuming that it is non-elliptic in 
$\omega$-all 
$T_n$, there are loxodromics for its action on 
$T_n$ for 
$\omega$-all 
$n$. Thus, retracing one last time the proof of Proposition 5.12 using part (2) of Proposition 5.6, we are necessarily in Case B, and we obtain a sequence of label-irreducible elements 
$g_n\in G$ (without loss of generality, not proper powers of elements of 
$G$) such that 
$Z=\bigcap _{\omega }Z_G(\varphi _n^{-1}(g_n))$. In addition, the 
$Z$-minimal subtree of 
$T_n$ is a line for 
$\omega$-all 
$n$, and we have 
$N_G(Z)=Z$.
The homomorphism 
$\rho \colon Z\rightarrow \mathbb {R}$ is obtained as the limit of the homomorphisms 
$\rho _n\colon Z\rightarrow \mathbb {R}$ giving translation lengths along the 
$Z$-invariant line in 
$T_n$. Each 
$\rho _n$ is the restriction to 
$Z$ of the composition 
$\eta _n\circ \varphi _n$, where 
$\eta _n\colon Z_G(g_n)\rightarrow \mathbb {R}$ is the homomorphism giving translation lengths in 
$\mathcal {T}_v$, rescaled by 
$\tau _n$. Note that 
$\eta _n$ has the same kernel as the straight projection 
$\pi _{g_n}\colon Z_G(g_n)\rightarrow \mathbb {Z}$ introduced in Remark 3.9(2). Recall that 
$\ker \pi _{g_n}$ is 
$G$-parabolic.
Proof of part (a) We have already observed that 
$N_G(Z)=Z$ and 
$Z=\bigcap _{\omega }Z_G(\varphi _n^{-1}(g_n))$. Let us show that we actually have 
$Z=Z_G(\varphi _n^{-1}(g_n))$ for 
$\omega$-all 
$n$.
Since 
$Z$ is finitely generated, we have 
$Z\leq Z_G(\varphi _n^{-1}(g_n))$ for 
$\omega$-all 
$n$, so 
$Z$ commutes with 
$\varphi _n^{-1}(g_n)$. Since 
$N_G(Z)=Z$, the elements 
$\varphi _n^{-1}(g_n)$ lie in the centre of 
$Z$ for 
$\omega$-all 
$n$. Thus, the 
$\varphi _n^{-1}(g_n)$ pairwise commute, hence the maximal cyclic groups containing their label-irreducible components are 
$\omega$-constant. This shows that 
$Z_G(\varphi _n^{-1}(g_n))$ is 
$\omega$-constant, hence it coincides with 
$Z$, as required.
Proof of part (b) First, suppose that 
$\ker \rho$ is elliptic in 
$\omega$-all 
$T_n$. We will show that 
$Z$ is a proper subgroup of 
$N_G(\ker \rho )$. Since 
$Z$ is 
$G$-semi-parabolic and 
$N_G(Z)=Z$, we can then use Proposition 3.35 to deduce that 
$\ker \rho$ is 
$G$-semi-parabolic, as required.
Since 
$\ker \rho$ is finitely generated and elliptic in 
$T_n$, we have 
$\ker \rho \leq \ker \rho _n$ for 
$\omega$-all 
$n$. Since 
$\rho$ is discrete, we have 
$Z/\ker \rho \simeq \mathbb {Z}$ (recall that 
$Z$ is non-elliptic in 
$T_n$, so 
$\ker \rho$ is a proper subgroup). Since we also have 
$Z/\ker \rho _n\simeq \mathbb {Z}$, this implies that 
$\ker \rho _n=\ker \rho$ for 
$\omega$-all 
$n$ (
$\mathbb {Z}$ is Hopfian). Recalling from part (a) that 
$Z=\varphi _n^{-1}(Z_G(g_n))$, it follows that
\[ Z\leq N_G(\ker\rho)=N_G(\ker\rho_n)=\varphi_n^{-1}N_G(\ker\eta_n)=\varphi_n^{-1}N_G(\ker\pi_{g_n}). \]
Suppose for the sake of contradiction that we have 
$Z=N_G(\ker \rho )$. Then 
$N_G(\ker \pi _{g_n})=\varphi _n(Z)=Z_G(g_n)$. Since 
$\ker \pi _{g_n}$ is 
$G$-parabolic, Corollary 3.21 shows that the centralisers 
$Z_G(g_n)$ are chosen from finitely many 
$G$-conjugacy classes of subgroups. Since the 
$g_n$ are all label-irreducible, it follows that there is a conjugacy class 
$\mathcal {C}\subseteq G$ such that 
$g_n\in \mathcal {C}$ for 
$\omega$-all 
$n$. This implies that the translation length of 
$g_n$ in 
$\mathcal {T}_v$ is uniformly bounded, so 
$\inf (\rho _n(Z)\cap \mathbb {R}_{>0})$ converges to zero. Since 
$\rho _n$ converges to 
$\rho$ and 
$\ker \rho _n=\ker \rho$ for 
$\omega$-all 
$n$, we conclude that 
$\rho$ is trivial and 
$Z=\ker \rho =\ker \rho _n$. This contradicts our assumption that 
$Z$ be non-elliptic in 
$\omega$-all 
$T_n$.
In order to complete the proof of part (b), suppose now that 
$\ker \rho$ is non-elliptic for 
$\omega$-all 
$T_n$. Let 
$h_1,\dots,h_k$ be a finite generating set for 
$\ker \rho$. The elements 
$h_i$ and 
$h_ih_j$ cannot all be elliptic in 
$T_n$ or 
$\ker \rho$ would also be elliptic in 
$T_n$ by Serre's lemma. This shows that there exists an element 
$h'\in \ker \rho$ such that 
$\rho _n(h')>0$ for 
$\omega$-all 
$n$. Hence 
$\inf (\rho _n(Z)\cap \mathbb {R}_{>0})\rightarrow 0$.
Now, let 
$Z_0$ denote the centre of 
$Z$. Recall that, if 
$G$ is, say, 
$q$-convex-cocompact, then 
$Z_G(g_n)$ has a subgroup of index 
$\leq q$ that splits as 
$\langle g_n\rangle \times \ker \pi _{g_n}$ (e.g. by Remark 3.7(6)). Thus, since we have seen in the proof of part (a) that 
$\varphi _n^{-1}(g_n)\in Z_0$ for 
$\omega$-all 
$n$, we have
\[ \inf(\rho_n(Z_0)\cap\mathbb{R}_{>0})\leq\eta_n(g_n)\leq q\cdot \inf(\eta_n(Z_G(g_n))\cap\mathbb{R}_{>0})=q\cdot \inf(\rho_n(Z)\cap\mathbb{R}_{>0})\rightarrow 0. \]
The subgroup 
$Z_0$ is free abelian, non-trivial and convex-cocompact (note that 
$Z_0$ is itself a centraliser). Thus, 
$Z_0$ admits a basis of label-irreducible elements 
$x_1,\dots,x_m$ with 
$m\geq 1$. Since 
$Z_0$ contains 
$\varphi _n^{-1}(g_n)$, on which 
$\rho _n$ does not vanish, we can assume that 
$\rho _n(x_1)>0$ for 
$\omega$-all 
$n$. If 
$x_1\in \ker \rho$, we can take 
$h=x_1$ and we are done. Note that this is always the case if 
$\ker \rho =Z=G_{\alpha }$.
Otherwise 
$\rho (x_1)\neq 0$, hence 
$\rho (Z_0)\neq \{0\}$. Modifying the basis of 
$Z_0$ if necessary (which can kill label-irreducibility of its elements), we can assume that 
$\rho (x_1)$ generates 
$\rho (Z_0)$, and 
$x_i\in \ker \rho$ for all 
$i\geq 2$. If 
$\rho _n$ vanished on all 
$x_i\neq x_1$ for 
$\omega$-all 
$n$, we would have 
$\inf (\rho _n(Z_0)\cap \mathbb {R}_{>0})=\rho _n(x_1)\rightarrow \rho (x_1)\neq 0$, contradicting the fact that 
$\inf (\rho _n(Z_0)\cap \mathbb {R}_{>0})\rightarrow 0$. Thus, there exists 
$i\geq 2$ such that 
$\rho _n(x_i)>0$ for 
$\omega$-all 
$n$, and 
$x_i$ lies in the centre of 
$\ker \rho$ as required. This proves part (b).
Proof of part (c) If 
$\ker \rho =Z$, then all statements are immediate. Indeed, 
$\rho$ is trivial (hence discrete), its kernel is the centraliser 
$Z$, and we cannot have 
$G=Z$, as 
$G$ would act elliptically on 
$T_{\omega }$. Thus, we assume in the rest of the proof that 
$\ker \rho \neq Z$.
Recall that there exist label-irreducible elements 
$g_n\in G$ such that 
$Z=\varphi _n^{-1}(Z_G(g_n))$ for 
$\omega$-all 
$n$. Also recall the notion of straight projection from Remark 3.9(2).
Claim The subgroup 
$\varphi _n(Z)=Z_G(g_n)$ does not lie in a single 
$G$-conjugacy class for 
$\omega$-all 
$n$.
Proof of Claim Under assumption (c2), this is immediate from part (a). Suppose instead that the automorphisms 
$\varphi _n$ are coarse-median preserving. Then Remark 3.9 shows that we have 
$g=\varphi _n^{-1}(g_n)$ for a fixed label-irreducible 
$g\in G$ and 
$\omega$-all 
$n$. In addition, 
$\ker \rho _n=\varphi _n^{-1}(\ker \pi _{g_n})=\ker \pi _g$, so 
$\ker \pi _g$ is contained in 
$\ker \rho$. Since 
$Z/\ker \pi _g\simeq \mathbb {Z}$ and 
$\ker \rho \neq Z$, this implies that 
$\ker \rho =\ker \pi _g$.
If the 
$\varphi _n(Z)=Z_G(g_n)$ lied in a single conjugacy class of subgroups, then the elements 
$\varphi _n(g)=g_n$ would lie in a single conjugacy class, since they are all label-irreducible. As in the proof of part (b), this would imply that 
$g$ is elliptic in 
$T_{\omega }$. In this case 
$g\in \ker \rho \setminus \ker \pi _g$, contradicting the fact that 
$\ker \rho =\ker \pi _g$.
The claim immediately implies that 
$G_{\alpha }=Z$ is a proper subgroup of 
$G$. We now prove the remaining statements.
Since 
$g_n\in Z_G(\ker \pi _{g_n})$, we have 
$\ker \pi _{g_n}\leq Z_GZ_G(\ker \pi _{g_n})\leq Z_G(g_n)$. Being a centraliser, 
$Z_GZ_G(\ker \pi _{g_n})$ is convex-cocompact and closed under taking roots. Thus, since 
$Z_G(g_n)$ virtually splits as 
$\langle g_n\rangle \times \ker \pi _{g_n}$, we must have either 
$Z_GZ_G(\ker \pi _{g_n})=\ker \pi _{g_n}$ or 
$Z_GZ_G(\ker \pi _{g_n})=Z_G(g_n)$.
Suppose first that 
$Z_GZ_G(\ker \pi _{g_n})=Z_G(g_n)$ for 
$\omega$-all 
$n$. Recall from Remark 3.9(2) that 
$\ker \pi _{g_n}$ is 
$G$-parabolic. Thus, Corollary 3.21 implies that the subgroups 
$Z_G(g_n)$ lie in finitely many 
$G$-conjugacy classes. It follows that 
$\varphi _n(Z)=Z_G(g_n)$ lies in a single 
$G$-conjugacy class for 
$\omega$-all 
$n$. This is ruled out by the claim.
Thus, we must have 
$Z_GZ_G(\ker \pi _{g_n})=\ker \pi _{g_n}$ for 
$\omega$-all 
$n$. In this case, 
$\ker \pi _{g_n}$ is a centraliser, so 
$\ker \rho _n=\varphi _n^{-1}(\ker \pi _{g_n})$ is a centraliser, and it is a convex-cocompact. Since 
$Z$ virtually splits as 
$\ker \rho _n\times \mathbb {Z}$, we conclude that the subgroup 
$\ker \rho _n$ is 
$\omega$-constant. It follows that 
$\ker \rho _n\leq \ker \rho$ for 
$\omega$-all 
$n$. Since 
$Z/\ker \rho _n\simeq \mathbb {Z}$ and we assumed that 
$\ker \rho \neq Z$, it follows that 
$\ker \rho _n=\ker \rho$ for 
$\omega$-all 
$n$. This shows that 
$\rho$ is discrete and 
$\ker \rho$ is a centraliser elliptic in 
$\omega$-all 
$T_n$.
Proof of part (d) Recall from the proof of part (a) that the elements 
$\varphi _n^{-1}(g_n)$ all lie in the centre of 
$Z$. Thus, the latter always has rank at least 
$1$. Suppose that the centre of 
$Z$ has rank 
$1$ and intersects 
$\ker \rho$ trivially. We will show that 
$\rho$ is discrete with 
$G$-semi-parabolic kernel.
Since the centre of 
$Z$ is cyclic, there exists an element 
$g\in G$ (now not necessarily label-irreducible) such that 
$g=\varphi _n^{-1}(g_n)$ for 
$\omega$-all 
$n$. Thus 
$\rho _n(g)=\eta _n(g_n)\in \mathbb {R}$ generates the image of 
$\rho _n$. If we had 
$\rho _n(g)\rightarrow 0$, then the centre of 
$Z$ would be elliptic in 
$T_{\omega }$, hence contained in 
$\ker \rho$. Thus, 
$\rho _n(g)$ must stay bounded away from zero, and the image of 
$\rho$ is discrete and generated by 
$\rho (g)$.
Now, 
$Z$ virtually splits as 
$\langle g\rangle \times P$ for some subgroup 
$P\leq Z$, which is necessarily finitely generated. Since 
$\rho (g)$ is non-trivial and generates the image of 
$\rho$, we deduce that 
$\ker \rho$ intersects 
$\langle g\rangle \times P$ in a subgroup that projects isomorphically onto 
$P$. In particular, 
$\ker \rho$ is finitely generated. Since the images of the 
$\rho _n$ stay bounded away from zero and 
$\ker \rho$ is finitely generated, we conclude that 
$\ker \rho$ is elliptic in 
$\omega$-all 
$T_n$. Finally, by part (b), 
$\ker \rho$ is 
$G$-semi-parabolic.
Proof of part (e) Since 
$\rho$ is non-discrete, there exists a loxodromic element 
$g\in Z$ with translation length small enough that there exists a point 
$x\in \beta$ such that 
$g^Nx\in \beta$, where 
$N=4\dim \mathcal {X}_{\Gamma }+1$. If 
$h\in G_{\beta }$, Lemma 3.8 shows that 
$h$ preserves the axis of 
$g$ in 
$T_n$ for 
$\omega$-all 
$n$. Thus, 
$h$ preserves the axis of 
$g$ in 
$T_{\omega }$, hence 
$h\in G_{\alpha }$ as required.
This completes the proof of Proposition 5.15.
Parts (c1) and (c2) of Proposition 5.15 are the key to Theorem A and Corollary D, respectively. The differences in the assumptions of Proposition 5.15(c2) and Corollary D can be reconciled using the following consequence of a providential result of B. H. Neumann.
Lemma 5.16 Let 
$G$ be a group with a countable collection 
$\mathscr {H}$ of 
$G$-conjugacy classes of subgroups. Suppose that, for every class 
$\mathcal {H}\in \mathscr {H}$, the 
$\operatorname {Out}(G)$-orbit of 
$\mathcal {H}$ is infinite. Then there exists a sequence 
$\phi _n\in \operatorname {Out}(G)$ such that, for every 
$\mathcal {H}\in \mathscr {H}$, the sequence 
$\phi _n(\mathcal {H})$ eventually consists of pairwise distinct classes.
Proof. Let 
$\dots \subseteq \mathscr {H}_n\subseteq \mathscr {H}_{n+1}\subseteq \dots$ be an exhaustion of 
$\mathscr {H}$ by finite subsets. We define 
$\phi _n$ inductively, starting with an arbitrary automorphism 
$\phi _1$. Suppose that 
$\phi _1,\dots,\phi _n$ have been defined. We would like to choose 
$\phi _{n+1}$ so that, for every 
$\mathcal {H}\in \mathscr {H}_n$, we have 
$\phi _{n+1}(\mathcal {H})\not \in \{\phi _1(\mathcal {H}),\dots,\phi _n(\mathcal {H})\}$. If this is possible for every 
$n$, then we obtain the required sequence of automorphisms.
Suppose instead that for some 
$n$, we cannot choose 
$\phi _{n+1}$ with this property. Then, for every 
$\phi \in \operatorname {Out}(G)$, there exists 
$\mathcal {H}\in \mathscr {H}_n$ such that 
$\phi (\mathcal {H})\in \{\phi _1(\mathcal {H}),\dots,\phi _n(\mathcal {H})\}$. Denoting by 
$\operatorname {Out}_{\mathcal {H}}(G)$ the stabiliser of 
$\mathcal {H}$ within 
$\operatorname {Out}(G)$, this means that 
$\operatorname {Out}(G)$ is covered by finitely many cosets of the infinite-index subgroups 
$\operatorname {Out}_{\mathcal {H}}(G)$ with 
$\mathcal {H}\in \mathscr {H}_n$. By [Reference NeumannNeu54, Lemma 4.1], this is impossible.
Finally, we record here the following result, which will be repeatedly needed in § 6.3.
Lemma 5.17 Let 
$\beta \subseteq T_{\omega }$ be an arc such that 
$G_{\beta }$ is finitely generated and elliptic in 
$\omega$-all 
$T_n$. If 
$\beta$ falls in case (2) of Proposition 5.12, assume in addition that 
$\rho$ has discrete image. Then there exists a sequence 
$\epsilon _n\rightarrow 0$ such that 
$Z_G(G_{\beta })$ acts on 
$\operatorname {Fix}(G_{\beta },T_n)$ with 
$\epsilon _n$-dense orbits.
Proof. Observe first that 
$\varphi _n(G_{\beta })$ is 
$G$-semi-parabolic for every 
$n$. Indeed, this is clear if 
$\beta$ falls in case (1) of Proposition 5.12, since then 
$G_{\beta }$ is a centraliser. Otherwise, Proposition 5.15(b) shows that 
$G_{\beta }$ is the kernel of a homomorphism 
$Z\rightarrow \mathbb {Z}$, where 
$Z$ is a centraliser and 
$Z$ is a proper subgroup of 
$N_G(G_{\beta })$. In this case, the group 
$\varphi _n(G_{\beta })$ is of the same form for every 
$n$, and Proposition 3.35 ensures that 
$\varphi _n(G_{\beta })$ is 
$G$-semi-parabolic.
Now, a consequence is that 
$\varphi _n(G_{\beta })$ is convex-cocompact in 
$G$ for all 
$n$. Recall that 
$T_G\subseteq \mathcal {T}_v$ is the 
$G$-minimal subtree. Thus, Lemma 3.22(2) shows that 
$\varphi _n(Z_G(G_{\beta }))=Z_G(\varphi _n(G_{\beta }))$ acts on 
$\operatorname {Fix}(\varphi _n(G_{\beta }),T_G)$ with 
$\leq c$ orbits of edges, where 
$c$ only depends on 
$G$ and its embedding in 
$\mathcal {A}_{\Gamma }$.
Since 
$T_n$ is a copy of 
$T_G$, twisted by 
$\varphi _n$ and rescaled by 
$\tau _n\rightarrow +\infty$, it follows that 
$Z_G(G_{\beta })$ acts on 
$\operatorname {Fix}(G_{\beta },T_n)$ with 
$\epsilon _n$-dense orbits, where 
$\epsilon _n:=c/\tau _n\rightarrow 0$.
6. From $\mathbb {R}$-trees to DLS automorphisms
In this section, we use the description of the limit tree 
$T_{\omega }$ obtained in § 5.4 to prove Theorems A and B and Corollary D.
First, in § 6.1, we review various standard results originating from ideas of Rips, Sela, Bestvina, Feighn and Guirardel. Then, in § 6.2, we briefly discuss how to ensure that DLS automorphisms are not inner. Finally, § 6.3 contains the core argument.
6.1 Actions on $\mathbb {R}$-trees
In this subsection, we review a few classical facts on actions on 
$\mathbb {R}$-trees.
A subtree of an 
$\mathbb {R}$-tree is non-degenerate if it is not a single point. Arcs are always assumed to be non-degenerate. A finite subtree is the convex hull of a finite set of points.
If 
$G$ is a group, we refer to 
$\mathbb {R}$-trees equipped with an isometric 
$G$-action simply as 
$G$-trees. A 
$G$-tree 
$T$ is minimal if it does not contain any proper 
$G$-invariant subtrees. A non-degenerate subtree 
$U\subseteq T$ is stable if all its arcs have the same 
$G$-stabiliser. We say that 
$T$ is BF-stable (after [Reference Bestvina and FeighnBF95]) if every arc of 
$T$ contains a stable sub-arc.
If 
$T_1$ and 
$T_2$ are 
$G$-trees, a morphism is a 
$G$-equivariant map 
$f\colon T_1\rightarrow T_2$ with the property that every arc of 
$T_1$ can be covered by finitely many arcs on which 
$f$ is isometric.
A 
$G$-tree is said to be geometric if it originates from a finite foliated 
$2$-complex 
$X$ with fundamental group 
$G$. The precise definition will not be relevant to us and is omitted. We instead refer the reader to [Reference Levitt and PaulinLP97] or [Reference GuirardelGui08, § 1.7] for additional details.
Remark 6.1 Let 
$T$ be a geometric 
$G$-tree. If 
$N$ is the kernel of the 
$G$-action, then 
$T$ is geometric also as a 
$G/N$-tree.
The following can be deduced for instance from [Reference Levitt and PaulinLP97, Theorem 2.2] or [Reference GuirardelGui98, § 2].
Proposition 6.2 Let 
$T$ be a minimal 
$G$-tree with 
$G$ finitely presented. To every finite subtree 
$K\subseteq T$, we can associate a geometric 
$G$-tree 
$\mathcal {G}_K$ and a morphism 
$f_K\colon \mathcal {G}_K\rightarrow T$ so that the following hold.
• There exists a finite subtree
$\widetilde K\subseteq \mathcal {G}_K$ such that $f_K$ is isometric on $\widetilde K$ and $f_K(\widetilde K)=K$.• If
$K\subseteq K'$, then there exists a morphism $f_K^{K'}\colon \mathcal {G}_K\rightarrow \mathcal {G}_{K'}$ such that $f_K=f_{K'}\circ f_K^{K'}$ and $f_K^{K'}(\widetilde K)\subseteq \widetilde K'$.• If
$H\leq G$ is finitely generated and fixes $K$, there exists $K'\supseteq K$ such that $H$ fixes $f_K^{K'}(\widetilde K)$.
We will refer to the morphisms 
$f\colon \mathcal {G}_K\rightarrow T$ provided by the previous proposition as geometric approximations of 
$T$.
Definition 6.3 [Reference GuirardelGui08, Definition 1.4]
A transverse covering of a 
$G$-tree 
$T$ is a 
$G$-invariant family 
$\mathcal {U}=\{U_i\}_{i\in I}$ of closed subtrees of 
$T$ that cover 
$T$ and satisfy the following.
• If
$i\neq j$, the intersection $U_i\cap U_j$ is empty or a singleton.• Every arc of
$T$ can be covered by finitely many elements of $\mathcal {U}$.
A transverse covering 
$\mathcal {U}$ of a 
$G$-tree 
$T$ always gives rise to a splitting of 
$G$. Indeed, we can construct an action without inversions on a simplicial tree 
$G\curvearrowright S_{\mathcal {U}}$ as follows [Reference GuirardelGui04, Lemma 4.7].
The vertex set of 
$S_{\mathcal {U}}$ is a disjoint union 
$V_0(S_{\mathcal {U}})\sqcup V_1(S_{\mathcal {U}})$, where 
$V_1(S_{\mathcal {U}})$ is identified with 
$\mathcal {U}$ and 
$V_0(\mathcal {S}_{\mathcal {U}})$ is the set of points appearing as the intersection of two elements of 
$\mathcal {U}$. The tree 
$S_{\mathcal {U}}$ is bipartite, with edges joining each point of 
$V_0(\mathcal {S}_{\mathcal {U}})$ to all elements of 
$\mathcal {U}=V_1(S_{\mathcal {U}})$ that contain it.
Note that, if 
$T$ is 
$G$-minimal, then so is 
$S_{\mathcal {U}}$.
Definition 6.4 [Reference GuirardelGui08, Definition 1.17]
Consider a 
$G$-tree 
$T$ and a subgroup 
$H\leq G$. A non-degenerate subtree 
$U\subseteq T$ is 
$H$-indecomposable if, for any two arcs 
$\beta,\beta '\subseteq U$, there exist elements 
$h_1,\dots,h_n\in H$ such that 
$\beta '\subseteq h_1\beta \cup \dots \cup h_n\beta$ and 
$h_i\beta \cap h_{i+1}\beta$ is an arc for each 
$1\leq i< n$.
Note that 
$U$ is not required to be 
$H$-invariant and the arcs 
$h_i\beta \cap h_{i+1}\beta$ can be disjoint from 
$U$.
The terminology is motivated by the fact that, if 
$\mathcal {U}$ is a transverse covering of 
$T$, then every 
$G$-indecomposable subtree of 
$T$ must be contained in one of the elements of 
$\mathcal {U}$ [Reference GuirardelGui08, Lemma 1.18].
We also record here part of Lemmas 1.19 and 1.20 in [Reference GuirardelGui08].
Lemma 6.5 Let 
$T$ be a 
$G$-tree with a 
$G$-indecomposable subtree 
$U\subseteq T$.
(1) If
$f\colon T\rightarrow T'$ is morphism, then $f(U)$ is $G$-indecomposable.(2) If
$G\curvearrowright T$ is BF–stable, then $U$ is a stable subtree.(3) If
$T$ is itself $G$-indecomposable, then it is $G$-minimal.
The following is a version of Imanishi's theorem [Reference ImanishiIma79] due to Guirardel.
Proposition 6.6 Let 
$T$ be a geometric 
$G$-tree with 
$G$ finitely presented. Then 
$T$ admits a unique transverse covering 
$\mathcal {U}=\{U_i\}_{i\in I}$ where, for each 
$i$:
• either
$U_i$ is a non-degenerate arc containing no branch points of $T$ in its interior;• or
$G_i\curvearrowright U_i$ is indecomposable and geometric, where $G_i\leq G$ the stabiliser of $U_i$.
Proof. Existence follows from Proposition 1.25 and Remark 1.29 in [Reference GuirardelGui08]. The additional hypothesis required for Guirardel's result is always satisfied for geometric actions of finitely presented groups (for instance, combining [Reference Levitt and PaulinLP97, Remark 2.3] with [Reference Levitt and PaulinLP97, Theorem 0.2(2)]). Uniqueness is due to [Reference GuirardelGui08, Lemma 1.18].
Definition 6.7 We refer to the elements of the transverse covering 
$\mathcal {U}$ provided by Proposition 6.6 as the components of 
$T$ (this is justified by uniqueness of 
$\mathcal {U}$).
The following classification result is due to Rips, and Bestvina and Feighn [Reference Bestvina and FeighnBF95]. This formulation is taken from [Reference GuirardelGui08, Proposition A.6].
Proposition 6.8 Let 
$T$ be a geometric 
$G$-tree with 
$G$ finitely presented and torsion-free. Suppose that 
$T$ has trivial arc-stabilisers and is 
$G$-indecomposable. Then 
$T$ is of one of the following types:
• axial:
$T$ is a line and $G$ is a free abelian group acting on $T$ with dense orbits;• surface:
$G$ is the fundamental group of a compact surface with boundary supporting an arational measured foliation that gives rise to $T$;• exotic: neither of the above.
We acknowledge that, with no requirement on exotic components, the previous proposition seems trivially satisfied. What we will actually need about these three types of 
$G$-trees is that they can be approximated by simplicial 
$G$-trees in a controlled way, as shown in [Reference GuirardelGui98]. We will refer the reader to precise statements when these will become necessary later in this section.
The following observation will allow us to apply Proposition 6.8 even though our actions normally have large arc-stabilisers.
Lemma 6.9 Let 
$T$ be a BF-stable 
$G$-tree, with 
$G$ finitely presented. Suppose that a geometric approximation 
$f\colon \mathcal {G}\rightarrow T$ admits an indecomposable component 
$U\subseteq \mathcal {G}$. Let 
$\beta \subseteq f(U)$ be an arc with finitely generated stabiliser 
$G_{\beta }$. Then there exists a geometric approximation 
$\mathcal {G}'\rightarrow T$ with an indecomposable component 
$U'\subseteq \mathcal {G}'$ such that:
(1)
$U'$ is invariant under the $G$-stabiliser of $U$;(2) the
$G$-stabiliser of every arc of $U'$ coincides with $G_{\beta }$.
Proof. By Proposition 6.2, there exists a geometric approximation 
$f'\colon \mathcal {G}'\rightarrow T$ such that 
$G_{\beta }$ is elliptic in 
$\mathcal {G}'$ and such that 
$f$ factors as the composition of 
$f'$ and a morphism 
$p\colon \mathcal {G}\rightarrow \mathcal {G}'$. Let 
$G_U$ be the 
$G$-stabiliser of 
$U\subseteq \mathcal {G}$. By Lemma 6.5(1), the image 
$p(U)\subseteq \mathcal {G}'$ is 
$G_U$-indecomposable, hence contained in an indecomposable component 
$U'\subseteq \mathcal {G}'$. Since distinct indecomposable components share at most one point, 
$U'$ must be 
$G_U$-invariant.
By Lemma 6.5, the image 
$f'(U')$ is 
$G$-indecomposable, hence a stable subtree of 
$T$. Since 
$f'(U')$ contains 
$f(U)$, which in turn contains 
$\beta$, we see that the stabiliser of every arc of 
$f'(U')$ is equal to 
$G_{\beta }$. In particular, since 
$f'(U')$ is 
$G_{U'}$-invariant and not a single point, the subgroup 
$G_{\beta }$ is normalised by 
$G_{U'}$.
Now, the subtree 
$\operatorname {Fix}(G_{\beta },\mathcal {G}')$ is non-empty and 
$G_{U'}$-invariant, thus it contains the 
$G_{U'}$-minimal subtree of 
$\mathcal {G}'$. By Lemma 6.5(3), the latter is 
$U'$. This shows that 
$G_{\beta }$ is contained in the stabiliser of every arc of 
$U'$. On the other hand, the 
$G$-stabiliser of an arc of 
$U'$ is contained in the 
$G$-stabiliser of an arc of 
$f'(U')$, since 
$f'$ is a morphism, hence it is contained in 
$G_{\beta }$. This shows that the 
$G$-stabiliser of every arc of 
$U'$ is exactly 
$G_{\beta }$, as required.
Finally, we record the following standard fact on refining simplicial splittings. We say that 
$G$ splits over a subgroup 
$C$ if it is an amalgamated product 
$G=A\ast _C B$ or an HNN extension 
$G=A\ast _C$.
Lemma 6.10 Let 
$G\curvearrowright T$ be a minimal action without inversions on a simplicial tree. Suppose that, for a vertex 
$v\in T$, the stabiliser 
$G_v$ splits over a subgroup 
$C\leq G_v$, with Bass–Serre tree 
$G_v\curvearrowright T'$. Suppose in addition that, for every edge 
$e\subseteq T$ incident to 
$v$, the stabiliser 
$G_e$ is elliptic in 
$T'$. Then 
$G$ splits over 
$C$. In addition, if the splitting of 
$G_v$ is HNN, then so is the one of 
$G$.
6.2 Outer DLS automorphisms
As mentioned in the Introduction, there are various situations in which a DLS automorphism turns out to be an inner automorphism in a non-obvious way. In this subsection, we provide two simple criteria to ensure that this does not happen.
Lemma 6.11 Consider a group 
$G$ with an HNN splitting 
$G=A\ast _C$. Suppose that 
$Z_C(C)$ commutes with the chosen stable letter 
$t\in G$. If the twist 
$\tau \in \operatorname {Aut}(G)$ induced by an element 
$c\in Z_C(C)\setminus \{1\}$ is an inner automorphism of 
$G$, then 
$c$ has finite order in 
$G$ and 
$C=A$.
Proof. Consider 
$c\in Z_C(C)\setminus \{1\}$ and the twist 
$\tau \in \operatorname {Aut}(G)$ with 
$\tau (t)=ct$ and 
$\tau (a)=a$ for every 
$a\in A$. Let 
$G\curvearrowright T$ be the Bass–Serre tree of the HNN extension. Let 
$\alpha$ and 
$\alpha '$ be the axes of 
$t$ and 
$ct$, respectively. There exists a point 
$x_0\in \alpha$ such that the stabiliser of 
$x_0$ is 
$A$ and the stabiliser of the edge 
$[x_0,tx_0]$ is 
$C$. Note that 
$[x_0,tx_0]$ is contained in the intersection 
$\alpha \cap \alpha '$.
Suppose 
$\tau$ is inner. Thus, there exists 
$g\in Z_G(A)$ such that 
$gtg^{-1}=ct$. In particular 
$g\alpha =\alpha '$, preserving the orientation induced by 
$t$ and 
$ct$. We distinguish three cases.
If 
$x_0$ is the only point of 
$T$ that is fixed by 
$A$, then 
$g$ must fix 
$x_0$. Since 
$g\alpha =\alpha '$, the edge 
$[x_0,tx_0]$ is also fixed by 
$g$, hence 
$g\in C$. Since 
$g\in Z_G(A)$, we have 
$g\in Z_C(C)$. By our assumptions, this implies that 
$g$ commutes with 
$t$, contradicting the fact that 
$gtg^{-1}=ct$.
If 
$A$ has more than one fixed point in 
$T$, then either 
$tAt^{-1}\geq A$ or 
$tAt^{-1}\leq A$. Suppose first that one of these inclusions is strict. Since 
$g\alpha =\alpha '$, there exists 
$n\in \mathbb {Z}$ such that 
$gt^n$ fixes the edge 
$[x_0,tx_0]$, hence 
$g=c't^{-n}$ for some 
$c'\in C$. This implies that either 
$gAg^{-1}\gneq A$ or 
$gAg^{-1}\lneq A$, contradicting the fact that 
$g\in Z_G(A)$.
Finally, suppose that 
$tAt^{-1}=A$. In this case, 
$C=A$ and 
$G=A\rtimes _{\psi }\langle t\rangle$ for some 
$\psi \in \operatorname {Aut}(A)$. Since 
$g\in Z_G(A)$, a standard computation shows that 
$g=xt^n$ for some 
$x\in A$ and 
$n\in \mathbb {Z}$ such that 
$\psi ^n(a)=x^{-1}ax$ for all 
$a\in A$. It follows that 
$g$ commutes with 
$t^n$. Since 
$C=A$, the centre of 
$A$ commutes with 
$t$, so 
$g\not \in Z_A(A)$, hence 
$n\neq 0$. Observing that 
$\tau (t^n)=c^nt^n=gt^ng^{-1}$, we conclude that 
$c^n=1$.
Lemma 6.12 Let a special group 
$G$ act on a simplicial tree 
$\mathcal {S}$ with a single orbit of edges and no inversions. Suppose that the stabiliser 
$C$ of an edge of 
$\mathcal {S}$ satisfies the following:
•
$C$ is convex-cocompact and closed under taking roots in $G$;•
$N_G(C)$ is not elliptic in $\mathcal {S}$;•
$N_G(C)/C$ is not cyclic, nor a free product of two virtually abelian groups elliptic in $\operatorname {Fix}(C,\mathcal {S})$.
Then this splitting of 
$G$ gives rise to a partial conjugation or a fold that has infinite order in 
$\operatorname {Out}(G)$.
Proof. Lemma 3.18 ensures that 
$C$ does not properly contain any of its conjugates, so the 
$G$-stabiliser of every edge of 
$\operatorname {Fix}(C,\mathcal {S})$ is equal to 
$C$. Since 
$G$ acts edge-transitively on 
$\mathcal {S}$, it follows that 
$N_G(C)$ acts edge-transitively on 
$\operatorname {Fix}(C,\mathcal {S})$. Thus, the induced action 
$N_G(C)/C\curvearrowright \operatorname {Fix}(C,\mathcal {S})$ gives a 
$1$-edge free splitting of 
$N_G(C)/C$.
Let 
$A$ and 
$B$ be 
$G$-stabilisers of adjacent vertices of 
$\operatorname {Fix}(C,\mathcal {S})$. Set 
$\overline {A}:=N_A(C)/C$ and 
$\overline {B}:=N_B(C)/C$. Depending on the number of orbits of vertices, we have 
$N_G(C)/C=\overline {A}\ast \overline {B}$ or 
$N_G(C)/C=\overline {A}\ast \mathbb {Z}$, where 
$\overline {A}$ and 
$\overline {B}$ are elliptic in 
$\operatorname {Fix}(C,\mathcal {S})$, while the 
$\mathbb {Z}$-factor is loxodromic. By our third assumption, 
$\overline {A}$ is not virtually abelian in the former case (up to swapping 
$A$ and 
$B$), and 
$\overline {A}$ is non-trivial in the latter.
By Corollary 2.13, 
$N_G(C)/C$ is virtually special, hence so is 
$\overline {A}$. In particular, the centre of 
$\overline {A}$ virtually splits as a direct factor. In addition, since 
$C$ is closed under taking roots, 
$N_G(C)/C$ is torsion-free. Thus, if 
$N_G(C)/C=\overline {A}\ast \overline {B}$, there exists 
$\overline {a}\in \overline {A}$ such that 
$\overline {a}$ projects to an infinite order element of 
$\overline {A}$ modulo its centre. If instead 
$N_G(C)/C=\overline {A}\ast \mathbb {Z}$, there exists 
$\overline {a}\in \overline {A}$ simply of infinite order in 
$\overline {A}$.
Let 
$\overline {\varphi }$ be the DLS automorphism of 
$N_G(C)/C$ induced by the above free splitting and the element 
$\overline {a}$. Recall that 
$\overline {\varphi }$ is the identity on 
$\overline {A}$ and the conjugation by 
$\overline {a}$ on 
$\overline {B}$. Since the splitting of 
$N_G(C)/C$ is free, and because of our choice of 
$\overline {a}$, it is straightforward to see that 
$\overline {\varphi }$ has infinite order in the outer automorphism group of 
$N_G(C)/C$.
Possibly replacing 
$\overline {a}$ with a power, Corollary 2.13 shows that there exists an element 
$a\in Z_A(C)$ projecting to 
$\overline {a}$. Let 
$\varphi$ be the DLS automorphism of 
$G$ induced by its splitting and the element 
$a$. Note that part (2) of Lemma 2.25 ensures that we can take 
$\langle a\rangle \perp C$, so that, in the HNN case, 
$\varphi$ is indeed a fold.
Since 
$\varphi |_C=\mathrm {id}_C$, the automorphism 
$\varphi$ leaves 
$N_G(C)$ invariant and projects to 
$\overline {\varphi }$ on 
$N_G(C)/C$. Also note that 
$\varphi$ is the identity on 
$A$. Thus, if a power of 
$\varphi$ were an inner automorphism of 
$G$, it would be the conjugation by an element of 
$Z_G(A)\leq N_G(C)$. This would contradict the fact that 
$\overline {\varphi }$ is an infinite-order outer automorphism of 
$N_G(C)/C$. This proves the lemma.
6.3 Proof of Theorems A and B
As discussed at the beginning of § 5.4, infinite sequences in 
$\operatorname {Out}(G)$ give rise to non-elliptic 
$G$-actions on 
$\mathbb {R}$-trees 
$G\curvearrowright T_{\omega }$. In this subsection, we show how to use such actions to obtain the required simplicial splittings of 
$G$, along with DLS automorphisms with infinite order in 
$\operatorname {Out}(G)$.
Throughout, we consider the setup of § 5.4. In particular, we use the notation 
$\varphi _n$, 
$T_n$ and 
$T_{\omega }$ with the same meaning as Assumption 5.11.
Having introduced BF-stability in § 6.1, we can now record the following immediate consequence of Proposition 5.12 and Lemma 3.36.
Corollary 6.13 The action 
$G\curvearrowright T_{\omega }$ is BF-stable.
Recall that the action 
$G\curvearrowright T_{\omega }$ is non-elliptic by construction, so the following makes sense.
Definition 6.14 We denote by 
$T\subseteq T_{\omega }$ the 
$G$-minimal subtree.
We now prove three long, technical propositions that make up the core of the proof of Theorems A and B. Each of them exploits certain features of the action 
$G\curvearrowright T$ to construct a splitting of 
$G$ and (possibly) a DLS automorphism. It is useful to recall Propositions 5.12 and 5.15 to better understand their relevance.
Proposition 6.15 Let 
$\alpha \subseteq T$ be a line acted upon by its stabiliser 
$Z$ via a non-trivial homomorphism 
$\rho \colon Z\rightarrow \mathbb {R}$. Then one of the following happens:
(1)
$\rho$ is discrete with $G$-semi-parabolic kernel;(2)
$G$ admits a splitting where $Z$ is a vertex group and each incident edge group is contained in $\ker \rho$ (we include here also the ‘trivial’ case when $G=Z$ and $T=\alpha$);(3) there exists a geometric approximation
$\mathcal {G}\rightarrow T$ and an indecomposable component $U\subseteq \mathcal {G}$ such that $U\not \simeq \mathbb {R}$ and the stabiliser of every arc of $U$ coincides with $\ker \rho$, which is a centraliser.
Proof. Assume throughout the proof that 
$\rho$ is not discrete with 
$G$-semi-parabolic kernel. We will either construct a splitting as in option (2) or find a component of a geometric approximation as in option (3). We remind the reader that 
$\ker \rho$ can be infinitely generated.
Observe that, by Lemma 3.33, either 
$\Gamma (\ker \rho )=\Gamma (Z)$, or an element of the centre of 
$Z$ lies outside 
$\ker \rho$. In addition, if 
$\Gamma (\ker \rho )\neq \Gamma (Z)$ then 
$\rho$ cannot be discrete, otherwise Proposition 3.35 would imply that 
$\ker \rho$ is 
$G$-semi-parabolic, violating our initial assumption.
Thus, it suffices to consider the following two cases, which we will treat by rather different arguments. Fix a finite generating set 
$Z_0\subseteq Z$ with 
$Z_0=Z_0^{-1}$ and 
$1\in Z_0$.
Case (a): 
$\rho$ is not discrete and there exists an element 
$\overline z\in Z_Z(Z)\setminus \ker \rho$. Since morphisms are 
$1$-Lipschitz, we have 
$\ell _{\mathcal {G}}(g)\geq \ell _T(g)$ for every geometric approximation 
$\mathcal {G}\rightarrow T$ and every element 
$g\in G$. Proposition 6.2 ensures that we can choose a geometric approximation 
$f\colon \mathcal {G}\rightarrow T$ such that each element of 
$Z_0\cup \{\overline z\}$ has the same translation length in 
$\mathcal {G}$ and 
$T$.
Now, since 
$\overline z$ is loxodromic in 
$\mathcal {G}$ and commutes with 
$Z$, its axis is 
$Z$-invariant. This shows that the 
$Z$-minimal subtree of 
$\mathcal {G}$ is a line 
$\widetilde \alpha$ with 
$f(\widetilde \alpha )=\alpha$. In addition, 
$Z$ translates along 
$\widetilde \alpha \subseteq \mathcal {G}$ and 
$\alpha \subseteq T$ according to the same homomorphism 
$\rho \colon Z\rightarrow \mathbb {R}$, since the elements of the generating set 
$Z_0$ have the same translation length in 
$\mathcal {G}$ and 
$T$.
Let 
$\mathcal {U}$ be the transverse covering of 
$\mathcal {G}$ provided by Proposition 6.6. Let 
$U\in \mathcal {U}$ be a component that shares an arc with 
$\widetilde \alpha$.
If 
$U$ is not indecomposable, then 
$U$ is an arc containing no branch points of 
$\mathcal {G}$ in its interior. In this case, we have 
$U\subseteq \widetilde \alpha$. Since 
$\rho$ is not discrete, there exist elements of 
$Z$ that translate arbitrarily little along 
$\widetilde \alpha$. It follows that 
$\widetilde \alpha$ contains no branch points of 
$\mathcal {G}$, hence 
$\mathcal {G}=\widetilde \alpha$ and 
$T=\alpha$. Thus 
$G=Z$ and we are in the ‘trivial’ case of option (2).
Suppose instead that 
$U$ is indecomposable and let 
$G_U\leq G$ be its stabiliser. Since 
$\rho$ is not discrete, for every 
$\epsilon >0$, the group 
$Z$ is generated by its elements with translation length 
$<\epsilon$. Thus, 
$Z$ is generated by elements 
$g\in Z$ such that 
$gU\cap U$ contains an arc, since 
$U$ and 
$\widetilde \alpha$ share an arc. Since 
$U$ is part of a transverse covering, these generators preserve 
$U$, hence 
$Z\leq G_U$. In particular, we have 
$\widetilde \alpha \subseteq U$.
If the image 
$f(U)$ is a line, then 
$f(U)=\alpha$, hence 
$G_U=Z$. Recall from the discussion after Definition 6.3 that 
$G_U$ is a vertex group in the splitting of 
$G$ given by the action 
$G\curvearrowright S_{\mathcal {U}}$. All stabilisers of incident edges are subgroups of 
$G_U=Z$ that are elliptic in 
$\mathcal {G}$, hence in 
$T$. This shows that they are contained in 
$\ker \rho$. Thus, this splitting is as required in option (2) of the proposition.
Finally, suppose that 
$f(U)$ is not a line. By Lemma 6.5, the action 
$G_U\curvearrowright f(U)$ is minimal. Since 
$\alpha \subseteq f(U)$, it follows that 
$f(U)$ contains an infinite tripod 
$\tau$ containing 
$\alpha$. Lemma 6.5 also shows that 
$f(U)$ is stable, so 
$G_{\tau }$ coincides with the 
$G$-stabiliser of any arc of 
$\alpha$. By Proposition 5.15(e), the latter is exactly 
$\ker \rho$, so 
$G_{\tau }=\ker \rho$. Proposition 5.13 now implies that 
$\ker \rho$ is a centraliser. In particular, 
$\ker \rho$ is finitely generated and, up to changing geometric approximation and indecomposable component, Lemma 6.9 allows us to assume that 
$\ker \rho$ is the stabiliser of every arc of 
$U$. This is the situation described in option (3) of the statement, so this completes the discussion of Case (a).
Case (b): we have 
$\Gamma (\ker \rho )=\Gamma (Z)$. In this case, we will show that we always fall in option (2) of the proposition. Let 
$K\leq \ker \rho$ be a finitely generated subgroup such that any centraliser containing 
$K$ contains 
$Z$, as provided by Remark 3.32.
Claim 1 We have 
$\operatorname {Fix}(K,T)=\alpha$ and the stabiliser of every arc of 
$\alpha$ is exactly 
$\ker \rho$.
Proof of Claim 1 It is clear that 
$\alpha \subseteq \operatorname {Fix}(K,T)$. Consider an arc 
$\eta \subseteq \operatorname {Fix}(K,T)$.
Observe that 
$\eta$ cannot fall in case (1) of Proposition 5.12. Indeed, 
$G_{\eta }$ would be a centraliser and, since 
$K$ is provided by Remark 3.32, it would follow that 
$Z\leq G_{\eta }$. However, this would contradict the fact that 
$Z$ is not elliptic in 
$T$ (since 
$\rho$ is non-trivial).
Thus, 
$\eta$ must fall in case (2) of Proposition 5.12. In particular, 
$G_{\eta }$ is the kernel of a homomorphism 
$\rho '\colon Z'\rightarrow \mathbb {R}$, where 
$Z'$ is a centraliser stabilising a line 
$\alpha '\subseteq T$ containing 
$\eta$. Again, we must have 
$Z\leq Z'$, so 
$Z$ stabilises 
$\alpha '$. Since 
$Z$ translates non-trivially along 
$\alpha$, we must have 
$\alpha =\alpha '$, hence 
$Z=Z'$. This shows that 
$\eta \subseteq \alpha$ and 
$G_{\eta }=\ker \rho$, thus proving the claim.
Fix a point 
$p\in \alpha$ and let 
$\beta \subseteq \alpha$ be the convex hull of the set 
$Z_0\cdot p$. Proposition 6.2 allows us to choose a geometric approximation 
$f\colon \mathcal {G}\rightarrow T$ so that 
$\beta$ lifts isometrically to a 
$K$-fixed arc 
$\widetilde \beta \subseteq \mathcal {G}$.
Since 
$\rho$ is non-trivial, 
$Z$ is not elliptic in 
$T$, nor can it be elliptic in 
$\mathcal {G}$. Let 
$\mathcal {S}_Z\subseteq \mathcal {G}$ be the 
$Z$-minimal subtree. Let 
$\mathcal {U}$ be the transverse covering of 
$\mathcal {G}$ provided by Proposition 6.6.
Claim 2 If 
$g\mathcal {S}_Z\cap \mathcal {S}_Z$ contains an arc, for some 
$g\in G$, then 
$g\in Z$. In addition, if some 
$U\in \mathcal {U}$ shares an arc with 
$\mathcal {S}_Z$, then 
$U\subseteq \mathcal {S}_Z$.
Proof of Claim 2 If 
$\widetilde p\in \widetilde \beta$ is the lift of 
$p$, the arc 
$\widetilde \beta$ contains 
$Z_0\cdot \widetilde p$. Recalling that 
$Z_0$ generates 
$Z$ and that 
$1\in Z_0=Z_0^{-1}$, we deduce that the 
$Z$-minimal subtree 
$\mathcal {S}_Z$ is contained in 
$Z\cdot \widetilde \beta$. In particular, every arc of 
$\mathcal {S}_Z$ contains a sub-arc that is fixed by a 
$Z$-conjugate of 
$K$.
Suppose that 
$g\mathcal {S}_Z\cap \mathcal {S}_Z$ contains a non-trivial arc 
$\eta$ for some 
$g\in G$. By the previous paragraph, we can choose 
$\eta$ so that it is simultaneously fixed by 
$z_1Kz_1^{-1}$ and 
$(gz_2)K(gz_2)^{-1}$, for some 
$z_1,z_2\in Z$. Up to shrinking 
$\eta$, the morphism 
$f$ is isometric on it, and 
$f(\eta )$ is an arc of 
$T$ fixed by 
$z_1Kz_1^{-1}$ and 
$(gz_2)K(gz_2)^{-1}$.
The first half of Claim 1 implies that 
$f(\eta )\subseteq \alpha \cap g\alpha$. In particular, 
$\alpha$ and 
$g\alpha$ share an arc, so the second half of Claim 1 implies that 
$g(\ker \rho )g^{-1}=\ker \rho$. Since 
$\Gamma (\ker \rho )=\Gamma (Z)$, Lemma 3.28(1) implies that 
$N_G(\ker \rho )\leq N_G(Z)=Z$. In conclusion, 
$g\in Z$ as required.
Now, suppose that a component 
$U\in \mathcal {U}$ shares an arc with 
$\mathcal {S}_Z$. If 
$U$ is not indecomposable, then 
$U$ is an arc containing no branch points of 
$\mathcal {G}$ in its interior, so it is clear that 
$U\subseteq \mathcal {S}_Z$.
Suppose instead that 
$U$ is indecomposable. As above, 
$f(U\cap \mathcal {S}_Z)$ contains an arc fixed by a 
$Z$-conjugate of 
$K$. Lemma 6.5 shows that 
$f(U)$ is a stable subtree of 
$T$, so 
$f(U)$ is fixed pointwise by a 
$Z$-conjugate of 
$K$. Claim 1 implies that 
$f(U)\subseteq \alpha$. Since 
$f$ is a morphism, 
$f(U)$ is not a single point and, by Lemma 6.5, it is 
$G_U$-minimal. We conclude that 
$f(U)=\alpha$, hence 
$G_U\leq Z$. Since 
$U$ is the 
$G_U$-minimal subtree of 
$\mathcal {G}$, it follows that 
$U\subseteq \mathcal {S}_Z$.
Note that 
$\mathcal {S}_Z$ is closed in 
$\mathcal {G}$. Indeed, every point 
$x\in \overline {\mathcal {S}}_Z$ is the missing endpoint of a half-open arc 
$\sigma \subseteq \mathcal {S}_Z$. By Definition 6.3, 
$\overline \sigma$ is covered by finitely many elements of 
$\mathcal {U}$, so one of these must intersect 
$\overline \sigma$ in an arc containing 
$x$. By Claim 2, this element of 
$\mathcal {U}$ is contained in 
$\mathcal {S}_Z$, hence 
$x\in \mathcal {S}_Z$.
Now, consider the covering 
$\mathcal {V}$ of 
$\mathcal {G}$ whose elements are either 
$G$-translates of 
$\mathcal {S}_Z$, or elements of 
$\mathcal {U}$ that are not contained in any 
$G$-translate of 
$\mathcal {S}_Z$. By Claim 2, 
$\mathcal {V}$ is a transverse covering of 
$\mathcal {G}$. Let 
$G\curvearrowright S_{\mathcal {V}}$ be the minimal action on a bipartite simplicial tree constructed as described after Definition 6.3.
By Claim 2, 
$Z$ is the 
$G$-stabiliser of 
$\mathcal {S}_Z$, which corresponds to a vertex of 
$S_{\mathcal {V}}$. Stabilisers of incident edges are 
$Z$-stabilisers of points of 
$\mathcal {S}_Z$. In particular, they are elliptic in 
$\mathcal {G}$, hence in 
$T$, so they must be contained in 
$\ker \rho$. In conclusion, we have realised the situation in option (2) of the proposition. This completes the proof.
In option (2) of Proposition 6.15 we will be able to obtain an HNN splitting of 
$G$ by applying Lemma 6.10 to the natural HNN splittings of 
$Z$ induced by 
$\rho$. The next result shows how to handle option (3) instead.
Proposition 6.16 Consider a geometric approximation 
$f\colon \mathcal {G}\rightarrow T$. Let 
$U\subseteq \mathcal {G}$ be an indecomposable component with 
$U\not \simeq \mathbb {R}$ such that every arc of 
$U$ has the same stabiliser 
$H\leq G$. Also suppose that 
$H$ is convex-cocompact and closed under taking roots in 
$G$. Then one of the following happens:
(a)
$G$ splits over $H$, giving rise to a fold or partial conjugation with infinite order in $\operatorname {Out}(G)$;(b)
$G$ splits over a centraliser $Z_G(k)$, where $k\in G$ is label-irreducible and $H\lhd Z_G(k)$ with $Z_G(k)/H\simeq \mathbb {Z}$. In addition, the twist $\psi \in \operatorname {Aut}(G)$ determined by $k$ and this splitting has infinite order in $\operatorname {Out}(G)$.
Proof. Let 
$G_U\leq G$ be the stabiliser of 
$U$. Clearly, 
$H$ is the kernel of the action 
$G_U\curvearrowright U$ and the induced action 
$G_U/H\curvearrowright U$ has trivial arc-stabilisers. The latter action is still indecomposable, and geometric by Remark 6.1. Note that 
$G_U/H$ is finitely presented, since 
$H$ is finitely generated, and torsion-free, since 
$H$ is closed under taking roots. Thus, we can invoke Proposition 6.8. The ‘axial’ case does not occur since 
$U$ is not a line. The two cases of the current proposition will correspond, respectively, to the ‘exotic’ and ‘surface’ cases.
Let 
$G\curvearrowright S_{\mathcal {U}}$ be the simplicial tree provided by Proposition 6.6 and the discussion after Definition 6.3. The subgroup 
$G_U$ is the stabiliser of a vertex 
$u\in S_{\mathcal {U}}$. Let 
$\mathscr {E}$ be the collection of stabilisers of edges of 
$S_{\mathcal {U}}$ incident to 
$u$. Note that 
$\mathscr {E}$ is a union of finitely many 
$G_U$-conjugacy classes of subgroups of 
$G_U$, and each element of 
$\mathscr {E}$ is the 
$G_U$-stabiliser of a point of 
$U$.
In view of Lemma 6.10, our goal is to construct a 
$1$-edge splitting of 
$G_U$ in which all elements of 
$\mathscr {E}$ are elliptic. For this purpose, it suffices to construct a 
$1$-edge splitting of 
$G_U/H$ in which all elements of the collection 
$\overline {\mathscr {E}}$ of projections of elements of 
$\mathscr {E}$ are elliptic. We treat the exotic and surface cases separately.
Case (a): the action 
$G_U/H\curvearrowright U$ is of exotic type. By Proposition 7.2 and Theorem 6.2 in [Reference GuirardelGui98], the action 
$G_U/H\curvearrowright U$ is a limit (in the length function topology) of actions on simplicial trees 
$G_U/H\curvearrowright \mathcal {S}_n$ where all edge stabilisers are trivial and all elements of 
$\overline {\mathscr {E}}$ are elliptic.
Picking any 
$\mathcal {S}_n$ and collapsing all orbits of edges but one, we obtain an action on a simplicial tree 
$G_U/H\curvearrowright \mathcal {S}$ with a single orbit of edges. This corresponds to a splitting of 
$G_U/H$ as 
$A\ast B$ or 
$A\ast \mathbb {Z}$, where every element of 
$\overline {\mathscr {E}}$ is conjugate into either 
$A$ or 
$B$, and the possible 
$\mathbb {Z}$-factor is loxodromic in 
$\mathcal {S}$. Via Lemma 6.10, this induces a 
$1$-edge splitting of 
$G$ over 
$H$.
Since 
$N_G(H)/H$ contains 
$G_U/H$, it is clear that 
$N_G(H)/H$ is not cyclic and that 
$N_G(H)$ is not elliptic in the Bass–Serre tree of the splitting of 
$G$. We would like to obtain a fold or partial conjugation with infinite order in 
$\operatorname {Out}(G)$ by applying Lemma 6.12. For this, it remains to ensure that 
$N_G(H)/H$ is not a free product of two virtually abelian groups elliptic in the Bass–Serre tree. In fact, it suffices to choose 
$\mathcal {S}$ so that 
$G_U/H$ is not a free product of two virtually abelian groups elliptic in 
$\mathcal {S}$.
Suppose that 
$G_U/H=V_1\ast V_2$, where the 
$V_i$ are non-trivial virtually abelian groups (otherwise any choice of 
$\mathcal {S}$ will do). If neither 
$V_1$ nor 
$V_2$ is isomorphic to 
$\mathbb {Z}$, then they are both elliptic in all the 
$\mathcal {S}_n$, hence they are elliptic in 
$U$. Since 
$G_U/H$ acts on 
$U$ with trivial arc-stabilisers, we obtain a 
$G_U$-invariant simplicial subtree of 
$U$, contradicting the fact that 
$U$ is indecomposable.
Thus, suppose that 
$V_2\simeq \mathbb {Z}$. If again 
$V_1\not \simeq \mathbb {Z}$, then 
$V_1$ is elliptic in all 
$\mathcal {S}_n$ and the same argument shows that 
$V_2$ must be loxodromic for large 
$n$. In this case, every element of 
$\overline {\mathscr {E}}$ is conjugate into 
$V_1$, so we can simply take 
$\mathcal {S}=\mathcal {S}_n$.
Finally, suppose that 
$G_U/H\simeq F_2$. Note that, for each 
$n$, every subgroup in 
$\overline {\mathscr {E}}$ is contained in a free factor of 
$F_2$ that is elliptic in 
$\mathcal {S}_n$. Since distinct free factors of 
$F_2$ intersect trivially, if a free factor contains a non-trivial element of 
$\overline {\mathscr {E}}$, then it must be elliptic in all 
$\mathcal {S}_n$, hence also in 
$U$. We conclude that there is at most one conjugacy class of free factors of 
$F_2$ that contains non-trivial elements of 
$\overline {\mathscr {E}}$. If 
$\langle x\rangle$ is one such free factor, it suffices to take 
$\mathcal {S}$ to be the HNN splitting 
$F_2=\langle x\rangle \ast _{\{1\}}$.
Case (b): the action 
$G_U/H\curvearrowright U$ is of surface type. In this case, we have 
$G_U/H=\pi _1\Sigma$ for a compact surface with boundary 
$\Sigma$. The action 
$\pi _1\Sigma \curvearrowright U$ is dual to an arational measured foliation on 
$\Sigma$. Since the subgroups 
$\overline {\mathscr {E}}$ are elliptic in 
$U$, they are contained in the fundamental groups of the boundary components of 
$\Sigma$.
Let 
$\gamma$ be an essential simple closed curve on 
$\Sigma$ representing a nonzero homology class in 
$H_1(\Sigma,\mathbb {Z})$. In particular, 
$\gamma$ is two-sided in 
$\Sigma$, and 
$\langle \gamma \rangle$ is a maximal cyclic subgroup of 
$\pi _1\Sigma$. Dual to 
$\gamma$, we have a simplicial 
$\pi _1\Sigma$-tree with edge-stabilisers conjugate to 
$\langle \gamma \rangle$, in which all elements of 
$\overline {\mathscr {E}}$ are elliptic.
Let 
$g\in G_U$ be a lift of 
$\gamma$. Note that 
$g$ is loxodromic in 
$U$, since the foliation on 
$\Sigma$ is arational. Lemma 6.10 gives a 
$1$-edge splitting of 
$G$ over the subgroup 
$C=H\rtimes \langle g\rangle$.
Claim There exists a label-irreducible element 
$k\in C$ such that 
$C=Z_G(k)$.
Proof of Claim Recall that 
$N_G(H)$ virtually splits as 
$H\times K$ with 
$K$ convex-cocompact in 
$G$. Thus, for some 
$n\geq 1$, we can write 
$g^n=hk$ with 
$h\in H$ and 
$k\in K$. Since 
$H$ and 
$g$ commute with 
$k$, we have 
$C\leq Z_G(k)$. Conversely, note that 
$g$ and 
$k$ are loxodromic in 
$\mathcal {G}$ with the same axis, which is contained in 
$U$. This axis is preserved by 
$Z_G(k)$, so 
$Z_G(k)\leq G_U$. Since 
$G_U/H$ is hyperbolic and 
$\langle g\rangle$ projects to a maximal cyclic subgroup of 
$G_U/H$, which also contains the projection of 
$k$, we conclude that 
$Z_G(k)\leq H\rtimes \langle g\rangle =C$. This shows that 
$C=Z_G(k)$.
In particular, 
$C$ is convex-cocompact in 
$G$ and it has a finite-index subgroup of the form 
$H\times \langle k\rangle$. Recalling that 
$K$ is convex-cocompact in 
$G$ and 
$K\cap H=\{1\}$, this shows that 
$\langle k\rangle =C\cap K$ is convex-cocompact. Hence 
$k$ is label-irreducible, proving the claim.
Finally, let 
$\psi \in \operatorname {Aut}(G)$ be the twist determined by 
$k$ and our splitting of 
$G$. Observe that 
$\psi |_H=\mathrm {id}_H$ and that 
$\psi (G_U)=G_U$, with the restriction to 
$G_U/H=\pi _1\Sigma$ being the (conventional) Dehn twist around 
$\gamma$ in the mapping class group of 
$\Sigma$. In particular, 
$\psi$ restricts to an automorphism of 
$G_U/H$ with infinite order in 
$\operatorname {Out}(G_U/H)$.
Also note that 
$\psi$ is the identity on 
$Z_G(k)$. Thus, if 
$\psi$ were an inner automorphism of 
$G$, then it would have to be the conjugation by an element of 
$Z_GZ_G(k)\leq Z_G(k)\leq G_U$. Hence 
$\psi$ would restrict to an inner automorphism of 
$G_U/H$, contradicting the previous paragraph. The same argument applies to powers of 
$\psi$, so 
$\psi$ has infinite order in 
$\operatorname {Out}(G)$, as required.
Finally, the next result covers the situation where every line in 
$T$ falls in option (1) of Proposition 6.15 and we are also unable to apply Proposition 6.16.
Proposition 6.17 Suppose that the following hold:
• every geometric approximation
$\mathcal {G}\rightarrow T$ is simplicial;• every line of
$T$ is acted upon discretely by its $G$-stabiliser;• the
$G$-stabiliser of every stable arc of $T$ is $G$-semi-parabolic;•
$T$ is not a line.
Then one of the following happens:
(1)
$G$ splits over the stabiliser of a stable arc of $T$, giving rise to a fold or partial conjugation with infinite order in $\operatorname {Out}(G)$;(2)
$G$ splits over some $Z_G(g)$, where $g\in G$ is label-irreducible and determines a twist with infinite order in $\operatorname {Out}(G)$;(3)
$T$ contains a line $\alpha$ falling in option (2) of Proposition 6.15.
Proof. Let 
$\beta \subseteq T$ be an arc such that 
$G_{\beta }$ is maximal among all stabilisers of arcs of 
$T$ (such an arc exists by Lemma 3.36). Note that 
$\beta$ is a stable arc and set 
$H:=G_{\beta }$ for simplicity.
By Proposition 6.2, we can choose a geometric approximation 
$f\colon \mathcal {G}\rightarrow T$ with an 
$H$-fixed edge 
$e\subseteq \mathcal {G}$ such that 
$f$ is isometric on 
$e$ and 
$\beta \subseteq f(e)$ (up to shrinking 
$\beta$).
Let 
$G\curvearrowright \mathcal {S}$ be the 
$1$-edge splitting obtained by collapsing all edges of 
$\mathcal {G}$ outside the orbit 
$G\cdot e$. Let 
$\overline {e}\subseteq \mathcal {S}$ be the projection of 
$e$, and let 
$A$ and 
$B$ be the 
$G$-stabilisers of its two vertices. Note that the stabilisers of 
$e$ and 
$\overline {e}$ coincide with 
$H$.
We divide the proof into three cases, depending on the behaviour of 
$H$ and its normaliser.
Case (a): 
$H$ is non-elliptic in 
$\omega$-all 
$T_n$. Then we are in case (2) of Proposition 5.12, so 
$H=\ker \rho$ for a homomorphism 
$\rho \colon Z\rightarrow \mathbb {R}$, where 
$Z$ is the stabiliser of a line 
$\alpha \subseteq T_{\omega }$ containing 
$\beta$.
Claim 1 We have 
$N_G(H)=Z$.
Proof of Claim 1 Recall from Proposition 5.12 that the 
$Z$-minimal subtree of 
$T_n$ is a line 
$\alpha _n$ and that the lines 
$\alpha _n$ converge to 
$\alpha$. Since 
$H$ is non-elliptic in 
$\omega$-all 
$T_n$, its minimal subtree coincides with 
$\alpha _n$. Thus, if 
$g\in N_G(H)$, we must have 
$g\alpha _n=\alpha _n$ for 
$\omega$-all 
$T_n$, hence 
$g\alpha =\alpha$. This shows that 
$N_G(H)\leq Z$, while the other inclusion is immediate.
Suppose first that 
$\rho$ is trivial, so that 
$H=Z$. In this case, Proposition 5.15(b) yields a label-irreducible element 
$h\in Z_H(H)$ that is loxodromic in 
$\omega$-all 
$T_n$ with 
$\ell _{T_n}(h)\rightarrow 0$. If 
$g\in G$ commutes with 
$h$, the argument in the proof of Claim 1 shows that 
$g\in Z$. In particular, we have 
$Z_G(h)=H$.
Let 
$\psi \in \operatorname {Aut}(G)$ be the twist or partial conjugation determined by 
$h$ and the splitting 
$G\curvearrowright \mathcal {S}$. In order to show that we fall in options (1) or (2) of the proposition, we only need to prove that 
$\psi$ has infinite order in 
$\operatorname {Out}(G)$.
Note that the standard argument from [Reference Rips and SelaRS94, § 6] applies in this case, yielding a sequence 
$k_n\rightarrow +\infty$ such that, for every finite generating set 
$F\subseteq G$, we have, for 
$\omega$-all 
$n$,
\[ \lim_{n\rightarrow+\infty}\inf_{x\in T_n}\max_{f\in F}d(x,\psi^{k_n}(f)x)<\inf_{x\in T}\max_{f\in F}d(x,fx), \quad \inf_{x\in T}\max_{f\in F}d(x,\psi(f)x)=\inf_{x\in T}\max_{f\in F}d(x,fx). \]
This shows that no power of 
$\psi$ can be an inner automorphism of 
$G$, as required.
Suppose now instead that 
$H=\ker \rho$ is a proper subgroup of 
$Z$. Recall that we are assuming that 
$\rho$ has discrete image and that 
$H=\ker \rho$ is 
$G$-semi-parabolic, hence convex-cocompact.
Thus, we can write 
$Z=H\rtimes \langle z\rangle$ for some 
$z\in Z$. Corollary 2.13(1) guarantees that 
$hz^k$ commutes with 
$H$ for some 
$h\in H$ and 
$k\geq 1$. This element commutes with a finite-index subgroup of 
$Z$, hence with the entire 
$Z$, because 
$G$ is a subgroup of 
$\mathcal {A}_{\Gamma }$. This shows that the centre of 
$Z$ contains an element outside 
$\ker \rho$.
Proceeding as in Case (a) of the proof of Proposition 6.15, we can ensure that the chosen geometric approximation 
$\mathcal {G}$ contains a 
$Z$-invariant line 
$\widetilde \alpha$ on which 
$Z$ acts via the homomorphism 
$\rho$. Note that 
$f(\widetilde \alpha )=\alpha$, so the 
$G$-stabiliser of 
$\widetilde \alpha$ must coincide with 
$Z$.
Note that distinct 
$G$-translates of 
$\widetilde \alpha$ can share at most one point. Indeed, if 
$g\widetilde \alpha$ and 
$\widetilde \alpha$ share an edge, then 
$gHg^{-1}$ fixes an arc of 
$\widetilde \alpha$, hence an arc of 
$\alpha$. Since we chose 
$H$ so that it is maximal among stabilisers of arcs of 
$T$, the stabiliser of every arc of 
$\alpha$ is equal to 
$H$. In conclusion, we have 
$gHg^{-1}\leq H$, and the symmetric argument yields 
$gHg^{-1}=H$. By Claim 1, we obtain 
$g\in Z$, hence 
$g\widetilde \alpha =\widetilde \alpha$.
Since 
$\mathcal {G}$ is simplicial, we obtain a transverse covering of 
$\mathcal {G}$ made up of the 
$G$-translates of 
$\widetilde \alpha$ and all edges of 
$\mathcal {G}$ that are not contained in any 
$G$-translate of 
$\widetilde \alpha$. Proceeding as at the end of Case (b) of Proposition 6.15, we end up in the situation of option (2) of Proposition 6.15 (which is option (3) of the current proposition).
This completes the discussion of Case (a). In the remaining two cases, we will always construct folds or partial conjugations arising from 
$G\curvearrowright \mathcal {S}$, thus ending up in option (1) of the proposition.
Before we proceed, recall that 
$A$ and 
$B$ are the stabilisers of the two vertices of 
$\overline {e}\subseteq \mathcal {S}$. The stabiliser of 
$\overline {e}$ is 
$H$. We make the following observations.
Claim 2 The sets 
$A\setminus H$ and 
$B\setminus H$ are both non-empty.
Proof of Claim 2 This is clear if 
$\mathcal {S}$ gives an amalgamated product splitting of 
$G$. If it gives an HNN splitting with stable letter 
$t$, we are also fine unless 
$A=H$ and either 
$tHt^{-1}\geq H$ or 
$tHt^{-1}\leq H$. Since 
$H$ is convex-cocompact, this can only occur if 
$t\in N_G(H)$, because of Lemma 3.18. But then Corollary 2.13(1) implies that 
$ht^k$ commutes with 
$H$ for some 
$h\in H$ and 
$k\geq 1$, so the axis of 
$ht^k$ in 
$T$ is 
$\langle H,t^k\rangle$-invariant, hence 
$G$-invariant. This implies that 
$T$ is a line, contradicting our assumptions.
Claim 3 If 
$H$ is elliptic in 
$\omega$-all 
$T_n$, then 
$N_G(H)$ is non-elliptic in 
$\omega$-all 
$T_n$ and the 
$N_G(H)$-minimal subtree of 
$\omega$-all 
$T_n$ is not a line.
Proof of Claim 3 By Lemma 5.17, there exists a sequence 
$\epsilon _n\rightarrow 0$ such that 
$N_G(H)$ acts with 
$\epsilon _n$-dense orbits on 
$\operatorname {Fix}(H,T_n)$. Since 
$\beta$ can be approximated by a sequence of arcs 
$\beta _n\subseteq \operatorname {Fix}(H,T_n)$, which have length bounded away from zero, this shows that 
$N_G(H)$ is non-elliptic in 
$\omega$-all 
$T_n$.
Since 
$\operatorname {Fix}(H,T_n)$ is 
$N_G(H)$-invariant, it contains the 
$N_G(H)$-minimal subtree as an 
$\epsilon _n$-dense subset. If the latter is a line 
$\alpha _n\subseteq T_n$ for 
$\omega$-all 
$n$, then these lines converge to an 
$N_G(H)$-invariant line 
$\alpha \subseteq T_{\omega }$. Again, since 
$\beta$ is approximated by arcs in 
$\operatorname {Fix}(H,T_n)$, we have 
$\beta \subseteq \alpha$.
Since 
$N_G(H)$ is not elliptic in 
$T_n$, we have 
$N_G(H)\neq H$. Thus, since 
$H=G_{\beta }$, the normaliser 
$N_G(H)$ must translate non-trivially along 
$\alpha$. This shows that 
$\alpha$ is contained in the 
$G$-minimal subtree 
$T\subseteq T_{\omega }$, so our assumptions guarantee that 
$N_G(H)$ acts discretely on 
$\alpha$. Since the kernel of the action on 
$\alpha$ is exactly 
$H$, it follows that 
$N_G(H)/H\simeq \mathbb {Z}$.
Now, let 
$g\in N_G(H)$ be an element generating this quotient. By the above discussion, we must have 
$\ell _{T_n}(g)\leq \epsilon _n\rightarrow 0$, contradicting the fact that 
$g$ is not elliptic in 
$T$.
Case (b): 
$H$ is elliptic in 
$\omega$-all 
$T_n$ and 
$N_G(H)$ is elliptic in 
$T$. Since 
$N_G(H)$ is finitely generated (e.g. by Corollary 2.13(3)), we can choose the geometric approximation 
$f\colon \mathcal {G}\rightarrow T$ so that 
$N_G(H)$ is elliptic in 
$\mathcal {G}$, hence in 
$\mathcal {S}$. Up to replacing 
$A,B,H$ with 
$G$-conjugates and swapping 
$A$ and 
$B$, we can assume that 
$N_G(H)\leq A$. In particular, 
$Z_G(H)=Z_A(H)$.
By Claim 2, we can pick elements 
$a\in A\setminus H$ and 
$b\in B\setminus H$.
Claim 4 There exist 
$n$ and 
$z\in Z_G(H)$ such that 
$z$ is loxodromic in 
$T_n$ with axis that has bounded (or empty) intersection with both 
$\mathrm {Min}(a,T_n)$ and 
$\mathrm {Min}(b,T_n)$.
Proof of Claim 4 Recall that 
$\langle H,Z_G(H)\rangle$ has finite index in 
$N_G(H)$ by Corollary 2.13(1). Thus, 
$Z_G(H)$ and 
$N_G(H)$ have the same minimal subtree in 
$\omega$-all 
$T_n$, since 
$H$ is elliptic. By Claim 3, this minimal subtree is well defined and its boundary is a Cantor set. On the other hand, if 
$a$ is loxodromic in 
$T_n$, then the boundary of its axis consists of only two points.
Approximate 
$\beta$ by a sequence of arcs 
$\beta _n\subseteq \operatorname {Fix}(H,T_n)$. If 
$a$ is elliptic in 
$T_n$, then the length of 
$\operatorname {Fix}(a,T_n)\cap \beta _n$ must go to zero, since 
$a$ does not fix any portion of the stable arc 
$\beta$. The same holds for 
$b$. Note that, for 
$\omega$-all 
$n$, the arc 
$\beta _n$ contains several branch points of 
$\operatorname {Fix}(H,T_n)$ because of Lemma 5.17.
We conclude that 
$\operatorname {Fix}(H,T_n)\setminus (\mathrm {Min}(a,T_n)\cup \mathrm {Min}(b,T_n))$ contains at least two disjoint rays, and the same holds for the 
$Z_G(H)$-minimal subtree. This yields the required element 
$z\in Z_G(H)$.
By Corollary 2.13(1) and Lemma 2.25(2), 
$Z_G(H)$ virtually splits as 
$Z_H(H)\times K$ with 
$K\perp H$. Since 
$H$ is elliptic in 
$T_n$, we can assume that the element 
$z$ provided by Claim 4 lies in 
$K$ (possibly replacing 
$z$ with a proper power and projecting it to 
$K$, which does not alter its axis in 
$T_n$). Also recall that 
$Z_G(H)=Z_A(H)$. Thus, 
$z$ and 
$\mathcal {S}$ determine a DLS automorphism 
$\psi \in \operatorname {Aut}(G)$, which is necessarily a fold or partial conjugation.
Note that 
$\psi ^k(a)=a$, while 
$\psi ^k(b)=z^kbz^{-k}$ for all 
$k\geq 1$. Since 
$\mathrm {Min}(a,T_n)$ and 
$\mathrm {Min}(b,T_n)$ have bounded projection to the axis of 
$z$ in 
$T_n$, the distance between 
$\mathrm {Min}(\psi ^k(a),T_n)$ and 
$\mathrm {Min}(\psi ^k(b),T_n)$ diverges for 
$k\rightarrow +\infty$. It follows that 
$\ell _{T_n}(\psi ^k(ab))$ diverges for 
$k\rightarrow +\infty$, showing that 
$\psi$ has infinite order in 
$\operatorname {Out}(G)$, as required.
Case (c): 
$H$ is elliptic in 
$\omega$-all 
$T_n$ and 
$N_G(H)$ is non-elliptic in 
$T$. Making sure that the chosen stable arc 
$\beta$ is contained in the axis of an element of 
$N_G(H)$, we can ensure that 
$N_G(H)$ remains non-elliptic in 
$\mathcal {S}$. Claim 3 guarantees that 
$N_G(H)/H$ is not cyclic.
Given Lemma 6.12, we are only left to consider the case when 
$N_G(H)/H$ is a free product of virtually abelian groups 
$V_1\ast V_2$. Recall that 
$\beta \subseteq T$ has been chosen so that its stabiliser is maximal among stabilisers of arcs of 
$T$ (at the beginning of the proof). This guarantees that the action 
$N_G(H)/H\curvearrowright \operatorname {Fix}(H,\mathcal {G})$ gives a free splitting of 
$N_G(H)/H$. The only situation where Lemma 6.12 cannot be applied is if both 
$V_1$ and 
$V_2$ are elliptic in 
$\mathcal {G}$ (and hence in 
$T$).
Let us show that 
$V_1$ and 
$V_2$ cannot both be elliptic in 
$T$. Suppose for the sake of contradiction that they are. Recall that 
$\mathfrak {T}(V_i,T_n)$ denotes 
$\operatorname {Fix}(V_i,T_n)$ if this is non-empty, and the 
$V_i$-minimal subtree of 
$T_n$ otherwise, which is necessarily a line. Since 
$N_G(H)$ is not elliptic in 
$T$, the fixed sets of 
$V_1$ and 
$V_2$ in 
$T$ have positive distance, say 
$D>0$. Thus, the subtrees 
$\mathfrak {T}(V_1,T_n)$ and 
$\mathfrak {T}(V_2,T_n)$ are at distance at least 
$D/2$ for 
$\omega$-all 
$n$.
Recall that Lemma 5.17 yields a sequence 
$\epsilon _n\rightarrow 0$ such that 
$V_1\ast V_2$ acts with 
$\epsilon _n$-dense orbits on 
$\operatorname {Fix}(H,T_n)$. In particular, note that 
$\operatorname {Fix}(H,T_n)$ and the 
$N_G(H)$-minimal subtree of 
$T_n$ are at Hausdorff distance 
$\leq \epsilon _n$. Thus, Corollary 4.20 shows that there exists a sequence 
$\epsilon _n'\rightarrow 0$ such that the actions of 
$V_1$ and 
$V_2$ on 
$\operatorname {Fix}(H,T_n)$ are both 
$\epsilon _n'$-rotating, in the sense of Definition 4.18.
Now, a straightforward ping-pong argument implies that an 
$N_G(H)$-orbit misses the ball of radius 
$D/4$ centred at the midpoint of the arc joining 
$\mathfrak {T}(V_1,T_n)$ and 
$\mathfrak {T}(V_2,T_n)$. For large 
$n$, we have 
$\epsilon _n< D/4$, so this is the required contradiction.
Remark 6.18 In Case (a) of the proof of Proposition 6.17, we have constructed a shortening automorphism in the sense of [Reference Rips and SelaRS94]. However, in Case (b), we have made the rather unusual choice of constructing a ‘lengthening automorphism’, and in Case (c) we have not described the resulting automorphism at all.
We followed this path in order to give a more direct proof of Proposition 6.17. Nevertheless, we want to emphasise that a shortening automorphism can indeed be constructed in each of the three cases of the proof of Proposition 6.17. This requires some more work, as one cannot simply ‘contract one edge’ as in [Reference Rips and SelaRS94, § 6], but rather needs to perform a folding procedure.
We are only left to record the following simple observation before we can begin with the proof of the main theorems.
Lemma 6.19 Suppose that 
$T\simeq \mathbb {R}$ and that 
$G\curvearrowright T$ has discrete orbits. If the kernel of the 
$G$-action is 
$G$-semi-parabolic, then it has non-trivial centre.
Proof. Let 
$H$ be the kernel of the 
$G$-action. Since 
$G$ acts discretely, there exists a loxodromic element 
$g\in G$ such that 
$G=H\rtimes \langle g\rangle$. Since 
$H$ is 
$G$-semi-parabolic, and in particular convex-cocompact, Corollary 2.13(1) shows that 
$hg^k$ commutes with 
$H$ for some 
$h\in H$ and 
$k\geq 1$.
If the centre of 
$H$ were trivial, then the centre of 
$G$ would be isomorphic to 
$\mathbb {Z}$ and it would contain the element 
$hg^k$. In particular, 
$\omega$-all automorphisms 
$\varphi _n$ would fix 
$hg^k$, hence 
${\ell _{T_n}(hg^k)\rightarrow 0}$. This would contradict the fact that 
$hg^k$ is loxodromic in 
$T$ and 
$T_{\omega }$.
We are finally ready to prove Theorems A and B and Corollary D.
Proof of Theorem A The fact that the DLS automorphisms appearing in the statement of the theorem are coarse-median preserving follows from Theorem E, which will be proved in § 7. Here we only show that such automorphisms exist and have infinite order in 
$\operatorname {Out}(G)$.
Let 
$G$ be a special group with 
$\operatorname {Out}_{\rm cmp}(G)$ infinite. Choose a sequence 
$\varphi _n\in \operatorname {Aut}_{\rm cmp}(G)$ projecting to an infinite sequence in 
$\operatorname {Out}_{\rm cmp}(G)$. We can apply the construction at the beginning of § 5.4 to obtain an action on an 
$\mathbb {R}$-tree 
$G\curvearrowright T_{\omega }$. Let 
$T\subseteq T_{\omega }$ be the 
$G$-minimal subtree.
By Propositions 5.12 and Proposition 5.15(c1), the 
$G$-stabiliser of every arc of 
$T$ is a centraliser, and every line of 
$T$ is acted upon discretely by its 
$G$-stabiliser. In addition, 
$T$ is not itself a line.
Suppose first that no geometric approximation 
$\mathcal {G}\rightarrow T$ admits indecomposable components in the transverse covering provided by Proposition 6.6, i.e. that all geometric approximations of 
$T$ are simplicial. Then we can apply Proposition 6.17. Note that option (3) never occurs: in the notation of the proof of Proposition 6.17, it corresponds to Case (a), when 
$\ker \rho$ is a proper subgroup of 
$Z$ and is non-elliptic in 
$\omega$-all 
$T_n$. This is ruled out by Proposition 5.15(c1).
In conclusion, we are in options (1) or (2) of Proposition 6.17, so 
$G$ splits over a centraliser, giving rise to a DLS automorphism that conforms to the requirements in the statement of Theorem A.
To complete the proof, it remains to consider the case when some geometric approximation 
$f\colon \mathcal {G}\rightarrow T$ admits an indecomposable component 
$U$. Up to replacing 
$\mathcal {G}$ and 
$U$, Lemma 6.9 allows us to assume that all arcs of 
$U$ have the same stabiliser 
$H$, which is also the stabiliser of a stable arc of 
$T$. In addition, 
$U$ is not a line, otherwise 
$f(U)\subseteq T$ would be a line with a non-discrete action by its stabiliser. Thus, we can apply Proposition 6.16, which shows that 
$G$ splits over a centraliser and admits a fold, partial conjugation or twist with infinite order in 
$\operatorname {Out}(G)$. Twists only occur in the ‘surface case’ and they satisfy the requirements of Theorem A.
This completes the proof.
Proof of Theorem B Let 
$G$ be a special group with 
$\operatorname {Out}(G)$ infinite. Any infinite sequence in 
$\operatorname {Out}(G)$ yields a 
$G$-tree 
$G\curvearrowright T_{\omega }$ as in § 5.4. Let 
$T\subseteq T_{\omega }$ be the 
$G$-minimal subtree.
Suppose first that one of the following happens:
(i) a line
$\alpha \subseteq T$ is acted upon non-discretely by its $G$-stabiliser;(ii) the
$G$-stabiliser of an arc $\beta \subseteq T$ is not $G$-semi-parabolic;(iii)
$T$ is a line.
In case (ii), 
$\beta$ necessarily falls into option (2) of Proposition 5.12 and we denote by 
$\alpha$ the line that it provides. In case (iii), we simply set 
$\alpha :=T$. In each of the three cases, we obtain a line 
$\alpha$ that is acted upon non-trivially by its 
$G$-stabiliser.
Now, we apply Proposition 6.15 to the line 
$\alpha$. Observe that, we can assume that we are in option (2) of Proposition 6.15. Indeed, this is clear in case (iii), since 
$\alpha =T$. Regarding instead cases (i) and (ii), we clearly cannot fall into option (1) of Proposition 6.15, whereas option (3) can be handled using Proposition 6.16, resulting in a DLS automorphism as in Theorem A.
In conclusion, suppose that we have a line 
$\alpha \subseteq T$ falling into option (2) of Proposition 6.15. Let 
$Z$ be the stabiliser of 
$\alpha$ and let 
$\rho \colon Z\rightarrow \mathbb {R}$ be the homomorphism giving translation lengths, which is non-trivial. Since 
$Z/\ker \rho$ is free abelian, there exists a homomorphism 
$\overline {\rho }\colon Z\rightarrow \mathbb {Z}$ such that 
$\ker \rho \leq \ker \overline {\rho }$. Note that 
$\overline {\rho }$ gives an HNN splitting of 
$Z$ over 
$\ker \overline {\rho }$, with stable letter in 
$Z$. Appealing to Lemma 6.10, this results in an HNN splitting of 
$G$ over 
$\ker \overline {\rho }$ with the same stable letter.
By Proposition 5.15(a), we have 
$Z=Z_G(x)$ for some 
$x\in G$. By Proposition 5.15(d) and Lemma 6.19, the centre of 
$\ker \overline {\rho }$ is non-trivial. By Remark 3.34, the centre of 
$\ker \overline {\rho }$ is contained in the centre of 
$Z$, so it commutes with the stable letter of the HNN splitting of 
$G$. Any element in the centre of 
$\ker \overline {\rho }$ gives a twist with infinite order in 
$\operatorname {Out}(G)$ by Lemma 6.11. In conclusion, we have constructed an automorphism as in type (3) in the statement of Theorem B.
By the above discussion, we can assume in the rest of the proof that cases (i)–(iii) do not occur, i.e. that 
$T$ is not a line, that all arc-stabilisers are 
$G$-semi-parabolic, and that every line in 
$T$ is acted upon discretely by its stabiliser. Note however that not all arc-stabilisers might be centralisers.
Now, we can conclude via Propositions 6.16 and 6.17 as in the proof of Theorem A. If option (3) of Proposition 6.17 presents itself, then we obtain an automorphism as in type (3) of Theorem B as above. In all other cases, we obtain a DLS automorphism that has infinite order in 
$\operatorname {Out}(G)$ and is coarse-median preserving by Theorem E. Thus, 
$\operatorname {Out}_{\rm cmp}(G)$ is infinite and, appealing to Theorem A, we obtain a DLS automorphism of the required form.
This completes the proof.
Proof of Corollary D Let 
$\mathscr {H}$ be the collection of subgroups of 
$G$ of the form 
$Z_G(x)$ with 
$x\in G$. Suppose that, for every 
$\mathcal {H}\in \mathscr {H}$, the 
$\operatorname {Out}(G)$-orbit of 
$\mathcal {H}$ is infinite. We will show that 
$\operatorname {Out}_{\rm cmp}(G)$ is infinite.
By Lemma 5.16, there exist automorphisms 
$\phi _n\in \operatorname {Out}(G)$ such that, for every 
$\mathcal {H}\in \mathscr {H}$, the sequence 
$\phi _n(\mathcal {H})$ eventually consists of pairwise distinct classes. Let us run the proof of Theorem A for this sequence of automorphisms. The only place where we used that the automorphisms were coarse-median preserving was when applying Proposition 5.15(c1), which we can now replace by Proposition 5.15(c2). Thus, we obtain a coarse-median preserving DLS automorphism with infinite order in 
$\operatorname {Out}(G)$, as required.
7. Coarse-median preserving DLS automorphisms
The goal of this section is the following result. The UCP (uniformly cocompact projections) condition is introduced in § 7.1.
Theorem 7.1 Let 
$G\curvearrowright X$ be a proper, cocompact, non-transverse action on a 
${\rm CAT(0)}$ cube complex. Suppose that 
$G$ splits as 
$G=A\ast _CB$ or 
$G=A\ast _C$, where 
$C$ is convex-cocompact, satisfies the UCP condition in 
$X$ and does not have any non-trivial finite normal subgroups. Then we have the following.
(1) All partial conjugations and folds determined by this splitting are coarse-median preserving.
(2) If
$z\in Z_C(C)$ is such that $\langle z\rangle$ is convex-cocompact in $X$ and $Z_G(c)$ is contained in a conjugate of $A$ for every $c\in C$ such that $\langle c\rangle \cap \langle z\rangle \neq \{1\}$, then the twist determined by $z$ is coarse-median preserving.(3) More generally, if, for every infinite-order element
$c\in C$ commuting with a finite-index subgroup of $C$, the centraliser $Z_G(c)$ is contained in a conjugate of $A$, then all transvections determined by the splitting $G=A\ast _C$ are coarse-median preserving.
The proof of Theorem 7.1 is simpler if the cube complex 
$X$ contains a collection of pairwise disjoint hyperplanes such that their dual tree is precisely the Bass–Serre tree 
$T$ of the splitting of 
$G$. This is the situation that we consider in § 7.4.
The previous subsections reduce the proof to this setting. The main idea is to ‘inflate’ a convex, 
$C$-invariant subcomplex of 
$X$ to a hyperplane. This is achieved by considering the 
$G$-action on the product 
$X\times T$, and recovering cocompactness by restricting to its ‘cubical Guirardel core’. This is a generalisation of the Guirardel core of a product of two trees [Reference GuirardelGui05] that we introduce in § 7.3. Our construction can also be viewed as a broad generalisation of the idea of Salvetti blowups from [Reference Charney, Stambaugh and VogtmannCSV17].
7.1 Uniformly cocompact projections
Let 
$G\curvearrowright X$ be a proper cocompact action on a 
${\rm CAT(0)}$ cube complex. We denote Hausdorff distances by 
$d_{\rm Haus}(\cdot,\cdot )$.
Lemma 7.2 Consider a subgroup 
$H\leq G$ and 
$H$-invariant, convex subcomplexes 
$Z,W\subseteq X$ with 
$d_{\rm Haus}(Z,W)=D$. Then 
$d_{\rm Haus}(\pi _Z(gZ),\pi _W(gW))\leq 3D$ for all 
$g\in G$.
Proof. Since 
$\pi _Z$ is 
$1$-Lipschitz, we have 
$d_{\rm Haus}(\pi _Z(gZ),\pi _Z(gW))\leq D$. In addition, for every 
$x\in X$
\begin{align*}
\mathscr{W}(\pi_Z(x)|\pi_W(x))=\mathscr{W}(x,\pi_Z(x)|\pi_W(x))\cup\mathscr{W}(\pi_Z(x)|x,\pi_W(x))
\subseteq\mathscr{W}(\pi_Z(x)|W)\cup\mathscr{W}(Z|\pi_W(x)),
\end{align*}
and hence 
$d(\pi _Z(x),\pi _W(x))\leq 2D$. It follows that 
$d_{\rm Haus}(\pi _Z(gZ),\pi _W(gW))\leq 3D$.
Definition 7.3 (Uniformly cocompact projections)
Let 
$H\leq G$ be convex-cocompact in 
$X$. Let 
$Z\subseteq X$ be any 
$H$-invariant, 
$H$-cocompact convex subcomplex. We say that 
$H$ satisfies the UCP condition in 
$X$ if there exists 
$N\geq 1$ such that, for every 
$g\in G$, the action 
$H\cap gHg^{-1}\curvearrowright \pi _Z(gZ)$ has at most 
$N$ orbits of vertices.
Since 
$X$ is uniformly locally finite, Lemma 7.2 shows that this property only depends on the subgroup 
$H\leq G$ and the action 
$G\curvearrowright X$, and not on the specific choice of 
$Z$.
Our interest in the UCP condition is exclusively related to Lemma 7.4 below. In Lemma 7.5, we will show that convex-cocompact subgroups of special groups satisfy the UCP condition in any cospecial cubulation. However, even when restricting to special groups 
$G$, we will need this property within non-cospecial cubulations of 
$G$ (see § 7.4).
Recall that a sequence of hyperplanes 
$\mathfrak {u}_1,\dots,\mathfrak {u}_k$ is said to be a chain of hyperplanes if, for each 
$2\leq i\leq k-1$, the hyperplane 
$\mathfrak {u}_i$ separates 
$\mathfrak {u}_{i-1}$ from 
$\mathfrak {u}_{i+1}$.
Lemma 7.4 Let 
$\mathfrak {w}\in \mathscr {W}(X)$ be a hyperplane. Let 
$H$ be its 
$G$-stabiliser and suppose that 
$H$ satisfies the UCP condition and acts non-transversely on 
$X$. Then there exists 
$K\geq 1$ such that, for every chain 
$\mathfrak {w},g_1\mathfrak {w},\dots,g_k\mathfrak {w}$ of 
$G$-translates of 
$\mathfrak {w}$ such that 
$\pi _{\mathfrak {w}}(g_1\mathfrak {w})\supsetneq \dots \supsetneq \pi _{\mathfrak {w}}(g_k\mathfrak {w})$, we have 
$k\leq K$.
Proof. Since 
$H$ satisfies the UCP condition, there exists 
$N\geq 1$ such that, for every 
$g\in G$, the subgroup 
$H\cap gHg^{-1}$ acts on 
$\pi _{\mathfrak {w}}(g\mathfrak {w})$ with at most 
$N$ orbits of vertices. As in the claim during the proof of Lemma 2.9, there exists 
$N'\geq 1$ such that, for every 
$p\in X$, there are at most 
$N'$ subgroups of 
$G$ that act with at most 
$N$ orbits of vertices on a convex subcomplex of 
$X$ containing 
$p$. We will show that 
$k\leq N\cdot N'$.
Since the hyperplanes 
$\mathfrak {w},g_1\mathfrak {w},\dots,g_k\mathfrak {w}$ form a chain and 
$H$ acts non-transversely on 
$X$, we have 
$g_1Hg_1^{-1}\cap H\geq \dots \geq g_kHg_k^{-1}\cap H$. By the previous paragraph, there are at most 
$N'$ distinct subgroups of 
$G$ among the 
$g_iHg_i^{-1}\cap H$. Thus, it suffices to assume that 
$g_iHg_i^{-1}\cap H$ is constant and show that 
$k\leq N$. The latter follows from the observation that, in this situation, the number of orbits in 
$\pi _{\mathfrak {w}}(g_i\mathfrak {w})$ is bounded above by 
$N$ and must strictly decrease as 
$i$ increases.
The following implies that convex-cocompact subgroups of special groups satisfy the UCP condition in any cospecial cubulation.
Lemma 7.5 Convex-cocompact subgroups of 
$\mathcal {A}_{\Gamma }$ satisfy the UCP condition in 
$\mathcal {X}_{\Gamma }$.
Proof. Let 
$H\leq \mathcal {A}_{\Gamma }$ be a convex-cocompact subgroup. Let 
$Z\subseteq \mathcal {X}_{\Gamma }$ be an 
$H$-invariant, 
$H$-cocompact, convex subcomplex. Let 
$Z_0\subseteq Z$ be a finite subset meeting every 
$H$-orbit.
Let 
$\mathscr {P}$ be the set of parabolic subgroups of 
$\mathcal {A}_{\Gamma }$ whose parabolic stratum meets 
$Z_0$. Note that 
$\mathscr {P}$ is finite. If 
$P\in \mathscr {P}$, recall that 
$\mathcal {W}_1(P)\subseteq \mathscr {W}(\mathcal {X}_{\Gamma })$ are the hyperplanes skewered by elements of 
$P$.
Claim If 
$g\in \mathcal {A}_{\Gamma }$ and 
$\pi _Z(gZ)\cap Z_0\neq \emptyset$, then there exist 
$\overline g\in \mathcal {A}_{\Gamma }$ and 
$P\in \mathscr {P}$ such that:
(1)
$\overline {g}Z\cap Z_0\neq \emptyset$ and $\mathscr {W}(\pi _Z(gZ))=\mathscr {W}(Z)\cap \mathscr {W}(\overline gZ)\cap \mathcal {W}_1(P)$;(2)
$H\cap gHg^{-1}=H\cap \overline {g}H\overline {g}^{-1}\cap P$.
Proof of Claim If 
$gZ\cap Z\neq \emptyset$, then 
$gZ$ meets 
$Z_0$, and we can take 
$\overline g=g$ and 
$P=\mathcal {A}_{\Gamma }$.
Otherwise, 
$\mathscr {W}(Z|gZ)$ is non-empty and we define 
$P\leq \mathcal {A}_{\Gamma }$ as the largest parabolic subgroup fixing 
$\mathscr {W}(Z|gZ)$ pointwise. Since 
$\pi _Z(gZ)$ meets 
$Z_0$, we have 
$P\in \mathscr {P}$. Note that 
$\mathcal {W}_1(P)\subseteq \mathscr {W}(\mathcal {X}_{\Gamma })$ coincides with the set of all hyperplanes transverse to 
$\mathscr {W}(Z|gZ)$.
Choose a pair of gates 
$z\in Z$, 
$z'\in gZ$ for 
$Z$ and 
$gZ$, with 
$z\in Z_0$. Choose 
$g'\in \mathcal {A}_{\Gamma }$ with 
$g'z'=z$. Observing that 
$H\cap gHg^{-1}\leq P$ and that 
$g'$ commutes with 
$P$ (e.g. by Lemma 3.4), we deduce that
\[ H\cap gHg^{-1}=H\cap gHg^{-1}\cap P=H\cap (g'g)H(g'g)^{-1}\cap P. \]
Setting 
$\overline {g}:=g'g$, condition (2) is satisfied. We also have 
$z\in \overline {g}Z\cap Z_0$, hence 
$\overline {g}Z\cap Z_0\neq \emptyset$.
Since 
$g'$ fixes 
$\mathcal {W}_1(P)$ pointwise and 
$\overline g=g'g$, we have 
$\mathscr {W}(\overline gZ)\cap \mathcal {W}_1(P)=\mathscr {W}(gZ)\cap \mathcal {W}_1(P)$. Recalling that 
$\mathcal {W}_1(P)$ is the set of hyperplanes transverse to 
$\mathscr {W}(Z|gZ)$, we obtain
\[ \mathscr{W}(\pi_Z(gZ))=\mathscr{W}(Z)\cap\mathscr{W}(gZ)=\mathscr{W}(Z)\cap\mathscr{W}(gZ)\cap\mathcal{W}_1(P)=\mathscr{W}(Z)\cap\mathscr{W}(\overline gZ)\cap\mathcal{W}_1(P), \]
which completes the proof of the claim.
Since the action 
$H\curvearrowright Z$ is cocompact, each point of 
$\mathcal {X}_{\Gamma }$ lies in only finitely many pairwise-distinct 
$\mathcal {A}_{\Gamma }$-translates of 
$Z$ (see Claim 1 in the proof of Lemma 2.8). Moreover, 
$H$ has finite index in the 
$\mathcal {A}_{\Gamma }$-stabiliser of 
$Z$. It follows that the set of elements 
$\overline g\in \mathcal {A}_{\Gamma }$ such that 
$\overline gZ\cap Z_0\neq \emptyset$ is a finite union of left cosets of 
$H$.
Note that, in order to prove the lemma, it suffices to show that the actions 
$H\cap gHg^{-1}\curvearrowright \pi _Z(gZ)$ are uniformly cocompact when 
$\pi _Z(gZ)\cap Z_0\neq \emptyset$. By the claim and the previous paragraph, there are only finitely many options for such subgroups 
$H\cap gHg^{-1}$ and sets 
$\pi _Z(gZ)$. So it suffices to show that each action 
$H\cap gHg^{-1}\curvearrowright \pi _Z(gZ)$ is cocompact, which follows from Lemma 2.8.
Proof of Theorem E Since 
$G$ is special, it admits a cospecial cubulation 
$G\curvearrowright X$. By Lemma 7.5, we can apply Theorem 7.1 to this action. To reconcile the differences in parts (2) and (3) between Theorems E and 7.1, it suffices to recall that 
$G$ is torsion-free and that elements of 
$G$ with commuting powers must themselves commute.
7.2 Panel collapse
Here, we record the following special case of the panel collapse procedure of Hagen and Touikan [Reference Hagen and TouikanHT19], restricting ourselves to non-transverse actions. Under this assumption, panel collapse, normally a fairly violent procedure, does not alter the coarse median structure.
Proposition 7.6 Let 
$G\curvearrowright X$ be a cocompact, non-transverse action on a 
${\rm CAT(0)}$ cube complex without inversions. Suppose that there exists a halfspace 
$\mathfrak {h}\in \mathscr {H}(X)$ that is minimal (under inclusion) among halfspaces transverse to a hyperplane 
$\mathfrak {w}\in \mathscr {W}(X)$. Then there exists 
$Y$ such that:
(1)
$Y$ is a $G$-invariant subcomplex of $X$ with $Y^{(0)}=X^{(0)}$;(2)
$Y$ is a ${\rm CAT(0)}$ cube complex (though not convex, nor a median subalgebra in $X$);(3)
$Y$ has strictly fewer $G$-orbits of edges than $X$;(4) the identity map
$X^{(0)}\rightarrow Y^{(0)}$ is coarse-median preserving;(5) the intersection
$\mathfrak {w}\cap Y$ is non-empty and connected.
Proof. Say that an edge 
$e\subseteq X$ is bad if there exists 
$g\in G$ such that 
$e$ is contained in 
$g\mathfrak {h}$ and crosses 
$g\mathfrak {w}$. Let 
$\mathcal {G}\subseteq X^{(1)}$ be the subgraph obtained by removing interiors of bad edges. Since the action 
$G\curvearrowright X$ is non-transverse and without inversions, then, for every cube 
$c\subseteq X$ with 
$\dim c\geq 2$, the intersection between 
$\mathcal {G}$ and the 
$1$-skeleton of 
$c$ is connected.
We define 
$Y$ as the full subcomplex of 
$X$ with 
$Y^{(1)}=\mathcal {G}$. Parts (1), (3) and (5) are immediate. Part (2) is proved in [Reference Hagen and TouikanHT19] (of which we are considering the simplest possible case, since 
$\mathcal {G}$ has connected intersection with 
$1$-skeletons of cubes of 
$X$).
It remains to prove part (4). We will speak of 
$X$-geodesics and 
$Y$-geodesics, depending on which of the two metrics we are considering. Let 
$m_X$ and 
$m_Y$ be the median operators on 
$X^{(0)}=Y^{(0)}$ induced by 
$X$ and 
$Y$, respectively. If 
$\alpha$ and 
$\beta$ are paths in 
$X^{(1)}$ (possibly containing edges outside 
$Y$), we write 
$\delta _Y(\alpha,\beta )$ for the Hausdorff distance in the metric of 
$Y$ between the two intersections 
$\alpha \cap X^{(0)}$ and 
$\beta \cap X^{(0)}$.
Claim For every 
$X$-geodesic 
$\alpha \subseteq X^{(1)}$, there exists a 
$Y$-geodesic 
$\beta \subseteq Y^{(1)}$ with the same endpoints and with 
$\delta _Y(\alpha,\beta )\leq 2$.
Assuming the claim, we prove part (4). Consider three points 
$x,y,z\in X^{(0)}$. By the claim, the point 
$m_X(x,y,z)$ is at distance 
$\leq 2$ in 
$Y$ from a 
$Y$-geodesic between any two of these three points. Thus, at most two hyperplanes of 
$Y$ separate 
$m_X(x,y,z)$ from any two among 
$x,y,z$. Hence at most six hyperplanes of 
$Y$ separate 
$m_X(x,y,z)$ and 
$m_Y(x,y,z)$, which shows part (4).
Now, in order to prove the claim, let 
$\alpha \subseteq X^{(1)}$ be an 
$X$-geodesic. Consider a bad edge 
$e\subseteq \alpha$, and let 
$g\in G$ be an element such that 
$e$ crosses 
$g\mathfrak {w}$ and is contained in 
$g\mathfrak {h}$. We say that 
$e$ is avoidable if 
$g\mathfrak {h}$ contains exactly one of the endpoints of 
$\alpha$.
Sub-claim There exists an 
$X$-geodesic 
$\alpha '\subseteq X^{(1)}$, with the same endpoints as 
$\alpha$, such that 
$\delta _Y(\alpha,\alpha ')\leq 1$ and 
$\alpha '$ contains no avoidable bad edges.
Proof of Sub-claim Let 
$e\subseteq \alpha$ be an avoidable bad edge, crossing a hyperplane 
$g\mathfrak {w}$ and contained in a halfspace 
$g\mathfrak {h}$. Let 
$\alpha _e\subseteq \alpha$ be the subsegment lying in the carrier of the hyperplane bounding 
$g\mathfrak {h}$. Let 
$\alpha _e'$ be the 
$X$-geodesic, with the same endpoints as 
$\alpha _e$, that is entirely contained in 
$g\mathfrak {h}^*$ except for its initial or terminal edge. Then 
$\delta _Y(\alpha _e,\alpha _e')=1$ and, by minimality of 
$\mathfrak {h}$, no edge of 
$\alpha _e'$ is bad.
Replacing the segment 
$\alpha _e\subseteq \alpha$ with 
$\alpha _e'$, then repeating the procedure for the two geodesics forming 
$\alpha \setminus \alpha _e$ yields the sub-claim.
Proof of Claim Now, let 
$e_1,\dots,e_k$ be the bad edges on 
$\alpha '$, in order of appearance along it. Let 
$g_i\in G$ be elements such that 
$e_i$ crosses 
$g_i\mathfrak {w}$ and is contained in 
$g_i\mathfrak {h}$. Since none of the 
$e_i$ is avoidable, we must have 
$\alpha '\subseteq g_i\mathfrak {h}$ for every 
$i$.
We define a new path 
$\beta \subseteq X^{(1)}$ as follows. Let 
$s$ be the highest index with 
$g_s\mathfrak {h}=g_1\mathfrak {h}$. Let 
$\gamma _1\subseteq \alpha '$ be the segment starting with 
$e_1$ and ending with 
$e_s$. We replace 
$\gamma _1$ with the path that immediately crosses into 
$g_1\mathfrak {h}^*$, then crosses the same hyperplanes as 
$\gamma _1$, and finally crosses back into 
$g_1\mathfrak {h}=g_s\mathfrak {h}$. We deal in a similar way with all other halfspaces 
$g_i\mathfrak {h}$ in order to avoid all bad edges on 
$\alpha '$.
Now, the path 
$\beta$ contains no bad edges. It is not an 
$X$-geodesic, but it is straightforward to check that it is a 
$Y$-geodesic. In addition, 
$\delta _Y(\alpha ',\beta )\leq 1$, hence 
$\delta _Y(\alpha,\beta )\leq 2$.
This completes the proof of the proposition.
Note that, by part (5), the intersection 
$\mathfrak {w}\cap Y$ is a hyperplane of 
$Y$. We can only apply Proposition 7.6 a finite number of times because of part (3). Eventually, we obtain the following.
Corollary 7.7 Let 
$G\curvearrowright X$ be a cocompact, non-transverse action on a 
${\rm CAT(0)}$ cube complex without inversions. Then there exists 
$Y\subseteq X$ such that:
(1)
$Y$ is a $G$-invariant subcomplex with $Y^{(0)}=X^{(0)}$;(2)
$Y$ is a ${\rm CAT(0)}$ cube complex (though not convex, nor a median subalgebra in $X$);(3) the action
$G\curvearrowright Y$ is hyperplane-essential;(4) the identity map
$X^{(0)}\rightarrow Y^{(0)}$ is coarse-median preserving.
In certain situations, it is convenient to prioritise connectedness of a certain hyperplane over essentiality of all other hyperplanes. This can be similarly achieved with a repeated application of Proposition 7.6.
Corollary 7.8 Given 
$\mathfrak {w}\in \mathscr {W}(X)$, property (3) in Corollary 7.7 can be replaced with:
(
$3'$) the intersection $\mathfrak {w}\cap Y$ is connected and the action $G_{\mathfrak {w}}\curvearrowright \mathfrak {w}\cap Y$ is essential.
7.3 Cubical Guirardel cores
Guirardel's notion of core for a product of actions on 
$\mathbb {R}$-trees 
$G\curvearrowright T_1\times T_2$ [Reference GuirardelGui05] can be rephrased purely in median-algebra terms: it is (closely related to) the median subalgebra of 
$T_1\times T_2$ generated by a 
$G$-orbit. As such, this notion can be naturally extended to products of 
${\rm CAT(0)}$ cube complexes.
In this subsection, we are concerned with cocompactness of this notion of core. The main result is Proposition 7.9, which we will only require in the special case of Corollary 7.14.
We remark that cocompactness of the core can be achieved more generally, but one must allow the core to be a non-
${\rm CAT(0)}$ cube complex, and thus abandon the setting of median algebras. This insight is explored in forthcoming work of Hagen and Wilton.
Proposition 7.9 Let 
$G$ act on 
${\rm CAT(0)}$ cube complexes 
$X$ and 
$Y$. Suppose that 
$G\curvearrowright X$ is proper and cocompact, while 
$G\curvearrowright Y$ is essential and has only finitely many orbits of hyperplanes. Then the following are equivalent.
(1) Every
$G$-orbit in the $0$-skeleton of $X\times Y$ generates a $G$-cofinite median subalgebra.(2) Some
$G$-orbit in the $0$-skeleton of $X\times Y$ generates a $G$-cofinite median subalgebra.(3) The stabiliser of every hyperplane of
$Y$ is convex-cocompact in $X$.
Before proving the proposition, we need to record a couple of observations.
Definition 7.10 Consider a group 
$\Gamma$, a subgroup 
$H\leq \Gamma$, and the action 
$H\curvearrowright \Gamma$ by left multiplication. An 
$H$-AIS (Almost Invariant Set) is a subset 
$A\subseteq \Gamma$ such that:
(1)
$A$ is $H$-invariant;(2) both
$A$ and its complement $\Gamma \setminus A$ contain infinitely many $H$-orbits;(3) for every
$g\in \Gamma$, the symmetric difference $Ag\triangle A$ is $H$-cofinite.
If 
$A$ is an 
$H$-AIS, then the set 
$A^*:=\Gamma \setminus A$ is another 
$H$-AIS.
Lemma 7.11 Let 
$G\curvearrowright X$ be a proper cocompact action on a 
${\rm CAT(0)}$ cube complex. Let 
$H\leq G$ be a convex-cocompact subgroup. Let 
$A\subseteq G$ be an 
$H$-AIS. Then, for every vertex 
$x_0\in X$, there exists a partition 
$X=C_-\sqcup C_0\sqcup C_+$ such that:
(1)
$C_0$ is an $H$-invariant convex subcomplex of $X$ on which $H$ acts cocompactly;(2)
$C_-$ and $C_+$ are $H$-invariant unions of connected components of $X\setminus C_0$;(3)
$A\cdot x_0\subseteq C_0\cup C_+$ and $A^*\cdot x_0\subseteq C_0\cup C_-$.
Proof. Choose 
$R\geq 0$ such that 
$G\cdot x_0$ is 
$R$-dense in 
$X$. Observing that 
$G$ is finitely generated, we can fix a word metric 
$(G,d)$. Choose 
$r\geq 0$ so that 
$d(g,h)\leq r$ for all 
$g,h\in G$ with 
$d(gx_0,hx_0)\leq 2R$. Let 
$\Delta \subseteq G$ be the intersection between 
$A^*\subseteq G$ and the 
$r$-neighbourhood of 
$A$ in 
$G$. Since 
$A$ is an 
$H$-AIS, 
$\Delta$ is 
$H$-cofinite.
Since 
$H$ is convex-cocompact, there exists an 
$H$-invariant convex subcomplex 
$K\subseteq X$ on which 
$H$ acts cocompactly. Since 
$\Delta$ is 
$H$-cofinite, there exists 
$L\geq 0$ such that the neighbourhood 
$N_L(K)$ contains the 
$R$-neighbourhood of 
$\Delta \cdot x_0$. We define 
$C_0$ as the convex hull of 
$N_L(K)$. This is clearly an 
$H$-invariant convex subcomplex of 
$X$. By [Reference BowditchBow13, Lemma 6.4], 
$C_0$ is at finite Hausdorff distance from 
$K$, so the action 
$H\curvearrowright C_0$ is again cocompact.
Now, define 
$C_+$ as the union of the connected components of 
$X\setminus C_0$ that intersect 
$A\cdot x_0$. Since 
$A\cdot x_0$ is 
$H$-invariant, so is 
$C_+$. The set 
$C_-$ is defined analogously using 
$A^*\cdot x_0$. We are only left to show that a single connected component of 
$X\setminus C_0$ cannot intersect both 
$A\cdot x_0$ and 
$A^*\cdot x_0$.
Suppose for the sake of contradiction that there exists a path 
$\alpha \subseteq X\setminus C_0$ joining a point of 
$A\cdot x_0$ to a point of 
$A^*\cdot x_0$. Since every point of 
$\alpha$ is at distance 
$\leq R$ from the orbit 
$G\cdot x_0$, there exist a point 
$y\in \alpha$ and elements 
$a\in A$, 
$a'\in A^*$ with 
$d(y,ax_0)\leq R$ and 
$d(y,a'x_0)\leq R$. In particular, 
$d(ax_0,a'x_0)\leq 2R$, hence 
$d(a,a')\leq r$. It follows that 
$a'\in \Delta$, so 
$d(y,\Delta \cdot x_0)\leq R$. Since 
$y\in X\setminus C_0$, this contradicts the fact that 
$C_0$ contains the 
$R$-neighbourhood of 
$\Delta \cdot x_0$.
Remark 7.12 Let 
$G\curvearrowright Y$ be an action on a 
${\rm CAT(0)}$ cube complex. Consider a basepoint 
$y_0\in Y$, a halfspace 
$\mathfrak {h}$ bounded by a hyperplane skewered by an element of 
$G$, and the subgroup 
$H\leq G$ stabilising 
$\mathfrak {h}$. Then the set 
$\{g\in G\mid gy_0\in \mathfrak {h}\}$ is an 
$H$-AIS.
Proof of Proposition 7.9 It is clear that (1)
$\Rightarrow$(2). Let us show that (2)
$\Rightarrow$(3). Assuming (2), let 
$M$ be a 
$G$-invariant, 
$G$-cofinite median subalgebra of the 
$0$-skeleton of 
$X\times Y$. Every hyperplane 
$\mathfrak {w}\in \mathscr {W}(Y)$ gives a hyperplane of 
$X\times Y$ skewered by some element of 
$G$, hence a wall 
$\mathfrak {w}'\in \mathscr {W}(M)$. By Chepoi–Roller duality, 
$M$ is the 
$0$-skeleton of a 
${\rm CAT(0)}$ cube complex 
$Z$ with a cocompact 
$G$-action. The stabiliser 
$G_{\mathfrak {w}}$ acts cocompactly on the carrier of 
$\mathfrak {w}'$ in 
$Z$, hence it is convex-cocompact in 
$Z$. The argument in the proof of Corollary 7.13(1) below implies that 
$G_{\mathfrak {w}}$ is convex-cocompact in 
$X$, as required.
We now prove the implication (3)
$\Rightarrow$(1), which is the main content of the proposition. Consider a vertex 
$p=(x_0,y_0)$ and let 
$M\subseteq X\times Y$ be the median algebra generated by the orbit 
$G\cdot p$.
By Lemma 7.11, to every hyperplane 
$\mathfrak {w}\in \mathscr {W}(Y)$ bounding halfspaces 
$\mathfrak {h}$ and 
$\mathfrak {h}^*$, we can associate a partition 
$X=C(\mathfrak {h}^*)\sqcup C(\mathfrak {w})\sqcup C(\mathfrak {h})$ with the following properties:
•
$C(\mathfrak {w})$ is a $G_{\mathfrak {h}}$-invariant, $G_{\mathfrak {h}}$-cocompact, convex subcomplex of $X$;•
$C(\mathfrak {h})$ and $C(\mathfrak {h}^*)$ are $G_{\mathfrak {h}}$-invariant unions of connected components of $X\setminus C(\mathfrak {w})$;• if
$g\in G$ and $gy_0\in \mathfrak {h}$, then $gx_0\in C(\mathfrak {w})\cup C(\mathfrak {h})$; if $gy_0\in \mathfrak {h}^*$, then $gx_0\in C(\mathfrak {w})\cup C(\mathfrak {h}^*)$;• if
$g\in G$, we have $C(g\mathfrak {w})=gC(\mathfrak {w})$ and $C(g\mathfrak {h})=gC(\mathfrak {h})$.
These properties imply the following.
Claim Consider hyperplanes 
$\mathfrak {v}\in \mathscr {W}(X)\sqcup \mathscr {W}(Y)$ and 
$\mathfrak {w}\in \mathscr {W}(Y)$ inducing transverse walls of 
$M$. Then 
$\mathfrak {v}\cap C(\mathfrak {w})\neq \emptyset$ if 
$\mathfrak {v}\in \mathscr {W}(X)$, and 
$C(\mathfrak {v})\cap C(\mathfrak {w})\neq \emptyset$ if 
$\mathfrak {v}\in \mathscr {W}(Y)$.
Proof of Claim We only consider the situation with 
$\mathfrak {v}\in \mathscr {W}(Y)$, as the argument for the case when 
$\mathfrak {v}\in \mathscr {W}(X)$ is entirely analogous.
Let 
$\mathfrak {v}^{\pm },\mathfrak {w}^{\pm }\in \mathscr {H}(Y)$ be the halfspaces bounded by 
$\mathfrak {v}$ and 
$\mathfrak {w}$. Suppose for the sake of contradiction that 
$C(\mathfrak {v})$ and 
$C(\mathfrak {w})$ are disjoint. Then 
$C(\mathfrak {w})$, being connected, is contained in a single connected component of 
$X\setminus C(\mathfrak {v})$. Without loss of generality, 
$C(\mathfrak {w})\subseteq C(\mathfrak {v}^+)$. It follows that the connected set 
$C(\mathfrak {v}^-)\cup C(\mathfrak {v})$ is disjoint from 
$C(\mathfrak {w})$, hence contained in a single connected component of 
$X\setminus C(\mathfrak {w})$. Thus, again without loss of generality, we have 
$C(\mathfrak {v}^-)\cup C(\mathfrak {v})\subseteq C(\mathfrak {w}^+)$, hence the sets 
$C(\mathfrak {v})\cup C(\mathfrak {v}^-)$ and 
$C(\mathfrak {w})\cup C(\mathfrak {w}^-)$ are disjoint.
However, since 
$\mathfrak {v}$ and 
$\mathfrak {w}$ induce transverse walls of 
$M=\langle G\cdot p\rangle$, there exists 
$g\in G$ such that 
$gp\in \mathfrak {v}^-\cap \mathfrak {w}^-$. Equivalently, 
$gy_0\in \mathfrak {v}^-\cap \mathfrak {w}^-$, hence 
$gx_0\in (C(\mathfrak {v})\cup C(\mathfrak {v}^-))\cap (C(\mathfrak {w})\cup C(\mathfrak {w}^-))$.
Now, let 
$\mathscr {T}(M)$ be the set of tuples of pairwise-transverse walls of 
$M$. Consider an element of 
$\mathscr {T}(M)$, say induced by tuples of hyperplanes 
$\mathfrak {u}_1,\dots,\mathfrak {u}_k\in \mathscr {W}(X)$ and 
$\mathfrak {v}_1,\dots,\mathfrak {v}_h\in \mathscr {W}(Y)$. By the claim, the collection of all carriers of the 
$\mathfrak {u}_i$ and all sets 
$C(\mathfrak {v}_i)$ consists of pairwise intersecting convex subsets of 
$X$. By Helly's lemma, the intersection of these convex sets is non-empty.
Fix a compact fundamental domain 
$K\subseteq X$ for the 
$G$-action. By the previous paragraph, there exists 
$g\in G$ such that the carrier of each 
$g\mathfrak {u}_i$ and every set 
$gC(\mathfrak {v}_i)$ meets 
$K$. Note that only finitely many hyperplanes of 
$X$ have carrier meeting the compact set 
$K$. Similarly, only finitely many hyperplanes 
$\mathfrak {v}\in \mathscr {W}(Y)$ satisfy 
$C(\mathfrak {v})\cap K\neq \emptyset$. This follows by combining the fact that the action 
$G\curvearrowright \mathscr {W}(Y)$ is cofinite with Claim 1 in the proof of Lemma 2.8.
The above discussion shows that the action 
$G\curvearrowright \mathscr {T}(M)$ has only finitely many orbits. By Chepoi–Roller duality, 
$M$ is the 
$0$-skeleton of a 
${\rm CAT(0)}$ cube complex with finitely many 
$G$-orbits of maximal cubes. This shows that the action 
$G\curvearrowright M$ is cofinite, as required.
For the next result, note that we can naturally extend the UCP property (Definition 7.3) to actions on discrete median algebras 
$M$. This is entirely equivalent to the UCP property for the action on the 
${\rm CAT(0)}$ cube complex associated with 
$M$ by Chepoi–Roller duality.
We will also speak of carriers and cubes in 
$M$, always referring to (vertex sets of) carriers and cubes in the associated 
${\rm CAT(0)}$ cube complex.
Corollary 7.13 Let 
$G$ act on 
$X$ and 
$Y$ satisfying both the assumptions and the equivalent conditions in Proposition 7.9. Let 
$M\subseteq X\times Y$ be the median subalgebra generated by a 
$G$-orbit.
(1) A subgroup
$H\leq G$ is convex-cocompact in $X$ if and only if $H$ is convex-cocompact in $M$.(2) If, in addition,
$H$ satisfies the UCP condition in $X$, then it also satisfies it in $M$.
Proof. Let 
$p_X\colon M\rightarrow X$ be the restriction of the factor projection. Since 
$G$ acts properly and cocompactly on both 
$M$ and 
$X$, and 
$p_X$ is a 
$1$-Lipschitz median morphism, we see that 
$M$ and 
$X$ induce the same coarse median structure on 
$G$. Along with Remark 2.21, this implies part (1).
Let us prove part (2). If 
$\mathfrak {w}\in \mathscr {W}(M)$, we denote by 
$C(\mathfrak {w})\subseteq X$ the convex hull of the image under 
$p_X$ of the carrier of 
$\mathfrak {w}$ in 
$M$. Since 
$G_{\mathfrak {w}}$ is convex-cocompact in 
$X$ by part (1), and 
$C(\mathfrak {w})$ is the convex hull of a 
$G_{\mathfrak {w}}$-cocompact subset of 
$X$, we conclude that the action 
$G_{\mathfrak {w}}\curvearrowright C(\mathfrak {w})$ is cocompact. Since 
$G\curvearrowright \mathscr {W}(M)$ is cofinite, there exists 
$N\geq 1$ such that every point of 
$X$ lies in 
$C(\mathfrak {w})$ for at most 
$N$ walls 
$\mathfrak {w}\in \mathscr {W}(M)$ (see Claim 1 in the proof of Lemma 2.8).
Let 
$Z\subseteq M$ be an 
$H$-invariant, 
$H$-cofinite, convex subset. As above, there exists an 
$H$-cocompact convex subcomplex 
$C(H)\subseteq X$ containing the projection 
$p_X(Z)$. Given 
$g\in G$, we denote by 
$\Pi _g$ the gate-projection of 
$gC(H)$ to 
$C(H)$. Since 
$H$ is UCP in 
$X$, there exists 
$N'\geq 1$ such that, for every 
$g\in G$, the group 
$H\cap gHg^{-1}$ acts on 
$\Pi _g$ with at most 
$N'$ orbits. Let 
$P_g\subseteq \Pi _g$ be a subset of cardinality 
$\leq N'$ meeting all these orbits.
Let 
$\mathscr {T}(g)$ be the set of tuples of pairwise-transverse walls of 
$M$ that cross both 
$Z$ and 
$gZ$. We need to show that the number of orbits of 
$H\cap gHg^{-1}\curvearrowright \mathscr {T}(g)$ is bounded independently of 
$g\in G$. This gives a uniform bound on the number of orbits of maximal cubes in 
$\pi _Z(gZ)$, hence on the number of vertices.
Consider 
$\underline {\mathfrak {u}}=(\mathfrak {u}_1,\dots,\mathfrak {u}_k)\in \mathscr {T}(g)$. The convex subcomplexes 
$C(\mathfrak {u}_1),\dots,C(\mathfrak {u}_k)\subseteq X$ pairwise intersect and they all meet both 
$C(H)$ and 
$gC(H)$. It follows that 
$C(\mathfrak {u}_1),\dots,C(\mathfrak {u}_k),\Pi _g$ pairwise intersect and, by Helly's lemma, their intersection contains a point 
$p\in \Pi _g$.
Up to translating 
$\underline {\mathfrak {u}}$ by an element of 
$H\cap gHg^{-1}$, we can assume that 
$p\in P_g$. Each point of 
$P_g$ lies in the set 
$C(\mathfrak {w})$ for at most 
$N$ walls 
$\mathfrak {w}\in \mathscr {W}(M)$. Thus, for each 
$k$, there are at most 
$N^k\cdot N'$ orbits of 
$k$-tuples for the action of 
$(H\cap gHg^{-1})$ on 
$\mathscr {T}(g)$. Observing that 
$\mathscr {T}(g)$ contains 
$k$-tuples only for finitely many integers 
$k$, since 
$M$ is finite-dimensional, this completes the proof.
Corollary 7.14 Let 
$G\curvearrowright X$ be a non-transverse, proper, cocompact action on a 
${\rm CAT(0)}$ cube complex. Let 
$G\curvearrowright T$ be a minimal action on a simplicial tree such that all edge-stabilisers are convex-cocompact in 
$X$. Then there exists an action on a 
${\rm CAT(0)}$ cube complex 
$G\curvearrowright Z$ such that:
(1)
$G\curvearrowright Z$ is non-transverse, proper, cocompact and without inversions;(2)
$G\curvearrowright Z$ and $G\curvearrowright X$ induce the same coarse median structure on $G$;(3) there exists a
$G$-equivariant, surjective median morphism $Z\rightarrow T$;(4) for every hyperplane
$\mathfrak {w}\in \mathscr {W}(Z)$ obtained as preimage of the midpoint of an edge of $T$, the action $G_{\mathfrak {w}}\curvearrowright \mathfrak {w}$ is essential;(5) if
$G$-stabilisers of edges of $T$ satisfy the UCP condition in $X$, they also do in $Z$.
Proof. Choose a basepoint 
$p\in X\times T$ and let 
$M$ be the median algebra generated by the orbit 
$G\cdot p$. Since the action 
$G\curvearrowright X\times T$ is proper and non-transverse, so is the action 
$G\curvearrowright M$. In addition, 
$G\curvearrowright M$ is cofinite by Proposition 7.9. Thus, by Chepoi–Roller duality, there exists a non-transverse, proper, cocompact action on a 
${\rm CAT(0)}$ cube complex 
$G\curvearrowright Y$ such that the 
$0$-skeleton of 
$Y$ is 
$G$-equivariantly isomorphic to 
$M$ as a median algebra.
The factor projection 
$X\times T\rightarrow T$ gives the required 
$G$-equivariant median morphism 
${M\rightarrow T}$. The projection, 
$X\times T\rightarrow X$, gives another 
$G$-equivariant median morphism 
$M\rightarrow X$; this ensures that 
$Y$ and 
$X$ induce the same coarse median structure on 
$G$. Condition (5) follows from Corollary 7.13. Up to subdividing, we can assume that 
$G\curvearrowright Y$ is without inversions.
We are only left to ensure that condition (4) is satisfied. By Corollary 7.8, it suffices to pass to a 
$G$-invariant (non-convex) 
${\rm CAT(0)}$ subcomplex 
$Z\subseteq Y$ inducing the same coarse median structure on 
$G$. It is immediate to check that the action 
$G\curvearrowright Z$ is again non-transverse, proper, cocompact and without inversions.
Let 
$\mathfrak {v}\in \mathscr {W}(Y)$ be the preimage of the midpoint of an edge of 
$T$. Since the intersection 
$\mathfrak {v}\cap Z$ is connected, condition (3) is not affected by passing to the subcomplex 
$Z$.
Finally, the 
$G$-stabiliser of 
$\mathfrak {v}\cap Z$ coincides with the stabiliser of 
$\mathfrak {v}$. The set of vertices in 
$Z^{(0)}=Y^{(0)}$ that are adjacent to a hyperplane of 
$Z$ transverse to both 
$g\mathfrak {v}\cap Z$ and 
$\mathfrak {v}\cap Z$ is clearly a subset of the set of vertices adjacent to a hyperplane of 
$Y$ transverse to both 
$g\mathfrak {v}$ and 
$\mathfrak {v}$. Thus, condition (5) remains satisfied in 
$Z$. This completes the proof of the corollary.
7.4 Earthquake maps
In this subsection, we prove Theorem 7.1. By Corollary 7.14, we can assume that we are in the following setting:
(1)
$G\curvearrowright X$ is a proper cocompact action on a ${\rm CAT(0)}$ cube complex without inversions;(2)
$G\curvearrowright X$ is also non-transverse;(3)
$G\curvearrowright T$ is the action on a tree obtained as restriction quotient of $X$ associated to an orbit of hyperplanes $G\cdot \mathfrak {w}\subseteq \mathscr {W}(X)$;(4)
$\mathfrak {A}$ and $\mathfrak {B}$ are the two connected components of $X\setminus G\cdot \mathfrak {w}$ adjacent to $\mathfrak {w}$, the subgroups $A,B\leq G$ are their stabilisers, and $C=A\cap B$ is the stabiliser of $\mathfrak {w}$;(5)
$C$ acts essentially on $\mathfrak {w}$, satisfies the UCP condition in $X$, and has no non-trivial finite normal subgroups;(6) we fix an element
$z\in Z_A(C)$;(7) depending on whether there are one or two
$G$-orbits of vertices in $T$, we denote by $\tau$ and $\sigma$, respectively, the transvection and the partial conjugation induced by $z$, as defined in the Introduction (in the definition of $\tau$, we fix as stable letter an element $t\in G$ with $t\mathfrak {A}=\mathfrak {B}$).
We emphasise that the element 
$z$ does not preserve the hyperplane 
$\mathfrak {w}$ in general.
Though they will not be part of our standing assumptions, it is convenient to give a name to the conditions in parts (2) and (3) of Theorem 7.1:
()
$z$ lies in $Z_C(C)$, the subgroup $\langle z\rangle$ is convex-cocompact in $X$, and $Z_G(c)$ fixes a point of $T$ for every $c\in C$ with $\langle c\rangle \cap \langle z\rangle \neq \{1\}$;() For every infinite-order element
$c\in C$ commuting with a finite-index subgroup of $C$, the centraliser $Z_G(c)$ fixes a point of $T$.
We begin with a few lemmas. If 
$\mathfrak {u}$ is a hyperplane of 
$X$, we denote by 
$\mathscr {T}(\mathfrak {u})\subseteq \mathscr {W}(X)$ the subset of hyperplanes transverse to 
$\mathfrak {u}$. Recall that 
$\mathfrak {u}$ has itself a structure of 
${\rm CAT(0)}$ cube complex whose hyperplanes are identified with hyperplanes of 
$X$ lying in 
$\mathscr {T}(\mathfrak {u})$.
Since 
$z$ acts non-transversely on 
$X$, note that every hyperplane in 
$\mathcal {W}_1(z)$ is skewered by 
$z$.
Lemma 7.15 The hyperplane 
$\mathfrak {w}$ splits as a product of cube complexes 
$\mathfrak {w}_0\times L_1\times \cdots \times L_m$, where 
$m\geq 0$ and each 
$L_i$ is a quasi-line. All hyperplanes of 
$X$ corresponding to the factor 
$\mathfrak {w}_0$ are preserved by 
$z$. All hyperplanes of 
$X$ corresponding to the factors 
$L_i$ are skewered by 
$z$.
Proof. Since 
$z$ commutes with 
$C$, the convex subcomplex 
$\overline {\mathcal {C}}(z)$ introduced in Proposition 2.1 is 
$C$-invariant. It follows that every hyperplane in 
$\mathcal {W}_1(C)$ crosses 
$\overline {\mathcal {C}}(z)$, hence 
$\mathcal {W}_1(C)\subseteq \overline {\mathcal {W}}_0(z)\sqcup \mathcal {W}_1(z)$. Since 
$G$ acts non-transversely and without inversions on 
$X$, every element of 
$\mathcal {W}_1(C)$ is either skewered or preserved by 
$z$. Since 
$C$ acts essentially on 
$\mathfrak {w}$, we have 
$\mathscr {T}(\mathfrak {w})=\mathcal {W}_1(C)$.
Since 
$\overline {\mathcal {W}}_0(z)$ is transverse to 
$\mathcal {W}_1(z)$, we have a transverse partition
\[ \mathscr{T}(\mathfrak{w})=(\mathscr{T}(\mathfrak{w})\cap\overline{\mathcal{W}}_0(z))\sqcup(\mathscr{T}(\mathfrak{w})\cap\mathcal{W}_1(z)), \]
which gives rise to a splitting 
$\mathfrak {w}=\mathfrak {w}_0\times \mathfrak {w}_1$ (see [Reference Caprace and SageevCS11, Lemma 2.5]). Every hyperplane of the factor 
$\mathfrak {w}_0$ is preserved by 
$z$, and every hyperplane of the factor 
$\mathfrak {w}_1$ is skewered by 
$z$. The cube complex 
$\mathfrak {w}_1$ is a restriction quotient of the convex hull in 
$X$ of any axis of 
$z$ in 
$X$. By [Reference Wise and WoodhouseWW17, Theorem 3.6], the latter splits as a product of quasi-lines. It follows that 
$\mathfrak {w}_1$ is a product of quasi-lines and bounded cube complexes. However, since 
$C$ acts essentially on 
$\mathfrak {w}$, there can be no bounded factors.
The previous lemma yields a partition:
\[ \mathscr{T}(\mathfrak{w})=\Omega_0\sqcup\Omega_1\sqcup\dots\sqcup\Omega_m. \]
The sets 
$\Omega _i$ are transverse to each other and, since 
$z$ acts non-transversely, they are all 
$\langle z\rangle$-invariant. In addition, 
$z$ fixes 
$\Omega _0$ pointwise and it skewers all other elements of 
$\mathscr {T}(\mathfrak {w})$.
Let 
$\mathfrak {w}_A,\mathfrak {w}_B\in \mathscr {H}(X)$ be the halfspaces bounded by 
$\mathfrak {w}$ containing 
$\mathfrak {A}$ and 
$\mathfrak {B}$, respectively.
Lemma 7.16 There exists a constant 
$D\geq 0$ such that:
(1) for every
$y\in \mathfrak {w}$, we have $d(y,zy)\leq D$;(2) for every
$x\in X$, we have $d(\pi _{\mathfrak {w}}(x),\pi _{\mathfrak {w}}(zx))\leq D$ and $\Omega _0\cap \mathscr {W}(x|zx)=\emptyset$.
Proof. Part (1) is immediate from the fact that 
$C$ acts cocompactly on 
$\mathfrak {w}$ and commutes with 
$z$. Regarding part (2), we need to bound uniformly the number of hyperplanes in 
$\mathscr {T}(\mathfrak {w})$ that separate 
$x\in X$ from 
$zx$.
Recall that 
$\mathscr {T}(\mathfrak {w})=\bigcup _{j\geq 0}\Omega _j$, where 
$z$ fixes 
$\Omega _0$ pointwise. Since 
$G$ acts on 
$X$ without inversions, every halfspace bounded by a hyperplane in 
$\Omega _0$ is left invariant by 
$z$. It follows that no element of 
$\Omega _0$ can separate 
$x$ and 
$zx$.
Let 
$H\subseteq X$ be the convex hull of an axis of 
$z$. Every hyperplane in 
$\mathscr {T}(\mathfrak {w})\setminus \Omega _0$ lies in 
$\mathcal {W}_1(z)$, hence it crosses 
$H$. Denoting by 
$\pi _H$ the gate-projection to 
$H$, we conclude that
\[ d(\pi_{\mathfrak{w}}(x),\pi_{\mathfrak{w}}(zx))\leq d(\pi_H(x),\pi_H(zx))=d(\pi_H(x),z\pi_H(x)), \]
since 
$H$ is 
$\langle z\rangle$-invariant. Since 
$G$ acts non-transversely, we have 
$d(y,zy)=\ell _X(z)$ for every 
$y\in H$ (for instance by [Reference Fernós, Forester and TaoFFT19, Proposition 3.17] or [Reference FioravantiFio21, Proposition 3.35]). This proves part (2) with 
$D=\ell _X(z)$.
Lemma 7.17 Consider 
$x\in \mathfrak {w}_B$ and 
$a\in A$.
(1) The projections
$\pi _{\mathfrak {w}}(ax)$ and $\pi _{\mathfrak {w}}(zaz^{-1}\cdot x)$ are at distance at most $2D$.(2) If
$\mathfrak {u}\in \mathscr {W}(X)$ is transverse to $a\mathfrak {w}$ and separates $\pi _{\mathfrak {w}}(ax)$ from $\pi _{\mathfrak {w}}(zaz^{-1}\cdot x)$, then there exists an index $j\neq 0$ such that $\mathfrak {u}\in \Omega _j\cap a\Omega _j$ and $\Omega _j\cap a\Omega _j\neq \Omega _j$.
Proof. We begin with part (1). Set 
$y:=\pi _{\mathfrak {w}}(x)$. Observing that the halfspaces 
$\mathfrak {w}_B$ and 
$a\mathfrak {w}_B$ are either equal or disjoint, we deduce that 
$\pi _{\mathfrak {w}}(ax)=\pi _{\mathfrak {w}}\pi _{a\mathfrak {w}}(ax)=\pi _{\mathfrak {w}}(ay)$. Similarly, 
$\pi _{\mathfrak {w}}(az^{-1}x)=\pi _{\mathfrak {w}}(az^{-1}y)$. Thus, Lemma 7.16 and the fact that gate-projections are 
$1$-Lipschitz yield
\begin{align*} d(\pi_{\mathfrak{w}}(ax),\pi_{\mathfrak{w}}(zaz^{-1}\cdot x))&\leq D+d(\pi_{\mathfrak{w}}(ax),\pi_{\mathfrak{w}}(az^{-1}x))=D+d(\pi_{\mathfrak{w}}(ay),\pi_{\mathfrak{w}}(az^{-1}y)) \\ &\leq D+d(ay,az^{-1}y)=D+d(y,z^{-1}y)\leq 2D. \end{align*}
We now prove part (2). Since 
$\mathfrak {u}$ separates two points of 
$\mathfrak {w}$, it lies in 
$\mathscr {T}(\mathfrak {w})$, hence 
$\mathfrak {u}\in \Omega _j$ for some 
$0\leq j\leq m$. Similarly, since 
$\mathfrak {u}$ is transverse to 
$a\mathfrak {w}$, we have 
$\mathfrak {u}\in a\Omega _{j'}$ for some 
$0\leq j'\leq m$. Since 
$G$ acts non-transversely on 
$X$, we must have 
$j=j'$.
If we had 
$j=0$, then 
$\mathfrak {u}$ would be preserved by both 
$z$ and 
$aza^{-1}$. Since 
$G$ acts without inversions, these elements would also leave invariant the two halfspaces bounded by 
$\mathfrak {u}$. This contradicts the fact that 
$\mathfrak {u}$ must separate the points 
$ax$ and 
$zaz^{-1}\cdot x=z\cdot az^{-1}a^{-1}\cdot ax$.
Thus 
$\mathfrak {u}\in \Omega _j\cap a\Omega _j$ for some 
$j\geq 1$. Suppose for the sake of contradiction that 
$\Omega _j\cap a\Omega _j=\Omega _j$. Consider the restriction quotient of 
$X$ determined by the orbit 
$G\cdot \mathfrak {u}$. This is a tree where 
$z$ and 
$aza^{-1}$ are loxodromics with the same translation length. Since 
$z$ acts non-transversely, we have 
$(G\cdot \mathfrak {u})\cap \mathcal {W}_1(z)\subseteq \Omega _j$ and 
$(G\cdot \mathfrak {u})\cap \mathcal {W}_1(aza^{-1})\subseteq a\Omega _j$. Thus, the fact that 
$\Omega _j\subseteq a\Omega _j$ implies that 
$z$ and 
$aza^{-1}$ have the same axis in the tree.
It follows that, for every point 
$y$ in this tree, the points 
$y$ and 
$z\cdot az^{-1}a^{-1}\cdot y$ have the same projection to the shared axis of 
$z$ and 
$aza^{-1}$. Since 
$\mathfrak {u}$ projects to the midpoint of an edge of this axis, it cannot separate the points 
$ax$ and 
$zaz^{-1}\cdot x=z\cdot az^{-1}a^{-1}\cdot ax$, which contradicts our supposition.
Lemma 7.18 There exists a constant 
$M\geq 0$ such that the following hold.
(1) For all
$g\in G$ and $j\neq 0$, either $\Omega _j\cap g\Omega _j=\Omega _j$ or $\#(\Omega _j\cap g\Omega _j)\leq M$.(2) Suppose that either
$(\ast )$ or $(\ast \ast )$ holds. If there exist $g\in G$ and $j\neq 0$ such that $\Omega _j\cap g\Omega _j=\Omega _j$, then there are at most $M$ elements of $G\cdot \mathfrak {w}$ separating $\mathfrak {w}$ and $g\mathfrak {w}$.
Proof. We begin with part (1). Consider 
$g\in G$. Since 
$\pi _{\mathfrak {w}}(g\mathfrak {w})$ is convex in 
$\mathfrak {w}$, the splitting 
$\mathfrak {w}=\mathfrak {w}_0\times L_1\times \cdots \times L_m$ given by Lemma 7.15 determines a splitting 
$\pi _{\mathfrak {w}}(g\mathfrak {w})=Y_0\times \cdots \times Y_m$. The set of hyperplanes of 
$X$ corresponding to the factor 
$Y_j$ is precisely 
$\Omega _j\cap g\Omega _j$. Indeed, recall that all intersections 
$\Omega _j\cap g\Omega _{j'}$ with 
$j\neq j'$ are empty because 
$G$ acts non-transversely on 
$X$.
Since 
$C$ satisfies the UCP condition in 
$X$, there exists a constant 
$N_1$ such that, for every 
$g\in G$, the subgroup 
$C\cap gCg^{-1}$ acts on 
$\pi _{\mathfrak {w}}(g\mathfrak {w})$ with at most 
$N_1$ orbits of vertices. This action preserves all factors in the above splitting of 
$\pi _{\mathfrak {w}}(g\mathfrak {w})$, since 
$C$ preserves the factors in the splitting of 
$\mathfrak {w}$. Hence 
$C\cap gCg^{-1}$ acts on each factor 
$Y_j$ with at most 
$N_1$ orbits of vertices.
Since each 
$L_j$ is an essential quasi-line and 
$Y_j$ is a cocompact convex subcomplex, 
$Y_j$ is either the entire 
$L_j$ or a compact subset. Thus, if 
$\Omega _j\cap g\Omega _j\neq \Omega _j$, then 
$C\cap gCg^{-1}$ fixes a point of 
$Y_j$, and it follows that the diameter of 
$Y_j$ is at most 
$N_1$. Since 
$Y_j$ is isomorphic to a subcomplex of 
$X$, which is locally finite, this results in a uniform bound on the number of vertices of 
$Y_j$, hence on the cardinality of 
$\Omega _j\cap g\Omega _j$. This proves part (1).
We now prove part (2), keeping the above notation. Since 
$C$ does not have any non-trivial finite normal subgroups, the action 
$C\curvearrowright \mathfrak {w}$ is faithful and we can apply Proposition 2.2. As a consequence, 
$C$ has a finite-index subgroup 
$C'=C_0\times \langle h_1,\dots,h_m\rangle$, where 
$\langle h_1,\dots,h_m\rangle \simeq \mathbb {Z}^m$, each 
$h_j$ acts trivially on 
$\mathfrak {w}_0$, and each 
$L_j$ is acted upon trivially by 
$C_0$ and all 
$h_i$ with 
$i\neq j$. If 
$N_2$ is the index of 
$C'$ in 
$C$, then the action 
$C'\cap gC'g^{-1}\curvearrowright \pi _{\mathfrak {w}}(g\mathfrak {w})$ has 
$\leq N_1N_2^2$ orbits of vertices for every 
$g\in G$. Let 
$N_3$ be the highest order of a finite-order element of 
$C_0$.
If 
$\Omega _j\cap g\Omega _j=\Omega _j$ for some 
$j\neq 0$, then 
$Y_j=L_j$. It follows that there exist an element 
$h\in C'\cap gC'g^{-1}$ and a point 
$x\in \pi _{\mathfrak {w}}(g\mathfrak {w})$ such that 
$0< d(x,hx)\leq N_1N_2^2$ and 
$\mathscr {W}(x|hx)\subseteq \Omega _j$. The latter implies that 
$h=h_0h_j^n$ for some 
$h_0\in C_0$ that is elliptic in 
$\mathfrak {w}_0$, while the former ensures that 
$n\leq N_1N_2^2$. Note that 
$h^{N_3}=h_j^{nN_3}$. In conclusion, 
$C'\cap gC'g^{-1}$ contains a power of 
$h_j$ of exponent at most 
$N_1N_2^2N_3$.
The cyclic subgroup 
$\langle h_j\rangle$ is convex-cocompact in 
$X$, since the convex hull of any of its axes is isomorphic to 
$L_j$. By Lemma 2.9, there exist finite subsets 
$F_{j,n}\subseteq G$ such that
\[ \{g\in G \mid h_j^n\in gCg^{-1}\}=Z_G(h_j^n)\cdot F_{j,n}\cdot C, \]
for all 
$j\neq 0$ and 
$n\geq 1$.
Summing up, if 
$\Omega _j\cap g\Omega _j=\Omega _j$ for some 
$j\neq 0$, then 
$g\mathfrak {w}$ belongs to the set 
$Z_G(h_j^n)F_{j,n}\cdot \mathfrak {w}$ for some 
$1\leq n\leq N_1N_2^2N_3$. Now, if 
$(\ast \ast )$ holds, then each subgroup 
$Z_G(h_j^n)$ is elliptic in the tree 
$T$. If instead 
$(\ast )$ holds, 
$\langle z\rangle$ is convex-cocompact and contained in 
$C$, so we have 
$m=1$ and 
$\mathcal {W}_1(z)=\Omega _1$. In this case, a power of 
$z$ lies in 
$C'=C_0\times \langle h_1\rangle$ and its projection to 
$C_0$ must have finite order. Thus, 
$z$ and 
$h_1$ have a common power, hence 
$Z_G(h_1^n)$ is again elliptic in 
$T$ by 
$(\ast )$.
In both cases, this gives a uniform bound to the maximum possible distance between the edges of 
$T$ corresponding to 
$\mathfrak {w}$ and 
$g\mathfrak {w}$, as required by part (2).
Note that the three options in part (b) of the next result correspond exactly to the three options in Theorem 7.1.
Proposition 7.19 Under the assumptions listed at the beginning of this subsection, the following hold.
(a) We have
$\sup _{x\in \mathfrak {w}}\sup _{g\in G}d(\pi _{\mathfrak {w}}(gx),\pi _{\mathfrak {w}}(\sigma (g)x))<+\infty$.(b) We have
$\sup _{x\in \mathfrak {w}}\sup _{g\in G}d(\pi _{\mathfrak {w}}(gx),\pi _{\mathfrak {w}}(\tau (g)x))<+\infty$, provided that either $\langle z\rangle \perp C$, or one among $(\ast )$ and $(\ast \ast )$ holds.
Proof. Let 
$K$ be the constant provided by Lemma 7.4 applied to 
$\mathfrak {w}$. Let 
$m$, 
$D$, 
$M$ be the constants provided by Lemmas 7.15, 7.16 and 7.18, respectively.
Recall that 
$G\curvearrowright T$ has either one or two orbits of vertices. We will have to treat separately these two situations, which correspond to parts (a) and (b) of the proposition.
Case (a): the action 
$G\curvearrowright T$ gives an amalgamated product splitting 
$G=A\ast _CB$. We consider the partial conjugation 
$\sigma$ with 
$\sigma (a)=a$ for 
$a\in A$ and 
$\sigma (b)=zbz^{-1}$ for 
$b\in B$. It is actually more convenient to consider the automorphism 
$\overline \sigma$ satisfying 
$\overline \sigma (a)=zaz^{-1}$ for 
$a\in A$ and 
$\overline \sigma (b)=b$ for 
$b\in B$. This differs from 
$\sigma ^{-1}$ by composition with an inner automorphism given by 
$z$. By Lemma 7.16, we have 
$d(\pi _{\mathfrak {w}}(\sigma ^{-1}(g)x),\pi _{\mathfrak {w}}(\overline \sigma (g)x))\leq 2D$ for every 
$x\in \mathfrak {w}$ and 
$g\in G$, so it suffices to prove the proposition for 
$\overline \sigma$.
We can write 
$g\in G$ as 
$g=a_0(b_1a_1\dots b_na_n)b_{n+1}$, with 
$n\geq 0$ and 
$a_i\in A\setminus C$, 
$b_i\in B\setminus C$, except for 
$a_0$ which is allowed to vanish, and 
$b_{n+1}$ which is allowed to lie in 
$C$. Consider a point 
$x\in \mathfrak {w}$.
For 
$0\leq i\leq n+1$, we introduce the following hyperplanes and points of 
$X$:
\[ \mathfrak{w}_i:=a_0b_1a_1\dots a_{i-1}b_i\cdot\mathfrak{w}, \quad y_i:=a_0b_1a_1\dots a_{i-1}b_i\cdot \overline\sigma(a_ib_{i+1}\dots b_na_nb_{n+1})\cdot x. \]
Thus 
$\mathfrak {w}_0=\mathfrak {w}$ and 
$\mathfrak {w}_{n+1}=g\mathfrak {w}$, while 
$y_0=\overline \sigma (g)x$ and 
$y_{n+1}=gx$. Observe that 
$\mathfrak {w}_0,\mathfrak {w}_1\dots,\mathfrak {w}_{n+1}$ is a chain of hyperplanes. For 
$1\leq i\leq n$, the hyperplane 
$\mathfrak {w}_i$ separates 
$y_i$ and 
$y_{i+1}$ from 
$\mathfrak {w}$.
Claim 1 At most 
$2KD$ elements of 
$\Omega _0$ separate 
$gx$ and 
$\overline \sigma (g)x$.
Proof of Claim 1 By our choice of 
$K$, there exists a subset 
$I\subseteq \{1,\dots,n\}$ such that 
$\#I\leq K$ and, for every 
$i\not \in I$, every hyperplane transverse to both 
$\mathfrak {w}$ and 
$\mathfrak {w}_i$ is also transverse to 
$\mathfrak {w}_{i+1}$.
Recall that, since 
$G$ acts non-transversely, an element of 
$\Omega _0$ can only be transverse to 
$\mathfrak {w}_i$ if it lies in the set 
$a_0b_1a_1\dots a_{i-1}b_i\cdot \Omega _0$.
By Lemma 7.17(1), the points 
$y_i$ and 
$y_{i+1}$ are separated by at most 
$2D$ hyperplanes in 
$\Omega _0\cap \mathscr {T}(\mathfrak {w}_i)$. By Lemma 7.17(2), none of these hyperplanes is transverse to 
$\mathfrak {w}_{i+1}$ (since 
$a_0b_1a_1\dots a_{i-1}b_ia_i\cdot \mathfrak {w}$ separates 
$\mathfrak {w}_i$ and 
$\mathfrak {w}_{i+1}$). So, if 
$y_i$ and 
$y_{i+1}$ are separated by an element of 
$\Omega _0\cap \mathscr {T}(\mathfrak {w}_i)$, then 
$i\in I$.
Since 
$\mathfrak {w}_i$ separates 
$y_i$ and 
$y_{i+1}$ from 
$\mathfrak {w}$, we deduce that 
$y_i$ and 
$y_{i+1}$ are separated by at most 
$2D$ elements of 
$\Omega _0$. In addition, they can only be separated by at least one element of 
$\Omega _0$ when 
$i\in I$. Since 
$\#I\leq K$, this shows that at most 
$2KD$ elements of 
$\Omega _0$ separate 
$y_0$ from 
$y_{n+1}$, as required.
Claim 2 For every 
$j\neq 0$, at most 
$2D(K+1)+M$ elements of 
$\Omega _j$ separate 
$gx$ and 
$\overline \sigma (g)x$.
Proof of Claim 2 Fix 
$j\neq 0$. By Lemma 7.18(1), there exists an index 
$0\leq k\leq n+1$ such that 
$\Omega _j\subseteq \mathscr {T}(\mathfrak {w}_i)$ for 
$i\leq k$, while 
$\#(\Omega _j\cap \mathscr {T}(\mathfrak {w}_i))\leq M$ for 
$i>k$.
Let 
$I$ be as in the proof of Claim 1. If 
$i\leq k-1$ and 
$i\not \in I$, Lemma 7.17(2) shows that no element of 
$\Omega _j$ separates 
$y_i$ and 
$y_{i+1}$. Thus, 
$y_0$ and 
$y_k$ are separated by at most 
$2DK$ elements of 
$\Omega _j$, using Lemma 7.17(1) as in Claim 1. Similarly, at most 
$2D$ elements of 
$\Omega _j$ separate 
$y_k$ and 
$y_{k+1}$.
Finally, every element of 
$\Omega _j$ separating 
$y_{k+1}$ and 
$y_{n+1}$ is transverse to 
$\mathfrak {w}_{k+1}$, hence there are at most 
$M$ such hyperplanes. This shows that at most 
$2D(K+1)+M$ elements of 
$\Omega _j$ separate 
$y_0$ and 
$y_{n+1}$, as required.
Combining the two claims with the fact that 
$\mathscr {T}(\mathfrak {w})=\bigcup _{j\geq 0}\Omega _j$, we obtain
\[ d(\pi_{\mathfrak{w}}(gx),\pi_{\mathfrak{w}}(\overline\sigma(g)x))\leq 2KD+m(2D(K+1)+M). \]
Case (b): the action 
$G\curvearrowright T$ gives an HNN splitting 
$G=A\ast _C$. We fix 
$t\in G$ with 
$t\mathfrak {A}=\mathfrak {B}$ and consider the transvection 
$\tau$ with 
$\tau (a)=a$ for 
$a\in A$ and 
$\tau (t)=zt$. We can write 
$g\in G$ as 
$g=a_1t^{\epsilon _1}\dots a_nt^{\epsilon _n}a_{n+1}$ with 
$n\geq 0$ and 
$a_i\in A$, 
$\epsilon _i\in \{\pm 1\}$. In addition, we can require that this word be reduced in the following sense.
• If
$\epsilon _{i-1}=-1$ and $\epsilon _i=+1$, then $a_i\not \in C$.• If
$\epsilon _{i-1}=+1$ and $\epsilon _i=-1$, then $a_i\not \in t^{-1}Ct$.
Note that 
$\tau (g)=\overline {a}_1t^{\epsilon _1}\dots \overline {a}_nt^{\epsilon _n}\overline {a}_{n+1}$, where:
•
$\overline {a}_i=a_i$ if $(\epsilon _{i-1},\epsilon _i)=(+1,-1)$;•
$\overline {a}_i=a_iz$ if $(\epsilon _{i-1},\epsilon _i)=(+1,+1)$, or $i=1$ and $\epsilon _1=+1$;•
$\overline {a}_i=z^{-1}a_i$ if $(\epsilon _{i-1},\epsilon _i)=(-1,-1)$, or $i=n+1$ and $\epsilon _n=-1$;•
$\overline {a}_i=z^{-1}a_iz$ if $(\epsilon _{i-1},\epsilon _i)=(-1,+1)$.
Since 
$z$ normalises 
$C$, this word representing 
$\tau (g)$ is again reduced as defined above. The words 
$a_1t^{\epsilon _1}\dots a_it^{\epsilon _i}\overline {a}_{i+1}t^{\epsilon _{i+1}}\dots \overline {a}_nt^{\epsilon _n}\overline {a}_{n+1}$ are also reduced.
Consider a point 
$x\in \mathfrak {w}$. For 
$0\leq i\leq n+1$, we introduce the following hyperplanes and points:
\[ \mathfrak{w}_i:=a_1t^{\epsilon_1}\dots a_it^{\epsilon_i}\cdot\mathfrak{w}, \quad y_i:=a_1t^{\epsilon_1}\dots a_it^{\epsilon_i}\overline{a}_{i+1}t^{\epsilon_{i+1}}\dots \overline{a}_nt^{\epsilon_n}\overline{a}_{n+1}\cdot x. \]
Again, we have 
$\mathfrak {w}_0=\mathfrak {w}$ and 
$\mathfrak {w}_{n+1}=g\mathfrak {w}$, while 
$y_0=\tau (g)x$ and 
$y_{n+1}=gx$. The hyperplanes 
$\mathfrak {w}=\mathfrak {w}_0,\mathfrak {w}_1\dots,\mathfrak {w}_n,\mathfrak {w}_{n+1}$ form a chain, possibly with 
$\mathfrak {w}_n=\mathfrak {w}_{n+1}$. For 
$1\leq i\leq n$, the hyperplane 
$\mathfrak {w}_i$ separates 
$y_i$ and 
$y_{i+1}$ from 
$\mathfrak {w}$, except if 
$i=n$ and 
$a_{n+1}\in C$ or 
$\overline {a}_{n+1}\in C$.
Claim 3 At most 
$2KD$ elements of 
$\Omega _0$ separate 
$gx$ and 
$\tau (g)x$.
Proof of Claim 3 This is proved exactly as in Claim 1. A little more care is only required when showing that 
$y_i$ and 
$y_{i+1}$ are separated by at most 
$2D$ elements of 
$\mathscr {T}(\mathfrak {w}_i)\cap \Omega _0$, and no element of 
$\mathscr {T}(\mathfrak {w}_{i+1})\cap \Omega _0$. We spend a few more words on this point.
If 
$\overline {a}_{i+1}=a_{i+1}$, this is obvious and, if 
$\overline {a}_{i+1}=z^{-1}a_{i+1}z$, we can repeat the argument in Claim 1. The cases when 
$\overline {a}_{i+1}=z^{-1}a_{i+1}$ or 
$\overline {a}_{i+1}=a_{i+1}z$ can be deduced from the previous two via Lemma 7.16(2).
If 
$\langle z\rangle \perp C$, then Lemma 2.25(1) shows that 
$\mathscr {T}(\mathfrak {w})=\Omega _0$. In this situation, Claim 3 immediately implies that 
$d(\pi _{\mathfrak {w}}(gx),\pi _{\mathfrak {w}}(\tau (g)x))\leq 2KD$, proving the proposition.
In the rest of the proof, we suppose that either 
$(\ast )$ or 
$(\ast \ast )$ is satisfied.
Claim 4 At most 
$mM+3D(M+2)$ elements of 
$\mathscr {T}(\mathfrak {w})\setminus \Omega _0$ separate 
$gx$ and 
$\tau (g)x$.
Proof of Claim 4 Lemma 7.18(2) rules out the existence of some 
$j\neq 0$ such that 
$\mathfrak {w}_{M+2}$ is transverse to every element of 
$\Omega _j$. Lemma 7.18(1) then shows that at most 
$M$ elements from each 
$\Omega _j$ are transverse to 
$\mathfrak {w}_{M+2}$. Since 
$\mathfrak {w}_{M+2}$ separates 
$y_{M+2}$ and 
$y_{n+1}$ from 
$\mathfrak {w}$, we deduce that 
$\pi _{\mathfrak {w}}(y_{M+2})$ and 
$\pi _{\mathfrak {w}}(y_{n+1})$ are separated by at most 
$M$ elements of each 
$\Omega _j$.
For every 
$i$, the projections of 
$y_i$ and 
$y_{i+1}$ to 
$\mathfrak {w}_i$ are at distance at most 
$3D$. This can be deduced from Lemma 7.17(1) and Lemma 7.16(2). Thus, the projections 
$\pi _{\mathfrak {w}}(y_i)$ and 
$\pi _{\mathfrak {w}}(y_{i+1})$ are also at distance at most 
$3D$. It follows that 
$\pi _{\mathfrak {w}}(y_0)$ and 
$\pi _{\mathfrak {w}}(y_{M+2})$ are at distance at most 
$3D(M+2)$.
Summing up, the projections 
$\pi _{\mathfrak {w}}(y_0)$ and 
$\pi _{\mathfrak {w}}(y_{n+1})$ are separated by at most 
${mM+3D(M+2)}$ elements of 
$\mathscr {T}(\mathfrak {w})\setminus \Omega _0$.
Combining Claims 3 and 4, we obtain
\[ d(\pi_{\mathfrak{w}}(gx),\pi_{\mathfrak{w}}(\tau(g)x))\leq 2KD+mM+3D(M+2). \]
This completes the proof of the proposition.
For simplicity, we introduce the notation 
$\varphi \in \operatorname {Aut}(G)$ to refer to either the partial conjugation 
$\sigma$ or the transvection 
$\tau$.
Definition 7.20 Consider the setting described at the beginning of this subsection and 
$\varphi \in \operatorname {Aut}(G)$ as above. The earthquake map is the only bijection 
$\Phi \colon X^{(0)}\rightarrow X^{(0)}$ that satisfies:
•
$\Phi (gx)=\varphi (g)\Phi (x)$ for all $x\in X$ and $g\in G$;•
$\Phi (p)=p$ for all $p\in \mathfrak {A}$, and $\Phi (q)=zq$ for all $q\in \mathfrak {B}$.
We leave to the reader the straightforward check that 
$\Phi$ exists and is unique. Note that 
$\Phi$ descends to an automorphism of the tree 
$T$.
Proposition 7.21 Under the assumptions of Proposition 7.19, the earthquake map 
$\Phi$ is 
$(D+1)$-Lipschitz and coarse-median preserving.
Proof. First, we prove that 
$\Phi$ is Lipschitz. It suffices to show that 
$d(\Phi (x),\Phi (y))\leq D+1$ whenever 
$x$ and 
$y$ are the endpoints of an edge of 
$X$. On each connected component of 
$X\setminus G\cdot \mathfrak {w}$, the map 
$\Phi$ is an isometry, so it is enough to consider the case when 
$x$ and 
$y$ are in distinct components.
Thus, suppose that there exist points 
$x'\in \mathfrak {A}$, 
$y'\in \mathfrak {B}$ and an element 
$g\in G$ such that 
$x=gx'$ and 
$y=gy'$. Now, since 
$\Phi (x)=\varphi (g)x'$ and 
$\Phi (y)=\varphi (g)zy'$, we have
\[ d(\Phi(x),\Phi(y))=d(x',zy')\leq 1+d(y',zy')\leq 1+D, \]
where the last inequality follows from Lemma 7.16(1).
Before showing that 
$\Phi$ is coarse-median preserving, we need to obtain the following.
Claim 1 We have 
$P:=\sup _{x\in X}d(\pi _{\mathfrak {w}}(x),\pi _{\mathfrak {w}}(\Phi (x)))<+\infty$.
Proof of Claim 1 Fix a point 
$w$ in the intersection between 
$\mathfrak {A}$ and the carrier of 
$\mathfrak {w}$. Let 
$L\geq 0$ be a constant such that the orbit 
$G\cdot w$ is 
$L$-dense in 
$X$. Since 
$\Phi$ is 
$(D+1)$-Lipschitz and 
$\pi _{\mathfrak {w}}$ is 
$1$-Lipschitz, we have
\begin{align*} \sup_{x\in X}d(\pi_{\mathfrak{w}}(x),\pi_{\mathfrak{w}}(\Phi(x)))&\leq \sup_{g\in G}d(\pi_{\mathfrak{w}}(gw),\pi_{\mathfrak{w}}(\Phi(gw)))+L+(D+1)L \\ &=\sup_{g\in G}d(\pi_{\mathfrak{w}}(gw),\pi_{\mathfrak{w}}(\varphi(g)w)))+L+(D+1)L. \end{align*}
The last quantity is finite by Proposition 7.19, which proves the claim.
Claim 2 For every hyperplane 
$\mathfrak {u}\in G\cdot \mathfrak {w}$ bounding the region 
$\mathfrak {A}$ and every 
$x\in X$, we have 
$d(\pi _{\mathfrak {u}}(x),\pi _{\mathfrak {u}}(\Phi (x)))\leq P+D$.
Proof of Claim 2 Suppose first that 
$\mathfrak {u}=a\mathfrak {w}$ for some 
$a\in A$. Then, since 
$\varphi (a)=a$, we have
\[ d(\pi_{a\mathfrak{w}}(x),\pi_{a\mathfrak{w}}(\Phi(x)))=d(\pi_{\mathfrak{w}}(a^{-1}x),\pi_{\mathfrak{w}}(a^{-1}\Phi(x)))=d(\pi_{\mathfrak{w}}(a^{-1}x),\pi_{\mathfrak{w}}(\Phi(a^{-1}x)))\leq P, \]
by Claim 1. The only other option (only in the HNN case) is that 
$\mathfrak {u}=at^{-1}\mathfrak {w}$ for some 
$a\in A$. By the above equalities, it suffices to consider the case 
$a=1$. Then, we have
\[ d(\pi_{t^{-1}\mathfrak{w}}(x),\pi_{t^{-1}\mathfrak{w}}(\Phi(x)))=d(\pi_{\mathfrak{w}}(tx),\pi_{\mathfrak{w}}(t\Phi(x)))=d(\pi_{\mathfrak{w}}(tx),\pi_{\mathfrak{w}}(\Phi(z^{-1}tx))). \]
Since 
$\pi _{\mathfrak {w}}(tx)$ and 
$\pi _{\mathfrak {w}}(z^{-1}tx)$ are at distance at most 
$D$ by Lemma 7.16(2), the above quantity is at most 
$P+D$, as required.
Now, consider vertices 
$x,y,p\in X$ with 
$p=m(x,y,p)$. We will show that there are at most 
$4P+2D$ hyperplanes in the set 
$\mathscr {W}(\Phi (p)|\Phi (x),\Phi (y))$. By Lemma 2.17, this shows that 
$\Phi$ is coarse-median preserving.
Since 
$\Phi$ is the restriction of an isometry on each connected component of 
$X\setminus G\cdot \mathfrak {w}$, we can assume that 
$x,y,p$ do not all lie in the same component of 
$X\setminus G\cdot \mathfrak {w}$. Thus, possibly swapping 
$x$ and 
$y$, the points 
$p$ and 
$y$ are separated by a hyperplane in the orbit 
$G\cdot \mathfrak {w}$. Translating 
$x,y,p$ by an element of 
$G$ does not alter the size of the set 
$\mathscr {W}(\Phi (p)|\Phi (x),\Phi (y))$ (by the first property in Definition 7.20), so we can assume that 
$\mathfrak {w}\in \mathscr {W}(p|y)$ and 
$p\in \mathfrak {A}\cup \mathfrak {B}$.
We only treat the case when 
$p\in \mathfrak {A}$. The other case is identical if we replace 
$\Phi$ with the map 
$z^{-1}\Phi$ and compose 
$\varphi$ with an inner automorphism of 
$G$ given by 
$z$.
By Claim 1, the projections 
$\pi _{\mathfrak {w}}(\Phi (x))$ and 
$\pi _{\mathfrak {w}}(\Phi (y))$ are at distance at most 
$P$ from the points 
$\pi _{\mathfrak {w}}(x)$ and 
$\pi _{\mathfrak {w}}(y)$, respectively. Since 
$x,p,y$ lie on a geodesic in this order, so do their projections 
$\pi _{\mathfrak {w}}(x)$, 
$\pi _{\mathfrak {w}}(p)$ and 
$\pi _{\mathfrak {w}}(y)$. Hence at most 
$2P$ hyperplanes can separate 
$\pi _{\mathfrak {w}}(p)$ from 
$\pi _{\mathfrak {w}}(\Phi (x))$ and 
$\pi _{\mathfrak {w}}(\Phi (y))$. In other words, at most 
$2P$ hyperplanes in 
$\mathscr {W}(p|\Phi (x),\Phi (y))$ are transverse to 
$\mathfrak {w}$.
In case 
$x\not \in \mathfrak {A}$, let 
$\mathfrak {u}\in G\cdot \mathfrak {w}$ be a hyperplane adjacent to 
$\mathfrak {A}$ and separating 
$\Phi (x)$ from 
$\mathfrak {A}$. With the argument in the previous paragraph, Claim 2 implies that at most 
$2(P+D)$ hyperplanes in 
$\mathscr {W}(p|\Phi (x),\Phi (y))$ are transverse to 
$\mathfrak {u}$.
Since 
$\varphi$ is the identity on 
$A$, note that 
$y$ and 
$\Phi (y)$ are on the same side of 
$\mathfrak {w}$ and, similarly, 
$x$ and 
$\Phi (x)$ are on the same side of 
$\mathfrak {u}$. Thus 
$\mathfrak {w}$ lies in 
$\mathscr {W}(p,\Phi (x) | y,\Phi (y))$ and, when defined, 
$\mathfrak {u}$ lies in 
$\mathscr {W}(p,\Phi (y) | x,\Phi (x))$.
Now, since the set 
$\mathscr {W}(p|x,y)$ is empty, we have
\[ \mathscr{W}(p|\Phi(x),\Phi(y))=\mathscr{W}(p,x|\Phi(x),\Phi(y))\cup\mathscr{W}(p,y|\Phi(x),\Phi(y)). \]
The set 
$\mathscr {W}(p,y|\Phi (x),\Phi (y))$ is transverse to the set 
$\mathscr {W}(p,\Phi (x) | y,\Phi (y))$, which contains 
$\mathfrak {w}$. Similarly, 
$\mathscr {W}(p,x|\Phi (x),\Phi (y))$ is transverse to 
$\mathscr {W}(p,\Phi (y) | x,\Phi (x))\ni \mathfrak {u}$ (or it is empty, if 
$x\in \mathfrak {A}$). In conclusion, every element of 
$\mathscr {W}(p|\Phi (x),\Phi (y))$ is transverse to either 
$\mathfrak {w}$ or 
$\mathfrak {u}$, and so there are at most 
$4P+2D$ hyperplanes in 
$\mathscr {W}(p|\Phi (x),\Phi (y))$. This completes the proof of the proposition.
Proof of Theorem 7.1 By Corollary 7.14, it suffices to prove the theorem under the assumptions of this subsection. Let 
$\varphi \in \operatorname {Aut}(G)$ be our DLS automorphism, as above. Applying Proposition 7.21 to both 
$\varphi$ and 
$\varphi ^{-1}$, we obtain a bi-Lipschitz, coarse-median preserving map 
$\Phi \colon X\rightarrow X$ satisfying 
$\Phi (gx)=\varphi (g)\Phi (x)$ for all 
$g\in G$ and 
$x\in X$. This shows that 
$\varphi$ preserves the coarse median structure on 
$G$ induced by 
$X$.
Acknowledgements
I warmly thank Daniel Groves for the many stimulating conversations on the content of this paper and the Conjecture. I am grateful to Anthony Genevois for pointing me to [Reference Crisp and WiestCW04], to Vincent Guirardel for dispelling some of my misconceptions on geometric trees, and to Michah Sageev for suggesting the first paragraph of the proof of Proposition 2.2. I also thank Montserrat Casals-Ruiz, Michael Hull, Gilbert Levitt, Ashot Minasyan and Zlil Sela for useful comments and interesting discussions related to this work. Finally, I am particularly grateful to the referee for their many helpful suggestions. I thank the Max Planck Institute for Mathematics in Bonn, the University of Bonn and Ursula Hamenstädt for their hospitality and financial support while this work was being completed.
Open access
