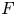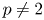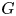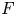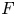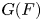1. Introduction
In 2001, Yu [Reference YuYu01] proposed a construction of smooth complex supercuspidal representations of ![]() $p$-adic groups that since then has been widely used, for example to study the Howe correspondence, to understand distinction of representations of
$p$-adic groups that since then has been widely used, for example to study the Howe correspondence, to understand distinction of representations of ![]() $p$-adic groups, to obtain character formulas and to construct an explicit local Langlands correspondence. However, Loren Spice noticed recently that Yu's proof relies on a misprintedFootnote 1 (and therefore false) statement in [Reference GérardinGér77] and therefore it became uncertain whether the representations constructed by Yu are irreducible and supercuspidal. In the present paper we illustrate the significance of this false statement on Yu's proof by providing a counterexample to Proposition 14.1 and Theorem 14.2 of [Reference YuYu01]. Proposition 14.1 and Theorem 14.2 are the main intertwining results in [Reference YuYu01] that form the heart of the proof. We also offer a different argument to show that nevertheless Yu's construction yields irreducible supercuspidal representations.
$p$-adic groups, to obtain character formulas and to construct an explicit local Langlands correspondence. However, Loren Spice noticed recently that Yu's proof relies on a misprintedFootnote 1 (and therefore false) statement in [Reference GérardinGér77] and therefore it became uncertain whether the representations constructed by Yu are irreducible and supercuspidal. In the present paper we illustrate the significance of this false statement on Yu's proof by providing a counterexample to Proposition 14.1 and Theorem 14.2 of [Reference YuYu01]. Proposition 14.1 and Theorem 14.2 are the main intertwining results in [Reference YuYu01] that form the heart of the proof. We also offer a different argument to show that nevertheless Yu's construction yields irreducible supercuspidal representations.
Let ![]() $F$ be a non-archimedean local field of residual characteristic
$F$ be a non-archimedean local field of residual characteristic ![]() $p \neq 2$. Let
$p \neq 2$. Let ![]() $G$ be a (connected) reductive group that splits over a tamely ramified field extension of
$G$ be a (connected) reductive group that splits over a tamely ramified field extension of ![]() $F$. In this paper we first describe the construction of Yu's representations in a way that we find more convenient for our purpose and then provide a proof that these representations are supercuspidal. All representations arise via compact induction from an irreducible representation
$F$. In this paper we first describe the construction of Yu's representations in a way that we find more convenient for our purpose and then provide a proof that these representations are supercuspidal. All representations arise via compact induction from an irreducible representation ![]() $\tilde \rho$ of a compact-mod-center open subgroup
$\tilde \rho$ of a compact-mod-center open subgroup ![]() $\tilde K$ of
$\tilde K$ of ![]() $G(F)$. Our proof only relies on the first part of Yu's proof and provides a shorter, alternative second part that does not rely on [Reference YuYu01, Proposition 14.1 and Theorem 14.2] and the misprinted version of [Reference GérardinGér77, Theorem 2.4(b)]. Yu's approach consists of following a strategy already employed by Bushnell and Kutzko that required to show that a certain space of intertwining operators has dimension precisely one, that is, in particular, is non-trivial. Our approach does not require such a result. Instead we use the structure of the constructed representation including the structure of Weil–Heisenberg representations, and the Bruhat–Tits building to show more directly that every element that intertwines
$G(F)$. Our proof only relies on the first part of Yu's proof and provides a shorter, alternative second part that does not rely on [Reference YuYu01, Proposition 14.1 and Theorem 14.2] and the misprinted version of [Reference GérardinGér77, Theorem 2.4(b)]. Yu's approach consists of following a strategy already employed by Bushnell and Kutzko that required to show that a certain space of intertwining operators has dimension precisely one, that is, in particular, is non-trivial. Our approach does not require such a result. Instead we use the structure of the constructed representation including the structure of Weil–Heisenberg representations, and the Bruhat–Tits building to show more directly that every element that intertwines ![]() $\tilde \rho$ is contained in
$\tilde \rho$ is contained in ![]() $\tilde K$, which implies the desired result. Our proof relies also less heavily on tameness assumptions, and our aim is to use a modification of it for the construction of supercuspidal representations beyond the tame setting when Yu's construction is not exhaustive.
$\tilde K$, which implies the desired result. Our proof relies also less heavily on tameness assumptions, and our aim is to use a modification of it for the construction of supercuspidal representations beyond the tame setting when Yu's construction is not exhaustive.
Note that Yu's construction yields all supercuspidal representations if ![]() $p$ does not divide the order of the Weyl group of
$p$ does not divide the order of the Weyl group of ![]() $G$ [Reference FintzenFin21, Reference KimKim07], a condition that guarantees that all tori of
$G$ [Reference FintzenFin21, Reference KimKim07], a condition that guarantees that all tori of ![]() $G$ split over a tamely ramified field extension of
$G$ split over a tamely ramified field extension of ![]() $F$.
$F$.
In the last section we provide a counterexample to [Reference YuYu01, Proposition 14.1 and Theorem 14.2] by considering the group ![]() $G=\operatorname {Sp}_{10}$ together with a twisted Levi subgroup
$G=\operatorname {Sp}_{10}$ together with a twisted Levi subgroup ![]() $G'$ of shape
$G'$ of shape ![]() $\operatorname {U}(1) \times \operatorname {Sp}_8$ and a well chosen point in the Bruhat–Tits building of
$\operatorname {U}(1) \times \operatorname {Sp}_8$ and a well chosen point in the Bruhat–Tits building of ![]() $G'$.
$G'$.
Conventions and notation
Let ![]() $F$ be a non-archimedean local field of residual characteristic
$F$ be a non-archimedean local field of residual characteristic ![]() $p \neq 2$. We denote by
$p \neq 2$. We denote by ![]() $\mathcal {O}$ the ring of integers of
$\mathcal {O}$ the ring of integers of ![]() $F$, and by
$F$, and by ![]() $\mathcal {P}$ the maximal ideal of
$\mathcal {P}$ the maximal ideal of ![]() $\mathcal {O}$. The residue field
$\mathcal {O}$. The residue field ![]() $\mathcal {O}/\mathcal {P}$ is denoted by
$\mathcal {O}/\mathcal {P}$ is denoted by ![]() $\mathbb {F}_q$, where
$\mathbb {F}_q$, where ![]() $q$ denotes the number of elements in
$q$ denotes the number of elements in ![]() $\mathbb {F}_q$. When considering field extensions of
$\mathbb {F}_q$. When considering field extensions of ![]() $F$ in this paper, we mean algebraic field extensions of
$F$ in this paper, we mean algebraic field extensions of ![]() $F$ and view them as contained in a fixed algebraic closure
$F$ and view them as contained in a fixed algebraic closure ![]() $\bar F$ of
$\bar F$ of ![]() $F$. We write
$F$. We write ![]() $F^{\rm sep}$ for the separable closure of F.
$F^{\rm sep}$ for the separable closure of F.
All reductive groups in this paper are required to be connected.
For a reductive group ![]() $G$ defined over
$G$ defined over ![]() $F$ we denote by
$F$ we denote by ![]() $\mathscr {B}(G,F)$ the (enlarged) Bruhat–Tits building [Reference Bruhat and TitsBT72, Reference Bruhat and TitsBT84] of
$\mathscr {B}(G,F)$ the (enlarged) Bruhat–Tits building [Reference Bruhat and TitsBT72, Reference Bruhat and TitsBT84] of ![]() $G$ over
$G$ over ![]() $F$, by
$F$, by ![]() $Z(G)$ the center of
$Z(G)$ the center of ![]() $G$ and by
$G$ and by ![]() $G^{\mathrm {der}}$ the derived subgroup of
$G^{\mathrm {der}}$ the derived subgroup of ![]() $G$. If
$G$. If ![]() $T$ is a maximal, maximally split torus of
$T$ is a maximal, maximally split torus of ![]() $G_E:=G \times _F E$ for some field extension
$G_E:=G \times _F E$ for some field extension ![]() $E$ over
$E$ over ![]() $F$, then
$F$, then ![]() $\mathscr {A}(T,E)$ denotes the apartment of
$\mathscr {A}(T,E)$ denotes the apartment of ![]() $T$ inside the Bruhat–Tits building
$T$ inside the Bruhat–Tits building ![]() $\mathscr {B}(G_E,E)$ of
$\mathscr {B}(G_E,E)$ of ![]() $G_E$ over
$G_E$ over ![]() $E$. Moreover, we write
$E$. Moreover, we write ![]() $\Phi (G_E,T)$ for the roots of
$\Phi (G_E,T)$ for the roots of ![]() $G_{E} \times _{E} \bar F$ with respect to
$G_{E} \times _{E} \bar F$ with respect to ![]() $T_{\bar F}$. We let
$T_{\bar F}$. We let ![]() $\tilde {\mathbb {R}}=\mathbb {R} \cup \{ {r+} \, | \, r \in \mathbb {R}\}$ with its usual order, that is, for
$\tilde {\mathbb {R}}=\mathbb {R} \cup \{ {r+} \, | \, r \in \mathbb {R}\}$ with its usual order, that is, for ![]() $r$ and
$r$ and ![]() $s$ in
$s$ in ![]() $\mathbb {R}$ with
$\mathbb {R}$ with ![]() $r< s$, we have
$r< s$, we have ![]() $r< r+< s< s+$. For
$r< r+< s< s+$. For ![]() $r \in \tilde {\mathbb {R}}_{\geq 0}$, we write
$r \in \tilde {\mathbb {R}}_{\geq 0}$, we write ![]() $G_{x,r}$ for the Moy–Prasad filtration subgroup of
$G_{x,r}$ for the Moy–Prasad filtration subgroup of ![]() $G(F)$ of depth
$G(F)$ of depth ![]() $r$ at a point
$r$ at a point ![]() $x \in \mathscr {B}(G,F)$. For
$x \in \mathscr {B}(G,F)$. For ![]() $r \in \tilde {\mathbb {R}}$, we write
$r \in \tilde {\mathbb {R}}$, we write ![]() $\mathfrak {g}_{x,r}$ for the Moy–Prasad filtration submodule of
$\mathfrak {g}_{x,r}$ for the Moy–Prasad filtration submodule of ![]() $\mathfrak {g}=\operatorname {Lie} G(F)$ of depth
$\mathfrak {g}=\operatorname {Lie} G(F)$ of depth ![]() $r$ at
$r$ at ![]() $x$, and
$x$, and ![]() $\mathfrak {g}^{*}_{x,r}$ for the Moy–Prasad filtration submodule of depth
$\mathfrak {g}^{*}_{x,r}$ for the Moy–Prasad filtration submodule of depth ![]() $r$ at
$r$ at ![]() $x$ of the linear dual
$x$ of the linear dual ![]() $\mathfrak {g}^{*}$ of
$\mathfrak {g}^{*}$ of ![]() $\mathfrak {g}$. If
$\mathfrak {g}$. If ![]() $x \in \mathscr {B}(G,F)$, then we denote by
$x \in \mathscr {B}(G,F)$, then we denote by ![]() $[x]$ its image in the reduced Bruhat–Tits building and we write
$[x]$ its image in the reduced Bruhat–Tits building and we write ![]() $G_{[x]}$ for the stabilizer of
$G_{[x]}$ for the stabilizer of ![]() $[x]$ in
$[x]$ in ![]() $G(F)$.
$G(F)$.
We call a subgroup ![]() $G'$ of
$G'$ of ![]() $G$ (defined over
$G$ (defined over ![]() $F$) a twisted Levi subgroup of
$F$) a twisted Levi subgroup of ![]() $G$ if
$G$ if ![]() $(G')_E$ is a Levi subgroup of
$(G')_E$ is a Levi subgroup of ![]() $G_E$ for some (finite) field extension
$G_E$ for some (finite) field extension ![]() $E$ of
$E$ of ![]() $F$. If
$F$. If ![]() $G'$ splits over a tamely ramified field extension of
$G'$ splits over a tamely ramified field extension of ![]() $F$, then, using (tame) Galois descent, we obtain an embedding of the corresponding Bruhat–Tits buildings
$F$, then, using (tame) Galois descent, we obtain an embedding of the corresponding Bruhat–Tits buildings ![]() $\mathscr {B}(G',F) \hookrightarrow \mathscr {B}(G,F)$. This embedding is only unique up to some translation, but its image is unique, and we will identify
$\mathscr {B}(G',F) \hookrightarrow \mathscr {B}(G,F)$. This embedding is only unique up to some translation, but its image is unique, and we will identify ![]() $\mathscr {B}(G',F)$ with its image in
$\mathscr {B}(G',F)$ with its image in ![]() $\mathscr {B}(G,F)$. All constructions in this paper are independent of the choice of such an identification.
$\mathscr {B}(G,F)$. All constructions in this paper are independent of the choice of such an identification.
Let ![]() $H$ be a group and
$H$ be a group and ![]() $\chi$ a character of
$\chi$ a character of ![]() $H$. Then we denote by
$H$. Then we denote by ![]() $\mathbb {C}_\chi$ the one-dimensional complex representation space on which
$\mathbb {C}_\chi$ the one-dimensional complex representation space on which ![]() $H$ acts via
$H$ acts via ![]() $\chi$. We also write
$\chi$. We also write ![]() $1$ to denote the one-dimensional trivial complex representation. If
$1$ to denote the one-dimensional trivial complex representation. If ![]() $K$ is a subgroup of
$K$ is a subgroup of ![]() $H$,
$H$, ![]() $h \in H$, and
$h \in H$, and ![]() $\rho$ a representation of
$\rho$ a representation of ![]() $K$, then we write
$K$, then we write ![]() $^{h}K$ to denote
$^{h}K$ to denote ![]() $hKh^{-1}$ and define
$hKh^{-1}$ and define ![]() ${{}^{h}\rho }(x)=\rho (h^{-1}xh)$ for
${{}^{h}\rho }(x)=\rho (h^{-1}xh)$ for ![]() $x \in K \cap {{}^{h}K}$. We say that
$x \in K \cap {{}^{h}K}$. We say that ![]() $h$ intertwines
$h$ intertwines ![]() $\rho$ if the space of intertwiners
$\rho$ if the space of intertwiners ![]() $\operatorname {Hom}_{K \cap {{}^{h}K}}(\rho, {{}^{h}\rho })$ is non-zero.
$\operatorname {Hom}_{K \cap {{}^{h}K}}(\rho, {{}^{h}\rho })$ is non-zero.
Throughout the paper we fix an additive character ![]() $\varphi : F \rightarrow \mathbb {C}^{*}$ of
$\varphi : F \rightarrow \mathbb {C}^{*}$ of ![]() $F$ of conductor
$F$ of conductor ![]() $\mathcal {P}$ and a reductive group
$\mathcal {P}$ and a reductive group ![]() $G$ that is defined over our non-archimedean local field
$G$ that is defined over our non-archimedean local field ![]() $F$ and that splits over a tamely ramified field extension of
$F$ and that splits over a tamely ramified field extension of ![]() $F$. All representations of
$F$. All representations of ![]() $G(F)$ in this paper have complex coefficients and are required to be smooth.
$G(F)$ in this paper have complex coefficients and are required to be smooth.
2. Construction of representations à la Yu
In this section we recall Yu's construction of representations but formulated in a way that is better adapted to our proof of supercuspidality.
2.1 The input
The input for Yu's construction of supercuspidal representations of ![]() $G(F)$ (using the conventions from [Reference FintzenFin21]; see Remark 2.4 for a comparison of Yu's notation with ours) is a tuple
$G(F)$ (using the conventions from [Reference FintzenFin21]; see Remark 2.4 for a comparison of Yu's notation with ours) is a tuple ![]() $((G_i)_{1 \leq i \leq n+1}, x, (r_i)_{1 \leq i \leq n}, \rho, (\phi _i)_{1 \leq i \leq n})$ for some non-negative integer
$((G_i)_{1 \leq i \leq n+1}, x, (r_i)_{1 \leq i \leq n}, \rho, (\phi _i)_{1 \leq i \leq n})$ for some non-negative integer ![]() $n$ where
$n$ where
(a)
 $G=G_1 \supseteq G_2 \supsetneq G_3 \supsetneq \ldots \supsetneq G_{n+1}$ are twisted Levi subgroups of
$G=G_1 \supseteq G_2 \supsetneq G_3 \supsetneq \ldots \supsetneq G_{n+1}$ are twisted Levi subgroups of  $G$ that split over a tamely ramified extension of
$G$ that split over a tamely ramified extension of  $F$,
$F$,(b)
 $x \in \mathscr {B}(G_{n+1},F)\subset \mathscr {B}(G,F)$,
$x \in \mathscr {B}(G_{n+1},F)\subset \mathscr {B}(G,F)$,(c)
 $r_1 > r_2 > \ldots > r_n >0$ are real numbers,
$r_1 > r_2 > \ldots > r_n >0$ are real numbers,(d)
 $\rho$ is an irreducible representation of
$\rho$ is an irreducible representation of  $(G_{n+1})_{[x]}$ that is trivial on
$(G_{n+1})_{[x]}$ that is trivial on  $(G_{n+1})_{x,0+}$,
$(G_{n+1})_{x,0+}$,(e)
 $\phi _i$, for
$\phi _i$, for  $1 \leq i \leq n$, is a character of
$1 \leq i \leq n$, is a character of  $G_{i+1}(F)$ of depth
$G_{i+1}(F)$ of depth  $r_i$ that is trivial on
$r_i$ that is trivial on  $(G_{i+1})_{x,r_i+}$,
$(G_{i+1})_{x,r_i+}$,
satisfying the following conditions:
(i)
 $Z(G_{n+1})/Z(G)$ is anisotropic;
$Z(G_{n+1})/Z(G)$ is anisotropic;(ii) the image of the point
 $x$ in
$x$ in  $\mathscr {B}(G_{n+1}^{\mathrm {der}},F)$ is a vertex;
$\mathscr {B}(G_{n+1}^{\mathrm {der}},F)$ is a vertex;(iii)
 $\rho |_{(G_{n+1})_{x,0}}$ is a cuspidal representation of
$\rho |_{(G_{n+1})_{x,0}}$ is a cuspidal representation of  $(G_{n+1})_{x,0}/(G_{n+1})_{x,0+}$;
$(G_{n+1})_{x,0}/(G_{n+1})_{x,0+}$;(iv)
 $\phi _i$ is
$\phi _i$ is  $G_i$-generic of depth
$G_i$-generic of depth  $r_i$ relative to
$r_i$ relative to  $x$ (in the sense of [Reference YuYu01, § 9, p. 599]) for all
$x$ (in the sense of [Reference YuYu01, § 9, p. 599]) for all  $1 \leq i \leq n$ with
$1 \leq i \leq n$ with  $G_i \neq G_{i+1}$ .
$G_i \neq G_{i+1}$ .
Remark 2.2 Note that for each apartment ![]() $\mathscr {A}$ of
$\mathscr {A}$ of ![]() $\mathscr {B}(G_{n+1},F)$, there exists a maximal torus
$\mathscr {B}(G_{n+1},F)$, there exists a maximal torus ![]() $T$ of
$T$ of ![]() $G_{n+1}$ that splits over a tamely ramified extension
$G_{n+1}$ that splits over a tamely ramified extension ![]() $E$ of
$E$ of ![]() $F$ such that
$F$ such that ![]() $\mathscr {A} \subset \mathscr {A}(T, E)$ (see, for example, [Reference YuYu01, § 2, pp. 585–586], which is based on [Reference Bruhat and TitsBT84, Reference RousseauRou77]). In particular, there exists a maximal torus
$\mathscr {A} \subset \mathscr {A}(T, E)$ (see, for example, [Reference YuYu01, § 2, pp. 585–586], which is based on [Reference Bruhat and TitsBT84, Reference RousseauRou77]). In particular, there exists a maximal torus ![]() $T$ of
$T$ of ![]() $G_{n+1}$ that splits over a tamely ramified extension
$G_{n+1}$ that splits over a tamely ramified extension ![]() $E$ of
$E$ of ![]() $F$ such that
$F$ such that ![]() $x \in \mathscr {A}(T, E)$.
$x \in \mathscr {A}(T, E)$.
Remark 2.3 By (the proof of) [Reference Moy and PrasadMP96, Proposition 6.8] requiring that the image of the point ![]() $x$ in
$x$ in ![]() $\mathscr {B}(G_{n+1}^{\mathrm {der}},F)$ is a vertex and that
$\mathscr {B}(G_{n+1}^{\mathrm {der}},F)$ is a vertex and that ![]() $\rho |_{(G_{n+1})_{x,0}}$ is a cuspidal representation of
$\rho |_{(G_{n+1})_{x,0}}$ is a cuspidal representation of ![]() $(G_{n+1})_{x,0}/(G_{n+1})_{x,0+}$ is equivalent to requiring that
$(G_{n+1})_{x,0}/(G_{n+1})_{x,0+}$ is equivalent to requiring that ![]() $\operatorname {c-ind}_{(G_{n+1})_{[x]}}^{G_{n+1}(F)}\rho$ is an irreducible supercuspidal representation. When
$\operatorname {c-ind}_{(G_{n+1})_{[x]}}^{G_{n+1}(F)}\rho$ is an irreducible supercuspidal representation. When ![]() $n=0$, then the tuple
$n=0$, then the tuple ![]() $((G_i)_{1 \leq i \leq n+1}, x, (r_i)_{1 \leq i \leq n}, \rho, (\phi _i)_{1 \leq i \leq n})$ consists only of the group
$((G_i)_{1 \leq i \leq n+1}, x, (r_i)_{1 \leq i \leq n}, \rho, (\phi _i)_{1 \leq i \leq n})$ consists only of the group ![]() $G=G_1=G_{n+1}$, a point
$G=G_1=G_{n+1}$, a point ![]() $x \in \mathscr {B}(G,F)$ whose image in
$x \in \mathscr {B}(G,F)$ whose image in ![]() $\mathscr {B}(G^{\mathrm {der}},F)$ is a vertex, and an irreducible representation
$\mathscr {B}(G^{\mathrm {der}},F)$ is a vertex, and an irreducible representation ![]() $\rho$ of
$\rho$ of ![]() $G_{[x]}$ that is trivial on
$G_{[x]}$ that is trivial on ![]() $G_{x,0+}$ and such that its restriction
$G_{x,0+}$ and such that its restriction ![]() $\rho |_{G_{x,0}}$ is a cuspidal representation of
$\rho |_{G_{x,0}}$ is a cuspidal representation of ![]() $G_{x,0}/G_{x,0+}$. This case recovers the depth-zero supercuspidal representations.
$G_{x,0}/G_{x,0+}$. This case recovers the depth-zero supercuspidal representations.
Remark 2.4 We use the conventions for notation from [Reference FintzenFin21] instead of from [Reference YuYu01]. The notation in [Reference YuYu01] (left-hand side) can be recovered from ours (right-hand side) as follows:
 \begin{align*} \vec G= (G^{0}, G^{1},
\ldots, G^{d}) &= \left\{ \begin{array}{@{}ll} (G_{n+1}, G_n,
\ldots, G_2, G_1=G) & \text{ if } G_2 \neq G_1 \text{ or }
n=0 \\ (G_{n+1}, G_n, \ldots, G_3, G_2=G) & \text{ if }
G_2=G_1, \end{array}\right.\\ \vec r & = \left\{
\begin{array}{@{}ll} (r_{n}, r_{n-1}, \ldots, r_2, r_1, r_\pi)
& \text{ if } G_2 \neq G_1 \text{ or } n=0 \\ (r_{n},
r_{n-1}, \ldots, r_2, r_1) & \text{ if } G_2=G_1,
\end{array}\right. \\ \vec \phi & = \left\{
\begin{array}{@{}ll} (\phi_{n}, \phi_{n-1}, \ldots, \phi_2,
\phi_1, 1) & \text{ if } G_2 \neq G_1 \text{ or } n=0 \\
(\phi_{n}, \phi_{n-1}, \ldots, \phi_2, \phi_1) & \text{ if
} G_2=G_1, \end{array}\right. \end{align*}
\begin{align*} \vec G= (G^{0}, G^{1},
\ldots, G^{d}) &= \left\{ \begin{array}{@{}ll} (G_{n+1}, G_n,
\ldots, G_2, G_1=G) & \text{ if } G_2 \neq G_1 \text{ or }
n=0 \\ (G_{n+1}, G_n, \ldots, G_3, G_2=G) & \text{ if }
G_2=G_1, \end{array}\right.\\ \vec r & = \left\{
\begin{array}{@{}ll} (r_{n}, r_{n-1}, \ldots, r_2, r_1, r_\pi)
& \text{ if } G_2 \neq G_1 \text{ or } n=0 \\ (r_{n},
r_{n-1}, \ldots, r_2, r_1) & \text{ if } G_2=G_1,
\end{array}\right. \\ \vec \phi & = \left\{
\begin{array}{@{}ll} (\phi_{n}, \phi_{n-1}, \ldots, \phi_2,
\phi_1, 1) & \text{ if } G_2 \neq G_1 \text{ or } n=0 \\
(\phi_{n}, \phi_{n-1}, \ldots, \phi_2, \phi_1) & \text{ if
} G_2=G_1, \end{array}\right. \end{align*}
where ![]() $r_\pi =r_1$ if
$r_\pi =r_1$ if ![]() $n \geq 1$ and
$n \geq 1$ and ![]() $r_\pi =0$ if
$r_\pi =0$ if ![]() $n=0$. Yu's convention has the advantage that it is adapted to associating a whole sequence of supercuspidal representations to a given datum (by only considering the groups
$n=0$. Yu's convention has the advantage that it is adapted to associating a whole sequence of supercuspidal representations to a given datum (by only considering the groups ![]() $G_i, G_{i+1}, \ldots, G_{n+1}$), while our convention is more natural when recovering the input from a given representation as can be seen in [Reference FintzenFin21]. We have chosen our convention for this paper as it has the advantage that our induction steps below start with
$G_i, G_{i+1}, \ldots, G_{n+1}$), while our convention is more natural when recovering the input from a given representation as can be seen in [Reference FintzenFin21]. We have chosen our convention for this paper as it has the advantage that our induction steps below start with ![]() $G_1$ and move from
$G_1$ and move from ![]() $G_i$ to
$G_i$ to ![]() $G_{i+1}$. Moreover, using our notation, we do not have to impose a condition on
$G_{i+1}$. Moreover, using our notation, we do not have to impose a condition on ![]() $\phi _d$ depending on whether
$\phi _d$ depending on whether ![]() $r_{d-1} < r_d$ or
$r_{d-1} < r_d$ or ![]() $r_{d-1}=r_d$ in Yu's notation; see [Reference YuYu01, p. 590 D5]. Hence the input looks more uniform. (Note that our condition
$r_{d-1}=r_d$ in Yu's notation; see [Reference YuYu01, p. 590 D5]. Hence the input looks more uniform. (Note that our condition ![]() $G_i \neq G_{i+1}$ in (iv) could be removed by extending the notion of ‘
$G_i \neq G_{i+1}$ in (iv) could be removed by extending the notion of ‘![]() $G_i$-generic’ to the case
$G_i$-generic’ to the case ![]() $G_i = G_{i+1}$.)
$G_i = G_{i+1}$.)
2.5 The construction
The (smooth complex) representation ![]() $\pi$ of
$\pi$ of ![]() $G(F)$ that Yu constructs from the given input
$G(F)$ that Yu constructs from the given input ![]() $((G_i)_{1 \leq i \leq n+1}, x, (r_i)_{1 \leq i \leq n}, \rho, (\phi _i)_{1 \leq i \leq n})$ is the compact induction
$((G_i)_{1 \leq i \leq n+1}, x, (r_i)_{1 \leq i \leq n}, \rho, (\phi _i)_{1 \leq i \leq n})$ is the compact induction ![]() $\operatorname {c-ind}_{\tilde K}^{G(F)} \tilde \rho$ of a representation
$\operatorname {c-ind}_{\tilde K}^{G(F)} \tilde \rho$ of a representation ![]() $\tilde \rho$ of a compact-mod-center, open subgroup
$\tilde \rho$ of a compact-mod-center, open subgroup ![]() $\tilde K \subset G(F)$.
$\tilde K \subset G(F)$.
In order to define ![]() $\tilde K$ and
$\tilde K$ and ![]() $\tilde \rho$ we introduce the following notation. For
$\tilde \rho$ we introduce the following notation. For ![]() $\tilde r \geq \tilde r' \geq {\tilde r}/{2}>0$ (
$\tilde r \geq \tilde r' \geq {\tilde r}/{2}>0$ (![]() $\tilde r, \tilde r' \in \tilde {\mathbb {R}}$) and
$\tilde r, \tilde r' \in \tilde {\mathbb {R}}$) and ![]() $1 \leq i \leq n$, we choose a maximal torus
$1 \leq i \leq n$, we choose a maximal torus ![]() $T$ of
$T$ of ![]() $G_{i+1}$ that splits over a tamely ramified extension
$G_{i+1}$ that splits over a tamely ramified extension ![]() $E$ of
$E$ of ![]() $F$ and such that
$F$ and such that ![]() $x \in \mathscr {A}(T,E)$. Then we define
$x \in \mathscr {A}(T,E)$. Then we define
 \begin{align*} (G_{i})_{x,\tilde r,\tilde r'} &:= G(F) \cap \\ &\qquad \big\langle T(E)_{\tilde r}, U_\alpha(E)_{x,\tilde r}, U_\beta(E)_{x,\tilde r'} \, | \, \alpha \in \Phi(G_i, T)\subset\Phi(G,T), \beta \in \Phi(G_i, T)-\Phi(G_{i+1}, T) \, \big\rangle, \end{align*}
\begin{align*} (G_{i})_{x,\tilde r,\tilde r'} &:= G(F) \cap \\ &\qquad \big\langle T(E)_{\tilde r}, U_\alpha(E)_{x,\tilde r}, U_\beta(E)_{x,\tilde r'} \, | \, \alpha \in \Phi(G_i, T)\subset\Phi(G,T), \beta \in \Phi(G_i, T)-\Phi(G_{i+1}, T) \, \big\rangle, \end{align*}
where ![]() $U_\alpha (E)_{x,r}$ denotes the Moy–Prasad filtration subgroup of depth
$U_\alpha (E)_{x,r}$ denotes the Moy–Prasad filtration subgroup of depth ![]() $r$ (at
$r$ (at ![]() $x$) of the root group
$x$) of the root group ![]() $U_\alpha (E) \subset G(E)$ corresponding to the root
$U_\alpha (E) \subset G(E)$ corresponding to the root ![]() $\alpha$. We define
$\alpha$. We define ![]() $(\mathfrak {g}_{i})_{x,\tilde r,\tilde r'}$ analogously for
$(\mathfrak {g}_{i})_{x,\tilde r,\tilde r'}$ analogously for ![]() $\mathfrak {g}_i=\operatorname {Lie}(G_i)(F)$. The group
$\mathfrak {g}_i=\operatorname {Lie}(G_i)(F)$. The group ![]() $(G_{i})_{x,\tilde r, \tilde r'}$ is denoted by
$(G_{i})_{x,\tilde r, \tilde r'}$ is denoted by ![]() $(G_{i+1},G_i)(F)_{x_i,\tilde r, \tilde r'}$ in [Reference YuYu01], and Yu [Reference YuYu01, pp. 585–586] shows that this definition is independent of the choice of
$(G_{i+1},G_i)(F)_{x_i,\tilde r, \tilde r'}$ in [Reference YuYu01], and Yu [Reference YuYu01, pp. 585–586] shows that this definition is independent of the choice of ![]() $T$ and
$T$ and ![]() $E$.
$E$.
We set
 \begin{align*} \tilde K &=(G_1)_{x,{r_1}/{2}}(G_2)_{x,{r_2}/{2}} \ldots (G_n)_{x,{r_n}/{2}}(G_{n+1})_{[x]} \\ &=(G_1)_{x,r_1,{r_1}/{2}}(G_2)_{x,r_2,{r_2}/{2}} \ldots (G_n)_{x,r_n,{r_n}/{2}}(G_{n+1})_{[x]}. \end{align*}
\begin{align*} \tilde K &=(G_1)_{x,{r_1}/{2}}(G_2)_{x,{r_2}/{2}} \ldots (G_n)_{x,{r_n}/{2}}(G_{n+1})_{[x]} \\ &=(G_1)_{x,r_1,{r_1}/{2}}(G_2)_{x,r_2,{r_2}/{2}} \ldots (G_n)_{x,r_n,{r_n}/{2}}(G_{n+1})_{[x]}. \end{align*}
Note that since we assume that ![]() $Z(G_{n+1})/Z(G)$ is anisotropic (see condition (i)), the subgroup
$Z(G_{n+1})/Z(G)$ is anisotropic (see condition (i)), the subgroup ![]() $\tilde K$ of
$\tilde K$ of ![]() $G(F)$ is compact mod center. Now the representation
$G(F)$ is compact mod center. Now the representation ![]() $\tilde \rho$ of
$\tilde \rho$ of ![]() $\tilde K$ is given by
$\tilde K$ is given by ![]() $\rho \otimes \kappa$, where
$\rho \otimes \kappa$, where ![]() $\rho$ also denotes the extension of
$\rho$ also denotes the extension of ![]() $\rho$ from
$\rho$ from ![]() $(G_{n+1})_{[x]}$ to
$(G_{n+1})_{[x]}$ to ![]() $\tilde K$ that is trivial on
$\tilde K$ that is trivial on ![]() $(G_1)_{x,{r_1}/{2}}(G_2)_{x,{r_2}/{2}} \ldots (G_n)_{x,{r_n}/{2}}$. In order to define
$(G_1)_{x,{r_1}/{2}}(G_2)_{x,{r_2}/{2}} \ldots (G_n)_{x,{r_n}/{2}}$. In order to define ![]() $\kappa$ we need some additional notation.
$\kappa$ we need some additional notation.
Following [Reference YuYu01, § 4], we denote by ![]() $\hat {\phi }_i$ for
$\hat {\phi }_i$ for ![]() $1 \leq i \leq n$ the unique character of
$1 \leq i \leq n$ the unique character of ![]() $(G_{n+1})_{[x]}(G_{i+1})_{x,0}G_{x,({r_i}/{2})+}$ that satisfies
$(G_{n+1})_{[x]}(G_{i+1})_{x,0}G_{x,({r_i}/{2})+}$ that satisfies
•
 $\hat {\phi }_i|_{(G_{n+1})_{[x]}(G_{i+1})_{x,0}}=\phi _i|_{(G_{n+1})_{[x]}(G_{i+1})_{x,0}}$, and
$\hat {\phi }_i|_{(G_{n+1})_{[x]}(G_{i+1})_{x,0}}=\phi _i|_{(G_{n+1})_{[x]}(G_{i+1})_{x,0}}$, and•
 $\hat {\phi }_i|_{G_{x,({r_i}/{2})+}}$ factors through
on which it is induced by
$\hat {\phi }_i|_{G_{x,({r_i}/{2})+}}$ factors through
on which it is induced by \begin{align*} G_{x,({r_i}/{2})+}/G_{x,r_i+} & \simeq \mathfrak{g}_{x,({r_i}/{2})+}/\mathfrak{g}_{x,r_i+} = (\mathfrak{g}_{i+1} \oplus \mathfrak{r}'')_{x, ({r_i}/{2})+}/(\mathfrak{g}_{i+1} \oplus \mathfrak{r}'')_{x,r_i+} \\ & \rightarrow (\mathfrak{g}_{i+1})_{x,({r_i}/{2})+}/(\mathfrak{g}_{i+1})_{x,r_i+} \simeq (G_{i+1})_{x,({r_i}/{2})+}/(G_{i+1})_{x,r_i+}, \end{align*}
\begin{align*} G_{x,({r_i}/{2})+}/G_{x,r_i+} & \simeq \mathfrak{g}_{x,({r_i}/{2})+}/\mathfrak{g}_{x,r_i+} = (\mathfrak{g}_{i+1} \oplus \mathfrak{r}'')_{x, ({r_i}/{2})+}/(\mathfrak{g}_{i+1} \oplus \mathfrak{r}'')_{x,r_i+} \\ & \rightarrow (\mathfrak{g}_{i+1})_{x,({r_i}/{2})+}/(\mathfrak{g}_{i+1})_{x,r_i+} \simeq (G_{i+1})_{x,({r_i}/{2})+}/(G_{i+1})_{x,r_i+}, \end{align*}
 $\phi _i$. Here
$\phi _i$. Here  $\mathfrak {r}''$ is defined to be
$\mathfrak {r}''$ is defined to be  $\mathfrak {g} \cap \bigoplus _{\alpha \in \Phi (G,T_E)-\Phi (G_{i+1},T_E)} (\mathfrak {g}_E)_\alpha$ for some maximal torus
$\mathfrak {g} \cap \bigoplus _{\alpha \in \Phi (G,T_E)-\Phi (G_{i+1},T_E)} (\mathfrak {g}_E)_\alpha$ for some maximal torus  $T$ of
$T$ of  $G_{i+1}$ that splits over a tame extension
$G_{i+1}$ that splits over a tame extension  $E$ of
$E$ of  $F$ with
$F$ with  $x \in \mathscr {A}(T,E)$, and the surjection
$x \in \mathscr {A}(T,E)$, and the surjection  $\mathfrak {g}_{i+1} \oplus \mathfrak {r}'' \twoheadrightarrow \mathfrak {g}_{i+1}$ sends
$\mathfrak {g}_{i+1} \oplus \mathfrak {r}'' \twoheadrightarrow \mathfrak {g}_{i+1}$ sends  $\mathfrak {r}''$ to zero. (Recall that
$\mathfrak {r}''$ to zero. (Recall that  $\mathfrak {g}=\operatorname {Lie}(G)(F)$, and
$\mathfrak {g}=\operatorname {Lie}(G)(F)$, and  $(\mathfrak {g}_E)_{\alpha }$ denotes the
$(\mathfrak {g}_E)_{\alpha }$ denotes the  $E$-subspace of
$E$-subspace of  $\operatorname {Lie}(G)(E)$ on which the torus acts via
$\operatorname {Lie}(G)(E)$ on which the torus acts via  $\alpha$.)
$\alpha$.)
Note that ![]() $(G_i)_{x,r_i,{r_i}/{2}}/\big ((G_i)_{x,r_i,({r_i}/{2})+} \cap \ker \hat {\phi }_i\big )$ is a Heisenberg
$(G_i)_{x,r_i,{r_i}/{2}}/\big ((G_i)_{x,r_i,({r_i}/{2})+} \cap \ker \hat {\phi }_i\big )$ is a Heisenberg ![]() $p$-group with center
$p$-group with center ![]() $(G_i)_{x,r_i,({r_i}/{2})+} / \big ((G_i)_{x,r_i,({r_i}/{2})+} \cap \ker \hat {\phi }_i\big )$ [Reference YuYu01, Proposition 11.4]. More precisely, set
$(G_i)_{x,r_i,({r_i}/{2})+} / \big ((G_i)_{x,r_i,({r_i}/{2})+} \cap \ker \hat {\phi }_i\big )$ [Reference YuYu01, Proposition 11.4]. More precisely, set
and equip it with the pairing ![]() $\big \langle \cdot, \cdot \big \rangle _i$ defined by
$\big \langle \cdot, \cdot \big \rangle _i$ defined by ![]() $\big \langle a,b\big \rangle _i=\hat {\phi }_i(aba^{-1}b^{-1})$. Then Yu shows in [Reference YuYu01, Proposition 11.4] that there is a canonical special isomorphism
$\big \langle a,b\big \rangle _i=\hat {\phi }_i(aba^{-1}b^{-1})$. Then Yu shows in [Reference YuYu01, Proposition 11.4] that there is a canonical special isomorphism
where ![]() $V_i^{\sharp }$ is the group with underlying set
$V_i^{\sharp }$ is the group with underlying set ![]() $V_i \times \mathbb {F}_p$ and with group law
$V_i \times \mathbb {F}_p$ and with group law ![]() $(v,a).(v',a')=(v+v', a+a'+\frac {1}{2}\big \langle v,v'\big \rangle _i)$.
$(v,a).(v',a')=(v+v', a+a'+\frac {1}{2}\big \langle v,v'\big \rangle _i)$.
Let ![]() $(\omega _i, V_{\omega _i})$ denote the Heisenberg representation of
$(\omega _i, V_{\omega _i})$ denote the Heisenberg representation of ![]() $(G_i)_{x,r_i,{r_i}/{2}}/\big ((G_i)_{x,r_i,({r_i}/{2})+} \cap \ker \hat {\phi }_i\big )$ (via the above special isomorphism) with central character
$(G_i)_{x,r_i,{r_i}/{2}}/\big ((G_i)_{x,r_i,({r_i}/{2})+} \cap \ker \hat {\phi }_i\big )$ (via the above special isomorphism) with central character ![]() $\hat {\phi }_i|_{(G_i)_{x,r_i,({r_i}/{2})+} }$. Then we define the space
$\hat {\phi }_i|_{(G_i)_{x,r_i,({r_i}/{2})+} }$. Then we define the space ![]() $V_\kappa$ underlying the representation
$V_\kappa$ underlying the representation ![]() $\kappa$ to be
$\kappa$ to be ![]() $\bigotimes _{i=1}^{n} V_{\omega _i}$. If
$\bigotimes _{i=1}^{n} V_{\omega _i}$. If ![]() $n=0$, then the empty tensor product should be taken to be a one-dimensional complex vector space and
$n=0$, then the empty tensor product should be taken to be a one-dimensional complex vector space and ![]() $\kappa$ is the trivial representation. In order to describe the action of
$\kappa$ is the trivial representation. In order to describe the action of ![]() $\tilde K$ on each
$\tilde K$ on each ![]() $V_{\omega _i}$ for
$V_{\omega _i}$ for ![]() $n \geq 1$, we describe the action of
$n \geq 1$, we describe the action of ![]() $(G_i)_{x,r_i,{r_i}/{2}}$ for
$(G_i)_{x,r_i,{r_i}/{2}}$ for ![]() $1 \leq i \leq n$ and of
$1 \leq i \leq n$ and of ![]() $(G_{n+1})_{[x]}$ separately.
$(G_{n+1})_{[x]}$ separately.
For ![]() $1 \leq i \leq n$, the action of
$1 \leq i \leq n$, the action of ![]() $(G_i)_{x,r_i,{r_i}/{2}}$ on
$(G_i)_{x,r_i,{r_i}/{2}}$ on ![]() $V_{\omega _i}$ should be given by letting
$V_{\omega _i}$ should be given by letting ![]() $(G_i)_{x,r_i,{r_i}/{2}}$ act via the Heisenberg representation
$(G_i)_{x,r_i,{r_i}/{2}}$ act via the Heisenberg representation ![]() $\omega _i$ of
$\omega _i$ of ![]() $(G_i)_{x,r_i,{r_i}/{2}}/\big ((G_i)_{x,r_i,({r_i}/{2})+} \cap \ker \hat {\phi }_i\big )$ with central character
$(G_i)_{x,r_i,{r_i}/{2}}/\big ((G_i)_{x,r_i,({r_i}/{2})+} \cap \ker \hat {\phi }_i\big )$ with central character ![]() $\hat {\phi }_i|_{(G_i)_{x,r_i,({r_i}/{2})+} }$. The action of
$\hat {\phi }_i|_{(G_i)_{x,r_i,({r_i}/{2})+} }$. The action of ![]() $(G_i)_{x,r_i,{r_i}/{2}}$ on
$(G_i)_{x,r_i,{r_i}/{2}}$ on ![]() $V_{\omega _j}$ for
$V_{\omega _j}$ for ![]() $j \neq i$ should be via the character
$j \neq i$ should be via the character ![]() $\hat {\phi }_j|_{(G_i)_{x,r_i,{r_i}/{2}}}$ (times identity).
$\hat {\phi }_j|_{(G_i)_{x,r_i,{r_i}/{2}}}$ (times identity).
The action of ![]() $(G_{n+1})_{[x]}$ on
$(G_{n+1})_{[x]}$ on ![]() $V_{\omega _i}$ for
$V_{\omega _i}$ for ![]() $1 \leq i \leq n$ is given by
$1 \leq i \leq n$ is given by ![]() $\phi _i|_{(G_{n+1})_{[x]}}$ times the following representation. Let
$\phi _i|_{(G_{n+1})_{[x]}}$ times the following representation. Let ![]() $(G_{n+1})_{[x]}/(G_{n+1})_{x,0+}$ act on
$(G_{n+1})_{[x]}/(G_{n+1})_{x,0+}$ act on ![]() $V_{\omega _i}$ by mapping
$V_{\omega _i}$ by mapping ![]() $(G_{n+1})_{[x]}/(G_{n+1})_{x,0+}$ to the symplectic group
$(G_{n+1})_{[x]}/(G_{n+1})_{x,0+}$ to the symplectic group ![]() $\operatorname {Sp}(V_i)$ of the corresponding symplectic
$\operatorname {Sp}(V_i)$ of the corresponding symplectic ![]() $\mathbb {F}_p$-vector space
$\mathbb {F}_p$-vector space ![]() $V_i=(G_i)_{x,r_i,{r_i}/{2}}/(G_i)_{x,r_i,({r_i}/{2})+}$ with pairing
$V_i=(G_i)_{x,r_i,{r_i}/{2}}/(G_i)_{x,r_i,({r_i}/{2})+}$ with pairing ![]() $\big \langle a,b\big \rangle _i=\hat {\phi }_i(aba^{-1}b^{-1})$ (after choosing a from now on fixed isomorphism between the
$\big \langle a,b\big \rangle _i=\hat {\phi }_i(aba^{-1}b^{-1})$ (after choosing a from now on fixed isomorphism between the ![]() $p$th roots of unity in
$p$th roots of unity in ![]() $\mathbb {C}^{*}$ and
$\mathbb {C}^{*}$ and ![]() $\mathbb {F}_p$) and composing this map with the Weil representation (defined in [Reference GérardinGér77]). Here the map from
$\mathbb {F}_p$) and composing this map with the Weil representation (defined in [Reference GérardinGér77]). Here the map from ![]() $(G_{n+1})_{[x]}/(G_{n+1})_{x,0+}$ to
$(G_{n+1})_{[x]}/(G_{n+1})_{x,0+}$ to ![]() $\operatorname {Sp}(V_i)$ is induced by the conjugation action of
$\operatorname {Sp}(V_i)$ is induced by the conjugation action of ![]() $(G_{n+1})_{[x]}$ on
$(G_{n+1})_{[x]}$ on ![]() $(G_i)_{x,r_i,{r_i}/{2}}$, which (together with the special isomorphism
$(G_i)_{x,r_i,{r_i}/{2}}$, which (together with the special isomorphism ![]() $j_i$) yields a symplectic action in the sense of [Reference YuYu01, § 10] by [Reference YuYu01, Proposition 11.4].
$j_i$) yields a symplectic action in the sense of [Reference YuYu01, § 10] by [Reference YuYu01, Proposition 11.4].
Then the resulting actions of ![]() $(G_i)_{x,r_i,{r_i}/{2}}$ for
$(G_i)_{x,r_i,{r_i}/{2}}$ for ![]() $1 \leq i \leq n$ and
$1 \leq i \leq n$ and ![]() $(G_{n+1})_{[x]}$ agree on the intersections and hence yield a representation
$(G_{n+1})_{[x]}$ agree on the intersections and hence yield a representation ![]() $\kappa$ of
$\kappa$ of ![]() $\tilde K$ on the space
$\tilde K$ on the space ![]() $V_\kappa$.
$V_\kappa$.
The representation ![]() $\pi =\operatorname {c-ind}_{\tilde K}^{G(F)} \rho \otimes \kappa$ is the smooth representation of
$\pi =\operatorname {c-ind}_{\tilde K}^{G(F)} \rho \otimes \kappa$ is the smooth representation of ![]() $G(F)$ that Yu attaches to the tuple
$G(F)$ that Yu attaches to the tuple ![]() $((G_i)_{1 \leq i \leq n+1}, x, (r_i)_{1 \leq i \leq n}, \rho, (\phi _i)_{1 \leq i \leq n})$, and we prove in the next section that
$((G_i)_{1 \leq i \leq n+1}, x, (r_i)_{1 \leq i \leq n}, \rho, (\phi _i)_{1 \leq i \leq n})$, and we prove in the next section that ![]() $\pi$ is an irreducible, supercuspidal representation.
$\pi$ is an irreducible, supercuspidal representation.
3. Proof that the representations are supercuspidal
We keep the notation from the previous section to prove the following theorem in this section.
Theorem 3.1 The representation ![]() $\operatorname {c-ind}_{\tilde K}^{G(F)} \tilde \rho$ is irreducible, hence supercuspidal.
$\operatorname {c-ind}_{\tilde K}^{G(F)} \tilde \rho$ is irreducible, hence supercuspidal.
Remark 3.2 This theorem follows from [Reference YuYu01, Theorem 15.1]. However, the proof in [Reference YuYu01] relies on [Reference GérardinGér77, Theorem 2.4(b)] and unfortunately the statement of [Reference GérardinGér77, Theorem 2.4(b)] contains a typo, as Loren Spice pointed out. Therefore Proposition 14.1 and Theorem 14.2 of [Reference YuYu01], on which Yu's proof relies, are no longer true. We provide a counterexample in § 4.
Here we use an alternative and shorter approach to prove Theorem 3.1 that uses ideas from the first part of Yu's paper [Reference YuYu01, Theorem 9.4], but that avoids the second part that relies on the misprinted version of the theorem in [Reference GérardinGér77]. In particular, we do not use [Reference YuYu01, Proposition 14.1 and Theorem 14.2].
In order to show that ![]() $\operatorname {c-ind}_{\tilde K}^{G(F)} \tilde \rho$ is irreducible, we first observe that
$\operatorname {c-ind}_{\tilde K}^{G(F)} \tilde \rho$ is irreducible, we first observe that ![]() $\tilde \rho$ is irreducible.
$\tilde \rho$ is irreducible.
Lemma 3.3 The representation ![]() $\tilde \rho$ of
$\tilde \rho$ of ![]() $\tilde K$ is irreducible.
$\tilde K$ is irreducible.
Proof. For ![]() $1 \leq i \leq n$ set
$1 \leq i \leq n$ set ![]() $K_i = (G_1)_{x,r_1,{r_1}/{2}}(G_2)_{x,r_2,{r_2}/{2}} \ldots (G_i)_{x,r_i,{r_i}/{2}}$ and
$K_i = (G_1)_{x,r_1,{r_1}/{2}}(G_2)_{x,r_2,{r_2}/{2}} \ldots (G_i)_{x,r_i,{r_i}/{2}}$ and ![]() $K_0=\{1\}$. We first prove by induction on
$K_0=\{1\}$. We first prove by induction on ![]() $i$ that
$i$ that ![]() $\bigotimes _{j=1}^{i} V_{\omega _j}$ is an irreducible representation of
$\bigotimes _{j=1}^{i} V_{\omega _j}$ is an irreducible representation of ![]() $K_i$ via the action described in § 2.5. For
$K_i$ via the action described in § 2.5. For ![]() $i=0$, we take
$i=0$, we take ![]() $\bigotimes _{j=1}^{i} V_{\omega _i}$ to be the trivial one-dimensional representation and the statement holds. Now assume the induction hypothesis that
$\bigotimes _{j=1}^{i} V_{\omega _i}$ to be the trivial one-dimensional representation and the statement holds. Now assume the induction hypothesis that ![]() $\bigotimes _{j=1}^{i-1} V_{\omega _{j}}$ is an irreducible representation of
$\bigotimes _{j=1}^{i-1} V_{\omega _{j}}$ is an irreducible representation of ![]() $K_{i-1}$. Suppose
$K_{i-1}$. Suppose ![]() $V' \subset \big (\bigotimes _{j=1}^{i-1} V_{\omega _{j}}\big ) \otimes V_{\omega _i}$ is a non-trivial subspace that is
$V' \subset \big (\bigotimes _{j=1}^{i-1} V_{\omega _{j}}\big ) \otimes V_{\omega _i}$ is a non-trivial subspace that is ![]() $K_i$-stable. Since
$K_i$-stable. Since ![]() $K_{i-1}$ acts on
$K_{i-1}$ acts on ![]() $V_{\omega _i}$ via a character (times identity), the subspace
$V_{\omega _i}$ via a character (times identity), the subspace ![]() $V'$ has to be of the form
$V'$ has to be of the form ![]() $\big (\bigotimes _{j=1}^{i-1} V_{\omega _{j}}\big ) \otimes V''$ for a
$\big (\bigotimes _{j=1}^{i-1} V_{\omega _{j}}\big ) \otimes V''$ for a ![]() $K_i$-stable non-trivial subspace
$K_i$-stable non-trivial subspace ![]() $V''$ of
$V''$ of ![]() $V_{\omega _i}$. However, since Heisenberg representations are irreducible,
$V_{\omega _i}$. However, since Heisenberg representations are irreducible, ![]() $V_{\omega _i}$ is irreducible as a representation of
$V_{\omega _i}$ is irreducible as a representation of ![]() $(G_i)_{x,r_i,\frac {r_i}{2}} \subset K_i$, and therefore
$(G_i)_{x,r_i,\frac {r_i}{2}} \subset K_i$, and therefore ![]() $V''=V_{\omega _i}$. Thus
$V''=V_{\omega _i}$. Thus ![]() $\bigotimes _{j=1}^{i} V_{\omega _j}$ is an irreducible representation of
$\bigotimes _{j=1}^{i} V_{\omega _j}$ is an irreducible representation of ![]() $K_i$, and by induction the representation
$K_i$, and by induction the representation ![]() $\kappa$ is an irreducible representation of
$\kappa$ is an irreducible representation of ![]() $K_n$.
$K_n$.
Since ![]() $K_n$ acts trivially on
$K_n$ acts trivially on ![]() $\rho$, every irreducible
$\rho$, every irreducible ![]() $\tilde K$-subrepresentation of
$\tilde K$-subrepresentation of ![]() $\tilde \rho =\rho \otimes \kappa$ has to be of the form
$\tilde \rho =\rho \otimes \kappa$ has to be of the form ![]() $\rho ' \otimes \kappa$ for an irreducible subrepresentation
$\rho ' \otimes \kappa$ for an irreducible subrepresentation ![]() $\rho '$ of
$\rho '$ of ![]() $\rho$. As
$\rho$. As ![]() $\rho$ is irreducible when restricted to
$\rho$ is irreducible when restricted to ![]() $(G_{n+1})_{[x]} \subset \tilde K$, we deduce that
$(G_{n+1})_{[x]} \subset \tilde K$, we deduce that ![]() $\tilde \rho$ is an irreducible representation of
$\tilde \rho$ is an irreducible representation of ![]() $\tilde K$.
$\tilde K$.
The remaining proof of Theorem 3.1 is concerned with showing that if ![]() $g$ intertwines
$g$ intertwines ![]() $\tilde \rho$, then
$\tilde \rho$, then ![]() $g \in \tilde K$, which then implies that
$g \in \tilde K$, which then implies that ![]() $\operatorname {ind}_{\tilde K}^{G(F)}\tilde \rho$ is irreducible and hence supercuspidal. Our proof consists of two parts. The first part is concerned with reducing the problem to considering
$\operatorname {ind}_{\tilde K}^{G(F)}\tilde \rho$ is irreducible and hence supercuspidal. Our proof consists of two parts. The first part is concerned with reducing the problem to considering ![]() $g \in G_{n+1}(F)$ using the characters
$g \in G_{n+1}(F)$ using the characters ![]() $\phi _i$ and is essentially [Reference YuYu01, Corollary 4.5]. The second part consists of deducing from there the theorem using the depth-zero representation
$\phi _i$ and is essentially [Reference YuYu01, Corollary 4.5]. The second part consists of deducing from there the theorem using the depth-zero representation ![]() $\rho$ together with the action of suitably chosen subgroups of higher depth and employing knowledge about the structure of Weil–Heisenberg representations. This is where our approach deviates crucially from Yu's approach by avoiding the wrong statements [Reference YuYu01, Proposition 14.1 and Theorem 14.2] in favor of a much shorter argument. For the first part, we will use the following result of Yu [Reference YuYu01, Theorem 9.4].
$\rho$ together with the action of suitably chosen subgroups of higher depth and employing knowledge about the structure of Weil–Heisenberg representations. This is where our approach deviates crucially from Yu's approach by avoiding the wrong statements [Reference YuYu01, Proposition 14.1 and Theorem 14.2] in favor of a much shorter argument. For the first part, we will use the following result of Yu [Reference YuYu01, Theorem 9.4].
Lemma 3.4 [Reference YuYu01]
Let ![]() $1 \leq i \leq n$ and
$1 \leq i \leq n$ and ![]() $g \in G_i(F)$. Suppose that
$g \in G_i(F)$. Suppose that ![]() $g$ intertwines
$g$ intertwines ![]() $\hat {\phi }_i|_{(G_i)_{x,r_i,({r_i}/{2})+}}$. Then
$\hat {\phi }_i|_{(G_i)_{x,r_i,({r_i}/{2})+}}$. Then ![]() $g \in (G_i)_{x,{r_i}/{2}}G_{i+1}(F)(G_i)_{x,{r_i}/{2}}$.
$g \in (G_i)_{x,{r_i}/{2}}G_{i+1}(F)(G_i)_{x,{r_i}/{2}}$.
Proof. This is (part of) [Reference YuYu01, Theorem 9.4].
Proof Proof of Theorem 3.1
Recall that ![]() $\tilde \rho$ is irreducible by Lemma 3.3. Thus, in order to show that
$\tilde \rho$ is irreducible by Lemma 3.3. Thus, in order to show that ![]() $\operatorname {c-ind}_{\tilde K}^{G(F)} \tilde \rho$ is irreducible, hence supercuspidal, we have to show that if
$\operatorname {c-ind}_{\tilde K}^{G(F)} \tilde \rho$ is irreducible, hence supercuspidal, we have to show that if ![]() $g \in G(F)$ such that
$g \in G(F)$ such that
then ![]() $g \in \tilde K$, where
$g \in \tilde K$, where ![]() $^{g}\tilde K$ denotes
$^{g}\tilde K$ denotes ![]() $g\tilde K g^{-1}$ and
$g\tilde K g^{-1}$ and ![]() $^{g}\tilde \rho (x)=\tilde \rho (g^{-1}xg)$.
$^{g}\tilde \rho (x)=\tilde \rho (g^{-1}xg)$.
Fix such a ![]() $g \in G(F)$ satisfying
$g \in G(F)$ satisfying ![]() $\operatorname {Hom}_{\tilde K \cap {{}^{g}\tilde K}}\big ( ^{g}\tilde \rho, \tilde \rho \big ) \neq \{0 \}$, and define
$\operatorname {Hom}_{\tilde K \cap {{}^{g}\tilde K}}\big ( ^{g}\tilde \rho, \tilde \rho \big ) \neq \{0 \}$, and define
We first prove by induction that ![]() $g \in \tilde K_n G_{n+1}(F)\tilde K_n$ using Lemma 3.4 (which is (part of) [Reference YuYu01, Theorem 9.4]). This is essentially [Reference YuYu01, Corollary 4.5], but we include a short proof for the convenience of the reader. Let
$g \in \tilde K_n G_{n+1}(F)\tilde K_n$ using Lemma 3.4 (which is (part of) [Reference YuYu01, Theorem 9.4]). This is essentially [Reference YuYu01, Corollary 4.5], but we include a short proof for the convenience of the reader. Let ![]() $1 \leq i \leq n$ and assume the induction hypothesis that
$1 \leq i \leq n$ and assume the induction hypothesis that ![]() $g \in \tilde K_{i-1}G_{i}(F)\tilde K_{i-1}$, which is obviously satisfied for
$g \in \tilde K_{i-1}G_{i}(F)\tilde K_{i-1}$, which is obviously satisfied for ![]() $i=1$. We need to show that
$i=1$. We need to show that ![]() $g \in \tilde K_{i}G_{i+1}(F)\tilde K_{i}$. Since
$g \in \tilde K_{i}G_{i+1}(F)\tilde K_{i}$. Since ![]() $\tilde K_{i-1} \subset \tilde K_i \subset \tilde K$, we may assume without loss of generality that
$\tilde K_{i-1} \subset \tilde K_i \subset \tilde K$, we may assume without loss of generality that ![]() $g \in G_i(F)$. Recall that by construction
$g \in G_i(F)$. Recall that by construction ![]() $\rho |_{(G_i)_{x,r_i,({r_i}/{2})+}}= \operatorname {Id}$ and
$\rho |_{(G_i)_{x,r_i,({r_i}/{2})+}}= \operatorname {Id}$ and ![]() $\kappa |_{(G_i)_{x,r_i,({r_i}/{2})+}}=\prod _{j=1}^{n} \hat {\phi }_j \cdot \operatorname {Id}$. Thus by restriction of the action in (1) to
$\kappa |_{(G_i)_{x,r_i,({r_i}/{2})+}}=\prod _{j=1}^{n} \hat {\phi }_j \cdot \operatorname {Id}$. Thus by restriction of the action in (1) to ![]() $(G_i)_{x,r_i,({r_i}/{2})+} \cap {{}^{g}(G_i)_{x,r_i,({r_i}/{2})+}}$ we conclude that
$(G_i)_{x,r_i,({r_i}/{2})+} \cap {{}^{g}(G_i)_{x,r_i,({r_i}/{2})+}}$ we conclude that ![]() $g$ intertwines
$g$ intertwines ![]() $(\prod _{j=1}^{n} \hat {\phi }_j)|_{(G_i)_{x,r_i,({r_i}/{2})+}}$. By the definition of
$(\prod _{j=1}^{n} \hat {\phi }_j)|_{(G_i)_{x,r_i,({r_i}/{2})+}}$. By the definition of ![]() $\hat {\phi }_j$ in § 2.5, we have that
$\hat {\phi }_j$ in § 2.5, we have that ![]() $\hat {\phi }_j|_{(G_i)_{x,r_i, ({r_i}/{2})+}}$ is trivial for
$\hat {\phi }_j|_{(G_i)_{x,r_i, ({r_i}/{2})+}}$ is trivial for ![]() $j>i$. Moreover, if
$j>i$. Moreover, if ![]() $j < i$, then for
$j < i$, then for ![]() $y\in (G_i)_{x,r_i,({r_i}/{2})+} \cap {{}^{g}(G_i)_{x,r_i,({r_i}/{2})+}}$ we have
$y\in (G_i)_{x,r_i,({r_i}/{2})+} \cap {{}^{g}(G_i)_{x,r_i,({r_i}/{2})+}}$ we have
Therefore we obtain that ![]() $g$ also intertwines
$g$ also intertwines ![]() $\hat {\phi }_i|_{(G_i)_{x,r_i,({r_i}/{2})+}}$. By Lemma 3.4 (which is (part of) [Reference YuYu01, Theorem 9.4]) we conclude that
$\hat {\phi }_i|_{(G_i)_{x,r_i,({r_i}/{2})+}}$. By Lemma 3.4 (which is (part of) [Reference YuYu01, Theorem 9.4]) we conclude that ![]() $g\in (G_i)_{x,{r_i}/{2}}G_{i+1}(F)(G_i)_{x,{r_i}/{2}}$, and hence
$g\in (G_i)_{x,{r_i}/{2}}G_{i+1}(F)(G_i)_{x,{r_i}/{2}}$, and hence ![]() $g \in \tilde K_i G_{i+1}(F)\tilde K_i$. This finishes the induction step and therefore we have shown that
$g \in \tilde K_i G_{i+1}(F)\tilde K_i$. This finishes the induction step and therefore we have shown that ![]() $g \in \tilde K_nG_{n+1}(F)\tilde K_n$.
$g \in \tilde K_nG_{n+1}(F)\tilde K_n$.
In order to prove that ![]() $g \in \tilde K$, we may therefore assume without loss of generality that
$g \in \tilde K$, we may therefore assume without loss of generality that ![]() $g \in G_{n+1}(F)$, and it suffices to prove that then
$g \in G_{n+1}(F)$, and it suffices to prove that then ![]() $g \in (G_{n+1})_{[x]}$. Let us assume the contrary, that
$g \in (G_{n+1})_{[x]}$. Let us assume the contrary, that ![]() $g \in G_{n+1}(F)-(G_{n+1})_{[x]}$, or, equivalently, that the images of
$g \in G_{n+1}(F)-(G_{n+1})_{[x]}$, or, equivalently, that the images of ![]() $g.x$ and
$g.x$ and ![]() $x$ in
$x$ in ![]() $\mathscr {B}(G_{n+1}^\textrm {{der}}, k)$ are distinct. Let
$\mathscr {B}(G_{n+1}^\textrm {{der}}, k)$ are distinct. Let ![]() $f$ be an element of
$f$ be an element of ![]() $\operatorname {Hom}_{\tilde K \cap {{}^{g}\tilde K}}\big (^{g}\tilde \rho, {\tilde \rho }\big ) - \{0\}$. We denote its image in the space
$\operatorname {Hom}_{\tilde K \cap {{}^{g}\tilde K}}\big (^{g}\tilde \rho, {\tilde \rho }\big ) - \{0\}$. We denote its image in the space ![]() $V_{\tilde \rho }$ of the representation of
$V_{\tilde \rho }$ of the representation of ![]() $\tilde \rho$ by
$\tilde \rho$ by ![]() $V_f$. We write
$V_f$. We write ![]() $H_{n+1}$ for the derived subgroup
$H_{n+1}$ for the derived subgroup ![]() $G_{n+1}^{\text {der}}$ of
$G_{n+1}^{\text {der}}$ of ![]() $G_{n+1}$ and denote by
$G_{n+1}$ and denote by ![]() $(H_{n+1})_{x,r}$ the Moy–Prasad filtration subgroup of depth
$(H_{n+1})_{x,r}$ the Moy–Prasad filtration subgroup of depth ![]() $r \in \mathbb {R}_{\geq 0}$ at the image of
$r \in \mathbb {R}_{\geq 0}$ at the image of ![]() $x$ in
$x$ in ![]() $\mathscr {B}(H_{n+1},F)$. Then
$\mathscr {B}(H_{n+1},F)$. Then ![]() $^{g}(H_{n+1})_{x,0}=(H_{n+1})_{g.x,0}$, and we have
$^{g}(H_{n+1})_{x,0}=(H_{n+1})_{g.x,0}$, and we have
By construction ![]() $\tilde \rho |_{(H_{n+1})_{x,0+}}=\hat {\phi }|_{(H_{n+1})_{x,0+}} \cdot \operatorname {Id} = \phi |_{(H_{n+1})_{x,0+}} \cdot \operatorname {Id}$, where
$\tilde \rho |_{(H_{n+1})_{x,0+}}=\hat {\phi }|_{(H_{n+1})_{x,0+}} \cdot \operatorname {Id} = \phi |_{(H_{n+1})_{x,0+}} \cdot \operatorname {Id}$, where
 \[ \hat{\phi} := \prod_{i=1}^{n} \hat{\phi}_i|_{(G_{n+1})_{[x]}G_{x,({r_1}/{2})+}}\quad \text{and}\quad \phi:=\prod_{i=1}^{n} \phi_i|_{G_{n+1}(F)}. \]
\[ \hat{\phi} := \prod_{i=1}^{n} \hat{\phi}_i|_{(G_{n+1})_{[x]}G_{x,({r_1}/{2})+}}\quad \text{and}\quad \phi:=\prod_{i=1}^{n} \phi_i|_{G_{n+1}(F)}. \]
In addition, for all ![]() $y \in (H_{n+1})_{g.x,0+}$ we have
$y \in (H_{n+1})_{g.x,0+}$ we have ![]() $^{g}\tilde \rho (y)=\hat \phi (g^{-1}yg)=\prod _{i=1}^{n} \phi _i(g^{-1}yg)=\prod _{i=1}^{n} \phi _i(y)=\phi (y)$, because
$^{g}\tilde \rho (y)=\hat \phi (g^{-1}yg)=\prod _{i=1}^{n} \phi _i(g^{-1}yg)=\prod _{i=1}^{n} \phi _i(y)=\phi (y)$, because ![]() $g \in G_{n+1}(F)$. Hence, by (3), the action of
$g \in G_{n+1}(F)$. Hence, by (3), the action of
on the image ![]() $V_f$ of
$V_f$ of ![]() $f$ via
$f$ via ![]() ${\tilde \rho }$ is given by
${\tilde \rho }$ is given by ![]() $\phi \cdot \operatorname {Id}$.
$\phi \cdot \operatorname {Id}$.
Recall that the image of ![]() $x$ in
$x$ in ![]() $\mathscr {B}(H_{n+1}, k)$ is a vertex by condition (ii) of the input in § 2.1. Hence the group
$\mathscr {B}(H_{n+1}, k)$ is a vertex by condition (ii) of the input in § 2.1. Hence the group ![]() $(((H_{n+1})_{x,0} \cap {(H_{n+1})_{g.x,0+}})(H_{n+1})_{x,0+})/(H_{n+1})_{x,0+}$ is the (
$(((H_{n+1})_{x,0} \cap {(H_{n+1})_{g.x,0+}})(H_{n+1})_{x,0+})/(H_{n+1})_{x,0+}$ is the (![]() $\mathbb {F}_q$-points of) a unipotent radical of a (proper) parabolic subgroup of
$\mathbb {F}_q$-points of) a unipotent radical of a (proper) parabolic subgroup of ![]() $(H_{n+1})_{x,0}/(H_{n+1})_{x,0+}$. We denote this subgroup by
$(H_{n+1})_{x,0}/(H_{n+1})_{x,0+}$. We denote this subgroup by ![]() $\bar {U}$.
$\bar {U}$.
In the remainder of the proof we exhibit a subspace ![]() $V_\kappa ' \subset V_\kappa$ such that
$V_\kappa ' \subset V_\kappa$ such that ![]() $V_f \subset V_\rho \otimes V_\kappa '$ and prove that the action of
$V_f \subset V_\rho \otimes V_\kappa '$ and prove that the action of ![]() ${U}$ on
${U}$ on ![]() $V_\kappa '$ via
$V_\kappa '$ via ![]() $\kappa$ is given by
$\kappa$ is given by ![]() $\phi \cdot \operatorname {Id}$. Hence, since
$\phi \cdot \operatorname {Id}$. Hence, since ![]() ${U}$ also acts via
${U}$ also acts via ![]() $\phi \cdot \operatorname {Id}$ on
$\phi \cdot \operatorname {Id}$ on ![]() $V_f \subset V_\rho \otimes V_\kappa '$, we deduce that
$V_f \subset V_\rho \otimes V_\kappa '$, we deduce that ![]() $(\rho |_{\bar {U}}, V_\rho )$ contains the trivial representation, which contradicts that
$(\rho |_{\bar {U}}, V_\rho )$ contains the trivial representation, which contradicts that ![]() $\rho |_{(G_{n+1})_{x,0}}$ is cuspidal (see condition (iii) of the input in § 2.1).
$\rho |_{(G_{n+1})_{x,0}}$ is cuspidal (see condition (iii) of the input in § 2.1).
Let ![]() $T$ be a maximal torus of
$T$ be a maximal torus of ![]() $G$ that splits over a tamely ramified extension
$G$ that splits over a tamely ramified extension ![]() $E$ of
$E$ of ![]() $F$ such that
$F$ such that ![]() $x$ and
$x$ and ![]() $g.x$ are contained in
$g.x$ are contained in ![]() $\mathscr {A}(T,E)$. (Such a torus exists by Remark 2.2.) Let
$\mathscr {A}(T,E)$. (Such a torus exists by Remark 2.2.) Let ![]() $\lambda \in X_*(T) \otimes _\mathbb {Z}\mathbb {R}=\operatorname {Hom}_{\bar F}(\mathbb {G}_m,T_{\bar F}) \otimes _\mathbb {Z} \mathbb {R}$ such that
$\lambda \in X_*(T) \otimes _\mathbb {Z}\mathbb {R}=\operatorname {Hom}_{\bar F}(\mathbb {G}_m,T_{\bar F}) \otimes _\mathbb {Z} \mathbb {R}$ such that ![]() $g.x = x + \lambda$, and observe that
$g.x = x + \lambda$, and observe that ![]() $\bar {U}$ is the image of
$\bar {U}$ is the image of
in ![]() $(H_{n+1})_{x,0}/(H_{n+1})_{x,0+}$. We define, for
$(H_{n+1})_{x,0}/(H_{n+1})_{x,0+}$. We define, for ![]() $1 \leq i \leq n$,
$1 \leq i \leq n$,
Note that ![]() ${{}^{g}(G_i)_{x,r_i,({r_i}/{2})+}}=(G_i)_{g.x,r_i,({r_i}/{2})+}$ and
${{}^{g}(G_i)_{x,r_i,({r_i}/{2})+}}=(G_i)_{g.x,r_i,({r_i}/{2})+}$ and ![]() $U_i \subset (G_i)_{x,r_i,{r_i}/{2}} \cap (G_i)_{g.x,r_i,({r_i}/{2})+} \subset \tilde K \cap {{}^{g}\tilde K}$. More precisely,
$U_i \subset (G_i)_{x,r_i,{r_i}/{2}} \cap (G_i)_{g.x,r_i,({r_i}/{2})+} \subset \tilde K \cap {{}^{g}\tilde K}$. More precisely, ![]() $U_i \subset (G_i)_{g.x,r_i+,({r_i}/{2})+}$, hence
$U_i \subset (G_i)_{g.x,r_i+,({r_i}/{2})+}$, hence ![]() ${{}^{{g}^{-1}}U_i} \subset (G_i)_{x,r_i+,({r_i}/{2})+}$ and
${{}^{{g}^{-1}}U_i} \subset (G_i)_{x,r_i+,({r_i}/{2})+}$ and ![]() $\hat {\phi }_j|_{{{}^{{g}^{-1}}U_i}}$ is trivial for
$\hat {\phi }_j|_{{{}^{{g}^{-1}}U_i}}$ is trivial for ![]() $j \geq i$. Thus, by (2), we obtain that
$j \geq i$. Thus, by (2), we obtain that ![]() $^{g}\tilde \rho |_{U_i} = \prod _{j=1}^{i-1} \hat \phi _j \cdot \operatorname {Id}$. Hence
$^{g}\tilde \rho |_{U_i} = \prod _{j=1}^{i-1} \hat \phi _j \cdot \operatorname {Id}$. Hence ![]() $U_i$ acts on
$U_i$ acts on ![]() $V_f$ via the character
$V_f$ via the character ![]() $\prod _{j=1}^{i-1} {\hat \phi _j}|_{U_i}=\prod _{1 \leq j \leq n \atop j \neq i} {\hat \phi _j}|_{U_i}$. Since
$\prod _{j=1}^{i-1} {\hat \phi _j}|_{U_i}=\prod _{1 \leq j \leq n \atop j \neq i} {\hat \phi _j}|_{U_i}$. Since ![]() $U_i$ acts trivially via
$U_i$ acts trivially via ![]() $\rho$ on the space
$\rho$ on the space ![]() $V_\rho$ underlying the representation of
$V_\rho$ underlying the representation of ![]() $\rho$ and
$\rho$ and ![]() $U_i$ acts via
$U_i$ acts via ![]() $\prod _{1 \leq j \leq n \atop j \neq i} {\hat \phi _j}|_{U_i}$ on
$\prod _{1 \leq j \leq n \atop j \neq i} {\hat \phi _j}|_{U_i}$ on ![]() $\bigotimes _{1 \leq j \leq n \atop j \neq i} V_{\omega _j}$, we obtain
$\bigotimes _{1 \leq j \leq n \atop j \neq i} V_{\omega _j}$, we obtain
 \[ V_f \subset V_\rho \otimes \bigotimes_{j=1}^{i-1} V_{\omega_j} \otimes V_{\omega_i}^{U_i} \otimes \bigotimes_{j=i+1}^{n} V_{\omega_j} \subset V_\rho \otimes \bigotimes_{i=1}^{n} V_{\omega_i} = V_\rho \otimes V_\kappa \]
\[ V_f \subset V_\rho \otimes \bigotimes_{j=1}^{i-1} V_{\omega_j} \otimes V_{\omega_i}^{U_i} \otimes \bigotimes_{j=i+1}^{n} V_{\omega_j} \subset V_\rho \otimes \bigotimes_{i=1}^{n} V_{\omega_i} = V_\rho \otimes V_\kappa \]
for ![]() $1 \leq i \leq n$. Hence we deduce that
$1 \leq i \leq n$. Hence we deduce that ![]() $V_f \subset V_\rho \otimes \bigotimes _{i=1}^{n} V_{\omega _i}^{U_i}$. We will see that
$V_f \subset V_\rho \otimes \bigotimes _{i=1}^{n} V_{\omega _i}^{U_i}$. We will see that ![]() $\bigotimes _{i=1}^{n} V_{\omega _i}^{U_i}$ is the subspace
$\bigotimes _{i=1}^{n} V_{\omega _i}^{U_i}$ is the subspace ![]() $V_\kappa ' \subset V_\kappa$ that we are looking for.
$V_\kappa ' \subset V_\kappa$ that we are looking for.
In order to study the subspace ![]() $V_{\omega _i}^{U_i}$ for
$V_{\omega _i}^{U_i}$ for ![]() $1 \leq i \leq n$, we recall that we write
$1 \leq i \leq n$, we recall that we write ![]() $V_i=(G_i)_{x,r_i,{r_i}/{2}}/(G_i)_{x,r_i,({r_i}/{2})+}$ and equip
$V_i=(G_i)_{x,r_i,{r_i}/{2}}/(G_i)_{x,r_i,({r_i}/{2})+}$ and equip ![]() $V_i$ with the pairing
$V_i$ with the pairing ![]() $\big \langle \cdot, \cdot \big \rangle _i$ defined by
$\big \langle \cdot, \cdot \big \rangle _i$ defined by ![]() $\big \langle a,b\big \rangle _i=\hat {\phi }_i(aba^{-1}b^{-1})$ (using the above fixed identification of the
$\big \langle a,b\big \rangle _i=\hat {\phi }_i(aba^{-1}b^{-1})$ (using the above fixed identification of the ![]() $p$th roots of unity in
$p$th roots of unity in ![]() $\mathbb {C}^{*}$ with
$\mathbb {C}^{*}$ with ![]() $\mathbb {F}_p$). We define the space
$\mathbb {F}_p$). We define the space ![]() $V_i^{+}$ to be the image of
$V_i^{+}$ to be the image of ![]() $U_i= G(F) \cap \big \langle U_\alpha (E)_{x,{r_i}/{2}} \, | \, \alpha \in \Phi (G_i, T)-\Phi (G_{i+1}, T), \lambda (\alpha )>0 \big \rangle$ in
$U_i= G(F) \cap \big \langle U_\alpha (E)_{x,{r_i}/{2}} \, | \, \alpha \in \Phi (G_i, T)-\Phi (G_{i+1}, T), \lambda (\alpha )>0 \big \rangle$ in ![]() $V_i$, the space
$V_i$, the space ![]() $V_i^{0}$ to be the image of
$V_i^{0}$ to be the image of ![]() $G(F) \cap \big \langle U_\alpha (E)_{x,{r_i}/{2}} \, | \, \alpha \in \Phi (G_i, T)-\Phi (G_{i+1}, T), \lambda (\alpha )=0 \big \rangle$ in
$G(F) \cap \big \langle U_\alpha (E)_{x,{r_i}/{2}} \, | \, \alpha \in \Phi (G_i, T)-\Phi (G_{i+1}, T), \lambda (\alpha )=0 \big \rangle$ in ![]() $V_i$, and
$V_i$, and ![]() $V_i^{-}$ to be the image of
$V_i^{-}$ to be the image of ![]() $G(F) \cap \big \langle U_\alpha (E)_{x,{r_i}/{2}} \, | \, \alpha \in \Phi (G_i, T)-\Phi (G_{i+1}, T), \lambda (\alpha )<0 \big \rangle$ in
$G(F) \cap \big \langle U_\alpha (E)_{x,{r_i}/{2}} \, | \, \alpha \in \Phi (G_i, T)-\Phi (G_{i+1}, T), \lambda (\alpha )<0 \big \rangle$ in ![]() $V_i$. Then
$V_i$. Then ![]() $V_i=V_i^{+} \oplus V_i^{0} \oplus V_i^{-}$ and the
$V_i=V_i^{+} \oplus V_i^{0} \oplus V_i^{-}$ and the ![]() $\mathbb {F}_p$-vector subspaces
$\mathbb {F}_p$-vector subspaces ![]() $V_i^{+}$ and
$V_i^{+}$ and ![]() $V_i^{-}$ are both totally isotropic. Since
$V_i^{-}$ are both totally isotropic. Since ![]() $\phi _i$ is
$\phi _i$ is ![]() $G_i$-generic of depth
$G_i$-generic of depth ![]() $r_i$ relative to
$r_i$ relative to ![]() $x$ the orthogonal complement of
$x$ the orthogonal complement of ![]() $V_i^{+}$ is
$V_i^{+}$ is ![]() $V_i^{+} \oplus V_i^{0}$, the orthogonal complement of
$V_i^{+} \oplus V_i^{0}$, the orthogonal complement of ![]() $V_i^{-}$ is
$V_i^{-}$ is ![]() $V_i^{0} \oplus V_i^{-}$, and
$V_i^{0} \oplus V_i^{-}$, and ![]() $V_i^{0}$ is a non-degenerate subspace of
$V_i^{0}$ is a non-degenerate subspace of ![]() $V_i$. We denote by
$V_i$. We denote by ![]() $P_i \subset \operatorname {Sp}(V_i)$ the (maximal) parabolic subgroup of
$P_i \subset \operatorname {Sp}(V_i)$ the (maximal) parabolic subgroup of ![]() $\operatorname {Sp}(V_i)$ that preserves the subspace
$\operatorname {Sp}(V_i)$ that preserves the subspace ![]() $V_i^{+}$ and that therefore also preserves
$V_i^{+}$ and that therefore also preserves ![]() $V_i^{+} \oplus V_i^{0}$. We obtain a surjection
$V_i^{+} \oplus V_i^{0}$. We obtain a surjection ![]() $\operatorname {pr}_{i,0}: P_i \twoheadrightarrow \operatorname {Sp}(V_i^{0})$ by composing restriction to
$\operatorname {pr}_{i,0}: P_i \twoheadrightarrow \operatorname {Sp}(V_i^{0})$ by composing restriction to ![]() $V_i^{0}$ with projection from
$V_i^{0}$ with projection from ![]() $V_i^{+} \oplus V_i^{0}$ to
$V_i^{+} \oplus V_i^{0}$ to ![]() $V_i^{0}$ with kernel
$V_i^{0}$ with kernel ![]() $V_i^{+}$. Note that the image
$V_i^{+}$. Note that the image ![]() $\bar {U}_{\operatorname {Sp}(V_i)}$ of
$\bar {U}_{\operatorname {Sp}(V_i)}$ of ![]() $\bar {U}$ in
$\bar {U}$ in ![]() $\operatorname {Sp}(V_i)$ is contained in
$\operatorname {Sp}(V_i)$ is contained in ![]() $P_i$ and that
$P_i$ and that ![]() $\operatorname {pr}_{i,0}(\bar {U}_{\operatorname {Sp}(V_i)})=\operatorname {Id}_{V_i^{0}}$.
$\operatorname {pr}_{i,0}(\bar {U}_{\operatorname {Sp}(V_i)})=\operatorname {Id}_{V_i^{0}}$.
Recall that ![]() $V_i^{\sharp }$ is the Heisenberg group with underlying set
$V_i^{\sharp }$ is the Heisenberg group with underlying set ![]() $V_i \times \mathbb {F}_p$ that is attached to the symplectic
$V_i \times \mathbb {F}_p$ that is attached to the symplectic ![]() $\mathbb {F}_p$-vector space
$\mathbb {F}_p$-vector space ![]() $V_i$ with pairing
$V_i$ with pairing ![]() $\big \langle \cdot, \cdot \big \rangle _i$, and note that the subset
$\big \langle \cdot, \cdot \big \rangle _i$, and note that the subset ![]() $V_i^{0} \times \mathbb {F}_p \subset V_i \times \mathbb {F}_p$ forms a subgroup, which is the Heisenberg group
$V_i^{0} \times \mathbb {F}_p \subset V_i \times \mathbb {F}_p$ forms a subgroup, which is the Heisenberg group ![]() $(V_i^{0})^{\sharp }$ attached to the symplectic vector space
$(V_i^{0})^{\sharp }$ attached to the symplectic vector space ![]() $V_i^{0}$ with the (restriction of the) pairing
$V_i^{0}$ with the (restriction of the) pairing ![]() $\big \langle \cdot, \cdot \big \rangle _i$. We denote by
$\big \langle \cdot, \cdot \big \rangle _i$. We denote by ![]() $V_{\omega _i}^{0}$ a Weil–Heisenberg representation of
$V_{\omega _i}^{0}$ a Weil–Heisenberg representation of ![]() $\operatorname {Sp}(V_i^{0}) \ltimes (V_i^{0})^{\sharp }$ corresponding to the same central character as the central character of
$\operatorname {Sp}(V_i^{0}) \ltimes (V_i^{0})^{\sharp }$ corresponding to the same central character as the central character of ![]() $V_i^{\sharp }$ acting on
$V_i^{\sharp }$ acting on ![]() $V_{\omega _i}$ (which in turn corresponds to the character
$V_{\omega _i}$ (which in turn corresponds to the character ![]() $\hat {\phi }_i|_{(G_i)_{x,r_i,({r_i}/{2})+}}$ via the special isomorphism
$\hat {\phi }_i|_{(G_i)_{x,r_i,({r_i}/{2})+}}$ via the special isomorphism ![]() $j_i$). By [Reference GérardinGér77, Theorem 2.4(b)] the restriction of the Weil–Heisenberg representation
$j_i$). By [Reference GérardinGér77, Theorem 2.4(b)] the restriction of the Weil–Heisenberg representation ![]() $V_{\omega _i}$ from
$V_{\omega _i}$ from ![]() $\operatorname {Sp}(V_i) \ltimes V_i^{\sharp }$ to
$\operatorname {Sp}(V_i) \ltimes V_i^{\sharp }$ to ![]() $P_i \ltimes V_i^{\sharp }$ is given by
$P_i \ltimes V_i^{\sharp }$ is given by
where the group ![]() $P_i \ltimes ( V_i^{+} \times (V_i^{0})^{\sharp })$ acts on
$P_i \ltimes ( V_i^{+} \times (V_i^{0})^{\sharp })$ acts on ![]() $V_{\omega _i}^{0}$ by composing the projection
$V_{\omega _i}^{0}$ by composing the projection
(where ![]() $\operatorname {pr}_{+0,0}: ( V_i^{+} \times (V_i^{0})^{\sharp }) \twoheadrightarrow (V_i^{0})^{\sharp }$ denotes the projection with kernel
$\operatorname {pr}_{+0,0}: ( V_i^{+} \times (V_i^{0})^{\sharp }) \twoheadrightarrow (V_i^{0})^{\sharp }$ denotes the projection with kernel ![]() $V_i^{+}$) with the Weil–Heisenberg representation of
$V_i^{+}$) with the Weil–Heisenberg representation of ![]() $\operatorname {Sp}(V_i^{0}) \ltimes (V_i^{0})^{\sharp }$, and
$\operatorname {Sp}(V_i^{0}) \ltimes (V_i^{0})^{\sharp }$, and ![]() $\mathbb {C}_{\chi ^{V_i^{+}}}$ is a one-dimensional space on which the action of
$\mathbb {C}_{\chi ^{V_i^{+}}}$ is a one-dimensional space on which the action of ![]() $P_i$ is given by a quadratic characterFootnote 2
$P_i$ is given by a quadratic characterFootnote 2 ![]() $\chi ^{V_i^{+}}$ that factors through the projection
$\chi ^{V_i^{+}}$ that factors through the projection ![]() $\operatorname {pr}_{i,+}: P_i \rightarrow \operatorname {GL}(V_i^{+})$ obtained by restricting elements in
$\operatorname {pr}_{i,+}: P_i \rightarrow \operatorname {GL}(V_i^{+})$ obtained by restricting elements in ![]() $P_i$ to
$P_i$ to ![]() $V_i^{+}$.
$V_i^{+}$.
Let ![]() $\bar U_{i}$ be the image of
$\bar U_{i}$ be the image of ![]() $U_i$ in the Heisenberg group
$U_i$ in the Heisenberg group ![]() $(G_i)_{x,r_i,{r_i}/{2}}/\big ((G_i)_{x,r_i,({r_i}/{2})+} \cap \ker (\hat {\phi }_i)\big )$. Then by Yu's construction of the special isomorphism
$(G_i)_{x,r_i,{r_i}/{2}}/\big ((G_i)_{x,r_i,({r_i}/{2})+} \cap \ker (\hat {\phi }_i)\big )$. Then by Yu's construction of the special isomorphism ![]() $j_i:(G_i)_{x,r_i,{r_i}/{2}}/\big ((G_i)_{x,r_i,({r_i}/{2})+} \cap \ker (\hat {\phi }_i)\big ) \rightarrow V_i^{\sharp }$ in [Reference YuYu01, Proposition 11.4], we have
$j_i:(G_i)_{x,r_i,{r_i}/{2}}/\big ((G_i)_{x,r_i,({r_i}/{2})+} \cap \ker (\hat {\phi }_i)\big ) \rightarrow V_i^{\sharp }$ in [Reference YuYu01, Proposition 11.4], we have ![]() $j_i(\bar U_{i})=V_i^{+} \times 0 \subset V_i \times \mathbb {F}_p$. Since the orthogonal complement of
$j_i(\bar U_{i})=V_i^{+} \times 0 \subset V_i \times \mathbb {F}_p$. Since the orthogonal complement of ![]() $V_i^{-}$ is
$V_i^{-}$ is ![]() $V_i^{0} \oplus V_i^{-}$, and hence for every element
$V_i^{0} \oplus V_i^{-}$, and hence for every element ![]() $v_- \in V_i^{-}$ there exists
$v_- \in V_i^{-}$ there exists ![]() $v_+ \in V_i^{+}$ such that
$v_+ \in V_i^{+}$ such that ![]() $\big \langle v_-,v_+\big \rangle _i \neq 0$, we have
$\big \langle v_-,v_+\big \rangle _i \neq 0$, we have
as a representation of ![]() $P_i$.
$P_i$.
Note that the image of ![]() $\bar {U}_{\operatorname {Sp}(V_i)}$ in
$\bar {U}_{\operatorname {Sp}(V_i)}$ in ![]() $\operatorname {GL}(V_i^{+})$ under the projection
$\operatorname {GL}(V_i^{+})$ under the projection ![]() $\operatorname {pr}_{i,+}:P_i \rightarrow \operatorname {GL}(V_i^{+})$ is unipotent since
$\operatorname {pr}_{i,+}:P_i \rightarrow \operatorname {GL}(V_i^{+})$ is unipotent since ![]() $\bar {U}$ is unipotent. Hence
$\bar {U}$ is unipotent. Hence ![]() $\operatorname {pr}_{i,+}(\bar {U}_{\operatorname {Sp}(V_i)})$ is contained in the commutator subgroup of
$\operatorname {pr}_{i,+}(\bar {U}_{\operatorname {Sp}(V_i)})$ is contained in the commutator subgroup of ![]() $\operatorname {GL}(V_i^{+})$, and
$\operatorname {GL}(V_i^{+})$, and ![]() $\chi ^{V_i^{+}}|_{\operatorname {pr}_{i,+}(\bar {U}_{\operatorname {Sp}(V_i)})}$ is trivial. Moreover, we observed above that
$\chi ^{V_i^{+}}|_{\operatorname {pr}_{i,+}(\bar {U}_{\operatorname {Sp}(V_i)})}$ is trivial. Moreover, we observed above that ![]() $\operatorname {pr}_{i,0}(\bar {U}_{\operatorname {Sp}(V_i)})=\operatorname {Id}_{V_i^{0}}$. Thus
$\operatorname {pr}_{i,0}(\bar {U}_{\operatorname {Sp}(V_i)})=\operatorname {Id}_{V_i^{0}}$. Thus ![]() $\bar {U}_{\operatorname {Sp}(V_i)}$ acts trivially on
$\bar {U}_{\operatorname {Sp}(V_i)}$ acts trivially on ![]() $V_{\omega _i}^{0} \otimes (\mathbb {C}_{\chi ^{V_i^{+}}} \ltimes 1)$.
$V_{\omega _i}^{0} \otimes (\mathbb {C}_{\chi ^{V_i^{+}}} \ltimes 1)$.
Recall that the action of ![]() ${U}$ on
${U}$ on ![]() $(V_{\omega _i})^{U_i}$ is given by the product of
$(V_{\omega _i})^{U_i}$ is given by the product of ![]() $\phi _i|_{U}$ with the above Weil representation construction; see § 2.5. Hence
$\phi _i|_{U}$ with the above Weil representation construction; see § 2.5. Hence ![]() ${U}$ acts on
${U}$ acts on ![]() $(V_{\omega _i})^{U_i}$ via the character
$(V_{\omega _i})^{U_i}$ via the character ![]() $\phi _i|_{U}$. Since we proved above that
$\phi _i|_{U}$. Since we proved above that ![]() ${U}$ acts via
${U}$ acts via ![]() $\phi =\prod _{i=1}^{n} \phi _i$ on
$\phi =\prod _{i=1}^{n} \phi _i$ on ![]() $V_f \subset V_\rho \otimes \bigotimes _{i=1}^{n} (V_{\omega _i})^{U_i}$, we deduce that there exists a non-trivial subspace
$V_f \subset V_\rho \otimes \bigotimes _{i=1}^{n} (V_{\omega _i})^{U_i}$, we deduce that there exists a non-trivial subspace ![]() $V_{\rho,f}$ of
$V_{\rho,f}$ of ![]() $V_\rho$ on which
$V_\rho$ on which ![]() ${U}$ acts trivially. Hence
${U}$ acts trivially. Hence ![]() $\rho |_{\bar {U}}$ contains the trivial representation, which contradicts that
$\rho |_{\bar {U}}$ contains the trivial representation, which contradicts that ![]() $\rho |_{(G_{n+1})_{x,0}}$ is cuspidal.
$\rho |_{(G_{n+1})_{x,0}}$ is cuspidal.
4. A counterexample
In this section we provide a counterexample to [Reference YuYu01, Proposition 14.1 and Theorem 14.2], whose proof relied on the misprinted version of [Reference GérardinGér77, Theorem 2.4(b)]. To state the content of the section more precisely, let ![]() $G'$ be a tamely ramified twisted Levi subgroup of
$G'$ be a tamely ramified twisted Levi subgroup of ![]() $G$, let
$G$, let ![]() $x \in \mathscr {B}(G', F)$, and let
$x \in \mathscr {B}(G', F)$, and let ![]() $\phi$ be a character of
$\phi$ be a character of ![]() $G'(F)$ that is
$G'(F)$ that is ![]() $G$-generic relative to
$G$-generic relative to ![]() $x$ of depth
$x$ of depth ![]() $r$ for some
$r$ for some ![]() $r \in \mathbb {R}_{>0}$, that is to say, we are in the setting of [Reference YuYu01, § 14]. Following [Reference YuYu01], we set
$r \in \mathbb {R}_{>0}$, that is to say, we are in the setting of [Reference YuYu01, § 14]. Following [Reference YuYu01], we set
 \begin{gather*} J=(G', G)(F)_{x,(r,{r}/{2})}, \quad J_+{=}(G', G)(F)_{x,(r,({r}/{2})+)}, \\ K=G'(F) \cap G_{[x]}, \quad K_+{=}G'(F) \cap G_{x,0+}, \quad N=\ker \hat{\phi}, \end{gather*}
\begin{gather*} J=(G', G)(F)_{x,(r,{r}/{2})}, \quad J_+{=}(G', G)(F)_{x,(r,({r}/{2})+)}, \\ K=G'(F) \cap G_{[x]}, \quad K_+{=}G'(F) \cap G_{x,0+}, \quad N=\ker \hat{\phi}, \end{gather*}
where ![]() $\hat {\phi }$ is defined as in [Reference YuYu01, §§ 4 and 9], see also p. 2736 of this paper, and we denote by
$\hat {\phi }$ is defined as in [Reference YuYu01, §§ 4 and 9], see also p. 2736 of this paper, and we denote by ![]() $\tilde {\phi }$ the representation of
$\tilde {\phi }$ the representation of ![]() $K \ltimes J$ which is the pull back of the Weil representation of
$K \ltimes J$ which is the pull back of the Weil representation of ![]() $\operatorname {Sp}(J/J_+) \ltimes (J / N)$ via the symplectic action given by [Reference YuYu01, Proposition 11.4], see also p. 2737 of this paper.
$\operatorname {Sp}(J/J_+) \ltimes (J / N)$ via the symplectic action given by [Reference YuYu01, Proposition 11.4], see also p. 2737 of this paper.
In this section, we provide an example for ![]() $G' \subset G$,
$G' \subset G$, ![]() $x$ and
$x$ and ![]() $\phi$ as above and
$\phi$ as above and ![]() $g \in G'(F)$ such that
$g \in G'(F)$ such that
Following [Reference YuYu01, §14], we denote by ![]() $\phi '$ the representation of
$\phi '$ the representation of ![]() $KJ$ whose inflation
$KJ$ whose inflation ![]() $\inf \phi '$ to
$\inf \phi '$ to ![]() $K \ltimes J$ yields
$K \ltimes J$ yields ![]() $\inf (\phi |_K) \otimes \tilde \phi$. By the discussion in [Reference YuYu01] immediately following Theorem 14.2 (see also Corollary 4.3 below), (6) implies that
$\inf (\phi |_K) \otimes \tilde \phi$. By the discussion in [Reference YuYu01] immediately following Theorem 14.2 (see also Corollary 4.3 below), (6) implies that
and therefore provides a counterexample to the claim that ![]() $\operatorname {Hom}_{KJ \cap {{}^{g}(KJ)}}(^{g}\phi ',\phi ')$ always has dimension one that was made in [Reference YuYu01, Proposition 14.1] and in its more general version [Reference YuYu01, Theorem 14.2].
$\operatorname {Hom}_{KJ \cap {{}^{g}(KJ)}}(^{g}\phi ',\phi ')$ always has dimension one that was made in [Reference YuYu01, Proposition 14.1] and in its more general version [Reference YuYu01, Theorem 14.2].
Consider the case ![]() $G=\operatorname {Sp}_{10}$ over
$G=\operatorname {Sp}_{10}$ over ![]() $F$ corresponding to the symplectic pairing given by
$F$ corresponding to the symplectic pairing given by ![]() $\big (\begin {smallmatrix}0 & J_5 \\ -J_5 & 0 \\ \end {smallmatrix}\big )$ where
$\big (\begin {smallmatrix}0 & J_5 \\ -J_5 & 0 \\ \end {smallmatrix}\big )$ where
 \[ J_5 = \begin{pmatrix} 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & -1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & -1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ \end{pmatrix} . \]
\[ J_5 = \begin{pmatrix} 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & -1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & -1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ \end{pmatrix} . \]
We assume that the residue field of ![]() $F$ is
$F$ is ![]() $\mathbb {F}_p$ for some prime number
$\mathbb {F}_p$ for some prime number ![]() $p>10$.
$p>10$.
Let ![]() $T \subset \operatorname {Sp}_{10}$ be the diagonal maximal torus using the standard coordinates, and write
$T \subset \operatorname {Sp}_{10}$ be the diagonal maximal torus using the standard coordinates, and write ![]() $\mathfrak {t}=\operatorname {Lie}(T)(F)$. We identify the apartment
$\mathfrak {t}=\operatorname {Lie}(T)(F)$. We identify the apartment ![]() $\mathscr {A}(T, F)$ with
$\mathscr {A}(T, F)$ with ![]() $X_*(T)\otimes \mathbb {R}$ (
$X_*(T)\otimes \mathbb {R}$ (![]() $X_*$ being, as above, the cocharacters over
$X_*$ being, as above, the cocharacters over ![]() $\bar F$, or, equivalently, the cocharacters over
$\bar F$, or, equivalently, the cocharacters over ![]() $F$) using the standard parametrization of the root groups as base point, that is, the point for which the attached parahoric subgroup is
$F$) using the standard parametrization of the root groups as base point, that is, the point for which the attached parahoric subgroup is ![]() $\operatorname {Sp}_{10}(\mathcal {O})$ in the standard coordinates. Identifying
$\operatorname {Sp}_{10}(\mathcal {O})$ in the standard coordinates. Identifying ![]() $X_*(T) \otimes _\mathbb {Z} \mathbb {R}$ with
$X_*(T) \otimes _\mathbb {Z} \mathbb {R}$ with ![]() $\mathbb {R}^{5}$ where the first standard basis vector corresponds to
$\mathbb {R}^{5}$ where the first standard basis vector corresponds to ![]() $t \rightarrow \operatorname {diag}(t, 1, 1, 1, 1, 1, 1, 1, 1, t^{-1})$, the second to
$t \rightarrow \operatorname {diag}(t, 1, 1, 1, 1, 1, 1, 1, 1, t^{-1})$, the second to ![]() $t \rightarrow \operatorname {diag}(1, t, 1, 1, 1, 1, 1, 1, t^{-1}, 1)$, and so on, we let
$t \rightarrow \operatorname {diag}(1, t, 1, 1, 1, 1, 1, 1, t^{-1}, 1)$, and so on, we let ![]() $x$ be the point of
$x$ be the point of ![]() $\mathscr {A}(T, F)$ corresponding to
$\mathscr {A}(T, F)$ corresponding to ![]() $(-\frac {1}{4}, 0, 0, \frac {1}{4}, \frac {1}{4})$.
$(-\frac {1}{4}, 0, 0, \frac {1}{4}, \frac {1}{4})$.
Let ![]() $\pi$ be a uniformizer of
$\pi$ be a uniformizer of ![]() $F$, and let
$F$, and let ![]() $\varpi$ in
$\varpi$ in ![]() $F^{\mathrm {sep}}$ such that
$F^{\mathrm {sep}}$ such that ![]() $\varpi ^{2}=\pi$. Let
$\varpi ^{2}=\pi$. Let ![]() $X \in \mathfrak {g}^{*}_{x,-{1}/{2}}$ be the element given by
$X \in \mathfrak {g}^{*}_{x,-{1}/{2}}$ be the element given by
We set ![]() $G'$ to be the centralizer
$G'$ to be the centralizer ![]() $\operatorname {Cent}_{G}(X)$ of
$\operatorname {Cent}_{G}(X)$ of ![]() $X$ in
$X$ in ![]() $G$. Note that
$G$. Note that
 \[ G'=\operatorname{Cent}_G\Bigg(\Bigg(\begin{array}{@{}ccc@{}} 0 & 0_{1 \times 8} & 1 \\ 0_{8 \times 1} & 0_{8\times 8} & 0_{8 \times 1} \\ \pi^{{-}1} & 0_{1 \times 8} & 0 \\ \end{array}\Bigg)\Bigg) \simeq \operatorname{U}(1) \times \operatorname{Sp}_8 \]
\[ G'=\operatorname{Cent}_G\Bigg(\Bigg(\begin{array}{@{}ccc@{}} 0 & 0_{1 \times 8} & 1 \\ 0_{8 \times 1} & 0_{8\times 8} & 0_{8 \times 1} \\ \pi^{{-}1} & 0_{1 \times 8} & 0 \\ \end{array}\Bigg)\Bigg) \simeq \operatorname{U}(1) \times \operatorname{Sp}_8 \]
is a twisted Levi subgroup of ![]() $G=\operatorname {Sp}_{10}$ (with anisotropic center).
$G=\operatorname {Sp}_{10}$ (with anisotropic center).
Lemma 4.1 The (restriction to ![]() $\mathfrak {g}'$ of the) element
$\mathfrak {g}'$ of the) element ![]() $X$ is
$X$ is ![]() $G$-generic of depth
$G$-generic of depth ![]() $r=\frac {1}{2}$ (for the pair
$r=\frac {1}{2}$ (for the pair ![]() $G'\subset G$), and the point
$G'\subset G$), and the point ![]() $x=(-\frac {1}{4}, 0, 0, \frac {1}{4}, \frac {1}{4}) \in \mathscr {A}(T,F)\subset \mathscr {B}(G,F)$ is contained in
$x=(-\frac {1}{4}, 0, 0, \frac {1}{4}, \frac {1}{4}) \in \mathscr {A}(T,F)\subset \mathscr {B}(G,F)$ is contained in ![]() $\mathscr {B}(G',F)$.
$\mathscr {B}(G',F)$.
Proof. First note that ![]() $X$ is
$X$ is ![]() $G'$-invariant by construction. Let
$G'$-invariant by construction. Let ![]() $\sqrt {2\varpi }$ in
$\sqrt {2\varpi }$ in ![]() $F^{\mathrm {sep}}$ such that
$F^{\mathrm {sep}}$ such that ![]() $\sqrt {2\varpi }^{2}=2 \varpi$. We consider the maximal torus
$\sqrt {2\varpi }^{2}=2 \varpi$. We consider the maximal torus
 \[ T'= \begin{pmatrix}
\frac{\varpi}{\sqrt{2\varpi}} & 0_{1 \times 8} &
\frac{-\varpi }{\sqrt{2\varpi}}\\ 0_{8
\times 1} & 1_{8\times 8} & 0_{8 \times 1}
\\ \frac{1}{\sqrt{2\varpi}} & 0_{1
\times 8} & \frac{1}{\sqrt{2\varpi}} \\
\end{pmatrix} T \begin{pmatrix} \frac{1}{{\sqrt{2\varpi}}}
& 0_{1 \times 8} & \frac{\varpi}{\sqrt{2\varpi}}
\\ 0_{8 \times 1} & 1_{8\times 8} & 0_{8
\times 1} \\ \frac{-1}{{\sqrt{2\varpi}}}
& 0_{1 \times 8} & \frac{\varpi}{\sqrt{2\varpi}} \\
\end{pmatrix} \]
\[ T'= \begin{pmatrix}
\frac{\varpi}{\sqrt{2\varpi}} & 0_{1 \times 8} &
\frac{-\varpi }{\sqrt{2\varpi}}\\ 0_{8
\times 1} & 1_{8\times 8} & 0_{8 \times 1}
\\ \frac{1}{\sqrt{2\varpi}} & 0_{1
\times 8} & \frac{1}{\sqrt{2\varpi}} \\
\end{pmatrix} T \begin{pmatrix} \frac{1}{{\sqrt{2\varpi}}}
& 0_{1 \times 8} & \frac{\varpi}{\sqrt{2\varpi}}
\\ 0_{8 \times 1} & 1_{8\times 8} & 0_{8
\times 1} \\ \frac{-1}{{\sqrt{2\varpi}}}
& 0_{1 \times 8} & \frac{\varpi}{\sqrt{2\varpi}} \\
\end{pmatrix} \]
of ![]() $G'$. Then the set
$G'$. Then the set ![]() $\{H_{\alpha }=d\check \alpha (1) \, | \, \alpha \in \Phi (G, T') \setminus \Phi (G',T')\}$, where
$\{H_{\alpha }=d\check \alpha (1) \, | \, \alpha \in \Phi (G, T') \setminus \Phi (G',T')\}$, where ![]() $\check \alpha$ denotes the dual root of
$\check \alpha$ denotes the dual root of ![]() $\alpha$, is given by
$\alpha$, is given by
 \[{\pm} \begin{pmatrix} 0 & 0_{1 \times 8} & \varpi \\ 0_{8 \times 1} & 0_{8\times 8} & 0_{8 \times 1} \\ \varpi^{{-}1} & 0_{1 \times 8} & 0 \\ \end{pmatrix} \]
\[{\pm} \begin{pmatrix} 0 & 0_{1 \times 8} & \varpi \\ 0_{8 \times 1} & 0_{8\times 8} & 0_{8 \times 1} \\ \varpi^{{-}1} & 0_{1 \times 8} & 0 \\ \end{pmatrix} \]
and sums of the former with a diagonal matrix of the form
Hence ![]() $\operatorname {val}(X(H_\alpha ))=\operatorname {val}(\pm 2\varpi ^{-1})=-\frac {1}{2}$ for all
$\operatorname {val}(X(H_\alpha ))=\operatorname {val}(\pm 2\varpi ^{-1})=-\frac {1}{2}$ for all ![]() $\alpha \in \Phi (G, T') \setminus \Phi (G',T')$, where
$\alpha \in \Phi (G, T') \setminus \Phi (G',T')$, where ![]() $\operatorname {val}$ denotes the valuation of
$\operatorname {val}$ denotes the valuation of ![]() $F$ with image
$F$ with image ![]() $\mathbb {Z}\cup \{\infty \}$. Moreover,
$\mathbb {Z}\cup \{\infty \}$. Moreover, ![]() $X$ is contained in
$X$ is contained in ![]() $(\mathfrak {g}')^{*}_{y,-{1}/{2}}$ for any point
$(\mathfrak {g}')^{*}_{y,-{1}/{2}}$ for any point ![]() $y \in \mathscr {B}(G', F)$ and its restriction to the Lie algebra of the identity component
$y \in \mathscr {B}(G', F)$ and its restriction to the Lie algebra of the identity component ![]() $Z(G')^{\circ }$ of the center of
$Z(G')^{\circ }$ of the center of ![]() $G'$ is contained in
$G'$ is contained in ![]() $\operatorname {Lie}^{*}(Z(G')^{\circ })_{-{1}/{2}}$. Since
$\operatorname {Lie}^{*}(Z(G')^{\circ })_{-{1}/{2}}$. Since ![]() $p>10$, that is,
$p>10$, that is, ![]() $p$ does not divide the order of the Weyl group of
$p$ does not divide the order of the Weyl group of ![]() $\operatorname {Sp}_{10}$, we conclude that
$\operatorname {Sp}_{10}$, we conclude that ![]() $X$ is
$X$ is ![]() $G$-generic of depth
$G$-generic of depth ![]() $\frac {1}{2}$.
$\frac {1}{2}$.
Let ![]() $E$ be a finite, tamely ramified extension of
$E$ be a finite, tamely ramified extension of ![]() $F$ that contains
$F$ that contains ![]() $\sqrt {2\varpi }$. Then
$\sqrt {2\varpi }$. Then ![]() $x$ is a vertex in
$x$ is a vertex in ![]() $\mathscr {B}(G,E)$ and it is an easy calculation to check that
$\mathscr {B}(G,E)$ and it is an easy calculation to check that
 \[ G_{x,0}(E)=\begin{pmatrix}
\frac{\varpi}{\sqrt{2\varpi}} & 0_{1 \times 8} &
\frac{-\varpi }{\sqrt{2\varpi}}\\ 0_{8
\times 1} & 1_{8\times 8} & 0_{8 \times 1}
\\ \frac{1}{\sqrt{2\varpi}} & 0_{1
\times 8} & \frac{1}{\sqrt{2\varpi}} \\
\end{pmatrix} G_{y,0}(E) \begin{pmatrix}
\frac{1}{{\sqrt{2\varpi}}} & 0_{1 \times 8} &
\frac{\varpi}{\sqrt{2\varpi}} \\ 0_{8
\times 1} & 1_{8\times 8} & 0_{8 \times 1}
\\ \frac{-1}{{\sqrt{2\varpi}}} & 0_{1
\times 8} & \frac{\varpi}{\sqrt{2\varpi}} \\ \end{pmatrix}
\]
\[ G_{x,0}(E)=\begin{pmatrix}
\frac{\varpi}{\sqrt{2\varpi}} & 0_{1 \times 8} &
\frac{-\varpi }{\sqrt{2\varpi}}\\ 0_{8
\times 1} & 1_{8\times 8} & 0_{8 \times 1}
\\ \frac{1}{\sqrt{2\varpi}} & 0_{1
\times 8} & \frac{1}{\sqrt{2\varpi}} \\
\end{pmatrix} G_{y,0}(E) \begin{pmatrix}
\frac{1}{{\sqrt{2\varpi}}} & 0_{1 \times 8} &
\frac{\varpi}{\sqrt{2\varpi}} \\ 0_{8
\times 1} & 1_{8\times 8} & 0_{8 \times 1}
\\ \frac{-1}{{\sqrt{2\varpi}}} & 0_{1
\times 8} & \frac{\varpi}{\sqrt{2\varpi}} \\ \end{pmatrix}
\]
for the point ![]() $y=(0,0,0,\frac {1}{4},\frac {1}{4}) \in \mathscr {A}(T,F) \subset \mathscr {A}(T,E)$. Hence
$y=(0,0,0,\frac {1}{4},\frac {1}{4}) \in \mathscr {A}(T,F) \subset \mathscr {A}(T,E)$. Hence
 \[ x=\begin{pmatrix} \frac{\varpi}{\sqrt{2\varpi}} & 0_{1 \times 8} & \frac{-\varpi }{\sqrt{2\varpi}}\\ 0_{8 \times 1} & 1_{8\times 8} & 0_{8 \times 1} \\ \frac{1}{\sqrt{2\varpi}} & 0_{1 \times 8} & \frac{1}{\sqrt{2\varpi}} \\ \end{pmatrix}.y, \]
\[ x=\begin{pmatrix} \frac{\varpi}{\sqrt{2\varpi}} & 0_{1 \times 8} & \frac{-\varpi }{\sqrt{2\varpi}}\\ 0_{8 \times 1} & 1_{8\times 8} & 0_{8 \times 1} \\ \frac{1}{\sqrt{2\varpi}} & 0_{1 \times 8} & \frac{1}{\sqrt{2\varpi}} \\ \end{pmatrix}.y, \]
which implies ![]() $x \in \mathscr {A}(T', E) \subset \mathscr {B}(G', E)$, and therefore
$x \in \mathscr {A}(T', E) \subset \mathscr {B}(G', E)$, and therefore ![]() $x \in \mathscr {B}(G', E) \cap \mathscr {B}(G, F) =\mathscr {B}(G',F)$.
$x \in \mathscr {B}(G', E) \cap \mathscr {B}(G, F) =\mathscr {B}(G',F)$.
The element ![]() $X$ yields a linear map from
$X$ yields a linear map from ![]() $\mathfrak {g}'_{x,{1}/{2}}$ to
$\mathfrak {g}'_{x,{1}/{2}}$ to ![]() $\mathcal {O}$ that sends
$\mathcal {O}$ that sends ![]() $\mathfrak {g}'_{x,({1}/{2})+}$ to
$\mathfrak {g}'_{x,({1}/{2})+}$ to ![]() $\varpi \mathcal {O}$ and defines a character of
$\varpi \mathcal {O}$ and defines a character of ![]() $G'_{x,{1}/{2}}$ that is trivial on
$G'_{x,{1}/{2}}$ that is trivial on ![]() $G'_{x,\frac {1}{2}+}$ and trivial on
$G'_{x,\frac {1}{2}+}$ and trivial on ![]() $G'_{x,{1}/{2}} \cap \operatorname {Sp}_8 \subset G'_{x,{1}/{2}} \cap (U(1) \times \operatorname {Sp}_8)(F) \simeq G'_{x,{1}/{2}}$. Since
$G'_{x,{1}/{2}} \cap \operatorname {Sp}_8 \subset G'_{x,{1}/{2}} \cap (U(1) \times \operatorname {Sp}_8)(F) \simeq G'_{x,{1}/{2}}$. Since ![]() $U(1)$ is abelian, we can extend this character to a character of
$U(1)$ is abelian, we can extend this character to a character of ![]() $G'(F)$ (trivial on
$G'(F)$ (trivial on ![]() $\operatorname {Sp}_8(F) \subset G'(F)$), which we denote by
$\operatorname {Sp}_8(F) \subset G'(F)$), which we denote by ![]() $\phi$. Since
$\phi$. Since ![]() $X$ is
$X$ is ![]() $G$-generic of depth
$G$-generic of depth ![]() $r=\frac {1}{2}$ (for the pair
$r=\frac {1}{2}$ (for the pair ![]() $G'\subset G$), the character
$G'\subset G$), the character ![]() $\phi$ is
$\phi$ is ![]() $G$-generic relative to
$G$-generic relative to ![]() $x$ of depth
$x$ of depth ![]() $r$ in the sense of Yu [Reference YuYu01, § 9].
$r$ in the sense of Yu [Reference YuYu01, § 9].
Proposition 4.2 Let ![]() $G'\subset G, \phi, x, r$ as above and
$G'\subset G, \phi, x, r$ as above and
 \[ g= \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & J_4^{+} & 0 & 0 \\ 0 & 0 & -J_4 ^{+} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \in G'(F),\quad \text{where } J_4^{+} = \begin{pmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ \end{pmatrix} . \]
\[ g= \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & J_4^{+} & 0 & 0 \\ 0 & 0 & -J_4 ^{+} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \in G'(F),\quad \text{where } J_4^{+} = \begin{pmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ \end{pmatrix} . \]
Then ![]() $\dim \operatorname {Hom}_{(K \cap {{}^{g}K}) \ltimes {(J \cap {{}^{g}J})}}({{}^{g}\tilde {\phi }}, \tilde {\phi }) =0.$
$\dim \operatorname {Hom}_{(K \cap {{}^{g}K}) \ltimes {(J \cap {{}^{g}J})}}({{}^{g}\tilde {\phi }}, \tilde {\phi }) =0.$
Proof. Using the standard coordinates we define the groups
 \[ {H_{23}}:= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & \operatorname{GL}_2(\mathcal{O}) & 0 & 0 & 0 \\ 0 & 0 & 1_{4 \times 4} & 0 & 0 \\ 0 & 0 & 0 & \operatorname{GL}_2(\mathcal{O}) & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{pmatrix} \cap \operatorname{Sp}_{10}(F) \subset G'_{x,0}, \]
\[ {H_{23}}:= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & \operatorname{GL}_2(\mathcal{O}) & 0 & 0 & 0 \\ 0 & 0 & 1_{4 \times 4} & 0 & 0 \\ 0 & 0 & 0 & \operatorname{GL}_2(\mathcal{O}) & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{pmatrix} \cap \operatorname{Sp}_{10}(F) \subset G'_{x,0}, \]
 \[ {H_{45}}:= \begin{pmatrix} 1_{3\times 3} & 0 & 0 & 0 \\ 0 & \operatorname{GL}_2(\mathcal{O}) & 0 & 0 \\ 0 & 0 & \operatorname{GL}_2(\mathcal{O}) & 0 \\ 0 & 0 & 0 & 1_{3\times 3} \\ \end{pmatrix} \cap \operatorname{Sp}_{10}(F) \subset G'_{x,0}. \]
\[ {H_{45}}:= \begin{pmatrix} 1_{3\times 3} & 0 & 0 & 0 \\ 0 & \operatorname{GL}_2(\mathcal{O}) & 0 & 0 \\ 0 & 0 & \operatorname{GL}_2(\mathcal{O}) & 0 \\ 0 & 0 & 0 & 1_{3\times 3} \\ \end{pmatrix} \cap \operatorname{Sp}_{10}(F) \subset G'_{x,0}. \]
Note that ![]() ${H_{23}} \simeq \operatorname {GL}_2(\mathcal {O}) \simeq {H_{45}}$, and
${H_{23}} \simeq \operatorname {GL}_2(\mathcal {O}) \simeq {H_{45}}$, and ![]() $g{H_{23}}g^{-1}={H_{45}}$ and
$g{H_{23}}g^{-1}={H_{45}}$ and ![]() $g{H_{45}}g^{-1}={H_{23}}$, hence
$g{H_{45}}g^{-1}={H_{23}}$, hence ![]() ${H_{23}} \in K \cap {{}^{g}K}$. Moreover, the image of
${H_{23}} \in K \cap {{}^{g}K}$. Moreover, the image of ![]() ${H_{23}}$ and the image of
${H_{23}}$ and the image of ![]() ${H_{45}}$ in
${H_{45}}$ in ![]() $G'_{x,0}/G'_{x,0+}$ are both isomorphic to
$G'_{x,0}/G'_{x,0+}$ are both isomorphic to ![]() $\operatorname {GL}_2(\mathbb {F}_p)$.
$\operatorname {GL}_2(\mathbb {F}_p)$.
We will show that ![]() $\dim \operatorname {Hom}_{{H_{23}}}({{}^{g}\tilde {\phi }}, \tilde {\phi })=0$, which implies that
$\dim \operatorname {Hom}_{{H_{23}}}({{}^{g}\tilde {\phi }}, \tilde {\phi })=0$, which implies that ![]() $\dim \operatorname {Hom}_{({K\cap {{}^{g}K}}) \ltimes ({J \cap {{}^{g}J}})}({{}^{g}\tilde {\phi }}, \tilde {\phi }) = 0$.
$\dim \operatorname {Hom}_{({K\cap {{}^{g}K}}) \ltimes ({J \cap {{}^{g}J}})}({{}^{g}\tilde {\phi }}, \tilde {\phi }) = 0$.
We write ![]() $V=J/J_+$, where we recall that
$V=J/J_+$, where we recall that
Let ![]() $\mathfrak {g}(\mathcal {O})$ be the
$\mathfrak {g}(\mathcal {O})$ be the ![]() $\mathcal {O}$-points of the Lie algebra of the reductive parahoric group scheme over
$\mathcal {O}$-points of the Lie algebra of the reductive parahoric group scheme over ![]() $\mathcal {O}$ corresponding to the base point
$\mathcal {O}$ corresponding to the base point ![]() $(0,0,0,0,0)$, that is, the Lie algebra of
$(0,0,0,0,0)$, that is, the Lie algebra of ![]() $\operatorname {Sp}_{10}$ defined over
$\operatorname {Sp}_{10}$ defined over ![]() $\mathcal {O}$ in the standard basis. We denote by
$\mathcal {O}$ in the standard basis. We denote by ![]() $\mathfrak {g}(\mathcal {O})_{t_1t_2^{-1}}$ the submodule of
$\mathfrak {g}(\mathcal {O})_{t_1t_2^{-1}}$ the submodule of ![]() $\mathfrak {g}(\mathcal {O})$ corresponding to the root
$\mathfrak {g}(\mathcal {O})$ corresponding to the root ![]() $\operatorname {diag}(t_1, t_2, t_3, t_4, t_5, t_5^{-1}, t_4^{-1}, t_3^{-1}, t_2^{-1}, t_1^{-1}) \mapsto t_1t_2^{-1}$, and analogously for all other indices. Then the four-dimensional
$\operatorname {diag}(t_1, t_2, t_3, t_4, t_5, t_5^{-1}, t_4^{-1}, t_3^{-1}, t_2^{-1}, t_1^{-1}) \mapsto t_1t_2^{-1}$, and analogously for all other indices. Then the four-dimensional ![]() $\mathbb {F}_p$-vector space
$\mathbb {F}_p$-vector space ![]() $V$ is spanned by the images of
$V$ is spanned by the images of
Each of these images is a one-dimensional ![]() $\mathbb {F}_p$-vector subspace of
$\mathbb {F}_p$-vector subspace of ![]() $V$, which we denote by
$V$, which we denote by ![]() $V_{t_2}$,
$V_{t_2}$, ![]() $V_{t_3}$,
$V_{t_3}$, ![]() $V_{t_2^{-1}}$ and
$V_{t_2^{-1}}$ and ![]() $V_{t_3^{-1}}$, respectively. The pairing on
$V_{t_3^{-1}}$, respectively. The pairing on ![]() $V=J/J_+$ defined by
$V=J/J_+$ defined by ![]() $\big \langle a,b\big \rangle =\hat {\phi }(aba^{-1}b^{-1})$ for
$\big \langle a,b\big \rangle =\hat {\phi }(aba^{-1}b^{-1})$ for ![]() $a, b \in J$,turns
$a, b \in J$,turns ![]() $V$ into a symplectic
$V$ into a symplectic ![]() $\mathbb {F}_p$-vector space, and
$\mathbb {F}_p$-vector space, and ![]() $V^{+}:=V_{t_2} \oplus V_{t_3}$ and
$V^{+}:=V_{t_2} \oplus V_{t_3}$ and ![]() $V^{-}:=V_{t_2^{-1}} \oplus V_{t_3^{-1}}$ are both maximal isotropic subspaces. Recall that
$V^{-}:=V_{t_2^{-1}} \oplus V_{t_3^{-1}}$ are both maximal isotropic subspaces. Recall that ![]() $\tilde {\phi }$ is defined to be the pullback to
$\tilde {\phi }$ is defined to be the pullback to ![]() $K\ltimes J$ of the Weil–Heisenberg representation of
$K\ltimes J$ of the Weil–Heisenberg representation of ![]() $\operatorname {Sp}(V) \ltimes (J/N)$ via the symplectic action defined in [Reference YuYu01, Proposition 11.4]. Hence the actions of
$\operatorname {Sp}(V) \ltimes (J/N)$ via the symplectic action defined in [Reference YuYu01, Proposition 11.4]. Hence the actions of ![]() ${H_{23}}$ and
${H_{23}}$ and ![]() ${H_{45}}$ on
${H_{45}}$ on ![]() $\tilde {\phi }$ factor through
$\tilde {\phi }$ factor through ![]() $\operatorname {Sp}(V)$, and therefore
$\operatorname {Sp}(V)$, and therefore ![]() ${H_{45}}$ acts trivially on
${H_{45}}$ acts trivially on ![]() $\tilde {\phi }$. Thus
$\tilde {\phi }$. Thus ![]() $^{g}\tilde {\phi }|_{{H_{23}}}={{}^{g}\tilde {\phi }}|_{g{H_{45}}g^{-1}}$ is trivial, and in order to prove that
$^{g}\tilde {\phi }|_{{H_{23}}}={{}^{g}\tilde {\phi }}|_{g{H_{45}}g^{-1}}$ is trivial, and in order to prove that ![]() $\dim \operatorname {Hom}_{{H_{23}}}({{}^{g}\tilde {\phi }}, \tilde {\phi })=0$ it suffices to show that the representation
$\dim \operatorname {Hom}_{{H_{23}}}({{}^{g}\tilde {\phi }}, \tilde {\phi })=0$ it suffices to show that the representation ![]() $\tilde {\phi }|_{{H_{23}}}$ has no non-zero
$\tilde {\phi }|_{{H_{23}}}$ has no non-zero ![]() ${H_{23}}$-fixed vector.
${H_{23}}$-fixed vector.
We denote by ![]() $P$ the parabolic subgroup of
$P$ the parabolic subgroup of ![]() $\operatorname {Sp}(V)$ that preserves
$\operatorname {Sp}(V)$ that preserves ![]() $V^{+}$. Then the image of
$V^{+}$. Then the image of ![]() ${H_{23}}$ in
${H_{23}}$ in ![]() $\operatorname {Sp}(V)$ is the Levi subgroup
$\operatorname {Sp}(V)$ is the Levi subgroup ![]() $M\simeq \operatorname {GL}(V^{+})\simeq \operatorname {GL}(V^{-})$ of
$M\simeq \operatorname {GL}(V^{+})\simeq \operatorname {GL}(V^{-})$ of ![]() $P$ that stabilizes
$P$ that stabilizes ![]() $V^{+}$ and
$V^{+}$ and ![]() $V^{-}$. Recall that we denote by
$V^{-}$. Recall that we denote by ![]() $V^{\sharp }$ the group with underlying set
$V^{\sharp }$ the group with underlying set ![]() $V \times \mathbb {F}_p$ and with group law
$V \times \mathbb {F}_p$ and with group law ![]() $(v,a).(v',a')=(v+v', a+a'+\frac {1}{2}\big \langle v,v'\big \rangle )$. By [Reference GérardinGér77, Theorem 2.4(b)] the restriction of the Weil–Heisenberg representation from
$(v,a).(v',a')=(v+v', a+a'+\frac {1}{2}\big \langle v,v'\big \rangle )$. By [Reference GérardinGér77, Theorem 2.4(b)] the restriction of the Weil–Heisenberg representation from ![]() $\operatorname {Sp}(V) \ltimes V^{\sharp }$ to
$\operatorname {Sp}(V) \ltimes V^{\sharp }$ to ![]() $P \ltimes V^{\sharp }$ is given by
$P \ltimes V^{\sharp }$ is given by
where ![]() $\chi ^{V^{+}}$ is the characterFootnote 3 of
$\chi ^{V^{+}}$ is the characterFootnote 3 of ![]() $P$ given by
$P$ given by ![]() $P \ni p \mapsto \det (p|_{V^{+}})^{({p-1})/{2}} \in \{ \pm 1\} \subset \mathbb {C}^{*}$ and by an abuse of notation we denote by
$P \ni p \mapsto \det (p|_{V^{+}})^{({p-1})/{2}} \in \{ \pm 1\} \subset \mathbb {C}^{*}$ and by an abuse of notation we denote by ![]() $\phi$ the (restriction to
$\phi$ the (restriction to ![]() $V^{+} \times \mathbb {F}_p$ of the) character
$V^{+} \times \mathbb {F}_p$ of the) character ![]() $\phi \circ j^{-1}$, where
$\phi \circ j^{-1}$, where ![]() $j:J/N \xrightarrow {\simeq } V^{\sharp }$ denotes the special isomorphism from [Reference YuYu01, Proposition 11.4].
$j:J/N \xrightarrow {\simeq } V^{\sharp }$ denotes the special isomorphism from [Reference YuYu01, Proposition 11.4].
Let ![]() $f: P \ltimes V^{\sharp } \rightarrow \mathbb {C}$ be an element of the representation space of
$f: P \ltimes V^{\sharp } \rightarrow \mathbb {C}$ be an element of the representation space of ![]() $\pi$ and suppose that
$\pi$ and suppose that ![]() $f$ is non-zero and
$f$ is non-zero and ![]() $M$-invariant. Hence there exists
$M$-invariant. Hence there exists ![]() $v \in V^{-}$ such that
$v \in V^{-}$ such that ![]() $f(1 \ltimes v) \neq 0$. Let
$f(1 \ltimes v) \neq 0$. Let ![]() $v' \in V^{-}$ so that
$v' \in V^{-}$ so that ![]() $v$ and
$v$ and ![]() $v'$ form a basis of
$v'$ form a basis of ![]() $V^{-}$ and let
$V^{-}$ and let ![]() $m=\big (\begin {smallmatrix} 1 & 0 \\ 0 & a \end {smallmatrix}\big ) \in \operatorname {GL}(V^{-})$ using the basis
$m=\big (\begin {smallmatrix} 1 & 0 \\ 0 & a \end {smallmatrix}\big ) \in \operatorname {GL}(V^{-})$ using the basis ![]() $(v, v')$ where
$(v, v')$ where ![]() $a \in \mathbb {F}_p$ such that
$a \in \mathbb {F}_p$ such that ![]() $a^{({p-1})/{2}}=-1$. Identifying
$a^{({p-1})/{2}}=-1$. Identifying ![]() $\operatorname {GL}(V^{-})$ with
$\operatorname {GL}(V^{-})$ with ![]() $M$ (via the action of
$M$ (via the action of ![]() $M$ on
$M$ on ![]() $V^{-}$), we obtain that
$V^{-}$), we obtain that
 \begin{align*} f(1\ltimes v) &= m.f(1 \ltimes v)=f((1 \ltimes v)(m \ltimes 1))=f((m \ltimes 1)(1 \ltimes m^{{-}1}.v)) \\ &=\chi^{V^{+}}(m)f(1 \ltimes m^{{-}1}.v) = \det(m|_{V^{+}})^{({p-1})/{2}}f(1 \ltimes v)=\det(m|_{V^{-}})^{({p-1})/{2}}f(1 \ltimes v)\\ &={-}f(1 \ltimes v). \end{align*}
\begin{align*} f(1\ltimes v) &= m.f(1 \ltimes v)=f((1 \ltimes v)(m \ltimes 1))=f((m \ltimes 1)(1 \ltimes m^{{-}1}.v)) \\ &=\chi^{V^{+}}(m)f(1 \ltimes m^{{-}1}.v) = \det(m|_{V^{+}})^{({p-1})/{2}}f(1 \ltimes v)=\det(m|_{V^{-}})^{({p-1})/{2}}f(1 \ltimes v)\\ &={-}f(1 \ltimes v). \end{align*}
This contradicts that ![]() $f(1 \ltimes v) \neq 0$, hence the representation
$f(1 \ltimes v) \neq 0$, hence the representation ![]() $\pi$ does not contain any non-zero element fixed under the action of
$\pi$ does not contain any non-zero element fixed under the action of ![]() $M$. Therefore
$M$. Therefore ![]() $\tilde {\phi }$ does not contain any non-zero element fixed under the action of
$\tilde {\phi }$ does not contain any non-zero element fixed under the action of ![]() ${H_{23}}$. Thus
${H_{23}}$. Thus ![]() $\dim \operatorname {Hom}_{{H_{23}}}({{}^{g}\tilde {\phi }}, \tilde {\phi })=0$.
$\dim \operatorname {Hom}_{{H_{23}}}({{}^{g}\tilde {\phi }}, \tilde {\phi })=0$.
Corollary 4.3 In the setting of Proposition 4.2, we have
Proof. This follows from the fact that ![]() $KJ \cap {{}^{g}(KJ)}=(K \cap {{}^{g}K})(J \cap {{}^{g}J})$ [Reference YuYu01, Lemma 13.7] as discussed in [Reference YuYu01] in the lines immediately following Theorem 14.2.
$KJ \cap {{}^{g}(KJ)}=(K \cap {{}^{g}K})(J \cap {{}^{g}J})$ [Reference YuYu01, Lemma 13.7] as discussed in [Reference YuYu01] in the lines immediately following Theorem 14.2.
Acknowledgements
The author thanks Loren Spice for pointing out that Yu's proof relies on a misprinted (and therefore false) statement in a paper by Gérardin, Tasho Kaletha for his encouragement to write up the proof that Yu's construction yields irreducible supercuspidal representations, and the referees for helpful feedback on the paper.
The author also thanks Jeffrey Adler, Stephen DeBacker, Tasho Kaletha, Loren Spice and Cheng-Chiang Tsai for helpful discussions related to the topic of this paper during their SQuaRE meetings at the American Institute of Mathematics, as well as the American Institute of Mathematics for supporting these meetings and providing a wonderful research environment.