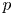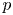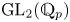1. Introduction
1.1 Statement of results
In this paper, we study the étale cohomology of Hilbert modular varieties, building on the methods introduced for unitary Shimura varieties in [Reference Caraiani and ScholzeCS17, Reference Caraiani and ScholzeCS19].
Let us first discuss a general vanishing conjecture for the cohomology of locally symmetric spaces. Let ![]() $G/\mathbb {Q}$ be a connected reductive group and let
$G/\mathbb {Q}$ be a connected reductive group and let ![]() $X$ be the symmetric space for
$X$ be the symmetric space for ![]() $G({\mathbb {R}})$, in the sense of [Reference Borel and SerreBS73]. For a neat compact open subgroup
$G({\mathbb {R}})$, in the sense of [Reference Borel and SerreBS73]. For a neat compact open subgroup ![]() $K\subset G({\mathbb {A}}_f)$, we can consider the associated locally symmetric space
$K\subset G({\mathbb {A}}_f)$, we can consider the associated locally symmetric space ![]() $X_K(G)$. Also define the invariantsFootnote 1
$X_K(G)$. Also define the invariantsFootnote 1
A folklore conjecture predicts that the cohomology of the locally symmetric space ![]() $X_K(G)$ with
$X_K(G)$ with ![]() ${\mathbb {Z}}_{\ell }$-coefficients vanishes, after imposing an appropriate non-degeneracy condition, outside the range of degrees
${\mathbb {Z}}_{\ell }$-coefficients vanishes, after imposing an appropriate non-degeneracy condition, outside the range of degrees ![]() $[q_0, q_0 +l_0]$ (which is symmetric about
$[q_0, q_0 +l_0]$ (which is symmetric about ![]() $\frac {1}{2}\dim _{{\mathbb {R}}} X$). See, for example, the discussion around [Reference EmertonEme14, Conjecture 3.3] and also [Reference Calegari and GeraghtyCG18, Conjecture B]. As these references explain, this conjecture has important consequences for automorphy lifting theorems and the
$\frac {1}{2}\dim _{{\mathbb {R}}} X$). See, for example, the discussion around [Reference EmertonEme14, Conjecture 3.3] and also [Reference Calegari and GeraghtyCG18, Conjecture B]. As these references explain, this conjecture has important consequences for automorphy lifting theorems and the ![]() $p$-adic Langlands programme.
$p$-adic Langlands programme.
When ![]() $F$ is a totally real field and
$F$ is a totally real field and ![]() $G:=\mathrm {Res}_{F/{\mathbb {Q}}}\operatorname {GL}_2$, the corresponding locally symmetric spaces are closely related to Hilbert modular varieties, which are (non-compact) Shimura varieties of abelian type. When working with Shimura varieties rather than with locally symmetric spaces, it is more natural to consider
$G:=\mathrm {Res}_{F/{\mathbb {Q}}}\operatorname {GL}_2$, the corresponding locally symmetric spaces are closely related to Hilbert modular varieties, which are (non-compact) Shimura varieties of abelian type. When working with Shimura varieties rather than with locally symmetric spaces, it is more natural to consider ![]() $l_0(G^{\mathrm {ad}})$, which is equal to
$l_0(G^{\mathrm {ad}})$, which is equal to ![]() $0$ by the second axiom in the definition of a Shimura datum. In this case, the conjecture mentioned above predicts that the non-degenerate part of the cohomology is concentrated in the middle degree.
$0$ by the second axiom in the definition of a Shimura datum. In this case, the conjecture mentioned above predicts that the non-degenerate part of the cohomology is concentrated in the middle degree.
To make this more precise, let ![]() $K\subset G({\mathbb {A}}_{f})$ be a neat compact open subgroup and let
$K\subset G({\mathbb {A}}_{f})$ be a neat compact open subgroup and let ![]() $Sh_K(G)$ be the corresponding Hilbert modular variety. This is a smooth, quasi-projective scheme over
$Sh_K(G)$ be the corresponding Hilbert modular variety. This is a smooth, quasi-projective scheme over ![]() ${\mathbb {Q}}$, of dimension
${\mathbb {Q}}$, of dimension ![]() $g:=[F:{\mathbb {Q}}]$. Its complex points can be described as
$g:=[F:{\mathbb {Q}}]$. Its complex points can be described as
Let ![]() $\ell$ be a prime number; we have a spherical Hecke algebra
$\ell$ be a prime number; we have a spherical Hecke algebra ![]() $\mathbb {T}$ defined in § 2.1.2, generated by the standard Hecke operators
$\mathbb {T}$ defined in § 2.1.2, generated by the standard Hecke operators ![]() $T_v, S_v^{\pm 1}$ for
$T_v, S_v^{\pm 1}$ for ![]() $v$ not belonging to a suitable finite set
$v$ not belonging to a suitable finite set ![]() $S$ of places of
$S$ of places of ![]() $F$. The algebra
$F$. The algebra ![]() $\mathbb {T}$ acts on the étale cohomology groups
$\mathbb {T}$ acts on the étale cohomology groups ![]() $H^i_{(c)}(Sh_K(G), {\mathbb {F}}_{\ell })$.Footnote 2 Take a maximal ideal
$H^i_{(c)}(Sh_K(G), {\mathbb {F}}_{\ell })$.Footnote 2 Take a maximal ideal ![]() $\mathfrak {m} \subset \mathbb {T}$ in the support of
$\mathfrak {m} \subset \mathbb {T}$ in the support of ![]() $H^i_{(c)}(Sh_K(G), {\mathbb {F}}_{\ell })$. It follows from Scholze's work, at least when
$H^i_{(c)}(Sh_K(G), {\mathbb {F}}_{\ell })$. It follows from Scholze's work, at least when ![]() $\ell >2$, cf. Theorem 2.2.1, that there exists a unique continuous, semisimple Galois representation
$\ell >2$, cf. Theorem 2.2.1, that there exists a unique continuous, semisimple Galois representation
where ![]() $\Gamma _F$ denotes the absolute Galois group of
$\Gamma _F$ denotes the absolute Galois group of ![]() $F$, which is characterised as follows: for every
$F$, which is characterised as follows: for every ![]() $v \not \in S$,
$v \not \in S$, ![]() $\bar {\rho }_\mathfrak {m}$ is unramified at
$\bar {\rho }_\mathfrak {m}$ is unramified at ![]() $v$ and the characteristic polynomial of
$v$ and the characteristic polynomial of ![]() $\bar {\rho }_{\mathfrak {m}}(\mathrm {Frob}_v)$ is equal to
$\bar {\rho }_{\mathfrak {m}}(\mathrm {Frob}_v)$ is equal to ![]() $X^2-T_vX+S_vN(v) \pmod {\mathfrak {m}}$.
$X^2-T_vX+S_vN(v) \pmod {\mathfrak {m}}$.
We say that ![]() $\mathfrak {m}$ is non-Eisenstein if
$\mathfrak {m}$ is non-Eisenstein if ![]() $\bar {\rho }_{\mathfrak {m}}$ is absolutely irreducible. The most optimistic vanishing conjecture predicts that the localisation
$\bar {\rho }_{\mathfrak {m}}$ is absolutely irreducible. The most optimistic vanishing conjecture predicts that the localisation ![]() $H^i_{(c)}(Sh_K(G), {\mathbb {F}}_{\ell })_{\mathfrak {m}}$ should be concentrated in the middle degree
$H^i_{(c)}(Sh_K(G), {\mathbb {F}}_{\ell })_{\mathfrak {m}}$ should be concentrated in the middle degree ![]() $i=g$ if
$i=g$ if ![]() $\mathfrak {m}$ is non-Eisenstein. We make significant progress towards this.
$\mathfrak {m}$ is non-Eisenstein. We make significant progress towards this.
Theorem A (see Theorem 7.1.1)
Let ![]() $\ell >2$ be a prime and let
$\ell >2$ be a prime and let ![]() $\mathfrak {m} \subset \mathbb {T}$ be a maximal ideal in the support of
$\mathfrak {m} \subset \mathbb {T}$ be a maximal ideal in the support of ![]() $H^i_{\rm c}(Sh_K(G), {\mathbb {F}}_{\ell })$ or
$H^i_{\rm c}(Sh_K(G), {\mathbb {F}}_{\ell })$ or ![]() $H^i(Sh_K(G), {\mathbb {F}}_{\ell })$. Assume that the image of
$H^i(Sh_K(G), {\mathbb {F}}_{\ell })$. Assume that the image of ![]() $\bar {\rho }_{\mathfrak {m}}$ is not solvable. Then
$\bar {\rho }_{\mathfrak {m}}$ is not solvable. Then ![]() $H^i(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}=H^i_c(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}$ is non-zero only for
$H^i(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}=H^i_c(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}$ is non-zero only for ![]() $i=g$.
$i=g$.
Remark 1.1.1 (i) By Dickson's theorem, cf. [Reference Darmon, Diamond and TaylorDDT97, Theorem 2.47 (b)], the projective image of ![]() $\bar {\rho }_{\mathfrak {m}}$ is either conjugate to a subgroup of the upper triangular matrices, or to
$\bar {\rho }_{\mathfrak {m}}$ is either conjugate to a subgroup of the upper triangular matrices, or to ![]() $\operatorname {PGL}_2({\mathbb {F}}_{\ell ^k})$ or
$\operatorname {PGL}_2({\mathbb {F}}_{\ell ^k})$ or ![]() $\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$, for some
$\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$, for some ![]() $k\geq 1$, or it is isomorphic to one of
$k\geq 1$, or it is isomorphic to one of ![]() $D_{2n}$, for some
$D_{2n}$, for some ![]() $n\in {\mathbb {Z}}_{> 1}$ prime to
$n\in {\mathbb {Z}}_{> 1}$ prime to ![]() $\ell$,
$\ell$, ![]() $A_4$,
$A_4$, ![]() $S_4$, or
$S_4$, or ![]() $A_5$. The image of
$A_5$. The image of ![]() $\bar {\rho }_\mathfrak {m}$ is not solvable if and only if the following condition is satisfied:
$\bar {\rho }_\mathfrak {m}$ is not solvable if and only if the following condition is satisfied:
(a) if
 $\ell = 3$, the projective image of
$\ell = 3$, the projective image of  $\bar {\rho }_{\mathfrak {m}}$ is isomorphic to
$\bar {\rho }_{\mathfrak {m}}$ is isomorphic to  $A_5$ or contains a conjugate of
$A_5$ or contains a conjugate of  $\operatorname {PSL}_2({\mathbb {F}}_9)$;
$\operatorname {PSL}_2({\mathbb {F}}_9)$;(b) if
 $\ell >3$, the projective image of
$\ell >3$, the projective image of  $\bar {\rho }_{\mathfrak {m}}$ is isomorphic to
$\bar {\rho }_{\mathfrak {m}}$ is isomorphic to  $A_5$ or contains a conjugate of
$A_5$ or contains a conjugate of  $\operatorname {PSL}_2({\mathbb {F}}_{\ell })$.
$\operatorname {PSL}_2({\mathbb {F}}_{\ell })$.
(ii) If ![]() $\mathfrak {m}$ is non-Eisenstein, then
$\mathfrak {m}$ is non-Eisenstein, then ![]() $H^i(Sh_K(G), {\mathbb {C}})_\mathfrak {m}$ is concentrated in the middle degree. This follows from the explicit description of the cohomology with complex coefficients of Hilbert modular varieties (see [Reference FreitagFre13, Chapter III]).
$H^i(Sh_K(G), {\mathbb {C}})_\mathfrak {m}$ is concentrated in the middle degree. This follows from the explicit description of the cohomology with complex coefficients of Hilbert modular varieties (see [Reference FreitagFre13, Chapter III]).
(iii) Previously, Dimitrov had obtained a vanishing theorem for the cohomology of Hilbert modular varieties with torsion coefficients in [Reference DimitrovDim09, Theorem 2.3] (see also [Reference DimitrovDim05]), under stronger assumptions. More precisely, Dimitrov proves a theorem for cohomology with coefficients in certain local systems on ![]() $Sh_K(G)$. In addition to a large image assumption on
$Sh_K(G)$. In addition to a large image assumption on ![]() $\bar {\rho }_{\mathfrak {m}}$, he also requires that the level is prime to
$\bar {\rho }_{\mathfrak {m}}$, he also requires that the level is prime to ![]() $\ell$ and that
$\ell$ and that ![]() $\ell$ is large compared to the weight giving rise to the local system. Since we make no assumption on the level at
$\ell$ is large compared to the weight giving rise to the local system. Since we make no assumption on the level at ![]() $\ell$, a standard argument using the Hochschild–Serre spectral sequence allows us to upgrade Theorem A to also apply to cohomology with twisted coefficients.
$\ell$, a standard argument using the Hochschild–Serre spectral sequence allows us to upgrade Theorem A to also apply to cohomology with twisted coefficients.
Let ![]() $p\not = \ell$ be a prime which splits completely in
$p\not = \ell$ be a prime which splits completely in ![]() $F$ and such that
$F$ and such that ![]() $\bar {\rho }_{\mathfrak {m}}$ is unramified at every place of
$\bar {\rho }_{\mathfrak {m}}$ is unramified at every place of ![]() $F$ above
$F$ above ![]() $p$. If
$p$. If ![]() $v$ is such a place, we say that
$v$ is such a place, we say that ![]() $\bar {\rho }_{\mathfrak {m}}$ is generic at
$\bar {\rho }_{\mathfrak {m}}$ is generic at ![]() $v$ if the eigenvalues of
$v$ if the eigenvalues of ![]() $\bar {\rho }_{\mathfrak {m}}(\mathrm {Frob}_v)$ have ratio different from
$\bar {\rho }_{\mathfrak {m}}(\mathrm {Frob}_v)$ have ratio different from ![]() $p^{\pm 1}$. If the projective image of
$p^{\pm 1}$. If the projective image of ![]() $\bar {\rho }_{\mathfrak {m}}$ satisfies the condition in Remark 1.1.1
$\bar {\rho }_{\mathfrak {m}}$ satisfies the condition in Remark 1.1.1![]() $(1)$, then the Chebotarev density theorem implies, cf. Lemma 7.1.8, that there exists a prime
$(1)$, then the Chebotarev density theorem implies, cf. Lemma 7.1.8, that there exists a prime ![]() $p$ as above such that
$p$ as above such that ![]() $\bar {\rho }_{\mathfrak {m}}$ is generic at every
$\bar {\rho }_{\mathfrak {m}}$ is generic at every ![]() $v\mid p$.Footnote 3 As in [Reference Caraiani and ScholzeCS17, Reference Caraiani and ScholzeCS19], Theorem A relies on the study of the cohomology of (perfectoid) Igusa varieties and on the geometry of the Hodge–Tate period map at the auxiliary prime
$v\mid p$.Footnote 3 As in [Reference Caraiani and ScholzeCS17, Reference Caraiani and ScholzeCS19], Theorem A relies on the study of the cohomology of (perfectoid) Igusa varieties and on the geometry of the Hodge–Tate period map at the auxiliary prime ![]() $p$.
$p$.
The key new idea in our situation is to establish a geometric Jacquet–Langlands transfer comparing the cohomology of Igusa varieties attached to different quaternionic Shimura varieties. This replaces the direct computation of the cohomology of Igusa varieties via the trace formula carried out in [Reference Caraiani and ScholzeCS17]. We also exploit the relation between Igusa varieties and fibres of the Hodge–Tate period map for compact quaternionic Shimura varieties. We explain this idea more in § 1.2.
Furthermore, Theorem A is obtained as a special case of the following more precise result, that probes the structure of the cohomology beyond the generic case. Given a prime ![]() $p$ which splits completely in
$p$ which splits completely in ![]() $F$ and such that
$F$ and such that ![]() $\bar {\rho }_{\mathfrak {m}}$ is unramified at every place of
$\bar {\rho }_{\mathfrak {m}}$ is unramified at every place of ![]() $F$ above
$F$ above ![]() $p$, denote by
$p$, denote by ![]() $\delta _p(\mathfrak {m})\in [0,g]$ the number of places above
$\delta _p(\mathfrak {m})\in [0,g]$ the number of places above ![]() $p$ where
$p$ where ![]() $\bar {\rho }_{\mathfrak {m}}$ is not generic.
$\bar {\rho }_{\mathfrak {m}}$ is not generic.
Theorem B see Theorem 7.1.6
Let ![]() $\ell >2$ be a prime. Let
$\ell >2$ be a prime. Let ![]() $p\not = \ell$ be an odd prime which splits completely in
$p\not = \ell$ be an odd prime which splits completely in ![]() $F$ and such that
$F$ and such that ![]() $K = K^pK_p$ with
$K = K^pK_p$ with ![]() $K_p$ hyperspecial. Let
$K_p$ hyperspecial. Let ![]() $\mathfrak {m}\subset \mathbb {T}$ be a non-Eisenstein maximal ideal. Then
$\mathfrak {m}\subset \mathbb {T}$ be a non-Eisenstein maximal ideal. Then
vanishes outside ![]() $i\in [g- \delta _p(\mathfrak {m}), g+\delta _p(\mathfrak {m})]$.
$i\in [g- \delta _p(\mathfrak {m}), g+\delta _p(\mathfrak {m})]$.
Theorem B is inspired by Arthur's conjectures [Reference ArthurArt96], describing the interplay between the Hecke action and the Lefschetz structure on the cohomology of Shimura varieties with ![]() ${\mathbb {C}}$-coefficients. Our result is consistent with the existence of such a structure on the cohomology with
${\mathbb {C}}$-coefficients. Our result is consistent with the existence of such a structure on the cohomology with ![]() ${\mathbb {F}}_{\ell }$-coefficients as well.
${\mathbb {F}}_{\ell }$-coefficients as well.
In the case of Harris–Taylor unitary Shimura varieties, Boyer established the analogue of Theorem B in [Reference BoyerBoy19] (see also the discussion around [Reference KoshikawaKos20, Theorem 1.3]). Our argument is partly inspired by Boyer's, but it is different: we rely on the ingredients mentioned above, as well as on the affineness and smoothness of Newton strata. This allows us to apply Artin vanishing at a crucial step in the proof, followed by Poincaré duality.
Remark 1.1.2 (i) If ![]() $\delta _p(\mathfrak {m}) = 0$, we expect that
$\delta _p(\mathfrak {m}) = 0$, we expect that ![]() $H^i_c(Sh_K(G), {\mathbb {F}}_{\ell })_{\mathfrak {m}} = 0$ for
$H^i_c(Sh_K(G), {\mathbb {F}}_{\ell })_{\mathfrak {m}} = 0$ for ![]() $i>g$ (and, dually,
$i>g$ (and, dually, ![]() $H^i(Sh_K(G), {\mathbb {F}}_{\ell })_{\mathfrak {m}}=0$ for
$H^i(Sh_K(G), {\mathbb {F}}_{\ell })_{\mathfrak {m}}=0$ for ![]() $i< g$) even without the non-Eisenstein assumption on
$i< g$) even without the non-Eisenstein assumption on ![]() $\mathfrak {m}$. This is the analogue of [Reference Caraiani and ScholzeCS19, Theorem 1.1] in our context. To establish this, one may need the semi-perversity result [Reference Caraiani and ScholzeCS19, Theorem 4.6.1] in our setting, which relies on a detailed understanding of toroidal compactifications of Igusa varieties.
$\mathfrak {m}$. This is the analogue of [Reference Caraiani and ScholzeCS19, Theorem 1.1] in our context. To establish this, one may need the semi-perversity result [Reference Caraiani and ScholzeCS19, Theorem 4.6.1] in our setting, which relies on a detailed understanding of toroidal compactifications of Igusa varieties.
(ii) Using the same method based on geometric Jacquet–Langlands, we also obtain analogues of Theorems A and B for compact quaternionic Shimura varieties, without the non-Eisenstein assumption: see Theorem 7.5.2.
As a quick application of Theorem A, we show that the ![]() $p$-adic local Langlands correspondence occurs in the completed homology of Hilbert modular varieties. More precisely, fix a prime
$p$-adic local Langlands correspondence occurs in the completed homology of Hilbert modular varieties. More precisely, fix a prime ![]() $p>3$ which splits completely in
$p>3$ which splits completely in ![]() $F$; in the following discussion, the prime
$F$; in the following discussion, the prime ![]() $p$ will play the role of the prime denoted by
$p$ will play the role of the prime denoted by ![]() $\ell$ above. Fix a large enough finite extension
$\ell$ above. Fix a large enough finite extension ![]() $L/{\mathbb {Q}}_p$ with ring of integers
$L/{\mathbb {Q}}_p$ with ring of integers ![]() ${\mathcal {O}}$. Under suitable assumptions (e.g. hypothesis
${\mathcal {O}}$. Under suitable assumptions (e.g. hypothesis ![]() $(3)$ in Theorem C) we can attach to the restriction of
$(3)$ in Theorem C) we can attach to the restriction of ![]() $\bar {\rho }_{\mathfrak {m}}$ to places
$\bar {\rho }_{\mathfrak {m}}$ to places ![]() $v\mid p$ a universal local deformation ring
$v\mid p$ a universal local deformation ring ![]() $R_p^{\mathrm {loc}} :=\hat {\otimes }_{v\mid p, {\mathcal {O}}} R_v^{\mathrm {def}}$ and an
$R_p^{\mathrm {loc}} :=\hat {\otimes }_{v\mid p, {\mathcal {O}}} R_v^{\mathrm {def}}$ and an ![]() $R_p^{\mathrm {loc}}$-module
$R_p^{\mathrm {loc}}$-module ![]() $P: =\hat {\otimes }_{v \mid p, {\mathcal {O}}}P_v$. The latter represents a large part of the
$P: =\hat {\otimes }_{v \mid p, {\mathcal {O}}}P_v$. The latter represents a large part of the ![]() $p$-adic local Langlands correspondence in this setting, cf. [Reference PaškūnasPaš13]. (See § 8 for more details on the notation.)
$p$-adic local Langlands correspondence in this setting, cf. [Reference PaškūnasPaš13]. (See § 8 for more details on the notation.)
Theorem C Let ![]() $p>3$ be a prime which splits completely in
$p>3$ be a prime which splits completely in ![]() $F$. Assume that the following assertions hold true.
$F$. Assume that the following assertions hold true.
(i) The projective image of the Galois representation
 $\bar {\rho }_\mathfrak {m}$ attached to
$\bar {\rho }_\mathfrak {m}$ attached to  $\mathfrak {m}$ contains a conjugate of
$\mathfrak {m}$ contains a conjugate of  $\operatorname {PSL}_2({\mathbb {F}}_p)$ or is isomorphic to
$\operatorname {PSL}_2({\mathbb {F}}_p)$ or is isomorphic to  $A_5$.
$A_5$.(ii) If
 $\bar {\rho }_\mathfrak {m}$ is ramified at some place
$\bar {\rho }_\mathfrak {m}$ is ramified at some place  $v$ not lying above
$v$ not lying above  $p$, then
$p$, then  $v$ is not a vexing prime.
$v$ is not a vexing prime.(iii) For each place
 $v \mid p$, the restriction of
$v \mid p$, the restriction of  $\bar {\rho }_\mathfrak {m}$ to
$\bar {\rho }_\mathfrak {m}$ to  $\Gamma _{F_v}$ is absolutely irreducible.
$\Gamma _{F_v}$ is absolutely irreducible.
Then the completed homology ![]() $\tilde {H}_g(\bar {K}_1(N(\bar {\rho }_\mathfrak {m}))^p, {\mathcal {O}})_\mathfrak {m}$, as a module over
$\tilde {H}_g(\bar {K}_1(N(\bar {\rho }_\mathfrak {m}))^p, {\mathcal {O}})_\mathfrak {m}$, as a module over ![]() $\mathbb {T}(\bar {K}_1(N(\bar {\rho }_\mathfrak {m}))^p)_\mathfrak {m}[\bar {G}({\mathbb {Q}}_p)]$, can be described as
$\mathbb {T}(\bar {K}_1(N(\bar {\rho }_\mathfrak {m}))^p)_\mathfrak {m}[\bar {G}({\mathbb {Q}}_p)]$, can be described as
for some ![]() $m \geq 1$.
$m \geq 1$.
Theorem C points towards an extension of Emerton's landmark local–global compatibility theorem for modular curves [Reference EmertonEme11] to the case of Hilbert modular varieties. Here, we apply the axiomatic approach via patching developed in [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and Woo ShinCEG+18, Reference Gee and NewtonGN22] in order to obtain an unconditional ‘proof of concept’. We note that, for this application, it is crucial to know that completed homology is a projective object in an appropriate category of ![]() $\prod _{v\mid p}\operatorname {PGL}_2({\mathbb {Z}}_p)$-modules. This relies on knowing Theorem A with twisted coefficients coming from arbitrary Serre weights, something that is not available from the earlier results of [Reference DimitrovDim09]. In Remark 8.2.3, we also sketch how to obtain a version of compatibility with the
$\prod _{v\mid p}\operatorname {PGL}_2({\mathbb {Z}}_p)$-modules. This relies on knowing Theorem A with twisted coefficients coming from arbitrary Serre weights, something that is not available from the earlier results of [Reference DimitrovDim09]. In Remark 8.2.3, we also sketch how to obtain a version of compatibility with the ![]() $p$-adic local Langlands correspondence without any assumptions on the tame level.
$p$-adic local Langlands correspondence without any assumptions on the tame level.
Theorem A should have numerous other applications to the ![]() $p$-adic Langlands programme for
$p$-adic Langlands programme for ![]() $\operatorname {GL}_2$ over a totally real field
$\operatorname {GL}_2$ over a totally real field ![]() $F$, including in the case when
$F$, including in the case when ![]() $p$ ramifies in
$p$ ramifies in ![]() $F$. Once cohomology is concentrated in one degree, one can combine the Taylor–Wiles–Kisin patching method with purely local techniques, as in [Reference Emerton, Gee and SavittEGS15, Reference Breuil, Hellmann and SchraenBHS19] (for example). Traditionally, these methods have been used for Shimura sets attached to definite unitary groups or for Shimura curves. The advantage of Hilbert modular varieties is that their (co)homology may be more suitable to studying low-weight forms, such as Hilbert modular forms of parallel weight
$F$. Once cohomology is concentrated in one degree, one can combine the Taylor–Wiles–Kisin patching method with purely local techniques, as in [Reference Emerton, Gee and SavittEGS15, Reference Breuil, Hellmann and SchraenBHS19] (for example). Traditionally, these methods have been used for Shimura sets attached to definite unitary groups or for Shimura curves. The advantage of Hilbert modular varieties is that their (co)homology may be more suitable to studying low-weight forms, such as Hilbert modular forms of parallel weight ![]() $1$.
$1$.
1.2 The method of proof
As we mentioned above, the proof of Theorems A and B uses the geometry of the Hodge–Tate period morphism at an auxiliary prime ![]() $p \neq \ell$ for quaternionic Shimura varieties, particularly the relation between fibres of this morphism and perfectoid Igusa varieties. The key new idea in the proof, inspired by the work of Tian and Xiao on the Goren–Oort stratification on quaternionic Shimura varieties [Reference Tian and XiaoTX16], is to establish instances of geometric Jacquet–Langlands functoriality for Igusa varieties. This idea, which was not present in either of [Reference Caraiani and ScholzeCS17, Reference Caraiani and ScholzeCS19], allows us to handle the cohomology of Igusa varieties. We exploit this (and further ingredients mentioned below) to transfer systems of Hecke eigenvalues in the cohomology of non-ordinary strata from Hilbert modular varieties to (perfectoid) compact quaternionic Shimura varieties. Using this we show that, in the setting of Theorem A, cohomology localised at
$p \neq \ell$ for quaternionic Shimura varieties, particularly the relation between fibres of this morphism and perfectoid Igusa varieties. The key new idea in the proof, inspired by the work of Tian and Xiao on the Goren–Oort stratification on quaternionic Shimura varieties [Reference Tian and XiaoTX16], is to establish instances of geometric Jacquet–Langlands functoriality for Igusa varieties. This idea, which was not present in either of [Reference Caraiani and ScholzeCS17, Reference Caraiani and ScholzeCS19], allows us to handle the cohomology of Igusa varieties. We exploit this (and further ingredients mentioned below) to transfer systems of Hecke eigenvalues in the cohomology of non-ordinary strata from Hilbert modular varieties to (perfectoid) compact quaternionic Shimura varieties. Using this we show that, in the setting of Theorem A, cohomology localised at ![]() $\mathfrak {m}$ must be supported on the ordinary locus; it is then relatively easy to prove that the cohomology is concentrated in one degree.
$\mathfrak {m}$ must be supported on the ordinary locus; it is then relatively easy to prove that the cohomology is concentrated in one degree.
We illustrate a version of the key new idea mentioned above first using the toy model of the modular curve, the Shimura variety for ![]() $G:=\operatorname {GL}_2/{\mathbb {Q}}$. Let
$G:=\operatorname {GL}_2/{\mathbb {Q}}$. Let ![]() $K^p\subset G({\mathbb {A}}_f)$ be a sufficiently small compact open subgroup. By [Reference ScholzeSch15, § 3], we have the Hodge–Tate period morphism
$K^p\subset G({\mathbb {A}}_f)$ be a sufficiently small compact open subgroup. By [Reference ScholzeSch15, § 3], we have the Hodge–Tate period morphism ![]() $\pi _{\mathrm {HT}}: \mathcal {S}h_{K^p}(G) \to \mathbb {P}^{1,\mathrm {ad}}$ and the Hodge–Tate period domain admits the Newton stratification
$\pi _{\mathrm {HT}}: \mathcal {S}h_{K^p}(G) \to \mathbb {P}^{1,\mathrm {ad}}$ and the Hodge–Tate period domain admits the Newton stratification
Here, ![]() $\mathbb {P}^1({\mathbb {Q}}_p)$ is the closed stratum corresponding to the ordinary locus and
$\mathbb {P}^1({\mathbb {Q}}_p)$ is the closed stratum corresponding to the ordinary locus and ![]() $\Omega ^2$, the Drinfeld upper half plane, is the open stratum corresponding to the supersingular locus. For every geometric point
$\Omega ^2$, the Drinfeld upper half plane, is the open stratum corresponding to the supersingular locus. For every geometric point ![]() $x: \mathrm {Spa} (C, \mathcal {O}_C)\to \Omega ^2$, the fibre
$x: \mathrm {Spa} (C, \mathcal {O}_C)\to \Omega ^2$, the fibre ![]() $\pi _{\mathrm {HT}}^{-1}(x)$ is a perfectoid version of a supersingular Igusa variety. In view of [Reference HoweHow22, Corollary 3.7.4] (which originates in an observation of Serre [Reference SerreSer96]), this can, in turn, be identified with the double coset
$\pi _{\mathrm {HT}}^{-1}(x)$ is a perfectoid version of a supersingular Igusa variety. In view of [Reference HoweHow22, Corollary 3.7.4] (which originates in an observation of Serre [Reference SerreSer96]), this can, in turn, be identified with the double coset ![]() $D^\times \backslash D^\times ({\mathbb {A}}_f)/K^p$, where
$D^\times \backslash D^\times ({\mathbb {A}}_f)/K^p$, where ![]() $D/{\mathbb {Q}}$ is the quaternion algebra that is ramified precisely at
$D/{\mathbb {Q}}$ is the quaternion algebra that is ramified precisely at ![]() $p$ and
$p$ and ![]() $\infty$. If
$\infty$. If ![]() $\mathfrak {m}\subset \mathbb {T}$ is a non-Eisenstein maximal ideal such that
$\mathfrak {m}\subset \mathbb {T}$ is a non-Eisenstein maximal ideal such that ![]() $(R\pi _{\mathrm {HT}*}{\mathbb {F}}_{\ell })_{\mathfrak {m}}$ is supported on
$(R\pi _{\mathrm {HT}*}{\mathbb {F}}_{\ell })_{\mathfrak {m}}$ is supported on ![]() $\Omega ^2$, then
$\Omega ^2$, then ![]() $\mathfrak {m}$ is also in the support of the module
$\mathfrak {m}$ is also in the support of the module ![]() $H^0(D^\times \backslash D^\times ({\mathbb {A}}_f)/K^p, {\mathbb {Q}}_{\ell })$. This means that there exists a cuspidal automorphic representation of
$H^0(D^\times \backslash D^\times ({\mathbb {A}}_f)/K^p, {\mathbb {Q}}_{\ell })$. This means that there exists a cuspidal automorphic representation of ![]() $D^\times$ whose associated Galois representation is a characteristic
$D^\times$ whose associated Galois representation is a characteristic ![]() $0$ lift of
$0$ lift of ![]() $\bar {\rho }_{\mathfrak {m}}$.
$\bar {\rho }_{\mathfrak {m}}$.
However, if we choose ![]() $p$ such that
$p$ such that ![]() $\bar {\rho }_{\mathfrak {m}}|_{\Gamma _{{\mathbb {Q}}_p}}$ is generic, then any characteristic
$\bar {\rho }_{\mathfrak {m}}|_{\Gamma _{{\mathbb {Q}}_p}}$ is generic, then any characteristic ![]() $0$ lift corresponds, under the classical local Langlands correspondence, to a generic principal series representation of
$0$ lift corresponds, under the classical local Langlands correspondence, to a generic principal series representation of ![]() $\operatorname {GL}_2({\mathbb {Q}}_p)$. Such a representation cannot be the local component at
$\operatorname {GL}_2({\mathbb {Q}}_p)$. Such a representation cannot be the local component at ![]() $p$ of the global Jacquet–Langlands transfer of a cuspidal automorphic representation of
$p$ of the global Jacquet–Langlands transfer of a cuspidal automorphic representation of ![]() $D^\times$. Therefore, if
$D^\times$. Therefore, if ![]() $\bar {\rho }_{\mathfrak {m}}$ is generic at
$\bar {\rho }_{\mathfrak {m}}$ is generic at ![]() $p$, then the complex of sheaves
$p$, then the complex of sheaves ![]() $(R\pi _{\mathrm {HT}*}{\mathbb {F}}_{\ell })_{\mathfrak {m}}$ is supported only on the ordinary locus
$(R\pi _{\mathrm {HT}*}{\mathbb {F}}_{\ell })_{\mathfrak {m}}$ is supported only on the ordinary locus ![]() $\mathbb {P}^1({\mathbb {Q}}_p)$.
$\mathbb {P}^1({\mathbb {Q}}_p)$.
Morally, the Hilbert case for a totally real field ![]() $F$ of degree
$F$ of degree ![]() $g$ behaves like a product of
$g$ behaves like a product of ![]() $g$ copies of the modular curve case. In this setting, Tian and Xiao establish geometric instances of the Jacquet–Langlands correspondence in [Reference Tian and XiaoTX16]. Inspired by their result in the case when
$g$ copies of the modular curve case. In this setting, Tian and Xiao establish geometric instances of the Jacquet–Langlands correspondence in [Reference Tian and XiaoTX16]. Inspired by their result in the case when ![]() $p$ splits completely in
$p$ splits completely in ![]() $F$, we express the geometric Jacquet–Langlands relation as a Hecke-equivariant isomorphism between Igusa varieties attached to different Shimura varieties, cf. Theorem 4.2.4.Footnote 4 In Theorem 6.3.3, we obtain a clean geometric description of the
$F$, we express the geometric Jacquet–Langlands relation as a Hecke-equivariant isomorphism between Igusa varieties attached to different Shimura varieties, cf. Theorem 4.2.4.Footnote 4 In Theorem 6.3.3, we obtain a clean geometric description of the ![]() $\mu$-ordinary locus at infinite level on quaternionic Shimura varieties. This relies on (a perfectoid version of) the Mantovan product formula [Reference MantovanMan05], established in § 5, and on the induced structure of the corresponding Rapoport–Zink spaces, cf. [Reference HansenHan21, Reference Gaisin and ImaiGI16]. Theorems 4.2.4 and 6.3.3 allow us to transfer systems of mod
$\mu$-ordinary locus at infinite level on quaternionic Shimura varieties. This relies on (a perfectoid version of) the Mantovan product formula [Reference MantovanMan05], established in § 5, and on the induced structure of the corresponding Rapoport–Zink spaces, cf. [Reference HansenHan21, Reference Gaisin and ImaiGI16]. Theorems 4.2.4 and 6.3.3 allow us to transfer systems of mod ![]() $\ell$ Hecke eigenvalues between different Shimura varieties, which forms the basis for an inductive argument to prove Theorem B.
$\ell$ Hecke eigenvalues between different Shimura varieties, which forms the basis for an inductive argument to prove Theorem B.
Some technical difficulties we encounter are that Hilbert modular varieties are Shimura varieties of abelian type and that they are non-compact. However, the non-compactness does not impose serious difficulties. The only Newton stratum that intersects the boundary of Hilbert modular varieties is the ordinary one. This, together with the geometric Jacquet–Langlands relation on the level of interior Igusa varieties, makes the analysis of interior Newton strata similar to that in [Reference Caraiani and ScholzeCS17]. Because we are localising at a non-Eisenstein maximal ideal, we avoid employing partial minimal and toroidal compactifications of Igusa varieties or semi-perversity; in particular, our argument is independent of [Reference Caraiani and ScholzeCS19], and only relies on the (easier) study of the geometry of the Hodge–Tate period map in the compact setting of [Reference Caraiani and ScholzeCS17].
Recently, Koshikawa [Reference KoshikawaKos21] gave a new strategy for proving the vanishing theorems of [Reference Caraiani and ScholzeCS17, Reference Caraiani and ScholzeCS19], removing most technical assumptions from these results. This strategy relies on [Reference Fargues and ScholzeFS21] together with the geometry of the Hodge–Tate period morphism. The idea is to show that only the cohomology of the ordinary locus contributes to the generic part of the cohomology of Shimura varieties, by proving a local vanishing theorem for the generic part of the cohomology of Rapoport–Zink spaces. After reducing to the ordinary locus, [Reference KoshikawaKos21] uses the semi-perversity result mentioned above to control the range of degrees of cohomology. Koshikawa's arguments could be applied in the Hilbert setting as well, though this would require some version of our results in § 5 and semi-perversity. One advantage of our method is that it gives information about the complexes of sheaves ![]() $(R\pi _{\mathrm {HT}*}{\mathbb {F}}_{\ell })_{\mathfrak {m}}$ rather that just the cohomology groups
$(R\pi _{\mathrm {HT}*}{\mathbb {F}}_{\ell })_{\mathfrak {m}}$ rather that just the cohomology groups ![]() $H^*(Sh_K(G), {\mathbb {F}}_{\ell })_{\mathfrak {m}}$.
$H^*(Sh_K(G), {\mathbb {F}}_{\ell })_{\mathfrak {m}}$.
1.3 Notation
We use the following notation throughout the paper, unless otherwise stated.
The cardinality of a set ![]() $T$ is denoted by
$T$ is denoted by ![]() $|T|$.
$|T|$.
The symbol ![]() $\otimes$ stands for
$\otimes$ stands for ![]() $\otimes _{{\mathbb {Z}}}$. If
$\otimes _{{\mathbb {Z}}}$. If ![]() $A$ is an abelian group, we let
$A$ is an abelian group, we let ![]() $\hat {A} = A\otimes \hat {{\mathbb {Z}}}$ and
$\hat {A} = A\otimes \hat {{\mathbb {Z}}}$ and ![]() $\hat {A}^{(p)} = A\otimes \hat {{\mathbb {Z}}}^{(p)}$. We also set
$\hat {A}^{(p)} = A\otimes \hat {{\mathbb {Z}}}^{(p)}$. We also set ![]() ${\mathbb {A}}_f = \hat {{\mathbb {Q}}}$, the finite adeles of
${\mathbb {A}}_f = \hat {{\mathbb {Q}}}$, the finite adeles of ![]() ${\mathbb {Q}}$, and
${\mathbb {Q}}$, and ![]() ${\mathbb {A}}_f^{(p)} = \hat {{\mathbb {Q}}}^{(p)}$, the finite adeles of
${\mathbb {A}}_f^{(p)} = \hat {{\mathbb {Q}}}^{(p)}$, the finite adeles of ![]() ${\mathbb {Q}}$ away from
${\mathbb {Q}}$ away from ![]() $p$.
$p$.
If ![]() $L$ is a perfect field, we denote by
$L$ is a perfect field, we denote by ![]() $\bar {L}$ an algebraic closure of
$\bar {L}$ an algebraic closure of ![]() $L$, and by
$L$, and by ![]() $\Gamma _L$ the absolute Galois group
$\Gamma _L$ the absolute Galois group ![]() $\operatorname {Gal}(\bar {L}/L)$. Assume now that
$\operatorname {Gal}(\bar {L}/L)$. Assume now that ![]() $L$ is a number field. If
$L$ is a number field. If ![]() $v$ is a finite place of
$v$ is a finite place of ![]() $L$, we denote by
$L$, we denote by ![]() $L_v$ the completion of
$L_v$ the completion of ![]() $L$ at
$L$ at ![]() $v$, and by
$v$, and by ![]() ${\mathcal {O}}_v$ the ring of integers of
${\mathcal {O}}_v$ the ring of integers of ![]() $L_v$. We denote by
$L_v$. We denote by ![]() $\varpi _v$ a uniformiser of
$\varpi _v$ a uniformiser of ![]() ${\mathcal {O}}_v$, and by
${\mathcal {O}}_v$, and by ![]() $N(v)$ the cardinality of the residue field
$N(v)$ the cardinality of the residue field ![]() ${\mathcal {O}}_v/(\varpi _v)$. We denote by
${\mathcal {O}}_v/(\varpi _v)$. We denote by ![]() $\mathrm {Frob}_v$ the geometric Frobenius at
$\mathrm {Frob}_v$ the geometric Frobenius at ![]() $v$. We let
$v$. We let ![]() ${\mathbb {A}}_{L,f} = \hat {L}$, the ring of finite adeles of
${\mathbb {A}}_{L,f} = \hat {L}$, the ring of finite adeles of ![]() $L$.
$L$.
If ![]() $A\to B$ is a ring morphism and
$A\to B$ is a ring morphism and ![]() $S\to \operatorname {Spec} A$ is a scheme, we denote by
$S\to \operatorname {Spec} A$ is a scheme, we denote by ![]() $S_B$ the base change
$S_B$ the base change ![]() $S\times _{\operatorname {Spec} A} \operatorname {Spec} B$. We use a similar notation for adic spaces. If
$S\times _{\operatorname {Spec} A} \operatorname {Spec} B$. We use a similar notation for adic spaces. If ![]() $S$,
$S$, ![]() $T$ are two schemes over
$T$ are two schemes over ![]() ${\mathbb {Q}}$, we denote by
${\mathbb {Q}}$, we denote by ![]() $S\times T$ the fibre product
$S\times T$ the fibre product ![]() $S\times _{\operatorname {Spec} {\mathbb {Q}}} T$.
$S\times _{\operatorname {Spec} {\mathbb {Q}}} T$.
If ![]() $L$ is a field and
$L$ is a field and ![]() $S$ is a variety or adic space over
$S$ is a variety or adic space over ![]() $L$, the symbols
$L$, the symbols ![]() $H^i(S, {\mathbb {F}}_{\ell })$,
$H^i(S, {\mathbb {F}}_{\ell })$, ![]() $H^i(S, {\mathbb {Z}}_{\ell })$ and
$H^i(S, {\mathbb {Z}}_{\ell })$ and ![]() $H^i(S, {\mathbb {Q}}_{\ell })$ denote the étale (respectively,
$H^i(S, {\mathbb {Q}}_{\ell })$ denote the étale (respectively, ![]() $\ell$-adic étale) cohomology of
$\ell$-adic étale) cohomology of ![]() $S_{\bar {L}}$.
$S_{\bar {L}}$.
2. Hilbert modular varieties and Galois representations
In this section, we establish some preliminary results about Hilbert modular varieties. In particular, we construct Galois representations attached to systems of Hecke eigenvalues occurring in their cohomology with ![]() ${\mathbb {F}}_{\ell }$-coefficients, using [Reference ScholzeSch15].
${\mathbb {F}}_{\ell }$-coefficients, using [Reference ScholzeSch15].
2.1 Shimura varieties and locally symmetric spaces for  $\mathrm {Res}_{F/{\mathbb {Q}}}\mathrm {GL}_2$
$\mathrm {Res}_{F/{\mathbb {Q}}}\mathrm {GL}_2$
Fix a totally real number field ![]() $F$ of degree
$F$ of degree ![]() $[F: {\mathbb {Q}}]=: g$, and let
$[F: {\mathbb {Q}}]=: g$, and let ![]() ${\mathcal {O}}_F$ be the ring of integers of
${\mathcal {O}}_F$ be the ring of integers of ![]() $F$. Totally positive elements in
$F$. Totally positive elements in ![]() $F$ (respectively,
$F$ (respectively, ![]() ${\mathcal {O}}_F$) will be denoted by
${\mathcal {O}}_F$) will be denoted by ![]() $F^+$ (respectively,
$F^+$ (respectively, ![]() ${\mathcal {O}}_F^+$). Let
${\mathcal {O}}_F^+$). Let ![]() $\Sigma _{\infty }: =\{\tau _1, \ldots, \tau _g\}$ be the set of real embeddings of
$\Sigma _{\infty }: =\{\tau _1, \ldots, \tau _g\}$ be the set of real embeddings of ![]() $F$; let
$F$; let ![]() $G:=\mathrm {Res}_{F/{\mathbb {Q}}}\mathrm {GL}_2$ with centre
$G:=\mathrm {Res}_{F/{\mathbb {Q}}}\mathrm {GL}_2$ with centre ![]() $Z \simeq \mathrm {Res}_{F/{\mathbb {Q}}}\mathbb {G}_m$.
$Z \simeq \mathrm {Res}_{F/{\mathbb {Q}}}\mathbb {G}_m$.
2.1.1
Let ![]() $\mathbb {S}:=\mathrm {Res}_{{\mathbb {C}}/{\mathbb {R}}}\mathbb {G}_m$ be the Deligne torus, and let
$\mathbb {S}:=\mathrm {Res}_{{\mathbb {C}}/{\mathbb {R}}}\mathbb {G}_m$ be the Deligne torus, and let ![]() $h : \mathbb {S} \rightarrow G_{{\mathbb {R}}}\simeq \prod _{i=1}^g \operatorname {GL}_{2, {\mathbb {R}}}$ be the morphism which on
$h : \mathbb {S} \rightarrow G_{{\mathbb {R}}}\simeq \prod _{i=1}^g \operatorname {GL}_{2, {\mathbb {R}}}$ be the morphism which on ![]() ${\mathbb {R}}$-points is given by
${\mathbb {R}}$-points is given by
Let ![]() $K^\circ _\infty : =\prod _{i=1}^g\mathrm {SO}_2({\mathbb {R}})\subset G({\mathbb {R}})$ (a maximal compact connected subgroup). The
$K^\circ _\infty : =\prod _{i=1}^g\mathrm {SO}_2({\mathbb {R}})\subset G({\mathbb {R}})$ (a maximal compact connected subgroup). The ![]() $G({\mathbb {R}})$-conjugacy class of
$G({\mathbb {R}})$-conjugacy class of ![]() $h$, denoted by
$h$, denoted by ![]() $X$, is identified with
$X$, is identified with ![]() $G({\mathbb {R}})/Z({\mathbb {R}})K^\circ _\infty \simeq ({\mathbb {C}}\smallsetminus {\mathbb {R}})^g$, and the couple
$G({\mathbb {R}})/Z({\mathbb {R}})K^\circ _\infty \simeq ({\mathbb {C}}\smallsetminus {\mathbb {R}})^g$, and the couple ![]() $(G, X)$ is a Shimura datum with reflex field
$(G, X)$ is a Shimura datum with reflex field ![]() ${\mathbb {Q}}$. For every compact open subgroup
${\mathbb {Q}}$. For every compact open subgroup ![]() $K \subset G({\mathbb {A}}_f)$ the Shimura variety
$K \subset G({\mathbb {A}}_f)$ the Shimura variety ![]() $Sh_K(G)$ is a quasi-projective variety with a canonical model over the reflex field
$Sh_K(G)$ is a quasi-projective variety with a canonical model over the reflex field ![]() ${\mathbb {Q}}$, with complex analytic uniformisation
${\mathbb {Q}}$, with complex analytic uniformisation
The Shimura varieties ![]() $Sh_K(G)$ are called Hilbert modular varieties. If
$Sh_K(G)$ are called Hilbert modular varieties. If ![]() $K\subset G({\mathbb {A}}_f)$ is neat (which we will always assume in what follows), then
$K\subset G({\mathbb {A}}_f)$ is neat (which we will always assume in what follows), then ![]() $Sh_K(G)$ is smooth; moreover, if
$Sh_K(G)$ is smooth; moreover, if ![]() $K'\subset K$ is a normal compact open subgroup then the map
$K'\subset K$ is a normal compact open subgroup then the map ![]() $Sh_{K'}(G)\rightarrow Sh_{K}(G)$ is a finite étale Galois cover.
$Sh_{K'}(G)\rightarrow Sh_{K}(G)$ is a finite étale Galois cover.
We have a map
induced by the map sending ![]() $(x_\infty, x_f) \in G({\mathbb {R}}) \times G({\mathbb {A}}_f)$ to
$(x_\infty, x_f) \in G({\mathbb {R}}) \times G({\mathbb {A}}_f)$ to ![]() $(\mathrm {sgn} \det x_\infty, \det x_f)$. An element in
$(\mathrm {sgn} \det x_\infty, \det x_f)$. An element in ![]() $F^\times$ acts on
$F^\times$ acts on ![]() $\{\pm 1\}^g$ by multiplying by the sign of the image via each real embedding. Fibres of the map in (2.1.1.1) are connected components of the source.
$\{\pm 1\}^g$ by multiplying by the sign of the image via each real embedding. Fibres of the map in (2.1.1.1) are connected components of the source.
2.1.2 Hecke action
We have the Hecke algebra ![]() $\mathbb {T}_K(G) :={\mathbb {Z}}[K\backslash G({\mathbb {A}}_f)/K]$ of compactly supported,
$\mathbb {T}_K(G) :={\mathbb {Z}}[K\backslash G({\mathbb {A}}_f)/K]$ of compactly supported, ![]() $K$-bi-invariant functions on
$K$-bi-invariant functions on ![]() $G({\mathbb {A}}_f)$, with multiplication given by convolution. Every element of
$G({\mathbb {A}}_f)$, with multiplication given by convolution. Every element of ![]() $\mathbb {T}_K(G)$ gives rise to a correspondence on
$\mathbb {T}_K(G)$ gives rise to a correspondence on ![]() $Sh_K(G)$ as follows: given
$Sh_K(G)$ as follows: given ![]() $g \in G({\mathbb {A}}_f)$, let
$g \in G({\mathbb {A}}_f)$, let ![]() $K_g:=K \cap g K g^{-1}$; we have a correspondence
$K_g:=K \cap g K g^{-1}$; we have a correspondence ![]() $[KgK]$ on
$[KgK]$ on ![]() $Sh_K(G)$ given by the following diagram.
$Sh_K(G)$ given by the following diagram.

Here the vertical maps are the canonical projections and the upper horizontal map on complex points is induced by right multiplication by ![]() $g$ on
$g$ on ![]() $G({\mathbb {A}}_f)$. Therefore, we obtain an action of
$G({\mathbb {A}}_f)$. Therefore, we obtain an action of ![]() $\mathbb {T}_K(G)$ on the cohomology groups
$\mathbb {T}_K(G)$ on the cohomology groups ![]() $H^i(Sh_K(G), {\mathbb {F}}_\ell )$ as well as on the cohomology groups with compact support
$H^i(Sh_K(G), {\mathbb {F}}_\ell )$ as well as on the cohomology groups with compact support ![]() $H^i_{\rm c}(Sh_K(G), {\mathbb {F}}_\ell )$, where
$H^i_{\rm c}(Sh_K(G), {\mathbb {F}}_\ell )$, where ![]() $\ell$ is a prime number. In the rest of the paper, we will rather work with a smaller Hecke algebra, defined as follows: fix a finite set
$\ell$ is a prime number. In the rest of the paper, we will rather work with a smaller Hecke algebra, defined as follows: fix a finite set ![]() $S$ of places of
$S$ of places of ![]() $F$ containing all the infinite places, all the places
$F$ containing all the infinite places, all the places ![]() $v\mid \ell$, and all the finite places
$v\mid \ell$, and all the finite places ![]() $v$ such that
$v$ such that ![]() $K_v$ is not conjugate to
$K_v$ is not conjugate to ![]() $\operatorname {GL}_2({\mathcal {O}}_v)$, where
$\operatorname {GL}_2({\mathcal {O}}_v)$, where ![]() ${\mathcal {O}}_v$ is the ring of integers in the completion
${\mathcal {O}}_v$ is the ring of integers in the completion ![]() $F_v$ of
$F_v$ of ![]() $F$ at
$F$ at ![]() $v$. Let
$v$. Let
denote the abstract spherical Hecke algebra away from ![]() $S$. For every
$S$. For every ![]() $v\not \in S$, choose a uniformiser
$v\not \in S$, choose a uniformiser ![]() $\varpi _v$ of
$\varpi _v$ of ![]() ${\mathcal {O}}_v$. We denote by
${\mathcal {O}}_v$. We denote by ![]() $T_v$ the double coset
$T_v$ the double coset ![]() $\operatorname {GL}_2({\mathcal {O}}_v)(\begin{smallmatrix} \varpi _v & 0\\ 0 & 1 \end{smallmatrix})\operatorname {GL}_2({\mathcal {O}}_v)$ and by
$\operatorname {GL}_2({\mathcal {O}}_v)(\begin{smallmatrix} \varpi _v & 0\\ 0 & 1 \end{smallmatrix})\operatorname {GL}_2({\mathcal {O}}_v)$ and by ![]() $S_v$ the double coset
$S_v$ the double coset ![]() $\operatorname {GL}_2({\mathcal {O}}_v)(\begin{smallmatrix} \varpi _v & 0\\ 0 & \varpi _v \end{smallmatrix})\operatorname {GL}_2({\mathcal {O}}_v)$, seen as elements of
$\operatorname {GL}_2({\mathcal {O}}_v)(\begin{smallmatrix} \varpi _v & 0\\ 0 & \varpi _v \end{smallmatrix})\operatorname {GL}_2({\mathcal {O}}_v)$, seen as elements of ![]() $\mathbb {T}$. The algebra
$\mathbb {T}$. The algebra ![]() $\mathbb {T}$ is commutative and is generated by the operators
$\mathbb {T}$ is commutative and is generated by the operators ![]() $T_v$,
$T_v$, ![]() $S_v^{\pm 1}$ for
$S_v^{\pm 1}$ for ![]() $v \not \in S$. The inversion map on
$v \not \in S$. The inversion map on ![]() $G$ induces a map
$G$ induces a map ![]() $\iota : \mathbb {T}\rightarrow \mathbb {T}$; for a maximal ideal
$\iota : \mathbb {T}\rightarrow \mathbb {T}$; for a maximal ideal ![]() $\mathfrak {m} \subset \mathbb {T}$ we denote by
$\mathfrak {m} \subset \mathbb {T}$ we denote by ![]() $\mathfrak {m}^\vee$ its image via
$\mathfrak {m}^\vee$ its image via ![]() $\iota$.
$\iota$.
2.1.3 Locally symmetric spaces
We have the locally symmetric space ![]() $X_K(G)$ attached to
$X_K(G)$ attached to ![]() $G$ and
$G$ and ![]() $K$, defined as follows:
$K$, defined as follows:
Letting ![]() $Z_K:=Z({\mathbb {Q}})\cap K$, the quotient
$Z_K:=Z({\mathbb {Q}})\cap K$, the quotient ![]() $T_K:=Z({\mathbb {R}})/\{\pm 1\}^g{\mathbb {R}}_{>0}Z_K$ is a torus of dimension
$T_K:=Z({\mathbb {R}})/\{\pm 1\}^g{\mathbb {R}}_{>0}Z_K$ is a torus of dimension ![]() $g-1$ by Dirichlet's unit theorem, and the projection
$g-1$ by Dirichlet's unit theorem, and the projection ![]() $X_K(G) \rightarrow Sh_K(G)$ is a
$X_K(G) \rightarrow Sh_K(G)$ is a ![]() $T_K$-bundle (see [Reference GrafGra16, Lemma 3.1.2]). Let us define
$T_K$-bundle (see [Reference GrafGra16, Lemma 3.1.2]). Let us define ![]() $K_\infty :=\prod _{i=1}^g\mathrm {O}_2({\mathbb {R}})$, and let us consider the space
$K_\infty :=\prod _{i=1}^g\mathrm {O}_2({\mathbb {R}})$, and let us consider the space
In other words, we are quotienting by a maximal compact subgroup at infinity instead of its connected component of the identity. This is the space used in [Reference ScholzeSch15] (see the introduction there). The matrix ![]() $(\begin{smallmatrix}-1 & 0\\ 0 & 1\end{smallmatrix})$ normalises
$(\begin{smallmatrix}-1 & 0\\ 0 & 1\end{smallmatrix})$ normalises ![]() $\mathrm {SO}_2({\mathbb {R}})$; hence, we get a right action of
$\mathrm {SO}_2({\mathbb {R}})$; hence, we get a right action of ![]() $C:=({\mathbb {Z}}/2{\mathbb {Z}})^g$ on
$C:=({\mathbb {Z}}/2{\mathbb {Z}})^g$ on ![]() $X_K(G)$, and we have
$X_K(G)$, and we have ![]() $\bar {X}_K(G)=X_K(G)/C$. The recipe given above endows the (Betti) cohomology of
$\bar {X}_K(G)=X_K(G)/C$. The recipe given above endows the (Betti) cohomology of ![]() $X_K(G)$ and
$X_K(G)$ and ![]() $\bar {X}_K(G)$ with an action of
$\bar {X}_K(G)$ with an action of ![]() $\mathbb {T}$, which commutes with the action of
$\mathbb {T}$, which commutes with the action of ![]() $C$. Furthermore, if we make
$C$. Furthermore, if we make ![]() $C$ act on
$C$ act on ![]() $F^\times \backslash \{\pm 1\}^g \times {\mathbb {A}}_{F, f}^\times / \det (K)$ by switching signs at archimedean places, then the map in (2.1.1.1) is
$F^\times \backslash \{\pm 1\}^g \times {\mathbb {A}}_{F, f}^\times / \det (K)$ by switching signs at archimedean places, then the map in (2.1.1.1) is ![]() $C$-equivariant.
$C$-equivariant.
Let ![]() $\hat {C}$ be the set of characters of
$\hat {C}$ be the set of characters of ![]() $C$ with values in
$C$ with values in ![]() ${\mathbb {F}}_\ell ^\times$. The following lemma relates the cohomology of the spaces
${\mathbb {F}}_\ell ^\times$. The following lemma relates the cohomology of the spaces ![]() $Sh_K(G), X_K(G)$ and
$Sh_K(G), X_K(G)$ and ![]() $\bar {X}_K(G)$.
$\bar {X}_K(G)$.
Lemma 2.1.4 Let ![]() $\ell$ be an odd prime.
$\ell$ be an odd prime.
(i) Assume that
 $\det (K)=K \cap Z({\mathbb {A}}_f)$. Then for every
$\det (K)=K \cap Z({\mathbb {A}}_f)$. Then for every  $i \geq 0$ the pullback map
$i \geq 0$ the pullback map  $H^i(Sh_K(G), {\mathbb {F}}_\ell ) \rightarrow H^i(X_K(G), {\mathbb {F}}_\ell )$ is injective.
$H^i(Sh_K(G), {\mathbb {F}}_\ell ) \rightarrow H^i(X_K(G), {\mathbb {F}}_\ell )$ is injective.(ii) Assume that
 $\det (K) \cap F^\times$ only consists of totally positive elements. Then there is a Hecke-equivariant decomposition
and pullback induces an isomorphism
$\det (K) \cap F^\times$ only consists of totally positive elements. Then there is a Hecke-equivariant decomposition
and pullback induces an isomorphism \[ H^*(X_K(G), {\mathbb{F}}_\ell)=\bigoplus_{\chi \in \hat{C}}H^*(X_K(G), {\mathbb{F}}_\ell)^\chi \]
\[ H^*(X_K(G), {\mathbb{F}}_\ell)=\bigoplus_{\chi \in \hat{C}}H^*(X_K(G), {\mathbb{F}}_\ell)^\chi \]
 $H^*(\bar {X}_K(G), {\mathbb {F}}_\ell )\simeq H^*(X_K(G), {\mathbb {F}}_\ell )^{\mathrm {Id}}$.
$H^*(\bar {X}_K(G), {\mathbb {F}}_\ell )\simeq H^*(X_K(G), {\mathbb {F}}_\ell )^{\mathrm {Id}}$.
Proof. (i) Under the assumption that ![]() $\det (K)=K \cap Z({\mathbb {A}}_f)$, [Reference GrafGra16, Proposition 3.3.9] constructs cohomology classes in
$\det (K)=K \cap Z({\mathbb {A}}_f)$, [Reference GrafGra16, Proposition 3.3.9] constructs cohomology classes in ![]() $H^*(X_K(G), {\mathbb {F}}_\ell )$ whose restrictions to each fibre of the map
$H^*(X_K(G), {\mathbb {F}}_\ell )$ whose restrictions to each fibre of the map ![]() $X_K(G)\rightarrow Sh_K(G)$ give a basis of its cohomology; the statement hence follows from the Leray–Hirsch theorem.
$X_K(G)\rightarrow Sh_K(G)$ give a basis of its cohomology; the statement hence follows from the Leray–Hirsch theorem.
(ii) Since ![]() $\det (K) \cap F^\times$ consists of totally positive elements by assumption, an explicit computation shows that
$\det (K) \cap F^\times$ consists of totally positive elements by assumption, an explicit computation shows that ![]() $C$ acts freely on
$C$ acts freely on ![]() $F^\times \backslash \{\pm 1\}^g \times {\mathbb {A}}_{F, f}^\times / \det (K)$. In other words, the group
$F^\times \backslash \{\pm 1\}^g \times {\mathbb {A}}_{F, f}^\times / \det (K)$. In other words, the group ![]() $C$ acts on
$C$ acts on ![]() $X_K(G)$ freely permuting connected components. This implies that
$X_K(G)$ freely permuting connected components. This implies that ![]() $H^*(\bar {X}_K(G), {\mathbb {F}}_\ell )\simeq H^*(X_K(G), {\mathbb {F}}_\ell )^{\mathrm {Id}}$. The Hecke-equivariance of the direct sum decomposition in the statement follows from the fact that the action of
$H^*(\bar {X}_K(G), {\mathbb {F}}_\ell )\simeq H^*(X_K(G), {\mathbb {F}}_\ell )^{\mathrm {Id}}$. The Hecke-equivariance of the direct sum decomposition in the statement follows from the fact that the action of ![]() $C$ commutes with the Hecke action.
$C$ commutes with the Hecke action.
2.2 Construction of Galois representations
The aim of this section is to prove the following result.
Theorem 2.2.1 Let ![]() $\ell$ be an odd prime and
$\ell$ be an odd prime and ![]() $K\subset G({\mathbb {A}}_f)$ a neat compact open subgroup. Let
$K\subset G({\mathbb {A}}_f)$ a neat compact open subgroup. Let ![]() $\mathfrak {m} \subset \mathbb {T}$ be a maximal ideal in the support of
$\mathfrak {m} \subset \mathbb {T}$ be a maximal ideal in the support of ![]() $H^i(Sh_K(G), {\mathbb {F}}_{\ell })$ or
$H^i(Sh_K(G), {\mathbb {F}}_{\ell })$ or ![]() $H^i_{\rm c}(Sh_K(G), {\mathbb {F}}_{\ell })$ for some
$H^i_{\rm c}(Sh_K(G), {\mathbb {F}}_{\ell })$ for some ![]() $i \geq 0$. There is a unique continuous, semisimple, totally odd Galois representation
$i \geq 0$. There is a unique continuous, semisimple, totally odd Galois representation
such that, for all but finitely many places ![]() $v$ of
$v$ of ![]() $F$,
$F$, ![]() $\bar {\rho }_\mathfrak {m}$ is unramified at
$\bar {\rho }_\mathfrak {m}$ is unramified at ![]() $v$ and the characteristic polynomial of
$v$ and the characteristic polynomial of ![]() $\bar {\rho }_{\mathfrak {m}}(\mathrm {Frob}_v)$ is equal to
$\bar {\rho }_{\mathfrak {m}}(\mathrm {Frob}_v)$ is equal to ![]() $X^2-T_vX+S_vN(v) \pmod {\mathfrak {m}}$.
$X^2-T_vX+S_vN(v) \pmod {\mathfrak {m}}$.
Remark 2.2.2 One could prove the above result by adapting the arguments in Chapter IV of [Reference ScholzeSch15]. The main technical point one needs to deal with is the construction of ad hoc compactifications of Hilbert modular varieties.Footnote 5 For the sake of brevity, we will instead explain below how to deduce the theorem from (a special case of) the main result of [Reference ScholzeSch15]; however, at the time of writing, the totally real case of the latter is conditional on Arthur's work [Reference ArthurArt13].
Proof. Uniqueness of ![]() $\bar {\rho }_\mathfrak {m}$ follows from the Chebotarev density theorem and the Brauer–Nesbitt theorem; to prove existence of
$\bar {\rho }_\mathfrak {m}$ follows from the Chebotarev density theorem and the Brauer–Nesbitt theorem; to prove existence of ![]() $\bar {\rho }_{\mathfrak {m}}$ it suffices to consider the cohomology groups
$\bar {\rho }_{\mathfrak {m}}$ it suffices to consider the cohomology groups ![]() $H^*(Sh_K(G), {\mathbb {F}}_{\ell })$ (by Poincaré duality and the discussion in [Reference Caraiani and ScholzeCS19, p. 35]). Furthermore, if
$H^*(Sh_K(G), {\mathbb {F}}_{\ell })$ (by Poincaré duality and the discussion in [Reference Caraiani and ScholzeCS19, p. 35]). Furthermore, if ![]() $K' \subset K$ is a normal compact open subgroup, then there is a Hecke-equivariant Hochschild–Serre spectral sequence relating cohomology of
$K' \subset K$ is a normal compact open subgroup, then there is a Hecke-equivariant Hochschild–Serre spectral sequence relating cohomology of ![]() $Sh_{K'}(G)$ and
$Sh_{K'}(G)$ and ![]() $Sh_K(G)$. Therefore, at the cost of possibly enlarging the set
$Sh_K(G)$. Therefore, at the cost of possibly enlarging the set ![]() $S$ in § 2.1.2, we may replace
$S$ in § 2.1.2, we may replace ![]() $K$ by a normal compact open subgroup. In particular, we may take
$K$ by a normal compact open subgroup. In particular, we may take ![]() $K=K(N)$ for
$K=K(N)$ for ![]() $N$ large enough, where
$N$ large enough, where ![]() $K(N):=\{M \in GL_2(\hat {\mathcal {O}}_F)\mid M \equiv (\begin{smallmatrix} 1 & 0\\ 0 & 1 \end{smallmatrix}) \pmod N\}$. This ensures that the assumption in the first point of Lemma 2.1.4 is satisfied. Furthermore, Chevalley's theorem on units guarantees that we may choose
$K(N):=\{M \in GL_2(\hat {\mathcal {O}}_F)\mid M \equiv (\begin{smallmatrix} 1 & 0\\ 0 & 1 \end{smallmatrix}) \pmod N\}$. This ensures that the assumption in the first point of Lemma 2.1.4 is satisfied. Furthermore, Chevalley's theorem on units guarantees that we may choose ![]() $N$ in such a way that the hypothesis in the second point of Lemma 2.1.4 is satisfied as well. We fix such an integer
$N$ in such a way that the hypothesis in the second point of Lemma 2.1.4 is satisfied as well. We fix such an integer ![]() $N$ from now on. By assumption there is
$N$ from now on. By assumption there is ![]() $i \geq 0$ such that
$i \geq 0$ such that ![]() $H^i(Sh_K(G), {\mathbb {F}}_\ell )_\mathfrak {m}\neq 0$. By Lemma 2.1.4 we deduce that
$H^i(Sh_K(G), {\mathbb {F}}_\ell )_\mathfrak {m}\neq 0$. By Lemma 2.1.4 we deduce that ![]() $H^i(X_K(G), {\mathbb {F}}_\ell )_\mathfrak {m} \neq 0$, hence
$H^i(X_K(G), {\mathbb {F}}_\ell )_\mathfrak {m} \neq 0$, hence ![]() $H^i(X_K(G), {\mathbb {F}}_\ell )_\mathfrak {m}^\chi \neq 0$ for some
$H^i(X_K(G), {\mathbb {F}}_\ell )_\mathfrak {m}^\chi \neq 0$ for some ![]() $\chi \in \hat {C}$. If
$\chi \in \hat {C}$. If ![]() $\chi$ is the trivial character, then by Lemma 2.1.4 we have
$\chi$ is the trivial character, then by Lemma 2.1.4 we have ![]() $H^i(\bar {X}_K(G), {\mathbb {F}}_\ell )_\mathfrak {m}\neq 0$, and by [Reference ScholzeSch15, Theorem 1.3] and [Reference Caraiani and Le HungCL16, Theorem 1.2] we can attach to
$H^i(\bar {X}_K(G), {\mathbb {F}}_\ell )_\mathfrak {m}\neq 0$, and by [Reference ScholzeSch15, Theorem 1.3] and [Reference Caraiani and Le HungCL16, Theorem 1.2] we can attach to ![]() $\mathfrak {m}$ a Galois representation as in the statement of the theorem.
$\mathfrak {m}$ a Galois representation as in the statement of the theorem.
Now let us suppose that ![]() $\chi$ is not the trivial character. The map
$\chi$ is not the trivial character. The map ![]() $\{\pm 1\}^g \rightarrow F^\times \backslash \{\pm 1\}^g \times {\mathbb {A}}_{F, f}^\times / \det (K)$ sending
$\{\pm 1\}^g \rightarrow F^\times \backslash \{\pm 1\}^g \times {\mathbb {A}}_{F, f}^\times / \det (K)$ sending ![]() $\varepsilon$ to the equivalence class of
$\varepsilon$ to the equivalence class of ![]() $(\varepsilon, 1)$ is injective. We may extend
$(\varepsilon, 1)$ is injective. We may extend ![]() $\chi : \{\pm 1\}^g\rightarrow {\mathbb {F}}_\ell ^\times$ to a character
$\chi : \{\pm 1\}^g\rightarrow {\mathbb {F}}_\ell ^\times$ to a character ![]() $\psi : F^\times \backslash \{\pm 1\}^g \times {\mathbb {A}}_{F, f}^\times / \det (K)\rightarrow k^\times$ for a large enough finite extension
$\psi : F^\times \backslash \{\pm 1\}^g \times {\mathbb {A}}_{F, f}^\times / \det (K)\rightarrow k^\times$ for a large enough finite extension ![]() $k$ of
$k$ of ![]() ${\mathbb {F}}_\ell$. The function
${\mathbb {F}}_\ell$. The function ![]() $\psi$ gives rise to a cohomology class
$\psi$ gives rise to a cohomology class ![]() $c_\psi \in H^0(X_K(G), k)$. Let
$c_\psi \in H^0(X_K(G), k)$. Let ![]() $f_\psi : \mathbb {T} \rightarrow \mathbb {T}$ the map sending the operator
$f_\psi : \mathbb {T} \rightarrow \mathbb {T}$ the map sending the operator ![]() $T_g$ attached to the double coset of
$T_g$ attached to the double coset of ![]() $g \in G({\mathbb {A}}_f)$ to
$g \in G({\mathbb {A}}_f)$ to ![]() $\psi (\det (g)^{-1})T_g$. Cup product with
$\psi (\det (g)^{-1})T_g$. Cup product with ![]() $c_\psi$ induces a map
$c_\psi$ induces a map ![]() $H^i(X_K(G), k)\rightarrow H^i(X_K(G), k)$ which is Hecke-equivariant if we endow the source (respectively, target) with the usual Hecke action (respectively, the composite of the usual Hecke action and
$H^i(X_K(G), k)\rightarrow H^i(X_K(G), k)$ which is Hecke-equivariant if we endow the source (respectively, target) with the usual Hecke action (respectively, the composite of the usual Hecke action and ![]() $f_\psi$). This is proved in great generality in [Reference Allen, Calegari, Caraiani, Gee, Helm, Le Hung, Newton, Scholze, Taylor and ThorneACC+23, Proposition 2.2.22], and it can be checked in our situation by a direct computation.
$f_\psi$). This is proved in great generality in [Reference Allen, Calegari, Caraiani, Gee, Helm, Le Hung, Newton, Scholze, Taylor and ThorneACC+23, Proposition 2.2.22], and it can be checked in our situation by a direct computation.
Furthermore, the above map sends ![]() $H^i(X_K(G), k)^\chi$ to
$H^i(X_K(G), k)^\chi$ to ![]() $H^i(X_K(G), k)^{\mathrm {Id}}$. Indeed, for
$H^i(X_K(G), k)^{\mathrm {Id}}$. Indeed, for ![]() $\varepsilon \in C$ we have
$\varepsilon \in C$ we have ![]() $\varepsilon ^*(c_\psi )=\chi (\varepsilon )c_\psi$; hence, for every
$\varepsilon ^*(c_\psi )=\chi (\varepsilon )c_\psi$; hence, for every ![]() $c \in H^i(X_K(G), k)^\chi$:
$c \in H^i(X_K(G), k)^\chi$:
The outcome of our discussion is that, letting ![]() $\mathfrak {m}(\psi ):=f_\psi (\mathfrak {m})$, we have the equivalence
$\mathfrak {m}(\psi ):=f_\psi (\mathfrak {m})$, we have the equivalence
We deduce that ![]() $H^i(\bar {X}_K(G), k)_{\mathfrak {m}(\psi )}\neq 0$, hence we have a Galois representation
$H^i(\bar {X}_K(G), k)_{\mathfrak {m}(\psi )}\neq 0$, hence we have a Galois representation ![]() $\bar {\rho }_{\mathfrak {m}(\psi )}$ attached to
$\bar {\rho }_{\mathfrak {m}(\psi )}$ attached to ![]() $\mathfrak {m}(\psi )$ by [Reference ScholzeSch15, Theorem 1.3]. We can finally take
$\mathfrak {m}(\psi )$ by [Reference ScholzeSch15, Theorem 1.3]. We can finally take ![]() $\bar {\rho }_\mathfrak {m}$ to be the twist of
$\bar {\rho }_\mathfrak {m}$ to be the twist of ![]() $\bar {\rho }_{\mathfrak {m}(\psi )}$ by the character of
$\bar {\rho }_{\mathfrak {m}(\psi )}$ by the character of ![]() $\Gamma _F$ corresponding to
$\Gamma _F$ corresponding to ![]() $\psi$ via global class field theory.
$\psi$ via global class field theory.
2.3 Cohomology of the boundary
Recall that a maximal ideal ![]() $\mathfrak {m}\subset \mathbb {T}$ in the support of
$\mathfrak {m}\subset \mathbb {T}$ in the support of ![]() $H^*(Sh_K(G), {\mathbb {F}}_\ell )$ is said to be non-Eisenstein if the associated Galois representation
$H^*(Sh_K(G), {\mathbb {F}}_\ell )$ is said to be non-Eisenstein if the associated Galois representation ![]() $\bar {\rho }_\mathfrak {m}$ is absolutely irreducible.
$\bar {\rho }_\mathfrak {m}$ is absolutely irreducible.
Lemma 2.3.1 Let ![]() $\ell >2$ be a prime and assume that
$\ell >2$ be a prime and assume that ![]() $\mathfrak {m}$ is non-Eisenstein. Then:
$\mathfrak {m}$ is non-Eisenstein. Then:
(i) for every integer
 $i$, the natural map from compactly supported cohomology to cohomology induces an isomorphism
$i$, the natural map from compactly supported cohomology to cohomology induces an isomorphism  $H^i_c(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}\simeq H^i(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}$;
$H^i_c(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}\simeq H^i(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}$;(ii) take
 $\delta \geq 0$ and assume that
$\delta \geq 0$ and assume that  $H^i_c(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}=H^i_c(Sh_K(G), {\mathbb {F}}_{\ell })_{\mathfrak {m}^\vee }=0$ for each
$H^i_c(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}=H^i_c(Sh_K(G), {\mathbb {F}}_{\ell })_{\mathfrak {m}^\vee }=0$ for each  $i < g-\delta$; then
$i < g-\delta$; then  $H^i(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ if
$H^i(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ if  $i$ is outside the interval
$i$ is outside the interval  $[g-\delta, g+\delta ]$.
$[g-\delta, g+\delta ]$.
Proof. Consider the Borel–Serre compactification ![]() $Sh_K(G)^{BS}$ of
$Sh_K(G)^{BS}$ of ![]() $Sh_K(G)$, constructed in [Reference HarderHar87], with boundary
$Sh_K(G)$, constructed in [Reference HarderHar87], with boundary ![]() $\partial$. Recall that the cohomology of
$\partial$. Recall that the cohomology of ![]() $Sh_K(G)^{BS}$ agrees with that of
$Sh_K(G)^{BS}$ agrees with that of ![]() $Sh_K(G)$, as the two spaces are homotopy equivalent, and the compactly supported cohomology of
$Sh_K(G)$, as the two spaces are homotopy equivalent, and the compactly supported cohomology of ![]() $Sh_K(G)$ coincides with the cohomology of
$Sh_K(G)$ coincides with the cohomology of ![]() $Sh_K(G)^{BS}$ relative to the boundary. Hence, we have a
$Sh_K(G)^{BS}$ relative to the boundary. Hence, we have a ![]() $\mathbb {T}$-equivariant long exact sequence
$\mathbb {T}$-equivariant long exact sequence
We claim that if ![]() $\mathfrak {m}$ is non-Eisenstein then cohomology of the boundary vanishes after localising at
$\mathfrak {m}$ is non-Eisenstein then cohomology of the boundary vanishes after localising at ![]() $\mathfrak {m}$; this implies the first point. The second follows using Poincaré duality (which interchanges
$\mathfrak {m}$; this implies the first point. The second follows using Poincaré duality (which interchanges ![]() $\mathfrak {m}$ and
$\mathfrak {m}$ and ![]() $\mathfrak {m}^\vee$, as in [Reference Caraiani and ScholzeCS19, p. 35]). It remains to justify our claim. By [Reference HarderHar87, p. 46] we have
$\mathfrak {m}^\vee$, as in [Reference Caraiani and ScholzeCS19, p. 35]). It remains to justify our claim. By [Reference HarderHar87, p. 46] we have ![]() $H^*(\partial, {\mathbb {F}}_\ell )\simeq H^*(P({\mathbb {Q}})\backslash ({\mathbb {C}} \smallsetminus {\mathbb {R}})^g \times G({\mathbb {A}}_f)/K, {\mathbb {F}}_\ell )$, where
$H^*(\partial, {\mathbb {F}}_\ell )\simeq H^*(P({\mathbb {Q}})\backslash ({\mathbb {C}} \smallsetminus {\mathbb {R}})^g \times G({\mathbb {A}}_f)/K, {\mathbb {F}}_\ell )$, where ![]() $P \subset G$ is the standard upper parabolic. To prove our claim we may replace
$P \subset G$ is the standard upper parabolic. To prove our claim we may replace ![]() $K$ by a normal compact open subgroup, so that the condition
$K$ by a normal compact open subgroup, so that the condition ![]() $\det (K)=K \cap Z({\mathbb {A}}_f)$ is satisfied. We will assume that this is the case in the rest of the proof. The space
$\det (K)=K \cap Z({\mathbb {A}}_f)$ is satisfied. We will assume that this is the case in the rest of the proof. The space ![]() $P({\mathbb {Q}})\backslash ({\mathbb {C}} \smallsetminus {\mathbb {R}})^g \times G({\mathbb {A}}_f)/K$ is a disjoint union of quotients
$P({\mathbb {Q}})\backslash ({\mathbb {C}} \smallsetminus {\mathbb {R}})^g \times G({\mathbb {A}}_f)/K$ is a disjoint union of quotients ![]() $P({\mathbb {Q}})\cap g_iKg_i^{-1}\backslash ({\mathbb {C}}\smallsetminus {\mathbb {R}})^g$, where
$P({\mathbb {Q}})\cap g_iKg_i^{-1}\backslash ({\mathbb {C}}\smallsetminus {\mathbb {R}})^g$, where ![]() $g_i$ runs over a set of representatives of
$g_i$ runs over a set of representatives of ![]() $P({\mathbb {Q}})\backslash G({\mathbb {A}}_f)/K$.
$P({\mathbb {Q}})\backslash G({\mathbb {A}}_f)/K$.
On the other hand, we have the locally symmetric space ![]() $X_K(G)$. The boundary of its Borel–Serre compactification is homotopy equivalent to the space
$X_K(G)$. The boundary of its Borel–Serre compactification is homotopy equivalent to the space ![]() $P({\mathbb {Q}}) \backslash G({\mathbb {R}})\times G({\mathbb {A}}_f)/({\mathbb {R}}_{>0}K^\circ _\infty ) K$ (see [Reference GrafGra16, p. 94]). The latter is a disjoint union of quotients
$P({\mathbb {Q}}) \backslash G({\mathbb {R}})\times G({\mathbb {A}}_f)/({\mathbb {R}}_{>0}K^\circ _\infty ) K$ (see [Reference GrafGra16, p. 94]). The latter is a disjoint union of quotients ![]() $P({\mathbb {Q}})\cap g_iKg_i^{-1}\backslash G({\mathbb {R}})/({\mathbb {R}}_{>0}K^\circ _\infty )$ with
$P({\mathbb {Q}})\cap g_iKg_i^{-1}\backslash G({\mathbb {R}})/({\mathbb {R}}_{>0}K^\circ _\infty )$ with ![]() $g_i$ as above. The action of
$g_i$ as above. The action of ![]() $Z({\mathbb {R}})$ on
$Z({\mathbb {R}})$ on ![]() $G({\mathbb {R}})/({\mathbb {R}}_{>0}K^\circ _\infty )$ induces an action on
$G({\mathbb {R}})/({\mathbb {R}}_{>0}K^\circ _\infty )$ induces an action on ![]() $P({\mathbb {Q}}) \backslash G({\mathbb {R}})\times G({\mathbb {A}}_f)/({\mathbb {R}}_{>0}K^\circ _\infty ) K$. This action preserves the fibres of the projection map
$P({\mathbb {Q}}) \backslash G({\mathbb {R}})\times G({\mathbb {A}}_f)/({\mathbb {R}}_{>0}K^\circ _\infty ) K$. This action preserves the fibres of the projection map
and factors through an action of the torus ![]() $T_K=Z({\mathbb {R}})/\{\pm 1\}^g{\mathbb {R}}_{>0}Z_K$. The argument in the proof of [Reference GrafGra16, Lemma 3.1.2] shows that each projection map
$T_K=Z({\mathbb {R}})/\{\pm 1\}^g{\mathbb {R}}_{>0}Z_K$. The argument in the proof of [Reference GrafGra16, Lemma 3.1.2] shows that each projection map ![]() $P({\mathbb {Q}})\cap g_iKg_i^{-1}\backslash G({\mathbb {R}})/({\mathbb {R}}_{>0}K^\circ _\infty ) \rightarrow P({\mathbb {Q}})\cap g_iKg_i^{-1}\backslash ({\mathbb {C}}\smallsetminus {\mathbb {R}})^g$ is a
$P({\mathbb {Q}})\cap g_iKg_i^{-1}\backslash G({\mathbb {R}})/({\mathbb {R}}_{>0}K^\circ _\infty ) \rightarrow P({\mathbb {Q}})\cap g_iKg_i^{-1}\backslash ({\mathbb {C}}\smallsetminus {\mathbb {R}})^g$ is a ![]() $T_K$-bundle. Hence, the same is true for the map in (2.3.1.1). Furthermore, we have the following commutative diagram.
$T_K$-bundle. Hence, the same is true for the map in (2.3.1.1). Furthermore, we have the following commutative diagram.

As we already mentioned, by [Reference GrafGra16, Lemma 3.1.2] the right vertical map is a ![]() $T_K$-bundle, and [Reference GrafGra16, Proposition 3.3.9] constructs cohomology classes in
$T_K$-bundle, and [Reference GrafGra16, Proposition 3.3.9] constructs cohomology classes in ![]() $H^*(X_K(G), {\mathbb {F}}_\ell )$ whose restrictions to each fibre of the right vertical map give a basis of its cohomology. Pulling back via the upper horizontal map we obtain classes in
$H^*(X_K(G), {\mathbb {F}}_\ell )$ whose restrictions to each fibre of the right vertical map give a basis of its cohomology. Pulling back via the upper horizontal map we obtain classes in ![]() $H^*(P({\mathbb {Q}}) \backslash G({\mathbb {R}})\times G({\mathbb {A}}_f)/({\mathbb {R}}_{>0}K^\circ _\infty ) K, {\mathbb {F}}_\ell )$ enjoying the same property. In particular, by Leray–Hirsch the pullback map in cohomology induced by the left vertical map is injective. Now assume that
$H^*(P({\mathbb {Q}}) \backslash G({\mathbb {R}})\times G({\mathbb {A}}_f)/({\mathbb {R}}_{>0}K^\circ _\infty ) K, {\mathbb {F}}_\ell )$ enjoying the same property. In particular, by Leray–Hirsch the pullback map in cohomology induced by the left vertical map is injective. Now assume that ![]() $H^*(\partial, {\mathbb {F}}_\ell )_\mathfrak {m}=H^*(P({\mathbb {Q}}) \backslash ({\mathbb {C}} \smallsetminus {\mathbb {R}})^g\times G({\mathbb {A}}_f)/K, {\mathbb {F}}_\ell )_\mathfrak {m}\neq 0$. We deduce that the cohomology
$H^*(\partial, {\mathbb {F}}_\ell )_\mathfrak {m}=H^*(P({\mathbb {Q}}) \backslash ({\mathbb {C}} \smallsetminus {\mathbb {R}})^g\times G({\mathbb {A}}_f)/K, {\mathbb {F}}_\ell )_\mathfrak {m}\neq 0$. We deduce that the cohomology ![]() $H^*(P({\mathbb {Q}}) \backslash G({\mathbb {R}})\times G({\mathbb {A}}_f)/({\mathbb {R}}_{>0}K^\circ _\infty ) K, {\mathbb {F}}_\ell )_\mathfrak {m}$ of the boundary of
$H^*(P({\mathbb {Q}}) \backslash G({\mathbb {R}})\times G({\mathbb {A}}_f)/({\mathbb {R}}_{>0}K^\circ _\infty ) K, {\mathbb {F}}_\ell )_\mathfrak {m}$ of the boundary of ![]() $X_K(G)$ is non-zero. Finally the argument in [Reference Newton and ThorneNT16, § 4] shows that
$X_K(G)$ is non-zero. Finally the argument in [Reference Newton and ThorneNT16, § 4] shows that ![]() $\mathfrak {m}$ must be Eisenstein.
$\mathfrak {m}$ must be Eisenstein.
3. Quaternionic and unitary Shimura varieties
In this section, we introduce quaternionic Shimura varieties as well as certain closely related unitary Shimura varieties that admit nice integral models.
3.1 Quaternionic Shimura data and the associated unitary Shimura data
3.1.1 Quaternionic Shimura data
As in the previous section we use the notation ![]() $G:=\mathrm {Res}_{F/{\mathbb {Q}}}\mathrm {GL}_2$; we also let
$G:=\mathrm {Res}_{F/{\mathbb {Q}}}\mathrm {GL}_2$; we also let ![]() $T_F:=\mathrm {Res}_{F/{\mathbb {Q}}}\mathbb {G}_m$. Let
$T_F:=\mathrm {Res}_{F/{\mathbb {Q}}}\mathbb {G}_m$. Let ![]() $K\subset G({\mathbb {A}}_f)$ be a neat compact open subgroup. Fix a prime
$K\subset G({\mathbb {A}}_f)$ be a neat compact open subgroup. Fix a prime ![]() $p>2$ which is totally split in
$p>2$ which is totally split in ![]() $F$ and such that
$F$ and such that ![]() $K=K^{p}K_p$ with
$K=K^{p}K_p$ with ![]() $K_p=\operatorname {GL}_2({\mathcal {O}}_F\otimes {\mathbb {Z}}_p)$.
$K_p=\operatorname {GL}_2({\mathcal {O}}_F\otimes {\mathbb {Z}}_p)$.
Recall that ![]() $\Sigma _\infty$ denotes the set of real places of
$\Sigma _\infty$ denotes the set of real places of ![]() $F$. We will denote by
$F$. We will denote by ![]() $\Sigma _p$ the set of embeddings of
$\Sigma _p$ the set of embeddings of ![]() $F$ into
$F$ into ![]() $\bar {{\mathbb {Q}}}_p$, which we identify with the set of prime ideals
$\bar {{\mathbb {Q}}}_p$, which we identify with the set of prime ideals ![]() $\mathfrak {p} \subset {\mathcal {O}}_F$ lying above
$\mathfrak {p} \subset {\mathcal {O}}_F$ lying above ![]() $p$. We fix an isomorphism
$p$. We fix an isomorphism ![]() $\iota _p : \bar {{\mathbb {Q}}}_p \buildrel \sim \over \to {\mathbb {C}}$, inducing a bijection
$\iota _p : \bar {{\mathbb {Q}}}_p \buildrel \sim \over \to {\mathbb {C}}$, inducing a bijection ![]() $\iota _{p, \infty }: \Sigma _p \buildrel \sim \over \to \Sigma _\infty$. For every subset
$\iota _{p, \infty }: \Sigma _p \buildrel \sim \over \to \Sigma _\infty$. For every subset ![]() $T \subset \Sigma _p$ we set
$T \subset \Sigma _p$ we set ![]() $T_\infty :=\iota _{p, \infty }(T)$ and we denote by
$T_\infty :=\iota _{p, \infty }(T)$ and we denote by ![]() $B_T$ the quaternion algebra over
$B_T$ the quaternion algebra over ![]() $F$ ramified precisely at
$F$ ramified precisely at ![]() $T \coprod T_\infty$. We let
$T \coprod T_\infty$. We let ![]() $G_T:=\mathrm {Res}_{F/{\mathbb {Q}}}B_T^\times$, and we fix an isomorphism
$G_T:=\mathrm {Res}_{F/{\mathbb {Q}}}B_T^\times$, and we fix an isomorphism ![]() $G_T({\mathbb {A}}_f^{(p)})\simeq G({\mathbb {A}}_f^{(p)})$. The group
$G_T({\mathbb {A}}_f^{(p)})\simeq G({\mathbb {A}}_f^{(p)})$. The group ![]() $G_{T, {\mathbb {R}}}$ is isomorphic to
$G_{T, {\mathbb {R}}}$ is isomorphic to ![]() $\prod _{\tau \in T_\infty } \mathbb {H}^\times \times \prod _{\tau \in \Sigma _\infty \smallsetminus T_\infty } \operatorname {GL}_{2, {\mathbb {R}}}$ where
$\prod _{\tau \in T_\infty } \mathbb {H}^\times \times \prod _{\tau \in \Sigma _\infty \smallsetminus T_\infty } \operatorname {GL}_{2, {\mathbb {R}}}$ where ![]() $\mathbb {H}$ is the algebra of Hamilton quaternions. Let
$\mathbb {H}$ is the algebra of Hamilton quaternions. Let ![]() $X_T$ be the
$X_T$ be the ![]() $G_T({\mathbb {R}})$-conjugacy class of the morphism
$G_T({\mathbb {R}})$-conjugacy class of the morphism ![]() $h_T: \mathbb {S} \rightarrow G_{T, {\mathbb {R}}}$ sending an
$h_T: \mathbb {S} \rightarrow G_{T, {\mathbb {R}}}$ sending an ![]() ${\mathbb {R}}$-point
${\mathbb {R}}$-point ![]() $z=a+ib \in \mathbb {S}({\mathbb {R}})$ to
$z=a+ib \in \mathbb {S}({\mathbb {R}})$ to ![]() $(z^\tau )_{\tau \in \Sigma _\infty }$, where
$(z^\tau )_{\tau \in \Sigma _\infty }$, where ![]() $z^\tau =1$ for
$z^\tau =1$ for ![]() $\tau \in T_\infty$ and
$\tau \in T_\infty$ and ![]() $z^\tau =(\begin{smallmatrix} a & b\\ -b & a \end{smallmatrix})$ if
$z^\tau =(\begin{smallmatrix} a & b\\ -b & a \end{smallmatrix})$ if ![]() $\tau \in \Sigma _\infty \smallsetminus T_\infty$. The couple
$\tau \in \Sigma _\infty \smallsetminus T_\infty$. The couple ![]() $(G_T, X_T)$ is a weak Shimura datum (in the sense of [Reference Tian and XiaoTX16, § 2.2]) whose reflex field
$(G_T, X_T)$ is a weak Shimura datum (in the sense of [Reference Tian and XiaoTX16, § 2.2]) whose reflex field ![]() $F_T$ can be described as follows: the group
$F_T$ can be described as follows: the group ![]() $\mathrm {Aut}({\mathbb {C}}/{\mathbb {Q}})$ acts on
$\mathrm {Aut}({\mathbb {C}}/{\mathbb {Q}})$ acts on ![]() $\Sigma _\infty$ by post-composition. Let
$\Sigma _\infty$ by post-composition. Let ![]() $\Gamma _T \subset \mathrm {Aut}({\mathbb {C}}/{\mathbb {Q}})$ be the subgroup preserving
$\Gamma _T \subset \mathrm {Aut}({\mathbb {C}}/{\mathbb {Q}})$ be the subgroup preserving ![]() $T_\infty$; then
$T_\infty$; then ![]() $F_T={\mathbb {C}}^{\Gamma _T}\subset {\mathbb {C}}$.
$F_T={\mathbb {C}}^{\Gamma _T}\subset {\mathbb {C}}$.
Let ![]() $K_T=K_{T, p}K^{p} \subset G_T({\mathbb {A}}_f)$ be the compact open subgroup such that
$K_T=K_{T, p}K^{p} \subset G_T({\mathbb {A}}_f)$ be the compact open subgroup such that ![]() $K^p\subset G_T({\mathbb {A}}_f^{(p)})\simeq G({\mathbb {A}}_f^{(p)})$ is the subgroup chosen above and
$K^p\subset G_T({\mathbb {A}}_f^{(p)})\simeq G({\mathbb {A}}_f^{(p)})$ is the subgroup chosen above and ![]() $K_{T, p}=\prod _{\mathfrak {p} \mid p}K_{T, \mathfrak {p}}$ is of the following type: if
$K_{T, p}=\prod _{\mathfrak {p} \mid p}K_{T, \mathfrak {p}}$ is of the following type: if ![]() $\mathfrak {p} \in \Sigma _p \smallsetminus T$, then we fix an isomorphism
$\mathfrak {p} \in \Sigma _p \smallsetminus T$, then we fix an isomorphism ![]() $\rho _\mathfrak {p}: B_T(F_\mathfrak {p})^\times \rightarrow \operatorname {GL}_2(F_\mathfrak {p})$ and we take
$\rho _\mathfrak {p}: B_T(F_\mathfrak {p})^\times \rightarrow \operatorname {GL}_2(F_\mathfrak {p})$ and we take ![]() $K_{T, \mathfrak {p}}:=\rho _\mathfrak {p}^{-1}(\operatorname {GL}_2(\mathcal {O}_\mathfrak {p}))$. If
$K_{T, \mathfrak {p}}:=\rho _\mathfrak {p}^{-1}(\operatorname {GL}_2(\mathcal {O}_\mathfrak {p}))$. If ![]() $\mathfrak {p} \in T$, then we take
$\mathfrak {p} \in T$, then we take ![]() $K_{T, \mathfrak {p}}$ to be the group of units in the unique maximal order in the division quaternion algebra
$K_{T, \mathfrak {p}}$ to be the group of units in the unique maximal order in the division quaternion algebra ![]() $B_T \otimes _F F_\mathfrak {p}$.
$B_T \otimes _F F_\mathfrak {p}$.
3.1.2 The auxiliary  $CM$ extension
$CM$ extension
Choose a ![]() $CM$ extension
$CM$ extension ![]() $E/F$ such that every place
$E/F$ such that every place ![]() $\mathfrak {p} \in \Sigma _p$ is inert in
$\mathfrak {p} \in \Sigma _p$ is inert in ![]() $E$; in particular,
$E$; in particular, ![]() $B_T \otimes _F E$ is isomorphic to the matrix algebra
$B_T \otimes _F E$ is isomorphic to the matrix algebra ![]() $M_2(E)$. Let
$M_2(E)$. Let ![]() $c \in \mathrm {Gal}(E/F)$ be the non trivial element and let
$c \in \mathrm {Gal}(E/F)$ be the non trivial element and let ![]() $\Sigma _{E, \infty }$ be the set of complex embeddings of
$\Sigma _{E, \infty }$ be the set of complex embeddings of ![]() $E$: it comes with a restriction map
$E$: it comes with a restriction map ![]() $\Sigma _{E, \infty }\rightarrow \Sigma _\infty$ whose fibres are the orbits for the action of
$\Sigma _{E, \infty }\rightarrow \Sigma _\infty$ whose fibres are the orbits for the action of ![]() $\mathrm {Gal}(E/F)$ sending an embedding
$\mathrm {Gal}(E/F)$ sending an embedding ![]() $\tilde {\tau } \in \Sigma _{E, \infty }$ to
$\tilde {\tau } \in \Sigma _{E, \infty }$ to ![]() $\tilde {\tau }^c:=\tilde {\tau }\circ c$. Choose a set
$\tilde {\tau }^c:=\tilde {\tau }\circ c$. Choose a set ![]() $\tilde {T} \subset \Sigma _{E, \infty }$ containing exactly one lift of each
$\tilde {T} \subset \Sigma _{E, \infty }$ containing exactly one lift of each ![]() $\tau \in T_\infty$. For every
$\tau \in T_\infty$. For every ![]() $\tilde {\tau } \in \Sigma _{E, \infty }$, define an integer
$\tilde {\tau } \in \Sigma _{E, \infty }$, define an integer ![]() $s_{\tilde {\tau }} \in \{0, 1, 2\}$ as follows:
$s_{\tilde {\tau }} \in \{0, 1, 2\}$ as follows:
• if
 $\tilde {\tau }_{|F} \not \in T_\infty$ then
$\tilde {\tau }_{|F} \not \in T_\infty$ then  $s_{\tilde {\tau }}=1$;
$s_{\tilde {\tau }}=1$;• if
 $\tilde {\tau } \in \tilde {T}$ then
$\tilde {\tau } \in \tilde {T}$ then  $s_{\tilde {\tau }}=0$;
$s_{\tilde {\tau }}=0$;• if
 $\tilde {\tau }^c \in \tilde {T}$ then
$\tilde {\tau }^c \in \tilde {T}$ then  $s_{\tilde {\tau }}=2$.
$s_{\tilde {\tau }}=2$.
For each ![]() $\tau \in T_\infty$ (respectively,
$\tau \in T_\infty$ (respectively, ![]() $\tau \in \Sigma _\infty \smallsetminus T_\infty$) we choose the isomorphism
$\tau \in \Sigma _\infty \smallsetminus T_\infty$) we choose the isomorphism ![]() $E\otimes _{F, \tau }{\mathbb {R}}\simeq {\mathbb {C}}$ induced by the embedding
$E\otimes _{F, \tau }{\mathbb {R}}\simeq {\mathbb {C}}$ induced by the embedding ![]() $\tilde {\tau } \in \Sigma _{E, \infty }\smallsetminus \tilde {T}$ lifting
$\tilde {\tau } \in \Sigma _{E, \infty }\smallsetminus \tilde {T}$ lifting ![]() $\tau$ (respectively, an arbitrary lift of
$\tau$ (respectively, an arbitrary lift of ![]() $\tau$). Let
$\tau$). Let ![]() $T_E:=\mathrm {Res}_{E/{\mathbb {Q}}}\mathbb {G}_m$; via the previous choices we obtain an isomorphism
$T_E:=\mathrm {Res}_{E/{\mathbb {Q}}}\mathbb {G}_m$; via the previous choices we obtain an isomorphism ![]() $T_{E}({\mathbb {R}})= \prod _{\tau \in \Sigma _\infty }(E\otimes _{F, \tau }{\mathbb {R}})^\times \simeq \prod _{\tau \in \Sigma _\infty }{\mathbb {C}}^\times$. Let
$T_{E}({\mathbb {R}})= \prod _{\tau \in \Sigma _\infty }(E\otimes _{F, \tau }{\mathbb {R}})^\times \simeq \prod _{\tau \in \Sigma _\infty }{\mathbb {C}}^\times$. Let ![]() $h_{T, E}: \mathbb {S} \rightarrow T_{E, {\mathbb {R}}}$ be the morphism which on
$h_{T, E}: \mathbb {S} \rightarrow T_{E, {\mathbb {R}}}$ be the morphism which on ![]() ${\mathbb {R}}$-points sends
${\mathbb {R}}$-points sends ![]() $z=a+ib \in \mathbb {S}({\mathbb {R}})$ to
$z=a+ib \in \mathbb {S}({\mathbb {R}})$ to ![]() $(z^\tau )_{\tau \in \Sigma _\infty }$, where
$(z^\tau )_{\tau \in \Sigma _\infty }$, where ![]() $z^\tau =z$ (respectively,
$z^\tau =z$ (respectively, ![]() $z^\tau =1$) if
$z^\tau =1$) if ![]() $\tau \in T_\infty$ (respectively,
$\tau \in T_\infty$ (respectively, ![]() $\tau \in \Sigma _\infty \smallsetminus T_\infty$). The reflex field
$\tau \in \Sigma _\infty \smallsetminus T_\infty$). The reflex field ![]() $E_T\supset F_T$ of the
$E_T\supset F_T$ of the ![]() $T_E({\mathbb {R}})-$conjugacy class of
$T_E({\mathbb {R}})-$conjugacy class of ![]() $h_{T, E}$ is the subfield of
$h_{T, E}$ is the subfield of ![]() ${\mathbb {C}}$ fixed by the stabiliser in
${\mathbb {C}}$ fixed by the stabiliser in ![]() $\mathrm {Aut}({\mathbb {C}}/{\mathbb {Q}})$ of
$\mathrm {Aut}({\mathbb {C}}/{\mathbb {Q}})$ of ![]() $\tilde {T}$.
$\tilde {T}$.
3.1.3 Unitary Shimura data
We denote by ![]() $H_T$ the algebraic group fitting in the exact sequence
$H_T$ the algebraic group fitting in the exact sequence
where the map ![]() $T_F \rightarrow G_T \times T_E$ is given by
$T_F \rightarrow G_T \times T_E$ is given by ![]() $a \mapsto (a, a^{-1})$. Note that, because of Hilbert's theorem 90, the map
$a \mapsto (a, a^{-1})$. Note that, because of Hilbert's theorem 90, the map ![]() $G_T \times T_E \rightarrow H_T$ induces surjections on
$G_T \times T_E \rightarrow H_T$ induces surjections on ![]() ${\mathbb {Q}}$-points and
${\mathbb {Q}}$-points and ![]() ${\mathbb {A}}_f$-points. The
${\mathbb {A}}_f$-points. The ![]() $(G_T \times T_E)({\mathbb {R}})-$conjugacy class of the map
$(G_T \times T_E)({\mathbb {R}})-$conjugacy class of the map ![]() $h_T\times h_{T, E}: \mathbb {S}\rightarrow (G_T \times T_E)_{\mathbb {R}}$ and the
$h_T\times h_{T, E}: \mathbb {S}\rightarrow (G_T \times T_E)_{\mathbb {R}}$ and the ![]() $H_T({\mathbb {R}})$-conjugacy class of the induced map
$H_T({\mathbb {R}})$-conjugacy class of the induced map ![]() $h_{H_T}: \mathbb {S}\rightarrow H_{T, {\mathbb {R}}}$ can both be identified with
$h_{H_T}: \mathbb {S}\rightarrow H_{T, {\mathbb {R}}}$ can both be identified with ![]() $X_T \simeq \prod _{\tau \in \Sigma _\infty \smallsetminus T_\infty }({\mathbb {C}} \smallsetminus {\mathbb {R}})$, and they give rise to weak Shimura data
$X_T \simeq \prod _{\tau \in \Sigma _\infty \smallsetminus T_\infty }({\mathbb {C}} \smallsetminus {\mathbb {R}})$, and they give rise to weak Shimura data ![]() $(G_T \times T_E, X_T)$ and
$(G_T \times T_E, X_T)$ and ![]() $(H_T, X_T)$ with reflex field
$(H_T, X_T)$ with reflex field ![]() $E_T$. We let
$E_T$. We let ![]() $X_{T}^+:=\prod _{\tau \in \Sigma _\infty \smallsetminus T_\infty }({\mathbb {C}} \smallsetminus {\mathbb {R}})^+$, where
$X_{T}^+:=\prod _{\tau \in \Sigma _\infty \smallsetminus T_\infty }({\mathbb {C}} \smallsetminus {\mathbb {R}})^+$, where ![]() $({\mathbb {C}} \smallsetminus {\mathbb {R}})^+ \subset ({\mathbb {C}} \smallsetminus {\mathbb {R}})$ is the upper half-plane.
$({\mathbb {C}} \smallsetminus {\mathbb {R}})^+ \subset ({\mathbb {C}} \smallsetminus {\mathbb {R}})$ is the upper half-plane.
Let us denote by ![]() $D_T$ the tensor product
$D_T$ the tensor product ![]() $B_T\otimes _F E$ and by
$B_T\otimes _F E$ and by ![]() $\overline {(\cdot )}: D_T \rightarrow D_T$ the tensor product of the main involution on
$\overline {(\cdot )}: D_T \rightarrow D_T$ the tensor product of the main involution on ![]() $B_T$ and complex conjugation on
$B_T$ and complex conjugation on ![]() $E$. For every
$E$. For every ![]() ${\mathbb {Q}}-$algebra
${\mathbb {Q}}-$algebra ![]() $R$ we have a canonical isomorphism
$R$ we have a canonical isomorphism
hence we get a map ![]() $G_T(R) \times T_E(R) \rightarrow (D_T \otimes _{\mathbb {Q}} R)^\times$. This yields an identification
$G_T(R) \times T_E(R) \rightarrow (D_T \otimes _{\mathbb {Q}} R)^\times$. This yields an identification
The latter description allows to see ![]() $H_T$ as a unitary group as follows: given an element
$H_T$ as a unitary group as follows: given an element ![]() $\sigma \in D_T$ such that
$\sigma \in D_T$ such that ![]() $\bar {\sigma }=-\sigma$ the map sending
$\bar {\sigma }=-\sigma$ the map sending ![]() $g \in D_T$ to
$g \in D_T$ to ![]() $g^*=\sigma ^{-1}\bar {g}\sigma$ is an involution of
$g^*=\sigma ^{-1}\bar {g}\sigma$ is an involution of ![]() $D_T$. Let us denote by
$D_T$. Let us denote by ![]() $V_T$ the
$V_T$ the ![]() ${\mathbb {Q}}$-vector space underlying
${\mathbb {Q}}$-vector space underlying ![]() $D_T$, together with its natural structure of left
$D_T$, together with its natural structure of left ![]() $D_T$-module, so that
$D_T$-module, so that ![]() $\mathrm {End}_{D_T}(V_T)=D_T^{op}$. Consider the skew-Hermitian pairing
$\mathrm {End}_{D_T}(V_T)=D_T^{op}$. Consider the skew-Hermitian pairing
for every ![]() $g \in D_T$ and
$g \in D_T$ and ![]() $v, w \in V_T$ we have
$v, w \in V_T$ we have
hence, for every ![]() ${\mathbb {Q}}$-algebra
${\mathbb {Q}}$-algebra ![]() $R$,
$R$,
3.2 Relation between quaternionic and unitary Shimura varieties
3.2.1
Fix a subset ![]() $T\subset \Sigma _p$; the reduced norm on
$T\subset \Sigma _p$; the reduced norm on ![]() $B_T$ gives rise to a map
$B_T$ gives rise to a map ![]() $\mathrm {Nm}: G_T \rightarrow T_F$. Let
$\mathrm {Nm}: G_T \rightarrow T_F$. Let ![]() $T_{H_T}:=(T_F \times T_E)/T_F$, where the embedding of
$T_{H_T}:=(T_F \times T_E)/T_F$, where the embedding of ![]() $T_F$ in
$T_F$ in ![]() $T_F \times T_E$ is given by
$T_F \times T_E$ is given by ![]() $a \mapsto (a^2, a^{-1})$. Letting
$a \mapsto (a^2, a^{-1})$. Letting ![]() $N_{H_T}: H_T \rightarrow T_{H_T}$ be the map induced by
$N_{H_T}: H_T \rightarrow T_{H_T}$ be the map induced by ![]() $\mathrm {Nm} \times \mathrm {Id}: G_T \times T_E \rightarrow T_F \times T_E$, we obtain a commutative diagram
$\mathrm {Nm} \times \mathrm {Id}: G_T \times T_E \rightarrow T_F \times T_E$, we obtain a commutative diagram

where the top arrow is compatible with the Deligne homomorphisms. Recall that we have fixed a compact open subgroup ![]() $K_T \subset G_T({\mathbb {A}}_f)$. Take a compact open subgroup
$K_T \subset G_T({\mathbb {A}}_f)$. Take a compact open subgroup ![]() $K_E=K_{E, p} K_E^{p} \subset T_E({\mathbb {A}}_f)$ and a compact open subgroup
$K_E=K_{E, p} K_E^{p} \subset T_E({\mathbb {A}}_f)$ and a compact open subgroup ![]() $U_T \subset H_T({\mathbb {A}}_f)$ containing the image of
$U_T \subset H_T({\mathbb {A}}_f)$ containing the image of ![]() $K_T \times K_E$. Let
$K_T \times K_E$. Let
 \begin{align*} C_{K_T}&:=F^{\times, +}\backslash {\mathbb{A}}_{F, f}^\times/\mathrm{Nm}(K_T), \quad C_{K_E}:=E^{\times}\backslash {\mathbb{A}}_{E, f}^\times/K_E\\ C_{K_T \times K_E}&:=C_{K_T}\times C_{K_E}, \quad C_{U_T}:=T_{H_T}({\mathbb{Q}})^+\backslash T_{H_T}({\mathbb{A}}_f)/N_{H_T}(U_T), \end{align*}
\begin{align*} C_{K_T}&:=F^{\times, +}\backslash {\mathbb{A}}_{F, f}^\times/\mathrm{Nm}(K_T), \quad C_{K_E}:=E^{\times}\backslash {\mathbb{A}}_{E, f}^\times/K_E\\ C_{K_T \times K_E}&:=C_{K_T}\times C_{K_E}, \quad C_{U_T}:=T_{H_T}({\mathbb{Q}})^+\backslash T_{H_T}({\mathbb{A}}_f)/N_{H_T}(U_T), \end{align*}
where ![]() $T_{H_T}({\mathbb {Q}})^+:=(F^{\times, +}\times E^\times )/F^\times$. We have maps
$T_{H_T}({\mathbb {Q}})^+:=(F^{\times, +}\times E^\times )/F^\times$. We have maps ![]() $C_{K_T}\rightarrow C_{K_T}\times C_{K_E} \rightarrow C_{U_T}$, where the first map sends
$C_{K_T}\rightarrow C_{K_T}\times C_{K_E} \rightarrow C_{U_T}$, where the first map sends ![]() $C_{K_T}$ to (the equivalence class of) 1 on the second component. Letting
$C_{K_T}$ to (the equivalence class of) 1 on the second component. Letting ![]() $G_T({\mathbb {Q}})^+\subset G_T({\mathbb {Q}})$ be the subgroup of elements with totally positive norm, and
$G_T({\mathbb {Q}})^+\subset G_T({\mathbb {Q}})$ be the subgroup of elements with totally positive norm, and ![]() $H_T({\mathbb {Q}})^+:=(G_T({\mathbb {Q}})^+\times T_E({\mathbb {Q}}))/T_F({\mathbb {Q}})$, we obtain the following commutative diagram.
$H_T({\mathbb {Q}})^+:=(G_T({\mathbb {Q}})^+\times T_E({\mathbb {Q}}))/T_F({\mathbb {Q}})$, we obtain the following commutative diagram.

If ![]() $T \neq \Sigma _p$ (so that the spaces in the top row are positive dimensional), the fibres of the vertical maps are connected components of the complex analytic spaces in the first row. The upper left (respectively, upper right) space is identified with the complex points of
$T \neq \Sigma _p$ (so that the spaces in the top row are positive dimensional), the fibres of the vertical maps are connected components of the complex analytic spaces in the first row. The upper left (respectively, upper right) space is identified with the complex points of ![]() $Sh_{K_T}(G_T)$ (respectively,
$Sh_{K_T}(G_T)$ (respectively, ![]() $Sh_{U_T}(H_T)$). If
$Sh_{U_T}(H_T)$). If ![]() $T=\Sigma _p$, then we take this as a definition of (the complex points of)
$T=\Sigma _p$, then we take this as a definition of (the complex points of) ![]() $Sh_{K_T}(G_T)$ and
$Sh_{K_T}(G_T)$ and ![]() $Sh_{U_T}(H_T)$.
$Sh_{U_T}(H_T)$.
Following [Reference Diamond, Kassei and SasakiDKS23], we will study the relation between the top left and the top right space of the above diagram. To do so, we introduce the following notion, borrowed from [Reference Diamond, Kassei and SasakiDKS23, § 2.3.1].
Definition 3.2.2 We say that ![]() $K_E$ is sufficiently small with respect to
$K_E$ is sufficiently small with respect to ![]() $K_T$ if the following conditions are satisfied:
$K_T$ if the following conditions are satisfied:
(i)
 $E^\times \cap \{ {y}/{y^c} \mid y \in K_E\}=\{1\}$;
$E^\times \cap \{ {y}/{y^c} \mid y \in K_E\}=\{1\}$;(ii)
 $K_E\cap T_F({\mathbb {A}}_f)\subset K_T$;
$K_E\cap T_F({\mathbb {A}}_f)\subset K_T$;(iii)
 $N_{E/F}(K_E)\subset \mathrm {Nm}(K_T)$.
$N_{E/F}(K_E)\subset \mathrm {Nm}(K_T)$.
3.2.3
Given ![]() $K_T$, it is always possible to choose
$K_T$, it is always possible to choose ![]() $K_E$ sufficiently small with respect to
$K_E$ sufficiently small with respect to ![]() $K_T$, cf. [Reference Diamond, Kassei and SasakiDKS23, § 2.3.1]. The main point is that the norm map
$K_T$, cf. [Reference Diamond, Kassei and SasakiDKS23, § 2.3.1]. The main point is that the norm map ![]() ${\mathcal {O}}_E^\times \rightarrow {\mathcal {O}}_F^\times$ has finite kernel, hence we can choose
${\mathcal {O}}_E^\times \rightarrow {\mathcal {O}}_F^\times$ has finite kernel, hence we can choose ![]() $K_E$ satisfying the first condition. Note that this can be done independently of
$K_E$ satisfying the first condition. Note that this can be done independently of ![]() $K_T$; given
$K_T$; given ![]() $K_T$, we can then shrink
$K_T$, we can then shrink ![]() $K_E$ so that it satisfies the second and third conditions. Furthermore, we may choose
$K_E$ so that it satisfies the second and third conditions. Furthermore, we may choose ![]() $K_E$ of the form
$K_E$ of the form ![]() $(\mathcal {O}_E\otimes {\mathbb {Z}}_p)^\times K_E^{p}$ (if
$(\mathcal {O}_E\otimes {\mathbb {Z}}_p)^\times K_E^{p}$ (if ![]() $K_T$ is as in § 3.1.1).
$K_T$ is as in § 3.1.1).
3.2.4 Hecke algebras
Let ![]() $u: G_T \rightarrow H_T$ be the composite of the inclusion
$u: G_T \rightarrow H_T$ be the composite of the inclusion ![]() $G_T \rightarrow G_T \times T_E$ (whose second component is the composition of the structure map and the identity section) and the projection
$G_T \rightarrow G_T \times T_E$ (whose second component is the composition of the structure map and the identity section) and the projection ![]() $G_T \times T_E \rightarrow H_T$. If
$G_T \times T_E \rightarrow H_T$. If ![]() $U_T \subset H_T({\mathbb {A}}_f)$ contains the image of
$U_T \subset H_T({\mathbb {A}}_f)$ contains the image of ![]() $K_T \times K_E$, then
$K_T \times K_E$, then ![]() $u$ induces a map
$u$ induces a map ![]() $K_T\backslash G_T({\mathbb {A}}_f)/K_T \rightarrow U_T\backslash H_T({\mathbb {A}}_f)/U_T$, which, in turn, induces a (set theoretic) pullback map
$K_T\backslash G_T({\mathbb {A}}_f)/K_T \rightarrow U_T\backslash H_T({\mathbb {A}}_f)/U_T$, which, in turn, induces a (set theoretic) pullback map ![]() $r: \mathbb {T}_{U_T}(H_T)\rightarrow \mathbb {T}_{K_T}(G_T)$. On the other hand, the inclusion
$r: \mathbb {T}_{U_T}(H_T)\rightarrow \mathbb {T}_{K_T}(G_T)$. On the other hand, the inclusion ![]() $G_T \rightarrow G_T \times T_E$ gives rise to a morphism of Hecke algebras
$G_T \rightarrow G_T \times T_E$ gives rise to a morphism of Hecke algebras ![]() $i: \mathbb {T}_{K_T}(G_T) \rightarrow \mathbb {T}_{U_T}(H_T)$ sending the characteristic function of a double coset
$i: \mathbb {T}_{K_T}(G_T) \rightarrow \mathbb {T}_{U_T}(H_T)$ sending the characteristic function of a double coset ![]() $K_TgK_T$ to that of
$K_TgK_T$ to that of ![]() $U_T(g, 1)U_T$.
$U_T(g, 1)U_T$.
Lemma 3.2.5 Assume that ![]() $K_E$ is sufficiently small with respect to
$K_E$ is sufficiently small with respect to ![]() $K_T$ and that
$K_T$ and that ![]() $U_T$ is the image of
$U_T$ is the image of ![]() $K_T \times K_E$. Then the composite
$K_T \times K_E$. Then the composite ![]() $r \circ i: \mathbb {T}_{K_T}(G_T)\rightarrow \mathbb {T}_{K_T}(G_T)$ is the identity.
$r \circ i: \mathbb {T}_{K_T}(G_T)\rightarrow \mathbb {T}_{K_T}(G_T)$ is the identity.
Proof. Let us see ![]() $G_T$ as a subgroup of
$G_T$ as a subgroup of ![]() $G_T \times T_E$ and denote by
$G_T \times T_E$ and denote by ![]() $q:(G_T \times T_E)(\mathbb {A}_f)\rightarrow H_T(\mathbb {A}_f)$ the quotient map. Given
$q:(G_T \times T_E)(\mathbb {A}_f)\rightarrow H_T(\mathbb {A}_f)$ the quotient map. Given ![]() $g \in G_T(\mathbb {A}_f)$, we need to prove that
$g \in G_T(\mathbb {A}_f)$, we need to prove that
Take ![]() $x$ belonging to the set on the left-hand side above. Then there exist
$x$ belonging to the set on the left-hand side above. Then there exist ![]() $(k_1, e_1), (k_2, e_2) \in K_T \times K_E$ and
$(k_1, e_1), (k_2, e_2) \in K_T \times K_E$ and ![]() $a \in T_F(\mathbb {A}_f)$ such that
$a \in T_F(\mathbb {A}_f)$ such that
As ![]() $x \in G_T(\mathbb {A}_f)$, we must have
$x \in G_T(\mathbb {A}_f)$, we must have ![]() $a^{-1}e_1e_2=1$, hence
$a^{-1}e_1e_2=1$, hence ![]() $e_1e_2=a \in T_F(\mathbb {A}_f)\cap K_E\subset K_T$. It follows that
$e_1e_2=a \in T_F(\mathbb {A}_f)\cap K_E\subset K_T$. It follows that
3.2.6
The above lemma implies, in particular, that the map ![]() $i: \mathbb {T}_{K_T}(G_T) \rightarrow \mathbb {T}_{U_T}(H_T)$ is injective. In what follows, we will use this map to identify
$i: \mathbb {T}_{K_T}(G_T) \rightarrow \mathbb {T}_{U_T}(H_T)$ is injective. In what follows, we will use this map to identify ![]() $\mathbb {T}_{K_T}(G_T)$ with a sub-algebra of
$\mathbb {T}_{K_T}(G_T)$ with a sub-algebra of ![]() $\mathbb {T}_{U_T}(H_T)$. We will work with the Hecke algebra
$\mathbb {T}_{U_T}(H_T)$. We will work with the Hecke algebra ![]() $\mathbb {T}=\bigotimes _{v}'{\mathbb {Z}}[\operatorname {GL}_2({\mathcal {O}}_v)\backslash \operatorname {GL}_2(F_v)/\operatorname {GL}_2({\mathcal {O}}_v)]$ as in
$\mathbb {T}=\bigotimes _{v}'{\mathbb {Z}}[\operatorname {GL}_2({\mathcal {O}}_v)\backslash \operatorname {GL}_2(F_v)/\operatorname {GL}_2({\mathcal {O}}_v)]$ as in ![]() $\S ~$2.1.2, where the product runs over the set of places of
$\S ~$2.1.2, where the product runs over the set of places of ![]() $F$ lying above a rational prime different from
$F$ lying above a rational prime different from ![]() $p$ and such that the component of
$p$ and such that the component of ![]() $K_T$ at
$K_T$ at ![]() $v$ is hyperspecial.
$v$ is hyperspecial.
The statements in the next lemma are established, in a slightly different setting, in the proof of [Reference Diamond, Kassei and SasakiDKS23, Lemma 2.3.1].
Lemma 3.2.7 Assume that ![]() $K_E$ is sufficiently small with respect to
$K_E$ is sufficiently small with respect to ![]() $K_T$ and that
$K_T$ and that ![]() $U_T$ is the image of
$U_T$ is the image of ![]() $K_T \times K_E$. Then we have the following.
$K_T \times K_E$. Then we have the following.
(i) The map
 $C_{K_T}\rightarrow C_{U_T}$ obtained composing the bottom arrows in (3.2.1.1) is injective.
$C_{K_T}\rightarrow C_{U_T}$ obtained composing the bottom arrows in (3.2.1.1) is injective.(ii) The map
 $j: Sh_{K_T}(G_T)({\mathbb {C}})\rightarrow Sh_{U_T}(H_T)({\mathbb {C}})$ obtained composing the top arrows in (3.2.1.1) restricts to an isomorphism between each connected component of
$j: Sh_{K_T}(G_T)({\mathbb {C}})\rightarrow Sh_{U_T}(H_T)({\mathbb {C}})$ obtained composing the top arrows in (3.2.1.1) restricts to an isomorphism between each connected component of  $Sh_{K_T}(G_T)({\mathbb {C}})$ and a connected component of the target.
$Sh_{K_T}(G_T)({\mathbb {C}})$ and a connected component of the target.
Proof. For the reader's convenience, let us briefly explain how the main points of the argument in the proof of [Reference Diamond, Kassei and SasakiDKS23, Lemma 2.3.1] adapt to our situation.
(i) This follows from the fact that the inclusion ![]() $T_F\rightarrow T_{H_T}$ sending
$T_F\rightarrow T_{H_T}$ sending ![]() $a$ to
$a$ to ![]() $(a, 1)$ is split by the map
$(a, 1)$ is split by the map ![]() $(a, b) \mapsto aN_{E/F}(b)$, which induces splittings
$(a, b) \mapsto aN_{E/F}(b)$, which induces splittings
 \begin{align*} T_{H_T}({\mathbb{Q}})^+=(F^{\times, +}\times E^\times)/F^\times & \rightarrow F^{\times, +} \; & \mathrm{N}_{H_T}(U_T)& \rightarrow \mathrm{Nm}(K_T)\\ (a, b) & \mapsto aN_{E/F}(b) & (\mathrm{Nm}(k), l) & \mapsto \mathrm{Nm}(k)N_{E/F}(l) \end{align*}
\begin{align*} T_{H_T}({\mathbb{Q}})^+=(F^{\times, +}\times E^\times)/F^\times & \rightarrow F^{\times, +} \; & \mathrm{N}_{H_T}(U_T)& \rightarrow \mathrm{Nm}(K_T)\\ (a, b) & \mapsto aN_{E/F}(b) & (\mathrm{Nm}(k), l) & \mapsto \mathrm{Nm}(k)N_{E/F}(l) \end{align*}
(note that the last formula gives a well-defined map ![]() $\mathrm {N}_{H_T}(U_T) \rightarrow \mathrm {Nm}(K_T)$ because of the assumptions that
$\mathrm {N}_{H_T}(U_T) \rightarrow \mathrm {Nm}(K_T)$ because of the assumptions that ![]() $U_T$ is the image of
$U_T$ is the image of ![]() $K_T \times K_E$ and
$K_T \times K_E$ and ![]() $N_{E/F}(K_E)\subset \mathrm {Nm}(K_T)$) of the inclusions
$N_{E/F}(K_E)\subset \mathrm {Nm}(K_T)$) of the inclusions
(ii) If ![]() $T=\Sigma _p$, there is nothing to prove. Assume that
$T=\Sigma _p$, there is nothing to prove. Assume that ![]() $T \neq \Sigma _p$. Then the claim follows from the equality, valid for every
$T \neq \Sigma _p$. Then the claim follows from the equality, valid for every ![]() $g \in G_T({\mathbb {A}}_f)$:
$g \in G_T({\mathbb {A}}_f)$:
Clearly the group on the left-hand side is contained in the group on the right-hand side. Conversely, let ![]() $h \in H_T({\mathbb {Q}})^+\cap g U_T g^{-1}$. On the one hand, we can write (the equivalence class of)
$h \in H_T({\mathbb {Q}})^+\cap g U_T g^{-1}$. On the one hand, we can write (the equivalence class of) ![]() $h$ as
$h$ as ![]() $h=a \cdot e$ for some
$h=a \cdot e$ for some ![]() $a \in G_T({\mathbb {Q}})^+, e \in E^\times$; on the other hand,
$a \in G_T({\mathbb {Q}})^+, e \in E^\times$; on the other hand, ![]() $h=g(k \cdot y)g^{-1}$ for some
$h=g(k \cdot y)g^{-1}$ for some ![]() $k \in K_T, y \in K_E$. It follows that
$k \in K_T, y \in K_E$. It follows that ![]() $ae=g(ky)g^{-1}$, which implies that
$ae=g(ky)g^{-1}$, which implies that ![]() $e\cdot c(e)^{-1}=y\cdot c(y)^{-1} \in E^\times \cap \{ {y}/{y^c} \mid y \in K_E\}=\{1\}$. Therefore,
$e\cdot c(e)^{-1}=y\cdot c(y)^{-1} \in E^\times \cap \{ {y}/{y^c} \mid y \in K_E\}=\{1\}$. Therefore, ![]() $y \in K_E \cap T_F({\mathbb {A}}_f)\subset K_T$. This yields
$y \in K_E \cap T_F({\mathbb {A}}_f)\subset K_T$. This yields ![]() $h \in G_T({\mathbb {Q}})^+\cap g K_T g^{-1}$.
$h \in G_T({\mathbb {Q}})^+\cap g K_T g^{-1}$.
3.2.8
Keeping the notation and assumptions of the previous lemma, we set ![]() $I:=C_{U_T}/C_{K_T}$. For each
$I:=C_{U_T}/C_{K_T}$. For each ![]() $\alpha \in I$, let
$\alpha \in I$, let ![]() $Sh_{U_T}^{\alpha }(H_T)({\mathbb {C}}) \subset Sh_{U_T}(H_T)({\mathbb {C}})$ be the subspace consisting of connected components mapping to the
$Sh_{U_T}^{\alpha }(H_T)({\mathbb {C}}) \subset Sh_{U_T}(H_T)({\mathbb {C}})$ be the subspace consisting of connected components mapping to the ![]() $C_{K_T}$-coset inside
$C_{K_T}$-coset inside ![]() $C_{U_T}$ given by
$C_{U_T}$ given by ![]() $\alpha$. We obtain a decomposition
$\alpha$. We obtain a decomposition
into open and closed subspaces; the subspace corresponding to the coset containing the identity is identified with ![]() $Sh_{K_{T}}(G_T)({\mathbb {C}})$ (if
$Sh_{K_{T}}(G_T)({\mathbb {C}})$ (if ![]() $\Sigma _p=T$, cf. the argument in the second part of the proof of [Reference Diamond, Kassei and SasakiDKS23, Lemma 2.3.1]).
$\Sigma _p=T$, cf. the argument in the second part of the proof of [Reference Diamond, Kassei and SasakiDKS23, Lemma 2.3.1]).
Corollary 3.2.9 Assume that ![]() $K_E$ is sufficiently small with respect to
$K_E$ is sufficiently small with respect to ![]() $K_T$ and that
$K_T$ and that ![]() $U_T$ is the image of
$U_T$ is the image of ![]() $K_T \times K_E$. Let
$K_T \times K_E$. Let ![]() $\mathfrak {m}\subset \mathbb {T}$ be a maximal ideal and
$\mathfrak {m}\subset \mathbb {T}$ be a maximal ideal and ![]() $i \geq 0$ an integer. Then:
$i \geq 0$ an integer. Then:
(i)
 $H^i(Sh_{K_T}(G_{T}), {\mathbb {F}}_{\ell })_{\mathfrak {m}}\neq 0$ if and only if
$H^i(Sh_{K_T}(G_{T}), {\mathbb {F}}_{\ell })_{\mathfrak {m}}\neq 0$ if and only if  $H^i(Sh_{U_T}(H_T), {\mathbb {F}}_{\ell })_{\mathfrak {m}}\neq 0$, and the same assertion is true for the cohomology with
$H^i(Sh_{U_T}(H_T), {\mathbb {F}}_{\ell })_{\mathfrak {m}}\neq 0$, and the same assertion is true for the cohomology with  ${\mathbb {Q}}_{\ell }$-coefficients;
${\mathbb {Q}}_{\ell }$-coefficients;(ii) the natural map
 $H^i_c(Sh_{U_T}(H_T), {\mathbb {F}}_{\ell })_\mathfrak {m}\rightarrow H^i(Sh_{U_T}(H_T), {\mathbb {F}}_{\ell })_\mathfrak {m}$ is an isomorphism if and only if the same is true for the map
$H^i_c(Sh_{U_T}(H_T), {\mathbb {F}}_{\ell })_\mathfrak {m}\rightarrow H^i(Sh_{U_T}(H_T), {\mathbb {F}}_{\ell })_\mathfrak {m}$ is an isomorphism if and only if the same is true for the map  $H^i_c(Sh_{K_T}(G_{T}), {\mathbb {F}}_{\ell })_{\mathfrak {m}}\rightarrow H^i(Sh_{K_T}(G_{T}), {\mathbb {F}}_{\ell })_{\mathfrak {m}}$.
$H^i_c(Sh_{K_T}(G_{T}), {\mathbb {F}}_{\ell })_{\mathfrak {m}}\rightarrow H^i(Sh_{K_T}(G_{T}), {\mathbb {F}}_{\ell })_{\mathfrak {m}}$.
Proof. We will work over the complex numbers throughout this proof, and omit this from the notation for simplicity. The decomposition ![]() $Sh_{U_T}(H_T)=\coprod _{\alpha \in I} Sh_{U_T}^{\alpha }(H_T)$ introduced above yields a direct sum decomposition
$Sh_{U_T}(H_T)=\coprod _{\alpha \in I} Sh_{U_T}^{\alpha }(H_T)$ introduced above yields a direct sum decomposition
and each summand on the right-hand side is preserved by the action of ![]() $\mathbb {T}$. Indeed, the Hecke algebra
$\mathbb {T}$. Indeed, the Hecke algebra ![]() $\mathbb {T}$ is spanned by characteristic functions of double cosets
$\mathbb {T}$ is spanned by characteristic functions of double cosets ![]() $K_TgK_T$, whose component at a place
$K_TgK_T$, whose component at a place ![]() $v$ is of the form
$v$ is of the form ![]() $\operatorname {GL}_2(\mathcal {O}_v)\big (\begin{smallmatrix} \varpi _v^{a_v} & 0\\ 0 & \varpi _v^{b_v} \end{smallmatrix}\big )\operatorname {GL}_2(\mathcal {O}_v)$, for some uniformiser
$\operatorname {GL}_2(\mathcal {O}_v)\big (\begin{smallmatrix} \varpi _v^{a_v} & 0\\ 0 & \varpi _v^{b_v} \end{smallmatrix}\big )\operatorname {GL}_2(\mathcal {O}_v)$, for some uniformiser ![]() $\varpi _v$ of
$\varpi _v$ of ![]() $\mathcal {O}_v$ and
$\mathcal {O}_v$ and ![]() $a_v, b_v \in {\mathbb {Z}}$. The group
$a_v, b_v \in {\mathbb {Z}}$. The group ![]() $K_E$ is sufficiently small with respect to
$K_E$ is sufficiently small with respect to ![]() $K_{T, g}:=K_T \cap gK_Tg^{-1}$; letting
$K_{T, g}:=K_T \cap gK_Tg^{-1}$; letting ![]() $U_{T, g}\subset H_T(\mathbb {A}_f)$ be the image of
$U_{T, g}\subset H_T(\mathbb {A}_f)$ be the image of ![]() $K_{T, g} \times K_E$ (which coincides with the group
$K_{T, g} \times K_E$ (which coincides with the group ![]() $U_{T} \cap gU_Tg^{-1}$), the Hecke correspondence
$U_{T} \cap gU_Tg^{-1}$), the Hecke correspondence

restricts to a correspondence on each ![]() $Sh_{U_T}^{\alpha }(H_T)$. Indeed, the map
$Sh_{U_T}^{\alpha }(H_T)$. Indeed, the map ![]() $Sh_{U_{T, g}}(H_T)\rightarrow Sh_{U_{T, g^{-1}}}(H_T)$ induced by right multiplication by
$Sh_{U_{T, g}}(H_T)\rightarrow Sh_{U_{T, g^{-1}}}(H_T)$ induced by right multiplication by ![]() $(g, 1) \in H_T({\mathbb {A}}_f)$ preserves each
$(g, 1) \in H_T({\mathbb {A}}_f)$ preserves each ![]() $Sh_{U_{T, g}}^\alpha (H_T)$, as
$Sh_{U_{T, g}}^\alpha (H_T)$, as ![]() $N_{H_T}((g, 1)) \in {\mathbb {A}}_{F, f}^\times \subset T_{H_T}({\mathbb {A}}_f)$. Hence, each summand in (3.2.9.1) is preserved by the action of
$N_{H_T}((g, 1)) \in {\mathbb {A}}_{F, f}^\times \subset T_{H_T}({\mathbb {A}}_f)$. Hence, each summand in (3.2.9.1) is preserved by the action of ![]() $\mathbb {T}$.
$\mathbb {T}$.
On the other hand, we have an action of ![]() $T_E(\mathbb {A}_f)$ on
$T_E(\mathbb {A}_f)$ on ![]() $Sh_{U_T}(H_{T})$: the action of
$Sh_{U_T}(H_{T})$: the action of ![]() $e \in T_E(\mathbb {A}_f)$ sends each
$e \in T_E(\mathbb {A}_f)$ sends each ![]() $Sh_{U_T}^{\alpha }(H_T)$ to
$Sh_{U_T}^{\alpha }(H_T)$ to ![]() $Sh_{U_T}^{e\alpha }(H_T)$. In particular,
$Sh_{U_T}^{e\alpha }(H_T)$. In particular, ![]() $T_E(\mathbb {A}_f)$ acts transitively on the set of subvarieties
$T_E(\mathbb {A}_f)$ acts transitively on the set of subvarieties ![]() $Sh_{U_T}^{\alpha }(H_T)$, inducing isomorphisms, for every
$Sh_{U_T}^{\alpha }(H_T)$, inducing isomorphisms, for every ![]() $\alpha \in I$:
$\alpha \in I$:
Finally, the action on cohomology induced by the ![]() $T_E(\mathbb {A}_f)$-action on
$T_E(\mathbb {A}_f)$-action on ![]() $Sh_{U_T}(H_{T})$ commutes with the action of
$Sh_{U_T}(H_{T})$ commutes with the action of ![]() $\mathbb {T}$. It follows that the above isomorphism induces an isomorphism
$\mathbb {T}$. It follows that the above isomorphism induces an isomorphism
The isomorphism (3.2.9.2) (which also holds with ![]() ${\mathbb {Q}}_\ell$-coefficients) implies part (i). Furthermore, the previous argument also applies to compactly supported cohomology, yielding a direct sum decomposition of
${\mathbb {Q}}_\ell$-coefficients) implies part (i). Furthermore, the previous argument also applies to compactly supported cohomology, yielding a direct sum decomposition of ![]() $H^i_c(Sh_{U_T}(H_T), {\mathbb {F}}_{\ell })_\mathfrak {m}$ as in (3.2.9.2). Hence we obtain a similar decomposition for the kernel and cokernel of the map
$H^i_c(Sh_{U_T}(H_T), {\mathbb {F}}_{\ell })_\mathfrak {m}$ as in (3.2.9.2). Hence we obtain a similar decomposition for the kernel and cokernel of the map ![]() $H^i_c(Sh_{U_T}(H_T), {\mathbb {F}}_{\ell })_\mathfrak {m}\rightarrow H^i(Sh_{U_T}(H_T), {\mathbb {F}}_{\ell })_\mathfrak {m}$, from which part (ii) follows.
$H^i_c(Sh_{U_T}(H_T), {\mathbb {F}}_{\ell })_\mathfrak {m}\rightarrow H^i(Sh_{U_T}(H_T), {\mathbb {F}}_{\ell })_\mathfrak {m}$, from which part (ii) follows.
3.3 Integral models of unitary Shimura varieties
3.3.1
Fix a totally negative element ![]() $\mathfrak {d} \in \mathcal {O}_F$ coprime to
$\mathfrak {d} \in \mathcal {O}_F$ coprime to ![]() $p$; choose isomorphisms
$p$; choose isomorphisms ![]() $\theta _T: M_2(E)=D_{\emptyset } \buildrel \sim \over \to D_{T}$ for every non-empty subset
$\theta _T: M_2(E)=D_{\emptyset } \buildrel \sim \over \to D_{T}$ for every non-empty subset ![]() $T \subset \Sigma _p$. For every such
$T \subset \Sigma _p$. For every such ![]() $T$, choose an element
$T$, choose an element ![]() $\delta _T \in D_T$ as in [Reference Tian and XiaoTX16, Lemma 3.8], and let
$\delta _T \in D_T$ as in [Reference Tian and XiaoTX16, Lemma 3.8], and let ![]() $\sigma _T=\sqrt {\mathfrak {d}}\delta _T$. Via the construction in § 3.1.3, such a choice gives an involution
$\sigma _T=\sqrt {\mathfrak {d}}\delta _T$. Via the construction in § 3.1.3, such a choice gives an involution ![]() $*_T$ on each
$*_T$ on each ![]() $D_T$. By [Reference Tian and XiaoTX16, Lemma 5.4] we may, and will, choose the elements
$D_T$. By [Reference Tian and XiaoTX16, Lemma 5.4] we may, and will, choose the elements ![]() $\delta _T$ in such a way that these involutions are respected by the isomorphisms
$\delta _T$ in such a way that these involutions are respected by the isomorphisms ![]() $\theta _T$. Let
$\theta _T$. Let ![]() $\mathcal {O}_{D_\emptyset }=M_2(\mathcal {O}_E)\subset D_{\emptyset }$ and
$\mathcal {O}_{D_\emptyset }=M_2(\mathcal {O}_E)\subset D_{\emptyset }$ and ![]() $\mathcal {O}_{D_T}=\theta _T(\mathcal {O}_{D_\emptyset })$ for every non-empty subset
$\mathcal {O}_{D_T}=\theta _T(\mathcal {O}_{D_\emptyset })$ for every non-empty subset ![]() $T \subset \Sigma _p$.
$T \subset \Sigma _p$.
Take ![]() $K_T\subset G_T(\mathbb {A}_f)$ as in § 3.1.1,
$K_T\subset G_T(\mathbb {A}_f)$ as in § 3.1.1, ![]() $K_E=(\mathcal {O}_E\otimes {\mathbb {Z}}_p)^\times K_E^{p} \subset T_E({\mathbb {A}}_f)$ sufficiently small with respect to
$K_E=(\mathcal {O}_E\otimes {\mathbb {Z}}_p)^\times K_E^{p} \subset T_E({\mathbb {A}}_f)$ sufficiently small with respect to ![]() $K_T$ and let
$K_T$ and let ![]() $U_T\subset H_T(\mathbb {A}_f)$ be the image of
$U_T\subset H_T(\mathbb {A}_f)$ be the image of ![]() $K_T \times K_E$. The inverse of the chosen isomorphism
$K_T \times K_E$. The inverse of the chosen isomorphism ![]() $\iota _p: \bar {{\mathbb {Q}}}_p \buildrel \sim \over \to {\mathbb {C}}$ determines a distinguished
$\iota _p: \bar {{\mathbb {Q}}}_p \buildrel \sim \over \to {\mathbb {C}}$ determines a distinguished ![]() $p$-adic place
$p$-adic place ![]() $\wp$ of the reflex field
$\wp$ of the reflex field ![]() $E_T \subset {\mathbb {C}}$. Let
$E_T \subset {\mathbb {C}}$. Let ![]() $E_\wp \subset \bar {{\mathbb {Q}}}_p$ be the completion of
$E_\wp \subset \bar {{\mathbb {Q}}}_p$ be the completion of ![]() $E_T$ at
$E_T$ at ![]() $\wp$, and
$\wp$, and ![]() ${\mathcal {O}}_\wp$ its ring of integers. Following [Reference Diamond, Kassei and SasakiDKS23, § 2] and [Reference Tian and XiaoTX16, § 3], an integral model of
${\mathcal {O}}_\wp$ its ring of integers. Following [Reference Diamond, Kassei and SasakiDKS23, § 2] and [Reference Tian and XiaoTX16, § 3], an integral model of ![]() $Sh_{U_T}(H_T)$ over
$Sh_{U_T}(H_T)$ over ![]() ${\mathcal {O}}_\wp$ can be constructed as follows. Consider the functor sending an
${\mathcal {O}}_\wp$ can be constructed as follows. Consider the functor sending an ![]() ${\mathcal {O}}_\wp$-scheme
${\mathcal {O}}_\wp$-scheme ![]() $S$ to the set of isomorphism classes of tuples
$S$ to the set of isomorphism classes of tuples ![]() $(A, \iota, \lambda, \eta )$ where:
$(A, \iota, \lambda, \eta )$ where:
(i)
 $A/S$ is an abelian scheme of dimension
$A/S$ is an abelian scheme of dimension  $4g$;
$4g$;(ii)
 $\iota : \mathcal {O}_{D_T}\rightarrow \mathrm {End}_S(A)$ is an embedding;
$\iota : \mathcal {O}_{D_T}\rightarrow \mathrm {End}_S(A)$ is an embedding;(iii)
 $\lambda : A \rightarrow A^\vee$ is a
$\lambda : A \rightarrow A^\vee$ is a  ${\mathbb {Z}}_{(p)}^\times$-polarisation whose attached Rosati involution coincides with
${\mathbb {Z}}_{(p)}^\times$-polarisation whose attached Rosati involution coincides with  $*_T$ on
$*_T$ on  $\mathcal {O}_{D_T}$;
$\mathcal {O}_{D_T}$;(iv)
 $\eta$ is a
$\eta$ is a  $U_T$-level structure, in the sense of [Reference Diamond, Kassei and SasakiDKS23, § 2.2.2].
$U_T$-level structure, in the sense of [Reference Diamond, Kassei and SasakiDKS23, § 2.2.2].
Furthermore, the above data are required to satisfy the following conditions.
(a) For every
 $b \in \mathcal {O}_E$, the characteristic polynomial of
$b \in \mathcal {O}_E$, the characteristic polynomial of  $\iota (b)$ acting on
$\iota (b)$ acting on  $\mathrm {Lie}(A/S)$ equals
where the integers
$\mathrm {Lie}(A/S)$ equals
where the integers \[ \prod_{\tilde{\tau} \in \Sigma_{E, \infty}}(X-\tilde{\tau}(b))^{2s_{\tilde{\tau}}}, \]
\[ \prod_{\tilde{\tau} \in \Sigma_{E, \infty}}(X-\tilde{\tau}(b))^{2s_{\tilde{\tau}}}, \]
 $s_{\tilde {\tau }}$ were defined in § 3.1.2.
$s_{\tilde {\tau }}$ were defined in § 3.1.2.(b) The kernel
 $\ker (\lambda [p^\infty ]): A[p^\infty ]\rightarrow A^\vee [p^\infty ]$ is a finite flat subgroup scheme contained in
$\ker (\lambda [p^\infty ]): A[p^\infty ]\rightarrow A^\vee [p^\infty ]$ is a finite flat subgroup scheme contained in  $\prod _{\mathfrak {p} \in T}A[\mathfrak {p}]$ and such that for each
$\prod _{\mathfrak {p} \in T}A[\mathfrak {p}]$ and such that for each  $\mathfrak {p} \in T$ the rank of
$\mathfrak {p} \in T$ the rank of  $\ker (\lambda [p^\infty ])\cap A[\mathfrak {p}]$ is
$\ker (\lambda [p^\infty ])\cap A[\mathfrak {p}]$ is  $p^4$.
$p^4$.(c) The cokernel of
 $\lambda _*: H_1^{dR}(A/S)\rightarrow H_1^{dR}(A^\vee /S)$ is locally free of rank two over
$\lambda _*: H_1^{dR}(A/S)\rightarrow H_1^{dR}(A^\vee /S)$ is locally free of rank two over  $\bigoplus _{\mathfrak {p} \in T} \mathcal {O}_S\otimes _{{\mathbb {Z}}_p} (\mathcal {O}_E\otimes _{\mathcal {O}_F}\mathcal {O}_F/\mathfrak {p})$ (here
$\bigoplus _{\mathfrak {p} \in T} \mathcal {O}_S\otimes _{{\mathbb {Z}}_p} (\mathcal {O}_E\otimes _{\mathcal {O}_F}\mathcal {O}_F/\mathfrak {p})$ (here  $H_1^{dR}(A/S)$ denotes the de Rham homology sheaf of
$H_1^{dR}(A/S)$ denotes the de Rham homology sheaf of  $A/S$).
$A/S$).
This functor is represented by a scheme ![]() $Y_{U_T}(H_T)$ which is an infinite disjoint union of smooth, quasi-projective (respectively, projective if
$Y_{U_T}(H_T)$ which is an infinite disjoint union of smooth, quasi-projective (respectively, projective if ![]() $T$ is non-empty)
$T$ is non-empty) ![]() ${\mathcal {O}}_\wp$-schemes. The group
${\mathcal {O}}_\wp$-schemes. The group ![]() $\mathcal {O}_{F, (p)}^{\times, +}$ acts on this scheme as follows: an element
$\mathcal {O}_{F, (p)}^{\times, +}$ acts on this scheme as follows: an element ![]() $u \in \mathcal {O}_{F, (p)}^{\times, +}$ sends
$u \in \mathcal {O}_{F, (p)}^{\times, +}$ sends ![]() $(A, \iota, \lambda, \eta )$ to
$(A, \iota, \lambda, \eta )$ to ![]() $(A, \iota, u\lambda, \eta )$. This action factors through the group
$(A, \iota, u\lambda, \eta )$. This action factors through the group ![]() $\mathcal {O}_{F, (p)}^{\times, +}/N_{E/F}(U_T \cap E^\times )$, and the resulting quotient is a smooth quasi-projective scheme giving the desired integral model of
$\mathcal {O}_{F, (p)}^{\times, +}/N_{E/F}(U_T \cap E^\times )$, and the resulting quotient is a smooth quasi-projective scheme giving the desired integral model of ![]() $Sh_{U_T}(H_T)$.
$Sh_{U_T}(H_T)$.
Remark 3.3.2 (i) More precisely, the above description of the moduli problem, using the level structure as in [Reference Diamond, Kassei and SasakiDKS23, § 2.2.2], is valid for locally noetherian schemes ![]() $S$. We will need later on to work with non-locally noetherian schemes as well; in this case, one can use a different definition of the level structure, adapting [Reference LanLan18, Definition 1.3.7.6].
$S$. We will need later on to work with non-locally noetherian schemes as well; in this case, one can use a different definition of the level structure, adapting [Reference LanLan18, Definition 1.3.7.6].
(ii) For any field extension ![]() $L$ of
$L$ of ![]() $E_T$, one can define schemes
$E_T$, one can define schemes ![]() $Y_{U_T}(H_T)_L$ over
$Y_{U_T}(H_T)_L$ over ![]() $\mathrm {Spec} \, L$ for arbitrary
$\mathrm {Spec} \, L$ for arbitrary ![]() $U_T=U_T^pU_{T, p}$ representing a moduli problem as above, including
$U_T=U_T^pU_{T, p}$ representing a moduli problem as above, including ![]() $U_{T, p}$-level structure.
$U_{T, p}$-level structure.
Remark 3.3.3 Note that, if ![]() $S$ is the spectrum of a ring where
$S$ is the spectrum of a ring where ![]() $p$ is nilpotent, then conditions (a), (b) and (c) in the definition of the above moduli problem can be stated in terms of the
$p$ is nilpotent, then conditions (a), (b) and (c) in the definition of the above moduli problem can be stated in terms of the ![]() $p$-divisible group (with
$p$-divisible group (with ![]() $\mathcal {O}_E$-action) of the abelian scheme
$\mathcal {O}_E$-action) of the abelian scheme ![]() $A$. Indeed, by [Reference MessingMes72, p. 164] the Lie algebra of
$A$. Indeed, by [Reference MessingMes72, p. 164] the Lie algebra of ![]() $A/S$ (respectively, of the universal vector extension of
$A/S$ (respectively, of the universal vector extension of ![]() $A/S$) is isomorphic to the Lie algebra of
$A/S$) is isomorphic to the Lie algebra of ![]() $A[p^\infty ]$ (respectively, of the universal vector extension of
$A[p^\infty ]$ (respectively, of the universal vector extension of ![]() $A[p^\infty ]$). Hence, the first condition is the Kottwitz condition on
$A[p^\infty ]$). Hence, the first condition is the Kottwitz condition on ![]() $A[p^\infty ]$; the second condition manifestly only depends on
$A[p^\infty ]$; the second condition manifestly only depends on ![]() $A[p^\infty ]$, and the same is true for the third, as the first de Rham cohomology of
$A[p^\infty ]$, and the same is true for the third, as the first de Rham cohomology of ![]() $A/S$ is identified with the Lie algebra of the universal vector extension of the dual of
$A/S$ is identified with the Lie algebra of the universal vector extension of the dual of ![]() $A$ by [Reference Mazur and MessingMM06, Chapter 1, § 4].
$A$ by [Reference Mazur and MessingMM06, Chapter 1, § 4].
4. Comparison of unitary Igusa varieties
In this section, we establish an isomorphism between Igusa varieties that are a priori attached to different unitary Shimura varieties. This relies on a reinterpretation of (some of) the arguments in [Reference Tian and XiaoTX16] in the case of a totally split prime.
4.1 Kottwitz sets
We keep the notation introduced in the previous section. In particular, we fixed in § 3.1.1 a prime ![]() $p$ which splits completely in
$p$ which splits completely in ![]() $F$; hence, we can write
$F$; hence, we can write ![]() $D_T\otimes _{{\mathbb {Q}}}{\mathbb {Q}}_p=\prod _{\mathfrak {p} \in \Sigma _p}D_{T, \mathfrak {p}}$ and
$D_T\otimes _{{\mathbb {Q}}}{\mathbb {Q}}_p=\prod _{\mathfrak {p} \in \Sigma _p}D_{T, \mathfrak {p}}$ and ![]() $H_{T, {\mathbb {Q}}_p}:=H_T \times _{\mathbb {Q}} {\mathbb {Q}}_p=\prod _{\mathfrak {p} \in \Sigma _p}H_{T, \mathfrak {p}}$, where
$H_{T, {\mathbb {Q}}_p}:=H_T \times _{\mathbb {Q}} {\mathbb {Q}}_p=\prod _{\mathfrak {p} \in \Sigma _p}H_{T, \mathfrak {p}}$, where ![]() $D_{T, \mathfrak {p}}:=D_T\otimes _F F_\mathfrak {p}$ and, for every
$D_{T, \mathfrak {p}}:=D_T\otimes _F F_\mathfrak {p}$ and, for every ![]() $F_\mathfrak {p}-$algebra
$F_\mathfrak {p}-$algebra ![]() $R$,
$R$,
According to [Reference Tian and XiaoTX16, Lemma 3.8], the subgroup defined by
is an unramified (respectively, non-quasi-split) group over ![]() $F_\mathfrak {p}$ if
$F_\mathfrak {p}$ if ![]() $\mathfrak {p} \in \Sigma _p \smallsetminus T$ (respectively,
$\mathfrak {p} \in \Sigma _p \smallsetminus T$ (respectively, ![]() $\mathfrak {p} \in T$). Furthermore, the natural maps
$\mathfrak {p} \in T$). Furthermore, the natural maps ![]() $G_T \leftarrow G_T \times T_E \rightarrow H_T$ are compatible with the Deligne homomorphisms and induce isomorphisms of derived and adjoint groups. Denoting by
$G_T \leftarrow G_T \times T_E \rightarrow H_T$ are compatible with the Deligne homomorphisms and induce isomorphisms of derived and adjoint groups. Denoting by ![]() $\mu _T$ the cocharacter of
$\mu _T$ the cocharacter of ![]() $H_{T, \bar {{\mathbb {Q}}}_p}$ induced by
$H_{T, \bar {{\mathbb {Q}}}_p}$ induced by ![]() $(H_T, X_T)$ and by the isomorphism
$(H_T, X_T)$ and by the isomorphism ![]() $\iota _p$, we have the Kottwitz set
$\iota _p$, we have the Kottwitz set ![]() $B(H_{T, {\mathbb {Q}}_p}, \mu _T)$. We can write
$B(H_{T, {\mathbb {Q}}_p}, \mu _T)$. We can write ![]() $B(H_{T, {\mathbb {Q}}_p}, \mu _T)=\prod _{\mathfrak {p} \in \Sigma _p} B(H_{T, \mathfrak {p}}, \mu _{T, \mathfrak {p}})$, where
$B(H_{T, {\mathbb {Q}}_p}, \mu _T)=\prod _{\mathfrak {p} \in \Sigma _p} B(H_{T, \mathfrak {p}}, \mu _{T, \mathfrak {p}})$, where ![]() $\mu _{T, \mathfrak {p}}$ is the
$\mu _{T, \mathfrak {p}}$ is the ![]() $\mathfrak {p}$-component of
$\mathfrak {p}$-component of ![]() $\mu _T$, and it follows from [Reference KottwitzKot97, (6.5.1), (6.5.2)] that
$\mu _T$, and it follows from [Reference KottwitzKot97, (6.5.1), (6.5.2)] that ![]() $B(H_{T, \mathfrak {p}}, \mu _{T, \mathfrak {p}})$ can be described as follows:
$B(H_{T, \mathfrak {p}}, \mu _{T, \mathfrak {p}})$ can be described as follows:
(i) it contains two elements, the basic one and the
 $\mu$-ordinary one, if
$\mu$-ordinary one, if  $\mathfrak {p} \in \Sigma _p \smallsetminus T$;
$\mathfrak {p} \in \Sigma _p \smallsetminus T$;(ii) it is a singleton if
 $\mathfrak {p} \in T$.
$\mathfrak {p} \in T$.
Let ![]() $b=(b_\mathfrak {p})_{\mathfrak {p} \in \Sigma _p} \in B(H_{T, {\mathbb {Q}}_p}, \mu _T)$ and let
$b=(b_\mathfrak {p})_{\mathfrak {p} \in \Sigma _p} \in B(H_{T, {\mathbb {Q}}_p}, \mu _T)$ and let ![]() $B \subset \Sigma _p \smallsetminus T$ be the set of places such that
$B \subset \Sigma _p \smallsetminus T$ be the set of places such that ![]() $b_\mathfrak {p}$ is basic. Let
$b_\mathfrak {p}$ is basic. Let ![]() $T':=T \coprod B$ and
$T':=T \coprod B$ and ![]() $b' \in B(H_{T', {\mathbb {Q}}_p}, \mu _{T'})$ be the element which is
$b' \in B(H_{T', {\mathbb {Q}}_p}, \mu _{T'})$ be the element which is ![]() $\mu$-ordinary at every place
$\mu$-ordinary at every place ![]() $\mathfrak {p} \in \Sigma _p \smallsetminus T'$. We call
$\mathfrak {p} \in \Sigma _p \smallsetminus T'$. We call ![]() $b'$ the element in
$b'$ the element in ![]() $B(H_{T', {\mathbb {Q}}_p}, \mu _{T'})$ associated with
$B(H_{T', {\mathbb {Q}}_p}, \mu _{T'})$ associated with ![]() $b$.
$b$.
4.2 Igusa varieties
Every ![]() $b \in B(H_{T, {\mathbb {Q}}_p}, \mu _T)$ corresponds to a Newton stratum in the special fibre of
$b \in B(H_{T, {\mathbb {Q}}_p}, \mu _T)$ corresponds to a Newton stratum in the special fibre of ![]() $Y_{U_T}(H_T)$, hence to a Newton stratum in the special fibre of
$Y_{U_T}(H_T)$, hence to a Newton stratum in the special fibre of ![]() $Sh_{U_T}(H_T)$. Let
$Sh_{U_T}(H_T)$. Let ![]() $(\mathbb {X}^b_T, \iota ^b_T, \lambda ^b_T)$ be a
$(\mathbb {X}^b_T, \iota ^b_T, \lambda ^b_T)$ be a ![]() $p$-divisible group with extra structure attached to an
$p$-divisible group with extra structure attached to an ![]() $\bar {\mathbb {F}}_p$-point in such a stratum. Note that, as
$\bar {\mathbb {F}}_p$-point in such a stratum. Note that, as ![]() $p$ splits completely in
$p$ splits completely in ![]() $F$, this datum is equivalent to the datum of a collection of
$F$, this datum is equivalent to the datum of a collection of ![]() $p$-divisible groups with extra structure
$p$-divisible groups with extra structure ![]() $(\mathbb {X}^{b_\mathfrak {p}}_T, \iota ^{b_\mathfrak {p}}_T, \lambda ^{b_\mathfrak {p}}_T)$, for each
$(\mathbb {X}^{b_\mathfrak {p}}_T, \iota ^{b_\mathfrak {p}}_T, \lambda ^{b_\mathfrak {p}}_T)$, for each ![]() $\mathfrak {p} \in \Sigma _p$. Similarly, if
$\mathfrak {p} \in \Sigma _p$. Similarly, if ![]() $({\mathcal {G}}, \iota _{\mathcal {G}}, \lambda _{\mathcal {G}})$ is a
$({\mathcal {G}}, \iota _{\mathcal {G}}, \lambda _{\mathcal {G}})$ is a ![]() $p$-divisible group with extra structure then an isomorphism (or, more generally, a quasi-isogeny)
$p$-divisible group with extra structure then an isomorphism (or, more generally, a quasi-isogeny) ![]() $\phi : \mathbb {X}^b_T \rightarrow \mathcal {G}$ commuting with the
$\phi : \mathbb {X}^b_T \rightarrow \mathcal {G}$ commuting with the ![]() ${\mathcal {O}}_{D_T}$-action splits as a sum of isomorphisms (or quasi-isogenies)
${\mathcal {O}}_{D_T}$-action splits as a sum of isomorphisms (or quasi-isogenies) ![]() $\phi _\mathfrak {p}$ indexed by places
$\phi _\mathfrak {p}$ indexed by places ![]() $\mathfrak {p} \in \Sigma _p$. We will write
$\mathfrak {p} \in \Sigma _p$. We will write ![]() $\phi =(\phi _\mathfrak {p})_{\mathfrak {p} \in \Sigma _p}$.
$\phi =(\phi _\mathfrak {p})_{\mathfrak {p} \in \Sigma _p}$.
4.2.1
Let ![]() $\overline {\mathrm {Ig}}_T^b$ be the scheme representing the functor that sends a ring
$\overline {\mathrm {Ig}}_T^b$ be the scheme representing the functor that sends a ring ![]() $R$ of characteristic
$R$ of characteristic ![]() $p$ to the set of isomorphism classes of data
$p$ to the set of isomorphism classes of data ![]() $(r, A, \iota, \lambda, \eta, \phi )$ defined as follows:
$(r, A, \iota, \lambda, \eta, \phi )$ defined as follows:
(i)
 $r: \bar {\mathbb {F}}_p\rightarrow R$ is a ring morphism;
$r: \bar {\mathbb {F}}_p\rightarrow R$ is a ring morphism;(ii)
 $(A, \iota, \lambda, \eta )/\mathrm {Spec} \, R$ is a datum as in the definition of the integral model of
$(A, \iota, \lambda, \eta )/\mathrm {Spec} \, R$ is a datum as in the definition of the integral model of  $Sh_{U_T}(H_T)$, satisfying conditions (a), (b) and (c) in § 3.3;
$Sh_{U_T}(H_T)$, satisfying conditions (a), (b) and (c) in § 3.3;(iii)
 $\phi =(\phi _\mathfrak {p})_{\mathfrak {p} \in \Sigma _p}: A[p^\infty ] \buildrel \sim \over \to \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p, r}R$ is an isomorphism commuting with the
$\phi =(\phi _\mathfrak {p})_{\mathfrak {p} \in \Sigma _p}: A[p^\infty ] \buildrel \sim \over \to \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p, r}R$ is an isomorphism commuting with the  $\mathcal {O}_{D_T}$-action and such that each
$\mathcal {O}_{D_T}$-action and such that each  $\phi _\mathfrak {p}$ respects the polarisation up to a
$\phi _\mathfrak {p}$ respects the polarisation up to a  ${\mathbb {Z}}_p^\times$-factor.
${\mathbb {Z}}_p^\times$-factor.
Two tuples ![]() $(r, A, \iota, \lambda, \eta, \phi ), (r', A', \iota ', \lambda ', \eta ', \phi ')$ are said to be isomorphic if
$(r, A, \iota, \lambda, \eta, \phi ), (r', A', \iota ', \lambda ', \eta ', \phi ')$ are said to be isomorphic if ![]() $r=r'$ and there is an isomorphism of abelian schemes over
$r=r'$ and there is an isomorphism of abelian schemes over ![]() $\mathrm {Spec} \, R$ between
$\mathrm {Spec} \, R$ between ![]() $A$ and
$A$ and ![]() $A'$ commuting with all the additional data.
$A'$ commuting with all the additional data.
Forgetting everything but the structure map ![]() $r$ we see that
$r$ we see that ![]() $\overline {\mathrm {Ig}}_T^b$ is fibred over
$\overline {\mathrm {Ig}}_T^b$ is fibred over ![]() $\bar {\mathbb {F}}_p$; in what follows, if there is no danger of confusion, we will abusively denote its points with values in an
$\bar {\mathbb {F}}_p$; in what follows, if there is no danger of confusion, we will abusively denote its points with values in an ![]() $\bar {\mathbb {F}}_p$-algebra
$\bar {\mathbb {F}}_p$-algebra ![]() $(R, r)$ just by
$(R, r)$ just by ![]() $(A, \iota, \lambda, \eta, \phi ) \in \overline {\mathrm {Ig}}_T^b(R)$. The functor defining
$(A, \iota, \lambda, \eta, \phi ) \in \overline {\mathrm {Ig}}_T^b(R)$. The functor defining ![]() $\overline {\mathrm {Ig}}_T^b$ is representable: indeed,
$\overline {\mathrm {Ig}}_T^b$ is representable: indeed, ![]() $\overline {\mathrm {Ig}}_T^b\rightarrow Y_{U_T}(H_T)_{\bar {\mathbb {F}}_p}$ relatively represents the moduli problem parametrising isomorphisms
$\overline {\mathrm {Ig}}_T^b\rightarrow Y_{U_T}(H_T)_{\bar {\mathbb {F}}_p}$ relatively represents the moduli problem parametrising isomorphisms ![]() $\phi : A[p^\infty ]\buildrel \sim \over \to \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p, r}R$ as above. By definition, such an isomorphisms is a compatible sequence of isomorphisms
$\phi : A[p^\infty ]\buildrel \sim \over \to \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p, r}R$ as above. By definition, such an isomorphisms is a compatible sequence of isomorphisms ![]() $\phi _k: A[p^k]\buildrel \sim \over \to \mathbb {X}^b_T[p^k]\times _{\bar {\mathbb {F}}_p, r}R$ for
$\phi _k: A[p^k]\buildrel \sim \over \to \mathbb {X}^b_T[p^k]\times _{\bar {\mathbb {F}}_p, r}R$ for ![]() $k \geq 0$. Hence
$k \geq 0$. Hence ![]() $\overline {\mathrm {Ig}}_T^b$ is the inverse limit of the schemes
$\overline {\mathrm {Ig}}_T^b$ is the inverse limit of the schemes ![]() $\overline {\mathrm {Ig}}_{T, k}^b\rightarrow Y_{U_T}(H_T)_{\bar {\mathbb {F}}_p}$ parametrising isomorphisms
$\overline {\mathrm {Ig}}_{T, k}^b\rightarrow Y_{U_T}(H_T)_{\bar {\mathbb {F}}_p}$ parametrising isomorphisms ![]() $\phi _k$ as above; each of these moduli problems is relatively representable (cf. [Reference Caraiani and ScholzeCS17, Proposition 4.3.3]) and the transition maps are finite.
$\phi _k$ as above; each of these moduli problems is relatively representable (cf. [Reference Caraiani and ScholzeCS17, Proposition 4.3.3]) and the transition maps are finite.
Recall that we have an action of ![]() ${\mathcal {O}}_{F, (p)}^{\times, +}$ on
${\mathcal {O}}_{F, (p)}^{\times, +}$ on ![]() $Y_{U_T}(H_T)_{\bar {\mathbb {F}}_p}$. For each
$Y_{U_T}(H_T)_{\bar {\mathbb {F}}_p}$. For each ![]() $k \geq 0$, consider the quotient
$k \geq 0$, consider the quotient ![]() $\Delta _k:=\mathcal {O}_{F, (p)}^\times /\{N_{E/F}(u), u \in U_T \cap \mathcal {O}_E^\times, u \equiv 1 \pmod {p^k}\}$; set
$\Delta _k:=\mathcal {O}_{F, (p)}^\times /\{N_{E/F}(u), u \in U_T \cap \mathcal {O}_E^\times, u \equiv 1 \pmod {p^k}\}$; set ![]() $\Delta :=\varprojlim _k \Delta _k$. The action of
$\Delta :=\varprojlim _k \Delta _k$. The action of ![]() $\mathcal {O}_{F, (p)}^{\times, +}$ on
$\mathcal {O}_{F, (p)}^{\times, +}$ on ![]() $\overline {\mathrm {Ig}}_{T, k}^b$ lifting the action on
$\overline {\mathrm {Ig}}_{T, k}^b$ lifting the action on ![]() $Y_{U_T}(H_T)_{\bar {\mathbb {F}}_p}$ factors through
$Y_{U_T}(H_T)_{\bar {\mathbb {F}}_p}$ factors through ![]() $\Delta _k$, hence we get an action of
$\Delta _k$, hence we get an action of ![]() $\Delta$ on
$\Delta$ on ![]() $\overline {\mathrm {Ig}}_T^b$. We define
$\overline {\mathrm {Ig}}_T^b$. We define ![]() $\mathrm {Ig}_T^b:=\overline {\mathrm {Ig}}_T^b/\Delta$.
$\mathrm {Ig}_T^b:=\overline {\mathrm {Ig}}_T^b/\Delta$.
For each ![]() $\mathfrak {p} \in \Sigma _p$ fix an element
$\mathfrak {p} \in \Sigma _p$ fix an element ![]() $x_\mathfrak {p} \in {\mathcal {O}}_F^+$ with
$x_\mathfrak {p} \in {\mathcal {O}}_F^+$ with ![]() $\mathfrak {p}$-adic valuation one, and with
$\mathfrak {p}$-adic valuation one, and with ![]() $\mathfrak {p}'$-adic valuation zero for every
$\mathfrak {p}'$-adic valuation zero for every ![]() $\mathfrak {p}' \in \Sigma _p \smallsetminus \{\mathfrak {p}\}$. The following lemma gives a description of the functor of points of
$\mathfrak {p}' \in \Sigma _p \smallsetminus \{\mathfrak {p}\}$. The following lemma gives a description of the functor of points of ![]() $\overline {\mathrm {Ig}}_T^b$ in terms of abelian schemes up to
$\overline {\mathrm {Ig}}_T^b$ in terms of abelian schemes up to ![]() $p$-quasi-isogeny; see also [Reference Caraiani and ScholzeCS17, Lemma 4.3.4].
$p$-quasi-isogeny; see also [Reference Caraiani and ScholzeCS17, Lemma 4.3.4].
Lemma 4.2.2 Let ![]() $R$ be a ring of characteristic
$R$ be a ring of characteristic ![]() $p$. There is a bijection, functorial in
$p$. There is a bijection, functorial in ![]() $R$, between
$R$, between ![]() $\overline {\mathrm {Ig}}_T^b(R)$ and the set of isomorphism classes of data
$\overline {\mathrm {Ig}}_T^b(R)$ and the set of isomorphism classes of data ![]() $(r, A, \iota, \lambda, \eta, \rho )$ defined as follows:
$(r, A, \iota, \lambda, \eta, \rho )$ defined as follows:
(i)
 $r: \bar {\mathbb {F}}_p\rightarrow R$ is a ring morphism;
$r: \bar {\mathbb {F}}_p\rightarrow R$ is a ring morphism;(ii)
 $A$ is an abelian scheme of dimension
$A$ is an abelian scheme of dimension  $4g$ over
$4g$ over  $\mathrm {Spec} \, R$;
$\mathrm {Spec} \, R$;(iii)
 $\iota : \mathcal {O}_{D_T}\rightarrow \mathrm {End}_R(A)$ is an embedding;
$\iota : \mathcal {O}_{D_T}\rightarrow \mathrm {End}_R(A)$ is an embedding;(iv)
 $\lambda : A \rightarrow A^\vee$ is a
$\lambda : A \rightarrow A^\vee$ is a  ${\mathbb {Z}}_{(p)}^\times$-polarisation such that the attached Rosati involution coincides with
${\mathbb {Z}}_{(p)}^\times$-polarisation such that the attached Rosati involution coincides with  $*_T$ on
$*_T$ on  $\mathcal {O}_{D_T}$;
$\mathcal {O}_{D_T}$;(v)
 $\eta$ is a level structure, defined as in § 3.3;
$\eta$ is a level structure, defined as in § 3.3;(vi)
 $\rho =(\rho _\mathfrak {p})_{\mathfrak {p} \in \Sigma _p}: A[p^\infty ] \rightarrow \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p, r}R$ is a quasi-isogeny commuting with
$\rho =(\rho _\mathfrak {p})_{\mathfrak {p} \in \Sigma _p}: A[p^\infty ] \rightarrow \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p, r}R$ is a quasi-isogeny commuting with  $\mathcal {O}_{D_T}$-action and such that each
$\mathcal {O}_{D_T}$-action and such that each  $\rho _\mathfrak {p}$ respects the polarisation up to a
$\rho _\mathfrak {p}$ respects the polarisation up to a  ${\mathbb {Q}}_p^\times$-factor.
${\mathbb {Q}}_p^\times$-factor.
Two tuples ![]() $(r, A, \iota, \lambda, \eta, \rho ), (r', A', \iota ', \lambda ', \eta ', \rho ')$ are regarded as isomorphic if
$(r, A, \iota, \lambda, \eta, \rho ), (r', A', \iota ', \lambda ', \eta ', \rho ')$ are regarded as isomorphic if ![]() $r=r'$ and there is a
$r=r'$ and there is a ![]() $p$-quasi-isogeny from
$p$-quasi-isogeny from ![]() $A$ to
$A$ to ![]() $A'$ commuting with
$A'$ commuting with ![]() $\mathcal {O}_{D_T}$-action, level structure and the quasi-isogenies
$\mathcal {O}_{D_T}$-action, level structure and the quasi-isogenies ![]() $\rho, \rho '$, and respecting polarisations up to a product of integral powers of the elements
$\rho, \rho '$, and respecting polarisations up to a product of integral powers of the elements ![]() $x_\mathfrak {p}$.
$x_\mathfrak {p}$.
Remark 4.2.3 Before proving the lemma, let us comment on its content. The first point is that the datum ![]() $(A, \iota, \lambda, \eta )$ is not a priori required to satisfy the conditions (a), (b) and (c) in § 3.3; the second point is that the isomorphism
$(A, \iota, \lambda, \eta )$ is not a priori required to satisfy the conditions (a), (b) and (c) in § 3.3; the second point is that the isomorphism ![]() $\phi$ in the definition of the moduli problem represented by
$\phi$ in the definition of the moduli problem represented by ![]() $\overline {\mathrm {Ig}}_T^b$ is replaced by a quasi-isogeny
$\overline {\mathrm {Ig}}_T^b$ is replaced by a quasi-isogeny ![]() $\rho$ (at the price of changing the notion of isomorphism of the data we are parametrising). Both points will be crucial in the next theorem.
$\rho$ (at the price of changing the notion of isomorphism of the data we are parametrising). Both points will be crucial in the next theorem.
Proof. Let ![]() $R$ be an
$R$ be an ![]() $\bar {\mathbb {F}}_p$-algebra. An isomorphism class of data
$\bar {\mathbb {F}}_p$-algebra. An isomorphism class of data ![]() $(A, \iota, \lambda, \eta, \phi )$ corresponding to an
$(A, \iota, \lambda, \eta, \phi )$ corresponding to an ![]() $R$-point of
$R$-point of ![]() $\overline {\mathrm {Ig}}_T^b$ gives rise to a tuple as in the statement of the lemma. Conversely, let
$\overline {\mathrm {Ig}}_T^b$ gives rise to a tuple as in the statement of the lemma. Conversely, let ![]() $(A, \iota, \lambda, \eta, \rho )$ be a datum as in the statement of the lemma; multiplying
$(A, \iota, \lambda, \eta, \rho )$ be a datum as in the statement of the lemma; multiplying ![]() $\rho$ by suitable powers of the elements
$\rho$ by suitable powers of the elements ![]() $x_\mathfrak {p}$ we obtain an isogeny, abusively still denoted by the same symbol,
$x_\mathfrak {p}$ we obtain an isogeny, abusively still denoted by the same symbol, ![]() $\rho : A[p^\infty ]\rightarrow \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p}R$, commuting with
$\rho : A[p^\infty ]\rightarrow \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p}R$, commuting with ![]() $\mathcal {O}_{D_T}$-action and polarisation (the latter up to a
$\mathcal {O}_{D_T}$-action and polarisation (the latter up to a ![]() ${\mathbb {Q}}_p^\times$-factor on each component). Letting
${\mathbb {Q}}_p^\times$-factor on each component). Letting ![]() $B=A/\ker (\rho )$, the map
$B=A/\ker (\rho )$, the map ![]() $\rho$ induces an isomorphism
$\rho$ induces an isomorphism ![]() $\bar {\rho }: B[p^\infty ]\xrightarrow {\sim } \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p}R$, and this property characterises uniquely
$\bar {\rho }: B[p^\infty ]\xrightarrow {\sim } \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p}R$, and this property characterises uniquely ![]() $B$ among abelian schemes in the
$B$ among abelian schemes in the ![]() $p$-power isogeny class of
$p$-power isogeny class of ![]() $A$. In order to complete the proof we need to endow
$A$. In order to complete the proof we need to endow ![]() $B$ with extra structures
$B$ with extra structures ![]() $\iota _B, \lambda _B, \eta _B, \phi$ in such a way that
$\iota _B, \lambda _B, \eta _B, \phi$ in such a way that ![]() $(B, \iota _B, \lambda _B, \eta _B, \phi )$ is a point of
$(B, \iota _B, \lambda _B, \eta _B, \phi )$ is a point of ![]() $\overline {\mathrm {Ig}}^b_T$, and the quotient map
$\overline {\mathrm {Ig}}^b_T$, and the quotient map ![]() $q: A\rightarrow B$ respects the extra structures as in the statement of the lemma.
$q: A\rightarrow B$ respects the extra structures as in the statement of the lemma.
Let us start by defining the ![]() $\mathcal {O}_{D_T}$-action on
$\mathcal {O}_{D_T}$-action on ![]() $B$. Given
$B$. Given ![]() $o \in \mathcal {O}_{D_T}$ we consider the self-quasi-isogeny
$o \in \mathcal {O}_{D_T}$ we consider the self-quasi-isogeny ![]() $\iota _B(o):=q \circ \iota (o) \circ q^{-1}$ of
$\iota _B(o):=q \circ \iota (o) \circ q^{-1}$ of ![]() $B$. Let us look at the following diagram.
$B$. Let us look at the following diagram.

By assumption, the largest square and the left square in the diagram commute; it follows that the right square also commutes. We deduce that ![]() $\iota _B(o): B \rightarrow B$ is a morphism (and not just a quasi-isogeny) as the same is true for
$\iota _B(o): B \rightarrow B$ is a morphism (and not just a quasi-isogeny) as the same is true for ![]() $\iota _T^b(o): \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p}R \rightarrow \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p}R$. Hence, the map sending
$\iota _T^b(o): \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p}R \rightarrow \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p}R$. Hence, the map sending ![]() $o$ to
$o$ to ![]() $\iota _B(o)$ endows
$\iota _B(o)$ endows ![]() $B$ with an
$B$ with an ![]() $\mathcal {O}_{D_T}$-action, which commutes with the quotient map
$\mathcal {O}_{D_T}$-action, which commutes with the quotient map ![]() $A \rightarrow B$ by construction.
$A \rightarrow B$ by construction.
Let us now define the polarisation ![]() $\lambda _B$. We consider the quasi-isogeny
$\lambda _B$. We consider the quasi-isogeny ![]() $\lambda '_B:=(q^\vee )^{-1}\circ \lambda \circ q^{-1}: B \rightarrow B^\vee$. It fits in the following diagram.
$\lambda '_B:=(q^\vee )^{-1}\circ \lambda \circ q^{-1}: B \rightarrow B^\vee$. It fits in the following diagram.

By assumption, the map ![]() $\rho =\bar {\rho }\circ q$ can be written as
$\rho =\bar {\rho }\circ q$ can be written as ![]() $\rho =(\rho _\mathfrak {p})_{\mathfrak {p} \in \Sigma _p}$ where each
$\rho =(\rho _\mathfrak {p})_{\mathfrak {p} \in \Sigma _p}$ where each ![]() $\rho _\mathfrak {p}$ respects polarisations on the
$\rho _\mathfrak {p}$ respects polarisations on the ![]() $\mathfrak {p}$-component of the relevant
$\mathfrak {p}$-component of the relevant ![]() $p$-divisible groups up to a factor
$p$-divisible groups up to a factor ![]() $c_\mathfrak {p} \in {\mathbb {Q}}_p^\times$, i.e. we have
$c_\mathfrak {p} \in {\mathbb {Q}}_p^\times$, i.e. we have ![]() $(\rho _\mathfrak {p}^\vee )^{-1} \circ \lambda _\mathfrak {p} \circ (\rho _\mathfrak {p})^{-1}=c_\mathfrak {p}\lambda _{\mathbb {X}^{b_\mathfrak {p}}_T}$. For each
$(\rho _\mathfrak {p}^\vee )^{-1} \circ \lambda _\mathfrak {p} \circ (\rho _\mathfrak {p})^{-1}=c_\mathfrak {p}\lambda _{\mathbb {X}^{b_\mathfrak {p}}_T}$. For each ![]() $\mathfrak {p}$ let
$\mathfrak {p}$ let ![]() $v_\mathfrak {p}$ be the valuation of
$v_\mathfrak {p}$ be the valuation of ![]() $c_\mathfrak {p}$, and set
$c_\mathfrak {p}$, and set ![]() $\lambda _B:=(\prod _{\mathfrak {p} \in \Sigma _p} x_\mathfrak {p}^{-v_\mathfrak {p}})\lambda '_B$; then the isomorphism
$\lambda _B:=(\prod _{\mathfrak {p} \in \Sigma _p} x_\mathfrak {p}^{-v_\mathfrak {p}})\lambda '_B$; then the isomorphism ![]() $\bar {\rho }$ commutes with the polarisations
$\bar {\rho }$ commutes with the polarisations ![]() $\lambda _B$ and
$\lambda _B$ and ![]() $\lambda _{\mathbb {X}^b_T}$ up to a
$\lambda _{\mathbb {X}^b_T}$ up to a ![]() ${\mathbb {Z}}_p^\times$-factor on each component.
${\mathbb {Z}}_p^\times$-factor on each component.
Let ![]() $\eta _B$ be the (prime to
$\eta _B$ be the (prime to ![]() $p$) level structure on
$p$) level structure on ![]() $B$ induced by
$B$ induced by ![]() $\eta$ and
$\eta$ and ![]() $q$. Let the isomorphism
$q$. Let the isomorphism ![]() $\phi$ be given by
$\phi$ be given by ![]() $\bar {\rho }$. Note that changing the polarisation on
$\bar {\rho }$. Note that changing the polarisation on ![]() $A$ by a product of powers of the elements
$A$ by a product of powers of the elements ![]() $x_\mathfrak {p}$ does not affect the polarisation
$x_\mathfrak {p}$ does not affect the polarisation ![]() $\lambda _B$, hence the isomorphism class of
$\lambda _B$, hence the isomorphism class of ![]() $(B, \iota _B, \lambda _B, \eta _B, \phi )$ only depends on the isomorphism class of
$(B, \iota _B, \lambda _B, \eta _B, \phi )$ only depends on the isomorphism class of ![]() $(A, \iota, \lambda, \eta, \rho )$ (in the sense of the lemma).
$(A, \iota, \lambda, \eta, \rho )$ (in the sense of the lemma).
Furthermore, by construction, the map ![]() $q$ commutes with polarisations up to a product of powers of the elements
$q$ commutes with polarisations up to a product of powers of the elements ![]() $x_\mathfrak {p}$, and respects all the other additional structures; therefore, the data
$x_\mathfrak {p}$, and respects all the other additional structures; therefore, the data ![]() $(A, \iota, \lambda, \eta, \rho )$ and
$(A, \iota, \lambda, \eta, \rho )$ and ![]() $(B, \iota _B, \lambda _B, \eta _B, \phi )$ are isomorphic in the sense of the lemma.
$(B, \iota _B, \lambda _B, \eta _B, \phi )$ are isomorphic in the sense of the lemma.
Finally, the datum ![]() $(B, \iota _B, \lambda _B, \eta _B)$ satisfies conditions (a), (b) and (c) in § 3.3, hence is a point of
$(B, \iota _B, \lambda _B, \eta _B)$ satisfies conditions (a), (b) and (c) in § 3.3, hence is a point of ![]() $\overline {\mathrm {Ig}}_T^b$. This follows from Remark 3.3.3 and from the fact that the
$\overline {\mathrm {Ig}}_T^b$. This follows from Remark 3.3.3 and from the fact that the ![]() $p$-divisible group
$p$-divisible group ![]() $\mathbb {X}^b_T$ comes from an abelian variety with extra structure satisfying the same conditions.
$\mathbb {X}^b_T$ comes from an abelian variety with extra structure satisfying the same conditions.
Theorem 4.2.4 Let ![]() $b \in B(H_{T, {\mathbb {Q}}_p}, \mu _T)$ and let
$b \in B(H_{T, {\mathbb {Q}}_p}, \mu _T)$ and let ![]() $B\subset \Sigma _p \smallsetminus T$ be the subset of places
$B\subset \Sigma _p \smallsetminus T$ be the subset of places ![]() $\mathfrak {p}$ such that
$\mathfrak {p}$ such that ![]() $b_\mathfrak {p}$ is basic. Let
$b_\mathfrak {p}$ is basic. Let ![]() $T'=T \coprod B$ and let
$T'=T \coprod B$ and let ![]() $b' \in B(H_{T', {\mathbb {Q}}_p}, \mu _{T'})$ be the element associated with
$b' \in B(H_{T', {\mathbb {Q}}_p}, \mu _{T'})$ be the element associated with ![]() $b$. Then there is an isomorphism
$b$. Then there is an isomorphism
whose induced map in cohomology is equivariant with respect to the action of the Hecke operators outside ![]() $p$.
$p$.
Proof. It suffices to produce an isomorphism ![]() $\overline {\mathrm {Ig}}^b_T \simeq \overline {\mathrm {Ig}}^{b'}_{T'}$ which satisfies the requirements in the theorem and is in addition
$\overline {\mathrm {Ig}}^b_T \simeq \overline {\mathrm {Ig}}^{b'}_{T'}$ which satisfies the requirements in the theorem and is in addition ![]() ${\mathcal {O}}_{F, (p)}^{\times, +}$-equivariant. Recall that in § 3.3 we have chosen isomorphisms
${\mathcal {O}}_{F, (p)}^{\times, +}$-equivariant. Recall that in § 3.3 we have chosen isomorphisms
i.e. isomorphisms ![]() $\theta _T: D_\emptyset \buildrel \sim \over \to D_T$ respecting orders and involutions; we use these isomorphisms to identify the above data, and we denote them by
$\theta _T: D_\emptyset \buildrel \sim \over \to D_T$ respecting orders and involutions; we use these isomorphisms to identify the above data, and we denote them by ![]() $(D, *, \mathcal {O}_D)$ in this proof. With this notation, Lemma 4.2.2 tells us that, for every
$(D, *, \mathcal {O}_D)$ in this proof. With this notation, Lemma 4.2.2 tells us that, for every ![]() $T \subset \Sigma _p$ and every
$T \subset \Sigma _p$ and every ![]() $\bar {\mathbb {F}}_p$-algebra
$\bar {\mathbb {F}}_p$-algebra ![]() $R$, the set
$R$, the set ![]() $\overline {\mathrm {Ig}}_T^b(R)$ is the set of isomorphism classes of data
$\overline {\mathrm {Ig}}_T^b(R)$ is the set of isomorphism classes of data ![]() $(A, \iota, \lambda, \eta, \rho )$ where:
$(A, \iota, \lambda, \eta, \rho )$ where:
(i)
 $A/\mathrm {Spec} \, R$ is an abelian scheme of dimension
$A/\mathrm {Spec} \, R$ is an abelian scheme of dimension  $4g$;
$4g$;(ii)
 $\iota : \mathcal {O}_{D}\rightarrow \mathrm {End}_R(A)$ is an embedding;
$\iota : \mathcal {O}_{D}\rightarrow \mathrm {End}_R(A)$ is an embedding;(iii)
 $\lambda : A \rightarrow A^\vee$ is a
$\lambda : A \rightarrow A^\vee$ is a  ${\mathbb {Z}}_{(p)}^\times$ polarisation whose attached Rosati involution coincides with
${\mathbb {Z}}_{(p)}^\times$ polarisation whose attached Rosati involution coincides with  $*$ on
$*$ on  $\mathcal {O}_{D}$;
$\mathcal {O}_{D}$;(iv)
 $\eta$ is a level structure, defined as in § 3.3;
$\eta$ is a level structure, defined as in § 3.3;(v)
 $\rho : A[p^\infty ]\rightarrow \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p}R$ is a quasi-isogeny commuting with
$\rho : A[p^\infty ]\rightarrow \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p}R$ is a quasi-isogeny commuting with  $\mathcal {O}_{D}$-action and polarisation (the latter up to a constant).
$\mathcal {O}_{D}$-action and polarisation (the latter up to a constant).
In particular, the only datum in the description of the functor of points of ![]() $\overline {\mathrm {Ig}}_T^b$ which depends on
$\overline {\mathrm {Ig}}_T^b$ which depends on ![]() $T$ is the quasi-isogeny
$T$ is the quasi-isogeny ![]() $\rho : A[p^\infty ]\rightarrow \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p}R$. Hence, in order to complete the proof it suffices to show that, if
$\rho : A[p^\infty ]\rightarrow \mathbb {X}^b_T\times _{\bar {\mathbb {F}}_p}R$. Hence, in order to complete the proof it suffices to show that, if ![]() $b$ is associated with
$b$ is associated with ![]() $b'$, then there is a quasi-isogeny
$b'$, then there is a quasi-isogeny ![]() $\rho _{T, T'}: \mathbb {X}^b_T\rightarrow \mathbb {X}^{b'}_{T'}$ commuting with the extra structure. The functor sending
$\rho _{T, T'}: \mathbb {X}^b_T\rightarrow \mathbb {X}^{b'}_{T'}$ commuting with the extra structure. The functor sending ![]() $(A, \iota, \lambda, \eta, \rho )$ to
$(A, \iota, \lambda, \eta, \rho )$ to ![]() $(A, \iota, \lambda, \eta, \rho _{T, T'}\circ \rho )$ will then give the desired isomorphism
$(A, \iota, \lambda, \eta, \rho _{T, T'}\circ \rho )$ will then give the desired isomorphism ![]() $\overline {\mathrm {Ig}}^b_T \simeq \overline {\mathrm {Ig}}^{b'}_{T'}$; as
$\overline {\mathrm {Ig}}^b_T \simeq \overline {\mathrm {Ig}}^{b'}_{T'}$; as ![]() ${\mathcal {O}}_{F, (p)}^{\times, +}$ only acts modifying polarisations by prime to
${\mathcal {O}}_{F, (p)}^{\times, +}$ only acts modifying polarisations by prime to ![]() $p$ quasi-isogenies, this isomorphism is
$p$ quasi-isogenies, this isomorphism is ![]() ${\mathcal {O}}_{F, (p)}^{\times, +}$-equivariant. The existence of a quasi-isogeny
${\mathcal {O}}_{F, (p)}^{\times, +}$-equivariant. The existence of a quasi-isogeny ![]() $\rho _{T, T'}$ as above follows from the construction in the proof of [Reference Tian and XiaoTX16, Lemma 5.18]. Indeed, letting
$\rho _{T, T'}$ as above follows from the construction in the proof of [Reference Tian and XiaoTX16, Lemma 5.18]. Indeed, letting ![]() ${\mathcal {D}}_T$ be the Dieudonné module of
${\mathcal {D}}_T$ be the Dieudonné module of ![]() $\mathbb {X}^b_T$, the argument in [Reference Tian and XiaoTX16, proof of Lemma 5.18, p. 2185] produces a Dieudonné module
$\mathbb {X}^b_T$, the argument in [Reference Tian and XiaoTX16, proof of Lemma 5.18, p. 2185] produces a Dieudonné module ![]() $p{\mathcal {D}}_T \subset N \subset {\mathcal {D}}_T$, giving rise to a closed finite subgroup scheme
$p{\mathcal {D}}_T \subset N \subset {\mathcal {D}}_T$, giving rise to a closed finite subgroup scheme ![]() $Z\subset \mathbb {X}^b_T[p]$; moreover
$Z\subset \mathbb {X}^b_T[p]$; moreover ![]() $\mathbb {X}^b_T/Z$ is isomorphic to
$\mathbb {X}^b_T/Z$ is isomorphic to ![]() $\mathbb {X}^{b'}_{T'}$, and the construction in [Reference Tian and XiaoTX16, proof of Lemma 5.18, p. 2185] endows the quotient
$\mathbb {X}^{b'}_{T'}$, and the construction in [Reference Tian and XiaoTX16, proof of Lemma 5.18, p. 2185] endows the quotient ![]() $\mathbb {X}^b_T/Z$ with extra structures respected by the isogeny
$\mathbb {X}^b_T/Z$ with extra structures respected by the isogeny ![]() $\mathbb {X}^b_T/Z\rightarrow \mathbb {X}^b_T$ whose composite with the quotient map is multiplication by
$\mathbb {X}^b_T/Z\rightarrow \mathbb {X}^b_T$ whose composite with the quotient map is multiplication by ![]() $p$.
$p$.
Remark 4.2.5 (i) The argument in [Reference Tian and XiaoTX16, p. 47] mentioned above constructs ![]() $N$ starting from the unitary Dieudonné module of
$N$ starting from the unitary Dieudonné module of ![]() $\mathbb {X}^b_T$ and using the Frobenius operator; a key point is that this results in a change of signature. The reader may find it helpful to check directly this phenomenon in the explicit examples given in [Reference Bültel and WedhornBW06, (3.2)].
$\mathbb {X}^b_T$ and using the Frobenius operator; a key point is that this results in a change of signature. The reader may find it helpful to check directly this phenomenon in the explicit examples given in [Reference Bültel and WedhornBW06, (3.2)].
(ii) With the notation as in the above theorem, the main result of [Reference Tian and XiaoTX16] implies that the Newton strata indexed by ![]() $b$ and
$b$ and ![]() $b'$ in the special fibres of the Shimura varieties attached to
$b'$ in the special fibres of the Shimura varieties attached to ![]() $H_T$ and
$H_T$ and ![]() $H_{T'}$ are isomorphic. The above result shows that the same is true for the corresponding Igusa varieties. This is natural to expect, in view of Lemma 4.2.2 and of the fact that the isomorphism in [Reference Tian and XiaoTX16] is obtained from a quasi-isogeny on the level of
$H_{T'}$ are isomorphic. The above result shows that the same is true for the corresponding Igusa varieties. This is natural to expect, in view of Lemma 4.2.2 and of the fact that the isomorphism in [Reference Tian and XiaoTX16] is obtained from a quasi-isogeny on the level of ![]() $p$-divisible groups. The existence of such isomorphisms between Igusa varieties is established much more systematically in the function field setting in Sempliner's PhD thesis.
$p$-divisible groups. The existence of such isomorphisms between Igusa varieties is established much more systematically in the function field setting in Sempliner's PhD thesis.
5. The geometry of the Hodge–Tate period morphism
The goal of this section is to establish the infinite-level Mantovan product formula for our abelian-type unitary Shimura varieties. As a consequence, we can compute the fibers of the Hodge–Tate period morphism in terms of Igusa varieties.
5.1 The product formula
Take ![]() $p$ as in the previous section and choose a subset
$p$ as in the previous section and choose a subset ![]() $T \subset \Sigma _p$; in order to simplify the notation, unless otherwise stated we will keep
$T \subset \Sigma _p$; in order to simplify the notation, unless otherwise stated we will keep ![]() $T$ fixed throughout this section, and omit it from the notation. Fix an element
$T$ fixed throughout this section, and omit it from the notation. Fix an element ![]() $b=(b_\mathfrak {p})_{\mathfrak {p} \in \Sigma _p} \in B(H_{{\mathbb {Q}}_p}, \mu )$, and let
$b=(b_\mathfrak {p})_{\mathfrak {p} \in \Sigma _p} \in B(H_{{\mathbb {Q}}_p}, \mu )$, and let ![]() $(\mathbb {X}^b, \iota ^b, \lambda ^b)$ be a
$(\mathbb {X}^b, \iota ^b, \lambda ^b)$ be a ![]() $p$-divisible group with extra structure attached to
$p$-divisible group with extra structure attached to ![]() $b$, giving rise to a collection of
$b$, giving rise to a collection of ![]() $p$-divisible groups with extra structure
$p$-divisible groups with extra structure ![]() $(\mathbb {X}^{b_\mathfrak {p}}, \iota ^{b_\mathfrak {p}}, \lambda ^{b_\mathfrak {p}})$, for
$(\mathbb {X}^{b_\mathfrak {p}}, \iota ^{b_\mathfrak {p}}, \lambda ^{b_\mathfrak {p}})$, for ![]() $\mathfrak {p} \in \Sigma _p$, as in the previous section.
$\mathfrak {p} \in \Sigma _p$, as in the previous section.
5.1.1
Let ![]() $\breve {{\mathcal {O}}}_\wp$ be the ring of integers of the completion of the maximal unramified extension of
$\breve {{\mathcal {O}}}_\wp$ be the ring of integers of the completion of the maximal unramified extension of ![]() $E_\wp$, and let
$E_\wp$, and let ![]() $\mathrm {Nilp}_{\breve {{\mathcal {O}}}_\wp }$ be the category of
$\mathrm {Nilp}_{\breve {{\mathcal {O}}}_\wp }$ be the category of ![]() $\breve {{\mathcal {O}}}_\wp$-algebras in which
$\breve {{\mathcal {O}}}_\wp$-algebras in which ![]() $p$ is nilpotent. Following [Reference Caraiani and ScholzeCS17, Definition 4.3.11], we consider the functor
$p$ is nilpotent. Following [Reference Caraiani and ScholzeCS17, Definition 4.3.11], we consider the functor ![]() $\mathfrak {X}^b: \mathrm {Nilp}_{\breve {{\mathcal {O}}}_\wp } \rightarrow \mathrm {Sets}$ sending
$\mathfrak {X}^b: \mathrm {Nilp}_{\breve {{\mathcal {O}}}_\wp } \rightarrow \mathrm {Sets}$ sending ![]() $R$ to the set of isomorphism classes of data
$R$ to the set of isomorphism classes of data ![]() $(A, \iota, \lambda, \eta, \varphi )$, where:
$(A, \iota, \lambda, \eta, \varphi )$, where:
(i)
 $(A, \iota, \lambda, \eta )/\mathrm {Spec} \, R$ is a datum as in § 3.3; and
$(A, \iota, \lambda, \eta )/\mathrm {Spec} \, R$ is a datum as in § 3.3; and(ii)
 $\varphi =\bigoplus _{\mathfrak {p} \in \Sigma _p}\varphi _\mathfrak {p}: A[p^\infty ]\times _{R} R/p=\bigoplus _{\mathfrak {p} \in \Sigma _p}A[\mathfrak {p}^\infty ]\times _{R} R/p\rightarrow \bigoplus _{\mathfrak {p} \in \Sigma _p} \mathbb {X}^{b_\mathfrak {p}}\times _{\bar {\mathbb {F}}_p}R/p$ is a quasi-isogeny commuting with the
$\varphi =\bigoplus _{\mathfrak {p} \in \Sigma _p}\varphi _\mathfrak {p}: A[p^\infty ]\times _{R} R/p=\bigoplus _{\mathfrak {p} \in \Sigma _p}A[\mathfrak {p}^\infty ]\times _{R} R/p\rightarrow \bigoplus _{\mathfrak {p} \in \Sigma _p} \mathbb {X}^{b_\mathfrak {p}}\times _{\bar {\mathbb {F}}_p}R/p$ is a quasi-isogeny commuting with the  ${\mathcal {O}}_D$-action, and such that each
${\mathcal {O}}_D$-action, and such that each  $\varphi _\mathfrak {p}$ respects the polarisation up to a
$\varphi _\mathfrak {p}$ respects the polarisation up to a  ${\mathbb {Q}}_p^\times$-factor.
${\mathbb {Q}}_p^\times$-factor.
We will now decompose ![]() $\mathfrak {X}^b$ as a product of Rapoport–Zink spaces and a formal lift of an Igusa variety we introduced before, as in [Reference Caraiani and ScholzeCS17, Lemma 4.3.12]. The existence of such lifts is a consequence of the next lemma, which is analogous to [Reference Caraiani and ScholzeCS17, Corollary 4.3.5].
$\mathfrak {X}^b$ as a product of Rapoport–Zink spaces and a formal lift of an Igusa variety we introduced before, as in [Reference Caraiani and ScholzeCS17, Lemma 4.3.12]. The existence of such lifts is a consequence of the next lemma, which is analogous to [Reference Caraiani and ScholzeCS17, Corollary 4.3.5].
Lemma 5.1.2 The scheme ![]() $\overline {\mathrm {Ig}}^b$ is perfect.
$\overline {\mathrm {Ig}}^b$ is perfect.
Proof. We have to show that, for every ring ![]() $R$, the absolute Frobenius
$R$, the absolute Frobenius ![]() $\mathrm {Fr}: \overline {\mathrm {Ig}}^b \rightarrow \overline {\mathrm {Ig}}^b$ induces a bijection on
$\mathrm {Fr}: \overline {\mathrm {Ig}}^b \rightarrow \overline {\mathrm {Ig}}^b$ induces a bijection on ![]() $R$-points. We will use the description of the functor of points of
$R$-points. We will use the description of the functor of points of ![]() $\overline {\mathrm {Ig}}^b$ given in Lemma 4.2.2. As the map
$\overline {\mathrm {Ig}}^b$ given in Lemma 4.2.2. As the map ![]() $\mathrm {Fr}$ is not a morphism of
$\mathrm {Fr}$ is not a morphism of ![]() $\bar {\mathbb {F}}_p$-schemes, in this proof we need to take the
$\bar {\mathbb {F}}_p$-schemes, in this proof we need to take the ![]() $\bar {\mathbb {F}}_p$-algebra structure on
$\bar {\mathbb {F}}_p$-algebra structure on ![]() $R$ into account. Let
$R$ into account. Let ![]() $(r, A, \iota, \lambda, \eta, \rho )$ be an
$(r, A, \iota, \lambda, \eta, \rho )$ be an ![]() $R$-point of
$R$-point of ![]() $\overline {\mathrm {Ig}}^b$; its image via Frobenius is the
$\overline {\mathrm {Ig}}^b$; its image via Frobenius is the ![]() $R$-point
$R$-point ![]() $(r^{(p)}, A^{(p)}, \iota ^{(p)}, \lambda ^{(p)}, \eta ^{(p)}, \rho ^{(p)})$ where:
$(r^{(p)}, A^{(p)}, \iota ^{(p)}, \lambda ^{(p)}, \eta ^{(p)}, \rho ^{(p)})$ where:
(i)
 $r^{(p)}$ is the composite of
$r^{(p)}$ is the composite of  $r$ and the Frobenius on
$r$ and the Frobenius on  $\bar {\mathbb {F}}_p$;
$\bar {\mathbb {F}}_p$;(ii)
 $A^{(p)}:=A \times _{R, \mathrm {Fr}_R}R$;
$A^{(p)}:=A \times _{R, \mathrm {Fr}_R}R$;(iii) (
 $\iota ^{(p)}, \lambda ^{(p)}, \eta ^{(p)}$) are induced from
$\iota ^{(p)}, \lambda ^{(p)}, \eta ^{(p)}$) are induced from  $(\iota, \lambda, \eta )$ by functoriality;
$(\iota, \lambda, \eta )$ by functoriality;(iv)
 $\rho ^{(p)}:=\rho \times \mathrm {Id}: A[p^\infty ] \times _{R, \mathrm {Fr}_R}R \rightarrow (\mathbb {X}^b\times _{\overline {\mathbb {F}}_p, r} R) \times _{R, \mathrm {Fr}_R} R = \mathbb {X}^b\times _{\overline {\mathbb {F}}_p, r^{(p)}} R$.
$\rho ^{(p)}:=\rho \times \mathrm {Id}: A[p^\infty ] \times _{R, \mathrm {Fr}_R}R \rightarrow (\mathbb {X}^b\times _{\overline {\mathbb {F}}_p, r} R) \times _{R, \mathrm {Fr}_R} R = \mathbb {X}^b\times _{\overline {\mathbb {F}}_p, r^{(p)}} R$.
Let ![]() $F_A: A \rightarrow A^{(p)}$ be the relative Frobenius morphism. Then
$F_A: A \rightarrow A^{(p)}$ be the relative Frobenius morphism. Then ![]() $F_A$ commutes with
$F_A$ commutes with ![]() $\iota, \iota ^{(p)}$ (as well as with the level structures) by functoriality. Furthermore, we have
$\iota, \iota ^{(p)}$ (as well as with the level structures) by functoriality. Furthermore, we have
where the first equality holds true by functoriality of relative Frobenius and the second follows from the fact that ![]() $(F_A)^\vee$ is the Verschiebung on
$(F_A)^\vee$ is the Verschiebung on ![]() $A^\vee$, and the composite of Verschiebung and Frobenius is multiplication by
$A^\vee$, and the composite of Verschiebung and Frobenius is multiplication by ![]() $p$. Finally, we have
$p$. Finally, we have
where ![]() $F_{\mathbb {X}^b}: \mathbb {X}^b \times _{\overline {\mathbb {F}}_p, r} R \rightarrow \mathbb {X}^b \times _{\overline {\mathbb {F}}_p, r^{(p)}} R$ is the relative Frobenius. Writing
$F_{\mathbb {X}^b}: \mathbb {X}^b \times _{\overline {\mathbb {F}}_p, r} R \rightarrow \mathbb {X}^b \times _{\overline {\mathbb {F}}_p, r^{(p)}} R$ is the relative Frobenius. Writing ![]() $\prod _{\mathfrak {p} \in \Sigma _p}x_\mathfrak {p}=pt$ with
$\prod _{\mathfrak {p} \in \Sigma _p}x_\mathfrak {p}=pt$ with ![]() $t \in {\mathcal {O}}_{F, (p)}^{\times, +}$, we deduce that the
$t \in {\mathcal {O}}_{F, (p)}^{\times, +}$, we deduce that the ![]() $R$-point
$R$-point ![]() $(r^{(p)}, A^{(p)}, \iota ^{(p)}, \lambda ^{(p)}, \eta ^{(p)}, \rho ^{(p)})$ coincides with the
$(r^{(p)}, A^{(p)}, \iota ^{(p)}, \lambda ^{(p)}, \eta ^{(p)}, \rho ^{(p)})$ coincides with the ![]() $R$-point
$R$-point
Let us denote by ![]() $r^{(-p)}$ the composition of
$r^{(-p)}$ the composition of ![]() $r$ and the inverse of Frobenius on
$r$ and the inverse of Frobenius on ![]() $\overline {\mathbb {F}}_p$; we have the Verschiebung map
$\overline {\mathbb {F}}_p$; we have the Verschiebung map ![]() $V_{\mathbb {X}^b}: \mathbb {X}^b \times _{\bar {\mathbb {F}}_p, r} R \rightarrow \mathbb {X}^b \times _{\bar {\mathbb {F}}_p, r^{(-p)}} R$, and the map
$V_{\mathbb {X}^b}: \mathbb {X}^b \times _{\bar {\mathbb {F}}_p, r} R \rightarrow \mathbb {X}^b \times _{\bar {\mathbb {F}}_p, r^{(-p)}} R$, and the map ![]() $\overline {\mathrm {Ig}}^b \rightarrow \overline {\mathrm {Ig}}^b$ which on
$\overline {\mathrm {Ig}}^b \rightarrow \overline {\mathrm {Ig}}^b$ which on ![]() $R$-points is given by
$R$-points is given by
is the inverse of the map induced by ![]() $\mathrm {Fr}: \overline {\mathrm {Ig}}^b \rightarrow \overline {\mathrm {Ig}}^b$.
$\mathrm {Fr}: \overline {\mathrm {Ig}}^b \rightarrow \overline {\mathrm {Ig}}^b$.
5.1.3 The formal Igusa variety
Since the Igusa variety ![]() $\overline {\mathrm {Ig}}^b$ is perfect, it lifts canonically to a flat
$\overline {\mathrm {Ig}}^b$ is perfect, it lifts canonically to a flat ![]() $p$-adic formal scheme
$p$-adic formal scheme ![]() $\overline {\mathfrak {Ig}}^b: \mathrm {Nilp}_{\breve {{\mathcal {O}}}_\wp } \rightarrow \mathrm {Sets}$ described as follows (see [Reference Caraiani and ScholzeCS17, p. 719]): fix a lift (up to quasi-isogeny)
$\overline {\mathfrak {Ig}}^b: \mathrm {Nilp}_{\breve {{\mathcal {O}}}_\wp } \rightarrow \mathrm {Sets}$ described as follows (see [Reference Caraiani and ScholzeCS17, p. 719]): fix a lift (up to quasi-isogeny) ![]() $\hat {\mathbb {X}}^{b}/\breve {{\mathcal {O}}}_\wp$ of
$\hat {\mathbb {X}}^{b}/\breve {{\mathcal {O}}}_\wp$ of ![]() $\mathbb {X}^b$ with extra structure. For
$\mathbb {X}^b$ with extra structure. For ![]() $R \in \mathrm {Nilp}_{\breve {{\mathcal {O}}}_\wp }$, the
$R \in \mathrm {Nilp}_{\breve {{\mathcal {O}}}_\wp }$, the ![]() $R$-points of
$R$-points of ![]() $\overline {\mathfrak {Ig}}^b$ are isomorphism classes of data
$\overline {\mathfrak {Ig}}^b$ are isomorphism classes of data ![]() $(A, \iota, \lambda, \eta, \phi )$ as in § 4.2.1, except that the target of
$(A, \iota, \lambda, \eta, \phi )$ as in § 4.2.1, except that the target of ![]() $\phi$ is
$\phi$ is ![]() $\hat {\mathbb {X}}^{b}_R:=\hat {\mathbb {X}}^{b}\times _{\breve {{\mathcal {O}}}_\wp }R$.
$\hat {\mathbb {X}}^{b}_R:=\hat {\mathbb {X}}^{b}\times _{\breve {{\mathcal {O}}}_\wp }R$.
The group ![]() $\Delta$ defined in § 4.2 acts on
$\Delta$ defined in § 4.2 acts on ![]() $\overline {\mathfrak {Ig}}^b$, and we set
$\overline {\mathfrak {Ig}}^b$, and we set ![]() $\mathfrak {Ig}^b:=\overline {\mathfrak {Ig}}^b/\Delta$.
$\mathfrak {Ig}^b:=\overline {\mathfrak {Ig}}^b/\Delta$.
5.1.4 Rapoport–Zink spaces
For every ![]() $\mathfrak {p} \in \Sigma _p$ we have the Rapoport–Zink space
$\mathfrak {p} \in \Sigma _p$ we have the Rapoport–Zink space ![]() $\mathfrak {M}^{b_\mathfrak {p}}$ which is the formal scheme
$\mathfrak {M}^{b_\mathfrak {p}}$ which is the formal scheme ![]() $\mathrm {Nilp}_{\breve {{\mathcal {O}}}_\wp } \rightarrow \mathrm {Sets}$ sending
$\mathrm {Nilp}_{\breve {{\mathcal {O}}}_\wp } \rightarrow \mathrm {Sets}$ sending ![]() $R$ to the set of isomorphism classes of data
$R$ to the set of isomorphism classes of data ![]() $({\mathcal {G}}, \iota, \lambda, \rho )$, where:
$({\mathcal {G}}, \iota, \lambda, \rho )$, where:
(i)
 ${\mathcal {G}}$ is a
${\mathcal {G}}$ is a  $p$-divisible group over
$p$-divisible group over  $R$;
$R$;(ii)
 $\iota : {\mathcal {O}}_{D, \mathfrak {p}}\rightarrow \mathrm {End}_R({\mathcal {G}})$ is an action of
$\iota : {\mathcal {O}}_{D, \mathfrak {p}}\rightarrow \mathrm {End}_R({\mathcal {G}})$ is an action of  ${\mathcal {O}}_{D, \mathfrak {p}}:={\mathcal {O}}_D\otimes _{{\mathcal {O}}_F}{\mathcal {O}}_{F_\mathfrak {p}}$;
${\mathcal {O}}_{D, \mathfrak {p}}:={\mathcal {O}}_D\otimes _{{\mathcal {O}}_F}{\mathcal {O}}_{F_\mathfrak {p}}$;(iii)
 $\lambda$ is a polarisation compatible with the involution on
$\lambda$ is a polarisation compatible with the involution on  ${\mathcal {O}}_{D, \mathfrak {p}}$ induced by
${\mathcal {O}}_{D, \mathfrak {p}}$ induced by  $*$ and such that the Kottwitz condition is satisfied;
$*$ and such that the Kottwitz condition is satisfied;(iv)
 $\rho : {\mathcal {G}} \times _{R}R/p \rightarrow \mathbb {X}^{b_\mathfrak {p}}\times _{\bar {\mathbb {F}}_p}R/p$ is a quasi-isogeny commuting with the
$\rho : {\mathcal {G}} \times _{R}R/p \rightarrow \mathbb {X}^{b_\mathfrak {p}}\times _{\bar {\mathbb {F}}_p}R/p$ is a quasi-isogeny commuting with the  ${\mathcal {O}}_{D, \mathfrak {p}}$-action, and respecting polarisations up to a
${\mathcal {O}}_{D, \mathfrak {p}}$-action, and respecting polarisations up to a  ${\mathbb {Q}}_p^\times$-factor.
${\mathbb {Q}}_p^\times$-factor.
Furthermore, we require ![]() $\lambda$ to be principal if
$\lambda$ to be principal if ![]() $\mathfrak {p} \not \in T$. If
$\mathfrak {p} \not \in T$. If ![]() $\mathfrak {p} \in T$, we ask the cokernel of the map induced by
$\mathfrak {p} \in T$, we ask the cokernel of the map induced by ![]() $\lambda$ on Lie algebras of the universal vector extensions of the relevant
$\lambda$ on Lie algebras of the universal vector extensions of the relevant ![]() $p$-divisible groups to be locally free of rank two over
$p$-divisible groups to be locally free of rank two over ![]() $R \otimes _{{\mathbb {Z}}_p}\mathcal {O}_E/\mathfrak {p}\mathcal {O}_E$.
$R \otimes _{{\mathbb {Z}}_p}\mathcal {O}_E/\mathfrak {p}\mathcal {O}_E$.
Two tuples ![]() $({\mathcal {G}}, \iota, \lambda, \rho )$ and
$({\mathcal {G}}, \iota, \lambda, \rho )$ and ![]() $({\mathcal {G}}', \iota ', \lambda ', \rho ')$ are regarded as isomorphic if there exists an isomorphism
$({\mathcal {G}}', \iota ', \lambda ', \rho ')$ are regarded as isomorphic if there exists an isomorphism ![]() ${\mathcal {G}} \rightarrow {\mathcal {G}}'$ commuting with
${\mathcal {G}} \rightarrow {\mathcal {G}}'$ commuting with ![]() $\iota$,
$\iota$, ![]() $\iota '$,
$\iota '$, ![]() $\rho$ and
$\rho$ and ![]() $\rho '$, and respecting polarisations up to a
$\rho '$, and respecting polarisations up to a ![]() ${\mathbb {Z}}_p^\times$-factor. Let
${\mathbb {Z}}_p^\times$-factor. Let ![]() $\mathfrak {M}^b:=\prod _{\mathfrak {p} \in \Sigma _p} \mathfrak {M}^{b_\mathfrak {p}}$.
$\mathfrak {M}^b:=\prod _{\mathfrak {p} \in \Sigma _p} \mathfrak {M}^{b_\mathfrak {p}}$.
5.1.5
We will now define a map ![]() $\alpha : \overline {\mathfrak {Ig}}^b \times _{\breve {{\mathcal {O}}}_\wp } \mathfrak {M}^b \rightarrow \mathfrak {X}^b$. We will denote the object to which some extra structure is attached by a subscript.
$\alpha : \overline {\mathfrak {Ig}}^b \times _{\breve {{\mathcal {O}}}_\wp } \mathfrak {M}^b \rightarrow \mathfrak {X}^b$. We will denote the object to which some extra structure is attached by a subscript.
Fix ![]() $R \in \mathrm {Nilp}_{\breve {{\mathcal {O}}}_\wp }$ and take
$R \in \mathrm {Nilp}_{\breve {{\mathcal {O}}}_\wp }$ and take
Let ![]() ${\mathcal {G}}=\bigoplus _{\mathfrak {p} \in \Sigma _p}{\mathcal {G}}_\mathfrak {p}$ and let
${\mathcal {G}}=\bigoplus _{\mathfrak {p} \in \Sigma _p}{\mathcal {G}}_\mathfrak {p}$ and let ![]() $\rho _ {\mathcal {G}}: {\mathcal {G}} \rightarrow \hat {\mathbb {X}}^b_R$ be the quasi-isogeny lifting
$\rho _ {\mathcal {G}}: {\mathcal {G}} \rightarrow \hat {\mathbb {X}}^b_R$ be the quasi-isogeny lifting ![]() $\bigoplus _{\mathfrak {p} \in \Sigma _p}\rho _{{\mathcal {G}}_\mathfrak {p}}$; we get a quasi-isogeny
$\bigoplus _{\mathfrak {p} \in \Sigma _p}\rho _{{\mathcal {G}}_\mathfrak {p}}$; we get a quasi-isogeny ![]() $\rho _{\mathcal {G}}^{-1}\circ \phi _A: A[p^\infty ]\rightarrow {\mathcal {G}}$ which commutes with the action of
$\rho _{\mathcal {G}}^{-1}\circ \phi _A: A[p^\infty ]\rightarrow {\mathcal {G}}$ which commutes with the action of ![]() ${\mathcal {O}}_D$ and such that each component respects polarisations up to a
${\mathcal {O}}_D$ and such that each component respects polarisations up to a ![]() ${\mathbb {Q}}_p^\times$-factor. We need to construct a point
${\mathbb {Q}}_p^\times$-factor. We need to construct a point ![]() $(B, \iota _{B}, \lambda _{B}, \eta _{B}, \varphi _{B}) \in \mathfrak {X}^b(R)$.
$(B, \iota _{B}, \lambda _{B}, \eta _{B}, \varphi _{B}) \in \mathfrak {X}^b(R)$.
Let ![]() $B$ be the unique abelian scheme in the
$B$ be the unique abelian scheme in the ![]() $p$-isogeny class of
$p$-isogeny class of ![]() $A$ such that
$A$ such that ![]() $\rho _{\mathcal {G}}^{-1}\circ \phi _A$ induces an isomorphism
$\rho _{\mathcal {G}}^{-1}\circ \phi _A$ induces an isomorphism ![]() $\gamma =(\gamma _\mathfrak {p})_{\mathfrak {p} \in \Sigma _p}: B[p^\infty ] \buildrel \sim \over \to {\mathcal {G}}$. We endow
$\gamma =(\gamma _\mathfrak {p})_{\mathfrak {p} \in \Sigma _p}: B[p^\infty ] \buildrel \sim \over \to {\mathcal {G}}$. We endow ![]() $B$ with an action
$B$ with an action ![]() $\iota _B:{\mathcal {O}}_D \rightarrow \mathrm {End}_R(B)$ and with a level structure
$\iota _B:{\mathcal {O}}_D \rightarrow \mathrm {End}_R(B)$ and with a level structure ![]() $\eta _{B}$ defined as in the proof of Lemma 4.2.2. To define the polarisation
$\eta _{B}$ defined as in the proof of Lemma 4.2.2. To define the polarisation ![]() $\lambda _{B}$, look at the following diagram.
$\lambda _{B}$, look at the following diagram.

As in the proof of Lemma 4.2.2 we may rescale the quasi-isogeny ![]() $(q^\vee )^{-1}\circ \lambda _A\circ q^{-1}$ and get a polarisation
$(q^\vee )^{-1}\circ \lambda _A\circ q^{-1}$ and get a polarisation ![]() $\lambda _B$ on
$\lambda _B$ on ![]() $B$ such that
$B$ such that ![]() $\gamma$ interchanges it with
$\gamma$ interchanges it with ![]() $\lambda _{\mathcal {G}}$ up to a
$\lambda _{\mathcal {G}}$ up to a ![]() ${\mathbb {Z}}_p^\times$-factor on each component. Finally, let
${\mathbb {Z}}_p^\times$-factor on each component. Finally, let ![]() $\bar {\gamma }$ be the reduction of
$\bar {\gamma }$ be the reduction of ![]() $\gamma$ modulo
$\gamma$ modulo ![]() $p$ and
$p$ and
Note that, by construction, the polarisation ![]() $\lambda _B$ is unchanged if
$\lambda _B$ is unchanged if ![]() ${\mathcal {G}}$ is replaced by a
${\mathcal {G}}$ is replaced by a ![]() $p$-divisible group
$p$-divisible group ![]() ${\mathcal {G}}'$ endowed with an isomorphism to
${\mathcal {G}}'$ endowed with an isomorphism to ![]() ${\mathcal {G}}$ respecting the extra structures, the polarisation being respected up to a
${\mathcal {G}}$ respecting the extra structures, the polarisation being respected up to a ![]() ${\mathbb {Z}}_p^\times$-factor on each component. Therefore, the resulting map
${\mathbb {Z}}_p^\times$-factor on each component. Therefore, the resulting map ![]() $\alpha : \overline {\mathfrak {Ig}}^b \times _{\breve {{\mathcal {O}}}_\wp } \mathfrak {M}^b \rightarrow \mathfrak {X}^b$ is well-defined.
$\alpha : \overline {\mathfrak {Ig}}^b \times _{\breve {{\mathcal {O}}}_\wp } \mathfrak {M}^b \rightarrow \mathfrak {X}^b$ is well-defined.
Lemma 5.1.6 The map ![]() $\alpha : \overline {\mathfrak {Ig}}^b \times _{\breve {{\mathcal {O}}}_\wp } \mathfrak {M}^b \rightarrow \mathfrak {X}^b$ is an isomorphism.
$\alpha : \overline {\mathfrak {Ig}}^b \times _{\breve {{\mathcal {O}}}_\wp } \mathfrak {M}^b \rightarrow \mathfrak {X}^b$ is an isomorphism.
Proof. We will construct an inverse ![]() $\beta : \mathfrak {X}^b \rightarrow \overline {\mathfrak {Ig}}^b \times _{\breve {{\mathcal {O}}}_\wp } \mathfrak {M}^b$ of the map
$\beta : \mathfrak {X}^b \rightarrow \overline {\mathfrak {Ig}}^b \times _{\breve {{\mathcal {O}}}_\wp } \mathfrak {M}^b$ of the map ![]() $\alpha$. Take
$\alpha$. Take ![]() $(B, \iota _{B}, \lambda _{B}, \eta _{B}, \varphi _{B}) \in \mathfrak {X}^b(R)$ and let
$(B, \iota _{B}, \lambda _{B}, \eta _{B}, \varphi _{B}) \in \mathfrak {X}^b(R)$ and let ![]() ${\mathcal {G}}:=B[p^\infty ]$, endowed with the additional structures coming from
${\mathcal {G}}:=B[p^\infty ]$, endowed with the additional structures coming from ![]() $B$, and with the trivialisation
$B$, and with the trivialisation ![]() $\rho _{\mathcal {G}}:=\varphi _B$. This gives an
$\rho _{\mathcal {G}}:=\varphi _B$. This gives an ![]() $R$-point of
$R$-point of ![]() $\mathfrak {M}^b$. Finally, define
$\mathfrak {M}^b$. Finally, define ![]() $(A, \iota _A, \lambda _A, \eta _A, \phi _A)$ as follows: the abelian scheme
$(A, \iota _A, \lambda _A, \eta _A, \phi _A)$ as follows: the abelian scheme ![]() $A$ is the unique one in the
$A$ is the unique one in the ![]() $p$-isogeny class of
$p$-isogeny class of ![]() $B$ such that the lift of
$B$ such that the lift of ![]() $\varphi _{B}$ induces an isomorphism
$\varphi _{B}$ induces an isomorphism ![]() $\phi _A: A[p^\infty ] \rightarrow \hat {\mathbb {X}}^b_R$, and the additional structures are obtained from those on
$\phi _A: A[p^\infty ] \rightarrow \hat {\mathbb {X}}^b_R$, and the additional structures are obtained from those on ![]() $B$ as in the discussion before the statement of the lemma.
$B$ as in the discussion before the statement of the lemma.
With the notation introduced in the construction of the map ![]() $\alpha$, the composite
$\alpha$, the composite ![]() $\beta \circ \alpha$ sends
$\beta \circ \alpha$ sends
to
The map ![]() $\gamma$ gives an isomorphism, respecting polarisations up to
$\gamma$ gives an isomorphism, respecting polarisations up to ![]() ${\mathbb {Z}}_p^\times$ on each factor, between
${\mathbb {Z}}_p^\times$ on each factor, between ![]() $(B[p^\infty ], \iota _B[p^\infty ], \lambda _B[p^\infty ], \bigoplus _{\mathfrak {p} \in \Sigma _p}\rho _{{\mathcal {G}}_\mathfrak {p}} \circ \bar {\gamma })$ and
$(B[p^\infty ], \iota _B[p^\infty ], \lambda _B[p^\infty ], \bigoplus _{\mathfrak {p} \in \Sigma _p}\rho _{{\mathcal {G}}_\mathfrak {p}} \circ \bar {\gamma })$ and ![]() $({\mathcal {G}}, \iota _{{\mathcal {G}}}, \lambda _{{\mathcal {G}}}, \bigoplus _{\mathfrak {p} \in \Sigma _p}\rho _{{\mathcal {G}}_\mathfrak {p}})$, hence
$({\mathcal {G}}, \iota _{{\mathcal {G}}}, \lambda _{{\mathcal {G}}}, \bigoplus _{\mathfrak {p} \in \Sigma _p}\rho _{{\mathcal {G}}_\mathfrak {p}})$, hence ![]() $\beta \circ \alpha$ is the identity map. Similarly one checks that
$\beta \circ \alpha$ is the identity map. Similarly one checks that ![]() $\alpha \circ \beta$ is the identity.
$\alpha \circ \beta$ is the identity.
5.2 The product formula at infinite level and the Hodge–Tate period map
We now wish to establish an analogue in our situation of [Reference Caraiani and ScholzeCS17, Lemma 4.3.20].
5.2.1 Generic fibres of formal schemes
We will need to work with the adic generic fibres of the formal schemes introduced in the previous section. Recall that to a formal scheme ![]() $\mathfrak {M}$ over
$\mathfrak {M}$ over ![]() $\breve {{\mathcal {O}}}_\wp$ (locally admitting a finitely generated ideal of definition) one can attach an adic space
$\breve {{\mathcal {O}}}_\wp$ (locally admitting a finitely generated ideal of definition) one can attach an adic space ![]() $\mathfrak {M}^{ad}$ as in [Reference Scholze and WeinsteinSW13, Proposition 2.2.1] over
$\mathfrak {M}^{ad}$ as in [Reference Scholze and WeinsteinSW13, Proposition 2.2.1] over ![]() $\mathrm {Spa}(\breve {{\mathcal {O}}}_\wp, \breve {{\mathcal {O}}}_\wp )$; one can then take the adic generic fibre
$\mathrm {Spa}(\breve {{\mathcal {O}}}_\wp, \breve {{\mathcal {O}}}_\wp )$; one can then take the adic generic fibre
where ![]() $\breve {E}_\wp$ is the fraction field of
$\breve {E}_\wp$ is the fraction field of ![]() $\breve {{\mathcal {O}}}_\wp$. With this notation, the product formula in Lemma 5.1.6 becomes, on the generic fibre:
$\breve {{\mathcal {O}}}_\wp$. With this notation, the product formula in Lemma 5.1.6 becomes, on the generic fibre:
The functors of points on complete affinoid ![]() $(\breve {E}_\wp, \breve {{\mathcal {O}}}_\wp )$-algebras of the adic spaces in the previous formula can be described using [Reference Scholze and WeinsteinSW13, Proposition 2.2.2]. It is easier, and sufficient for our purposes, to give such a description restricted to the category
$(\breve {E}_\wp, \breve {{\mathcal {O}}}_\wp )$-algebras of the adic spaces in the previous formula can be described using [Reference Scholze and WeinsteinSW13, Proposition 2.2.2]. It is easier, and sufficient for our purposes, to give such a description restricted to the category ![]() $\mathrm {Perf}_{\breve {E}_\wp }$ of perfectoid Huber pairs
$\mathrm {Perf}_{\breve {E}_\wp }$ of perfectoid Huber pairs ![]() $(R, R^+)$ over
$(R, R^+)$ over ![]() $(\breve {E}_\wp, \breve {{\mathcal {O}}}_\wp )$. For example, the functor of points of
$(\breve {E}_\wp, \breve {{\mathcal {O}}}_\wp )$. For example, the functor of points of ![]() $\mathcal {X}^b$ is the sheafification in the analytic topology of the functor
$\mathcal {X}^b$ is the sheafification in the analytic topology of the functor
 \begin{align*} \mathrm{Perf}_{\breve{E}_\wp} & \rightarrow \mathrm{Sets}\\ (R, R^+) & \mapsto \varprojlim_n \mathfrak{X}^b(R^+/p^n). \end{align*}
\begin{align*} \mathrm{Perf}_{\breve{E}_\wp} & \rightarrow \mathrm{Sets}\\ (R, R^+) & \mapsto \varprojlim_n \mathfrak{X}^b(R^+/p^n). \end{align*}
In other words, up to sheafification, an ![]() $(R, R^+)$-point of
$(R, R^+)$-point of ![]() $\mathcal {X}^b$ is a compatible collection of data
$\mathcal {X}^b$ is a compatible collection of data ![]() $(A_n, \iota _n, \lambda _n, \eta _n, \varphi _n)$ over
$(A_n, \iota _n, \lambda _n, \eta _n, \varphi _n)$ over ![]() $R^+/p^n$ as defined in § 5.1. Note that giving a compatible sequence of quasi-isogenies
$R^+/p^n$ as defined in § 5.1. Note that giving a compatible sequence of quasi-isogenies ![]() $\varphi _n$ just amounts to giving
$\varphi _n$ just amounts to giving ![]() $\varphi _1$; on the other hand, we may see the compatible sequence
$\varphi _1$; on the other hand, we may see the compatible sequence ![]() $(A_n, \iota _n, \lambda _n, \eta _n)$ as a formal scheme with extra structure over
$(A_n, \iota _n, \lambda _n, \eta _n)$ as a formal scheme with extra structure over ![]() $\operatorname {Spf} R^+$, which as above can be regarded as an adic space; we will denote it by
$\operatorname {Spf} R^+$, which as above can be regarded as an adic space; we will denote it by ![]() $(\mathcal {A}, \iota, \lambda, \eta )$. Hence, the compatible sequence of data
$(\mathcal {A}, \iota, \lambda, \eta )$. Hence, the compatible sequence of data ![]() $(A_n, \iota _n, \lambda _n, \eta _n, \varphi _n)$ uniquely corresponds to a datum of the form
$(A_n, \iota _n, \lambda _n, \eta _n, \varphi _n)$ uniquely corresponds to a datum of the form ![]() $(\mathcal {A}, \iota, \lambda, \eta, \varphi )$.
$(\mathcal {A}, \iota, \lambda, \eta, \varphi )$.
A similar description can be given of the functor of points of the other objects appearing in (5.2.1.1), as well as of the good reduction locus ![]() $\mathcal {Y}_{U}(H)^\circ$ inside the analytification
$\mathcal {Y}_{U}(H)^\circ$ inside the analytification ![]() $\mathcal {Y}_{U}(H)$ of the space
$\mathcal {Y}_{U}(H)$ of the space ![]() $Y_{U}(H)_{E_\wp }$; the space
$Y_{U}(H)_{E_\wp }$; the space ![]() $\mathcal {Y}_{U}(H)^\circ$ is defined as the generic fibre of the completion along the special fibre of
$\mathcal {Y}_{U}(H)^\circ$ is defined as the generic fibre of the completion along the special fibre of ![]() $Y_{U, {\mathcal {O}}_\wp }(H)$. In particular, [Reference Scholze and WeinsteinSW13, Lemma 2.2.2] applies and yields a description of the functor of points of
$Y_{U, {\mathcal {O}}_\wp }(H)$. In particular, [Reference Scholze and WeinsteinSW13, Lemma 2.2.2] applies and yields a description of the functor of points of ![]() $\mathcal {Y}_{U}(H)^\circ$ similar to that discussed above for
$\mathcal {Y}_{U}(H)^\circ$ similar to that discussed above for ![]() $\mathcal {X}^b$. Note that the inclusion
$\mathcal {X}^b$. Note that the inclusion ![]() $\mathcal {Y}_{U}(H)^\circ \subset \mathcal {Y}_{U}(H)$ is an equality if
$\mathcal {Y}_{U}(H)^\circ \subset \mathcal {Y}_{U}(H)$ is an equality if ![]() $T$ is non-empty, but it is strict if
$T$ is non-empty, but it is strict if ![]() $T$ is empty.
$T$ is empty.
We will now introduce versions with infinite level at ![]() $p$ of the spaces considered so far.
$p$ of the spaces considered so far.
5.2.2 The space  $\mathcal {M}^b_{\infty }$
$\mathcal {M}^b_{\infty }$
We will first define the Rapoport–Zink space at infinite level ![]() $\mathcal {M}^b_{\infty }:=\prod _{\mathfrak {p} \in \Sigma _p}\mathcal {M}^{b_\mathfrak {p}}_{\infty }$. Each
$\mathcal {M}^b_{\infty }:=\prod _{\mathfrak {p} \in \Sigma _p}\mathcal {M}^{b_\mathfrak {p}}_{\infty }$. Each ![]() $\mathcal {M}^{b_\mathfrak {p}}_{\infty }$ is a pro-étale cover of the generic fibre
$\mathcal {M}^{b_\mathfrak {p}}_{\infty }$ is a pro-étale cover of the generic fibre ![]() $\mathcal {M}^{b_\mathfrak {p}}$ of the adic space attached to the formal scheme
$\mathcal {M}^{b_\mathfrak {p}}$ of the adic space attached to the formal scheme ![]() $\mathfrak {M}^{b_\mathfrak {p}}$.
$\mathfrak {M}^{b_\mathfrak {p}}$.
Fix ![]() $\mathfrak {p} \in \Sigma _p$; as recalled above, the functor of points
$\mathfrak {p} \in \Sigma _p$; as recalled above, the functor of points ![]() $\mathrm {Perf}_{\breve {E}_\wp } \rightarrow \mathrm {Sets}$ of
$\mathrm {Perf}_{\breve {E}_\wp } \rightarrow \mathrm {Sets}$ of ![]() $\mathcal {M}^{b_\mathfrak {p}}$ is the sheafification of the functor sending
$\mathcal {M}^{b_\mathfrak {p}}$ is the sheafification of the functor sending ![]() $(R, R^+)$ to
$(R, R^+)$ to ![]() $\varprojlim _n \mathfrak {M}^{b_\mathfrak {p}}(R^+/p^n)$. Giving such a compatible system of
$\varprojlim _n \mathfrak {M}^{b_\mathfrak {p}}(R^+/p^n)$. Giving such a compatible system of ![]() $(R^+/p^n)$-points amounts to giving a compatible collection of
$(R^+/p^n)$-points amounts to giving a compatible collection of ![]() $p$-divisible groups with extra structure
$p$-divisible groups with extra structure ![]() $(\mathcal {G}_n, \iota _n, \lambda _n)$ as in § 5.1.4 and a quasi-isogeny (respecting extra structures)
$(\mathcal {G}_n, \iota _n, \lambda _n)$ as in § 5.1.4 and a quasi-isogeny (respecting extra structures) ![]() $\rho : \mathcal {G}_1 \rightarrow \mathbb {X}^{b_\mathfrak {p}} \times _{\bar {\mathbb {F}}_p} R^+/p$. Now, by [Reference MessingMes72, Lemma (4.16)], giving a compatible sequence of
$\rho : \mathcal {G}_1 \rightarrow \mathbb {X}^{b_\mathfrak {p}} \times _{\bar {\mathbb {F}}_p} R^+/p$. Now, by [Reference MessingMes72, Lemma (4.16)], giving a compatible sequence of ![]() $p$-divisible groups with extra-structure
$p$-divisible groups with extra-structure ![]() $(\mathcal {G}_n, \iota _n, \lambda _n)$ is equivalent to giving a
$(\mathcal {G}_n, \iota _n, \lambda _n)$ is equivalent to giving a ![]() $p$-divisible group with extra structure
$p$-divisible group with extra structure ![]() $(\mathcal {G}, \iota, \lambda )$ over
$(\mathcal {G}, \iota, \lambda )$ over ![]() $R^+$. For every
$R^+$. For every ![]() $n \geq 1$, the Tate module functor
$n \geq 1$, the Tate module functor ![]() $T(\mathcal {G}_n)$ from
$T(\mathcal {G}_n)$ from ![]() $R^+/p^n$-algebras to sets sending
$R^+/p^n$-algebras to sets sending ![]() $S$ to
$S$ to ![]() $\varprojlim _{k}\mathcal {G}_n[p^k](S)$ is represented by an affine scheme, flat over
$\varprojlim _{k}\mathcal {G}_n[p^k](S)$ is represented by an affine scheme, flat over ![]() $\operatorname {Spec}(R^+/p^n)$, by [Reference Scholze and WeinsteinSW13, Proposition 3.3.1]. Taking the limit over
$\operatorname {Spec}(R^+/p^n)$, by [Reference Scholze and WeinsteinSW13, Proposition 3.3.1]. Taking the limit over ![]() $n$ and passing to the adic generic fibre we obtain an adic space which we denote by
$n$ and passing to the adic generic fibre we obtain an adic space which we denote by ![]() $\mathcal {T}(\mathcal {G})$.
$\mathcal {T}(\mathcal {G})$.
The space ![]() $\mathcal {M}^{b_\mathfrak {p}}_{\infty }$ parametrises trivialisations of the local system on
$\mathcal {M}^{b_\mathfrak {p}}_{\infty }$ parametrises trivialisations of the local system on ![]() $\mathcal {M}^{b_\mathfrak {p}}$ given by
$\mathcal {M}^{b_\mathfrak {p}}$ given by ![]() $\mathcal {T}(\mathcal {G})$. More precisely, let
$\mathcal {T}(\mathcal {G})$. More precisely, let ![]() $\Lambda _\mathfrak {p}=\Big (\begin{smallmatrix} \mathcal {O}_{E_\mathfrak {p}} & \mathcal {O}_{E_\mathfrak {p}}\\ \mathcal {O}_{E_\mathfrak {p}} & \mathcal {O}_{E_\mathfrak {p}} \end{smallmatrix}\Big )$ if
$\Lambda _\mathfrak {p}=\Big (\begin{smallmatrix} \mathcal {O}_{E_\mathfrak {p}} & \mathcal {O}_{E_\mathfrak {p}}\\ \mathcal {O}_{E_\mathfrak {p}} & \mathcal {O}_{E_\mathfrak {p}} \end{smallmatrix}\Big )$ if ![]() $\mathfrak {p} \in \Sigma _p \smallsetminus T$ and
$\mathfrak {p} \in \Sigma _p \smallsetminus T$ and ![]() $\Lambda _\mathfrak {p}=\Big (\begin{smallmatrix} \mathfrak {p}\mathcal {O}_{E_\mathfrak {p}} & \mathcal {O}_{E_\mathfrak {p}}\\ \mathfrak {p}\mathcal {O}_{E_\mathfrak {p}} & \mathcal {O}_{E_\mathfrak {p}} \end{smallmatrix}\Big )$ if
$\Lambda _\mathfrak {p}=\Big (\begin{smallmatrix} \mathfrak {p}\mathcal {O}_{E_\mathfrak {p}} & \mathcal {O}_{E_\mathfrak {p}}\\ \mathfrak {p}\mathcal {O}_{E_\mathfrak {p}} & \mathcal {O}_{E_\mathfrak {p}} \end{smallmatrix}\Big )$ if ![]() $\mathfrak {p} \in T$ (as in [Reference Tian and XiaoTX16, p. 2154]). Following [Reference Scholze and WeinsteinSW13, Definition 6.5.3], we define
$\mathfrak {p} \in T$ (as in [Reference Tian and XiaoTX16, p. 2154]). Following [Reference Scholze and WeinsteinSW13, Definition 6.5.3], we define
as the sheafification of the functor sending ![]() $(R, R^+)$ to the set of isomorphism classes of data
$(R, R^+)$ to the set of isomorphism classes of data ![]() $(\mathcal {G}, \iota, \lambda, \rho, \alpha )$, where
$(\mathcal {G}, \iota, \lambda, \rho, \alpha )$, where ![]() $(\mathcal {G}, \iota, \lambda, \rho )$ is a datum as above, and
$(\mathcal {G}, \iota, \lambda, \rho )$ is a datum as above, and
is an ![]() ${\mathcal {O}}_{D, \mathfrak {p}}$-linear map. We require that there is a compatible choice of
${\mathcal {O}}_{D, \mathfrak {p}}$-linear map. We require that there is a compatible choice of ![]() $p$-power roots of unity in
$p$-power roots of unity in ![]() $R^+$, yielding a map
$R^+$, yielding a map ![]() $\varepsilon : {\mathbb {Z}}_p \rightarrow \mathcal {T}(\mu _{p^\infty })(R, R^+)$, such that the pairing
$\varepsilon : {\mathbb {Z}}_p \rightarrow \mathcal {T}(\mu _{p^\infty })(R, R^+)$, such that the pairing ![]() $\mathrm {Tr} (\psi ):\Lambda _\mathfrak {p} \times \Lambda _\mathfrak {p} \rightarrow {\mathbb {Z}}_p$ and the pairing
$\mathrm {Tr} (\psi ):\Lambda _\mathfrak {p} \times \Lambda _\mathfrak {p} \rightarrow {\mathbb {Z}}_p$ and the pairing ![]() $\mathcal {T}\mathcal {G}(R, R^+) \times \mathcal {T}\mathcal {G}(R, R^+) \rightarrow \mathcal {T}(\mu _{p^\infty })(R, R^+)$ induced by the polarisation are identified via the maps
$\mathcal {T}\mathcal {G}(R, R^+) \times \mathcal {T}\mathcal {G}(R, R^+) \rightarrow \mathcal {T}(\mu _{p^\infty })(R, R^+)$ induced by the polarisation are identified via the maps ![]() $\alpha$ and
$\alpha$ and ![]() $\varepsilon$. Furthermore, we ask that for every map
$\varepsilon$. Furthermore, we ask that for every map ![]() $x: \mathrm {Spa}(K, K^+) \rightarrow \mathrm {Spa}(R, R^+)$ with
$x: \mathrm {Spa}(K, K^+) \rightarrow \mathrm {Spa}(R, R^+)$ with ![]() $K$ a perfectoid field, the induced map
$K$ a perfectoid field, the induced map ![]() $\Lambda _\mathfrak {p} \rightarrow \mathcal {T}(\mathcal {G})(K, K^+)$ is an isomorphism.
$\Lambda _\mathfrak {p} \rightarrow \mathcal {T}(\mathcal {G})(K, K^+)$ is an isomorphism.
5.2.3 The space  $\mathcal {Y}_{U^p}(H)^{\circ }$
$\mathcal {Y}_{U^p}(H)^{\circ }$
Let ![]() $\mathcal {Y}_{U^p}(H)/\breve {E}_\wp$ be the inverse limit of the diamonds attached to the analytifications of the varieties
$\mathcal {Y}_{U^p}(H)/\breve {E}_\wp$ be the inverse limit of the diamonds attached to the analytifications of the varieties ![]() $Y_{U^pU_p}(H)_{\breve {E}_\wp }$, as the compact open subgroup
$Y_{U^pU_p}(H)_{\breve {E}_\wp }$, as the compact open subgroup ![]() $U_p\subset H({\mathbb {Q}}_p)$ varies (cf. Remark 3.3.2). We denote by
$U_p\subset H({\mathbb {Q}}_p)$ varies (cf. Remark 3.3.2). We denote by ![]() $\mathcal {Y}_{U^p}(H)^\circ \subset \mathcal {Y}_{U^p}(H)$ the preimage of
$\mathcal {Y}_{U^p}(H)^\circ \subset \mathcal {Y}_{U^p}(H)$ the preimage of ![]() $\mathcal {Y}_{U}(H)^\circ _{\breve {E}_\wp }$ via the natural projection map. The same argument used in § 5.2.1 shows that
$\mathcal {Y}_{U}(H)^\circ _{\breve {E}_\wp }$ via the natural projection map. The same argument used in § 5.2.1 shows that ![]() $\mathcal {Y}_{U}(H)^\circ : \mathrm {Perf}_{\breve {E}_\mathfrak {p}} \rightarrow \mathrm {Sets}$ is the sheafification of the functor sending
$\mathcal {Y}_{U}(H)^\circ : \mathrm {Perf}_{\breve {E}_\mathfrak {p}} \rightarrow \mathrm {Sets}$ is the sheafification of the functor sending ![]() $(R, R^+)$ to the set of isomorphism classes of data
$(R, R^+)$ to the set of isomorphism classes of data ![]() $(\mathcal {A}, \iota, \lambda, \eta )/\operatorname {Spf} R^+$. On the other hand
$(\mathcal {A}, \iota, \lambda, \eta )/\operatorname {Spf} R^+$. On the other hand ![]() $\mathcal {Y}_{U^p}(H)$ is the inverse limit of the analytifications of schemes over
$\mathcal {Y}_{U^p}(H)$ is the inverse limit of the analytifications of schemes over ![]() $Y_{U}(H)_{\breve {E}_\wp }$ relatively representing trivialisations (respecting extra structure) of the
$Y_{U}(H)_{\breve {E}_\wp }$ relatively representing trivialisations (respecting extra structure) of the ![]() $p^n$-torsion in the universal abelian scheme. It follows that
$p^n$-torsion in the universal abelian scheme. It follows that ![]() $\mathcal {Y}_{U^p}(H)^\circ : \mathrm {Perf}_{\breve {E}_\wp } \rightarrow \mathrm {Sets}$ is the sheafification of the functor sending
$\mathcal {Y}_{U^p}(H)^\circ : \mathrm {Perf}_{\breve {E}_\wp } \rightarrow \mathrm {Sets}$ is the sheafification of the functor sending ![]() $(R, R^+)$ to the set of isomorphism classes of data
$(R, R^+)$ to the set of isomorphism classes of data ![]() $(\mathcal {A}, \iota, \lambda, \eta, \alpha )$, where
$(\mathcal {A}, \iota, \lambda, \eta, \alpha )$, where ![]() $\alpha : \Lambda _p=\bigoplus _{\mathfrak {p} \in \Sigma _p}\Lambda _\mathfrak {p} \rightarrow \mathcal {T}(\mathcal {A}[p^\infty ])(R, R^+)$ is a trivialisation in the sense of § 5.2.2.
$\alpha : \Lambda _p=\bigoplus _{\mathfrak {p} \in \Sigma _p}\Lambda _\mathfrak {p} \rightarrow \mathcal {T}(\mathcal {A}[p^\infty ])(R, R^+)$ is a trivialisation in the sense of § 5.2.2.
There is a continuous specialisation map ![]() $\mathcal {Y}_{U}(H)^\circ \rightarrow Y_{U}(H)\times _{\breve {{\mathcal {O}}}_\wp } \bar {{\mathbb {F}}}_p$; define
$\mathcal {Y}_{U}(H)^\circ \rightarrow Y_{U}(H)\times _{\breve {{\mathcal {O}}}_\wp } \bar {{\mathbb {F}}}_p$; define ![]() $\mathcal {Y}_{U^p}(H)^{b} \subset \mathcal {Y}_{U^p}(H)^{\circ }$ to be the preimage of the Newton stratum in
$\mathcal {Y}_{U^p}(H)^{b} \subset \mathcal {Y}_{U^p}(H)^{\circ }$ to be the preimage of the Newton stratum in ![]() $Y_{U}(H)\times _{\breve {{\mathcal {O}}}_\wp } \bar {{\mathbb {F}}}_p$ corresponding to
$Y_{U}(H)\times _{\breve {{\mathcal {O}}}_\wp } \bar {{\mathbb {F}}}_p$ corresponding to ![]() $b \in B(H_{{\mathbb {Q}}_p}, \mu )$ via the composition of the specialisation map and the projection map
$b \in B(H_{{\mathbb {Q}}_p}, \mu )$ via the composition of the specialisation map and the projection map ![]() $\mathcal {Y}_{U^p}(H)^{\circ } \rightarrow \mathcal {Y}_{U}(H)^\circ _{\breve {E}_\wp }$. Hence,
$\mathcal {Y}_{U^p}(H)^{\circ } \rightarrow \mathcal {Y}_{U}(H)^\circ _{\breve {E}_\wp }$. Hence, ![]() $\mathcal {Y}_{U^p}(H)^{b}$ is a locally closed subspace of (the topological space underlying)
$\mathcal {Y}_{U^p}(H)^{b}$ is a locally closed subspace of (the topological space underlying) ![]() $\mathcal {Y}_{U^p}(H)^{\circ }$.
$\mathcal {Y}_{U^p}(H)^{\circ }$.
5.2.4 The space  $\mathcal {X}^b_{\infty }$
$\mathcal {X}^b_{\infty }$
Finally, we will need the infinite level version of the space ![]() $\mathcal {X}^b$. This is the sheafification of the functor sending
$\mathcal {X}^b$. This is the sheafification of the functor sending ![]() $(R, R^+) \in \mathrm {Perf}_{\breve {E}_\wp }$ to the set of isomorphism classes of data
$(R, R^+) \in \mathrm {Perf}_{\breve {E}_\wp }$ to the set of isomorphism classes of data ![]() $(\mathcal {A}, \iota, \lambda, \eta, \varphi, \alpha )$ where
$(\mathcal {A}, \iota, \lambda, \eta, \varphi, \alpha )$ where ![]() $(\mathcal {A}, \iota, \lambda, \eta, \varphi )$ is as in § 5.2.1, and
$(\mathcal {A}, \iota, \lambda, \eta, \varphi )$ is as in § 5.2.1, and ![]() $\alpha$ is a trivialisation of
$\alpha$ is a trivialisation of ![]() $\mathcal {T}(\mathcal {A}[p^\infty ])(R, R^+)$ in the sense defined above.
$\mathcal {T}(\mathcal {A}[p^\infty ])(R, R^+)$ in the sense defined above.
5.2.5
From now on, unless otherwise stated we will regard all our objects as diamonds over ![]() $\mathrm {Spd}(\breve {E}_\wp, \breve {{\mathcal {O}}}_\wp )$; in particular, to define maps between them it suffices to give natural transformations between the functors on
$\mathrm {Spd}(\breve {E}_\wp, \breve {{\mathcal {O}}}_\wp )$; in particular, to define maps between them it suffices to give natural transformations between the functors on ![]() $\mathrm {Perf}_{\breve {E}_\wp }$ described above. We have a map
$\mathrm {Perf}_{\breve {E}_\wp }$ described above. We have a map ![]() $\mathcal {X}^b_{\infty }\rightarrow \mathcal {M}^b_\infty$, obtained sending an abelian scheme with extra structure to the associated
$\mathcal {X}^b_{\infty }\rightarrow \mathcal {M}^b_\infty$, obtained sending an abelian scheme with extra structure to the associated ![]() $p$-divisible group with extra structure. This fits into the following cartesian diagram.
$p$-divisible group with extra structure. This fits into the following cartesian diagram.

Indeed, the above diagram is clearly cartesian on the non-sheafified functors of points, and sheafification commutes with finite limits. It follows that ![]() $\mathcal {X}^b_{\infty }$ is representable by an adic space. Furthermore, the product formula (5.2.1.1) is still true at infinite level, as
$\mathcal {X}^b_{\infty }$ is representable by an adic space. Furthermore, the product formula (5.2.1.1) is still true at infinite level, as
The diamond ![]() $\mathcal {X}^b_\infty$ maps to
$\mathcal {X}^b_\infty$ maps to ![]() $\mathcal {Y}_{U^p}(H)^{\circ }$ forgetting the quasi-isogeny
$\mathcal {Y}_{U^p}(H)^{\circ }$ forgetting the quasi-isogeny ![]() $\varphi$; the underlying map of topological spaces factors through a map
$\varphi$; the underlying map of topological spaces factors through a map
We warn the reader that the subset ![]() $\mathcal {Y}_{U^p}(H)^{b}\subset \mathcal {Y}_{U^p}(H)$ is not necessarily generalising, hence it may not be the underlying topological space of a subdiamond of
$\mathcal {Y}_{U^p}(H)^{b}\subset \mathcal {Y}_{U^p}(H)$ is not necessarily generalising, hence it may not be the underlying topological space of a subdiamond of ![]() $\mathcal {Y}_{U^p}(H)$. For
$\mathcal {Y}_{U^p}(H)$. For ![]() $(R, R^+) \in \mathrm {Perf}_{\breve {E}_\wp }$, we will denote by
$(R, R^+) \in \mathrm {Perf}_{\breve {E}_\wp }$, we will denote by ![]() $\mathcal {Y}_{U^p}(H)^{b}(R, R^+)$ the set of maps from
$\mathcal {Y}_{U^p}(H)^{b}(R, R^+)$ the set of maps from ![]() $\mathrm {Spa}(R, R^+)$ to
$\mathrm {Spa}(R, R^+)$ to ![]() $\mathcal {Y}_{U^p}(H)$ whose image is contained in
$\mathcal {Y}_{U^p}(H)$ whose image is contained in ![]() $\mathcal {Y}_{U^p}(H)^{b}$.
$\mathcal {Y}_{U^p}(H)^{b}$.
Finally, we have global and local Hodge–Tate period maps
 \begin{align*} \pi_{\mathrm{HT}}^\circ:
\mathcal{Y}_{U^p}(H)^{\circ} & \rightarrow
\mathscr{F}\ell_{H_{{\mathbb{Q}}_p}, \mu^{-1}}\\
\pi_{\mathrm{HT}}^b: \mathcal{M}^b_\infty & \rightarrow
\mathscr{F}\ell_{H_{{\mathbb{Q}}_p}, \mu^{-1}}.
\end{align*}
\begin{align*} \pi_{\mathrm{HT}}^\circ:
\mathcal{Y}_{U^p}(H)^{\circ} & \rightarrow
\mathscr{F}\ell_{H_{{\mathbb{Q}}_p}, \mu^{-1}}\\
\pi_{\mathrm{HT}}^b: \mathcal{M}^b_\infty & \rightarrow
\mathscr{F}\ell_{H_{{\mathbb{Q}}_p}, \mu^{-1}}.
\end{align*}
We can now state and prove an analogue of [Reference Caraiani and ScholzeCS17, Lemma 4.3.20].
Proposition 5.2.6 The following diagram (of functors on ![]() $\mathrm {Perf}_{\breve {E}_\wp }$) is cartesian.
$\mathrm {Perf}_{\breve {E}_\wp }$) is cartesian.

Proof. As sheafification commutes with finite limits, it is enough to prove the statement at the level of non-sheafified functors of points.
(i) First we show that the diagram commutes. It is enough to prove this for ![]() $\mathrm {Spa}(K, K^+)$-points with
$\mathrm {Spa}(K, K^+)$-points with ![]() $K$ a complete algebraically closed field and
$K$ a complete algebraically closed field and ![]() $K^+ \subset K$ an open bounded valuation subring, and replacing
$K^+ \subset K$ an open bounded valuation subring, and replacing ![]() $\mathcal {Y}_{U^p}(H)^{b}$ with
$\mathcal {Y}_{U^p}(H)^{b}$ with ![]() $\mathcal {Y}_{U^p}(H)$. Because
$\mathcal {Y}_{U^p}(H)$. Because ![]() $\mathscr {F}\ell _{H_{{\mathbb {Q}}_p}, \mu^{-1}}$ is separated (it is even proper), we are reduced to prove commutativity on
$\mathscr {F}\ell _{H_{{\mathbb {Q}}_p}, \mu^{-1}}$ is separated (it is even proper), we are reduced to prove commutativity on ![]() $\mathrm {Spa}(K, {\mathcal {O}}_K)$-points. In this case, it follows from the compatibility of the Hodge–Tate filtration for an abelian variety and the associated
$\mathrm {Spa}(K, {\mathcal {O}}_K)$-points. In this case, it follows from the compatibility of the Hodge–Tate filtration for an abelian variety and the associated ![]() $p$-divisible group [Reference ScholzeSch13, Proposition 4.15].
$p$-divisible group [Reference ScholzeSch13, Proposition 4.15].
(ii) It remains to prove that the diagram is cartesian. Let ![]() $(R, R^+) \in \mathrm {Perf}_{\breve {E}_\wp }$ and take two points
$(R, R^+) \in \mathrm {Perf}_{\breve {E}_\wp }$ and take two points
mapping to the same ![]() $(R, R^+)$-point of the flag variety. The map
$(R, R^+)$-point of the flag variety. The map ![]() $\alpha _{\mathcal {G}} \circ \alpha _A^{-1}: \mathcal {T}_p(\mathcal {A})(R, R^+)\rightarrow \mathcal {T}_p(\mathcal {G})(R, R^+)$ becomes an isomorphism when pulled back to any geometric rank one point
$\alpha _{\mathcal {G}} \circ \alpha _A^{-1}: \mathcal {T}_p(\mathcal {A})(R, R^+)\rightarrow \mathcal {T}_p(\mathcal {G})(R, R^+)$ becomes an isomorphism when pulled back to any geometric rank one point ![]() $\mathrm {Spa}(K, {\mathcal {O}}_K)$, and it is induced by an isomorphism
$\mathrm {Spa}(K, {\mathcal {O}}_K)$, and it is induced by an isomorphism ![]() $\phi : \mathcal {A}[p^\infty ]_R\buildrel \sim \over \to \mathcal {G}_R$ respecting the extra structures. Furthermore, as
$\phi : \mathcal {A}[p^\infty ]_R\buildrel \sim \over \to \mathcal {G}_R$ respecting the extra structures. Furthermore, as ![]() $x$ and
$x$ and ![]() $y$ map to the same point in the flag variety, the map
$y$ map to the same point in the flag variety, the map ![]() $\alpha _{\mathcal {G}} \circ \alpha _A^{-1}$ respects the Hodge–Tate filtrations (on Tate modules tensored by
$\alpha _{\mathcal {G}} \circ \alpha _A^{-1}$ respects the Hodge–Tate filtrations (on Tate modules tensored by ![]() $K$). Finally, since the image of
$K$). Finally, since the image of ![]() $y$ is contained in
$y$ is contained in ![]() $\mathcal {Y}_{U^p}(H)^{b}$, the Newton polygon of
$\mathcal {Y}_{U^p}(H)^{b}$, the Newton polygon of ![]() $\mathcal {A}[p^\infty ]\times _{R^+}R^+/p$ is constant. Hence, by [Reference Scholze and WeinsteinSW13, Theorem B] and [Reference Caraiani and ScholzeCS17, Lemma 4.2.15], the isomorphism
$\mathcal {A}[p^\infty ]\times _{R^+}R^+/p$ is constant. Hence, by [Reference Scholze and WeinsteinSW13, Theorem B] and [Reference Caraiani and ScholzeCS17, Lemma 4.2.15], the isomorphism ![]() $\phi$ extends to an isomorphism, abusively denoted by the same symbol,
$\phi$ extends to an isomorphism, abusively denoted by the same symbol, ![]() $\phi : \mathcal {A}[p^\infty ]\buildrel \sim \over \to \mathcal {G}$. We get a (unique)
$\phi : \mathcal {A}[p^\infty ]\buildrel \sim \over \to \mathcal {G}$. We get a (unique) ![]() $(R, R^+)$-point
$(R, R^+)$-point ![]() $(\mathcal {A}, \iota _\mathcal {A}, \lambda _\mathcal {A}, \eta _\mathcal {A}, \alpha _\mathcal {A}, \rho _{\mathcal {G}} \circ \phi )$ of
$(\mathcal {A}, \iota _\mathcal {A}, \lambda _\mathcal {A}, \eta _\mathcal {A}, \alpha _\mathcal {A}, \rho _{\mathcal {G}} \circ \phi )$ of ![]() $\mathcal {X}^b_{\infty }$ mapping to
$\mathcal {X}^b_{\infty }$ mapping to ![]() $x$ and
$x$ and ![]() $y$.
$y$.
5.2.7
We have a natural map from ![]() $\mathcal {Y}_{U^p}(H)=\varprojlim _{U_p}\mathcal {Y}_{U^pU_p}$ to the inverse limit
$\mathcal {Y}_{U^p}(H)=\varprojlim _{U_p}\mathcal {Y}_{U^pU_p}$ to the inverse limit ![]() $\mathcal {S}h_{U^p}(H)$ of the analytifications
$\mathcal {S}h_{U^p}(H)$ of the analytifications ![]() $\mathcal {S}h_{U^pU_p}(H)$ of the Shimura varieties with level
$\mathcal {S}h_{U^pU_p}(H)$ of the Shimura varieties with level ![]() $U^pU_p$; this map is a torsor for the group
$U^pU_p$; this map is a torsor for the group ![]() $\Delta =\varprojlim _k \Delta _k$ defined in § 4.2. We let
$\Delta =\varprojlim _k \Delta _k$ defined in § 4.2. We let ![]() $\mathcal {S}h_{U^pU_{p}}(H)^\circ =\mathcal {Y}_{U^pU_p}^\circ /\Delta$ and
$\mathcal {S}h_{U^pU_{p}}(H)^\circ =\mathcal {Y}_{U^pU_p}^\circ /\Delta$ and ![]() $\mathcal {S}h_{U^p}(H)^\circ =\mathcal {Y}^\circ _{U^p}(H)/\Delta$, so that
$\mathcal {S}h_{U^p}(H)^\circ =\mathcal {Y}^\circ _{U^p}(H)/\Delta$, so that ![]() $\mathcal {S}h_{U^p}(H)^\circ /U_p\simeq \mathcal {S}h_{U^pU_p}(H)^\circ$. Similarly, we set
$\mathcal {S}h_{U^p}(H)^\circ /U_p\simeq \mathcal {S}h_{U^pU_p}(H)^\circ$. Similarly, we set ![]() $\mathcal {S}h_{U^p}(H)^b=\mathcal {Y}_{U^p}(H)^b/\Delta$ for
$\mathcal {S}h_{U^p}(H)^b=\mathcal {Y}_{U^p}(H)^b/\Delta$ for ![]() $b \in B(H_{{\mathbb {Q}}_p}, \mu )$.
$b \in B(H_{{\mathbb {Q}}_p}, \mu )$.
5.3 Fibres of the Hodge–Tate period map
Recall that we have fixed a subset ![]() $T \subset \Sigma _p$; we have a Hodge–Tate period map
$T \subset \Sigma _p$; we have a Hodge–Tate period map
induced by the map (abusively denoted with the same symbol) ![]() $\pi _{\mathrm {HT}}^\circ : \mathcal {Y}_{U^p}(H)^{\circ } \rightarrow \mathscr {F}\ell _{H_{{\mathbb {Q}}_p}, \mu^{-1} }$ introduced above, which is equivariant with respect to the
$\pi _{\mathrm {HT}}^\circ : \mathcal {Y}_{U^p}(H)^{\circ } \rightarrow \mathscr {F}\ell _{H_{{\mathbb {Q}}_p}, \mu^{-1} }$ introduced above, which is equivariant with respect to the ![]() $\Delta$-action (trivial on the target). Take an element
$\Delta$-action (trivial on the target). Take an element ![]() $b \in B(H_{{\mathbb {Q}}_\mathfrak {p}}, \mu )$, and fix a
$b \in B(H_{{\mathbb {Q}}_\mathfrak {p}}, \mu )$, and fix a ![]() $p$-divisible group
$p$-divisible group ![]() $\mathbb {X}^b$ (with extra structure) corresponding to it.
$\mathbb {X}^b$ (with extra structure) corresponding to it.
Proposition 5.3.1 For every geometric point ![]() $\tilde {x}$ of
$\tilde {x}$ of ![]() $\mathscr {F}\ell ^b_{H_{{\mathbb {Q}}_p}, \mu^{-1} }$ and every
$\mathscr {F}\ell ^b_{H_{{\mathbb {Q}}_p}, \mu^{-1} }$ and every ![]() $i \geq 0$ there is a Hecke-equivariant isomorphism
$i \geq 0$ there is a Hecke-equivariant isomorphism
Proof. This follows from Proposition 5.2.6 with the same argument as in [Reference Caraiani and ScholzeCS17, § 4.4]. More precisely, we may assume that ![]() $\tilde {x}= \mathrm {Spa}(C, \mathcal {O}_C)$ is a rank one point; any rank one point in the preimage of
$\tilde {x}= \mathrm {Spa}(C, \mathcal {O}_C)$ is a rank one point; any rank one point in the preimage of ![]() $\tilde {x}$ in
$\tilde {x}$ in ![]() $\mathcal {Y}_{U^p}(H)^{\circ }$ is contained in
$\mathcal {Y}_{U^p}(H)^{\circ }$ is contained in ![]() $\mathcal {Y}_{U^p}(H)^{b}$. The cartesian diagram in Proposition 5.2.6, [Reference Caraiani and ScholzeCS17, Lemma 4.2.18] and the product formula for
$\mathcal {Y}_{U^p}(H)^{b}$. The cartesian diagram in Proposition 5.2.6, [Reference Caraiani and ScholzeCS17, Lemma 4.2.18] and the product formula for ![]() $\mathcal {X}^{b}_\infty$ (5.2.5.1) imply that the fibre of
$\mathcal {X}^{b}_\infty$ (5.2.5.1) imply that the fibre of ![]() $\pi _{\mathrm {HT}}^\circ : \mathcal {Y}_{U^p}(H)^{b} \rightarrow \mathscr {F}\ell ^b_{H_{{\mathbb {Q}}_p}, \mu^{-1} }$ at
$\pi _{\mathrm {HT}}^\circ : \mathcal {Y}_{U^p}(H)^{b} \rightarrow \mathscr {F}\ell ^b_{H_{{\mathbb {Q}}_p}, \mu^{-1} }$ at ![]() $\tilde {x}$ is isomorphic to
$\tilde {x}$ is isomorphic to ![]() $\overline {\mathcal {I}g^b}_{(C, \mathcal {O}_C)}$, hence the fibre of
$\overline {\mathcal {I}g^b}_{(C, \mathcal {O}_C)}$, hence the fibre of ![]() $\pi _{\mathrm {HT}}^\circ : \mathcal {S}h_{U^p}(H)^{b} \rightarrow \mathscr {F}\ell ^b_{H_{{\mathbb {Q}}_p}, \mu^{-1} }$ is isomorphic to
$\pi _{\mathrm {HT}}^\circ : \mathcal {S}h_{U^p}(H)^{b} \rightarrow \mathscr {F}\ell ^b_{H_{{\mathbb {Q}}_p}, \mu^{-1} }$ is isomorphic to ![]() $\mathcal {I}g^b_{(C, \mathcal {O}_C)}$. The result now follows as in [Reference Caraiani and ScholzeCS17, pp. 728 and 729].
$\mathcal {I}g^b_{(C, \mathcal {O}_C)}$. The result now follows as in [Reference Caraiani and ScholzeCS17, pp. 728 and 729].
6. The structure of the  $\mu$-ordinary stratum at infinite level
$\mu$-ordinary stratum at infinite level
In this section, we show that the ![]() $\mu$-ordinary locus at infinite level is parabolically induced from the corresponding perfectoid Igusa variety.
$\mu$-ordinary locus at infinite level is parabolically induced from the corresponding perfectoid Igusa variety.
6.1 Setup
Fix a prime ![]() $p$ and a subset
$p$ and a subset ![]() $T \subsetneq \Sigma _p$ as in the previous section; we will mostly omit
$T \subsetneq \Sigma _p$ as in the previous section; we will mostly omit ![]() $T$ from our notations: for example, we denote
$T$ from our notations: for example, we denote ![]() $H_T$ by
$H_T$ by ![]() $H$. As explained in § 4.1 we have
$H$. As explained in § 4.1 we have ![]() $B(H_{{\mathbb {Q}}_p}, \mu )=\prod _{\mathfrak {p} \in \Sigma _p} B(H_{\mathfrak {p}}, \mu _{\mathfrak {p}})$, where
$B(H_{{\mathbb {Q}}_p}, \mu )=\prod _{\mathfrak {p} \in \Sigma _p} B(H_{\mathfrak {p}}, \mu _{\mathfrak {p}})$, where ![]() $B(H_{\mathfrak {p}}, \mu _{\mathfrak {p}})$ is a singleton if
$B(H_{\mathfrak {p}}, \mu _{\mathfrak {p}})$ is a singleton if ![]() $\mathfrak {p} \in T$ and has two elements, the basic one and the
$\mathfrak {p} \in T$ and has two elements, the basic one and the ![]() $\mu _\mathfrak {p}$-ordinary one, if
$\mu _\mathfrak {p}$-ordinary one, if ![]() $\mathfrak {p} \in \Sigma _p \smallsetminus T$. Consider the
$\mathfrak {p} \in \Sigma _p \smallsetminus T$. Consider the ![]() $\mu$-ordinary element
$\mu$-ordinary element ![]() $b^{\mathrm {ord}}=(b_\mathfrak {p})_{\mathfrak {p} \in \Sigma _p}$ where
$b^{\mathrm {ord}}=(b_\mathfrak {p})_{\mathfrak {p} \in \Sigma _p}$ where ![]() $b_\mathfrak {p}$ is the non-basic element for every
$b_\mathfrak {p}$ is the non-basic element for every ![]() $\mathfrak {p} \in \Sigma _p \smallsetminus T$. Our aim is to study the structure of the stratum
$\mathfrak {p} \in \Sigma _p \smallsetminus T$. Our aim is to study the structure of the stratum ![]() $\mathcal {S}h_{U^p}(H)^{b^\mathrm {ord}}$, proving that it is parabolically induced from the corresponding perfectoid Igusa variety. This rests on the product formula
$\mathcal {S}h_{U^p}(H)^{b^\mathrm {ord}}$, proving that it is parabolically induced from the corresponding perfectoid Igusa variety. This rests on the product formula
we proved in the previous section and on the fact that the relevant Rapoport–Zink spaces are parabolically induced.
6.1.1 The group  $\mathcal {J}^{b^\mathrm {ord}}$
$\mathcal {J}^{b^\mathrm {ord}}$
Let ![]() $\mathcal {J}^{b^\mathrm {ord}}=\prod _{\mathfrak {p} \in \Sigma _p}\mathcal {J}^{b_\mathfrak {p}}$ be the group of self-quasi-isogenies (respecting extra structure) of
$\mathcal {J}^{b^\mathrm {ord}}=\prod _{\mathfrak {p} \in \Sigma _p}\mathcal {J}^{b_\mathfrak {p}}$ be the group of self-quasi-isogenies (respecting extra structure) of ![]() $\mathbb {X}^{b^\mathrm {ord}}$, seen as a functor
$\mathbb {X}^{b^\mathrm {ord}}$, seen as a functor ![]() $\mathrm {Perf}_{\breve {E}_\wp } \to \mathrm {Sets}$ sending
$\mathrm {Perf}_{\breve {E}_\wp } \to \mathrm {Sets}$ sending ![]() $(R, R^+)$ to the set of self-quasi-isogenies of
$(R, R^+)$ to the set of self-quasi-isogenies of ![]() $\mathbb {X}^{b^\mathrm {ord}}\times _{\bar {{\mathbb {F}}}_p}R^+/p$. If
$\mathbb {X}^{b^\mathrm {ord}}\times _{\bar {{\mathbb {F}}}_p}R^+/p$. If ![]() $\mathfrak {p} \in T$, then
$\mathfrak {p} \in T$, then ![]() $\mathcal {J}^{b_\mathfrak {p}}$ is just the constant group diamond attached to
$\mathcal {J}^{b_\mathfrak {p}}$ is just the constant group diamond attached to ![]() $H_\mathfrak {p}({\mathbb {Q}}_p)$, which will be denoted by
$H_\mathfrak {p}({\mathbb {Q}}_p)$, which will be denoted by ![]() $\underline {H_\mathfrak {p}({\mathbb {Q}}_p)}$. If
$\underline {H_\mathfrak {p}({\mathbb {Q}}_p)}$. If ![]() $\mathfrak {p} \in \Sigma _p \smallsetminus T$ then we can write
$\mathfrak {p} \in \Sigma _p \smallsetminus T$ then we can write ![]() $\mathcal {J}^{b_\mathfrak {p}}=\underline {L_{\mathfrak {p}}({\mathbb {Q}}_p)} \ltimes \mathcal {J}_\mathfrak {p}^{U}$ where
$\mathcal {J}^{b_\mathfrak {p}}=\underline {L_{\mathfrak {p}}({\mathbb {Q}}_p)} \ltimes \mathcal {J}_\mathfrak {p}^{U}$ where ![]() $L_{\mathfrak {p}}\subset H_\mathfrak {p}$ is a Levi and
$L_{\mathfrak {p}}\subset H_\mathfrak {p}$ is a Levi and ![]() $\mathcal {J}_\mathfrak {p}^{U}$ is a (positive-dimensional) group diamond (cf. [Reference Caraiani and ScholzeCS17, Proposition 4.2.11]). On the other hand, we can attach to
$\mathcal {J}_\mathfrak {p}^{U}$ is a (positive-dimensional) group diamond (cf. [Reference Caraiani and ScholzeCS17, Proposition 4.2.11]). On the other hand, we can attach to ![]() $\mathbb {X}^{b^\mathrm {ord}}$ an
$\mathbb {X}^{b^\mathrm {ord}}$ an ![]() $H_{{\mathbb {Q}}_p}$-bundle
$H_{{\mathbb {Q}}_p}$-bundle ![]() $\mathcal {E}^{b^\mathrm {ord}}_{(R, R^+)}$ on the Fargues–Fontaine curve
$\mathcal {E}^{b^\mathrm {ord}}_{(R, R^+)}$ on the Fargues–Fontaine curve ![]() $X_{(R^\flat, R^{\flat,+})}$ for each
$X_{(R^\flat, R^{\flat,+})}$ for each ![]() $(R, R^+) \in \mathrm {Perf}_{\breve {E}_\wp }$, and look at the corresponding automorphism group functor
$(R, R^+) \in \mathrm {Perf}_{\breve {E}_\wp }$, and look at the corresponding automorphism group functor ![]() $\mathrm {Aut}(\mathcal {E}^{b^\mathrm {ord}}): \mathrm {Perf}_{\breve {E}_\wp } \to \mathrm {Sets}$.
$\mathrm {Aut}(\mathcal {E}^{b^\mathrm {ord}}): \mathrm {Perf}_{\breve {E}_\wp } \to \mathrm {Sets}$.
We claim that ![]() $\mathrm {Aut}(\mathcal {E}^{b^\mathrm {ord}})\simeq \mathcal {J}^{b^\mathrm {ord}}$. Indeed, for
$\mathrm {Aut}(\mathcal {E}^{b^\mathrm {ord}})\simeq \mathcal {J}^{b^\mathrm {ord}}$. Indeed, for ![]() $\mathfrak {p} \in \Sigma _p \smallsetminus T$, [Reference Fargues and ScholzeFS21, Proposition III.5.1] describes
$\mathfrak {p} \in \Sigma _p \smallsetminus T$, [Reference Fargues and ScholzeFS21, Proposition III.5.1] describes ![]() $\mathrm {Aut}(\mathcal {E}^{b_\mathfrak {p}})$ in terms of
$\mathrm {Aut}(\mathcal {E}^{b_\mathfrak {p}})$ in terms of ![]() $\underline {L_{\mathfrak {p}}({\mathbb {Q}}_p)}$ and of Banach–Colmez spaces. On the other hand, the computation in the proof of [Reference Caraiani and ScholzeCS17, Proposition 4.2.11] gives a similar description of
$\underline {L_{\mathfrak {p}}({\mathbb {Q}}_p)}$ and of Banach–Colmez spaces. On the other hand, the computation in the proof of [Reference Caraiani and ScholzeCS17, Proposition 4.2.11] gives a similar description of ![]() $\mathcal {J}^{b_\mathfrak {p}}$, with the universal cover of suitable
$\mathcal {J}^{b_\mathfrak {p}}$, with the universal cover of suitable ![]() $p$-divisible groups in place of Banach–Colmez spaces. The desired isomorphism follows from the identification between these two objects, cf. [Reference Scholze and WeinsteinSW20, § 15.2].
$p$-divisible groups in place of Banach–Colmez spaces. The desired isomorphism follows from the identification between these two objects, cf. [Reference Scholze and WeinsteinSW20, § 15.2].
6.1.2
The description of the Igusa variety in Lemma 4.2.2 implies that ![]() $\mathcal {J}^{b^\mathrm {ord}}$ acts on the left on
$\mathcal {J}^{b^\mathrm {ord}}$ acts on the left on ![]() $\overline {\mathcal {I}g}^{b^{\mathrm {ord}}}$, changing the trivialisation
$\overline {\mathcal {I}g}^{b^{\mathrm {ord}}}$, changing the trivialisation ![]() $\rho$. For the same reason,
$\rho$. For the same reason, ![]() $\mathcal {J}^{b^\mathrm {ord}}$ acts on the left on
$\mathcal {J}^{b^\mathrm {ord}}$ acts on the left on ![]() $\mathcal {M}_\infty ^{b^{\mathrm {ord}}}$ and
$\mathcal {M}_\infty ^{b^{\mathrm {ord}}}$ and ![]() $\mathcal {X}_\infty ^{b^\mathrm {ord}}$. The stratum
$\mathcal {X}_\infty ^{b^\mathrm {ord}}$. The stratum ![]() $\mathcal {Y}_{U^p}(H)^{b^\mathrm {ord}}\subset \mathcal {Y}_{U^p}(H)^\circ$ is open and contained in the preimage via
$\mathcal {Y}_{U^p}(H)^{b^\mathrm {ord}}\subset \mathcal {Y}_{U^p}(H)^\circ$ is open and contained in the preimage via ![]() $\pi _{HT}^\circ$ of the
$\pi _{HT}^\circ$ of the ![]() $\mu$-ordinary stratum in the flag variety. As the latter is a diamond, the same is true for
$\mu$-ordinary stratum in the flag variety. As the latter is a diamond, the same is true for ![]() $\mathcal {Y}_{U^p}(H)^{b^\mathrm {ord}}$. The map
$\mathcal {Y}_{U^p}(H)^{b^\mathrm {ord}}$. The map ![]() $\mathcal {X}^{b^\mathrm {ord}}_{\infty } \rightarrow \mathcal {Y}_{U^p}(H)^{b^\mathrm {ord}}$ is invariant with respect to the action of
$\mathcal {X}^{b^\mathrm {ord}}_{\infty } \rightarrow \mathcal {Y}_{U^p}(H)^{b^\mathrm {ord}}$ is invariant with respect to the action of ![]() $\mathcal {J}^{b^\mathrm {ord}}$ on the source.
$\mathcal {J}^{b^\mathrm {ord}}$ on the source.
Lemma 6.1.3
(i) The map
 $\mathcal {J}^{b^\mathrm {ord}} \backslash \mathcal {X}^{b^\mathrm {ord}}_{\infty } \rightarrow \mathcal {Y}_{U^p}(H)^{b^\mathrm {ord}}$ is an isomorphism.
$\mathcal {J}^{b^\mathrm {ord}} \backslash \mathcal {X}^{b^\mathrm {ord}}_{\infty } \rightarrow \mathcal {Y}_{U^p}(H)^{b^\mathrm {ord}}$ is an isomorphism.(ii) The induced map
 $\mathcal {J}^{b^\mathrm {ord}} \backslash (\mathcal {I}g^{b^{\mathrm {ord}}} \times \mathcal {M}_\infty ^{b^{\mathrm {ord}}}) \rightarrow \mathcal {S}h_{U^p}(H)^{b^\mathrm {ord}}$ is an isomorphism.
$\mathcal {J}^{b^\mathrm {ord}} \backslash (\mathcal {I}g^{b^{\mathrm {ord}}} \times \mathcal {M}_\infty ^{b^{\mathrm {ord}}}) \rightarrow \mathcal {S}h_{U^p}(H)^{b^\mathrm {ord}}$ is an isomorphism.
Proof. The second point follows from the first and the product formula: indeed, as the map in (5.2.1.1) (as well as its counterpart at infinite level (5.2.5.1)) is ![]() $\mathcal {J}^{b^\mathrm {ord}}$-equivariant, we get an isomorphism
$\mathcal {J}^{b^\mathrm {ord}}$-equivariant, we get an isomorphism
The above isomorphism is equivariant with respect to the ![]() $\Delta$-action on
$\Delta$-action on ![]() $\overline {\mathcal {I}g^{b^{\mathrm {ord}}}}$ and on
$\overline {\mathcal {I}g^{b^{\mathrm {ord}}}}$ and on ![]() $\mathcal {Y}_{U^p}(H)^{b^\mathrm {ord}}$; hence, quotienting by this action we obtain the desired isomorphism.
$\mathcal {Y}_{U^p}(H)^{b^\mathrm {ord}}$; hence, quotienting by this action we obtain the desired isomorphism.
To prove the first point, we need to show that the map (of pro-étale sheaves) ![]() $\mathcal {X}^{b^\mathrm {ord}}_{\infty } \rightarrow \mathcal {Y}_{U^p}(H)^{b^\mathrm {ord}}$ is surjective. Let
$\mathcal {X}^{b^\mathrm {ord}}_{\infty } \rightarrow \mathcal {Y}_{U^p}(H)^{b^\mathrm {ord}}$ is surjective. Let ![]() $(R, R^+) \in \mathrm {Perf}_{\breve {E}_\wp }$ and let
$(R, R^+) \in \mathrm {Perf}_{\breve {E}_\wp }$ and let ![]() $\mathcal {G}/R^+$ be the
$\mathcal {G}/R^+$ be the ![]() $p$-divisible group with extra structure attached to an
$p$-divisible group with extra structure attached to an ![]() $(R, R^+)$-point of the target. Then, after base change to any geometric point of
$(R, R^+)$-point of the target. Then, after base change to any geometric point of ![]() $\mathrm {Spa}(R, R^+)$, we have a quasi-isogeny respecting extra structures between
$\mathrm {Spa}(R, R^+)$, we have a quasi-isogeny respecting extra structures between ![]() $\mathcal {G}\times _{R^+}R^+/p$ and
$\mathcal {G}\times _{R^+}R^+/p$ and ![]() $\mathbb {X}^{b^\mathrm {ord}}\times _{\bar {\mathbb {F}}_p}R^+/p$. Therefore, the isocrystal attached to the
$\mathbb {X}^{b^\mathrm {ord}}\times _{\bar {\mathbb {F}}_p}R^+/p$. Therefore, the isocrystal attached to the ![]() $p$-divisible group with extra structure
$p$-divisible group with extra structure ![]() $\mathcal {G}\times _{R^+}R^+/p$ gives rise to an
$\mathcal {G}\times _{R^+}R^+/p$ gives rise to an ![]() $H$-bundle
$H$-bundle ![]() $\mathcal {E}_{\mathcal {G}}$ on the Fargues–Fontaine curve
$\mathcal {E}_{\mathcal {G}}$ on the Fargues–Fontaine curve ![]() $X_{(R^\flat, R^{\flat,+})}$ which is geometrically fibrewise isomorphic to the
$X_{(R^\flat, R^{\flat,+})}$ which is geometrically fibrewise isomorphic to the ![]() $H$-bundle
$H$-bundle ![]() $\mathcal {E}^{b^{\mathrm {ord}}}$ corresponding to
$\mathcal {E}^{b^{\mathrm {ord}}}$ corresponding to ![]() $b^{\mathrm {ord}}$. By [Reference Fargues and ScholzeFS21, Proposition III.5.3], there is, pro-étale locally on
$b^{\mathrm {ord}}$. By [Reference Fargues and ScholzeFS21, Proposition III.5.3], there is, pro-étale locally on ![]() $\mathrm {Spa}(R^\flat, R^{+, \flat })$, an isomorphism
$\mathrm {Spa}(R^\flat, R^{+, \flat })$, an isomorphism ![]() $\mathcal {E}_{\mathcal {G}}\simeq \mathcal {E}^{b^{\mathrm {ord}}}$, yielding, pro-étale locally, a quasi-isogeny respecting extra-structures between
$\mathcal {E}_{\mathcal {G}}\simeq \mathcal {E}^{b^{\mathrm {ord}}}$, yielding, pro-étale locally, a quasi-isogeny respecting extra-structures between ![]() $\mathcal {G}\times _{R^+}R^+/p$ and
$\mathcal {G}\times _{R^+}R^+/p$ and ![]() $\mathbb {X}^{b^\mathrm {ord}}\times _{\bar {\mathbb {F}}_p}R^+/p$.
$\mathbb {X}^{b^\mathrm {ord}}\times _{\bar {\mathbb {F}}_p}R^+/p$.
6.2 The structure of  $\mu$-ordinary Rapoport–Zink spaces
$\mu$-ordinary Rapoport–Zink spaces
6.2.1 Moduli spaces of shtukas
Given ![]() $\mathfrak {p} \in \Sigma _p$, we can attach to
$\mathfrak {p} \in \Sigma _p$, we can attach to ![]() $(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ a diamond
$(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ a diamond ![]() $Sht_\infty (H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ over
$Sht_\infty (H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ over ![]() $\mathrm {Spd}(\breve {E}_\wp, \breve {\mathcal {O}}_{\wp })$ parametrising
$\mathrm {Spd}(\breve {E}_\wp, \breve {\mathcal {O}}_{\wp })$ parametrising ![]() $H_\mathfrak {p}$-shtukas with infinite level structure, as in [Reference Scholze and WeinsteinSW20, § 23]. More precisely, the functor
$H_\mathfrak {p}$-shtukas with infinite level structure, as in [Reference Scholze and WeinsteinSW20, § 23]. More precisely, the functor ![]() $Sht_\infty (H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p}): \mathrm {Perf}_{\bar {{\mathbb {F}}}_p}\rightarrow \mathrm {Sets}$ sends
$Sht_\infty (H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p}): \mathrm {Perf}_{\bar {{\mathbb {F}}}_p}\rightarrow \mathrm {Sets}$ sends ![]() $(R, R^+)$ to the set of isomorphism classes of data of the form
$(R, R^+)$ to the set of isomorphism classes of data of the form ![]() $(S^\sharp, \mathcal {E}, \mathcal {E}', \phi, \rho, \rho _{\infty })$, where:
$(S^\sharp, \mathcal {E}, \mathcal {E}', \phi, \rho, \rho _{\infty })$, where:
(i)
 $S^\sharp /\mathrm {Spa}(\breve {E}_\wp, \breve {\mathcal {O}}_\wp )$ is an untilt of
$S^\sharp /\mathrm {Spa}(\breve {E}_\wp, \breve {\mathcal {O}}_\wp )$ is an untilt of  $S:=\mathrm {Spa}(R, R^+)$;
$S:=\mathrm {Spa}(R, R^+)$;(ii)
 $\mathcal {E}, \mathcal {E}'$ are
$\mathcal {E}, \mathcal {E}'$ are  $H_\mathfrak {p}$-bundles over the relative Fargues-Fontaine curve
$H_\mathfrak {p}$-bundles over the relative Fargues-Fontaine curve  $X_S$;
$X_S$;(iii)
 $\phi$ is an isomorphism between
$\phi$ is an isomorphism between  $\mathcal {E}$ and
$\mathcal {E}$ and  $\mathcal {E}'$ outside
$\mathcal {E}'$ outside  $S^\sharp$, which is a modification of type
$S^\sharp$, which is a modification of type  $\mu _\mathfrak {p}$ at
$\mu _\mathfrak {p}$ at  $S^\sharp$;
$S^\sharp$;(iv)
 $\rho : \mathcal {E}' \rightarrow \mathcal {E}^{b_\mathfrak {p}}$ is an isomorphism, where
$\rho : \mathcal {E}' \rightarrow \mathcal {E}^{b_\mathfrak {p}}$ is an isomorphism, where  $\mathcal {E}^{b_\mathfrak {p}}$ is the
$\mathcal {E}^{b_\mathfrak {p}}$ is the  $H_\mathfrak {p}$-bundle on
$H_\mathfrak {p}$-bundle on  $X_S$ coming from (the isocrystal attached to)
$X_S$ coming from (the isocrystal attached to)  $\mathbb {X}^{b_\mathfrak {p}}$;
$\mathbb {X}^{b_\mathfrak {p}}$;(v)
 $\rho _\infty : \mathcal {E}^1 \rightarrow \mathcal {E}$ is an isomorphism, where
$\rho _\infty : \mathcal {E}^1 \rightarrow \mathcal {E}$ is an isomorphism, where  $\mathcal {E}^1$ is the trivial
$\mathcal {E}^1$ is the trivial  $H_\mathfrak {p}$-bundle on
$H_\mathfrak {p}$-bundle on  $X_S$.
$X_S$.
By [Reference Scholze and WeinsteinSW20, Corollary 24.3.5], the diamond ![]() $Sht_\infty (H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ is isomorphic to
$Sht_\infty (H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ is isomorphic to ![]() $\mathcal {M}^{b_\mathfrak {p}}_\infty$.
$\mathcal {M}^{b_\mathfrak {p}}_\infty$.
We have a left (respectively, right) action of ![]() $\mathcal {J}^{b_\mathfrak {p}}=\mathcal {A}ut(\mathcal {E}^{b_\mathfrak {p}})$ (respectively,
$\mathcal {J}^{b_\mathfrak {p}}=\mathcal {A}ut(\mathcal {E}^{b_\mathfrak {p}})$ (respectively, ![]() $\underline {H_\mathfrak {p}({\mathbb {Q}}_p)}=\mathcal {A}ut(\mathcal {E}^1)$) on the space
$\underline {H_\mathfrak {p}({\mathbb {Q}}_p)}=\mathcal {A}ut(\mathcal {E}^1)$) on the space ![]() $Sht_\infty (H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$, changing the trivialisation
$Sht_\infty (H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$, changing the trivialisation ![]() $\rho$ (respectively,
$\rho$ (respectively, ![]() $\rho _\infty$). The former corresponds to the action of
$\rho _\infty$). The former corresponds to the action of ![]() $\mathcal {J}^{b_\mathfrak {p}}$ on
$\mathcal {J}^{b_\mathfrak {p}}$ on ![]() $\mathcal {M}^{b_\mathfrak {p}}_\infty$ recalled above.
$\mathcal {M}^{b_\mathfrak {p}}_\infty$ recalled above.
6.2.2 The space  $\mathcal {M}^{b_\mathfrak {p}}_\infty$ for
$\mathcal {M}^{b_\mathfrak {p}}_\infty$ for  $\mathfrak {p} \in T$
$\mathfrak {p} \in T$
If ![]() $\mathfrak {p} \in T$, then the cocharacter
$\mathfrak {p} \in T$, then the cocharacter ![]() $\mu _\mathfrak {p}$ is central, hence the flag variety
$\mu _\mathfrak {p}$ is central, hence the flag variety ![]() $\mathscr {F}\ell _{H_{\mathfrak {p}}, \mu _\mathfrak {p}}$ is a point. By [Reference Scholze and WeinsteinSW20, Proposition 19.4.2] and [Reference Scholze and WeinsteinSW20, proof of Proposition 23.3.3] the diamond
$\mathscr {F}\ell _{H_{\mathfrak {p}}, \mu _\mathfrak {p}}$ is a point. By [Reference Scholze and WeinsteinSW20, Proposition 19.4.2] and [Reference Scholze and WeinsteinSW20, proof of Proposition 23.3.3] the diamond ![]() $\mathcal {M}^{b_\mathfrak {p}}_\infty$ is isomorphic to the diamond
$\mathcal {M}^{b_\mathfrak {p}}_\infty$ is isomorphic to the diamond ![]() $\underline {H_\mathfrak {p}({\mathbb {Q}}_p)}$ attached to the locally profinite set
$\underline {H_\mathfrak {p}({\mathbb {Q}}_p)}$ attached to the locally profinite set ![]() $H_\mathfrak {p}({\mathbb {Q}}_p)$. Hence, the product
$H_\mathfrak {p}({\mathbb {Q}}_p)$. Hence, the product ![]() $\mathcal {M}_{T, \infty }:=\prod _{\mathfrak {p} \in T} \mathcal {M}^{b_\mathfrak {p}}_\infty$ is isomorphic to
$\mathcal {M}_{T, \infty }:=\prod _{\mathfrak {p} \in T} \mathcal {M}^{b_\mathfrak {p}}_\infty$ is isomorphic to ![]() $\prod _{\mathfrak {p} \in T}\underline {H_\mathfrak {p}({\mathbb {Q}}_p)}$.
$\prod _{\mathfrak {p} \in T}\underline {H_\mathfrak {p}({\mathbb {Q}}_p)}$.
6.2.3 The space  $\mathcal {M}^{b_\mathfrak {p}}_\infty$ for
$\mathcal {M}^{b_\mathfrak {p}}_\infty$ for  $\mathfrak {p} \in \Sigma _p \smallsetminus T$
$\mathfrak {p} \in \Sigma _p \smallsetminus T$
Now fix ![]() $\mathfrak {p} \in \Sigma _p \smallsetminus T$ and let
$\mathfrak {p} \in \Sigma _p \smallsetminus T$ and let ![]() $b_\mathfrak {p} \in B(H_\mathfrak {p}, \mu _\mathfrak {p})$ be the
$b_\mathfrak {p} \in B(H_\mathfrak {p}, \mu _\mathfrak {p})$ be the ![]() $\mu _\mathfrak {p}$-ordinary element. The structure of
$\mu _\mathfrak {p}$-ordinary element. The structure of ![]() $Sht_\infty (H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ is studied in [Reference Gaisin and ImaiGI16] (generalising [Reference HansenHan21]), whose main result we now recall in the situation of interest to us: we warn the reader that our notation differs from that in [Reference Gaisin and ImaiGI16]. We have a forgetful map from
$Sht_\infty (H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ is studied in [Reference Gaisin and ImaiGI16] (generalising [Reference HansenHan21]), whose main result we now recall in the situation of interest to us: we warn the reader that our notation differs from that in [Reference Gaisin and ImaiGI16]. We have a forgetful map from ![]() $Sht_\infty (H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ to the Hecke stack
$Sht_\infty (H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ to the Hecke stack ![]() $\mathrm {Hecke}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ which parametrises data
$\mathrm {Hecke}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ which parametrises data ![]() $(S^\sharp, \mathcal {E}, \mathcal {E}', \phi )$ as above, such that
$(S^\sharp, \mathcal {E}, \mathcal {E}', \phi )$ as above, such that ![]() $\mathcal {E}'$ (respectively,
$\mathcal {E}'$ (respectively, ![]() $\mathcal {E}$) is fibrewise isomorphic to
$\mathcal {E}$) is fibrewise isomorphic to ![]() $\mathcal {E}^{b_\mathfrak {p}}$ (respectively,
$\mathcal {E}^{b_\mathfrak {p}}$ (respectively, ![]() $\mathcal {E}^1$). The Grassmannian
$\mathcal {E}^1$). The Grassmannian ![]() $Gr(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ is the
$Gr(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ is the ![]() $\underline {H_\mathfrak {p}({\mathbb {Q}}_p)}$-torsor over
$\underline {H_\mathfrak {p}({\mathbb {Q}}_p)}$-torsor over ![]() $\mathrm {Hecke}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ parametrising trivialisations
$\mathrm {Hecke}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ parametrising trivialisations ![]() $\rho _\infty : \mathcal {E}^1 \rightarrow \mathcal {E}$. Consider the subfunctor
$\rho _\infty : \mathcal {E}^1 \rightarrow \mathcal {E}$. Consider the subfunctor ![]() $\mathcal {C}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})\subset Gr(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ obtained imposing the condition that
$\mathcal {C}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})\subset Gr(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ obtained imposing the condition that ![]() $\rho _\infty$ and
$\rho _\infty$ and ![]() $\phi$ are compatible with the filtrations, in the sense of [Reference Gaisin and ImaiGI16, p. 9]. The right action of
$\phi$ are compatible with the filtrations, in the sense of [Reference Gaisin and ImaiGI16, p. 9]. The right action of ![]() $\underline {H_\mathfrak {p}({\mathbb {Q}}_p)}$ on
$\underline {H_\mathfrak {p}({\mathbb {Q}}_p)}$ on ![]() $Gr(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ induces a right action of a parabolic
$Gr(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ induces a right action of a parabolic ![]() $\underline {P_\mathfrak {p}({\mathbb {Q}}_p)}\supset \underline {L_\mathfrak {p}({\mathbb {Q}}_p)}$ on the subspace
$\underline {P_\mathfrak {p}({\mathbb {Q}}_p)}\supset \underline {L_\mathfrak {p}({\mathbb {Q}}_p)}$ on the subspace ![]() $\mathcal {C}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})\subset Gr(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$. The natural map
$\mathcal {C}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})\subset Gr(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$. The natural map ![]() $\mathcal {C}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})\times \underline {H_\mathfrak {p}({\mathbb {Q}}_p)}\rightarrow Gr(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ is invariant with respect to the left action of
$\mathcal {C}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})\times \underline {H_\mathfrak {p}({\mathbb {Q}}_p)}\rightarrow Gr(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ is invariant with respect to the left action of ![]() $\underline {P_\mathfrak {p}({\mathbb {Q}}_p)}$ on the source given by the product of the inverse of the right action on
$\underline {P_\mathfrak {p}({\mathbb {Q}}_p)}$ on the source given by the product of the inverse of the right action on ![]() $\mathcal {C}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ and the left action by multiplication on
$\mathcal {C}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ and the left action by multiplication on ![]() $\underline {H_\mathfrak {p}({\mathbb {Q}}_p)}$. By [Reference Gaisin and ImaiGI16, Proposition 4.13] the induced map
$\underline {H_\mathfrak {p}({\mathbb {Q}}_p)}$. By [Reference Gaisin and ImaiGI16, Proposition 4.13] the induced map
is an isomorphism.
Now let us consider the moduli space of shtukas ![]() $Sht_{P_\mathfrak {p}}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ with ‘parabolic level structure’, defined as the fibre product as follows.
$Sht_{P_\mathfrak {p}}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ with ‘parabolic level structure’, defined as the fibre product as follows.

The isomorphism (6.2.3.1) yields an isomorphism
6.2.4 The structure of  $Sht_{P_\mathfrak {p}}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$
$Sht_{P_\mathfrak {p}}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$
The data ![]() $b_\mathfrak {p}, \mu _\mathfrak {p}$ are induced by analogous data for the Levi
$b_\mathfrak {p}, \mu _\mathfrak {p}$ are induced by analogous data for the Levi ![]() $L_\mathfrak {p}$, which we will abusively denote by the same symbol. In other words, our data are HN-reducible in the sense of [Reference Gaisin and ImaiGI16, Definition 4.5] (note that only one of the elements
$L_\mathfrak {p}$, which we will abusively denote by the same symbol. In other words, our data are HN-reducible in the sense of [Reference Gaisin and ImaiGI16, Definition 4.5] (note that only one of the elements ![]() $b$,
$b$, ![]() $b'$ considered in [Reference Gaisin and ImaiGI16, Definition 4.5] is non-trivial in our case). We can consider the corresponding moduli space of shtukas
$b'$ considered in [Reference Gaisin and ImaiGI16, Definition 4.5] is non-trivial in our case). We can consider the corresponding moduli space of shtukas ![]() $Sht_\infty (L_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$; in fact, as
$Sht_\infty (L_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$; in fact, as ![]() $L_\mathfrak {p}$ is abelian, the same argument used above shows that
$L_\mathfrak {p}$ is abelian, the same argument used above shows that ![]() $Sht_\infty (L_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ is just the diamond attached to the locally profinite set
$Sht_\infty (L_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$ is just the diamond attached to the locally profinite set ![]() $L_\mathfrak {p}({\mathbb {Q}}_p)$. Inducing bundles from
$L_\mathfrak {p}({\mathbb {Q}}_p)$. Inducing bundles from ![]() $L_\mathfrak {p}$ to
$L_\mathfrak {p}$ to ![]() $H_\mathfrak {p}$ we obtain a map
$H_\mathfrak {p}$ we obtain a map ![]() $Sht_\infty (L_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})\rightarrow Sht_{P_\mathfrak {p}}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$. Finally, the group object
$Sht_\infty (L_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})\rightarrow Sht_{P_\mathfrak {p}}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$. Finally, the group object ![]() $\mathcal {J}_\mathfrak {p}^{U}$ acts on the left on
$\mathcal {J}_\mathfrak {p}^{U}$ acts on the left on ![]() $Sht_{P_\mathfrak {p}}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$, hence we obtain a map
$Sht_{P_\mathfrak {p}}(H_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$, hence we obtain a map
By [Reference Gaisin and ImaiGI16, Proposition 4.21] the above map is an isomorphism. Joining this with (6.2.3.2) we obtain the following isomorphism, where fibre products are taken over ![]() $\mathrm {Spd}(\breve {E}_\wp, \breve {\mathcal {O}}_{\wp })$, which is omitted from the notation:
$\mathrm {Spd}(\breve {E}_\wp, \breve {\mathcal {O}}_{\wp })$, which is omitted from the notation:
Define ![]() $Sht_\infty (L^T, b^T, \mu ^T):=\prod _{\mathfrak {p} \in \Sigma _p \smallsetminus T}Sht_\infty (L_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$; similarly, we denote by
$Sht_\infty (L^T, b^T, \mu ^T):=\prod _{\mathfrak {p} \in \Sigma _p \smallsetminus T}Sht_\infty (L_\mathfrak {p}, b_\mathfrak {p}, \mu _\mathfrak {p})$; similarly, we denote by ![]() $P^{T}({\mathbb {Q}}_p), \mathcal {J}^{U, T}$ and
$P^{T}({\mathbb {Q}}_p), \mathcal {J}^{U, T}$ and ![]() $H^T({\mathbb {Q}}_p)$ the product of the objects
$H^T({\mathbb {Q}}_p)$ the product of the objects ![]() $P_\mathfrak {p}({\mathbb {Q}}_p), \mathcal {J}^U_\mathfrak {p}$ and
$P_\mathfrak {p}({\mathbb {Q}}_p), \mathcal {J}^U_\mathfrak {p}$ and ![]() $H_\mathfrak {p}({\mathbb {Q}}_p)$ for
$H_\mathfrak {p}({\mathbb {Q}}_p)$ for ![]() $\mathfrak {p} \in \Sigma _p \smallsetminus T$. With this notation, the space
$\mathfrak {p} \in \Sigma _p \smallsetminus T$. With this notation, the space ![]() $\mathcal {M}^{b_\mathrm {ord}}_\infty$ can be written as
$\mathcal {M}^{b_\mathrm {ord}}_\infty$ can be written as
6.3 The almost product formula on the  $\mu$-ordinary stratum
$\mu$-ordinary stratum
6.3.1
We can now join Lemma 6.1.3 and the above description of ![]() $\mathcal {M}^{b_\mathrm {ord}}_\infty$. Let
$\mathcal {M}^{b_\mathrm {ord}}_\infty$. Let ![]() $\mathcal {J}^T:=\prod _{\mathfrak {p} \in \Sigma _p \smallsetminus T}\mathcal {J}^{b_\mathfrak {p}}$. Since for
$\mathcal {J}^T:=\prod _{\mathfrak {p} \in \Sigma _p \smallsetminus T}\mathcal {J}^{b_\mathfrak {p}}$. Since for ![]() $\mathfrak {p} \in T$ we have
$\mathfrak {p} \in T$ we have ![]() $\mathcal {M}^{b_\mathfrak {p}}_\infty \simeq \mathcal {J}^{b_\mathfrak {p}}\simeq \underline {H_\mathfrak {p}({\mathbb {Q}}_p)}$ we obtain the following description of the ordinary stratum
$\mathcal {M}^{b_\mathfrak {p}}_\infty \simeq \mathcal {J}^{b_\mathfrak {p}}\simeq \underline {H_\mathfrak {p}({\mathbb {Q}}_p)}$ we obtain the following description of the ordinary stratum ![]() $\mathcal {S}h_{U^p}(H)^{b^\mathrm {ord}}$:
$\mathcal {S}h_{U^p}(H)^{b^\mathrm {ord}}$:
We will now show that the space on the right-hand side is isomorphic to
where ![]() $\underline {P^{T}({\mathbb {Q}}_p)}$ acts on the left on
$\underline {P^{T}({\mathbb {Q}}_p)}$ acts on the left on ![]() $\mathcal {I}g^{b^\mathrm {ord}}$ via the natural inclusion in
$\mathcal {I}g^{b^\mathrm {ord}}$ via the natural inclusion in ![]() $\mathcal {J}^T$ and on
$\mathcal {J}^T$ and on ![]() $\underline {H^T({\mathbb {Q}}_p)}$ via left multiplication.
$\underline {H^T({\mathbb {Q}}_p)}$ via left multiplication.
Sending (the equivalence class of) a point ![]() $(i, g)$ to (the equivalence class of)
$(i, g)$ to (the equivalence class of) ![]() $(i, ((1, 1), g))$ gives a well-defined map from the space in (6.3.1.1) to
$(i, ((1, 1), g))$ gives a well-defined map from the space in (6.3.1.1) to ![]() $\mathcal {S}h_{U^p}(H)^{b^\mathrm {ord}}$. This map is surjective because
$\mathcal {S}h_{U^p}(H)^{b^\mathrm {ord}}$. This map is surjective because ![]() $\mathcal {J}^{T}$ acts transitively on
$\mathcal {J}^{T}$ acts transitively on ![]() $Sht_\infty (L^T, b^T, \mu ^T)\times \mathcal {J}^{U, T}$; injectivity can be checked directly. Hence, we obtain an isomorphism
$Sht_\infty (L^T, b^T, \mu ^T)\times \mathcal {J}^{U, T}$; injectivity can be checked directly. Hence, we obtain an isomorphism
which is equivariant with respect to the right action of ![]() $\underline {H({\mathbb {Q}}_p)}$ on the source and the target (here
$\underline {H({\mathbb {Q}}_p)}$ on the source and the target (here ![]() $\underline {H^T({\mathbb {Q}}_p)}$ acts on the target via right multiplication on itself).
$\underline {H^T({\mathbb {Q}}_p)}$ acts on the target via right multiplication on itself).
Notation 6.3.2 In the next theorem and its proof we will use the following notation. We set ![]() $P({\mathbb {Q}}_p):=\prod _{\mathfrak {p} \in T}H_\mathfrak {p}({\mathbb {Q}}_p)\times \prod _{\mathfrak {p} \in \Sigma _p \smallsetminus T}P_\mathfrak {p}({\mathbb {Q}}_p) \subset H({\mathbb {Q}}_p)$; similarly, let
$P({\mathbb {Q}}_p):=\prod _{\mathfrak {p} \in T}H_\mathfrak {p}({\mathbb {Q}}_p)\times \prod _{\mathfrak {p} \in \Sigma _p \smallsetminus T}P_\mathfrak {p}({\mathbb {Q}}_p) \subset H({\mathbb {Q}}_p)$; similarly, let ![]() $P({\mathbb {Z}}_p):=\prod _{\mathfrak {p} \in T}H_\mathfrak {p}({\mathbb {Z}}_p)\times \prod _{\mathfrak {p} \in \Sigma _p \smallsetminus T}P_\mathfrak {p}({\mathbb {Z}}_p) \subset H({\mathbb {Z}}_p)$. We will denote by
$P({\mathbb {Z}}_p):=\prod _{\mathfrak {p} \in T}H_\mathfrak {p}({\mathbb {Z}}_p)\times \prod _{\mathfrak {p} \in \Sigma _p \smallsetminus T}P_\mathfrak {p}({\mathbb {Z}}_p) \subset H({\mathbb {Z}}_p)$. We will denote by ![]() $\mathrm {Ind}$ smooth induction.
$\mathrm {Ind}$ smooth induction.
Theorem 6.3.3
(i) There is an
 $\underline {H({\mathbb {Q}}_p)}$-equivariant isomorphism
$\underline {H({\mathbb {Q}}_p)}$-equivariant isomorphism
 \[ \mathcal{S}h_{U^p}(H)^{b^\mathrm{ord}}\simeq \underline{P^T({\mathbb{Q}}_p)} \backslash \big(\mathcal{I}g^{b^\mathrm{ord}}\times \underline{H^T({\mathbb{Q}}_p)} \big). \]
\[ \mathcal{S}h_{U^p}(H)^{b^\mathrm{ord}}\simeq \underline{P^T({\mathbb{Q}}_p)} \backslash \big(\mathcal{I}g^{b^\mathrm{ord}}\times \underline{H^T({\mathbb{Q}}_p)} \big). \]
(ii) Let us turn the left action of
 $\underline {P({\mathbb {Q}}_p)}$ on
$\underline {P({\mathbb {Q}}_p)}$ on  $\mathcal {I}g^{b^\mathrm {ord}}$ into a right action taking the inverse. Then the cohomology of
$\mathcal {I}g^{b^\mathrm {ord}}$ into a right action taking the inverse. Then the cohomology of  $\mathcal {I}g^{b^\mathrm {ord}}$ (respectively,
$\mathcal {I}g^{b^\mathrm {ord}}$ (respectively,  $\mathcal {S}h_{U^p}(H)^{b^\mathrm {ord}}$) carries a left action of
$\mathcal {S}h_{U^p}(H)^{b^\mathrm {ord}}$) carries a left action of  $P({\mathbb {Q}}_p)$ (respectively,
$P({\mathbb {Q}}_p)$ (respectively,  $H({\mathbb {Q}}_p)$). For each
$H({\mathbb {Q}}_p)$). For each  $i \geq 0$, we have an isomorphism of smooth
$i \geq 0$, we have an isomorphism of smooth  $H({\mathbb {Q}}_p)$-representations
$H({\mathbb {Q}}_p)$-representations
 \[ H^i(\mathcal{S}h_{U^p}(H)^{b^\mathrm{ord}}, {\mathbb{F}}_{\ell})\simeq \mathrm{Ind}_{P({\mathbb{Q}}_p)}^{H({\mathbb{Q}}_p)}\big( H^i(\mathcal{I}g^{b^\mathrm{ord}}, {\mathbb{F}}_{\ell})\big). \]
\[ H^i(\mathcal{S}h_{U^p}(H)^{b^\mathrm{ord}}, {\mathbb{F}}_{\ell})\simeq \mathrm{Ind}_{P({\mathbb{Q}}_p)}^{H({\mathbb{Q}}_p)}\big( H^i(\mathcal{I}g^{b^\mathrm{ord}}, {\mathbb{F}}_{\ell})\big). \]
Proof. The first point was established before the statement of the theorem; let us prove the second point. Fix ![]() $i \geq 0$ and let
$i \geq 0$ and let ![]() $I:=\mathcal {I}g^{b^\mathrm {ord}}$ and
$I:=\mathcal {I}g^{b^\mathrm {ord}}$ and ![]() $V:=H^i(I, {\mathbb {F}}_\ell )$. The subgroup
$V:=H^i(I, {\mathbb {F}}_\ell )$. The subgroup ![]() $P({\mathbb {Z}}_p)\subset P({\mathbb {Q}}_p)$ acts freely on
$P({\mathbb {Z}}_p)\subset P({\mathbb {Q}}_p)$ acts freely on ![]() $\overline {\mathcal {I}g^{b^\mathrm {ord}}}$. On the other hand, for
$\overline {\mathcal {I}g^{b^\mathrm {ord}}}$. On the other hand, for ![]() $u \in \mathcal {O}_{E}^{\times }\cap U^p$, the action of
$u \in \mathcal {O}_{E}^{\times }\cap U^p$, the action of ![]() $N_{E/F}(u)$ (changing polarisation) on
$N_{E/F}(u)$ (changing polarisation) on ![]() $\overline {\mathcal {I}g^{b^\mathrm {ord}}}$ agrees with the action of
$\overline {\mathcal {I}g^{b^\mathrm {ord}}}$ agrees with the action of ![]() $u^{-1} \in P({\mathbb {Z}}_p)$. The induced action of
$u^{-1} \in P({\mathbb {Z}}_p)$. The induced action of ![]() $P({\mathbb {Z}}_p)$ on
$P({\mathbb {Z}}_p)$ on ![]() $I$ hence factors through a free action of
$I$ hence factors through a free action of ![]() $P({\mathbb {Z}}_p)/C$, where
$P({\mathbb {Z}}_p)/C$, where ![]() $C:=\varprojlim _k(\mathcal {O}_E^{\times }\cap U^p/\{u \in \mathcal {O}_E^{\times }\cap U^p \mid u \equiv 1 \pmod {p^k}\})$.
$C:=\varprojlim _k(\mathcal {O}_E^{\times }\cap U^p/\{u \in \mathcal {O}_E^{\times }\cap U^p \mid u \equiv 1 \pmod {p^k}\})$.
The action of ![]() $P({\mathbb {Q}}_p)$ on
$P({\mathbb {Q}}_p)$ on ![]() $I$ induces a map
$I$ induces a map ![]() $\rho : P({\mathbb {Q}}_p) \rightarrow \mathrm {Aut}(V)$. The map
$\rho : P({\mathbb {Q}}_p) \rightarrow \mathrm {Aut}(V)$. The map ![]() $\iota : I \rightarrow \underline {P({\mathbb {Q}}_p)}\backslash I \times \underline {H({\mathbb {Q}}_p)}$ sending
$\iota : I \rightarrow \underline {P({\mathbb {Q}}_p)}\backslash I \times \underline {H({\mathbb {Q}}_p)}$ sending ![]() $x$ to
$x$ to ![]() $(x, 1)$ is equivariant with respect to the right
$(x, 1)$ is equivariant with respect to the right ![]() $\underline {P({\mathbb {Q}}_p)}$-action on source and target, hence it induces a
$\underline {P({\mathbb {Q}}_p)}$-action on source and target, hence it induces a ![]() $P({\mathbb {Q}}_p)$-equivariant map
$P({\mathbb {Q}}_p)$-equivariant map
We therefore have an ![]() $H({\mathbb {Q}}_p)$-equivariant map
$H({\mathbb {Q}}_p)$-equivariant map
induced by ![]() $\iota ^*$ via Frobenius reciprocity, which sends a cohomology class
$\iota ^*$ via Frobenius reciprocity, which sends a cohomology class ![]() $c$ to the function
$c$ to the function ![]() $H({\mathbb {Q}}_p)\rightarrow V$ sending
$H({\mathbb {Q}}_p)\rightarrow V$ sending ![]() $h$ to
$h$ to ![]() $\iota ^*\circ h^{*}(c)$. For every compact open subgroup
$\iota ^*\circ h^{*}(c)$. For every compact open subgroup ![]() $K \subset H({\mathbb {Q}}_p)$ we have the space
$K \subset H({\mathbb {Q}}_p)$ we have the space ![]() $I_{K}:=\underline {P({\mathbb {Q}}_p)}\backslash (I \times \underline {H({\mathbb {Q}}_p)}/\underline {K})$ and the natural map
$I_{K}:=\underline {P({\mathbb {Q}}_p)}\backslash (I \times \underline {H({\mathbb {Q}}_p)}/\underline {K})$ and the natural map ![]() $q_K: \underline {P({\mathbb {Q}}_p)}\backslash (I \times \underline {H({\mathbb {Q}}_p)}) \rightarrow I_K$. On the other hand, let
$q_K: \underline {P({\mathbb {Q}}_p)}\backslash (I \times \underline {H({\mathbb {Q}}_p)}) \rightarrow I_K$. On the other hand, let
so that ![]() $\mathrm {Ind}_{P({\mathbb {Q}}_p)}^{H({\mathbb {Q}}_p)}(\rho )=\varinjlim _{K} S_{K}$. We may, and will, restrict to pro-
$\mathrm {Ind}_{P({\mathbb {Q}}_p)}^{H({\mathbb {Q}}_p)}(\rho )=\varinjlim _{K} S_{K}$. We may, and will, restrict to pro-![]() $p$ compact open subgroups
$p$ compact open subgroups ![]() $K\subset H({\mathbb {Z}}_p)$; to complete the proof, we will show that the composite
$K\subset H({\mathbb {Z}}_p)$; to complete the proof, we will show that the composite ![]() $a_{\iota ^*}\circ q_K^*$ induces an isomorphism
$a_{\iota ^*}\circ q_K^*$ induces an isomorphism ![]() $H^i(I_{K}, {\mathbb {F}}_\ell ) \simeq S_{K}$.
$H^i(I_{K}, {\mathbb {F}}_\ell ) \simeq S_{K}$.
Choose a set of representatives ![]() $R=\{h_1, \ldots, h_r\}$ of the (finite) double coset
$R=\{h_1, \ldots, h_r\}$ of the (finite) double coset ![]() $P({\mathbb {Q}}_p) \backslash H({\mathbb {Q}}_p)/K$ such that each
$P({\mathbb {Q}}_p) \backslash H({\mathbb {Q}}_p)/K$ such that each ![]() $h_j$ belongs to
$h_j$ belongs to ![]() $H({\mathbb {Z}}_p)$ (this is possible because of the Iwasawa decomposition of
$H({\mathbb {Z}}_p)$ (this is possible because of the Iwasawa decomposition of ![]() $H({\mathbb {Q}}_p)$). Evaluation at elements of
$H({\mathbb {Q}}_p)$). Evaluation at elements of ![]() $R$ yields an injection
$R$ yields an injection ![]() $S_K \hookrightarrow V^R$; an explicit computation shows that the image is
$S_K \hookrightarrow V^R$; an explicit computation shows that the image is ![]() $\bigoplus _{R}V^{\Gamma _j}$, where
$\bigoplus _{R}V^{\Gamma _j}$, where ![]() $\Gamma _j:=P({\mathbb {Q}}_p) \cap h_jKh_j^{-1}$. Consider the composite of the map
$\Gamma _j:=P({\mathbb {Q}}_p) \cap h_jKh_j^{-1}$. Consider the composite of the map ![]() $a_{\iota ^*}\circ q_K^*$ and of the injection
$a_{\iota ^*}\circ q_K^*$ and of the injection ![]() $S_K \hookrightarrow V^R$, and let
$S_K \hookrightarrow V^R$, and let ![]() $\phi _j$ be its
$\phi _j$ be its ![]() $h_j$th component. Then
$h_j$th component. Then ![]() $\phi _j$ sends
$\phi _j$ sends ![]() $c\in H^i(I_K, {\mathbb {F}}_\ell )$ to
$c\in H^i(I_K, {\mathbb {F}}_\ell )$ to ![]() $\iota ^*\circ h_j^* \circ q_K^*(c)$.
$\iota ^*\circ h_j^* \circ q_K^*(c)$.
We can write
The isomorphism is induced on the ![]() $h_j$th component by the composite of the map
$h_j$th component by the composite of the map
given by right multiplication by ![]() $h_j$ and the map
$h_j$ and the map
sending everything to the identity on the second component. Therefore, via the isomorphism in (6.3.3.1), the map ![]() $\phi _j$ is identified with the pullback
$\phi _j$ is identified with the pullback ![]() $H^i(\underline {\Gamma _j}\backslash I, {\mathbb {F}}_\ell )\rightarrow H^i(I, {\mathbb {F}}_\ell )$.
$H^i(\underline {\Gamma _j}\backslash I, {\mathbb {F}}_\ell )\rightarrow H^i(I, {\mathbb {F}}_\ell )$.
It remains to show that each of the pullback maps above induces an isomorphism ![]() $H^i(\underline {\Gamma _j}\backslash I, {\mathbb {F}}_\ell )\xrightarrow {\sim } V^{\Gamma _j}$. Each group
$H^i(\underline {\Gamma _j}\backslash I, {\mathbb {F}}_\ell )\xrightarrow {\sim } V^{\Gamma _j}$. Each group ![]() $\Gamma _j$ is contained in
$\Gamma _j$ is contained in ![]() $P({\mathbb {Z}}_p)$, hence the action of
$P({\mathbb {Z}}_p)$, hence the action of ![]() $\Gamma _j/(\Gamma _j\cap C)$ on
$\Gamma _j/(\Gamma _j\cap C)$ on ![]() $I$ is free. Therefore, as
$I$ is free. Therefore, as ![]() $K$ is a pro-
$K$ is a pro-![]() $p$ group and
$p$ group and ![]() $p \neq \ell$, the desired isomorphism follows from [Reference WeinsteinWei17, Proposition 4.3.2] and [Reference Caraiani, Gulotta, Hsu, Johansson, Mocz, Reinecke and ShihCGH+20, Theorem 2.2.7].
$p \neq \ell$, the desired isomorphism follows from [Reference WeinsteinWei17, Proposition 4.3.2] and [Reference Caraiani, Gulotta, Hsu, Johansson, Mocz, Reinecke and ShihCGH+20, Theorem 2.2.7].
7. The structure of the cohomology in the non-Eisenstein case
The aim of this section is to prove our main results on the cohomology of Hilbert modular varieties after localisation at a non-Eisenstein maximal ideal. These are Theorems 7.1.1 and 7.1.6 stated below. We also establish analogous results for quaternionic Shimura varieties: see Theorem 7.5.2.
7.1 Main results: statements
Theorem 7.1.1 Let ![]() $\ell >2$ be a prime,
$\ell >2$ be a prime, ![]() $K\subset G({\mathbb {A}}_f)$ a neat compact open and
$K\subset G({\mathbb {A}}_f)$ a neat compact open and ![]() $\mathfrak {m} \subset \mathbb {T}$ a maximal ideal in the support of
$\mathfrak {m} \subset \mathbb {T}$ a maximal ideal in the support of ![]() $H^i(Sh_K(G), {\mathbb {F}}_{\ell })$. Let
$H^i(Sh_K(G), {\mathbb {F}}_{\ell })$. Let ![]() $\bar {\rho }_{\mathfrak {m}}$ be the Galois representation attached to
$\bar {\rho }_{\mathfrak {m}}$ be the Galois representation attached to ![]() $\mathfrak {m}$ by Theorem 2.2.1. Assume that the image of
$\mathfrak {m}$ by Theorem 2.2.1. Assume that the image of ![]() $\bar {\rho }_{\mathfrak {m}}$ is not solvable. Then
$\bar {\rho }_{\mathfrak {m}}$ is not solvable. Then ![]() $H^i(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}=H^i_c(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}$ is non-zero only for
$H^i(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}=H^i_c(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}$ is non-zero only for ![]() $i=g$.
$i=g$.
Corollary 7.1.2 With the same notation and assumptions as in Theorem 7.1.1, we have ![]() $H^i(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m}\neq 0$ if and only if
$H^i(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m}\neq 0$ if and only if ![]() $i=g$, and
$i=g$, and ![]() $H^g(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m}$ is torsion-free. The same is true for compactly supported cohomology.
$H^g(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m}$ is torsion-free. The same is true for compactly supported cohomology.
Proof. Looking at the long exact sequence in Betti cohomology coming from the short exact sequence ![]() $0 \rightarrow {\mathbb {Z}}_{\ell } \rightarrow {\mathbb {Z}}_{\ell } \rightarrow {\mathbb {F}}_{\ell }\rightarrow 0$ we see that multiplication by
$0 \rightarrow {\mathbb {Z}}_{\ell } \rightarrow {\mathbb {Z}}_{\ell } \rightarrow {\mathbb {F}}_{\ell }\rightarrow 0$ we see that multiplication by ![]() $\ell$ is surjective on
$\ell$ is surjective on ![]() $H^i(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m}$ if
$H^i(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m}$ if ![]() $i \neq g$, hence
$i \neq g$, hence ![]() $H^i(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m}=0$ for
$H^i(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m}=0$ for ![]() $i \neq g$. On the other hand, we have
$i \neq g$. On the other hand, we have
as the first term vanishes, we deduce that ![]() $H^g(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m}$ is torsion-free, hence free. Finally, the cokernel of the map
$H^g(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m}$ is torsion-free, hence free. Finally, the cokernel of the map ![]() $H^g(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m} \rightarrow H^g(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}$ injects into
$H^g(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m} \rightarrow H^g(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}$ injects into ![]() $H^{g+1}(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m}=0$, hence
$H^{g+1}(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m}=0$, hence ![]() $H^g(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m} \neq 0$. The result for
$H^g(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m} \neq 0$. The result for ![]() $H^*_{\rm c}(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m}$ follows as in Lemma 2.3.1.
$H^*_{\rm c}(Sh_K(G), {\mathbb {Z}}_{\ell })_\mathfrak {m}$ follows as in Lemma 2.3.1.
To proceed, we make the following definition.
Definition 7.1.3
(i) Let
 $v$ be a place of
$v$ be a place of  $F$ above a prime
$F$ above a prime  $p\not =\ell$ which splits completely in
$p\not =\ell$ which splits completely in  $F$. We say that
$F$. We say that  $\bar {\rho }_\mathfrak {m}$ is generic at
$\bar {\rho }_\mathfrak {m}$ is generic at  $v$ if it is unramified at
$v$ if it is unramified at  $v$ and the eigenvalues of Frobenius at
$v$ and the eigenvalues of Frobenius at  $v$ have ratio different from
$v$ have ratio different from  $p^{\pm 1}$.
$p^{\pm 1}$.(ii) Let
 $p \neq \ell$ be a prime. We say that
$p \neq \ell$ be a prime. We say that  $p$ is a decomposed generic prime for
$p$ is a decomposed generic prime for  $\bar {\rho }_\mathfrak {m}$ if
$\bar {\rho }_\mathfrak {m}$ if  $p$ splits completely in
$p$ splits completely in  $F$ and
$F$ and  $\bar {\rho }_{\mathfrak {m}}$ is generic at
$\bar {\rho }_{\mathfrak {m}}$ is generic at  $v$ for every place
$v$ for every place  $v$ of
$v$ of  $F$ above
$F$ above  $p$.
$p$.(iii) We say that
 $\bar {\rho }_{\mathfrak {m}}$ is decomposed generic if there exists a prime
$\bar {\rho }_{\mathfrak {m}}$ is decomposed generic if there exists a prime  $p \neq \ell$ which is decomposed generic for
$p \neq \ell$ which is decomposed generic for  $\bar {\rho }_{\mathfrak {m}}$.
$\bar {\rho }_{\mathfrak {m}}$.
7.1.4
Assume that ![]() $\bar {\rho }_{\mathfrak {m}}$ is generic at some place
$\bar {\rho }_{\mathfrak {m}}$ is generic at some place ![]() $v$ of
$v$ of ![]() $F$. Then any characteristic zero lift of the restriction of
$F$. Then any characteristic zero lift of the restriction of ![]() $\bar {\rho }_{\mathfrak {m}}$ to
$\bar {\rho }_{\mathfrak {m}}$ to ![]() $\Gamma _{F_v}$ cannot be associated via the local Langlands correspondence to an irreducible smooth representation of
$\Gamma _{F_v}$ cannot be associated via the local Langlands correspondence to an irreducible smooth representation of ![]() $\operatorname {GL}_2(F_v)$ which transfers to the non-split quaternion algebra over
$\operatorname {GL}_2(F_v)$ which transfers to the non-split quaternion algebra over ![]() $F_v$.
$F_v$.
Notation 7.1.5 Let ![]() $p \neq \ell$ be a prime which splits completely in
$p \neq \ell$ be a prime which splits completely in ![]() $F$ and such that
$F$ and such that ![]() $\bar {\rho }_\mathfrak {m}$ is unramified at every place of
$\bar {\rho }_\mathfrak {m}$ is unramified at every place of ![]() $F$ above
$F$ above ![]() $p$. We will denote by
$p$. We will denote by ![]() $\delta _p(\mathfrak {m})$ the number of places above
$\delta _p(\mathfrak {m})$ the number of places above ![]() $p$ at which
$p$ at which ![]() $\bar {\rho }_\mathfrak {m}$ is not generic.
$\bar {\rho }_\mathfrak {m}$ is not generic.
Theorem 7.1.6 Let ![]() $\ell >2$ be a prime. Let
$\ell >2$ be a prime. Let ![]() $p \neq \ell$ be an odd prime which splits completely in
$p \neq \ell$ be an odd prime which splits completely in ![]() $F$ and such that
$F$ and such that ![]() $K=K^pK_p$ with
$K=K^pK_p$ with ![]() $K_p$ hyperspecial. Let
$K_p$ hyperspecial. Let ![]() $\mathfrak {m} \subset \mathbb {T}$ be a non-Eisenstein maximal ideal. Then
$\mathfrak {m} \subset \mathbb {T}$ be a non-Eisenstein maximal ideal. Then ![]() $H^*_c(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}=H^*(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}$ vanishes outside the interval
$H^*_c(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}=H^*(Sh_K(G), {\mathbb {F}}_{\ell })_\mathfrak {m}$ vanishes outside the interval ![]() $[g-\delta _p(\mathfrak {m}), g+\delta _p(\mathfrak {m})]$.
$[g-\delta _p(\mathfrak {m}), g+\delta _p(\mathfrak {m})]$.
Remark 7.1.7 For a maximal ideal ![]() $\mathfrak {m} \subset \mathbb {T}$ in the support of
$\mathfrak {m} \subset \mathbb {T}$ in the support of ![]() $H^i(Sh_K(G), {\mathbb {F}}_{\ell })$, the projective image
$H^i(Sh_K(G), {\mathbb {F}}_{\ell })$, the projective image ![]() $I$ of the Galois representation
$I$ of the Galois representation ![]() $\bar {\rho }_\mathfrak {m}$ is a finite subgroup of
$\bar {\rho }_\mathfrak {m}$ is a finite subgroup of ![]() $\operatorname {PGL}_2(\bar {{\mathbb {F}}}_\ell )$. By Dickson's theorem, cf. [Reference Darmon, Diamond and TaylorDDT97, Theorem 2.47 (b)], the group
$\operatorname {PGL}_2(\bar {{\mathbb {F}}}_\ell )$. By Dickson's theorem, cf. [Reference Darmon, Diamond and TaylorDDT97, Theorem 2.47 (b)], the group ![]() $I$ is either conjugate to a subgroup of the upper triangular matrices, or to
$I$ is either conjugate to a subgroup of the upper triangular matrices, or to ![]() $\operatorname {PGL}_2({\mathbb {F}}_{\ell ^k})$ or
$\operatorname {PGL}_2({\mathbb {F}}_{\ell ^k})$ or ![]() $\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$, for some
$\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$, for some ![]() $k\geq 1$, or it is isomorphic to one of
$k\geq 1$, or it is isomorphic to one of ![]() $D_{2n}$, for some
$D_{2n}$, for some ![]() $n\in {\mathbb {Z}}_{> 1}$ prime to
$n\in {\mathbb {Z}}_{> 1}$ prime to ![]() $\ell$,
$\ell$, ![]() $A_4$,
$A_4$, ![]() $S_4$ or
$S_4$ or ![]() $A_5$. It follows that the image of
$A_5$. It follows that the image of ![]() $\bar {\rho }_\mathfrak {m}$ is not solvable if and only if the following holds:
$\bar {\rho }_\mathfrak {m}$ is not solvable if and only if the following holds:
(i) if
 $\ell =3$, then
$\ell =3$, then  $I$ is isomorphic to
$I$ is isomorphic to  $A_5$ or it contains a conjugate of
$A_5$ or it contains a conjugate of  $\operatorname {PSL}_2({\mathbb {F}}_9)$;
$\operatorname {PSL}_2({\mathbb {F}}_9)$;(ii) if
 $\ell >3$, then
$\ell >3$, then  $I$ is isomorphic to
$I$ is isomorphic to  $A_5$ or it contains a conjugate of
$A_5$ or it contains a conjugate of  $\operatorname {PSL}_2({\mathbb {F}}_{\ell })$.
$\operatorname {PSL}_2({\mathbb {F}}_{\ell })$.
Theorem 7.1.1 follows from Theorem 7.1.6 in view of the following lemma (more precisely, observe that the proof of the lemma allows to produce ![]() $p$ as in Definition 7.1.3(iii) satisfying the conditions of Theorem 7.1.6).
$p$ as in Definition 7.1.3(iii) satisfying the conditions of Theorem 7.1.6).
Lemma 7.1.8 Assume that ![]() $\ell >2$ and that the image of
$\ell >2$ and that the image of ![]() $\bar {\rho }_{\mathfrak {m}}$ is not solvable. Then
$\bar {\rho }_{\mathfrak {m}}$ is not solvable. Then ![]() $\bar {\rho }_{\mathfrak {m}}$ is decomposed generic in the sense of Definition 7.1.3.
$\bar {\rho }_{\mathfrak {m}}$ is decomposed generic in the sense of Definition 7.1.3.
Proof. This is a variation of [Reference Allen and NewtonAN20, Lemma 2.3]; following [Reference Allen and NewtonAN20, Lemma 2.3], we prove that there are infinitely many primes ![]() $p\equiv 1 \pmod {\ell }$, totally split in
$p\equiv 1 \pmod {\ell }$, totally split in ![]() $F$, and such that
$F$, and such that ![]() $\bar {\rho }_\mathfrak {m}$ is generic at every place above
$\bar {\rho }_\mathfrak {m}$ is generic at every place above ![]() $p$. This is deduced from our large image assumption using the Chebotarev density theorem.
$p$. This is deduced from our large image assumption using the Chebotarev density theorem.
We first make some preliminary reductions. Let ![]() $\tilde {F}$ be the normal closure of
$\tilde {F}$ be the normal closure of ![]() $F$ in
$F$ in ![]() ${\mathbb {C}}$; notice that
${\mathbb {C}}$; notice that ![]() $\tilde {F}$ is also a totally real field. Let
$\tilde {F}$ is also a totally real field. Let ![]() $\mathrm {pr}: \operatorname {GL}_2(\bar {{\mathbb {F}}}_{\ell })\rightarrow \operatorname {PGL}_2(\bar {{\mathbb {F}}}_{\ell })$ be the projection map. As observed before the statement of the theorem, the image
$\mathrm {pr}: \operatorname {GL}_2(\bar {{\mathbb {F}}}_{\ell })\rightarrow \operatorname {PGL}_2(\bar {{\mathbb {F}}}_{\ell })$ be the projection map. As observed before the statement of the theorem, the image ![]() $I$ of
$I$ of
is isomorphic to ![]() $A_5$, or conjugate to one of
$A_5$, or conjugate to one of ![]() $\operatorname {PGL}_2({\mathbb {F}}_{\ell ^k})$ or
$\operatorname {PGL}_2({\mathbb {F}}_{\ell ^k})$ or ![]() $\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$, where
$\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$, where ![]() $k\geq 2$ if
$k\geq 2$ if ![]() $\ell = 3$ and
$\ell = 3$ and ![]() $k\geq 1$ if
$k\geq 1$ if ![]() $\ell >3$. We claim that the same is true for the image
$\ell >3$. We claim that the same is true for the image ![]() $\tilde {I}$ of
$\tilde {I}$ of ![]() $\mathrm {pr} \circ \bar {\rho }_{\mathfrak {m}|\Gamma _{\tilde {F}}}: \Gamma _{\tilde {F}} \rightarrow \operatorname {PGL}_2(\bar {{\mathbb {F}}}_\ell )$. Since
$\mathrm {pr} \circ \bar {\rho }_{\mathfrak {m}|\Gamma _{\tilde {F}}}: \Gamma _{\tilde {F}} \rightarrow \operatorname {PGL}_2(\bar {{\mathbb {F}}}_\ell )$. Since ![]() $\tilde {F}/F$ is Galois, the group
$\tilde {F}/F$ is Galois, the group ![]() $\tilde {I}$ is a normal subgroup of
$\tilde {I}$ is a normal subgroup of ![]() $I$.
$I$.
(i) Assume first that the group
 $I$ is isomorphic to
$I$ is isomorphic to  $A_5$. Since
$A_5$. Since  $A_5$ is simple and
$A_5$ is simple and  $\tilde {I}$ is a normal subgroup of
$\tilde {I}$ is a normal subgroup of  $I$, it is enough to show that
$I$, it is enough to show that  $\tilde {I}$ is non-trivial. This is true because
$\tilde {I}$ is non-trivial. This is true because  $\tilde {I}$ contains the image under
$\tilde {I}$ contains the image under  $\mathrm {pr}\circ \bar {\rho }_{\mathfrak {m}|\Gamma _{\tilde {F}}}$ of any complex conjugation in
$\mathrm {pr}\circ \bar {\rho }_{\mathfrak {m}|\Gamma _{\tilde {F}}}$ of any complex conjugation in  $\Gamma _{\tilde {F}}$, which is conjugate to the matrix
$\Gamma _{\tilde {F}}$, which is conjugate to the matrix  $(\begin{smallmatrix} 1 & 0\\ 0 & -1 \end{smallmatrix})$ because
$(\begin{smallmatrix} 1 & 0\\ 0 & -1 \end{smallmatrix})$ because  $\bar {\rho }_{\mathfrak {m}}$ is totally odd.
$\bar {\rho }_{\mathfrak {m}}$ is totally odd.(ii) Assume now that the group
 $I$ is conjugate to
$I$ is conjugate to  $\operatorname {PGL}_2({\mathbb {F}}_{\ell ^k})$ or
$\operatorname {PGL}_2({\mathbb {F}}_{\ell ^k})$ or  $\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$. We conjugate everything so that
$\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$. We conjugate everything so that  $I$ is identified with
$I$ is identified with  $\operatorname {PGL}_2({\mathbb {F}}_{\ell ^k})$ or
$\operatorname {PGL}_2({\mathbb {F}}_{\ell ^k})$ or  $\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$ inside
$\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$ inside  $\operatorname {PGL}_2(\bar {{\mathbb {F}}}_\ell )$. It is enough to prove that
$\operatorname {PGL}_2(\bar {{\mathbb {F}}}_\ell )$. It is enough to prove that  $\tilde {I}\supseteq \operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$. As the representation
$\tilde {I}\supseteq \operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$. As the representation  $\bar {\rho }_{\mathfrak {m}}$ is totally odd, the image via
$\bar {\rho }_{\mathfrak {m}}$ is totally odd, the image via  $\bar {\rho }_{\mathfrak {m}|\Gamma _{\tilde {F}}}$ of any complex conjugation
$\bar {\rho }_{\mathfrak {m}|\Gamma _{\tilde {F}}}$ of any complex conjugation  $c\in \Gamma _{\tilde {F}}$ is a non-scalar semisimple element. As a normal subgroup of
$c\in \Gamma _{\tilde {F}}$ is a non-scalar semisimple element. As a normal subgroup of  $I$, the group
$I$, the group  $\tilde {I}$ contains the projective image of every
$\tilde {I}$ contains the projective image of every  $\operatorname {SL}_2({\mathbb {F}}_{\ell ^k})$-conjugate of
$\operatorname {SL}_2({\mathbb {F}}_{\ell ^k})$-conjugate of  $\bar {\rho }_{\mathfrak {m}}(c)$. In particular,
$\bar {\rho }_{\mathfrak {m}}(c)$. In particular,  $\tilde {I}\cap \operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$ contains the ratio of any two distinct such conjugates and is, therefore, a non-trivial normal subgroup of
$\tilde {I}\cap \operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$ contains the ratio of any two distinct such conjugates and is, therefore, a non-trivial normal subgroup of  $\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$. Finally, the groups
$\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$. Finally, the groups  $\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$, with
$\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$, with  $k\geq 2$ if
$k\geq 2$ if  $\ell =3$ and
$\ell =3$ and  $k\geq 1$ if
$k\geq 1$ if  $\ell >3$, are simple. Therefore,
$\ell >3$, are simple. Therefore,  $\tilde {I}\supseteq \operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$.
$\tilde {I}\supseteq \operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$.
This proves the claim. Up to replacing ![]() $\tilde {F}$ by a finite abelian extension
$\tilde {F}$ by a finite abelian extension ![]() $F'$ and conjugating
$F'$ and conjugating ![]() $\bar {\rho }_{\mathfrak {m}}$, we may ensure that the image
$\bar {\rho }_{\mathfrak {m}}$, we may ensure that the image ![]() $I'$ of
$I'$ of ![]() $\mathrm {pr} \circ \bar {\rho }_{\mathfrak {m}|\Gamma _{F'}}$ equals either
$\mathrm {pr} \circ \bar {\rho }_{\mathfrak {m}|\Gamma _{F'}}$ equals either ![]() $A_5$ or
$A_5$ or ![]() $\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$, with
$\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$, with ![]() $k\geq 2$ if
$k\geq 2$ if ![]() $\ell =3$ and
$\ell =3$ and ![]() $k\geq 1$ if
$k\geq 1$ if ![]() $\ell >3$. As
$\ell >3$. As ![]() $A_5$ and
$A_5$ and ![]() $\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$ are both simple,
$\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$ are both simple, ![]() $I'$ is unchanged if we replace
$I'$ is unchanged if we replace ![]() $F'$ by its normal closure. For the same reason we may adjoin
$F'$ by its normal closure. For the same reason we may adjoin ![]() $\zeta _{\ell }$ to
$\zeta _{\ell }$ to ![]() $F'$ without changing
$F'$ without changing ![]() $I'$.
$I'$.
Let ![]() $\Gamma$ denote either one of the finite simple groups
$\Gamma$ denote either one of the finite simple groups ![]() $A_5$ or
$A_5$ or ![]() $\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$. Let
$\operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$. Let ![]() $L$ be the normal closure of the extension of
$L$ be the normal closure of the extension of ![]() $F'$ cut out by
$F'$ cut out by ![]() $I'$. Since
$I'$. Since ![]() $\Gamma$ is simple, Goursat's lemma implies that
$\Gamma$ is simple, Goursat's lemma implies that ![]() $\operatorname {Gal}(L/F')\simeq \Gamma ^t$ for some
$\operatorname {Gal}(L/F')\simeq \Gamma ^t$ for some ![]() $t\geq 1$. We claim that we can choose an element
$t\geq 1$. We claim that we can choose an element ![]() $1\neq g\in \Gamma$ which is semisimple when viewed as an element of
$1\neq g\in \Gamma$ which is semisimple when viewed as an element of ![]() $\operatorname {PGL}_2(\bar {{\mathbb {F}}}_{\ell })$. In the case
$\operatorname {PGL}_2(\bar {{\mathbb {F}}}_{\ell })$. In the case ![]() $\Gamma = \operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$, this is clear. In the case
$\Gamma = \operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$, this is clear. In the case ![]() $\Gamma = A_5$, choose any element of order
$\Gamma = A_5$, choose any element of order ![]() $2$; since
$2$; since ![]() $\ell \not =2$, such an element must be semisimple. The Chebotarev density theorem ensures the existence of a place
$\ell \not =2$, such an element must be semisimple. The Chebotarev density theorem ensures the existence of a place ![]() $\mathfrak {p}$ of
$\mathfrak {p}$ of ![]() $F'$ with residue field
$F'$ with residue field ![]() ${\mathbb {F}}_p$ with
${\mathbb {F}}_p$ with ![]() $p \neq \ell$ unramified in
$p \neq \ell$ unramified in ![]() $F$ and such that
$F$ and such that ![]() $\mathrm {Frob}_\mathfrak {p}^{L/F'}$ is conjugate to
$\mathrm {Frob}_\mathfrak {p}^{L/F'}$ is conjugate to ![]() $(g, g, \ldots, g)$. Since
$(g, g, \ldots, g)$. Since ![]() $F'/{\mathbb {Q}}$ is Galois,
$F'/{\mathbb {Q}}$ is Galois, ![]() $p$ is totally split in
$p$ is totally split in ![]() $F'$. We claim that, for every place
$F'$. We claim that, for every place ![]() $\mathfrak {p}'$ of
$\mathfrak {p}'$ of ![]() $F'$ above
$F'$ above ![]() $p$, the element
$p$, the element ![]() $\bar {\rho }_\mathfrak {m}(\mathrm {Frob}_{\mathfrak {p}'})$ is semisimple and different from the identity in
$\bar {\rho }_\mathfrak {m}(\mathrm {Frob}_{\mathfrak {p}'})$ is semisimple and different from the identity in ![]() $\operatorname {PGL}_2(\bar {{\mathbb {F}}}_{\ell })$. In the case
$\operatorname {PGL}_2(\bar {{\mathbb {F}}}_{\ell })$. In the case ![]() $\Gamma = \operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$, this follows as in [Reference Allen and NewtonAN20, Lemma 2.3]. In the case
$\Gamma = \operatorname {PSL}_2({\mathbb {F}}_{\ell ^k})$, this follows as in [Reference Allen and NewtonAN20, Lemma 2.3]. In the case ![]() $\Gamma = A_5$, the argument in [Reference Allen and NewtonAN20, Lemma 2.3] shows that each such element has order
$\Gamma = A_5$, the argument in [Reference Allen and NewtonAN20, Lemma 2.3] shows that each such element has order ![]() $2$ in
$2$ in ![]() $\operatorname {PGL}_2(\bar {{\mathbb {F}}}_{\ell })$, which implies that it must also be semisimple and different from the identity. As
$\operatorname {PGL}_2(\bar {{\mathbb {F}}}_{\ell })$, which implies that it must also be semisimple and different from the identity. As ![]() $\zeta _{\ell } \in F'$ we have
$\zeta _{\ell } \in F'$ we have ![]() $p \equiv 1 \pmod {\ell }$, hence the eigenvalues of each
$p \equiv 1 \pmod {\ell }$, hence the eigenvalues of each ![]() $\bar {\rho }_\mathfrak {m}(\mathrm {Frob}_{\mathfrak {p}'})$ cannot have ratio
$\bar {\rho }_\mathfrak {m}(\mathrm {Frob}_{\mathfrak {p}'})$ cannot have ratio ![]() $p^{\pm 1}$.
$p^{\pm 1}$.
7.2 Proof of Theorem 7.1.6
7.2.1 Step 1: setup and choice of the auxiliary data
Note that the quantity ![]() $\delta _p(\mathfrak {m}) = \delta _p(\mathfrak {m}^\vee )$. By Lemma 2.3.1 it suffices to show the following implication:
$\delta _p(\mathfrak {m}) = \delta _p(\mathfrak {m}^\vee )$. By Lemma 2.3.1 it suffices to show the following implication:
Choose an auxiliary ![]() $CM$ extension
$CM$ extension ![]() $E$ of
$E$ of ![]() $F$ such that every
$F$ such that every ![]() $\mathfrak {p} \in \Sigma _p$ is inert in
$\mathfrak {p} \in \Sigma _p$ is inert in ![]() $E$, and choose
$E$, and choose ![]() $K_E=(\mathcal {O}_E\otimes {\mathbb {Z}}_p)^\times K_E^{p}\subset T_E({\mathbb {A}}_f)$ sufficiently small with respect to
$K_E=(\mathcal {O}_E\otimes {\mathbb {Z}}_p)^\times K_E^{p}\subset T_E({\mathbb {A}}_f)$ sufficiently small with respect to ![]() $K$. With the notation of § 3.1.3, consider the unitary group
$K$. With the notation of § 3.1.3, consider the unitary group ![]() $H:=H_{\emptyset }$ and let
$H:=H_{\emptyset }$ and let ![]() $U \subset H({\mathbb {A}}_f)$ be the image of
$U \subset H({\mathbb {A}}_f)$ be the image of ![]() $K \times K_E$. Recall that the Hecke algebra
$K \times K_E$. Recall that the Hecke algebra ![]() $\mathbb {T}$ (defined in § 3.2.6) acts on the cohomology of
$\mathbb {T}$ (defined in § 3.2.6) acts on the cohomology of ![]() $Sh_{U}(H)$, and Corollary 3.2.9 ensures that, for
$Sh_{U}(H)$, and Corollary 3.2.9 ensures that, for ![]() $i \geq 0$,
$i \geq 0$,
Therefore, for the sake of proving Theorem 7.1.6, we may (and will) work with ![]() $Sh_U(H)$. Let
$Sh_U(H)$. Let ![]() $\overline {Sh}_U(H)$ be the base change to
$\overline {Sh}_U(H)$ be the base change to ![]() $\bar {{\mathbb {F}}}_p$ of its integral model. We have isomorphisms, for
$\bar {{\mathbb {F}}}_p$ of its integral model. We have isomorphisms, for ![]() $i \geq 0$,
$i \geq 0$,
The first is obtained as in [Reference Lan and StrohLS18, Corollary 5.20]; the second follows from the fact that the complex of nearby cycles ![]() $R\Psi {\mathbb {F}}_{\ell }$ is quasi-isomorphic to the constant sheaf
$R\Psi {\mathbb {F}}_{\ell }$ is quasi-isomorphic to the constant sheaf ![]() ${\mathbb {F}}_{\ell }$ as the integral model is smooth. Hence, it suffices to show the implication
${\mathbb {F}}_{\ell }$ as the integral model is smooth. Hence, it suffices to show the implication
7.2.2 Step 2: the Newton stratification
We have a Newton stratification on ![]() $\overline {Sh}_U(H)$ indexed by elements
$\overline {Sh}_U(H)$ indexed by elements ![]() $b=(b_1, \ldots, b_g)$ with
$b=(b_1, \ldots, b_g)$ with ![]() $b_j \in B(H_{\mathfrak {p}_j}, \mu _{\mathfrak {p}_j})$. Recall that each
$b_j \in B(H_{\mathfrak {p}_j}, \mu _{\mathfrak {p}_j})$. Recall that each ![]() $B(H_{\mathfrak {p}_j}, \mu _{\mathfrak {p}_j})$ consists of one
$B(H_{\mathfrak {p}_j}, \mu _{\mathfrak {p}_j})$ consists of one ![]() $\mu$-ordinary and one basic element. We denote by
$\mu$-ordinary and one basic element. We denote by ![]() $\overline {Sh}_U(H)^b \subset \overline {Sh}_U(H)$ the stratum corresponding to
$\overline {Sh}_U(H)^b \subset \overline {Sh}_U(H)$ the stratum corresponding to ![]() $b$. More generally, for each
$b$. More generally, for each ![]() $0 \leq k \leq g$ and every
$0 \leq k \leq g$ and every ![]() $c \in \prod _{j \leq k}B(H_{\mathfrak {p}_j}, \mu _{\mathfrak {p}_j})$ we let
$c \in \prod _{j \leq k}B(H_{\mathfrak {p}_j}, \mu _{\mathfrak {p}_j})$ we let ![]() $\overline {Sh}_U(H)^c \subset \overline {Sh}_U(H)$ be the union of the Newton strata corresponding to elements
$\overline {Sh}_U(H)^c \subset \overline {Sh}_U(H)$ be the union of the Newton strata corresponding to elements ![]() $b=(b_1, \ldots, b_g)$ such that
$b=(b_1, \ldots, b_g)$ such that ![]() $(b_1, \ldots, b_k)=c$. In particular, for
$(b_1, \ldots, b_k)=c$. In particular, for ![]() $k=0$ we obtain
$k=0$ we obtain ![]() $\overline {Sh}_U(H)$ and for
$\overline {Sh}_U(H)$ and for ![]() $k=g$ we recover Newton strata.
$k=g$ we recover Newton strata.
As we are excluding from ![]() $\mathbb {T}$ the Hecke operators at places above
$\mathbb {T}$ the Hecke operators at places above ![]() $p$, the Hecke algebra acts on the cohomology of each stratum. The first (elementary) observation is that it suffices to show (7.2.1.2) for each Newton stratum.
$p$, the Hecke algebra acts on the cohomology of each stratum. The first (elementary) observation is that it suffices to show (7.2.1.2) for each Newton stratum.
Lemma 7.2.3 Assume that ![]() $H^i_{\rm c}(\overline {Sh}_U(H)^b, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for every
$H^i_{\rm c}(\overline {Sh}_U(H)^b, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for every ![]() $i< g-\delta _p(\mathfrak {m})$ and every
$i< g-\delta _p(\mathfrak {m})$ and every ![]() $b \in B(H_{{\mathbb {Q}}_p}, \mu )$. Then
$b \in B(H_{{\mathbb {Q}}_p}, \mu )$. Then ![]() $H^i_{\rm c}(\overline {Sh}_U(H), {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for
$H^i_{\rm c}(\overline {Sh}_U(H), {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for ![]() $i< g-\delta _p(\mathfrak {m})$.
$i< g-\delta _p(\mathfrak {m})$.
Proof. This follows from additivity of compactly supported cohomology. To be precise, we show by descending induction on ![]() $0 \leq k \leq g$ that
$0 \leq k \leq g$ that
By hypothesis the statement is true for ![]() $k=g$. Now take
$k=g$. Now take ![]() $k< g$ and assume that the statement is true for
$k< g$ and assume that the statement is true for ![]() $k+1$. Take
$k+1$. Take ![]() $c \in \prod _{j \leq k}B(H_{\mathfrak {p}_j}, \mu _{\mathfrak {p}_j})$. Let
$c \in \prod _{j \leq k}B(H_{\mathfrak {p}_j}, \mu _{\mathfrak {p}_j})$. Let ![]() $o$ (respectively,
$o$ (respectively, ![]() $b$) be the non-basic (respectively, basic) element in
$b$) be the non-basic (respectively, basic) element in ![]() $B(H_{\mathfrak {p}_{k+1}}, \mu _{\mathfrak {p}_{k+1}})$ and consider
$B(H_{\mathfrak {p}_{k+1}}, \mu _{\mathfrak {p}_{k+1}})$ and consider ![]() $(c, o), (c, b) \in \prod _{j \leq k+1}B(H_{\mathfrak {p}_j}, \mu _{\mathfrak {p}_j})$. We have
$(c, o), (c, b) \in \prod _{j \leq k+1}B(H_{\mathfrak {p}_j}, \mu _{\mathfrak {p}_j})$. We have
furthermore, ![]() $\overline {Sh}_U(H)^{(c, o)}$ is open in
$\overline {Sh}_U(H)^{(c, o)}$ is open in ![]() $\overline {Sh}_U(H)^c$ and
$\overline {Sh}_U(H)^c$ and ![]() $\overline {Sh}_U(H)^{(c, b)}$ is the closed complement. By induction, we know that
$\overline {Sh}_U(H)^{(c, b)}$ is the closed complement. By induction, we know that ![]() $H^i_c(\overline {Sh}_U(H)^{(c, o)}, {\mathbb {F}}_{\ell })_\mathfrak {m}=H^i_c(\overline {Sh}_U(H)^{(c, b)}, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for
$H^i_c(\overline {Sh}_U(H)^{(c, o)}, {\mathbb {F}}_{\ell })_\mathfrak {m}=H^i_c(\overline {Sh}_U(H)^{(c, b)}, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for ![]() $i< g-\delta _p(\mathfrak {m})$. The exact sequence
$i< g-\delta _p(\mathfrak {m})$. The exact sequence
implies that ![]() $H^i_c(\overline {Sh}_U(H)^{c}, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for
$H^i_c(\overline {Sh}_U(H)^{c}, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for ![]() $i< g-\delta _p(\mathfrak {m})$.
$i< g-\delta _p(\mathfrak {m})$.
We need to show that the assumption of the lemma holds true in our situation. The first key ingredient is the following.
Lemma 7.2.4 Let ![]() $b \in B(H_{{\mathbb {Q}}_p}, \mu )$.
$b \in B(H_{{\mathbb {Q}}_p}, \mu )$.
(i) If
 $b$ is not the
$b$ is not the  $\mu$-ordinary element, then the stratum
$\mu$-ordinary element, then the stratum  $\overline {Sh}_U(H)^b$ is smooth, affine and of dimension the number of non-basic coordinates of
$\overline {Sh}_U(H)^b$ is smooth, affine and of dimension the number of non-basic coordinates of  $b$.
$b$.(ii) If
 $b$ is the
$b$ is the  $\mu$-ordinary element, then
$\mu$-ordinary element, then  $\overline {Sh}_U(H)^b$ is smooth of dimension
$\overline {Sh}_U(H)^b$ is smooth of dimension  $g$, and the partial minimal compactification of
$g$, and the partial minimal compactification of  $\overline {Sh}_U(H)^b$ (i.e. the union of
$\overline {Sh}_U(H)^b$ (i.e. the union of  $\overline {Sh}_U(H)^b$ and the cusps in the minimal compactification of
$\overline {Sh}_U(H)^b$ and the cusps in the minimal compactification of  $\overline {Sh}_U(H)$) is affine.
$\overline {Sh}_U(H)$) is affine.
Proof. The dimension of strata can be obtained from [Reference Tian and XiaoTX16, Proposition 4.7]. As ![]() $p$ splits completely in
$p$ splits completely in ![]() $F$ Newton strata coincide with Ekedahl–Oort strata. Each of them is smooth by [Reference Shen and ZhangSZ22, Theorem 3.4.7]. Furthermore, recall that
$F$ Newton strata coincide with Ekedahl–Oort strata. Each of them is smooth by [Reference Shen and ZhangSZ22, Theorem 3.4.7]. Furthermore, recall that ![]() $\overline {Sh}_U(H)$ is a finite union of quotients of connected components of integral models of Hodge-type Shimura varieties by finite groups. Each Ekedahl–Oort stratum in
$\overline {Sh}_U(H)$ is a finite union of quotients of connected components of integral models of Hodge-type Shimura varieties by finite groups. Each Ekedahl–Oort stratum in ![]() $\overline {Sh}_U(H)$ decomposes accordingly, hence its partial minimal compactification is affine by [Reference Goldring and KoskivirtaGK19, Proposition 6.3.1] (see also [Reference BoxerBox15]). Finally, the
$\overline {Sh}_U(H)$ decomposes accordingly, hence its partial minimal compactification is affine by [Reference Goldring and KoskivirtaGK19, Proposition 6.3.1] (see also [Reference BoxerBox15]). Finally, the ![]() $\mu$-ordinary stratum is the only one intersecting the boundary, hence the lemma follows.
$\mu$-ordinary stratum is the only one intersecting the boundary, hence the lemma follows.
Corollary 7.2.5 Let ![]() $b \in B(H_{{\mathbb {Q}}_p}, \mu )$ be such that
$b \in B(H_{{\mathbb {Q}}_p}, \mu )$ be such that ![]() $\dim \overline {Sh}_U(H)^b\geq g-\delta _p(\mathfrak {m})$. Then for every
$\dim \overline {Sh}_U(H)^b\geq g-\delta _p(\mathfrak {m})$. Then for every ![]() $i< g-\delta _p(\mathfrak {m})$ we have
$i< g-\delta _p(\mathfrak {m})$ we have ![]() $H^i_c(\overline {Sh}_U(H)^b, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$.
$H^i_c(\overline {Sh}_U(H)^b, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$.
Proof. Let us first assume that ![]() $b$ is not the
$b$ is not the ![]() $\mu$-ordinary element and let us set
$\mu$-ordinary element and let us set ![]() $d_b:=\dim \overline {Sh}_U(H)^b$. By Artin vanishing
$d_b:=\dim \overline {Sh}_U(H)^b$. By Artin vanishing ![]() $H^i(\overline {Sh}_U(H)^b, {\mathbb {F}}_{\ell })=0$ for
$H^i(\overline {Sh}_U(H)^b, {\mathbb {F}}_{\ell })=0$ for ![]() $i>d_b$, and by Poincaré duality
$i>d_b$, and by Poincaré duality ![]() $H^i_c(\overline {Sh}_U(H)^b, {\mathbb {F}}_{\ell })=0$ for
$H^i_c(\overline {Sh}_U(H)^b, {\mathbb {F}}_{\ell })=0$ for ![]() $i< d_b$. In particular,
$i< d_b$. In particular, ![]() $H^i_c(\overline {Sh}_U(H)^b, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for
$H^i_c(\overline {Sh}_U(H)^b, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for ![]() $i< g-\delta _p(\mathfrak {m})$.
$i< g-\delta _p(\mathfrak {m})$.
Now let us consider the ordinary stratum ![]() $\overline {Sh}_U(H)^b$ and its partial minimal compactification
$\overline {Sh}_U(H)^b$ and its partial minimal compactification ![]() $\overline {Sh}_U(H)^{b, *}$, with boundary
$\overline {Sh}_U(H)^{b, *}$, with boundary ![]() $\partial$. Let
$\partial$. Let ![]() $j^b: \overline {Sh}_U(H)^b \rightarrow \overline {Sh}_U(H)^{b, *}$ and
$j^b: \overline {Sh}_U(H)^b \rightarrow \overline {Sh}_U(H)^{b, *}$ and ![]() $i^b: \partial \rightarrow \overline {Sh}_U(H)^{b, *}$ be the inclusions. By Artin vanishing
$i^b: \partial \rightarrow \overline {Sh}_U(H)^{b, *}$ be the inclusions. By Artin vanishing ![]() $H^i(\overline {Sh}_U(H)^{b, *}, j^b_!{\mathbb {F}}_{\ell })=0$ for
$H^i(\overline {Sh}_U(H)^{b, *}, j^b_!{\mathbb {F}}_{\ell })=0$ for ![]() $i>g$, and by Verdier duality
$i>g$, and by Verdier duality ![]() $H^i_c(\overline {Sh}_U(H)^{b, *}, Rj^b_*{\mathbb {F}}_{\ell })=0$ for
$H^i_c(\overline {Sh}_U(H)^{b, *}, Rj^b_*{\mathbb {F}}_{\ell })=0$ for ![]() $i< g$. Finally, we have an exact sequence
$i< g$. Finally, we have an exact sequence
To end the proof it suffices to show that ![]() $H^*_c(\partial, i^{b, *}Rj^b_*{\mathbb {F}}_{\ell })_\mathfrak {m}=0$. Denoting by
$H^*_c(\partial, i^{b, *}Rj^b_*{\mathbb {F}}_{\ell })_\mathfrak {m}=0$. Denoting by ![]() $j: \overline {Sh}_U(H) \rightarrow \overline {Sh}_U(H)^{*}$ and
$j: \overline {Sh}_U(H) \rightarrow \overline {Sh}_U(H)^{*}$ and ![]() $i: \partial \rightarrow \overline {Sh}_U(H)^{*}$ the inclusions we have
$i: \partial \rightarrow \overline {Sh}_U(H)^{*}$ the inclusions we have ![]() $i^{b, *}Rj^{b}_*{\mathbb {F}}_\ell \simeq i^{*}Rj_*{\mathbb {F}}_\ell$. It follows that it suffices to prove that, after localisation at
$i^{b, *}Rj^{b}_*{\mathbb {F}}_\ell \simeq i^{*}Rj_*{\mathbb {F}}_\ell$. It follows that it suffices to prove that, after localisation at ![]() $\mathfrak {m}$, the maps
$\mathfrak {m}$, the maps ![]() $H^*_c(\overline {Sh}_U(H), {\mathbb {F}}_\ell )\rightarrow H^*_c(\overline {Sh}_U(H)^{*}, Rj_*{\mathbb {F}}_\ell )$ are bijective. In other words, we have to show that the natural maps
$H^*_c(\overline {Sh}_U(H), {\mathbb {F}}_\ell )\rightarrow H^*_c(\overline {Sh}_U(H)^{*}, Rj_*{\mathbb {F}}_\ell )$ are bijective. In other words, we have to show that the natural maps
are isomorphisms. Using [Reference Lan and StrohLS18, Corollary 5.20] we see that we can replace ![]() $\overline {Sh}_U(H)$ by
$\overline {Sh}_U(H)$ by ![]() $Sh_U(H)$; since
$Sh_U(H)$; since ![]() $\mathfrak {m}$ is non-Eisenstein, the conclusion then follows from Lemma 2.3.1 and Corollary 3.2.9.
$\mathfrak {m}$ is non-Eisenstein, the conclusion then follows from Lemma 2.3.1 and Corollary 3.2.9.
To show Theorem 7.1.6 it remains to prove the following result.
Proposition 7.2.6 Let ![]() $b \in B(H_{{\mathbb {Q}}_p}, \mu )$ and let
$b \in B(H_{{\mathbb {Q}}_p}, \mu )$ and let ![]() $\mathfrak {m} \subset \mathbb {T}$ be a non-Eisenstein maximal ideal. If
$\mathfrak {m} \subset \mathbb {T}$ be a non-Eisenstein maximal ideal. If ![]() $\dim \overline {Sh}_U(H)^b< g-\delta _p(\mathfrak {m})$, then for every
$\dim \overline {Sh}_U(H)^b< g-\delta _p(\mathfrak {m})$, then for every ![]() $i\geq 0$ we have
$i\geq 0$ we have ![]() $H^i(\overline {Sh}_U(H)^b, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$.
$H^i(\overline {Sh}_U(H)^b, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$.
Indeed, applying the above proposition to ![]() $\mathfrak {m}^\vee$ and using Corollary 7.2.5 we obtain that
$\mathfrak {m}^\vee$ and using Corollary 7.2.5 we obtain that ![]() $H^i_c(\overline {Sh}_U(H)^b, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for
$H^i_c(\overline {Sh}_U(H)^b, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for ![]() $i< g-\delta _p(\mathfrak {m})$ and for every
$i< g-\delta _p(\mathfrak {m})$ and for every ![]() $b \in B(H_{{\mathbb {Q}}_p}, \mu )$. By Lemma 7.2.3 we conclude that
$b \in B(H_{{\mathbb {Q}}_p}, \mu )$. By Lemma 7.2.3 we conclude that ![]() $H^i_{\rm c}(\overline {Sh}_U(H), {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for
$H^i_{\rm c}(\overline {Sh}_U(H), {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for ![]() $i< g-\delta _p(\mathfrak {m})$.
$i< g-\delta _p(\mathfrak {m})$.
Finally, we will deduce Proposition 7.2.6 from the following result, whose proof will be given below.
Proposition 7.2.7 If ![]() $\dim \overline {Sh}_U(H)^b< g-\delta _p(\mathfrak {m})$, then
$\dim \overline {Sh}_U(H)^b< g-\delta _p(\mathfrak {m})$, then ![]() $H^i(\mathrm {Ig}^b, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for every
$H^i(\mathrm {Ig}^b, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for every ![]() $i$.
$i$.
7.2.8
Assuming Proposition 7.2.7, let us prove Proposition 7.2.6. Observe that the stratum ![]() $\overline {Sh}_U(H)^b$ consists of a unique leaf; let
$\overline {Sh}_U(H)^b$ consists of a unique leaf; let ![]() $\mathbb {X}^b$ be the
$\mathbb {X}^b$ be the ![]() $p$-divisible group attached to a geometric point in the leaf, and
$p$-divisible group attached to a geometric point in the leaf, and ![]() $\Gamma ^b$ the automorphism group of
$\Gamma ^b$ the automorphism group of ![]() $\mathbb {X}^b$ (respecting extra structures). Let
$\mathbb {X}^b$ (respecting extra structures). Let ![]() $Y_U(H)_{\bar {{\mathbb {F}}}_p}^{b, \mathrm {perf}}$ be the perfection of
$Y_U(H)_{\bar {{\mathbb {F}}}_p}^{b, \mathrm {perf}}$ be the perfection of ![]() $Y_U(H)_{\bar {{\mathbb {F}}}_p}^b$; the forgetful map
$Y_U(H)_{\bar {{\mathbb {F}}}_p}^b$; the forgetful map ![]() $\overline {\mathrm {Ig}}^b\rightarrow Y_U(H)_{\bar {{\mathbb {F}}}_p}^b$ factors through a map
$\overline {\mathrm {Ig}}^b\rightarrow Y_U(H)_{\bar {{\mathbb {F}}}_p}^b$ factors through a map ![]() $\overline {\mathrm {Ig}}^b\rightarrow Y_U(H)_{\bar {{\mathbb {F}}}_p}^{b, \mathrm {perf}}$, which is a
$\overline {\mathrm {Ig}}^b\rightarrow Y_U(H)_{\bar {{\mathbb {F}}}_p}^{b, \mathrm {perf}}$, which is a ![]() $\Gamma ^b$-torsor (cf. [Reference Caraiani and ScholzeCS19, Proposition 2.2.6]). For
$\Gamma ^b$-torsor (cf. [Reference Caraiani and ScholzeCS19, Proposition 2.2.6]). For ![]() $u \in \mathcal {O}_{E}^{\times }\cap U^p$, the action of
$u \in \mathcal {O}_{E}^{\times }\cap U^p$, the action of ![]() $N_{E/F}(u)$ on
$N_{E/F}(u)$ on ![]() $\overline {\mathrm {Ig}}^b$ changing the polarisation agrees with the action of
$\overline {\mathrm {Ig}}^b$ changing the polarisation agrees with the action of ![]() $u^{-1}$ on
$u^{-1}$ on ![]() $\overline {\mathrm {Ig}}^b$ via the inclusion
$\overline {\mathrm {Ig}}^b$ via the inclusion ![]() $\mathcal {O}_{E}^{\times } \hookrightarrow \Gamma ^b$. Hence, the induced map
$\mathcal {O}_{E}^{\times } \hookrightarrow \Gamma ^b$. Hence, the induced map ![]() $\mathrm {Ig}^b\rightarrow \overline {Sh}_U(H)^{b, \mathrm {perf}}$ is a torsor for the group
$\mathrm {Ig}^b\rightarrow \overline {Sh}_U(H)^{b, \mathrm {perf}}$ is a torsor for the group ![]() $\Gamma ^b/\varprojlim _k(\mathcal {O}_E^{\times }\cap U/\{u \in \mathcal {O}_E^{\times }\cap U \mid u \equiv 1 \pmod {p^k}\})$. Therefore, there is a Hecke-equivariant Hochschild–Serre spectral sequence relating the cohomology of
$\Gamma ^b/\varprojlim _k(\mathcal {O}_E^{\times }\cap U/\{u \in \mathcal {O}_E^{\times }\cap U \mid u \equiv 1 \pmod {p^k}\})$. Therefore, there is a Hecke-equivariant Hochschild–Serre spectral sequence relating the cohomology of ![]() $\mathrm {Ig}^b$ and the cohomology of
$\mathrm {Ig}^b$ and the cohomology of ![]() $\overline {Sh}_U(H)^{b, \mathrm {perf}}$. The latter agrees with étale cohomology of
$\overline {Sh}_U(H)^{b, \mathrm {perf}}$. The latter agrees with étale cohomology of ![]() $\overline {Sh}_U(H)^b$ by topological invariance of the étale site; hence, if
$\overline {Sh}_U(H)^b$ by topological invariance of the étale site; hence, if ![]() $H^i(\mathrm {Ig}^b, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for every
$H^i(\mathrm {Ig}^b, {\mathbb {F}}_{\ell })_\mathfrak {m}=0$ for every ![]() $i$, then the same is true for
$i$, then the same is true for ![]() $H^i(\overline {Sh}_U(H)^b, {\mathbb {F}}_{\ell })_\mathfrak {m}$.
$H^i(\overline {Sh}_U(H)^b, {\mathbb {F}}_{\ell })_\mathfrak {m}$.
7.3 The excision triangle for diamonds
In the proof of Proposition 7.2.7, given in the next section, we will make use of the long exact sequence relating, under suitable assumptions, sheaves on a diamond to their restriction to an open subdiamond and its closed complement. The existence of such an exact sequence is well-known; for the reader's convenience, we will briefly explain how to obtain it.
7.3.1
Fix a locally spatial diamond ![]() $X$; let
$X$; let ![]() $X_{\mathrm {\acute {e}t}}$ be the étale site of
$X_{\mathrm {\acute {e}t}}$ be the étale site of ![]() $X$, defined in [Reference ScholzeSch17, Definition 14.1], and
$X$, defined in [Reference ScholzeSch17, Definition 14.1], and ![]() $|X|$ the underlying topological space of
$|X|$ the underlying topological space of ![]() $X$, defined in [Reference ScholzeSch17, Definition 11.14]. One can attach to each
$X$, defined in [Reference ScholzeSch17, Definition 11.14]. One can attach to each ![]() $x \in |X|$ a quasi-pro-étale map
$x \in |X|$ a quasi-pro-étale map ![]() $\bar {x}=\mathrm {Spa}(C(x), C(x)^+)\rightarrow X$, with
$\bar {x}=\mathrm {Spa}(C(x), C(x)^+)\rightarrow X$, with ![]() $C(x)$ an algebraically closed perfectoid field, mapping the closed point of
$C(x)$ an algebraically closed perfectoid field, mapping the closed point of ![]() $\mathrm {Spa}(C(x), C(x)^+)$ to
$\mathrm {Spa}(C(x), C(x)^+)$ to ![]() $x$ (see [Reference ScholzeSch17, Proposition 14.3] and [Reference Caraiani, Gulotta, Hsu, Johansson, Mocz, Reinecke and ShihCGH+20, Lemma 2.2.2]). We call
$x$ (see [Reference ScholzeSch17, Proposition 14.3] and [Reference Caraiani, Gulotta, Hsu, Johansson, Mocz, Reinecke and ShihCGH+20, Lemma 2.2.2]). We call ![]() $\bar {x}$ a geometric point of
$\bar {x}$ a geometric point of ![]() $X$ (with the important caveat that as a set
$X$ (with the important caveat that as a set ![]() $\bar {x}$ may not be a singleton), and we denote by
$\bar {x}$ may not be a singleton), and we denote by ![]() $F_{\bar {x}}$ the stalk of a sheaf
$F_{\bar {x}}$ the stalk of a sheaf ![]() $F$ at
$F$ at ![]() $\bar {x}$. By [Reference ScholzeSch17, Proposition 14.3] we may check if a sequence of étale sheaves on
$\bar {x}$. By [Reference ScholzeSch17, Proposition 14.3] we may check if a sequence of étale sheaves on ![]() $X$ is exact looking at stalks at each geometric point.
$X$ is exact looking at stalks at each geometric point.
7.3.2
Fix an open subspace of ![]() $|X|$, corresponding, by [Reference ScholzeSch17, Proposition 11.15], to a subdiamond
$|X|$, corresponding, by [Reference ScholzeSch17, Proposition 11.15], to a subdiamond ![]() $j: U \rightarrow X$; assume that the closed complement
$j: U \rightarrow X$; assume that the closed complement ![]() $|X|\smallsetminus |U|$ is generalising, so that, by [Reference Anschütz, Gleason, Lourenço and RicharzAGLR22, Lemma 2.7] and [Reference ScholzeSch17, Proposition 11.20], it is the underlying topological space of a canonical locally spatial subdiamond
$|X|\smallsetminus |U|$ is generalising, so that, by [Reference Anschütz, Gleason, Lourenço and RicharzAGLR22, Lemma 2.7] and [Reference ScholzeSch17, Proposition 11.20], it is the underlying topological space of a canonical locally spatial subdiamond ![]() $i: Z \rightarrow X$.Footnote 6 Since
$i: Z \rightarrow X$.Footnote 6 Since ![]() $|Z|$ is generalising, geometric points of
$|Z|$ is generalising, geometric points of ![]() $X$ are a disjoint union of geometric points of
$X$ are a disjoint union of geometric points of ![]() $U$ and of
$U$ and of ![]() $Z$. We have the extension by zero functor
$Z$. We have the extension by zero functor ![]() $j_!: \mathrm {Ab}(U_{\mathrm {\acute {e}t}})\rightarrow \mathrm {Ab}(X_{\mathrm {\acute {e}t}})$, defined as for schemes (cf. the discussion before [Reference Caraiani, Gulotta, Hsu, Johansson, Mocz, Reinecke and ShihCGH+20, Lemma 2.2.6]), which is exact and left-adjoint to
$j_!: \mathrm {Ab}(U_{\mathrm {\acute {e}t}})\rightarrow \mathrm {Ab}(X_{\mathrm {\acute {e}t}})$, defined as for schemes (cf. the discussion before [Reference Caraiani, Gulotta, Hsu, Johansson, Mocz, Reinecke and ShihCGH+20, Lemma 2.2.6]), which is exact and left-adjoint to ![]() $j^*$. The stalk of
$j^*$. The stalk of ![]() $j_!F$ at
$j_!F$ at ![]() $x \in |U|$ (respectively,
$x \in |U|$ (respectively, ![]() $x \in |Z|$) is isomorphic to
$x \in |Z|$) is isomorphic to ![]() $F_{\bar {x}}$ (respectively, is zero).
$F_{\bar {x}}$ (respectively, is zero).
Lemma 7.3.3 Let ![]() $x \in |X|$ and let
$x \in |X|$ and let ![]() $\bar {x}$ be the associated geometric point; let
$\bar {x}$ be the associated geometric point; let ![]() $F$ be an étale sheaf (of abelian groups) on
$F$ be an étale sheaf (of abelian groups) on ![]() $Z$. If
$Z$. If ![]() $x \not \in |Z|$, then
$x \not \in |Z|$, then ![]() $(i_*F)_{\bar {x}}=0$; if
$(i_*F)_{\bar {x}}=0$; if ![]() $x \in |Z|$, then
$x \in |Z|$, then ![]() $(i_{*}F)_{\bar {x}}=F_{\bar {x}}$.
$(i_{*}F)_{\bar {x}}=F_{\bar {x}}$.
Proof. If ![]() $x \not \in |Z|$, then
$x \not \in |Z|$, then ![]() $x \in |U|$, hence there is a cofinal systems of étale neighbourhoods
$x \in |U|$, hence there is a cofinal systems of étale neighbourhoods ![]() $V \rightarrow X$ of
$V \rightarrow X$ of ![]() $x$ factoring through
$x$ factoring through ![]() $U$; therefore,
$U$; therefore, ![]() $i_*F(V)=0$ and
$i_*F(V)=0$ and ![]() $(i_*F)_{\bar {x}}=0$. Now take
$(i_*F)_{\bar {x}}=0$. Now take ![]() $x \in |Z|$; then
$x \in |Z|$; then ![]() $(i_*F)_{\bar {x}}=\varinjlim _{V} F(V \times _X Z)$, where
$(i_*F)_{\bar {x}}=\varinjlim _{V} F(V \times _X Z)$, where ![]() $V$ runs over the objects
$V$ runs over the objects ![]() $V\rightarrow X \in X_{\mathrm {\acute {e}t}}$ through which
$V\rightarrow X \in X_{\mathrm {\acute {e}t}}$ through which ![]() $\bar {x}$ factors. We may restrict to
$\bar {x}$ factors. We may restrict to ![]() $V$ spatial and such that
$V$ spatial and such that ![]() $V \rightarrow X$ factors through a fixed spatial open subdiamond of
$V \rightarrow X$ factors through a fixed spatial open subdiamond of ![]() $X$. Using [Reference ScholzeSch17, Proposition 14.9], the description of
$X$. Using [Reference ScholzeSch17, Proposition 14.9], the description of ![]() $\bar {x}$ before [Reference Caraiani, Gulotta, Hsu, Johansson, Mocz, Reinecke and ShihCGH+20, Lemma 2.2.2], and the fact that
$\bar {x}$ before [Reference Caraiani, Gulotta, Hsu, Johansson, Mocz, Reinecke and ShihCGH+20, Lemma 2.2.2], and the fact that ![]() $\bar {x} \rightarrow X$ factors through
$\bar {x} \rightarrow X$ factors through ![]() $Z$, we have
$Z$, we have
Proposition 7.3.4 Let ![]() $X$ be a locally spatial diamond, and
$X$ be a locally spatial diamond, and ![]() $j: U \rightarrow X$ an open subdiamond with generalising closed complement underlying a subdiamond
$j: U \rightarrow X$ an open subdiamond with generalising closed complement underlying a subdiamond ![]() $i: Z\rightarrow X$. For every étale sheaf
$i: Z\rightarrow X$. For every étale sheaf ![]() $F$ of abelian groups on
$F$ of abelian groups on ![]() $X$ the sequence
$X$ the sequence
is exact.
Proof. It suffices to check this on stalks at each geometric point ![]() $\bar {x} \rightarrow X$. If
$\bar {x} \rightarrow X$. If ![]() $\bar {x}$ factors through
$\bar {x}$ factors through ![]() $U$ we get
$U$ we get ![]() $0 \rightarrow F_{\bar {x}}\xrightarrow {\mathrm {Id}} F_{\bar {x}}\rightarrow 0 \rightarrow 0$. If it factors through
$0 \rightarrow F_{\bar {x}}\xrightarrow {\mathrm {Id}} F_{\bar {x}}\rightarrow 0 \rightarrow 0$. If it factors through ![]() $Z$, then
$Z$, then ![]() $(j_!j^{*}F)_{\bar {x}}=0$. On the other hand, setting
$(j_!j^{*}F)_{\bar {x}}=0$. On the other hand, setting ![]() $G=i^{*}F$ we have
$G=i^{*}F$ we have ![]() $(i_{*}G)_{\bar {x}}=G_{\bar {x}}$ by the previous lemma, and
$(i_{*}G)_{\bar {x}}=G_{\bar {x}}$ by the previous lemma, and ![]() $G_{\bar {x}}=F_{\bar {x}}$. Hence we get
$G_{\bar {x}}=F_{\bar {x}}$. Hence we get ![]() $0 \rightarrow 0 \rightarrow F_{\bar {x}}\xrightarrow {\mathrm {Id}} F_{\bar {x}}\rightarrow 0$.
$0 \rightarrow 0 \rightarrow F_{\bar {x}}\xrightarrow {\mathrm {Id}} F_{\bar {x}}\rightarrow 0$.
7.4 Proof of Proposition 7.2.7
7.4.1
Let ![]() $b=(b_\mathfrak {p})_{\mathfrak {p} \in \Sigma _p}\in B(H_{{\mathbb {Q}}_p}, \mu )$ be an element such that
$b=(b_\mathfrak {p})_{\mathfrak {p} \in \Sigma _p}\in B(H_{{\mathbb {Q}}_p}, \mu )$ be an element such that ![]() $R\Gamma (\mathrm {Ig}^b, {\mathbb {F}}_{\ell })_\mathfrak {m}$ is non-trivial and such that the dimension
$R\Gamma (\mathrm {Ig}^b, {\mathbb {F}}_{\ell })_\mathfrak {m}$ is non-trivial and such that the dimension ![]() $d^{\mathrm {min}}$ of
$d^{\mathrm {min}}$ of ![]() $\overline {Sh}_U(H)^b$ is as small as possible. Let
$\overline {Sh}_U(H)^b$ is as small as possible. Let ![]() $\varepsilon$ be the cardinality of the set
$\varepsilon$ be the cardinality of the set ![]() $T\subset \Sigma _p$ consisting of places
$T\subset \Sigma _p$ consisting of places ![]() $\mathfrak {p}$ such that
$\mathfrak {p}$ such that ![]() $b_\mathfrak {p}$ is basic. Then
$b_\mathfrak {p}$ is basic. Then ![]() $d^{\mathrm {min}}=g-\varepsilon$, so we need to prove that
$d^{\mathrm {min}}=g-\varepsilon$, so we need to prove that
If ![]() $\varepsilon =0$ there is nothing to prove; hence let us assume
$\varepsilon =0$ there is nothing to prove; hence let us assume ![]() $\varepsilon >0$, so that
$\varepsilon >0$, so that ![]() $T$ is non-empty. Let
$T$ is non-empty. Let ![]() $H_T$ be the unitary group attached to
$H_T$ be the unitary group attached to ![]() $T$, defined in § 3.1.3, and
$T$, defined in § 3.1.3, and ![]() $\mathrm {Ig}_T^{\mathrm {ord}}$ the associated
$\mathrm {Ig}_T^{\mathrm {ord}}$ the associated ![]() $\mu _T$-ordinary Igusa variety. Consider the Hodge–Tate period map
$\mu _T$-ordinary Igusa variety. Consider the Hodge–Tate period map
Our assumption and Theorem 4.2.4 imply that ![]() $R\Gamma (\mathrm {Ig}_T^{\mathrm {ord}}, {\mathbb {F}}_{\ell })_\mathfrak {m}$ is non-trivial. Because of Proposition 5.3.1 we deduce that
$R\Gamma (\mathrm {Ig}_T^{\mathrm {ord}}, {\mathbb {F}}_{\ell })_\mathfrak {m}$ is non-trivial. Because of Proposition 5.3.1 we deduce that ![]() $(R\pi _{\mathrm {HT}, *}^T {\mathbb {F}}_{\ell })_\mathfrak {m}$ has non-trivial cohomology on the
$(R\pi _{\mathrm {HT}, *}^T {\mathbb {F}}_{\ell })_\mathfrak {m}$ has non-trivial cohomology on the ![]() $\mu _T$-ordinary stratum. Better, we have the following.
$\mu _T$-ordinary stratum. Better, we have the following.
Lemma 7.4.2 The ![]() $\mu _T$-ordinary stratum is the only one where
$\mu _T$-ordinary stratum is the only one where ![]() $(R\pi _{\mathrm {HT}, *}^T{\mathbb {F}}_{\ell })_\mathfrak {m}$ has non-zero cohomology.
$(R\pi _{\mathrm {HT}, *}^T{\mathbb {F}}_{\ell })_\mathfrak {m}$ has non-zero cohomology.
Proof. Assume the contrary. Then using Proposition 5.3.1 we find that there is a non-ordinary element ![]() $b'_T \in B(H_{T, {\mathbb {Q}}_p}, \mu _T)$ such that
$b'_T \in B(H_{T, {\mathbb {Q}}_p}, \mu _T)$ such that ![]() $H^*(\mathrm {Ig}^{b'_T}_T, {\mathbb {F}}_{\ell })_\mathfrak {m}$ is non-zero. Consider the element
$H^*(\mathrm {Ig}^{b'_T}_T, {\mathbb {F}}_{\ell })_\mathfrak {m}$ is non-zero. Consider the element ![]() $b' \in B(H_{{\mathbb {Q}}_p}, \mu )$ which is basic precisely at places in
$b' \in B(H_{{\mathbb {Q}}_p}, \mu )$ which is basic precisely at places in ![]() $T$ and at places outside
$T$ and at places outside ![]() $T$ where
$T$ where ![]() $b'_T$ is basic. By Theorem 4.2.4 the cohomology
$b'_T$ is basic. By Theorem 4.2.4 the cohomology ![]() $H^*(\mathrm {Ig}^{b'}, {\mathbb {F}}_{\ell })_\mathfrak {m}$ is not identically zero; however the dimension of
$H^*(\mathrm {Ig}^{b'}, {\mathbb {F}}_{\ell })_\mathfrak {m}$ is not identically zero; however the dimension of ![]() $\overline {Sh}_U(H)^{b'}$ is strictly smaller than the dimension of
$\overline {Sh}_U(H)^{b'}$ is strictly smaller than the dimension of ![]() $\overline {Sh}_U(H)^b$, hence we obtain a contradiction.
$\overline {Sh}_U(H)^b$, hence we obtain a contradiction.
7.4.3
We now come back to the proof of Proposition 7.2.7. Perversity of the complex ![]() $R\pi ^T_{\mathrm {HT}, *}{\mathbb {F}}_{\ell }[g-\varepsilon ]$ and the fact that it is concentrated on one stratum after localisation at
$R\pi ^T_{\mathrm {HT}, *}{\mathbb {F}}_{\ell }[g-\varepsilon ]$ and the fact that it is concentrated on one stratum after localisation at ![]() $\mathfrak {m}$ imply that
$\mathfrak {m}$ imply that ![]() $H^i(\mathrm {Ig}_T^{\mathrm {ord}}, {\mathbb {F}}_{\ell })_\mathfrak {m}$ is non-zero only in middle degree
$H^i(\mathrm {Ig}_T^{\mathrm {ord}}, {\mathbb {F}}_{\ell })_\mathfrak {m}$ is non-zero only in middle degree ![]() $g-\varepsilon$ (cf. [Reference Caraiani and ScholzeCS17, Corollary 6.1.4]). Theorem 6.3.3 (together with the fact that smooth parabolic induction of a non-zero representation is non-zero) implies that
$g-\varepsilon$ (cf. [Reference Caraiani and ScholzeCS17, Corollary 6.1.4]). Theorem 6.3.3 (together with the fact that smooth parabolic induction of a non-zero representation is non-zero) implies that
Let ![]() $Z\subset \mathscr {F}\ell _{H_{T}, \mu _T}$ be the
$Z\subset \mathscr {F}\ell _{H_{T}, \mu _T}$ be the ![]() $\mu _T$-ordinary locus, and
$\mu _T$-ordinary locus, and ![]() $V:=\mathscr {F}\ell _{H_{T}, \mu_T^{-1}}\smallsetminus Z$. We have an inclusion
$V:=\mathscr {F}\ell _{H_{T}, \mu_T^{-1}}\smallsetminus Z$. We have an inclusion
which induces a bijection on rank one points. The ordinary locus ![]() $\mathcal {S}h_{U^p}(H_T)^{b^\mathrm {ord}}$ is open and quasi-compact, as it is the preimage of a quasi-compact open subspace in the special fibre via the specialisation map, which is continuous and spectral. By [Reference Caraiani and ScholzeCS17, Lemma 4.4.2] the map induced in cohomology by (7.4.3.2) is an isomorphism, hence the equivalence in (7.4.3.1) holds true for the cohomology of
$\mathcal {S}h_{U^p}(H_T)^{b^\mathrm {ord}}$ is open and quasi-compact, as it is the preimage of a quasi-compact open subspace in the special fibre via the specialisation map, which is continuous and spectral. By [Reference Caraiani and ScholzeCS17, Lemma 4.4.2] the map induced in cohomology by (7.4.3.2) is an isomorphism, hence the equivalence in (7.4.3.1) holds true for the cohomology of ![]() $(\pi _{\mathrm {HT}}^{T})^{-1}(Z)$ as well. Let
$(\pi _{\mathrm {HT}}^{T})^{-1}(Z)$ as well. Let ![]() $i_Z: Z \rightarrow \mathscr {F}\ell _{H_{T}, \mu_T^{-1}}$ and
$i_Z: Z \rightarrow \mathscr {F}\ell _{H_{T}, \mu_T^{-1}}$ and ![]() $i_V : V \rightarrow \mathscr {F}\ell _{H_{T}, \mu _T}$ be the inclusion maps. The assumptions of Proposition 7.3.4 are satisfied, hence for every
$i_V : V \rightarrow \mathscr {F}\ell _{H_{T}, \mu _T}$ be the inclusion maps. The assumptions of Proposition 7.3.4 are satisfied, hence for every ![]() $j \geq 0$ we have an exact sequence
$j \geq 0$ we have an exact sequence
Lemma 7.4.2 ensures that the first term vanishes after localisation at ![]() $\mathfrak {m}$; therefore, we deduce that
$\mathfrak {m}$; therefore, we deduce that ![]() $H^i(\mathscr {F}\ell _{H_{T}, \mu_T^{-1}}, R^j\pi ^T_{\mathrm {HT}, *}{\mathbb {F}}_{\ell })_\mathfrak {m}=H^i(Z, R^j\pi ^T_{\mathrm {HT}, *}{\mathbb {F}}_{\ell })_\mathfrak {m}$. The outcome of our discussion is that cohomology of
$H^i(\mathscr {F}\ell _{H_{T}, \mu_T^{-1}}, R^j\pi ^T_{\mathrm {HT}, *}{\mathbb {F}}_{\ell })_\mathfrak {m}=H^i(Z, R^j\pi ^T_{\mathrm {HT}, *}{\mathbb {F}}_{\ell })_\mathfrak {m}$. The outcome of our discussion is that cohomology of ![]() $\mathcal {S}h_{U^p}(H_T)$ coincides with cohomology of its ordinary locus, after localisation at
$\mathcal {S}h_{U^p}(H_T)$ coincides with cohomology of its ordinary locus, after localisation at ![]() $\mathfrak {m}$; hence
$\mathfrak {m}$; hence ![]() $H^i(\mathcal {S}h_{U^p}(H_T), {\mathbb {F}}_{\ell })_\mathfrak {m} \neq 0$ if and only if
$H^i(\mathcal {S}h_{U^p}(H_T), {\mathbb {F}}_{\ell })_\mathfrak {m} \neq 0$ if and only if ![]() $i=g-\varepsilon$.
$i=g-\varepsilon$.
Now ![]() $\mathcal {S}h_{U^p}(H_T)$ is the inverse limit (as a diamond) of the spaces
$\mathcal {S}h_{U^p}(H_T)$ is the inverse limit (as a diamond) of the spaces ![]() $\mathcal {S}h_{U^pU_{T, p}}(H_T)$ for
$\mathcal {S}h_{U^pU_{T, p}}(H_T)$ for ![]() $U_{T, p}\subset H_T({\mathbb {Q}}_p)$ running over compact open subgroups. There is a cofinal system of subgroups
$U_{T, p}\subset H_T({\mathbb {Q}}_p)$ running over compact open subgroups. There is a cofinal system of subgroups ![]() $U_{T, p}$ which are images in
$U_{T, p}$ which are images in ![]() $H_T({\mathbb {Q}}_p)$ of subgroups of the form
$H_T({\mathbb {Q}}_p)$ of subgroups of the form ![]() $K_{T, p}\times K_{E, p}\subset G_T({\mathbb {Q}}_p)\times T_E({\mathbb {Q}}_p)$, where
$K_{T, p}\times K_{E, p}\subset G_T({\mathbb {Q}}_p)\times T_E({\mathbb {Q}}_p)$, where ![]() $K_{E, p}$ is such that
$K_{E, p}$ is such that ![]() $K_{E, p}K_{E}^p$ is sufficiently small with respect to
$K_{E, p}K_{E}^p$ is sufficiently small with respect to ![]() $K_{T, p}K^p$, in the sense of Definition 3.2.2. For
$K_{T, p}K^p$, in the sense of Definition 3.2.2. For ![]() $U_{T, p}$ of this form and small enough, we must have
$U_{T, p}$ of this form and small enough, we must have
where the first equality holds because a small enough subgroup ![]() $U_{T, p}$ is a pro-
$U_{T, p}$ is a pro-![]() $p$ group, hence the map from the cohomology of
$p$ group, hence the map from the cohomology of ![]() $\mathcal {S}h_{U^pU_{T, p}}(H_T)$ to the cohomology of
$\mathcal {S}h_{U^pU_{T, p}}(H_T)$ to the cohomology of ![]() $\mathcal {S}h_{U^p}(H_T)$ is injective. The argument in the proof of Corollary 7.1.2 shows that
$\mathcal {S}h_{U^p}(H_T)$ is injective. The argument in the proof of Corollary 7.1.2 shows that ![]() $H^{g-\varepsilon }(Sh_{U^pU_{T, p}}(H_T), {\mathbb {Z}}_{\ell })_\mathfrak {m}$ is non-zero and torsion free, therefore we deduce that
$H^{g-\varepsilon }(Sh_{U^pU_{T, p}}(H_T), {\mathbb {Z}}_{\ell })_\mathfrak {m}$ is non-zero and torsion free, therefore we deduce that
Applying Corollary 3.2.9 once more we obtain that ![]() $H^{g-\varepsilon }(Sh_{K^pK_{T, p}}(G_T), {\mathbb {Q}}_{\ell })_\mathfrak {m}\neq 0$. We claim that this implies that
$H^{g-\varepsilon }(Sh_{K^pK_{T, p}}(G_T), {\mathbb {Q}}_{\ell })_\mathfrak {m}\neq 0$. We claim that this implies that ![]() $\bar {\rho }_\mathfrak {m}$ cannot be generic at places in
$\bar {\rho }_\mathfrak {m}$ cannot be generic at places in ![]() $T$; this yields the desired inequality
$T$; this yields the desired inequality ![]() $\varepsilon \leq \delta _p(\mathfrak {m})$ and ends the proof of Proposition 7.2.7.
$\varepsilon \leq \delta _p(\mathfrak {m})$ and ends the proof of Proposition 7.2.7.
To justify our claim, recall that ![]() $H^{g-\varepsilon }(Sh_{K^pK_{T, p}}(G_T), \bar {{\mathbb {Q}}}_{\ell })$ can be described in terms of automorphic representations of
$H^{g-\varepsilon }(Sh_{K^pK_{T, p}}(G_T), \bar {{\mathbb {Q}}}_{\ell })$ can be described in terms of automorphic representations of ![]() $G_T$ as in [Reference NekovářNek18, (5.9)–(5.11)]. The Hecke algebra acts on the universal part of cohomology (corresponding to one-dimensional automorphic representations, and called case (A) in [Reference NekovářNek18]) via the degree character. Hence, this part of cohomology vanishes after localisation at
$G_T$ as in [Reference NekovářNek18, (5.9)–(5.11)]. The Hecke algebra acts on the universal part of cohomology (corresponding to one-dimensional automorphic representations, and called case (A) in [Reference NekovářNek18]) via the degree character. Hence, this part of cohomology vanishes after localisation at ![]() $\mathfrak {m}$, since
$\mathfrak {m}$, since ![]() $\mathfrak {m}$ is non-Eisenstein. Therefore, as in [Reference NekovářNek18, (5.11)(B)], there is an automorphic representation
$\mathfrak {m}$ is non-Eisenstein. Therefore, as in [Reference NekovářNek18, (5.11)(B)], there is an automorphic representation ![]() $\pi _T$ of
$\pi _T$ of ![]() $G_T$ which transfers to an automorphic representation
$G_T$ which transfers to an automorphic representation ![]() $\pi$ of
$\pi$ of ![]() $\operatorname {GL}_{2, F}$ attached to a (holomorphic) cuspidal Hilbert newform
$\operatorname {GL}_{2, F}$ attached to a (holomorphic) cuspidal Hilbert newform ![]() $f$ such that almost all the Hecke eigenvalues of
$f$ such that almost all the Hecke eigenvalues of ![]() $f$ modulo
$f$ modulo ![]() $\ell$ are given by the image of the map
$\ell$ are given by the image of the map ![]() $\mathbb {T} \rightarrow \mathbb {T}/\mathfrak {m}$. Letting
$\mathbb {T} \rightarrow \mathbb {T}/\mathfrak {m}$. Letting ![]() $\rho _\pi : \Gamma _F \rightarrow \operatorname {GL}_2(\bar {{\mathbb {Q}}}_{\ell })$ be the Galois representation attached to
$\rho _\pi : \Gamma _F \rightarrow \operatorname {GL}_2(\bar {{\mathbb {Q}}}_{\ell })$ be the Galois representation attached to ![]() $\pi$, we deduce that the reduction modulo
$\pi$, we deduce that the reduction modulo ![]() $\ell$ of (a lattice in)
$\ell$ of (a lattice in) ![]() $\rho _\pi$ is isomorphic to
$\rho _\pi$ is isomorphic to ![]() $\bar {\rho }_\mathfrak {m}$. Let
$\bar {\rho }_\mathfrak {m}$. Let ![]() $v$ be a place in
$v$ be a place in ![]() $T$; by [Reference CarayolCar86, Theorem A] the Galois representation attached to
$T$; by [Reference CarayolCar86, Theorem A] the Galois representation attached to ![]() $\pi _v$ lifts
$\pi _v$ lifts ![]() $\bar {\rho }_{\mathfrak {m}|\Gamma _{F_v}}$. As
$\bar {\rho }_{\mathfrak {m}|\Gamma _{F_v}}$. As ![]() $\pi _v$ is the Jacquet–Langlands transfer of a representation of the non-split quaternion algebra over
$\pi _v$ is the Jacquet–Langlands transfer of a representation of the non-split quaternion algebra over ![]() $F_v$, we deduce using § 7.1.4 that
$F_v$, we deduce using § 7.1.4 that ![]() $\bar {\rho }_\mathfrak {m}$ is not generic at
$\bar {\rho }_\mathfrak {m}$ is not generic at ![]() $v$.
$v$.
Remark 7.4.4 In the above proof, we used the parabolically induced structure of the ordinary locus to deduce that ![]() $H^*(\mathcal {S}h_{U^p}(H_T)^{b^\mathrm {ord}}, {\mathbb {F}}_{\ell })_\mathfrak {m}$ is non-zero and concentrated in one degree from the analogous properties of cohomology of the Igusa variety. One could also argue computing cohomology of
$H^*(\mathcal {S}h_{U^p}(H_T)^{b^\mathrm {ord}}, {\mathbb {F}}_{\ell })_\mathfrak {m}$ is non-zero and concentrated in one degree from the analogous properties of cohomology of the Igusa variety. One could also argue computing cohomology of ![]() $\mathcal {S}h_{U^p}(H_T)^{b^\mathrm {ord}}$ via the Leray spectral sequence, and using the fact that the ordinary locus in the flag variety is a profinite set (hence, a sheaf on it with a non-zero stalk has non-zero global sections and vanishing higher cohomology).
$\mathcal {S}h_{U^p}(H_T)^{b^\mathrm {ord}}$ via the Leray spectral sequence, and using the fact that the ordinary locus in the flag variety is a profinite set (hence, a sheaf on it with a non-zero stalk has non-zero global sections and vanishing higher cohomology).
7.5 Cohomology of quaternionic Shimura varieties
7.5.1
Let ![]() $\ell$ be a prime number. In this section, we explain how the arguments used in this paper can be extended to study the cohomology with
$\ell$ be a prime number. In this section, we explain how the arguments used in this paper can be extended to study the cohomology with ![]() ${\mathbb {F}}_\ell$-coefficients of quaternionic Shimura varieties attached to non-split quaternion algebras. In a nutshell, the strategy we used for Hilbert modular varieties can be applied in this generality, with the difference that we do not need to restrict to non-Eisenstein maximal ideals, as Shimura varieties attached to non-split quaternion algebras have no boundary. The construction of Galois representations is also simpler in this case, therefore some results also apply to the case
${\mathbb {F}}_\ell$-coefficients of quaternionic Shimura varieties attached to non-split quaternion algebras. In a nutshell, the strategy we used for Hilbert modular varieties can be applied in this generality, with the difference that we do not need to restrict to non-Eisenstein maximal ideals, as Shimura varieties attached to non-split quaternion algebras have no boundary. The construction of Galois representations is also simpler in this case, therefore some results also apply to the case ![]() $\ell = 2$.
$\ell = 2$.
We fix a non-split quaternion algebra ![]() $B$ over a totally real number field
$B$ over a totally real number field ![]() $F$ of degree
$F$ of degree ![]() $g$. Let
$g$. Let ![]() $R$ (respectively,
$R$ (respectively, ![]() $R_\infty$) be the set of places (respectively, infinite places) of
$R_\infty$) be the set of places (respectively, infinite places) of ![]() $F$ where
$F$ where ![]() $B$ is ramified. In this section, we will denote by
$B$ is ramified. In this section, we will denote by ![]() $G$ the group
$G$ the group ![]() $\mathrm {Res}_{F/{\mathbb {Q}}}B^\times$; we fix a neat compact open subgroup
$\mathrm {Res}_{F/{\mathbb {Q}}}B^\times$; we fix a neat compact open subgroup ![]() $K \subset G({\mathbb {A}}_f)$ and we denote by
$K \subset G({\mathbb {A}}_f)$ and we denote by ![]() $Sh_K(G)$ the corresponding Shimura variety, of dimension
$Sh_K(G)$ the corresponding Shimura variety, of dimension ![]() $d:=g-|R_\infty |$. Let
$d:=g-|R_\infty |$. Let ![]() $\mathbb {T}$ be the Hecke algebra generated by operators at places of residue characteristic different from
$\mathbb {T}$ be the Hecke algebra generated by operators at places of residue characteristic different from ![]() $\ell$ where
$\ell$ where ![]() $B$ is unramified and
$B$ is unramified and ![]() $K$ is hyperspecial. Given a prime
$K$ is hyperspecial. Given a prime ![]() $p$ totally split in
$p$ totally split in ![]() $F$, fix an isomorphism
$F$, fix an isomorphism ![]() $\bar {{\mathbb {Q}}}_p \simeq {\mathbb {C}}$, inducing a bijection between the set
$\bar {{\mathbb {Q}}}_p \simeq {\mathbb {C}}$, inducing a bijection between the set ![]() $\Sigma _\infty$ of infinite places and the set
$\Sigma _\infty$ of infinite places and the set ![]() $\Sigma _p$ of
$\Sigma _p$ of ![]() $p$-adic places of
$p$-adic places of ![]() $F$. We denote by
$F$. We denote by ![]() $R_p$ the set of
$R_p$ the set of ![]() $p$-adic places corresponding to
$p$-adic places corresponding to ![]() $R_\infty$. The cocharacter of
$R_\infty$. The cocharacter of ![]() $G_{\bar {{\mathbb {Q}}}_p}$ induced by the cocharacter coming from the Shimura datum attached to
$G_{\bar {{\mathbb {Q}}}_p}$ induced by the cocharacter coming from the Shimura datum attached to ![]() $G$ is central at places in
$G$ is central at places in ![]() $R_p$. In the rest of the section we will discuss the proof of the following result.
$R_p$. In the rest of the section we will discuss the proof of the following result.
Theorem 7.5.2 Let ![]() $\ell$ be a prime number and
$\ell$ be a prime number and ![]() $\mathfrak {m} \subset \mathbb {T}$ a maximal ideal in the support of
$\mathfrak {m} \subset \mathbb {T}$ a maximal ideal in the support of ![]() $H^*(Sh_K(G), {\mathbb {F}}_\ell )$.
$H^*(Sh_K(G), {\mathbb {F}}_\ell )$.
(i) There exists a unique Galois representation
 $\bar {\rho }_\mathfrak {m}: \Gamma _F \rightarrow \operatorname {GL}_2(\bar {{\mathbb {F}}}_\ell )$ attached to
$\bar {\rho }_\mathfrak {m}: \Gamma _F \rightarrow \operatorname {GL}_2(\bar {{\mathbb {F}}}_\ell )$ attached to  $\mathfrak {m}$, in the sense of Theorem 2.2.1.
$\mathfrak {m}$, in the sense of Theorem 2.2.1.(ii) Let
 $p\neq \ell$ be an odd prime number which splits completely in
$p\neq \ell$ be an odd prime number which splits completely in  $F$ and such that
$F$ and such that  $B$ is unramified at every place above
$B$ is unramified at every place above  $p$ and
$p$ and  $K=K^pK_p$ with
$K=K^pK_p$ with  $K_p \subset G({\mathbb {Q}}_p)$ hyperspecial. Let
$K_p \subset G({\mathbb {Q}}_p)$ hyperspecial. Let  $\delta _p(\mathfrak {m})$ be the cardinality of the set of places
$\delta _p(\mathfrak {m})$ be the cardinality of the set of places  $v \in \Sigma _p \smallsetminus R_p$ such that
$v \in \Sigma _p \smallsetminus R_p$ such that  $\bar {\rho }_\mathfrak {m}$ is not generic at
$\bar {\rho }_\mathfrak {m}$ is not generic at  $v$. Then
$v$. Then
 \[ i \not \in [d-\delta_p(\mathfrak{m}), d+\delta_p(\mathfrak{m})]\Rightarrow H^i(Sh_K(G), {\mathbb{F}}_\ell)_\mathfrak{m} = 0. \]
\[ i \not \in [d-\delta_p(\mathfrak{m}), d+\delta_p(\mathfrak{m})]\Rightarrow H^i(Sh_K(G), {\mathbb{F}}_\ell)_\mathfrak{m} = 0. \]
(iii) If
 $\ell >2$ and the image of
$\ell >2$ and the image of  $\bar {\rho }_{\mathfrak {m}}$ is not solvable, then
$\bar {\rho }_{\mathfrak {m}}$ is not solvable, then
 \[ i \neq d \Rightarrow H^i(Sh_K(G), {\mathbb{F}}_\ell)_\mathfrak{m} = 0. \]
\[ i \neq d \Rightarrow H^i(Sh_K(G), {\mathbb{F}}_\ell)_\mathfrak{m} = 0. \]
7.5.3
Take a prime ![]() $p$ as in point (ii) of the theorem. We choose an auxiliary
$p$ as in point (ii) of the theorem. We choose an auxiliary ![]() $CM$ extension
$CM$ extension ![]() $E/F$ such that every finite place in
$E/F$ such that every finite place in ![]() $R$ is inert in
$R$ is inert in ![]() $E$, and a place of
$E$, and a place of ![]() $F$ above
$F$ above ![]() $p$ is split (respectively, inert) in
$p$ is split (respectively, inert) in ![]() $E$ if it belongs (respectively, does not belong) to
$E$ if it belongs (respectively, does not belong) to ![]() $R_p$. We consider the auxiliary unitary group
$R_p$. We consider the auxiliary unitary group ![]() $H_\emptyset$ constructed as in § 3.1.3; we will denote
$H_\emptyset$ constructed as in § 3.1.3; we will denote ![]() $H_\emptyset$ by
$H_\emptyset$ by ![]() $H$ for simplicity. We can write the Kottwitz set
$H$ for simplicity. We can write the Kottwitz set ![]() $B(H_{{\mathbb {Q}}_p}, \mu )$ as a product
$B(H_{{\mathbb {Q}}_p}, \mu )$ as a product ![]() $B(H_{{\mathbb {Q}}_p}, \mu )=\prod _{\Sigma _p}B(H_{\mathfrak {p}}, \mu _{\mathfrak {p}})$, where
$B(H_{{\mathbb {Q}}_p}, \mu )=\prod _{\Sigma _p}B(H_{\mathfrak {p}}, \mu _{\mathfrak {p}})$, where ![]() $B(H_{\mathfrak {p}}, \mu _{\mathfrak {p}})$ has one element (respectively, two elements, the basic and the
$B(H_{\mathfrak {p}}, \mu _{\mathfrak {p}})$ has one element (respectively, two elements, the basic and the ![]() $\mu _\mathfrak {p}$-ordinary element) if
$\mu _\mathfrak {p}$-ordinary element) if ![]() $\mathfrak {p} \in R_p$ (respectively, if
$\mathfrak {p} \in R_p$ (respectively, if ![]() $\mathfrak {p} \in \Sigma _p \smallsetminus R_p$). We fix a compact open subgroup
$\mathfrak {p} \in \Sigma _p \smallsetminus R_p$). We fix a compact open subgroup ![]() $K_E=(\mathcal {O}_E \otimes {\mathbb {Z}}_p)^\times K_E^{p}$ sufficiently small with respect to
$K_E=(\mathcal {O}_E \otimes {\mathbb {Z}}_p)^\times K_E^{p}$ sufficiently small with respect to ![]() $K$, and we let
$K$, and we let ![]() $U\subset H({\mathbb {A}}_f)$ be the image of
$U\subset H({\mathbb {A}}_f)$ be the image of ![]() $K_E \times K$. Given
$K_E \times K$. Given ![]() $b=(b_\mathfrak {p})_{\mathfrak {p} \in \Sigma _p} \in B(H_{{\mathbb {Q}}_p}, \mu )$ we have the corresponding Newton stratum
$b=(b_\mathfrak {p})_{\mathfrak {p} \in \Sigma _p} \in B(H_{{\mathbb {Q}}_p}, \mu )$ we have the corresponding Newton stratum ![]() $\overline {Sh}^b_{U}(H)$ which is affine and smooth, of dimension
$\overline {Sh}^b_{U}(H)$ which is affine and smooth, of dimension ![]() $d-\varepsilon _b$, where
$d-\varepsilon _b$, where ![]() $\varepsilon _b$ denotes the number of places
$\varepsilon _b$ denotes the number of places ![]() $\mathfrak {p} \in \Sigma _p \smallsetminus R_p$ such that
$\mathfrak {p} \in \Sigma _p \smallsetminus R_p$ such that ![]() $b_\mathfrak {p}$ is basic.
$b_\mathfrak {p}$ is basic.
Given a set ![]() $T \subset \Sigma _p \smallsetminus R_p$, let
$T \subset \Sigma _p \smallsetminus R_p$, let ![]() $B_T$ be the quaternion algebra over
$B_T$ be the quaternion algebra over ![]() $F$ ramified at places in
$F$ ramified at places in ![]() $R$ as well as at places in
$R$ as well as at places in ![]() $T$ and at the corresponding infinite places. We let
$T$ and at the corresponding infinite places. We let ![]() $G_T:=\mathrm {Res}_{F/{\mathbb {Q}}}B_T^\times$; fix an isomorphism
$G_T:=\mathrm {Res}_{F/{\mathbb {Q}}}B_T^\times$; fix an isomorphism ![]() $G({\mathbb {A}}_f^{(p)})\simeq G_T({\mathbb {A}}_f^{(p)})$, allowing us to see
$G({\mathbb {A}}_f^{(p)})\simeq G_T({\mathbb {A}}_f^{(p)})$, allowing us to see ![]() $K^p$ as a subgroup of
$K^p$ as a subgroup of ![]() $G_T({\mathbb {A}}_f^{(p)})$. The arguments in §§ 3.2 and 3.3 go through in this setting; in particular, one can define moduli problems giving rise to integral models of the Shimura varieties attached to the groups
$G_T({\mathbb {A}}_f^{(p)})$. The arguments in §§ 3.2 and 3.3 go through in this setting; in particular, one can define moduli problems giving rise to integral models of the Shimura varieties attached to the groups ![]() $H$ and
$H$ and ![]() $H_T$; this makes it possible to define Igusa varieties, and Theorem 4.2.4 has an analogue in this setting. Similarly, we have a description of the fibres of the relevant Hodge–Tate period maps in terms of Igusa varieties, and of the
$H_T$; this makes it possible to define Igusa varieties, and Theorem 4.2.4 has an analogue in this setting. Similarly, we have a description of the fibres of the relevant Hodge–Tate period maps in terms of Igusa varieties, and of the ![]() $\mu$-ordinary locus at infinite level as being parabolically induced from the corresponding Igusa variety.
$\mu$-ordinary locus at infinite level as being parabolically induced from the corresponding Igusa variety.
Theorem 7.5.2 will follow from the following proposition.
Proposition 7.5.4 Take ![]() $b=(b_\mathfrak {p})_{\mathfrak {p} \in \Sigma _p} \in B(H_{{\mathbb {Q}}_p}, \mu )$ corresponding to a Newton stratum with smallest possible dimension such that
$b=(b_\mathfrak {p})_{\mathfrak {p} \in \Sigma _p} \in B(H_{{\mathbb {Q}}_p}, \mu )$ corresponding to a Newton stratum with smallest possible dimension such that ![]() $H^*(\overline {Sh}^b_{U}(H), {\mathbb {F}}_\ell )_\mathfrak {m} \neq 0$. Let
$H^*(\overline {Sh}^b_{U}(H), {\mathbb {F}}_\ell )_\mathfrak {m} \neq 0$. Let ![]() $T \subset \Sigma _p \smallsetminus R_p$ be the set of places
$T \subset \Sigma _p \smallsetminus R_p$ be the set of places ![]() $\mathfrak {p}$ such that
$\mathfrak {p}$ such that ![]() $b_\mathfrak {p}$ is basic. Then there is a compact open subgroup
$b_\mathfrak {p}$ is basic. Then there is a compact open subgroup ![]() $K_{T, p}\subset G_T({\mathbb {Q}}_p)$ such that
$K_{T, p}\subset G_T({\mathbb {Q}}_p)$ such that
Proof. As ![]() $H^*(\overline {Sh}^b_{U}(H), {\mathbb {F}}_\ell )_\mathfrak {m} \neq 0$ we deduce that
$H^*(\overline {Sh}^b_{U}(H), {\mathbb {F}}_\ell )_\mathfrak {m} \neq 0$ we deduce that ![]() $H^*(\mathrm {Ig}^b, {\mathbb {F}}_\ell )_\mathfrak {m} \neq 0$, hence by Theorem 4.2.4 we get
$H^*(\mathrm {Ig}^b, {\mathbb {F}}_\ell )_\mathfrak {m} \neq 0$, hence by Theorem 4.2.4 we get ![]() $H^*(\mathrm {Ig}_T^{{\mathrm {ord}}}, {\mathbb {F}}_\ell )_\mathfrak {m} \neq 0$. Denoting by
$H^*(\mathrm {Ig}_T^{{\mathrm {ord}}}, {\mathbb {F}}_\ell )_\mathfrak {m} \neq 0$. Denoting by ![]() $\pi _{\mathrm {HT}}^T$ the Hodge–Tate period map for
$\pi _{\mathrm {HT}}^T$ the Hodge–Tate period map for ![]() $\mathcal {S}h_{U^p}(H_T)$, we deduce as in Lemma 7.4.2 that
$\mathcal {S}h_{U^p}(H_T)$, we deduce as in Lemma 7.4.2 that ![]() $(R\pi _{\mathrm {HT}, *}^T {\mathbb {F}}_{\ell })_\mathfrak {m}$ is supported only on the
$(R\pi _{\mathrm {HT}, *}^T {\mathbb {F}}_{\ell })_\mathfrak {m}$ is supported only on the ![]() $\mu _T$-ordinary locus. Perversity (up to shift) of
$\mu _T$-ordinary locus. Perversity (up to shift) of ![]() $R\pi _{\mathrm {HT}, *}^T {\mathbb {F}}_{\ell }$ implies that
$R\pi _{\mathrm {HT}, *}^T {\mathbb {F}}_{\ell }$ implies that ![]() $H^*(\mathrm {Ig}_T^{\mathrm {ord}}, {\mathbb {F}}_\ell )_\mathfrak {m}$ is non-zero only in middle degree; the same argument as in § 7.4.3 then shows that
$H^*(\mathrm {Ig}_T^{\mathrm {ord}}, {\mathbb {F}}_\ell )_\mathfrak {m}$ is non-zero only in middle degree; the same argument as in § 7.4.3 then shows that ![]() $H^*(\mathcal {S}h_{U^p}(H_T), {\mathbb {F}}_\ell )_\mathfrak {m}$ is concentrated in middle degree. We can finally descend to an appropriate finite level and apply Corollary 3.2.9 to deduce that
$H^*(\mathcal {S}h_{U^p}(H_T), {\mathbb {F}}_\ell )_\mathfrak {m}$ is concentrated in middle degree. We can finally descend to an appropriate finite level and apply Corollary 3.2.9 to deduce that ![]() $H^*(Sh_{K^{p}K_{T, p}}(G_T), {\mathbb {F}}_\ell )_\mathfrak {m}$ is concentrated in middle degree, hence
$H^*(Sh_{K^{p}K_{T, p}}(G_T), {\mathbb {F}}_\ell )_\mathfrak {m}$ is concentrated in middle degree, hence ![]() $H^*(Sh_{K^{p}K_{T, p}}(G_T), {\mathbb {Q}}_\ell )_\mathfrak {m}\neq 0$.
$H^*(Sh_{K^{p}K_{T, p}}(G_T), {\mathbb {Q}}_\ell )_\mathfrak {m}\neq 0$.
7.5.5 Proof of Theorem 7.5.2
The existence of ![]() $\bar {\rho }_\mathfrak {m}$ follows combining Proposition 7.5.4, the description of the cohomology of
$\bar {\rho }_\mathfrak {m}$ follows combining Proposition 7.5.4, the description of the cohomology of ![]() $Sh_{K^{p}K_{T, p}}(G_T)$ with characteristic zero coefficients in terms of automorphic forms and the existence of Galois representations attached to quaternionic automorphic forms. The second point is proved adapting the argument in §§ 7.2 and 7.4.3. The third point follows from the second and from Lemma 7.1.8.
$Sh_{K^{p}K_{T, p}}(G_T)$ with characteristic zero coefficients in terms of automorphic forms and the existence of Galois representations attached to quaternionic automorphic forms. The second point is proved adapting the argument in §§ 7.2 and 7.4.3. The third point follows from the second and from Lemma 7.1.8.
8. Compatibility with the  $p$-adic local Langlands correspondence
$p$-adic local Langlands correspondence
Fix a prime ![]() $p$ throughout this section, which will play the role of the prime denoted by
$p$ throughout this section, which will play the role of the prime denoted by ![]() $\ell$ above. The aim of this section is to relate the completed homology of Hilbert modular varieties and the
$\ell$ above. The aim of this section is to relate the completed homology of Hilbert modular varieties and the ![]() $p$-adic Langlands correspondence, building on [Reference Gee and NewtonGN22].
$p$-adic Langlands correspondence, building on [Reference Gee and NewtonGN22].
8.1 Completed homology
8.1.1
Following [Reference Gee and NewtonGN22] we work with locally symmetric spaces attached to ![]() $\operatorname {PGL}_{2, F}$ rather than
$\operatorname {PGL}_{2, F}$ rather than ![]() $\operatorname {GL}_{2, F}$. Let
$\operatorname {GL}_{2, F}$. Let ![]() $G:=\mathrm {Res}_{F/{\mathbb {Q}}}\operatorname {GL}_{2}$ and
$G:=\mathrm {Res}_{F/{\mathbb {Q}}}\operatorname {GL}_{2}$ and ![]() $\bar {G}:=\mathrm {Res}_{F/{\mathbb {Q}}}\operatorname {PGL}_{2}$. Given a compact open subgroup
$\bar {G}:=\mathrm {Res}_{F/{\mathbb {Q}}}\operatorname {PGL}_{2}$. Given a compact open subgroup ![]() $\bar {K}\subset \bar {G}({\mathbb {A}}_f)$ we have the locally symmetric space
$\bar {K}\subset \bar {G}({\mathbb {A}}_f)$ we have the locally symmetric space
Fix a compact open subgroup ![]() $\bar {K}^p\bar {K}_0$ which is good in the sense of [Reference Gee and NewtonGN22, § 2.1], with
$\bar {K}^p\bar {K}_0$ which is good in the sense of [Reference Gee and NewtonGN22, § 2.1], with ![]() $\bar {K}_0=\prod _{v \mid p}\operatorname {PGL}_2({\mathcal {O}}_{F_v})$. Consider the completed homology groups
$\bar {K}_0=\prod _{v \mid p}\operatorname {PGL}_2({\mathcal {O}}_{F_v})$. Consider the completed homology groups
Let ![]() $\mathbb {T}(\bar {K}^p)$ be the big Hecke algebra defined in [Reference Gee and NewtonGN22, Definition 2.1.11] (beware that our notation differs from that used there). It maps to the Hecke algebra
$\mathbb {T}(\bar {K}^p)$ be the big Hecke algebra defined in [Reference Gee and NewtonGN22, Definition 2.1.11] (beware that our notation differs from that used there). It maps to the Hecke algebra ![]() $\mathbb {T}(\bar {K}^p\bar {K}_p, {\mathbb {Z}}/p^s{\mathbb {Z}})$ acting on homology with
$\mathbb {T}(\bar {K}^p\bar {K}_p, {\mathbb {Z}}/p^s{\mathbb {Z}})$ acting on homology with ![]() ${\mathbb {Z}}/p^s{\mathbb {Z}}$-coefficients of the locally symmetric space of level
${\mathbb {Z}}/p^s{\mathbb {Z}}$-coefficients of the locally symmetric space of level ![]() $\bar {K}^p\bar {K}_p$ for each
$\bar {K}^p\bar {K}_p$ for each ![]() $\bar {K}_p$ and each
$\bar {K}_p$ and each ![]() $s \geq 1$. Completed homology
$s \geq 1$. Completed homology ![]() $\tilde {H}_*(\bar {K}^p, {\mathbb {Z}}_p)$ carries an action of
$\tilde {H}_*(\bar {K}^p, {\mathbb {Z}}_p)$ carries an action of ![]() $\mathbb {T}(\bar {K}^p)$ as well as of
$\mathbb {T}(\bar {K}^p)$ as well as of ![]() $\bar {G}({\mathbb {Q}}_p)$; we fix a maximal ideal
$\bar {G}({\mathbb {Q}}_p)$; we fix a maximal ideal ![]() $\mathfrak {m}\subset \mathbb {T}(\bar {K}^p)$. For
$\mathfrak {m}\subset \mathbb {T}(\bar {K}^p)$. For ![]() $\bar {K}_p$ small enough, the ideal
$\bar {K}_p$ small enough, the ideal ![]() $\mathfrak {m}$ is the preimage of a maximal ideal in
$\mathfrak {m}$ is the preimage of a maximal ideal in ![]() $\mathbb {T}(\bar {K}^p\bar {K}_p, {\mathbb {Z}}/p{\mathbb {Z}})$, which we will abusively denote by the same symbol (in fact any pro-
$\mathbb {T}(\bar {K}^p\bar {K}_p, {\mathbb {Z}}/p{\mathbb {Z}})$, which we will abusively denote by the same symbol (in fact any pro-![]() $p$ group
$p$ group ![]() $\bar {K}_p$ does the job, cf. the proof of [Reference Gee and NewtonGN22, Lemma 2.1.14]). Hence, setting
$\bar {K}_p$ does the job, cf. the proof of [Reference Gee and NewtonGN22, Lemma 2.1.14]). Hence, setting ![]() $\bar {K}=\bar {K}^p\bar {K}_p$, we have
$\bar {K}=\bar {K}^p\bar {K}_p$, we have ![]() $H^*(X_{\bar {K}}(\bar {G}), {\mathbb {F}}_p)_\mathfrak {m}\simeq H_*(X_{\bar {K}}(\bar {G}), {\mathbb {F}}_p)_\mathfrak {m} \neq 0$.
$H^*(X_{\bar {K}}(\bar {G}), {\mathbb {F}}_p)_\mathfrak {m}\simeq H_*(X_{\bar {K}}(\bar {G}), {\mathbb {F}}_p)_\mathfrak {m} \neq 0$.
8.1.2
Let us now assume that ![]() $p>3$; we take
$p>3$; we take ![]() $\bar {K}$ as above, and assume in addition that it is the image of a compact open subgroup
$\bar {K}$ as above, and assume in addition that it is the image of a compact open subgroup ![]() $K \subset G({\mathbb {A}}_f)$. The natural map
$K \subset G({\mathbb {A}}_f)$. The natural map ![]() $Sh_K(G) \rightarrow X_{\bar {K}}(\bar {G})$ is a finite étale Galois cover, hence
$Sh_K(G) \rightarrow X_{\bar {K}}(\bar {G})$ is a finite étale Galois cover, hence ![]() $H^*(Sh_K(G), {\mathbb {F}}_p)_{\mathfrak {m}}\neq 0$. By Theorem 2.2.1 there is a Galois representation
$H^*(Sh_K(G), {\mathbb {F}}_p)_{\mathfrak {m}}\neq 0$. By Theorem 2.2.1 there is a Galois representation ![]() $\bar {\rho }_\mathfrak {m}: \Gamma _F \rightarrow \operatorname {GL}_2(\bar {{\mathbb {F}}}_p)$ attached to
$\bar {\rho }_\mathfrak {m}: \Gamma _F \rightarrow \operatorname {GL}_2(\bar {{\mathbb {F}}}_p)$ attached to ![]() $\mathfrak {m}$. Let us suppose that the projective image of
$\mathfrak {m}$. Let us suppose that the projective image of ![]() $\bar {\rho }_\mathfrak {m}$ contains a conjugate of
$\bar {\rho }_\mathfrak {m}$ contains a conjugate of ![]() $\operatorname {PSL}_2({\mathbb {F}}_p)$ or is isomorphic to
$\operatorname {PSL}_2({\mathbb {F}}_p)$ or is isomorphic to ![]() $A_5$; then Theorem 7.1.1 implies that, for every
$A_5$; then Theorem 7.1.1 implies that, for every ![]() $K'_p\subset K_{p}$, we have
$K'_p\subset K_{p}$, we have
for ![]() $i< g$; the Hochschild–Serre spectral sequence attached to the Galois cover
$i< g$; the Hochschild–Serre spectral sequence attached to the Galois cover ![]() $Sh_{K^pK'_p}(G)\rightarrow X_{\overline {K^pK'_p}}(\bar {G})$ implies that the same property holds true for the cohomology of
$Sh_{K^pK'_p}(G)\rightarrow X_{\overline {K^pK'_p}}(\bar {G})$ implies that the same property holds true for the cohomology of ![]() $X_{\overline {K^pK'_p}}(\bar {G})$, hence
$X_{\overline {K^pK'_p}}(\bar {G})$, hence ![]() $H^*(X_{\overline {K^pK'_p}}(\bar {G}), {\mathbb {F}}_p)_\mathfrak {m}\simeq H_*(X_{\overline {K^pK'_p}}(\bar {G}), {\mathbb {F}}_p)_\mathfrak {m}$ is concentrated in degree
$H^*(X_{\overline {K^pK'_p}}(\bar {G}), {\mathbb {F}}_p)_\mathfrak {m}\simeq H_*(X_{\overline {K^pK'_p}}(\bar {G}), {\mathbb {F}}_p)_\mathfrak {m}$ is concentrated in degree ![]() $g$. Therefore, assumptions (a) and (b) of [Reference Gee and NewtonGN22, Proposition 4.2.1] are satisfied (note that assumption (b) trivially holds since, with the notation of [Reference Gee and NewtonGN22, Proposition 4.2.1], we have
$g$. Therefore, assumptions (a) and (b) of [Reference Gee and NewtonGN22, Proposition 4.2.1] are satisfied (note that assumption (b) trivially holds since, with the notation of [Reference Gee and NewtonGN22, Proposition 4.2.1], we have ![]() $l_0=0$ in our situation). Thanks to [Reference Gee and NewtonGN22, Proposition 4.2.1] we obtain that
$l_0=0$ in our situation). Thanks to [Reference Gee and NewtonGN22, Proposition 4.2.1] we obtain that ![]() $\tilde {H}_i(\bar {K}^p, {\mathbb {Z}}_p)_\mathfrak {m}=0$ if
$\tilde {H}_i(\bar {K}^p, {\mathbb {Z}}_p)_\mathfrak {m}=0$ if ![]() $i \neq g$ and
$i \neq g$ and ![]() $\tilde {H}_g(\bar {K}^p, {\mathbb {Z}}_p)_\mathfrak {m}$ is a projective,
$\tilde {H}_g(\bar {K}^p, {\mathbb {Z}}_p)_\mathfrak {m}$ is a projective, ![]() $p$-torsion-free
$p$-torsion-free ![]() ${\mathbb {Z}}_p[[\bar {K}_{0}]]$-module. Furthermore, there is a Galois representation
${\mathbb {Z}}_p[[\bar {K}_{0}]]$-module. Furthermore, there is a Galois representation
lifting ![]() $\bar {\rho }_\mathfrak {m}$, as in [Reference Gee and NewtonGN22, Conjecture 3.3.3(2)]. It can be constructed as in [Reference ScholzeSch18, § 5]: the argument in [Reference ScholzeSch18, § 5], glueing representations valued in Hecke algebras at increasing finite level, can be applied in our situation as (co)homology with
$\bar {\rho }_\mathfrak {m}$, as in [Reference Gee and NewtonGN22, Conjecture 3.3.3(2)]. It can be constructed as in [Reference ScholzeSch18, § 5]: the argument in [Reference ScholzeSch18, § 5], glueing representations valued in Hecke algebras at increasing finite level, can be applied in our situation as (co)homology with ![]() ${\mathbb {Z}}_p$-coefficients is concentrated in one degree and torsion-free after localisation at
${\mathbb {Z}}_p$-coefficients is concentrated in one degree and torsion-free after localisation at ![]() $\mathfrak {m}$, and cohomology with
$\mathfrak {m}$, and cohomology with ![]() ${\mathbb {Q}}_p$-coefficients localised at
${\mathbb {Q}}_p$-coefficients localised at ![]() $\mathfrak {m}$ is described in terms of Hilbert cusp forms.
$\mathfrak {m}$ is described in terms of Hilbert cusp forms.
8.2  $p$-adic local Langlands
$p$-adic local Langlands
Assume from now on that ![]() $p$ is totally split in
$p$ is totally split in ![]() $F$. We want to describe the relation between completed homology of Hilbert modular varieties and the
$F$. We want to describe the relation between completed homology of Hilbert modular varieties and the ![]() $p$-adic Langlands correspondence for
$p$-adic Langlands correspondence for ![]() $\operatorname {GL}_2({\mathbb {Q}}_p)$, using the machinery of [Reference Gee and NewtonGN22]. As remarked in [Reference Gee and NewtonGN22, § 5.4], assumption (a) of [Reference Gee and NewtonGN22, Proposition 4.2.1], which we established above, is the key input needed to apply the results in [Reference Gee and NewtonGN22].
$\operatorname {GL}_2({\mathbb {Q}}_p)$, using the machinery of [Reference Gee and NewtonGN22]. As remarked in [Reference Gee and NewtonGN22, § 5.4], assumption (a) of [Reference Gee and NewtonGN22, Proposition 4.2.1], which we established above, is the key input needed to apply the results in [Reference Gee and NewtonGN22].
8.2.1
We first need to introduce some notation. We replace ![]() ${\mathbb {Z}}_p$ by the ring of integers
${\mathbb {Z}}_p$ by the ring of integers ![]() ${\mathcal {O}}$ of a finite extension of
${\mathcal {O}}$ of a finite extension of ![]() ${\mathbb {Q}}_p$, with residue field
${\mathbb {Q}}_p$, with residue field ![]() $k$, so that
$k$, so that ![]() $\bar {\rho }_\mathfrak {m}$ takes values in
$\bar {\rho }_\mathfrak {m}$ takes values in ![]() $\operatorname {GL}_2(k)$. Furthermore, up to further extending
$\operatorname {GL}_2(k)$. Furthermore, up to further extending ![]() $\mathcal {O}$, we may, and will, assume that
$\mathcal {O}$, we may, and will, assume that ![]() $k$ contains all the eigenvalues of the elements in the image of
$k$ contains all the eigenvalues of the elements in the image of ![]() $\bar {\rho }_\mathfrak {m}$ (as in [Reference Gee and NewtonGN22, § 3.2]). We denote by
$\bar {\rho }_\mathfrak {m}$ (as in [Reference Gee and NewtonGN22, § 3.2]). We denote by ![]() $L$ the fraction field of
$L$ the fraction field of ![]() ${\mathcal {O}}$. For a place
${\mathcal {O}}$. For a place ![]() $v \mid p$, under suitable assumptions on
$v \mid p$, under suitable assumptions on ![]() $\bar {\rho }_{\mathfrak {m}_{|\Gamma _{F_v}}}$ (for example, if it is absolutely irreducible) we have the universal local deformation ring
$\bar {\rho }_{\mathfrak {m}_{|\Gamma _{F_v}}}$ (for example, if it is absolutely irreducible) we have the universal local deformation ring ![]() $R_v^{\mathrm {def}}$ of
$R_v^{\mathrm {def}}$ of ![]() $\bar {\rho }_{\mathfrak {m} \mid \Gamma _{F_v}}$. We denote by
$\bar {\rho }_{\mathfrak {m} \mid \Gamma _{F_v}}$. We denote by ![]() $\pi _v$ the
$\pi _v$ the ![]() $k$-representation of
$k$-representation of ![]() $\operatorname {PGL}_2(F_v)$ attached to
$\operatorname {PGL}_2(F_v)$ attached to ![]() $\bar {\rho }_{\mathfrak {m} \mid \Gamma _{F_v}}$, and we let
$\bar {\rho }_{\mathfrak {m} \mid \Gamma _{F_v}}$, and we let ![]() $P_v$ be the projective envelope of
$P_v$ be the projective envelope of ![]() $\pi _v^\vee$ in the Pontryagin dual of the category of locally admissible
$\pi _v^\vee$ in the Pontryagin dual of the category of locally admissible ![]() ${\mathcal {O}}$-representations of
${\mathcal {O}}$-representations of ![]() $\operatorname {PGL}_2(F_v)$. We set
$\operatorname {PGL}_2(F_v)$. We set ![]() $R_p^{\mathrm {loc}}:=\hat {\otimes }_{v\mid p, {\mathcal {O}}} R_v^{\mathrm {def}}$; then
$R_p^{\mathrm {loc}}:=\hat {\otimes }_{v\mid p, {\mathcal {O}}} R_v^{\mathrm {def}}$; then ![]() $P:=\hat {\otimes }_{v \mid p, {\mathcal {O}}}P_v$ has an
$P:=\hat {\otimes }_{v \mid p, {\mathcal {O}}}P_v$ has an ![]() $R_p^{\mathrm {loc}}$-module structure, cf. [Reference PaškūnasPaš13, Proposition 6.3, Corollary 8.7] (see also [Reference Gee and NewtonGN22, § 5.1]). Finally, the representation
$R_p^{\mathrm {loc}}$-module structure, cf. [Reference PaškūnasPaš13, Proposition 6.3, Corollary 8.7] (see also [Reference Gee and NewtonGN22, § 5.1]). Finally, the representation ![]() $\rho _\mathfrak {m}$ gives rise to a map
$\rho _\mathfrak {m}$ gives rise to a map ![]() $R_{p}^{\mathrm {loc}}\rightarrow \mathbb {T}(\bar {K}^p)_\mathfrak {m}$. Let
$R_{p}^{\mathrm {loc}}\rightarrow \mathbb {T}(\bar {K}^p)_\mathfrak {m}$. Let ![]() $N(\bar {\rho }_\mathfrak {m})$ be the prime-to-
$N(\bar {\rho }_\mathfrak {m})$ be the prime-to-![]() $p$-conductor of
$p$-conductor of ![]() $\bar {\rho }_\mathfrak {m}$ and let
$\bar {\rho }_\mathfrak {m}$ and let ![]() $\bar {K}_1(N(\bar {\rho }_\mathfrak {m}))$ be the image of
$\bar {K}_1(N(\bar {\rho }_\mathfrak {m}))$ be the image of ![]() $\{M \in \operatorname {GL}_2(\hat {\mathcal {O}}_F)\mid M \equiv (\begin{smallmatrix}* & *\\ 0 & 1\end{smallmatrix}) \pmod {N(\bar {\rho }_\mathfrak {m})}\}$ (more precisely, if this group is not good, we make it smaller at places where
$\{M \in \operatorname {GL}_2(\hat {\mathcal {O}}_F)\mid M \equiv (\begin{smallmatrix}* & *\\ 0 & 1\end{smallmatrix}) \pmod {N(\bar {\rho }_\mathfrak {m})}\}$ (more precisely, if this group is not good, we make it smaller at places where ![]() $\bar {\rho }_\mathfrak {m}$ admits no ramified deformations).
$\bar {\rho }_\mathfrak {m}$ admits no ramified deformations).
Theorem 8.2.2 Let ![]() $p>3$ be a prime which splits completely in
$p>3$ be a prime which splits completely in ![]() $F$. Assume that the following assertions hold true.
$F$. Assume that the following assertions hold true.
(i) The projective image of the Galois representation
 $\bar {\rho }_\mathfrak {m}$ attached to
$\bar {\rho }_\mathfrak {m}$ attached to  $\mathfrak {m}$ contains a conjugate of
$\mathfrak {m}$ contains a conjugate of  $\operatorname {PSL}_2({\mathbb {F}}_p)$ or is isomorphic to
$\operatorname {PSL}_2({\mathbb {F}}_p)$ or is isomorphic to  $A_5$.
$A_5$.(ii) If
 $\bar {\rho }_\mathfrak {m}$ is ramified at some place
$\bar {\rho }_\mathfrak {m}$ is ramified at some place  $v$ not lying above
$v$ not lying above  $p$, then
$p$, then  $v$ is not a vexing prime.
$v$ is not a vexing prime.(iii) For each place
 $v \mid p$, the restriction of
$v \mid p$, the restriction of  $\bar {\rho }_\mathfrak {m}$ to
$\bar {\rho }_\mathfrak {m}$ to  $\Gamma _{F_v}$ is absolutely irreducible.
$\Gamma _{F_v}$ is absolutely irreducible.
Then there is an isomorphism of ![]() $\mathbb {T}(\bar {K}_1(N(\bar {\rho }_\mathfrak {m}))^p)_\mathfrak {m}[\bar {G}({\mathbb {Q}}_p)]$-modules
$\mathbb {T}(\bar {K}_1(N(\bar {\rho }_\mathfrak {m}))^p)_\mathfrak {m}[\bar {G}({\mathbb {Q}}_p)]$-modules
for some ![]() $m \geq 1$.
$m \geq 1$.
Proof. This is [Reference Gee and NewtonGN22, Proposition 5.1.4], which follows from [Reference Gee and NewtonGN22, Conjecture 5.1.2]. Let us explain why this and other conjectures formulated in [Reference Gee and NewtonGN22] hold true in our setting, and the various assumptions made in [Reference Gee and NewtonGN22] are satisfied.
(i) In [Reference Gee and NewtonGN22, § 4.1] the authors assume that the image of restriction of
 $\bar {\rho }_\mathfrak {m}$ to
$\bar {\rho }_\mathfrak {m}$ to  $\Gamma _{F(\zeta _p)}$ is enormous. This is needed for the construction of Taylor–Wiles data, as in [Reference Gee and NewtonGN22, Lemma 3.3.1]. Our large image assumption and [Reference Gee and NewtonGN22, Lemma 3.2.3] imply that the group
$\Gamma _{F(\zeta _p)}$ is enormous. This is needed for the construction of Taylor–Wiles data, as in [Reference Gee and NewtonGN22, Lemma 3.3.1]. Our large image assumption and [Reference Gee and NewtonGN22, Lemma 3.2.3] imply that the group  $\bar {\rho }_\mathfrak {m}(\Gamma _{F(\zeta _p)})$ is enormous if
$\bar {\rho }_\mathfrak {m}(\Gamma _{F(\zeta _p)})$ is enormous if  $p>5$. If
$p>5$. If  $p=5$, our assumption does not guarantee that
$p=5$, our assumption does not guarantee that  $\bar {\rho }_\mathfrak {m}(\Gamma _{F(\zeta _p)})$ is enormous. However, in this case, one can work under the assumption [Reference ScholzeSch18, Hypothesis 9.1], which originates in [Reference KisinKis09, Theorem 3.5.5] and which is satisfied in our situation. Indeed, if the image of
$\bar {\rho }_\mathfrak {m}(\Gamma _{F(\zeta _p)})$ is enormous. However, in this case, one can work under the assumption [Reference ScholzeSch18, Hypothesis 9.1], which originates in [Reference KisinKis09, Theorem 3.5.5] and which is satisfied in our situation. Indeed, if the image of  $\mathrm {pr}\circ \bar {\rho }_\mathfrak {m}: \Gamma _F \rightarrow \operatorname {PGL}_2(\bar {{\mathbb {F}}}_5)$ is conjugate to
$\mathrm {pr}\circ \bar {\rho }_\mathfrak {m}: \Gamma _F \rightarrow \operatorname {PGL}_2(\bar {{\mathbb {F}}}_5)$ is conjugate to  $\operatorname {PGL}_2({\mathbb {F}}_5)$ and its kernel fixes
$\operatorname {PGL}_2({\mathbb {F}}_5)$ and its kernel fixes  $F(\zeta _5)$ then
$F(\zeta _5)$ then  $[F(\zeta _5): F]=2$, which cannot happen if
$[F(\zeta _5): F]=2$, which cannot happen if  $p=5$ is unramified in
$p=5$ is unramified in  $F$.
$F$.(ii) The assumption that
 $\bar {\rho }_\mathfrak {m}\neq \bar {\rho }_\mathfrak {m}\otimes \bar {\epsilon }$, where
$\bar {\rho }_\mathfrak {m}\neq \bar {\rho }_\mathfrak {m}\otimes \bar {\epsilon }$, where  $\bar {\epsilon }$ is the mod
$\bar {\epsilon }$ is the mod  $p$ cyclotomic character (see [Reference Gee and NewtonGN22, p. 18]) holds. Indeed because
$p$ cyclotomic character (see [Reference Gee and NewtonGN22, p. 18]) holds. Indeed because  $p$ is unramified
$p$ is unramified  $F$, the fields
$F$, the fields  $F$ and
$F$ and  ${\mathbb {Q}}(\zeta _p)$ are linearly disjoint over
${\mathbb {Q}}(\zeta _p)$ are linearly disjoint over  ${\mathbb {Q}}$; hence
${\mathbb {Q}}$; hence  $\bar {\epsilon }: \Gamma _F \rightarrow ({\mathbb {Z}}/p{\mathbb {Z}})^\times$ is surjective. In particular, there is
$\bar {\epsilon }: \Gamma _F \rightarrow ({\mathbb {Z}}/p{\mathbb {Z}})^\times$ is surjective. In particular, there is  $\gamma \in \Gamma _F$ such that
$\gamma \in \Gamma _F$ such that  $\bar {\epsilon }(\gamma )^2 \neq 1$, hence
$\bar {\epsilon }(\gamma )^2 \neq 1$, hence  $\det \bar {\rho }_\mathfrak {m}(\gamma )\neq \det (\bar {\epsilon }\otimes \bar {\rho }_\mathfrak {m})(\gamma )$. For the same reason the first assumption in [Reference Gee and NewtonGN22, Hypothesis 4.1.3] is satisfied.
$\det \bar {\rho }_\mathfrak {m}(\gamma )\neq \det (\bar {\epsilon }\otimes \bar {\rho }_\mathfrak {m})(\gamma )$. For the same reason the first assumption in [Reference Gee and NewtonGN22, Hypothesis 4.1.3] is satisfied.(iii) Conjecture 3.3.7 of [Reference Gee and NewtonGN22] holds: the representation denoted by
 $\rho _{\mathfrak {m}, Q}$ in [Reference Gee and NewtonGN22] can be constructed as explained before the statement of the theorem, and the desired local–global compatibility follows from the analogous statement for Hilbert modular forms.
$\rho _{\mathfrak {m}, Q}$ in [Reference Gee and NewtonGN22] can be constructed as explained before the statement of the theorem, and the desired local–global compatibility follows from the analogous statement for Hilbert modular forms.(iv) The second assumption in [Reference Gee and NewtonGN22, Hypothesis 4.1.3] holds in view of the hypothesis that there are no vexing primes.
The upshot of the above discussion is that all the assumptions made at the beginning of [Reference Gee and NewtonGN22, § 5] are verified. Therefore, by [Reference Gee and NewtonGN22, Corollary 5.3.2], Conjecture 5.1.2 follows from Conjecture 5.1.12 in [Reference Gee and NewtonGN22].
It remains to justify why Conjecture 5.1.12 holds. Let ![]() $Q$ be a set of Taylor–Wiles primes and
$Q$ be a set of Taylor–Wiles primes and ![]() $\sigma =(\sigma _v)_{v \mid p}$ an irreducible
$\sigma =(\sigma _v)_{v \mid p}$ an irreducible ![]() $L$-representation of
$L$-representation of ![]() $\bar {K}_0$, with
$\bar {K}_0$, with ![]() $\bar {K}_0$-stable
$\bar {K}_0$-stable ![]() ${\mathcal {O}}$ lattice
${\mathcal {O}}$ lattice ![]() $\sigma ^\circ$ as in [Reference Gee and NewtonGN22, p. 34]. Let
$\sigma ^\circ$ as in [Reference Gee and NewtonGN22, p. 34]. Let ![]() $X_{\bar {K}_1(Q)}(\bar {G})$ be the space with level
$X_{\bar {K}_1(Q)}(\bar {G})$ be the space with level ![]() $\bar {K}_0$ at
$\bar {K}_0$ at ![]() $p$ and
$p$ and ![]() $\bar {K}_1(Q)_v$ at each place
$\bar {K}_1(Q)_v$ at each place ![]() $v \in Q$. We need to show that the action of
$v \in Q$. We need to show that the action of ![]() $R_p^{\mathrm {loc}}$ on
$R_p^{\mathrm {loc}}$ on ![]() $H_*(X_{\bar {K}_1(Q)}(\bar {G}), \sigma ^\circ )_{\mathfrak {m}_{Q, 1}}$ factors through
$H_*(X_{\bar {K}_1(Q)}(\bar {G}), \sigma ^\circ )_{\mathfrak {m}_{Q, 1}}$ factors through ![]() $R_p^{\mathrm {loc}}(\sigma )$, where the ideal
$R_p^{\mathrm {loc}}(\sigma )$, where the ideal ![]() $\mathfrak {m}_{Q, 1}$ is defined in [Reference Gee and NewtonGN22, Proposition 3.3.6]. Let
$\mathfrak {m}_{Q, 1}$ is defined in [Reference Gee and NewtonGN22, Proposition 3.3.6]. Let ![]() $\mathbb {T}(\bar {K}_1(Q), \sigma )_{\mathfrak {m}_{Q, 1}}$ be the image of the Hecke algebra in the endomorphism ring of
$\mathbb {T}(\bar {K}_1(Q), \sigma )_{\mathfrak {m}_{Q, 1}}$ be the image of the Hecke algebra in the endomorphism ring of ![]() $H_g(X_{\bar {K}_1(Q)}(\bar {G}), \sigma ^\circ )_{\mathfrak {m}_{Q, 1}}$. By assumption (i) the homology
$H_g(X_{\bar {K}_1(Q)}(\bar {G}), \sigma ^\circ )_{\mathfrak {m}_{Q, 1}}$. By assumption (i) the homology ![]() $H_*(X_{\bar {K}_1(Q)}(\bar {G}), \sigma ^\circ )_{\mathfrak {m}_{Q, 1}}$ is concentrated in middle degree, and
$H_*(X_{\bar {K}_1(Q)}(\bar {G}), \sigma ^\circ )_{\mathfrak {m}_{Q, 1}}$ is concentrated in middle degree, and ![]() $H_g(X_{\bar {K}_1(Q)}(\bar {G}), \sigma ^\circ )_{\mathfrak {m}_{Q, 1}}$ is torsion-free; furthermore
$H_g(X_{\bar {K}_1(Q)}(\bar {G}), \sigma ^\circ )_{\mathfrak {m}_{Q, 1}}$ is torsion-free; furthermore ![]() $\mathbb {T}(\bar {K}_1(Q), \sigma )_{\mathfrak {m}_{Q, 1}}$ is reduced. As in the proof of the first part of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and Woo ShinCEG+16, Lemma 4.17], it suffices to show that, for any
$\mathbb {T}(\bar {K}_1(Q), \sigma )_{\mathfrak {m}_{Q, 1}}$ is reduced. As in the proof of the first part of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and Woo ShinCEG+16, Lemma 4.17], it suffices to show that, for any ![]() $\bar {{\mathbb {Q}}}_p$-point of
$\bar {{\mathbb {Q}}}_p$-point of ![]() $\mathbb {T}(\bar {K}_1(Q), \sigma )_{\mathfrak {m}_{Q, 1}}$, the restriction to
$\mathbb {T}(\bar {K}_1(Q), \sigma )_{\mathfrak {m}_{Q, 1}}$, the restriction to ![]() $\Gamma _{F_v}$ (for
$\Gamma _{F_v}$ (for ![]() $v \mid p$) of the associated Galois representation with
$v \mid p$) of the associated Galois representation with ![]() $\bar {{\mathbb {Q}}}_p$-coefficients is crystalline of type
$\bar {{\mathbb {Q}}}_p$-coefficients is crystalline of type ![]() $\sigma _v$. The space
$\sigma _v$. The space ![]() $H_*(X_{\bar {K}_1(Q)}(\bar {G}), \sigma )_{\mathfrak {m}_{Q, 1}}$ can be described in terms of Hilbert cusp forms with algebraic weight, hence the desired result follows from local–global compatibility at places above
$H_*(X_{\bar {K}_1(Q)}(\bar {G}), \sigma )_{\mathfrak {m}_{Q, 1}}$ can be described in terms of Hilbert cusp forms with algebraic weight, hence the desired result follows from local–global compatibility at places above ![]() $p$ (see [Reference KisinKis08, Theorem 4.3]). This establishes the first assertion in [Reference Gee and NewtonGN22, Conjecture 5.1.12]; the second one can be proved similarly, following the strategy in the second part of the proof of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and Woo ShinCEG+16, Lemma 4.17].
$p$ (see [Reference KisinKis08, Theorem 4.3]). This establishes the first assertion in [Reference Gee and NewtonGN22, Conjecture 5.1.12]; the second one can be proved similarly, following the strategy in the second part of the proof of [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and Woo ShinCEG+16, Lemma 4.17].
Remark 8.2.3 In fact, one should be able to prove a version of compatibility with the ![]() $p$-adic local Langlands correspondence without any assumptions on the tame level, for example the analogue to this setting of [Reference PanPan22b, Corollary 6.3.6]. That this would follow from Theorem A and the machinery developed by Paškūnas is more or less known to experts. We sketch the argument in this remark.
$p$-adic local Langlands correspondence without any assumptions on the tame level, for example the analogue to this setting of [Reference PanPan22b, Corollary 6.3.6]. That this would follow from Theorem A and the machinery developed by Paškūnas is more or less known to experts. We sketch the argument in this remark.
One can consider the completed cohomology of a Hilbert modular variety with ![]() ${\mathbb {Z}}_p$-coefficients. After localisation at a maximal ideal
${\mathbb {Z}}_p$-coefficients. After localisation at a maximal ideal ![]() $\mathfrak {m}$ whose associated residual Galois representation is non-solvable, Theorem A implies that this is concentrated in one degree. As in [Reference PanPan22b, Corollary 6.3.6], the key point is to prove the analogue of [Reference PanPan22b, Theorem 6.3.5] that compares two actions of the local pseudo-deformation ring with fixed determinant on completed cohomology localised at
$\mathfrak {m}$ whose associated residual Galois representation is non-solvable, Theorem A implies that this is concentrated in one degree. As in [Reference PanPan22b, Corollary 6.3.6], the key point is to prove the analogue of [Reference PanPan22b, Theorem 6.3.5] that compares two actions of the local pseudo-deformation ring with fixed determinant on completed cohomology localised at ![]() $\mathfrak {m}$. (See [Reference PanPan22a, Theorem 3.5.5] for the statement in the case when there are multiple split places above
$\mathfrak {m}$. (See [Reference PanPan22a, Theorem 3.5.5] for the statement in the case when there are multiple split places above ![]() $p$, which relies on [Reference PanPan22a, Corollary 3.4.12].)
$p$, which relies on [Reference PanPan22a, Corollary 3.4.12].)
The comparison of the two pseudo-deformation ring actions can be done using the method of [Reference PaškūnasPaš22, Corollary 5.6]. The key facts that would need checking are: density of those locally algebraic vectors for which the smooth part is a specific principal series representation, and semi-simplicity of the usual Hecke action on the non-Eisenstein cohomology of Hilbert modular varieties. The latter can be deduced from the Eichler–Shimura isomorphism and the existence of the Petersson inner product on Hilbert cusp forms. Density of locally algebraic vectors follows from [Reference Dospinescu, Paškūnas and SchraenDPS20, Corollary 7.8] and the fact that completed cohomology localised at ![]() $\mathfrak {m}$ with fixed central character is a direct summand of a space of continuous functions with fixed central character as in the proof of [Reference Dospinescu, Paškūnas and SchraenDPS20, Theorem 9.24]. Finally, the latter fact follows from projectivity of completed homology localised at
$\mathfrak {m}$ with fixed central character is a direct summand of a space of continuous functions with fixed central character as in the proof of [Reference Dospinescu, Paškūnas and SchraenDPS20, Theorem 9.24]. Finally, the latter fact follows from projectivity of completed homology localised at ![]() $\mathfrak {m}$ (cf. [Reference Dospinescu, Paškūnas and SchraenDPS20, Lemma 9.16(i)]). As in § 8.1.2, to establish this last property one crucially uses Theorem A.
$\mathfrak {m}$ (cf. [Reference Dospinescu, Paškūnas and SchraenDPS20, Lemma 9.16(i)]). As in § 8.1.2, to establish this last property one crucially uses Theorem A.
Acknowledgements
We are grateful to David Hansen for asking us to consider the cohomology of Hilbert modular varieties with torsion coefficients. A.C. would like to thank X. Zhu for the invitation to a 2019 AIM workshop on geometric instances of the Jacquet–Langlands correspondences, which inspired our method. We are grateful to F. Calegari, T. Gee, J. Newton, V. Paškūnas and J. Sempliner for useful conversations and correspondence, and to C. Cornut, T. Gee, J. Lourenço, S. Morra and P. Scholze for comments on a previous draft of this paper.
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement No. 804176). A.C. was supported by a Royal Society University Research Fellowship.
Conflicts of Interest
None.