We introduce 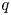$q$-stability conditions 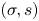$(\sigma,s)$ on Calabi–Yau-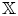$\mathbb {X}$ categories 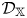$\mathcal {D}_\mathbb {X}$, where 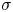$\sigma$ is a stability condition on 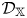$\mathcal {D}_\mathbb {X}$ and 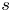$s$ a complex number. We prove the corresponding deformation theorem, that 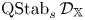$\operatorname {QStab}_s\mathcal {D}_\mathbb {X}$ is a complex manifold of dimension 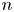$n$ for fixed 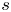$s$, where 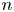$n$ is the rank of the Grothendieck group of 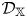$\mathcal {D}_\mathbb {X}$ over $\mathbb {Z}[q^{\pm 1}]$. When $s=N$ is an integer, we show that 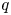$q$-stability conditions can be identified with the stability conditions on 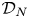$\mathcal {D}_N$, provided the orbit category 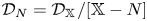$\mathcal {D}_N=\mathcal {D}_\mathbb {X}/[\mathbb {X}-N]$ is well defined. To attack the questions on existence and deformation along the 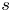$s$ direction, we introduce the inducing method. Sufficient and necessary conditions are given, for a stability condition on an $\mathbb {X}$-baric heart (that is, a usual triangulated category) of 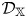$\mathcal {D}_\mathbb {X}$ to induce 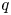$q$-stability conditions on 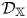$\mathcal {D}_\mathbb {X}$. As a consequence, we show that the space 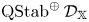$\operatorname {QStab}^\oplus \mathcal {D}_\mathbb {X}$ of (induced) open 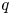$q$-stability conditions is a complex manifold of dimension 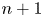$n+1$. Our motivating examples for 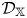$\mathcal {D}_\mathbb {X}$ are coming from (Keller's) Calabi–Yau-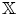$\mathbb {X}$ completions of dg algebras. In the case of smooth projective varieties, the 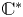$\mathbb {C}^*$-equivariant coherent sheaves on canonical bundles provide the Calabi–Yau-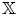$\mathbb {X}$ categories. Another application is that we show perfect derived categories can be realized as cluster-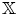$\mathbb {X}$ categories for acyclic quivers.