Hostname: page-component-89b8bd64d-x2lbr Total loading time: 0 Render date: 2026-05-05T15:30:35.899Z Has data issue: false hasContentIssue false
  • English
  • Français

$\tau $-tilting theory

Part of: Representation theory of rings and algebras Abelian categories Modules, bimodules and ideals

Published online by Cambridge University Press:  03 December 2013

Takahide Adachi ,
Osamu Iyama  and
Idun Reiten
Takahide Adachi
Affiliation:
Graduate School of Mathematics, Nagoya University, Chikusa-ku, Nagoya 464-8602, Japan email m09002b@math.nagoya-u.ac.jp
Osamu Iyama
Affiliation:
Graduate School of Mathematics, Nagoya University, Chikusa-ku, Nagoya 464-8602, Japan email iyama@math.nagoya-u.ac.jp
Idun Reiten
Affiliation:
Department of Mathematical Sciences, Norges teknisk-naturvitenskapelige universitet, 7491 Trondheim, Norway email idunr@math.ntnu.no
Get access Rights & Permissions [Opens in a new window]

Abstract

The aim of this paper is to introduce $\tau $-tilting theory, which ‘completes’ (classical) tilting theory from the viewpoint of mutation. It is well known in tilting theory that an almost complete tilting module for any finite-dimensional algebra over a field 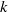$k$ is a direct summand of exactly one or two tilting modules. An important property in cluster-tilting theory is that an almost complete cluster-tilting object in a 2-CY triangulated category is a direct summand of exactly two cluster-tilting objects. Reformulated for path algebras 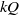$kQ$, this says that an almost complete support tilting module has exactly two complements. We generalize (support) tilting modules to what we call (support) $\tau $-tilting modules, and show that an almost complete support $\tau $-tilting module has exactly two complements for any finite-dimensional algebra. For a finite-dimensional 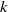$k$-algebra 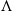$\Lambda $, we establish bijections between functorially finite torsion classes in 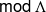$ \mathsf{mod} \hspace{0.167em} \Lambda $, support $\tau $-tilting modules and two-term silting complexes in ${ \mathsf{K} }^{\mathrm{b} } ( \mathsf{proj} \hspace{0.167em} \Lambda )$. Moreover, these objects correspond bijectively to cluster-tilting objects in 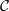$ \mathcal{C} $ if 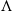$\Lambda $ is a 2-CY tilted algebra associated with a 2-CY triangulated category 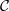$ \mathcal{C} $. As an application, we show that the property of having two complements holds also for two-term silting complexes in 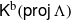${ \mathsf{K} }^{\mathrm{b} } ( \mathsf{proj} \hspace{0.167em} \Lambda )$.

Keywords

τ-tilting moduletilting moduletorsion classsilting complexcluster-tilting objectE-invariant

MSC classification

Secondary: 16D20: Bimodules 16G20: Representations of quivers and partially ordered sets 18E40: Torsion theories, radicals

Information

Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 3 , March 2014 , pp. 415 - 452
Copyright
© The Author(s) 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abe, H., Tilting modules arising from two-term tilting complexes, Preprint (2011), arXiv:1104.0627.Google Scholar
Adachi, T., $\tau $-tilting modules over Nakayama algebras, Preprint (2013), arXiv:1309.2216.Google Scholar
Aihara, T., Tilting-connected symmetric algebras, Algebr. Represent. Theory 16 (2013), 873–894.Google Scholar
Aihara, T. and Iyama, O., Silting mutation in triangulated categories, J. Lond. Math. Soc. 85 (2012), 633–668.CrossRefGoogle Scholar
Amiot, C., Cluster categories for algebras of global dimension 2 and quiver with potential, Ann. Inst. Fourier 59 (2009), 2525–2590.Google Scholar
Assem, I., Simson, D. and Skowronski, A., Elements of the representation theory of associative algebras, Vol. 65 (Cambridge University Press, Cambridge, 2006).CrossRefGoogle Scholar
Auslander, M., Platzeck, M. I. and Reiten, I., Coxeter functions without diagrams, Trans. Amer. Math. Soc. 250 (1979), 1–12.Google Scholar
Auslander, M. and Reiten, I., Representation theory of Artin algebras III: almost split sequences, Comm. Algebra 3 (1975), 239–294.CrossRefGoogle Scholar
Auslander, M. and Reiten, I., Representation theory of Artin algebras V: methods for computing almost split sequences and irreducible morphisms, Comm. Algebra 5 (1977), 519–554.Google Scholar
Auslander, M. and Reiten, I., Modules determined by their composition factors, Illinois J. Math. 29 (1985), 280–301.Google Scholar
Auslander, M. and Reiten, I., Applications of contravariantly finite subcategories, Adv. Math. 86 (1991), 111–152.Google Scholar
Auslander, M., Reiten, I. and Smalø, S. O., Representation theory of Artin algebras, Cambridge Studies in Advanced Mathematics, vol. 36 (Cambridge University Press, Cambridge, 1995).Google Scholar
Auslander, M. and Smalø, S. O., Almost split sequences in subcategories, J. Algebra 69 (1981), 426–454. Addendum: J. Algebra 71 (1981), 592–594.Google Scholar
Bernstein, I. N., Gelfand, I. M. and Ponomarev, V. A., Coxeter functors and Gabriel’s theorem, Russian Math. Surveys 28 (1973), 17–32.Google Scholar
Bongartz, K., Tilted algebras, in Proc. ICRA III (Puebla 1980), Lecture Notes in Mathematics, vol. 903 (Springer, New York, 1981), 26–38.Google Scholar
Brenner, S. and Butler, M. C. R., Generalization of the Bernstein–Gelfand–Ponomarev reflection functors, Lecture Notes in Mathematics, vol. 839 (Springer, New York, 1980), 103–169.Google Scholar
Buan, A., Iyama, O., Reiten, I. and Smith, D., Mutation of cluster-tilting objects and potentials, Amer. J. Math. 133 (2011), 835–887.CrossRefGoogle Scholar
Buan, A. B., Marsh, R., Reineke, M., Reiten, I. and Todorov, G., Tilting theory and cluster combinatorics, Adv. Math. 204 (2006), 572–618.Google Scholar
Buan, A. B., Marsh, R. and Reiten, I., Denominators of cluster variables, J. Lond. Math. Soc. (2) 79 (2006), 589–611.Google Scholar
Buan, A. B., Marsh, R. and Reiten, I., Cluster-tilted algebras, Trans. Amer. Math. Soc. 359 (2007), 323–332.Google Scholar
Buan, A. B., Marsh, R., Reiten, I. and Todorov, G., Clusters and seeds in acyclic cluster algebras, Proc. Amer. Math. Soc. 135 (2007), 3049–3060; with an appendix coauthored in addition by P. Caldero and B. Keller.Google Scholar
Buan, A. B., Reiten, I. and Thomas, H., Three kinds of mutation, J. Algebra 339 (2011), 97–113.Google Scholar
Caldero, P. and Keller, B., From triangulated categories to cluster algebras II, Ann. Sci Éc. Norm. Supér. (4) 39 (2006), 983–1009.Google Scholar
Cerulli Irelli, G., Labardini-Fragoso, D. and Schröer, J., Caldero–Chapoton algebras, Trans. Amer. Math. Soc., to appear, arXiv:1208.3310.Google Scholar
Dehy, R. and Keller, B., On the combinatorics of rigid objects in 2-Calabi–Yau categories, Int. Math. Res. Not. IMRN (2008), Art. ID rnn029.Google Scholar
Derksen, H. and Fei, J., General presentations of algebras, Preprint (2009), arXiv:0911.4913.Google Scholar
Derksen, H., Weyman, J. and Zelevinsky, A., Quivers with potentials and their representations II: applications to cluster algebras, J. Amer. Math. Soc. 23 (2010), 749–790.Google Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras IV: coefficients, Compositio Math. 143 (2007), 112–164.Google Scholar
Fu, C. and Liu, P., Lifting to cluster-tilting objects in 2-Calabi–Yau triangulated categories, Comm. Algebra 37 (2009), 2410–2418.Google Scholar
Happel, D., Triangulated categories in the representation theory of finite-dimensional algebras, London Mathematical Society Lecture Note Series, vol. 119 (Cambridge University Press, Cambridge, 1988).Google Scholar
Happel, D. and Ringel, C. M., Tilted algebras, Trans. Amer. Math. Soc. 274 (1982), 399–443.Google Scholar
Happel, D. and Unger, L., Almost complete tilting modules, Proc. Amer. Math. Soc. 107 (1989), 603–610.Google Scholar
Happel, D. and Unger, L., On a partial order of tilting modules, Algebr. Represent. Theory 8 (2005), 147–156.Google Scholar
Hoshino, M., Tilting modules and torsion theories, Bull. Lond. Math. Soc. 14 (1982), 334–336.Google Scholar
Hoshino, M., Kato, Y. and Miyachi, J., On $t$-structures and torsion theories induced by compact objects, J. Pure Appl. Algebra 167 (2002), 15–35.Google Scholar
Ingalls, C. and Thomas, H., Noncrossing partitions and representations of quivers, Compositio Math. 145 (2009), 1533–1562.Google Scholar
Iyama, O. and Yoshino, Y., Mutations in triangulated categories and rigid Cohen–Macaulay modules, Invent. Math. 172 (2008), 117–168.Google Scholar
Jasso, G., Reduction of $\tau $-tilting modules and torsion pairs, Preprint (2013), arXiv:1302.2709.Google Scholar
Keller, B. and Reiten, I., Cluster-tilted algebras are Gorenstein and stably Calabi–Yau, Adv. Math. 211 (2007), 123–151.Google Scholar
Keller, B. and Vossieck, D., Aisles in derived categories, in Deuxieme Contact Franco-Belge en Algebre (Faulx-les-Thombes, 1987), Bull. Soc. Math. Belg. 40 (1988), 239–253.Google Scholar
König, S. and Yang, D., Silting objects, simple-minded collections, $t$-structures and co- $t$-structures for finite-dimensional algebras, Preprint (2012), arXiv:1203.5657.Google Scholar
Miyashita, Y., Tilting modules of finite projective dimension, Math. Z. 193 (1986), 113–146.Google Scholar
Mizuno, Y., Classifying $\tau $-tilting modules over preprojective algebras of Dynkin type, Preprint (2013), arXiv:1304.0667.Google Scholar
Palu, Y., Cluster characters for 2-Calabi–Yau triangulated categories, Ann. Inst. Fourier (Grenoble) 58 (2008), 2221–2248.CrossRefGoogle Scholar
Riedtmann, C. and Schofield, A., On a simplicial complex associated with tilting modules, Comment. Math. Helv. 66 (1991), 70–78.Google Scholar
Rickard, J., Morita theory for derived categories, J. Lond. Math. Soc. (2) 39 (1989), 436–456.CrossRefGoogle Scholar
Ringel, C. M., Some remarks concerning tilting modules and tilted algebras. Origin. Relevance. Future, in Handbook of tilting theory, London Mathematical Society Lecture Note Series, vol. 332 (Cambridge University Press, 2007), 49–104.Google Scholar
Skowronski, A., Regular Auslander–Reiten components containing directing modules, Proc. Amer. Math. Soc. 120 (1994), 19–26.Google Scholar
Smalø, S. O., Torsion theory and tilting modules, Bull. Lond. Math. Soc. 16 (1984), 518–522.Google Scholar
Smith, D., On tilting modules over cluster-tilted algebras, Illinois J. Math. 52 (2008), 1223–1247.Google Scholar
Unger, L., Schur modules over wild, finite-dimensional path algebras with three simple modules, J. Pure Appl. Algebra 64 (1990), 205–222.Google Scholar
Zhang, X., $\tau $-rigid modules for algebras with radical square zero, Preprint (2012), arXiv:1211.5622.Google Scholar
Zhou, Y. and Zhu, B., Maximal rigid subcategories in 2-Calabi–Yau triangulated categories, J. Algebra 348 (2011), 49–60.Google Scholar