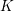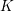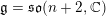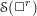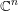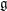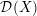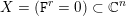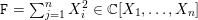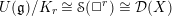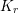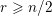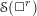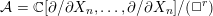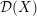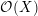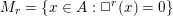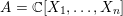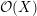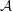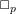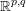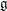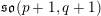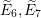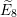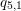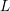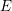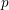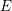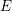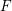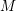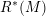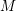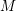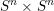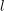In 2005, Knutson–Vakil conjectured a puzzle rule for equivariant K$K$-theory of Grassmannians. We resolve this conjecture. After giving a correction, we establish a modified rule by combinatorially connecting it to the authors’ recently proved tableau rule for the same Schubert calculus problem.

We study the interplay between the minimal representations of the orthogonal Lie algebra 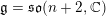\mathfrak{g}=\mathfrak{so}(n+2,\mathbb{C})$\mathfrak{g}=\mathfrak{so}(n+2,\mathbb{C})$ and the algebra of symmetries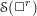\mathscr{S}(\Box ^{r})$\mathscr{S}(\Box ^{r})$ of powers of the Laplacian \Box$\Box$ on 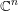\mathbb{C}^{n}$\mathbb{C}^{n}$. The connection is made through the construction of a highest-weight representation of 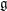\mathfrak{g}$\mathfrak{g}$ via the ring of differential operators 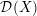{\mathcal{D}}(X)${\mathcal{D}}(X)$ on the singular scheme 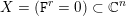X=(\mathtt{F}^{r}=0)\subset \mathbb{C}^{n}$X=(\mathtt{F}^{r}=0)\subset \mathbb{C}^{n}$, for 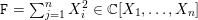\mathtt{F}=\sum _{j=1}^{n}X_{i}^{2}\in \mathbb{C}[X_{1},\ldots ,X_{n}]$\mathtt{F}=\sum _{j=1}^{n}X_{i}^{2}\in \mathbb{C}[X_{1},\ldots ,X_{n}]$. In particular, we prove that 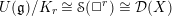U(\mathfrak{g})/K_{r}\cong \mathscr{S}(\Box ^{r})\cong {\mathcal{D}}(X)$U(\mathfrak{g})/K_{r}\cong \mathscr{S}(\Box ^{r})\cong {\mathcal{D}}(X)$ for a certain primitive ideal 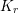K_{r}$K_{r}$. Interestingly, if (and only if) n$n$ is even with 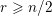r\geqslant n/2$r\geqslant n/2$, then both 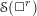\mathscr{S}(\Box ^{r})$\mathscr{S}(\Box ^{r})$ and its natural module 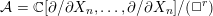{\mathcal{A}}=\mathbb{C}[\unicode[STIX]{x2202}/\unicode[STIX]{x2202}X_{n},\ldots ,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}X_{n}]/(\Box ^{r})${\mathcal{A}}=\mathbb{C}[\unicode[STIX]{x2202}/\unicode[STIX]{x2202}X_{n},\ldots ,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}X_{n}]/(\Box ^{r})$ have a finite-dimensional factor. The same holds for the 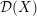{\mathcal{D}}(X)${\mathcal{D}}(X)$-module 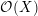{\mathcal{O}}(X)${\mathcal{O}}(X)$. We also study higher-dimensional analogues 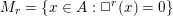M_{r}=\{x\in A:\Box ^{r}(x)=0\}$M_{r}=\{x\in A:\Box ^{r}(x)=0\}$ of the module of harmonic elements in 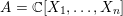A=\mathbb{C}[X_{1},\ldots ,X_{n}]$A=\mathbb{C}[X_{1},\ldots ,X_{n}]$ and of the space of ‘harmonic densities’. In both cases we obtain a minimal 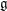\mathfrak{g}$\mathfrak{g}$-representation that is closely related to the 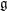\mathfrak{g}$\mathfrak{g}$-modules 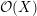{\mathcal{O}}(X)${\mathcal{O}}(X)$ and 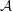{\mathcal{A}}${\mathcal{A}}$. Essentially all these results have real analogues, with the Laplacian replaced by the d’Alembertian 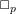\Box _{p}$\Box _{p}$ on the pseudo-Euclidean space 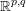\mathbb{R}^{p,q}$\mathbb{R}^{p,q}$ and with 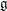\mathfrak{g}$\mathfrak{g}$ replaced by the real Lie algebra 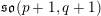\mathfrak{so}(p+1,q+1)$\mathfrak{so}(p+1,q+1)$.

A log symplectic manifold is a complex manifold equipped with a complex symplectic form that has simple poles on a hypersurface. The possible singularities of such a hypersurface are heavily constrained. We introduce the notion of an elliptic point of a log symplectic structure, which is a singular point at which a natural transversality condition involving the modular vector field is satisfied, and we prove a local normal form for such points that involves the simple elliptic surface singularities \widetilde{E}_{6},\widetilde{E}_{7}$\widetilde{E}_{6},\widetilde{E}_{7}$ and \widetilde{E}_{8}$\widetilde{E}_{8}$. Our main application is to the classification of Poisson brackets on Fano fourfolds. For example, we show that Feigin and Odesskii’s Poisson structures of type q_{5,1}$q_{5,1}$ are the only log symplectic structures on projective four-space whose singular points are all elliptic.

We introduce coarse flow spaces for relatively hyperbolic groups and use them to verify a regularity condition for the action of relatively hyperbolic groups on their boundaries. As an application the Farrell–Jones conjecture for relatively hyperbolic groups can be reduced to the peripheral subgroups (up to index-2 overgroups in the L$L$-theory case).

We prove that the p$p$-completed Brown–Peterson spectrum is a retract of a product of Morava E$E$-theory spectra. As a consequence, we generalize results of Kashiwabara and of Ravenel, Wilson and Yagita from spaces to spectra and deduce that the notion of a good group is determined by Brown–Peterson cohomology. Furthermore, we show that rational factorizations of the Morava E$E$-theory of certain finite groups hold integrally up to bounded torsion with height-independent exponent, thereby lifting these factorizations to the rationalized Brown–Peterson cohomology of such groups.

We show that any Kawamata log terminal del Pezzo surface over an algebraically closed field of large characteristic is globally F$F$-regular or it admits a log resolution which lifts to characteristic zero. As a consequence, we prove the Kawamata–Viehweg vanishing theorem for klt del Pezzo surfaces of large characteristic.

We study tautological rings for high-dimensional manifolds, that is, for each smooth manifold M$M$ the ring R^{\ast }(M)$R^{\ast }(M)$ of those characteristic classes of smooth fibre bundles with fibre M$M$ which is generated by generalised Miller–Morita–Mumford classes. We completely describe these rings modulo nilpotent elements, when M$M$ is a connected sum of copies of S^{n}\times S^{n}$S^{n}\times S^{n}$ for n$n$ odd.

We prove analogs of the Bezout and the Bernstein–Kushnirenko–Khovanskii theorems for systems of algebraic differential conditions over differentially closed fields. Namely, given a system of algebraic conditions on the first l$l$ derivatives of an n$n$-tuple of functions, which admits finitely many solutions, we show that the number of solutions is bounded by an appropriate constant (depending singly-exponentially on n$n$ and l$l$) times the volume of the Newton polytope of the set of conditions. This improves a doubly-exponential estimate due to Hrushovski and Pillay. We illustrate the application of our estimates in two diophantine contexts: to counting transcendental lattice points on algebraic subvarieties of semi-abelian varieties, following Hrushovski and Pillay; and to counting the number of intersections between isogeny classes of elliptic curves and algebraic varieties, following Freitag and Scanlon. In both cases we obtain bounds which are singly-exponential (improving the known doubly-exponential bounds) and which exhibit the natural asymptotic growth with respect to the degrees of the equations involved.