Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T17:35:55.609Z Has data issue: false hasContentIssue false
  • English
  • Français

ESTIMATION FOR A NONSTATIONARY SEMI-STRONG GARCH(1,1) MODEL WITH HEAVY-TAILED ERRORS

Published online by Cambridge University Press:  19 June 2009

Oliver Linton ,
Jiazhu Pan  and
Hui Wang
Oliver Linton*
Affiliation:
London School of Economics
Jiazhu Pan*
Affiliation:
University of Strathclyde and Peking University
Hui Wang
Affiliation:
Central University of Finance and Economics, China
*
†Oliver Linton, Department of Economics, London School of Economics, Houghton Street, London, WC2A 2AE, U.K.; e-mail: o.linton@lse.ac.uk.
*Address correspondence to Jiazhu Pan, Department of Mathematics and Statistics, University of Strathclyde, Richmond Street, Glasgow, G1 1XH, U.K.; e-mail: jiazhu.pan@strath.ac.uk.
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper studies the estimation of a semi-strong GARCH(1,1) model when it does not have a stationary solution, where semi-strong means that we do not require the errors to be independent over time. We establish necessary and sufficient conditions for a semi-strong GARCH(1,1) process to have a unique stationary solution. For the nonstationary semi-strong GARCH(1,1) model, we prove that a local minimizer of the least absolute deviations (LAD) criterion converges at the rate 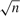to a normal distribution under very mild moment conditions for the errors. Furthermore, when the distributions of the errors are in the domain of attraction of a stable law with the exponent κ ∈ (1, 2), it is shown that the asymptotic distribution of the Gaussian quasi-maximum likelihood estimator (QMLE) is non-Gaussian but is some stable law with the exponent κ ∈ (0, 2). The asymptotic distribution is difficult to estimate using standard parametric methods. Therefore, we propose a percentile-t subsampling bootstrap method to do inference when the errors are independent and identically distributed, as in Hall and Yao (2003). Our result implies that the least absolute deviations estimator (LADE) is always asymptotically normal regardless of whether there exists a stationary solution or not, even when the errors are heavy-tailed. So the LADE is more appealing when the errors are heavy-tailed. Numerical results lend further support to our theoretical results.

Type
ARTICLES
Information
Econometric Theory , Volume 26 , Issue 1 , February 2010 , pp. 1 - 28
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Berkes, I., Horváth, L., & Kokoszka, P. (2003) GARCH processes: Structure and estimation. Bernoulli 9(2), 201–227.CrossRefGoogle Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley.Google Scholar
Bollerslev, T. (1986) Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31, 307–327.Google Scholar
Bougerol, P. & Picard, N. (1992) Stationarity of GARCH process and of some nonnegative time series. Journal of Econometrics 52, 115–127.CrossRefGoogle Scholar
Breiman, L. (1965) On some limit theorems similar to the arc-sin law. Teor. Verojatnost. i Primenen 10, 351–360.Google Scholar
Brown, B.M. (1971) Martingale central limit theorems. Annals of Mathematical Statistics 42, 59–66.CrossRefGoogle Scholar
Davis, R.A. & Dunsmuir, W.T.M. (1997) Least absolute deviation estimation for regression with ARMA errors. Journal of Theoretical Probability 10, 481–497.Google Scholar
Davis, R.A. & Mikosch, T. (1998) The sample autocorrelations of heavy-tailed processes with applications to ARCH. Annals of Statistics 26, 2049–2080.CrossRefGoogle Scholar
de la Pena, V.H., Ibragimov, R., & Sharakhmetov, S. (2003) On extremal distributions and sharp Lp-bounds for sums of multilinear forms. Annals of Probability 31, 630–675.Google Scholar
Drost, F.C. & Nijman, T.E. (1993) Temporal aggregation of GARCH processes. Econometrica 61, 909–927.CrossRefGoogle Scholar
Embrechts, P., Klüppelberg, C., & Mikosch, T. (1997) Modelling Extremal Events for Insurance and Finance, 1st ed.Springer.Google Scholar
Engle, R.F. (1982) Autoregressive conditional heteroskedasticity with estimates of the variance of U.K. inflation. Econometrica 50, 987–1007.Google Scholar
Engle, R.F. & Rangel, J.G. (2005) The Spline GARCH Model for Unconditional Volatility and Its Global Macroeconomic Causes. Working paper, NYU Stern School.CrossRefGoogle Scholar
Feller, W. (1971) An Introduction to Probability Theory and Its Applications, vol. II. Wiley.Google Scholar
Hall, P. & Yao, Q. (2003) Inference in ARCH and GARCH models with heavy-tailed errors. Econometrica 71, 285–317.CrossRefGoogle Scholar
Ibragimov, R. (2004) On the Robustness of Economic Models to Heavy-Tailedness Assumptions. Manuscript, Yale University.Google Scholar
Jensen, S.T. & Rahbek, A. (2004a) Asymptotic normality of the QMLE estimator of ARCH in the nonstationary case. Econometrica 72, 641–646.CrossRefGoogle Scholar
Jensen, S.T. & Rahbek, A. (2004b) Asymptotic inference for nonstationary GARCH. Econometric Theory 20, 1203–1226.Google Scholar
Lee, S.-W. & Hansen, B.E. (1994) Asymptotic theory for the GARCH (1,1) quasi-maximum likelihood estimator. Econometric Theory 10, 29–52.CrossRefGoogle Scholar
Leadbetter, M.R., Lindgren, G., & Rootzén, H. (1983) Extremes and Related Properties of Random Sequences and Processes. Springer.Google Scholar
Lumsdaine, R.L. (1996) Consistency and asymptotic normality of the quasi-maximum likelihood estimator in IGARCH(1,1) and covariance stationary GARCH (1,1) models. Econometrica 64, 575–596.Google Scholar
Mandelbrot, B. (1963) The variation of certain speculative prices. Journal of Business 36, 394–419.Google Scholar
Mikosch, T. & Stărică, C. (2000) Limit theory for the sample autocorrelations and extremes of a GARCH(1, 1) process. Annals of Statistics 28, 1427–1451.CrossRefGoogle Scholar
Mikosch, T. & Straumann, D. (2002) Whittle estimation in a heavy-tailed GARCH(1,1) model. Stochastic Processes and Their Applications 100, 187–222.Google Scholar
Mittnik, S. & Rachev, S.T. (2000) Stable Paretian Models in Finance. Wiley.Google Scholar
Mittnik, S., Rachev, S.T., & Paolella, M.S. (1998) Stable Paretian modelling in finance: Some empirical and theoretical aspects. In Adler, R.J., Feldman, R.E., and Taqqu, M.S. (eds.), A Practical Guide to Heavy Tails, pp. 79–110. Birkhäuser.Google Scholar
Nelson, D.B. (1990) Stationarity and persistence in the GARCH(1,1) model. Econometric Theory 6, 318–334.Google Scholar
Nze, P.A. & Doukhan, P. (2004) Weak dependence: Models and applications to econometrics. Econometric Theory 20, 995–1045.CrossRefGoogle Scholar
Pan, J., Wang, H., & Tong, H. (2008) Estimation and tests for power-transformed and threshold GARCH models. Journal of Econometrics 142, 352–378.CrossRefGoogle ScholarPubMed
Pan, J., Wang, H., & Yao, Q. (2007) Weighted least absolute deviations estimation for ARMA models with infinite variance. Econometric Theory 23, 852–879.Google Scholar
Peng, L. & Yao, Q. (2003) Least absolute deviation estimation for ARCH and GARCH models. Biometrika 90, 967–975.CrossRefGoogle Scholar
Polzehl, J. & Spokoiny, V. (2004) Varying Coefficient GARCH Versus Local Constant Volatility Modeling. Comparison of the Predictive Power. No. 977, Weierstrass Institute.Google Scholar
Resnick, S.I. (1987) Extreme Values, Regular Variation, Point Processes. Springer.CrossRefGoogle Scholar
Rydberg, T. (2000) Realistic statistical modelling of financial data. International Statistical Review 68, 233–258.CrossRefGoogle Scholar
Shephard, N. (1996) Statistical aspects of ARCH and stochastic volatility. In Cox, D.R., Hinkley, D.V., and Barndorff-Nielsen, O.E. (eds.), Time Series Models in Econometrics, Finance and Other Fields, pp. 1–67. Chapman and Hall.Google Scholar
Straumann, D. (2005) Estimation in Conditionally Heteroskedastic Time Series Models. Lecture notes in Statistics 181. Springer.Google Scholar
Weiss, A. (1986) Asymptotic theory for ARCH models: Estimation and testing. Econometric Theory 2, 107–131.Google Scholar