Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-27T03:59:23.772Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON MINIMAX REGRET RULES WITH MULTIPLE TREATMENTS IN FINITE SAMPLES

Published online by Cambridge University Press:  27 February 2025

Haoning Chen  and
Patrik Guggenberger Open the ORCID record for Patrik Guggenberger [Opens in a new window]
Haoning Chen
Affiliation:
Pennsylvania State University
Patrik Guggenberger*
Affiliation:
Pennsylvania State University
*
Address correspondence to Patrik Guggenberger, Department of Economics, Pennsylvania State University, State College, PA, USA; e-mail: pxg27@psu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We study minimax regret treatment rules under matched treatment assignment in a setup where a policymaker, informed by a sample of size N, needs to decide between T different treatments for a 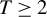$T\geq 2$. Randomized rules are allowed for. We show that the generalization of the minimax regret rule derived in Schlag (2006, ELEVEN—Tests needed for a recommendation, EUI working paper) and Stoye (2009, Journal of Econometrics 151, 70–81) for the case $T=2$ is minimax regret for general finite 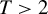$T>2$ and also that the proof structure via the Nash equilibrium and the “coarsening” approaches generalizes as well. We also show by example, that in the case of random assignment the generalization of the minimax rule in Stoye (2009, Journal of Econometrics 151, 70–81) to the case 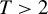$T>2$ is not necessarily minimax regret and derive minimax regret rules for a few small sample cases, e.g., for 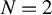$N=2$ when 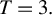$T=3.$

In the case where a covariate x is included, it is shown that a minimax regret rule is obtained by using minimax regret rules in the “conditional-on-x” problem if the latter are obtained as Nash equilibria.

Type
ARTICLES
Information
Econometric Theory , First View , pp. 1 - 27
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

We would like to thank the Editor Peter Phillips, the Co-Editor Matias Cattaneo, and three referees for very helpful comments and suggestions. We thank Kei Hirano, Jiaqi Huang, Matt Masten, Chen Qiu, Karl Schlag, Joerg Stoye, and Aleksey Tetenov for comments and helpful information about this research agenda. We thank seminar participants at Brisbane, Cambridge, Colorado Boulder, Exeter, Frankfurt, Heidelberg, Konstanz, LMU, Macquarie, Manchester, NTU, NUS, McGill, Oxford, Regensburg, SMU, SUNY Stony Brook, UC Davis, UCL, UC Riverside, University of Sydney, and UNSW, and participants at the ‘Advances in Econometrics Conference and Festschrift in Honor of Joon Y. Park’ in 2023, the ‘New York Camp Econometrics conference’, and the Rochester conference in Econometrics in 2024.

References

REFERENCES

Aradillas Fernández, A., Blanchet, J., Montiel Olea, J. L., Qiu, C., Stoye, J., & Tan, L. (2024). $\epsilon$ -Minimax solutions of statistical decision problems. Unpublished working paper. Cornell University.Google Scholar
Aradillas Fernández, A., Olea, J. L. M., Qiu, C., Stoye, J., & Tinda, S. (2024). Robust Bayes treatment choice with partial identification. Preprint, arXiv:2408.11621.Google Scholar
Bahadur, R. (1950). On a problem in the theory of k populations. The Annals of Mathematical Statistics , 21, 362–375.CrossRefGoogle Scholar
Bahadur, R., & Goodman, L. (1952). Impartial decision rules and sufficient statistics. The Annals of Mathematical Statistics , 23, 553–562.CrossRefGoogle Scholar
Berger, J. (1985). Statistical decision theory and Bayesian analysis (2nd ed.). Springer-Verlag.CrossRefGoogle Scholar
Chamberlain, G. (2000). Econometric applications of maxmin expected utility. Journal of Applied Econometrics , 15, 625–644.CrossRefGoogle Scholar
Christensen, T., Moon, R., & Schorfheide, F. (2023). Optimal discrete decisions when payoffs are partially identified. Unpublished working paper.Google Scholar
Cucconi, O. (1968). Contributi all’analisi sequenziale nel controllo di accettazione per variabili. Atti dell’ Associazione Italiana per il Controllo della Qualità , 6, 171–186.Google Scholar
Guggenberger, P., & Huang, J. (2024). On the numerical approximation to minimax regret rules via fictitious play. Unpublished working paper. Pennsylvania State University.Google Scholar
Guggenberger, P., Mehta, N., & Pavlov, N. (2024). Minimax regret treatment rules with finite samples when a quantile is the object of interest. Unpublished working paper. Pennsylvania State University.Google Scholar
Gupta, S., & Hande, S. (1992). On some nonparametric selection procedures. In Saleh, A. K. Md. E. (Ed.), Nonparametric statistics and related topics . Elsevier.Google Scholar
Hirano, K., & Porter, J. (2009). Asymptotics for statistical treatment rules. Econometrica , 77, 1683–1701.Google Scholar
Kitagawa, T., & Tetenov, A. (2018), Who should be treated? Empirical welfare maximization methods for treatment choice. Econometrica , 86, 591–616.CrossRefGoogle Scholar
Kitagawa, T., Lee, S., & Qiu, C. (2024). Treatment choice with nonlinear regret. Preprint, arXiv:2205.08586.Google Scholar
Lehmann, E. (1966). On a theorem of Bahadur and Goodman. The Annals of Mathematical Statistics , 37, 1–6.CrossRefGoogle Scholar
Manski, C. (2004). Statistical treatment rules for heterogeneous populations. Econometrica , 72,221–246.CrossRefGoogle Scholar
Manski, C., & Tetenov, A. (2007). Admissible treatment rules for a risk-averse planner with experimental data on an innovation. Journal of Statistical Planning and Inference , 137, 1998–2010.CrossRefGoogle Scholar
Manski, C., & Tetenov, A. (2023). Statistical decision theory respecting stochastic dominance. The Japanese Economic Review , 74, 447–469.CrossRefGoogle Scholar
Masten, M. (2023). Minimax-regret treatment rules with many treatments. The Japanese Economic Review , 74, 501–537.CrossRefGoogle Scholar
Montiel Olea, J. L., Qiu, C., & Stoye, J. (2023), Decision theory for treatment choice with partial identification. Preprint, arXiv:2312.17623.Google Scholar
Robinson, J. (1951). An iterative method of solving a game. Annals of Mathematics , 54(2), 296–301.CrossRefGoogle Scholar
Savage, L. (1954), The foundations of statistics . Wiley.Google Scholar
Schlag, K. (2003). How to minimize maximum regret under repeated decision-making. EUI working paper.Google Scholar
Schlag, K. (2006). ELEVEN—Tests needed for a recommendation. EUI working paper. ECO No. 2006/2.Google Scholar
Song, K. (2014). Point decisions for interval-identified parameters. Econometric Theory , 30, 334–356.CrossRefGoogle Scholar
Stein, C. (1956). Inadmissibility of the usual estimator for the mean of a multivariate normal distribution. In Proceeding of the third Berkeley symposium on mathematical statistics and probability , 1, (pp. 197–206).CrossRefGoogle Scholar
Stoye, J. (2007). Minimax regret treatment choice with incomplete data and many treatments. Econometric Theory , 23(1), 190–199.CrossRefGoogle Scholar
Stoye, J. (2009). Minimax regret treatment choice with finite samples. Journal of Econometrics , 151, 70–81.CrossRefGoogle Scholar
Stoye, J. (2012). Minimax regret treatment choice with covariates or with limited validity of experiments. Journal of Econometrics , 166, 138–156.CrossRefGoogle Scholar
Tetenov, A. (2012). Statistical treatment choice based on asymmetric minimax regret criteria. Journal of Econometrics , 166, 157–165.CrossRefGoogle Scholar
Wald, A. (1950). Statistical decision functions , Wiley.Google Scholar
Yata, K. (2023). Optimal decision rules under partial identification. Preprint, arXiv:2111.04926.Google Scholar