Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T14:45:20.963Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE CONVERGENCE RATE OF POTENTIALS OF BRENIER MAPS

Published online by Cambridge University Press:  15 February 2021

Florian F. Gunsilius
Florian F. Gunsilius*
Affiliation:
University of Michigan
*
Address correspondence to Florian F. Gunsilius, University of Michigan, Ann Arbor, MI 48109, USA; e-mail: ffg@umich.edu.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The theory of optimal transportation has experienced a sharp increase in interest in many areas of economic research such as optimal matching theory and econometric identification. A particularly valuable tool, due to its convenient representation as the gradient of a convex function, has been the Brenier map: the matching obtained as the optimizer of the Monge–Kantorovich optimal transportation problem with the euclidean distance as the cost function. Despite its popularity, the statistical properties of the Brenier map have yet to be fully established, which impedes its practical use for estimation and inference. This article takes a first step in this direction by deriving a convergence rate for the simple plug-in estimator of the potential of the Brenier map via the semi-dual Monge–Kantorovich problem. Relying on classical results for the convergence of smoothed empirical processes, it is shown that this plug-in estimator converges in standard deviation to its population counterpart under the minimax rate of convergence of kernel density estimators if one of the probability measures satisfies the Poincaré inequality. Under a normalization of the potential, the result extends to convergence in the 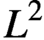$L^2$ norm, while the Poincaré inequality is automatically satisfied. The main mathematical contribution of this article is an analysis of the second variation of the semi-dual Monge–Kantorovich problem, which is of independent interest.

Type
MISCELLANEA
Information
Econometric Theory , Volume 38 , Issue 2 , April 2022 , pp. 381 - 417
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Footnotes

I would like to thank the Editor Peter Phillips, the Co-Editor Ivan Fernandez-Val, and especially two referees for their effort and important comments which helped me improve the paper substantially. I would also like to thank Susanne Schennach for helpful feedback. I wrote the initial version of this paper while a graduate student in the Economics Department at Brown University. All errors are mine.

References

REFERENCES

Aleksandrov, A. (1939) Almost everywhere existence of the second differential of a convex function and some properties of convex surfaces connected with it. Leningrad State University Annals [Uchenye Zapiski] 37, 3–35.Google Scholar
Aliprantis, C.D. & Border, K. (2006) Infinite Dimensional Analysis: A Hitchhiker’s Guide. Springer Science & Business Media.Google Scholar
Athey, S. & Imbens, G.W. (2006) Identification and inference in nonlinear difference-in-differences models. Econometrica 74(2), 431–497.CrossRefGoogle Scholar
Attouch, H. & Wets, R.J.B. (1986) Isometries for the Legendre–Fenchel transform. Transactions of the American Mathematical Society 296(1), 33–60.CrossRefGoogle Scholar
Bačák, M. & Borwein, J.M. (2011) On difference convexity of locally Lipschitz functions. Optimization 60(8–9), 961–978.CrossRefGoogle Scholar
Bakry, D., Barthe, F., Cattiaux, P., & Guillin, A. (2008) A simple proof of the Poincaré inequality for a large class of probability measures. Electronic Communications in Probability 13, 60–66.CrossRefGoogle Scholar
Benamou, J.D. & Brenier, Y. (2000) A computational fluid mechanics solution to the Monge–Kantorovich mass transfer problem. Numerische Mathematik 84(3), 375–393.CrossRefGoogle Scholar
Benamou, J.D., Froese, B.D., & Oberman, A.M. (2014) Numerical solution of the optimal transportation problem using the Monge–Ampère equation. Journal of Computational Physics 260, 107–126.CrossRefGoogle Scholar
Brenier, Y. (1991) Polar factorization and monotone rearrangement of vector-valued functions. Communications on Pure and Applied Mathematics 44(4), 375–417.CrossRefGoogle Scholar
Caffarelli, L.A. (1990). Interior ${W}^{2,p}$ estimates for solutions of the Monge–Ampère equation. Annals of Mathematics 131(1), 135–150.CrossRefGoogle Scholar
Carlier, G., Chernozhukov, V., & Galichon, A. (2016) Vector quantile regression: An optimal transport approach. Annals of Statistics 44(3), 1165–1192.CrossRefGoogle Scholar
Chartrand, R., Wohlberg, B., Vixie, K., & Bollt, E. (2009) A gradient descent solution to the Monge–Kantorovich problem. Applied Mathematical Sciences 3(22), 1071–1080.Google Scholar
Chernozhukov, V., Galichon, A., Hallin, M., & Henry, M. (2017) Monge–Kantorovich depth, quantiles, ranks and signs. Annals of Statistics 45(1), 223–256.CrossRefGoogle Scholar
Chernozhukov, V., Galichon, A., Henry, M., & Pass, B. (2019) Single Market Nonparametric Identification of Multi-Attribute Hedonic Equilibrium Models. Cemmap Working paper, CWP 27/19.Google Scholar
Chiappori, P.A., McCann, R.J., & Nesheim, L.P. (2010) Hedonic price equilibria, stable matching, and optimal transport: Equivalence, topology, and uniqueness Economic Theory 42(2), 317–354.CrossRefGoogle Scholar
Clarke, F.H. (1975) Generalized gradients and applications. Transactions of the American Mathematical Society 205, 247–262.CrossRefGoogle Scholar
Cuturi, M. (2013) Sinkhorn distances: Lightspeed computation of optimal transport. In Advances in Neural Information Processing Systems. Edited by Burges, C. J. C., Bottou, L., Welling, M., Ghahramani, Z. and Weinberger, K. Q., 26, 2292–2300. Curran Associates, Inc. Google Scholar
Dalalyan, A. & Reiß, M. (2007) Asymptotic statistical equivalence for ergodic diffusions: The multidimensional case. Probability Theory and Related Fields 137(1–2), 25–47.CrossRefGoogle Scholar
de Philippis, G. & Figalli, A. (2013) Second order stability for the Monge–Ampère equation and strong Sobolev convergence of optimal transport maps. Analysis & PDE 6(4), 993–1000.CrossRefGoogle Scholar
del Barrio, E. & Loubes, J.-M. (2019) Central limit theorems for empirical transportation cost in general dimension. The Annals of Probability 47(2), 926–951.CrossRefGoogle Scholar
Ekeland, I., Galichon, A., & Henry, M. (2010) Optimal transportation and the falsifiability of incompletely specified economic models. Economic Theory 42(2), 355–374.CrossRefGoogle Scholar
Folland, G.B. (2013) Real Analysis: Modern Techniques and Their Applications. John Wiley & Sons.Google Scholar
Galichon, A. (2016) Optimal Transport Methods in Economics. Princeton University Press.CrossRefGoogle Scholar
Galichon, A. (2017) A survey of some recent applications of optimal transport methods to econometrics. The Econometrics Journal 20(2), C1–C11.CrossRefGoogle Scholar
Gangbo, W. (1994) An elementary proof of the polar factorization of vector-valued functions. Archive for Rational Mechanics and Analysis 128(4), 381–399.CrossRefGoogle Scholar
Gilbarg, D. & Trudinger, N.S. (1998) Elliptic Partial Differential Equations of Second Order. Springer.Google Scholar
Giné, E. & Nickl, R. (2008) Uniform central limit theorems for kernel density estimators. Probability Theory and Related Fields 141(3–4), 333–387.CrossRefGoogle Scholar
Gozlan, N., Roberto, C., & Samson, P.-M. (2015) From dimension free concentration to the Poincaré inequality. Calculus of Variations and Partial Differential Equations 52(3–4), 899–925.CrossRefGoogle Scholar
Griewank, A. & Rabier, P. (1990) On the smoothness of convex envelopes. Transactions of the American Mathematical Society 322(2), 691–709.CrossRefGoogle Scholar
Gunsilius, F.F. & Schennach, S.M. (2019) Independent Nonlinear Component Analysis, Cemmap Working paper, CWP 46/19.Google Scholar
Henry-Labordère, P. (2017) Model-Free Hedging: A Martingale Optimal Transport Viewpoint. CRC Press.CrossRefGoogle Scholar
Hiriart-Urruty, J.B. (1985) Generalized differentiability/duality and optimization for problems dealing with differences of convex functions. In Convexity and Duality in Optimization, pp. 37–70. Springer.CrossRefGoogle Scholar
Hütter, J.C. & Rigollet, P. (2019) Minimax Rates of Estimation for Smooth Optimal Transport Maps. arXiv preprint 1905.05828.Google Scholar
Ibragimov, R. (2009) Copula-based characterizations for higher order Markov processes. Econometric Theory 25(3), 819–846.CrossRefGoogle Scholar
Kirchheim, B. & Kristensen, J. (2001) Differentiability of convex envelopes. Comptes Rendus de l’Académie des Sciences-Series I-Mathematics 333(8), 725–728.CrossRefGoogle Scholar
Ledoux, M. (2001) The Concentration of Measure Phenomenon. American Mathematical Society.Google Scholar
Lee, Y.J. (2018) Sieve Estimation of Optimal Transport with Applications to Multivariate Quantiles and Matching. UCL Job market paper.Google Scholar
Lindenlaub, I. (2017) Sorting multidimensional types: Theory and application. The Review of Economic Studies 84(2), 718–789.Google Scholar
Lindsey, M. & Rubinstein, Y.A. (2017) Optimal transport via a Monge–Ampère optimization problem. SIAM Journal on Mathematical Analysis 49(4), 3073–3124.CrossRefGoogle Scholar
Radulović, D. & Wegkamp, M. (2000) Weak convergence of smoothed empirical processes: Beyond Donsker classes. In High Dimensional Probability II, pp. 89–105. Springer.CrossRefGoogle Scholar
Rockafellar, R.T. (1977) Higher derivatives of conjugate convex functions. Journal of Applied Analysis 1(1), 41–43.Google Scholar
Rockafellar, R.T. (1997) Convex Analysis. Princeton University Press.Google Scholar
Rohde, A. & Strauch, C. (2010) Uniform Central Limit Theorems for Multidimensional Diffusions. arXiv preprint 1010.3604.Google Scholar
Rubinstein, Y.A. (2008) Geometric quantization and dynamical constructions on the space of Kähler metrics. PhD thesis, Massachusetts Institute of Technology.Google Scholar
Santambrogio, F. (2015) Optimal Transport for Applied Mathematicians. Progress in Nonlinear Differential Equations and Their Applications, 87. Birkhäuser Basel.CrossRefGoogle Scholar
Seguy, V., Damodaran, B.B., Flamary, R., Courty, N., Rolet, A., & Blondel, M. (2017) Large-Scale Optimal Transport and Mapping Estimation. arXiv preprint 1711.02283.Google Scholar
Sinkhorn, R. (1967) Diagonal equivalence to matrices with prescribed row and column sums. The American Mathematical Monthly 74(4), 402–405.CrossRefGoogle Scholar
Sommerfeld, M. & Munk, A. (2018) Inference for empirical Wasserstein distances on finite spaces. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 80(1), 219–238.CrossRefGoogle Scholar
Stern, A. (2010) Lp Change of Variables Inequalities on Manifolds. arXiv preprint 1004.0401.Google Scholar
Trudinger, N.S. & Wang, X.-J. (2008) The Monge–Ampère equation and its geometric applications. In Handbook of Geometric Analysis, vol. 1, pp. 467–524. International Press.Google Scholar
Tsybakov, A.B. (2008) Introduction to Nonparametric Estimation. Springer Science & Business Media.Google Scholar
van der Vaart, A. (1994) Weak convergence of smoothed empirical processes. Scandinavian Journal of Statistics 21(4), 501–504.Google Scholar
van der Vaart, A. & Wellner, J. (2013) Weak Convergence and Empirical Processes: With Applications to Statistics. Springer Science & Business Media.Google Scholar
Villani, C. (2003) Topics in Optimal Transportation, Graduate Studies in Mathematics, 58. American Mathematical Society.CrossRefGoogle Scholar
Villani, C. (2008) Optimal Transport: Old and New, Grundlehren der Mathematischen Wissenschaften, 338. Springer Science & Business Media.Google Scholar
Yukich, J.E. (1992) Weak convergence of smoothed empirical processes. Scandinavian Journal of Statistics 19, 271–279.Google Scholar
Zeidler, E. (1985) Nonlinear Functional Analysis and Its Applications III: Variational Methods and Optimization. Springer.Google Scholar