Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-21T19:48:06.521Z Has data issue: false hasContentIssue false
  • English
  • Français

SEMI-PARAMETRIC SEASONAL UNIT ROOT TESTS

Published online by Cambridge University Press:  09 April 2017

Tomás del Barrio Castro ,
Paulo M.M. Rodrigues  and
A.M. Robert Taylor
Tomás del Barrio Castro
Affiliation:
University of the Balearic Islands
Paulo M.M. Rodrigues
Affiliation:
Universidade Nova de Lisboa
A.M. Robert Taylor*
Affiliation:
University of Essex
*
*Address correspondence to Robert Taylor, Essex Business School, University of Essex, Wivenhoe Park, Colchester CO4 3SQ, UK; e-mail: rtaylor@essex.ac.uk.
Get access Rights & Permissions [Opens in a new window]

Abstract

We extend the 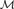${\cal M}$ class of unit root tests introduced by Stock (1999, Cointegration, Causality and Forecasting. A Festschrift in Honour of Clive W.J. Granger. Oxford University Press), Perron and Ng (1996, Review of Economic Studies 63, 435–463) and Ng and Perron (2001, Econometrica 69, 1519–1554) to the seasonal case, thereby developing semi-parametric alternatives to the regression-based augmented seasonal unit root tests of Hylleberg, Engle, Granger, and Yoo (1990, Journal of Econometrics 44, 215–238). The success of this class of unit root tests to deliver good finite sample size control even in the most problematic (near-cancellation) case where the shocks contain a strong negative moving average component is shown to carry over to the seasonal case as is the superior size/power trade-off offered by these tests relative to other available tests.

Type
ARTICLES
Information
Econometric Theory , Volume 34 , Issue 2 , April 2018 , pp. 447 - 476
Copyright
Copyright © Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

We are grateful to the Editor, Peter Phillips, the Co-Editor, Michael Jansson and two anonymous referees for their helpful and constructive comments. Tomás del Barrio Castro acknowledges financial support from projects ECO2011-23934 and ECO2014-58991-C3-3-R.

References

REFERENCES

del Barrio Castro, T., Osborn, D.R., & Taylor, A.M.R. (2016) The performance of lag selection and detrending methods for HEGY seasonal unit root tests. Econometric Reviews 35, 122–168.CrossRefGoogle Scholar
del Barrio Castro, T., Rodrigues, P.M.M., & Taylor, A.M.R. (2015) Semi-Parametric Seasonal Unit Root Tests. Essex Finance Centre Working Paper Series number 16807. Available at http://repository.essex.ac.uk/16807/.Google Scholar
Berk, K.N. (1974) Consistent autoregressive spectral estimates. The Annals of Statistics 2, 389–502.CrossRefGoogle Scholar
Bhargava, A. (1986) On the theory of testing for unit roots in observed time series. Review of Economic Studies 53, 369–384.CrossRefGoogle Scholar
Box, G.E.P. & Jenkins, G.M. (1976) Time Series Analysis: Forecasting and Control, Revised ed. Holden-Day.Google Scholar
Breitung, J. & Franses, P.H. (1998) On Phillips-Perron type tests for seasonal unit roots. Econometric Theory 14, 200–221.Google Scholar
Elliott, G., Rothenberg, T.J., & Stock, J.H. (1996) Efficient tests for an autoregressive unit root. Econometrica 64, 813–836.CrossRefGoogle Scholar
Ghysels, E. & Osborn, D.R. (2001) The Econometric Analysis of Seasonal Time Series. CUP.Google Scholar
Granger, C.W.J. & Hatanaka, M. (1964) Spectral Analysis of Economic Time Series. Princeton University Press.Google Scholar
Gregoir, S. (1999) Multivariate time series with various hidden unit roots, Part I: Integral operator algebra and representation theory. Econometric Theory 15, 435–468.Google Scholar
Gregoir, S. (2006) Efficient tests for the presence of a pair of complex conjugate unit roots in real time series. Journal of Econometrics 130, 45–100.Google Scholar
Haldrup, N. & Jansson, M. (2006) Improving power and size in unit root testing. In Mills, T.C. & Patterson, K. (eds.), Palgrave Handbooks of Econometrics: Vol. 1 Econometric Theory, Chapter 7, pp. 252–277. Palgrave MacMillan.Google Scholar
Hylleberg, S., Engle, R.F., Granger, C.W.J., & Yoo, B.S. (1990) Seasonal integration and cointegration. Journal of Econometrics 44, 215–238.CrossRefGoogle Scholar
Jansson, M. (2002) Consistent covariance matrix estimation for linear processes. Econometric Theory 18, 1449–1459.Google Scholar
Jansson, M. & Nielsen, M.Ø. (2011) Nearly efficient likelihood ratio tests for seasonal unit roots. Journal of Time Series Econometrics 3(1), Article 5, 1–19.Google Scholar
Müller, U.K. & Elliott, G. (2003) Tests for unit roots and the initial condition. Econometrica 71, 1269–1286.Google Scholar
Ng, S. & Perron, P. (2001) Lag length selection and the construction of unit root tests with good size and power. Econometrica 69, 1519–1554.Google Scholar
Perron, P. & Qu, Z. (2007) A simple modification to improve the finite sample properties of Ng and Perrons unit root tests. Economics Letters 94, 12–19.CrossRefGoogle Scholar
Perron, P. & Ng, S. (1996) Useful modifications to some unit root tests with dependent errors and their local asymptotic properties. Review of Economic Studies 63, 435–463.CrossRefGoogle Scholar
Perron, P. & Ng, S. (1998) An autoregressive spectral density estimator at frequency zero for nonstationarity tests. Econometric Theory 14, 560–603.CrossRefGoogle Scholar
Phillips, P.C.B. & Perron, P. (1988) Testing for a unit root in time series regression. Biometrika 75, 335–346.Google Scholar
Rodrigues, P.M.M. & Taylor, A.M.R. (2007) Efficient tests of the seasonal unit root hypothesis. Journal of Econometrics 141, 548–573.Google Scholar
Smith, R.J., Taylor, A.M.R., & del Barrio Castro, T. (2009) Regression-based seasonal unit root tests. Econometric Theory 25, 527–560.Google Scholar
Stock, J.H. (1999) A class of tests for integration and cointegration. In Engle, R.F. & White, H. (eds.), Cointegration, Causality and Forecasting. A Festschrift in Honour of Clive W.J. Granger, pp. 137–167. Oxford University Press.Google Scholar
Supplementary material: PDF

del Barrio Castro supplementary material

Online Appendix

Download del Barrio Castro supplementary material(PDF)
PDF 385.9 KB