Introduction
The World Health Organisation (WHO) describes antimicrobial resistance (AMR) as ‘a problem so serious that it threatens the achievements of modern medicine’ [1]. The effective prevention and treatment of an increasing range of bacterial, viral, fungal and parasitic infections is a challenge in many parts of the world where high rates of resistance are observed. Increases in mortality, length of hospitalisation and costs of care are associated with the development of resistance in several important bacterial pathogens [Reference Cosgrove2]. A recent report on AMR [Reference O'Neill3] estimates that 10 million more people are expected to die every year by 2050 if resistance is left unchecked; while the size of this figure has been met with skepticism [Reference de Kraker, Stewardson and Harbarth4], there is clearly a large clinical and public health burden related to AMR. Indeed, the World Bank estimates that the annual global gross domestic product (GDP) would fall by 1.1% by 2050 under even a modest ‘low impact’ AMR scenario [5].
Selective pressure exerted by the widespread use of antimicrobial drugs is accelerating the development of resistant populations of bacteria and other pathogens [1, Reference O'Neill3]. The development of resistance is a normal evolutionary process for microorganisms [1] and even the ‘appropriate’ use of antimicrobials selects for preexisting resistant populations in nature [Reference O'Neill3, Reference Spellberg, Bartlett and Glibert6]. The AMR issue is exacerbated by the ongoing misuse and overuse of antibiotic drugs in humans and food-producing animals [1, Reference O'Neill3]; further, the ‘collapse of the antibiotic research-and-development pipeline’ [Reference Spellberg, Bartlett and Glibert6] is a related problem underscoring the need for urgent solutions. The epidemiology of AMR is exceedingly complex and effective solutions must necessarily involve a coordinated effort by many sectors. Resistant bacteria and resistant genes do not recognise ecologic and geographic borders [7] and the transmission between human, animal [Reference Silbergeld, Graham and Price8, Reference Landers9] and environmental [Reference Allen10] domains is of shared concern. The WHO, World Organisation for Animal Health (OIE) and Food and Agriculture Organisation are thus mobilising a ‘One Health’ response in a tripartite collaboration on AMR [7].
Systems science and AMR
AMR has been framed by several experts as a ‘super-wicked’ problem [Reference Littman11], a specific type of policy challenge defined by the problem's inherent complexity, the interrelatedness of multiple fields and the potential for conflict arising from competing goals. There is a critical role for the ‘systems science approach’ to optimise intervention strategies for problems of this nature [Reference Littman11, Reference Gröhn12]. While traditional scientific approaches might examine how mechanisms work in isolation, a systems science approach makes it possible to examine the relationships between many interdependent components by integrating existing epidemiological data [Reference Gröhn12–Reference Bonten, Austin and Lipsitch14]. Dynamic modelling methods are used to develop mathematical representations of systems characterised by nonlinearities, feedback loops and multiple variables that evolve over time [Reference Marshall15]. Representations of this type are necessarily a simplification of the system of interest [Reference Bonten, Austin and Lipsitch14, Reference Grundmann and Hellriegel16], but can help identify the critical functional aspects of a system via experimentation with scenarios under various conditions [Reference Marshall15, Reference Grundmann and Hellriegel16]. By defining the conditions under which an intervention is likely to work [Reference Lipsitch and Samore17], dynamic or mathematical models offer insights on which to build effective policy responses [Reference Gröhn12, Reference Smith, Dushoff and Morris18]. Furthermore, models of this sort challenge researchers to both share and scrutinise their assumptions and/or hypotheses about how a system works. Risk assessment (RA) is a related and complementary approach for data integration and was the focus of a parallel review (unpublished).
Temime et al. [Reference Temime19] previously demonstrated the growing interest in mathematical modelling approaches to evaluate antibiotic resistance. In particular, these models have been used extensively to explore the development and spread of multi-drug resistant bacteria in hospital settings [Reference Bonten, Austin and Lipsitch14, Reference Grundmann and Hellriegel16, Reference Opatowski20, Reference Doan21]. Interventions of interest include those with implications for physical infection control strategies (e.g. isolation, hand hygiene) [Reference Grundmann and Hellriegel16] and to a lesser extent, antibiotic restriction [Reference Doan21] and other prescription strategies [Reference Bonten, Austin and Lipsitch14]. Mathematical modelling is a valuable tool with which to generate hypotheses about the relationship between antimicrobial use (AMU) and AMR at the population level [Reference Lipsitch and Samore17]. However, the scope of work undertaken for this purpose in both healthcare and other relevant domains has yet to be fully characterised [Reference Austin and Anderson22, Reference Levin23]. Of special interest to this research team is the use of dynamic models as they pertain to AMR in agricultural and food system settings; this is notably relevant in light of the recent suggestion that veterinary epidemiologists should progress to the multi-scale modelling of food animal systems [Reference Gröhn12].
Scope of inquiry
The purpose of this scoping review was to identify and describe how researchers have used dynamic modelling techniques to explore and advance policies that limit AMR-related risk arising from AMU. To establish an effective search strategy, a broad research question should be combined with a clearly articulated scope of inquiry, including the concept, target population and health outcomes of interest [Reference Levac, Colquhoun and O'Brien24]. This review was thus conceived as a means to summarise the range of studies that use dynamic models to analyse the problem of bacterial resistance in relation to antibacterial use in humans and animals. The intended focus was studies which generate and draw conclusions from simulated data using aggregate or individual-based dynamic models of resistance development and spread. Population-level outcomes of interest included the frequency of resistant hosts, the likelihood of morbidity and mortality arising from resistant infections and/or the costs associated with resistant infections.
Arksey and O'Malley [Reference Arksey and O'Malley25] describe several reasons for conducting a scoping review, several of which may be relevant for the overall purpose [Reference Levac, Colquhoun and O'Brien24]. This review combines multiple objectives, namely to describe the specific contexts to which these models are applied, to summarise the approches to model building and to identify where gaps exist in the peer-reviewed literature. Furthermore, the effort was motivated in part by this group's interest in the documentation and reporting of models in relation to recommended guidelines. In 2012, the Good Research Practices in Modeling Task Force published a series of articles describing best practices for designing and building dynamic models [Reference Pitman26], analysing uncertainty [Reference Briggs27] and achieving transparency [Reference Eddy28]. Several of the questions in the ‘Data charting’ section was developed with reference to this framework [Reference Pitman26–Reference Eddy28] and to related materials concerning the responsible conduct of research with simulation models [Reference Kijowski29].
Methods
The scoping study team consisted of members with the appropriate content and methodological knowledge to perform this review [Reference Levac, Colquhoun and O'Brien24] and included expertise in the areas of AMR, infectious and veterinary epidemiology, food system safety, dynamic modelling and RA techniques and scoping review methodology. As is typical of scoping reviews, the process of selecting relevant studies and charting the data was non-linear [Reference Levac, Colquhoun and O'Brien24, Reference Arksey and O'Malley25]; frequent team discussions were necessary to refine the inclusion/exclusion criteria and extraction variables over the course of this review. The criteria and questions described below reflect the multiple iterations and improvements gleaned through the team's increasing familiarity with the literature.
Search terms and strategy
In consultation with a research librarian, the team developed a strategy to search the peer-reviewed literature for studies modelling AMR in humans, animals and the environments with which they interact. The search was limited to English language publications but was otherwise deliberately broad to ensure a comprehensive review of the literature. There were no limitations on the date nor geographical origin of publication. Four databases were included in the search (PubMed, Scopus, Agricola and CAB Abstracts) and identical search terms were modified only to reflect the differing indexing schemes. The PubMed search in particular made use of Medical Subject Headings (MeSH) terms, the US National Library of Medicine's controlled vocabulary thesaurus.
The search was comprised of concatenated descriptors from three general areas: the first concerned study subject and included variations on the terms humans, patients, hospitals, domestic and companion animals, farms, water and soils; the second concerned methodological approach and included variations on the terms simulation and dynamic models; the third concerned general content area and included variations on the terms antibacterial use and resistance. A full list of terms included in the search is available in the online Supplementary Material. The search was initially conducted on 28 February 2016 and updated with additional terms on 5 November 2016; in an effort to establish reproducibility, the search was performed independently by two reviewers (JI and DR). Reference information for the identified articles was exported to and de-duplicated using Zotero, a web-based reference management program. De-duplicated references were exported to an Excel spreadsheet for sorting and screening.
In order to identify relevant studies missed by the database search, the team conducted a supplementary review of reference lists from pertinent articles. Included in this subset of articles were previous reviews of studies modelling bacterial resistance [Reference Opatowski30–Reference Arepeva32] and studies published between 2013 and 2016 and retained for inclusion after full-text review (see the ‘Article screening’ section). The reference lists of retained studies concerning food-producing animals [e.g. Reference Abatih33–Reference Graesbøll34], cost outcomes [e.g. Reference Jansen, Kumar and Carmeli35] and network modelling [e.g. Reference Karlsson36, Reference Geli37] were likewise reviewed, given that these were comparably unique and suggestive of missed search terms. Retained studies published prior to 2013 were not reviewed further, as this time period was comprehensively covered by [Reference Opatowski30–Reference Arepeva32] and new articles were no longer being identified. As the focus of this review was peer-reviewed literature, the team chose not to include grey literature in the search.
Article screening
Two reviewers (JI and DR) independently performed the title and abstract screens. A third reviewer (CW) was consulted when agreement could not be reached on a particular reference at either the title or abstract screening stages. Articles were excluded if they were not in English, if they were not published in a peer-reviewed journal and if they did not present novel findings (e.g. literature reviews, commentaries, editorials or methodological descriptions). Because the focus of this review was bacterial resistance, studies which were specific to non-bacterial pathogens (e.g. viruses, fungi, parasites or mycobacteria) were excluded, as were those addressing non-infectious disease outcomes. Studies which were strictly observational in nature, including case series and prevalence surveys, were likewise excluded at this stage.
Where the article title was not sufficiently informative to make an inclusion/exclusion decision, the reference was retained for abstract screening. In addition to the aforementioned criteria, studies were excluded at this stage if they concerned pharmacodynamic-pharmacokinetic models, or if they focused exclusively on susceptible bacterial variants. Studies which were strictly experimental in nature, including microbiological investigations, were likewise excluded at this stage.
An additional level of screening was performed at the stage of full-text review and data extraction/charting. A series of questions was applied to each remaining reference to ensure the final subset was reflective of the review's scope of inquiry. The list of questions appears below and evolved over several iterations of review, analysis and discussion.
(1) Does this study possess a dynamic component (i.e. does the outcome vary over time, in contrast to studies where the outcome is independent of time, as in static assessments of risk)?
(2) Does this study generate data using simulation(s) and/or draw conclusions from simulated data?
(3) Does this study concern the development or spread of bacterial strains with inherited antibiotic resistance (i.e. is not exclusive to susceptible bacteria and/or bacterial strains with non-inherited antibiotic resistance)?
(4) Does this study investigate the dynamics of resistant bacteria in the presence of antibacterial treatment/use, either in the baseline or counterfactual scenarios?
(5) Does this study endeavour to examine the dynamics of resistant bacteria at the population or inter-host level (i.e. is not strictly an intra-host model)?
The reference was excluded if a ‘no’ answer was observed for any of the above questions. A sample of 30 full-text articles over several iterations was screened independently by two reviewers (CW and DR) to evaluate reviewer agreement. As there were no significant disagreements or challenges related to study selection using this framework, a single reviewer (DR) screened the full texts of remaining articles. When the decision to include/exclude was uncertain, a second reviewer (CW) determined the final inclusion. Articles were not excluded on the basis of quality. A PRISMA diagram depicts the flow of information through the identification, screening and eligibility stages in Figure 1.

Fig. 1. PRISMA flow diagram depicting the number of articles at each of the identification, screening and eligibility stages.
Data charting
The review team developed a data charting form in Microsoft Excel in which to capture variables relevant to the study's scope. As is recommended by Levac et al. [Reference Levac, Colquhoun and O'Brien24], the data charting form was frequently updated in concert with the team's increasing familiarity with the studies retained for inclusion (n = 81). The charting questions appear below and are organised by category to highlight distinct contextual and methodological model features.
Model type and context
(1) What type of model was built for this study?
(2) What is the setting or context for the system represented by this model?
(3) Which bacterial host(s) is/are represented in this model, if any?
(4) Which bacterial organism(s) is/are of interest in this model, if any?
(5) Which resistance pattern(s) (e.g. cephalosporin resistance) is/are of interest in this model, if any?
(6) Which particular antibiotic treatment/application(s) is/are simulated in this model, if any?
Model construction and parameterisation
(1) Does the study describe and/or justify the assumptions made in constructing this model?
(2) Does the paper provide a visual depiction of the system represented by this model (e.g. compartmental diagram)?
(3) Does the paper detail and/or solve the differential equations for the system represented by this model (where applicable, as in compartmental models)?
(4) What source(s) of data are used to generate input values for this model?
(5) Do the authors use a range or distribution of values for one or several parameters in the baseline scenario?
(6) Do the authors calibrate (i.e. ‘fit’) the model to empirical data in order to generate input values?
Model outputs and validation
(1) Which emergent property or endogenous variable(s) (i.e. outputs) of interest is/are generated by this model?
(2) For a particular set of assumptions, is the output of this model represented by a single possible outcome (arising from deterministic models) or a distribution of possible outcomes (arising from stochastic processes)?
(3) Does the paper report the time units and/or length of time over which the output is observed (i.e. the simulation length)?
(4) Do the authors perform sensitivity analyses to identify parameters which strongly affect the outputs of this model (i.e. explicitly characterise the uncertainty associated with model inputs)?
(5) Do the authors attempt to validate this model by reproducing observed or empirical data?
Model applications
(1) Does this study attempt to explain an observed epidemiological phenomenon or investigate a future and/or counterfactual state, given a set of initial conditions?
(2) If the model's purpose is explicative, do the authors compare competing hypotheses for observed phenomena?
(3) If the model's purpose is investigative, do the authors examine the impact of changes to the system in alternative or counterfactual scenarios?
(4) What type of system change(s) and/or intervention(s) are of interest in this study, if any?
(5) Do the results or conclusions reported in the paper have the potential to inform policy development or decision-making?
The required responses were either binary (i.e. yes/no) or restricted to a defined list of descriptors. Data from a sample of 10 included studies were extracted independently by two reviewers (CW and DR) to evaluate reviewer agreement and consistency. As there were no significant disagreements or challenges related to data extraction using the charting form, a single reviewer (DR) charted the data for the remaining articles. The responses were summarised across the included studies and reported in a tabular format where appropriate (see the ‘Results’ section).
Results
The review identified 81 articles for inclusion at the stage of full-text screening and data charting [Reference Abatih33–Reference Sun, Lu and Ruan113]. Nine articles (11%) were published before 2000, 25 articles (31%) were published between 2000 and 2009 (inclusive) and 47 (58%) articles were published between 2010 and the most recent database search in November 2016. Twenty-two of the included articles (27%) were published after 2012, the most recent year covered by a review in our supplemental search [Reference Arepeva32]. The corresponding author in nearly half of the articles (43%) was affiliated with an American institution; 12 articles (15%) and eight articles (10%) were affiliated with corresponding authors based in France and the UK, respectively. The map in Figure 2 highlights the national affiliation of the corresponding author for articles included in the review.

Fig. 2. National affiliation of corresponding author for articles included in the scoping review.
Model type and context
The studies are summarised by model setting and bacterial host(s) in Table 1 and are further subdivided by model type and behaviour. Thirty-three articles (41%) feature models relevant to healthcare settings (i.e. hospitals or clinics), while 31 articles (38%) feature models based in human communities; six additional articles (7%) model the interaction between healthcare and community settings [Reference Kardas-Sloma56, Reference Kouyos, zur Wiesch and Bonhoeffer57, Reference Kouyos, Klein and Grenfell59, Reference Obolski, Stein and Hadany66, Reference Smith71, Reference Talaminos73]. Only two articles examine antibacterial resistance in an exclusively agricultural setting at the inter-host level [Reference Abatih33, Reference Graesbøll34]. Humans are the relevant bacterial hosts in most of the included studies, with some notable exceptions where pigs [Reference Abatih33, Reference Graesbøll34], dogs [Reference Suthar72] and food-producing animals [Reference Gao, Pan and He85] are the hosts of interest. In eight articles with non-specific settings, the model simulates antibacterial resistance development/spread in a generic ‘host’ population.
Table 1. Summary of studies included in the final review (n = 81), organised by model context and type

Most of the included studies (86%) represent the system of interest with a compartmental or aggregate model. Of the 70 compartmental-type models, 84% exhibit exclusively deterministic behaviour (i.e. a single possible outcome is determined by the system's initial conditions). Six models treat the transitions between compartments as random phenomena and thus exhibit stochastic behaviour [Reference Graesbøll34, Reference Austin38, Reference Domenech de Cellès49, Reference Kouyos, zur Wiesch and Bonhoeffer57, Reference Kouyos, zur Wiesch and Bonhoeffer58, Reference Mitchell, Lipsitch and Hanage91]. In five studies, the authors perform both deterministic and stochastic simulations of the same compartmental model [Reference Haber, Levin and Kramarz52, Reference zur Wiesch76, Reference Handel, Regoes and Antia86, Reference Temime98, Reference Temime, Boëlle and Thomas100]. Individual or agent-based models (ABM) are described in four studies [Reference Kardas-Sloma55, Reference Sébille and Valleron69, Reference Suthar72, Reference Hui87]; a single study combines compartmental and individual-based components in a hybrid model [Reference Kardas-Sloma56]. In [Reference D'Agata47] and [Reference Samore96], the authors compare simulations arising from compartmental and individual-based models representing the same system.
The studies are summarised by the bacterial organism(s) and resistance pattern(s) of interest in Table 2; an organism was considered to be ‘of interest’ if it was the motivation for model building [e.g. Reference Gao, Lietman and Porco84, Reference Smith97, Reference Wang and Lipsitch104], or if the model was parameterised and/or validated with data specific to that bacteria. In 40% of the articles (n = 32), resistance is modelled for a generic or non-specific bacterial organism. An additional six articles model resistance in otherwise unspecified Enterobacteriaceae species [Reference Domenech de Cellès49, Reference Suthar72] or commensals [Reference Lipsitch, Bergstrom and Levin61, Reference Austin, Kakehashi and Anderson77, Reference Levin110, Reference Stewart112]. Vancomycin-resistant enterococci (n = 5) and methicillin-resistant Staphylococcus aureus (MRSA) (n = 4) are of frequent interest in hospital settings. In the community setting, the bacteria of interest are most often Streptococcus pneumoniae (n = 18) and Neisseria gonorrhoeae (n = 6).
Table 2. Bacterial organism(s) and resistance pattern(s) of interest for studies included in the final review (n = 81)
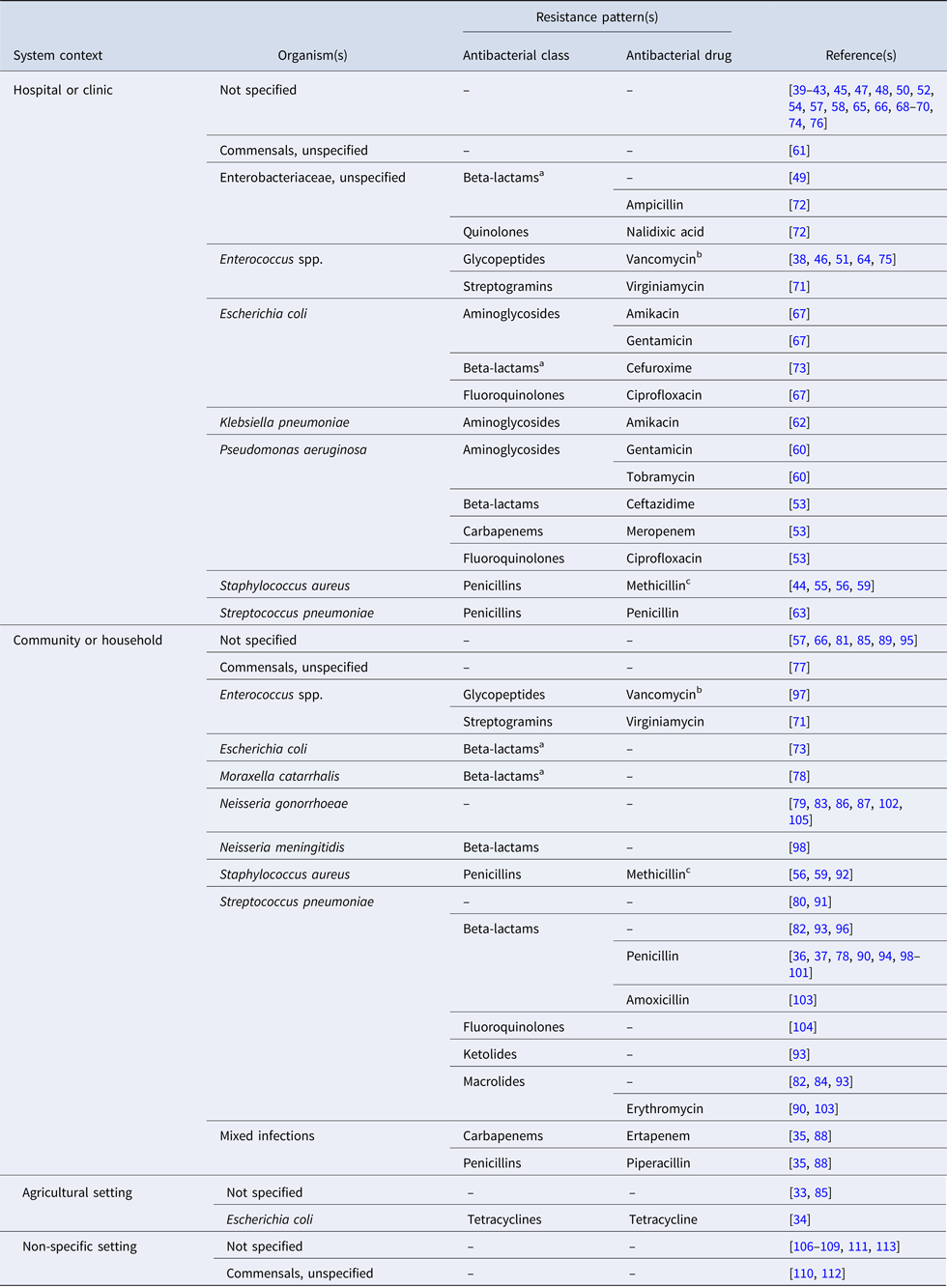
‘–’ indicates the antimicrobial class and/or antimicrobial drug was not specified in the study.
a Beta-lactamase or extended-spectrum beta-lactamase-producing bacteria.
b Vancomycin-resistant enterococci (VRE).
c Methicillin-resistant staphylococcus aureus (MRSA).
Of the 43 articles which specify the bacteria of interest, eight (19%) do not indicate the resistance pattern of interest. Resistance to penicillin in Streptococcus pneumoniae is the most frequently modeled phenotype (n = 10); beta-lactamase-producing bacteria are considered in only three studies [Reference Domenech de Cellès49, Reference Talaminos73, Reference Austin, Kristinsson and Anderson78]. In 74% of the articles (n = 60), the antibiotic applied to the bacterial host(s) in the model is generic or non-specific. Twelve studies simulate treatment with antibiotics from multiple classes [Reference Jansen, Kumar and Carmeli35, Reference Hurford53, Reference Kardas-Sloma55, Reference Kardas-Sloma56, Reference Obolski67, Reference Talaminos73, Reference Domenech de Celles82, Reference Jansen, Kumar and Carmeli88, Reference McCormick90, Reference Opatowski93, Reference Samore96, Reference Van Effelterre103]. Treatment with beta-lactams (including carbapenems, cephalosporins and penicillins) is most frequently simulated (n = 17), while fluoroquinolone [Reference Hurford53, Reference Obolski67, Reference Talaminos73] and macrolide [Reference Domenech de Celles82, Reference McCormick90, Reference Opatowski93, Reference Van Effelterre103] treatments are simulated less often. The single example of treatment with tetracycline concerns the spread of tetracycline-resistant Escherichia coli in pigs [Reference Graesbøll34].
Model construction and parameterisation
Many of the included articles (77%) provide a visual depiction of the system represented by the model (e.g. a compartmental diagram or other schematic representation, as in [Reference Kardas-Sloma55, Reference Sébille and Valleron69, Reference Suthar72]). In 84% of the 70 strictly compartmental-style models, the paper details the differential equations representing the system of interest; the relevant equations are also highlighted for the deterministic component or formulation in [Reference D'Agata47, Reference Kardas-Sloma56, Reference Samore96]. While most articles describe to some extent the source(s) of data used to parameterise the model (86%), 11 articles do not comment on the source of the input values [Reference Bergstrom, Lo and Lipsitch41, Reference Reluga68, Reference Smith71, Reference Webb74, Reference Austin, Kakehashi and Anderson77, Reference Gao, Lietman and Porco84, Reference Gao, Pan and He85, Reference Levin, Baquero and Johnsen89, Reference Bonhoeffer, Lipsitch and Levin107, Reference Boni and Feldman108, Reference Sun, Lu and Ruan113]. An additional eight articles rely solely on expert opinion or ‘guesstimates’ to parameterise the model and/or purposively choose values in order to highlight specific dynamic behaviours [Reference Abatih33, Reference Beardmore and Pena-Miller40, Reference Haber, Levin and Kramarz52, Reference Colijn and Cohen81, Reference Handel, Regoes and Antia86, Reference Porco95, Reference Beams106, Reference Levin110].
Of the 70 articles for which the source(s) of data are described, 50% make use of empirical data either collected by the study's authors (n = 11) or published in a report of particular relevance (n = 25). In 22 studies, the authors estimate previously unknown parameters by calibrating or ‘fitting’ model outputs to empirical data. The published literature and/or expert opinion was used to generate at least one parameter in 74% and 64% of studies for which the input value source could be identified with reasonable confidence, respectively. These percentages should be interpreted as relative trends and not conclusive findings, given that the data source(s) for unique inputs were frequently unreported or otherwise not easily gleaned from the article.
Model output and validation
In most of the included articles (84%), the proportion of resistant patients is an emergent property of primary or secondary interest. Variations of the term proportion in this subset include ‘fraction’, ‘frequency’, or ‘prevalence’ of resistance; likewise, variants of the term resistant patients including ‘colonisation with resistant bacteria’, ‘resistant infections’ or ‘resistant strains’ were assigned to this outcome category. Additional outcomes of interest include the likelihood of and/or time to resistance emergence or extinction [Reference Obolski and Hadany65, Reference Obolski, Stein and Hadany66, Reference Austin, Kristinsson and Anderson78, Reference Fingerhuth83, Reference Handel, Regoes and Antia86, Reference Hui87, Reference Mitchell, Lipsitch and Hanage91, Reference Opatowski93, Reference Smith97, Reference Temime98, Reference Levin110], the likelihood of coexistence (i.e. of sensitive and resistant strains) [Reference Kouyos, Klein and Grenfell59, Reference Massad, Lundberg and Yang62, Reference Colijn80, Reference Beams106], the fraction of resistant infections attributable to antibiotic use [Reference Smith71, Reference Samore96, Reference Smith97, Reference Temime101] and the number of treatment failures or inappropriately-treated patients [Reference Kouyos, zur Wiesch and Bonhoeffer58, Reference Obolski, Stein and Hadany66, Reference Wang and Lipsitch104]. The outcome of interest in four articles [Reference Opatowski94, Reference Temime98–Reference Temime, Boëlle and Thomas100] is the distribution of resistance levels determined by the minimum inhibitory concentration.
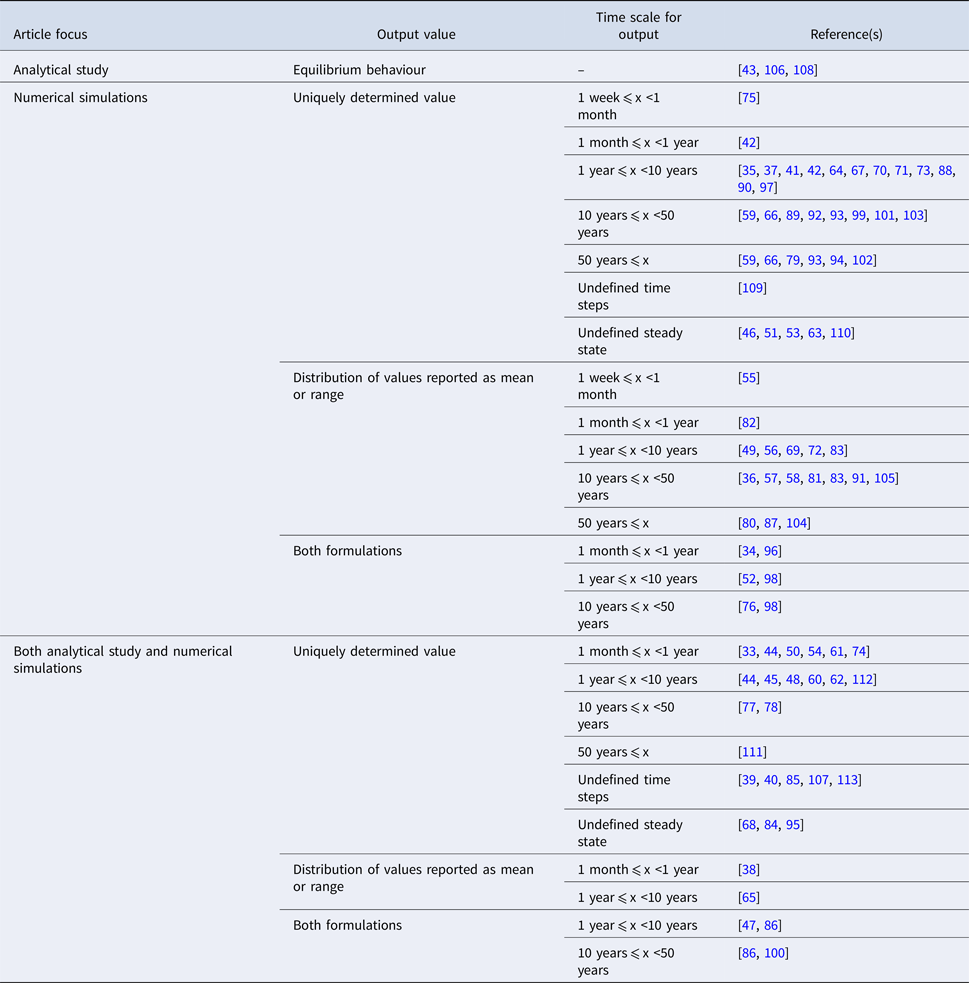
The studies are summarised by the characteristics of their reported outputs in Table 3. ‘Uniquely determined’ outputs (i.e. outcomes with a single possible value) are observed for models with deterministic behaviour and inputs represented by point estimates (n = 52). Conversely, distributions of output values are observed for models with stochastic behaviour (see Table 1), or for models with deterministic behaviour that draw multiple parameter sets from input distributions [e.g. Reference Obolski and Hadany65, Reference Colijn and Cohen81, Reference Wang and Lipsitch104]. In order to highlight different scales of temporal abstraction, the articles are further subdivided by the length of time over which the output is observed (i.e. the simulation time). Models which were simulated to equilibrium or ‘steady state’ values were classified based on the time reported in the associated graphical output [e.g. Reference Chamchod and Ruan44, Reference Joyner, Manning and Canter54, Reference Austin, Kakehashi and Anderson77]. There was no specific time associated with the equilibrium state in eight articles; in six additional articles, time is measured in otherwise undefined ‘steps’.
Table 3. Characteristics of the reported output arising from dynamic modelling effort in included studies (n = 81)
In 53% of included articles, the author(s) perform sensitivity analyses to identify parameters and/or structural features which exert a strong effect on the model's outputs. In addition to the term sensitivity, related concepts including ‘uncertainty’ or ‘robust(ness)’ were suggestive of an attempt to formally characterise the impact on the outcome of model assumptions. As with the sources for input data, relevant analyses are often incompletely described and this estimate should be interpreted in that context. An effort is made to formally validate the relevant model by reproducing empirical data in 17 of the included articles [Reference Geli37, Reference Austin38, Reference Domenech de Cellès49, Reference Hurford53, Reference Kardas-Sloma56, Reference Massad, Lundberg and Yang62, Reference Massad, Burattini and Coutinho63, Reference Austin, Kristinsson and Anderson78, Reference Domenech de Celles82, Reference Fingerhuth83, Reference Hui87, Reference McCormick90, Reference Opatowski93, Reference Opatowski94, Reference Temime98, Reference Van Effelterre103, Reference Xiridou105]. Less formal comparisons between model outputs and historical trends are explored in seven additional articles [Reference Graesbøll34, Reference Bergstrom, Lo and Lipsitch41, Reference Suthar72, Reference Talaminos73, Reference zur Wiesch76, Reference Nielsen92, Reference Temime, Guillemot and Boëlle99].
Model applications
The reported study purpose is to investigate one or several counterfactual and/or future states in 75% of the included articles; in five articles, the purpose of the study is to explain or interpret an epidemiological phenomenon [Reference Kouyos, Klein and Grenfell59, Reference Massad, Lundberg and Yang62, Reference Colijn80, Reference Domenech de Celles82, Reference Fingerhuth83]. In 15 additional articles, the model is used both to explain phenomena and to examine the system's dynamics in competing or alternative scenarios. ‘Intervention(s)’ representing theoretically modifiable system change(s) were explored in 90% of the included articles (n = 73). The intervention type and potential relevance of study results and/or conclusions for policy development are summarised in Table 4. Note that in 25 articles, the author(s) examine the effect of multiple intervention types on the system of interest; the total number of interventions reported in the table is thus larger than 73.
Table 4. Modifiable intervention types investigated in hypothetical and/or counterfactual scenarios (n = 73)

Interventions involving a change to the overall consumption of antibiotics were the most frequently investigated (n = 37); pertinent examples explore changes in antibiotic use frequency, duration and dose. Other interventions with particular relevance for antibiotic use policy include changes to antibiotic management strategies (n = 21) and changes to antibiotic category or class (n = 15). In the former category, deployment strategies of interest include cycling, mixing or combining antibiotics at the institutional or population level; in the latter, shifts in antibiotic use within and between classes are highlighted. Eight (10%) of the included studies do not impose a theoretically modifiable change on the system of interest. A subset of these articles nevertheless has the potential to inform antibiotic use [Reference Geli37, Reference Colijn80, Reference Fingerhuth83, Reference McCormick90] and/or hygiene and infection control [Reference Colijn80, Reference Fingerhuth83] policies. The results from six articles have relevant implications for antibiotic use in companion animals [Reference Suthar72] and food-producing animals [Reference Abatih33, Reference Graesbøll34, Reference Smith71, Reference Gao, Pan and He85, Reference Smith97].
Discussion and implications
Given the increasing interest in [Reference Temime19] and projected value of [Reference Lipsitch and Samore17] mathematical modelling to generate hypotheses about the AMU/AMR relationship, the authors endeavoured to better characterise the peer-reviewed literature in this domain. This review identified 81 studies which used simulated data from dynamic models to analyse the problem of bacterial resistance in relation to antibiotic use in humans or animals [Reference Abatih33–Reference Sun, Lu and Ruan113]. Note that the focus of this work was resistance dynamics at the population or inter-host level and thus strictly intra-host models are excluded from this count. As was expected, the number of included articles grew in each 5-year increment since 2000, in parallel with the AMR modelling literature more generally. The articles’ corresponding authors are affiliated with 14 countries on five continents, although most articles (70%) emerged out of three countries (USA, UK and France). This observation is likely explained in part by the English language limitations of our search, but might also indicate that well-resourced institutions are better able to engage in the ‘systems science approach’ and with its associated methodologies. In particular, the National Institutes of Health (NIH) has played a leading role in the promotion and funding of systems science projects at American institutions.
Model type and context
Aggregate models comprise the vast majority of studies included in this subset of articles (86%). In most instances and unless they are simulated stochastically as in [Reference Austin38, Reference Beardmore and Pena-Miller39, Reference Kouyos, zur Wiesch and Bonhoeffer57, Reference Kouyos, zur Wiesch and Bonhoeffer58, Reference Mitchell, Lipsitch and Hanage91], compartmental models exhibit deterministic behaviour. Models of this type describe the average behaviour of a system and are most appropriate when the population is sufficiently large to minimise the impact of differences between individuals. While compartmental models have the advantage of being comparably easy to parameterise and calibrate, they cannot account for individual heterogeneity nor the substantial impact of chance events in smaller populations (e.g. closed hospital wards). In contrast, individual or ABM represent the system as a population of heterogeneous entities engaged in local interactions; models of this type better capture the stochastic behaviour of a system but impose opportunity costs related to model construction, parameterisation and computing time [Reference Osgood and Sterman114]. Opatowski and colleagues [Reference Opatowski30] argue that increasingly realistic predictions arising from ABM models are likely to advance the utility of computer simulations for decision support. Only seven articles in this series develop individual-based representations of the system of interest [Reference D'Agata47, Reference Kardas-Sloma55, Reference Kardas-Sloma56, Reference Sébille and Valleron69, Reference Suthar72, Reference Hui87, Reference Samore96], suggesting that ABMs have been infrequently used to examine the AMU/AMR relationship at the population level.
While experts decidedly agree that AMR is a ‘One Health’ problem requiring multi-sectoral action [7], there are few examples of inter-host models outside of strictly human contexts. Further, there are only two models in this subset which incorporate multiple host species in shared environments [Reference Suthar72, Reference Gao, Pan and He85]. Antibiotic use in agricultural settings accounts for a substantial proportion of global antimicrobial consumption [Reference Silbergeld, Graham and Price8] and global AMU in livestock is expected to rise significantly through 2030 [Reference Van Boeckel115]. These observations highlight the potential role for dynamic models to inform strategies that limit the inter-ecosystem spread of AMR arising from AMU in food-producing animals. Recent and impressive examples exist at the within-host level; for instance, Volkova and colleagues examine the effect of antibiotic therapy on the dynamics of ceftiofur-resistant commensal Escherichia coli in the large intestine of cattle in [Reference Volkova116, Reference Volkova117]. At the inter-host level, dynamic models have been used to investigate the persistence of resistant bacteria following a clinical outbreak of Salmonella typhimurium in dairy cows [Reference Lanzas118] and in the context of non-AMU interventions targeting Escherichia coli commensals in beef cattle [Reference Volkova119].
Model applications
Models included in the final subset range from general or hypothetical [e.g. Reference Beardmore and Pena-Miller39, Reference Bergstrom, Lo and Lipsitch41] to those with a single, specific application [e.g. Reference D'Agata, Webb and Horn46, Reference Hurford53]. The purpose of the model is primarily theoretical in 40% and 74% of articles where resistance is modelled for a generic bacterial organism and/or a generic antibiotic, respectively. Articles in which the organism of interest is explicitly identified are more useful for decision support [Reference Opatowski30] and frequently concern ‘priority’ [Reference Garner120] or ‘urgent’ [121] AMR disease threats. Indeed, drug-resistant Streptococcus pneumoniae (n = 18), Neisseria gonnorhoeae (n = 6) and MRSA (n = 5) are well represented in this dataset and appear on WHO's list of bacteria of international concern [1]. Extended-spectrum beta-lactamase-producing Enterobacteriaceae are routinely identified as high priority threats [1, Reference Garner120, 121], but are the focus of only two studies reported here [Reference Domenech de Cellès49, Reference Talaminos73]; no studies examine the urgent threat of carbapenem-resistant Enterobacteriaceae. Further, there are no studies which model resistance in zoonotic bacterial pathogens that are important sources of infection for humans (e.g. Salmonella spp. or Campylobacter jejuni). Normally commensal bacteria that may harbour resistant genes, including Enterococcus spp. (n = 7), are better represented in this dataset.
This review was limited to models in which antibacterial treatment or use is directly simulated; the inclusion criteria are thus reflected in the scope and types of interventions applied in this subset of articles. Sixty-seven articles (83%) impose at least one antibiotic use-related intervention, ranging from institutional drug management strategies (e.g. cycling antibiotics) to drug category changes (e.g. switching from a first to a second-line drug). Antibiotic stewardship is one component of a necessarily multifaceted approach to the AMR problem [Reference Fishman122]; there are only 22 articles (27%) which examine an antibacterial use intervention in combination with another approach. Future consideration should be given to the impact on system behaviour of the interactions between prudent antibiotic use and other biological or behavioural interventions. While they do not simulate treatment directly, several related models estimate the relative importance of resistant bacterial acquisition by the endogenous route (i.e. arising from the selective pressure of antibiotics) [e.g. Reference Pelupessy, Bonten and Diekmann123, Reference Bootsma124]. There are likewise numerous articles which model the acquisition of resistant bacteria via the exogenous route (i.e. via direct or indirect transmission) in the absence of selective treatment pressure [e.g. Reference Raboud125, Reference Barnes126].
Model transparency and uncertainty
Responses to the charting questions were limited to yes/no selections or an otherwise restricted set of descriptors; this review thus summarises but does not offer a critical appraisal of the included studies. Nevertheless, some broad generalisations can be made with respect to the achievement of transparency and management of uncertainty in this set of articles. Modelers can enhance credibility by clearly describing the model structure, assumptions and parameter values [Reference Briggs27, Reference Eddy28]. While several studies offer robust, defensible explanations for the assumed model properties [e.g. Reference Fingerhuth83, Reference Hui87], others provide only limited support in this regard. Rather than assume a particular model structure, some notable examples [e.g. Reference Geli37, Reference Colijn80] compare several possible configurations to arrive at the best representation. The articles likewise vary considerably by both the source of model inputs (see the ‘Model construction and parameterisation’ section) and the clarity with which the sources are reported. Readers should be provided with sufficient information to understand the model's limitations, including those arising from uncertain or estimated inputs [Reference Eddy28]; parameter tables are used in many studies [e.g. Reference D'Agata48, Reference Suthar72] and are a particularly transparent means of reporting input values.
The Good Research Practices in Modeling Task Force describes the importance of reporting uncertainty analyses in modeling studies [Reference Pitman26, Reference Briggs27]. As a complement to uncertainty or sensitivity analyses, ‘scenario analyses’ report alternative outcomes under discrete assumptions (i.e. values) for a parameter of primary interest [Reference Briggs27]. Only half of the included articles (n = 43) performed and clearly reported a deterministic or probabilistic sensitivity analyses [e.g. Reference Temime, Guillemot and Boëlle99, Reference Wang and Lipsitch104]. In many articles, it is difficult to distinguish sensitivity analyses from attempts to examine the impact of interventions in unique ‘scenarios’. Sensitivity analyses are one component of the formal process for external validation [Reference Eddy28], wherein a model's results are compared to actual event data. Simulated outcomes are compared to observed results in only 21% of the articles, suggesting that models in this domain are not routinely assessed for accuracy in making relevant predictions. Most examples in this dataset use the same source to estimate model parameters and to validate the model (i.e. dependent validation) [e.g. Reference Massad, Burattini and Coutinho63, Reference Opatowski94], which is less rigorous than independent or blinded validation [Reference Eddy28]. In the absence of a full sensitivity analysis and validation effort, it is a challenge for decision-makers to ascertain the value of the model for informing a course of action [Reference Briggs27, Reference Eddy28].
Limitations and conclusions
Several limitations of this work deserve mentioning. In addition to the English language restriction, the team did not search the grey literature for non-peer-reviewed studies. The inadvertent exclusion of relevant search terms could have similarly impacted the number of database ‘hits’. For both reasons, it is possible that models fitting the inclusion criteria were overlooked in this review. Models specific to bacteria with non-inherited resistance (i.e. phenotypically resistant or ‘persister’ cells) rather than inherited resistance were likewise excluded from consideration [e.g. Reference Levin and Rozen127, Reference Bootsma128]. The data charting questions were refined and updated over several iterations, but nevertheless, reflect in part the particular interests of this review team. The extent to which these models are constructed in line with best practices [Reference Pitman26, Reference Eddy28] may require further scrutiny. Dynamic models capture the non-linear relationships and feedback loops characteristic of communicable disease spread. ABM are only infrequently used to model the AMU/AMR relationship at the population level, limiting their usefulness for decision support; the popularity of ABM is likely to increase as ‘big data’ becomes more readily accessible. Models investigating AMR in agricultural and/or environmental settings are critically underrepresented in this dataset, in spite of recent efforts to promote farm animal populations as models for disease transmission [Reference Lanzas129]. Finally, there is substantial room to improve the clarity and transparency of reporting in the AMR modelling literature.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/S0950268818002091.
Acknowledgement
This work was supported by Alberta Agriculture and Forestry (grant number 2015E017R).
Conflict of interest
None.








