INTRODUCTION
Host population reduction is a common strategy used to reduce infection prevalence in wildlife and livestock. For infections in host populations which are relatively freely mixing and for which transmission depends on social contacts, reductions in the population will lead to a reduced frequency of contacts between individuals and therefore fewer transmission events. However, for infections which occur in socially structured populations, the effects of population reduction are more difficult to predict, due to the complex interplay between disease development within individuals and its transmissibility between individuals, which depends on host behaviour and population structure [Reference Dobson and Foufopoulos1–Reference Cross3].
Host population reduction can produce a more fractured contact structure, which reduces mixing and leaves the infection more vulnerable to localized chance extinctions, but this effect is dependent on the spatial and social structure of the host population. Failure to take this into account can lead to inappropriate conclusions regarding infection management. For example, based on a non-spatial model, Swinton et al. [Reference Swinton4] predicted that large reductions in prevalence of bovine tuberuclosis in badgers could be achieved by only moderate reductions in badger populations, whereas White & Harris [Reference White and Harris5], using a spatial stochastic model, found that >90% of the badger population needed to be culled to ensure a reasonable probability of control. This conclusion has been borne out by the subsequent failure of control strategies based on relatively inefficient badger culling to reduce bovine tuberculosis in cattle [6], and highlights the need to incorporate host social structure into the development of disease control strategies. This is further underpinned by the observations that culling can change the behaviour of the remaining individuals in socially and spatially structured populations (e.g. badgers [Reference Tuyttens7–Reference Woodroffe9]), with resultant increases in the contact and transmission rate negating any potential benefits of control through population reduction [Reference Donnelly10]. Removal of individual animals may therefore have a different impact on control than measures which remove entire social groups, which has important practical implications for the control of infectious disease.
Paratuberculosis (also known as Johne's disease) is a chronic, usually fatal, enteritis of wild and domestic ruminants, with purported links to Crohn's disease in humans [Reference Naser11], caused by Mycobacterium avium subsp. paratuberculosis (Map). It causes not only great economic losses but also welfare issues for the agricultural industry worldwide [Reference Sweeney and Sweeney12]. The disease is notoriously difficult to control in ruminant livestock populations, a difficulty that may be partially accounted for by the recent extension of the known host range to include a number of non-ruminant wildlife species [Reference Daniels13]. Among these, rabbits are likely to have a particularly important role, following recent evidence that livestock and rabbits share the same Map strains and for high levels of livestock exposure to Map from rabbits via the faecal–oral route (ingestion of rabbit faecal pellets) [Reference Judge14] and the persistence of infection in rabbit populations over long timescales [Reference Judge15]. This persistence suggests that control of the infection in rabbit populations should be included in any strategies directed at reducing human and livestock exposure to the organism.
The aim of the present study is to use an existing simulation model of paratuberculosis dynamics in rabbit populations to quantify the relative effectiveness of removing hosts at different control efficiencies under different control scenarios, with control directed either at the individual or social group level, as single unrepeated measures or as long-term repeated strategies.
METHODS
The model
An existing model of Map dynamics in rabbit populations was used to address the aims of the study [Reference Judge15]. This is a stochastic compartmental model in which individuals make transitions between states representing different attributes of that individual, e.g. age classes (infant, adolescent or mature) and disease states (in this case individuals are simply classified as either susceptible or infected). Other transitions, such as birth or death of an individual, also occur which change the state of the population as a whole, rather than that of one individual. In addition to the age and disease states, each individual belongs to one of N social groups, which for the runs carried out here was chosen to be 100, and the model also tracks the gender of each individual. The carrying capacity for the social groups was set to 90, although actual populations are likely to remain somewhat below this level due to a density-dependent birth process which depends logistically on the total population. The location of the social groups is taken from a bivariate uniform distribution over a square domain with periodic boundary conditions. Movement rates between social groups are dependent on an exponentially decaying distance kernel, as described by Judge et al. [Reference Judge15]. Thus the complete configuration of the system is specified by the age class, sex, infection status and location (social group) of each animal.
For each possible transition a rate of occurrence is defined, which is in general a function of the states of the entire population; for example the rate of becoming infected depends on the total number of infected individuals with which the individual in question is in contact. Thus the set of rates change after each event (e.g. if an individual becomes infected the rates of infection for all susceptible individuals in contact with it will increase). The infection is modelled as being spread either horizontally (with a rate proportional to the number of infective individuals) or vertically (with a fixed probability when a birth occurs). After each event the set of rates is used in a Poisson process [Reference Renshaw16] to stochastically determine which the next event will be and how much time has elapsed, the rates then being recalculated after making the transition.
The Poisson process is equivalent to assigning an exponential distribution of inter-event times to each possible transition. This exponential probability distribution has the corresponding event rate as a parameter, and it is straightforward to show that by drawing inter-event times from such a distribution the average number of events per unit time is indeed equal to the supplied rate. By drawing samples in this way the model progresses through time. The resulting time evolution of the system (realization) is random, so averages over many realizations must be generated in order to present meaningful results (e.g. means, variances or distributions) from a stochastic model. (For a full description of the model see [Reference Judge15].)
Model parameter estimation
The rabbit population dynamics and infection parameter values were taken from Judge et al. [Reference Judge15] and are given in Table 1. All rates are expressed as a mean number of events per month and therefore one unit of model time corresponds to one month real time. The parameters defining rabbit demography were obtained from the literature sources noted in the table. The estimations of the infection transmission parameters are taken from data collected in a previous study from a low- to moderate-density wild Scottish population of rabbits naturally infected with Map, for which a maximum-likelihood fitting procedure was used to derive probabilities of vertical and horizontal transmission from the field data [Reference Judge17]. The probability of transmission via vertical routes, p v, is 0·326. The horizontal transmission coefficient per infective individual per month (β), based on the monthly per capita rate of infection from the empirical study, was estimated to be in the range between 0·013 and 0·046 [Reference Judge17]. When simulating rabbit control a β value of 0·019 was used (see below for discussion on this β value).
Table 1. Model parameters and values used
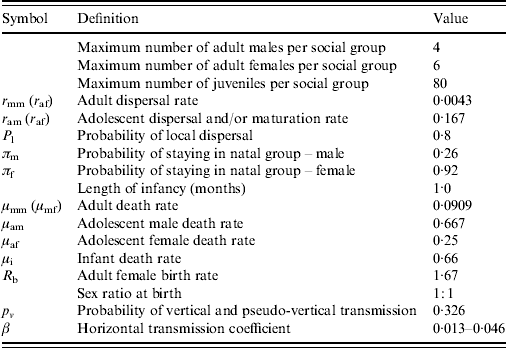
For the origin of these values see Judge et al. [Reference Judge15].
Model runs performed
The stochastic nature of the model causes the state at any one time to rapidly be diluted away, so that as long as the possibility of stochastic extinctions is avoided by using sufficiently large initial values for the population and number infected, the initial configuration is immaterial. Once both population and infection have reached their equilibrium values, the control measure is implemented by removing a fixed number of randomly selected individuals or social groups.
Three techniques of rabbit control were simulated:
(1) Single unrepeated culls of random rabbits (similar to shooting). One-off rabbit culls were simulated by instantaneous removal of a specified fraction of randomly selected individual rabbits from the host population.
(2) Single unrepeated culls of complete social groups (similar to warren removal techniques). In this control measure, a fixed number of groups were completely emptied, leaving their nest sites free for expansion of the remaining groups.
(3) Repeated culls of random rabbits (similar to repeated shooting events). The slow recovery rate of the infection after a single cull event suggests that repeated culling may have a more significant impact upon prevalence. Repeated culls were simulated by repeating control option (1) on an annual basis. Repeated removal of individuals was chosen over repeated removal of groups on the basis of the results from the unrepeated culls.
To quantify the probability of extinction of the infection in the wake of a cull, the number of realizations of the stochastic process (individual model runs) in which the infection became extinct was recorded. From the distribution of the total number of infected rabbits remaining after the population cull(s) across realizations, the proportion of the distribution crossing the y axis was taken as the probability of the infection becoming extinct.
RESULTS
One-off culls to remove individual rabbits
Single population reduction events targeting individual animals of up to 96% do not result in any noticeable chance of infection extinction (Fig. 1), while culls at the unrealistically high levels of 98% and 99% of the population yield infection extinction probabilities of 0·08 and 0·34 respectively.
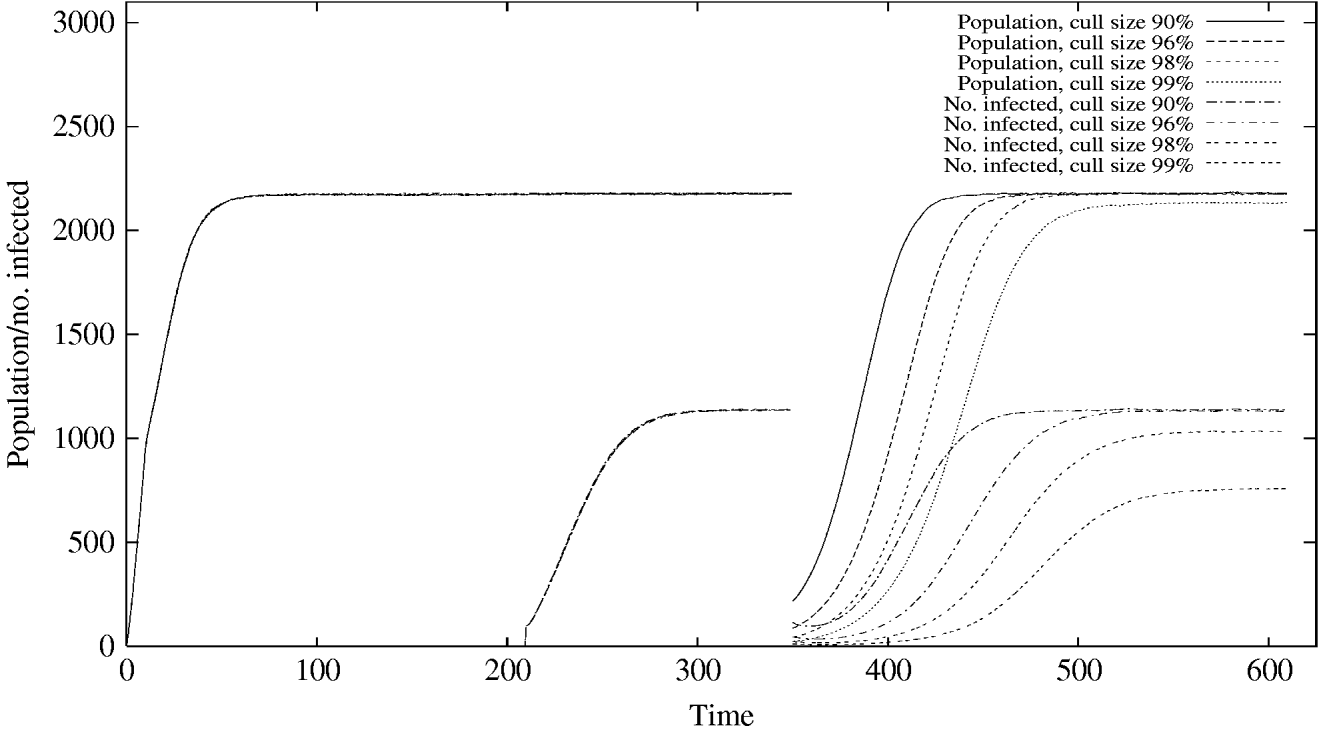
Fig. 1. The evolution of the mean population and number of rabbits infected, up to and after a cull at t=350. For some cull sizes the equilibrium values of these means are lowered after the cull, as a result of extinction of either the population or the infection in a proportion of the stochastic realizations. In the initialization period leading up to the cull the curves for the various cull sizes coincide.
For larger culls the infection takes slightly longer to recover to its full equilibrium level, but in all cases, the slow transmission rate of Map means that this takes around 180 months. These results can also be seen in Figure 2a, where the distribution of the number of infected animals among realizations immediately after a population reduction event is shown. Although no realizations were infection-free immediately, even with the 98% and 99% culls, many were left with a very small number of infected individuals (e.g. only a mean of 11 infected individuals in the case of a 99% cull) which resulted in chance eradication in the subsequent recovery period due to small populations being more susceptible to stochastic effects.
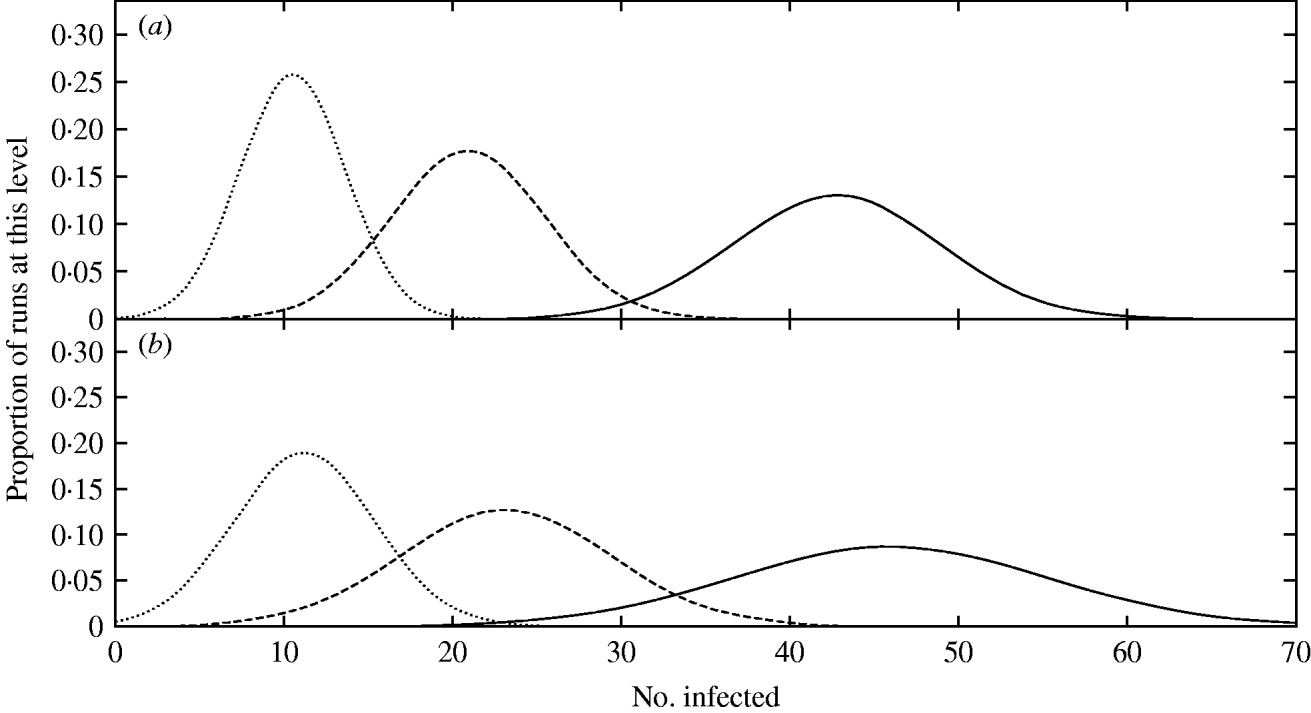
Fig. 2. The distribution among realizations of the number of infected individuals immediately after a cull event. Gaussian curves have been fitted to the data-points, which have been omitted for clarity as they closely follow the curves. Three levels of culling are shown: 96% removal (——), 98% removal (- - -) and 99% removal (. . . . . . .). Removing individuals (a) results in a lower variance than removing entire groups (b), and it can be seen that more of the mass in each distribution lies close to the origin in the latter case, giving rise to a greater extinction probability.
One-off culls to remove social groups
A slight broadening in the distributions of the population size and number of infected animals among realizations is apparent when targeting social groups for removal from the population compared to targeting individuals (Fig. 2). In the 99% cull, some realizations become extinct as a direct consequence of the cull, with an eradication probability immediately post-cull of 0·02, as visible in the non-zero y-intercept of the post-cull distribution at this cull size (see Fig. 2b). After allowing the system to recover to equilibrium, the final eradication probabilities were 0·01 and 0·16 for cull levels of 98% and 99% respectively. These values are considerably poorer than removal of individuals, despite a better performance immediately post-cull, a consequence of the faster recovery time of the infection in this case due to clustering of the remaining individuals, leaving a small but highly connected population. This points to removal of individuals as a superior approach when employing repeated cull strategies.
Repeated culling strategies to remove individual rabbits
Repeated annual population reductions are more effective than single one-off reductions with annual reductions of ⩾45% resulting in infection eradication (Fig. 3). These culls are carried out after a period long enough to allow the population and infection levels to stabilize, being stopped when the mean number of infected individuals either reaches zero or levels out, so that the number of infected individuals culled is equal to the number of re-infections in the inter-cull period. The 45% threshold in the cull size will be reduced if more frequent culls are performed. Overall reductions in prevalence come both from realizations in which the infection is eradicated and those in which the prevalence is reduced but the infection is not completely eradicated which, if no further culls are carried out, will recover to their previous values. From Figure 3 it can be seen that, for this cull frequency, a cull size of around 45% will eradicate the infection, but not the population. At 50% there is a considerable probability that the population itself will become extinct, while at 40% there is no appreciable probability of infection eradication. The infection eradication probability as a function of time is also shown in Figure 3 for the 45% annual cull.
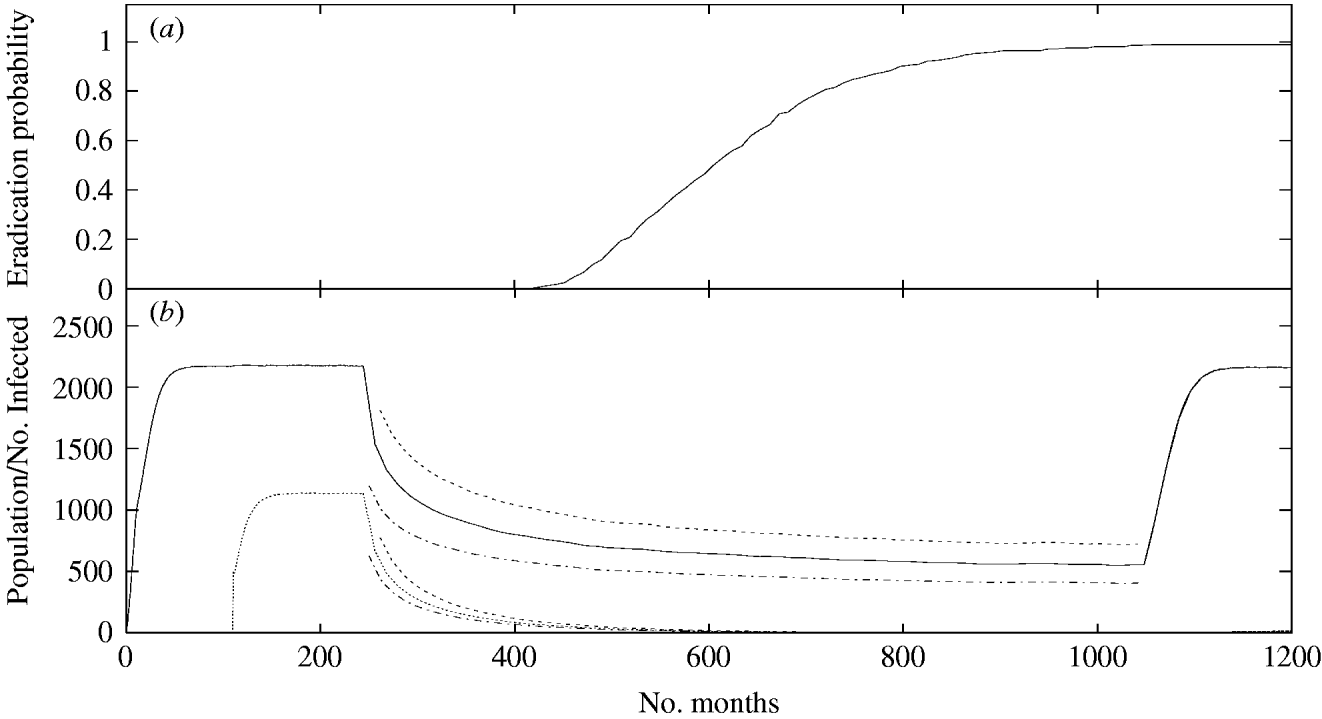
Fig. 3. (a) The mean population size (——) and prevalence of infection (. . . . . . .) among 200 realizations of the model for a 45% annual cull. Culling commences once population and infection are at equilibrium, here at 240 months, and continues annually for a further 840 months. During this period numbers oscillate, reaching an annual maximum just before the cull and a minimum directly afterwards. These maxima and minima are represented by the lines surrounding each of the curves displaying the means. As the annual minimum decreases, the probability of stochastic fluctuations causing extinction increases. (b) The growth of the probability of extinction of the infection over the same period. As shown here, it is possible to choose the size of the annual cull so that extinction of the infection becomes highly likely in the large time limit, while the population remains stable. Higher levels of annual cull result in a quicker growth of the extinction probability, but may give rise to extinction of the entire population.
DISCUSSION
Through the use of a numerical stochastic model, likely outcomes have been demonstrated for three different control strategies for Map: random removal of individuals; random removal of social groups; and repeated random removal of individuals on an annual basis. Extremely high rabbit population reduction levels (>96%) are necessary if either of the one-off rabbit cull strategies is to have even a small probability of eradicating the infection. At these high reduction levels the main contribution to this small eradication probability emerges not from the contribution of the probability of removing all infected individuals at the cull (which is highly unlikely), but from subsequent fluctuations while the infection remains for a short time at the reduced prevalence brought about by the cull. This effect can only be captured with a stochastic model. That these fluctuations are only able to bring about infection eradication in such extreme cases demonstrates the highly persistent nature of this infection and the difficulty associated with managing it.
It has been shown that targeting entire social groups for removal results in a higher probability of eradicating the infection during the cull event itself than random removal of individuals at an equivalent level. This is reflected in a higher degree of variability post-cull in the distribution of the number of individuals infected. It is likely that this broadening of the post-cull distribution of infection is due to correlations in the infective status of individuals in the same group, arising from the within-group component of the horizontal transmission. Consequently removal of some groups will have a very large impact on the number of infected individuals, while removal of others will have very little impact, giving the variability mentioned above. Although a better result is obtained in the immediate aftermath of the cull, the prevalence remains low for a much smaller amount of time as the remaining population is clustered in the few remaining groups and so has a higher contact rate. This faster recovery of the prevalence leaves less opportunity for fluctuations to take the system to the infection-free state, and gives rise to a worse long-term performance.
The ineffectiveness of single-cull strategies, together with the difference in population and infection recovery rates, points to the use of repeated cull strategies. For these the random removal of individuals is superior to group removal due to the faster infection recovery rate in the latter. The differential response of the population and infection gives rise to a lag between the respective times to recovery to equilibrium. Thus a point in time will be reached when the population has almost fully recovered but the infection has not. At this point, a further cull would bring the expected prevalence to a lower level than a cull of the same size would upon an equilibrated population. Repetition of this procedure should result in a much depleted infection level, distinctly increasing the probability of eradicating the infection but without causing the population to go extinct. This hypothesis was investigated by exploring different cull sizes while keeping the cull frequency fixed, in this case at one cull per year. The findings indicate that the infection can feasibly be eradicated from rabbit populations using repeated culls, although this is likely to take a number of years to achieve. In the case of an annual cull removing 45% of the population, this time period may be as long as 33 years, although this period is for the eradication probability to approach 1, so that in most cases eradication would be achieved before this time. Eradicating Map whilst maintaining the rabbit population is only possible due to the fact that rabbits reproduce faster than Map transmits between rabbits.
The finding that Map is extremely persistent in rabbit populations and requires significant and prolonged effort to achieve control is likely to be conservative – for example, if the recent findings by Jenkins et al. [Reference Jenkins18] that population reduction may increase contact rates and impair infection control are applicable to rabbits, any increase in movement rate would act to increase infection persistence and reduce control efficacy (R. S. Davidson & M. R. Hutchings, unpublished data). Furthermore, landowners often attempt to prevent immigration of rabbits by rabbit netting their land to create a closed population as simulated here. The use of rabbit fencing and population reduction has been shown to be effective at reducing levels of rabbit faecal contamination of pasture [Reference Daniels19]. When such measures are absent or non-effective and immigration is non-zero, background infection from contiguous neighbours acts to reinforce infection levels, further slowing control. In short, many years of control are needed, even if a landowner could completely close the local population and any immigration would act to prolong the control effort needed to eradicate the infection.
Although Map has been used as a case study, these results apply in principle to other infections with low transmission rates and hence low rates of recovery of the infection. With any infection at high prevalence, a single cull is highly unlikely to eradicate it, although it will produce short-term reductions in prevalence. Repeated culls at moderate efficiencies will eradicate the infection and the level of culling necessary will be a function of the frequency with which it is carried out. Cull sizes beyond the threshold level for a given inter-cull period will lead to faster eradication of the infection, but with a greater impact on the population. Beyond a second threshold the population will also be driven to extinction.
Eradication of both the population and the infection may, in the case of rabbits and Map, be seen as advantageous as the rabbit is a pest species. However, the possibility of removing the infection without the population may have advantages from an infection control point of view, as competition effects could act to reduce the rates of immigration from outside areas post-cull and consequently slow re-infection. The study of such effects would require an extended model with external sources of infection. Another potential advantage occurs where the host population is a species of conservation importance (e.g. bovine tuberculosis in badgers in the United Kingdom; bovine tuberculosis and brucellosis in bison in Canada [Reference Joly and Messier20]), in which case eradication without population removal is an ideal scenario. The results presented here suggest that this effect is a theoretical possibility for any infection for which transmission occurs at a lower rate than reproduction, as with rabbits and Map. It should be noted, however, that recent findings on bovine tuberculosis in badgers indicate that culling disrupts social structure and leads to a scattering of infected individuals in neighbouring areas. The dynamics which give rise to such an effect are not included in the model used here.
The horizontal transmission rate used here is taken from a range of estimates given in Judge et al. [Reference Judge17]. There the real value was considered to be at the higher end of the range, however a value towards the lower end of the range has been considered here, giving a lower bound on times to reach a given eradication probability. Higher values of β will give rise to larger values for these eradication times. However, the simulations used here with the lower β value suggest that Map is extremely persistent and difficult to eradicate, with repeated culling strategies taking many years before achieving success. As such it is likely that sustained effort over extended periods is required to control Map in rabbit populations and this effort is likely to be greater than that predicted here. Increases in the value of β result in a faster recovery of the infection in rabbit populations after a population reduction event. At β values >0·034, the infection recovers faster than the population and the effect described above, where optimal culling rates result in the eradication of infection but the survival of the population, is not achievable. The parameters used represent a typical set estimated from field data, but uncertainty in these values leads to inevitable uncertainty in estimates of the extinction times. The lack of data on Map makes a more precise statistical inference of eradication probabilities, optimal cull frequency and size, and consequently the time to eradication unfeasible, however, the low recovery rate means that the conclusions on the efficacy of repeated culling strategies are likely to remain the same.
In conclusion, paratuberculosis control strategies based on one-off rabbit population reduction events require unrealistically high proportions of the rabbit population to achieve Map eradication. Control strategies based on repeated population reduction events have greater chances of success in eradicating Map from the rabbit population. The persistence of Map in livestock systems despite control seems to be mirrored in infected rabbit populations, with significant effort over an extended period (i.e. many years) being required to eradicate Map from rabbit populations. The difficulties in controlling Map in rabbit populations demonstrated here further highlight the risk rabbits pose to livestock, especially given the high levels of exposure of cattle to rabbit faeces and the likely persistence of infection in rabbit populations in the absence of control. Currently Map-infected rabbit populations may be considered relatively rare in the United Kingdom. However, given the ubiquitous distribution of the rabbit in the country and the likely persistence of infection in rabbit populations, the use of repeated control strategies may be advisable, and where possible these should be conducted at the landscape scale via landowner cooperation.
ACKNOWLEDGEMENTS
BioSS and SAC receive funding from the Scottish Executive. M.R.H. held a Scottish Executive Senior Research Fellowship.
DECLARATION OF INTEREST
None.





