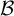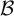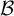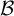1 Introduction
1.1 Toeplitz subshifts
Let
![]() $\eta \in \{0,1\}^{\mathbb Z}$
be a non-periodic Toeplitz sequence [Reference Jacobs and Keane17] with period structure
$\eta \in \{0,1\}^{\mathbb Z}$
be a non-periodic Toeplitz sequence [Reference Jacobs and Keane17] with period structure
![]() $p_1\mid p_2\mid p_3 \ldots \to \infty $
. That means for each
$p_1\mid p_2\mid p_3 \ldots \to \infty $
. That means for each
![]() $k\in {\mathbb Z}$
, there exists
$k\in {\mathbb Z}$
, there exists
![]() $n\ge 1$
such that
$n\ge 1$
such that
![]() $\eta _{|k+p_n{\mathbb Z}}$
is constant, but
$\eta _{|k+p_n{\mathbb Z}}$
is constant, but
![]() $\eta $
is not periodic (the latter excludes trivial cases). Denote the orbit closure of
$\eta $
is not periodic (the latter excludes trivial cases). Denote the orbit closure of
![]() $\eta $
under the left shift
$\eta $
under the left shift
![]() $\sigma $
on
$\sigma $
on
![]() $\{0,1\}^{\mathbb Z}$
by
$\{0,1\}^{\mathbb Z}$
by
![]() $X_\eta $
. Each such subshift is called a Toeplitz shift. It follows from the work of Williams [Reference Williams25] that such systems are in fact almost 1-1 extensions of their maximal equicontinuous factor (MEF), in this case of an associated odometer
$X_\eta $
. Each such subshift is called a Toeplitz shift. It follows from the work of Williams [Reference Williams25] that such systems are in fact almost 1-1 extensions of their maximal equicontinuous factor (MEF), in this case of an associated odometer
![]() $(G,T)$
, where G is the compact topological group
$(G,T)$
, where G is the compact topological group
![]() $\varprojlim {\mathbb Z}/p_n{\mathbb Z}$
built from the period structure
$\varprojlim {\mathbb Z}/p_n{\mathbb Z}$
built from the period structure
![]() $(p_n)_{n\ge 1}$
, and T is the translation by
$(p_n)_{n\ge 1}$
, and T is the translation by
![]() $(1, 1,\ldots )$
. Recall that odometers are minimal, equicontinuous and zero-dimensional dynamical systems, and the conjunction of these three properties characterizes them among all topological dynamical systems, see [Reference Downarowicz, Kolyada, Manin and Ward8].
$(1, 1,\ldots )$
. Recall that odometers are minimal, equicontinuous and zero-dimensional dynamical systems, and the conjunction of these three properties characterizes them among all topological dynamical systems, see [Reference Downarowicz, Kolyada, Manin and Ward8].
1.2 The centralizer
For any subshift
![]() $(Y,\sigma )$
, that is, a shift invariant closed subset
$(Y,\sigma )$
, that is, a shift invariant closed subset
![]() $Y\subseteq \{0,1\}^{\mathbb Z}$
, the automorphism group (or centralizer) is the group of all homeomorphisms
$Y\subseteq \{0,1\}^{\mathbb Z}$
, the automorphism group (or centralizer) is the group of all homeomorphisms
![]() $U\colon Y\to Y$
which commute with
$U\colon Y\to Y$
which commute with
![]() $\sigma $
. Its elements are sliding block codes [Reference Hedlund16]. Therefore, the automorphism group is countable. Since all powers of the shift are elements of the centralizer, it contains a copy of
$\sigma $
. Its elements are sliding block codes [Reference Hedlund16]. Therefore, the automorphism group is countable. Since all powers of the shift are elements of the centralizer, it contains a copy of
![]() ${\mathbb Z}$
as a normal subgroup. We say that the automorphism group is trivial if it consists solely of powers of the shift.
${\mathbb Z}$
as a normal subgroup. We say that the automorphism group is trivial if it consists solely of powers of the shift.
Centralizers are studied for various classes of systems. Bułatek and Kwiatkowski [Reference Bułatek and Kwiatkowski2] do it for Toeplitz subshifts with separated holes (Sh) using elements of the associated odometer
![]() $(G,T)$
. Moreover, in [Reference Bułatek and Kwiatkowski3], they deliver examples of Toeplitz subshifts with positive topological entropy and trivial automorphism group. More recently, Cyr and Kra study automorphism groups of subshifts of subquadratic and linear growth in [Reference Cyr and Kra4, Reference Cyr and Kra5]. In [Reference Cyr and Kra5], they prove that the cosets of powers of the shift in the centralizer of any topologically transitive subshift of subquadratic growth form a periodic group. In [Reference Cyr and Kra4], they show that any minimal subshift with non-superlinear complexity has a virtually
$(G,T)$
. Moreover, in [Reference Bułatek and Kwiatkowski3], they deliver examples of Toeplitz subshifts with positive topological entropy and trivial automorphism group. More recently, Cyr and Kra study automorphism groups of subshifts of subquadratic and linear growth in [Reference Cyr and Kra4, Reference Cyr and Kra5]. In [Reference Cyr and Kra5], they prove that the cosets of powers of the shift in the centralizer of any topologically transitive subshift of subquadratic growth form a periodic group. In [Reference Cyr and Kra4], they show that any minimal subshift with non-superlinear complexity has a virtually
![]() ${\mathbb Z}$
automorphism group, answering the question asked in [Reference Salo and Törmä24]. In [Reference Donoso, Durand, Maass and Petite6], the same result is shown independently with different methods by Donoso et al. However, the centralizer can be quite a complicated group. In [Reference Salo23], Salo gives an example of a Toeplitz subshift with not finitely generated automorphism group. We provide another example with this property, see equation (53) and Corollary 3.25.
${\mathbb Z}$
automorphism group, answering the question asked in [Reference Salo and Törmä24]. In [Reference Donoso, Durand, Maass and Petite6], the same result is shown independently with different methods by Donoso et al. However, the centralizer can be quite a complicated group. In [Reference Salo23], Salo gives an example of a Toeplitz subshift with not finitely generated automorphism group. We provide another example with this property, see equation (53) and Corollary 3.25.
1.3 This paper’s contributions to general Toeplitz shifts
Let
![]() $\eta $
be a Toeplitz sequence with period structure
$\eta $
be a Toeplitz sequence with period structure
![]() $(p_n)_{n\ge 1}$
and recall from [Reference Bułatek and Kwiatkowski2] that a position
$(p_n)_{n\ge 1}$
and recall from [Reference Bułatek and Kwiatkowski2] that a position
![]() $k\in {\mathbb Z}$
is called a hole at level N if
$k\in {\mathbb Z}$
is called a hole at level N if
![]() $\eta _{|k+p_N{\mathbb Z}}$
is not constant. We refine this concept and call such a hole essential if the residue class
$\eta _{|k+p_N{\mathbb Z}}$
is not constant. We refine this concept and call such a hole essential if the residue class
![]() $k+p_N{\mathbb Z}$
contains holes of each level
$k+p_N{\mathbb Z}$
contains holes of each level
![]() $n\ge N$
, see Definition 2.2. The minimal period
$n\ge N$
, see Definition 2.2. The minimal period
![]() $\tilde {\tau }_N$
of the set of essential holes at level N divides
$\tilde {\tau }_N$
of the set of essential holes at level N divides
![]() $p_N$
and, under a (seemingly strong) additional assumption, Theorem 2.8 provides restrictions on the size of the centralizer in terms of the quotients
$p_N$
and, under a (seemingly strong) additional assumption, Theorem 2.8 provides restrictions on the size of the centralizer in terms of the quotients
![]() $p_N/\tilde {\tau }_N$
. A direct application of this result to a variant of the Garcia–Hedlund sequence is discussed in Example 2.19. After that, using a mixture of topological and arithmetic arguments, we show that the additional assumption is satisfied more often than one may expect—the main tool is Theorem 2.31. Along this way, we exploit suitable topological variants of the separated holes condition (Sh) from [Reference Bułatek and Kwiatkowski2] in Proposition 2.16, and verify these conditions under arithmetic assumptions tailor-made for the
$p_N/\tilde {\tau }_N$
. A direct application of this result to a variant of the Garcia–Hedlund sequence is discussed in Example 2.19. After that, using a mixture of topological and arithmetic arguments, we show that the additional assumption is satisfied more often than one may expect—the main tool is Theorem 2.31. Along this way, we exploit suitable topological variants of the separated holes condition (Sh) from [Reference Bułatek and Kwiatkowski2] in Proposition 2.16, and verify these conditions under arithmetic assumptions tailor-made for the
![]() ${\mathcal B}$
-free case in Proposition 2.30. We note that our techniques generalize the setting from [Reference Bułatek and Kwiatkowski2], but are kind of transverse to the setting from [Reference Bułatek and Kwiatkowski3], see Remark 2.10.
${\mathcal B}$
-free case in Proposition 2.30. We note that our techniques generalize the setting from [Reference Bułatek and Kwiatkowski2], but are kind of transverse to the setting from [Reference Bułatek and Kwiatkowski3], see Remark 2.10.
1.4 The centralizer of
 ${\mathcal B}$
-free Toeplitz shifts
${\mathcal B}$
-free Toeplitz shifts
For any set
![]() ${\mathcal B}\subseteq \{2,3,\ldots \}$
, let
${\mathcal B}\subseteq \{2,3,\ldots \}$
, let
be the set of multiples of
![]() ${\mathcal B}$
and
${\mathcal B}$
and
the set of
![]() ${\mathcal B}$
-free numbers. One can easily modify a set
${\mathcal B}$
-free numbers. One can easily modify a set
![]() ${\mathcal B}$
to have the same set of multiples and to be primitive, that is,
${\mathcal B}$
to have the same set of multiples and to be primitive, that is,
![]() $b\nmid b'$
for different
$b\nmid b'$
for different
![]() $b,b'\in {\mathcal B}$
. So, we will tacitly assume that
$b,b'\in {\mathcal B}$
. So, we will tacitly assume that
![]() ${\mathcal B}$
is primitive. The investigation of sets of multiples and
${\mathcal B}$
is primitive. The investigation of sets of multiples and
![]() ${\mathcal B}$
-free numbers has a quite long history, see [Reference Hall15]. Recently, the subshifts associated with
${\mathcal B}$
-free numbers has a quite long history, see [Reference Hall15]. Recently, the subshifts associated with
![]() ${\mathcal B}$
-free numbers are under intensive study, see e.g. [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk12, Reference Kasjan, Keller and Lemańczyk18] and references therein. Namely, let
${\mathcal B}$
-free numbers are under intensive study, see e.g. [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk12, Reference Kasjan, Keller and Lemańczyk18] and references therein. Namely, let
![]() $\eta \in \{0,1\}^{\mathbb Z}$
be the characteristic function of the
$\eta \in \{0,1\}^{\mathbb Z}$
be the characteristic function of the
![]() ${\mathcal B}$
-free numbers. Minimality of
${\mathcal B}$
-free numbers. Minimality of
![]() $(X_\eta ,\sigma )$
is equivalent to
$(X_\eta ,\sigma )$
is equivalent to
![]() $\eta $
being Toeplitz is shown in [Reference Kasjan, Keller and Lemańczyk18, Theorem B], whenever
$\eta $
being Toeplitz is shown in [Reference Kasjan, Keller and Lemańczyk18, Theorem B], whenever
![]() ${\mathcal B}$
is taut. The tautness assumption was removed in [Reference Dymek, Kasjan and Kułaga-Przymus11, Theorem 3.7]. So, in the
${\mathcal B}$
is taut. The tautness assumption was removed in [Reference Dymek, Kasjan and Kułaga-Przymus11, Theorem 3.7]. So, in the
![]() ${\mathcal B}$
-free context,
${\mathcal B}$
-free context,
![]() $(X_\eta ,\sigma )$
is minimal if and only if
$(X_\eta ,\sigma )$
is minimal if and only if
![]() $\eta $
is a Toeplitz sequence.
$\eta $
is a Toeplitz sequence.
In the case of
![]() ${\mathcal B}$
-free Toeplitz subshifts, the previously cited results for low complexity systems are not useful, because even very simple
${\mathcal B}$
-free Toeplitz subshifts, the previously cited results for low complexity systems are not useful, because even very simple
![]() ${\mathcal B}$
-free Toeplitz systems may have superpolynomial complexity, see §3.6, where this is shown for
${\mathcal B}$
-free Toeplitz systems may have superpolynomial complexity, see §3.6, where this is shown for
![]() ${\mathcal B}={\mathcal B}_1:=\{2^nc_n:n\in {\mathbb N}\}$
with pairwise coprime odd
${\mathcal B}={\mathcal B}_1:=\{2^nc_n:n\in {\mathbb N}\}$
with pairwise coprime odd
![]() $c_n$
. Although the separated holes condition (Sh) is satisfied for this simple example, we were not able to use the results from [Reference Bułatek and Kwiatkowski2] to determine the centralizer. However, its triviality was shown with more direct methods in [Reference Dymek10]. Nevertheless, there are many
$c_n$
. Although the separated holes condition (Sh) is satisfied for this simple example, we were not able to use the results from [Reference Bułatek and Kwiatkowski2] to determine the centralizer. However, its triviality was shown with more direct methods in [Reference Dymek10]. Nevertheless, there are many
![]() ${\mathcal B}$
-free Toeplitz systems which do not satisfy (Sh) anyway, see the example discussed at the end of this introduction, so that there is need for techniques relying neither on low complexity nor on (Sh).
${\mathcal B}$
-free Toeplitz systems which do not satisfy (Sh) anyway, see the example discussed at the end of this introduction, so that there is need for techniques relying neither on low complexity nor on (Sh).
We mention briefly that Mentzen [Reference Mentzen22] proves the triviality of the automorphism group for any Erdős
![]() ${\mathcal B}$
-free subshift, that is, when
${\mathcal B}$
-free subshift, that is, when
![]() ${\mathcal B}$
is infinite, pairwise coprime and
${\mathcal B}$
is infinite, pairwise coprime and
![]() $\sum _{b\in {\mathcal B}}({1}/b)<\infty $
. This is extended to taut
$\sum _{b\in {\mathcal B}}({1}/b)<\infty $
. This is extended to taut
![]() ${\mathcal B}$
containing an infinite pairwise coprime subset in [Reference Keller19, Reference Keller, Lemańczyk, Richard and Sell20]. This class of
${\mathcal B}$
containing an infinite pairwise coprime subset in [Reference Keller19, Reference Keller, Lemańczyk, Richard and Sell20]. This class of
![]() ${\mathcal B}$
-free subshifts is kind of opposite to the
${\mathcal B}$
-free subshifts is kind of opposite to the
![]() ${\mathcal B}$
-free Toeplitz shifts.
${\mathcal B}$
-free Toeplitz shifts.
1.5 This paper’s contributions to
 ${\mathcal B}$
-free Toeplitz shifts
${\mathcal B}$
-free Toeplitz shifts
In §3, the results from §2 are applied to
![]() ${\mathcal B}$
-free examples. This is possible because Theorem 3.17 provides an arithmetic characterization of the sets of essential holes in terms of sets of multiples derived explicitly from the set
${\mathcal B}$
-free examples. This is possible because Theorem 3.17 provides an arithmetic characterization of the sets of essential holes in terms of sets of multiples derived explicitly from the set
![]() ${\mathcal B}$
. Then we can use the general results to produce examples of minimal
${\mathcal B}$
. Then we can use the general results to produce examples of minimal
![]() ${\mathcal B}$
-free systems, including not only the case
${\mathcal B}$
-free systems, including not only the case
![]() ${\mathcal B}={\mathcal B}_1$
treated in [Reference Dymek10] but also many systems violating the separated holes condition (Sh), which have trivial centralizers, see §3.3. (The reader will notice that a very broad class of examples can be treated along the same lines.) The fact that the general results fail to guarantee triviality of the centralizer for some examples, to which even the basic Theorem 2.8 applies, is not a shortcoming of our approach. This is illustrated in §3.4, where we consider simple variants of
${\mathcal B}={\mathcal B}_1$
treated in [Reference Dymek10] but also many systems violating the separated holes condition (Sh), which have trivial centralizers, see §3.3. (The reader will notice that a very broad class of examples can be treated along the same lines.) The fact that the general results fail to guarantee triviality of the centralizer for some examples, to which even the basic Theorem 2.8 applies, is not a shortcoming of our approach. This is illustrated in §3.4, where we consider simple variants of
![]() ${\mathcal B}={\mathcal B}_1$
, still satisfying condition (Sh), but having non-trivial centralizers—just as big as Theorem 2.8 allows them to be. This provides a negative answer to [Reference Ferenczi, Kułaga Przymus, Lemańczyk, Ferenczi, Kułaga-Przymus and Lemańczyk13, Question 11]. Indeed, a slight generalization of this construction provides examples for which the centralizer contains elements of arbitrarily large finite order, see Remark 3.24. It should be noticed that our examples have superpolynomial complexity, see Proposition 3.30, so that the complexity based results from the literature discussed above do not apply.
${\mathcal B}={\mathcal B}_1$
, still satisfying condition (Sh), but having non-trivial centralizers—just as big as Theorem 2.8 allows them to be. This provides a negative answer to [Reference Ferenczi, Kułaga Przymus, Lemańczyk, Ferenczi, Kułaga-Przymus and Lemańczyk13, Question 11]. Indeed, a slight generalization of this construction provides examples for which the centralizer contains elements of arbitrarily large finite order, see Remark 3.24. It should be noticed that our examples have superpolynomial complexity, see Proposition 3.30, so that the complexity based results from the literature discussed above do not apply.
1.6 The formal setting
We recall some notation and results from [Reference Baake, Jäger and Lenz1], where a cut-and-project scheme is associated with a Toeplitz sequence
![]() $\eta \in \{0,1\}^{\mathbb Z}$
.
$\eta \in \{0,1\}^{\mathbb Z}$
.
-
(i)
 $p_1\mid p_2\mid p_3 \ldots \to \infty $
is a period structure of
$p_1\mid p_2\mid p_3 \ldots \to \infty $
is a period structure of
 $\eta $
.
$\eta $
. -
(ii)
 ${\mathcal P}_n^i:=\{k\in {\mathbb Z}: \eta _{|k+p_n{\mathbb Z}}=i\}$
denotes
${\mathcal P}_n^i:=\{k\in {\mathbb Z}: \eta _{|k+p_n{\mathbb Z}}=i\}$
denotes
 $p_n$
-periodic positions of
$p_n$
-periodic positions of
 $i=0,1$
on
$i=0,1$
on
 $\eta $
and
$\eta $
and
 ${\mathcal H}_n:={\mathbb Z}\setminus ({\mathcal P}_n^0\cup {\mathcal P}_n^1)$
denotes the set of holes at level n.
${\mathcal H}_n:={\mathbb Z}\setminus ({\mathcal P}_n^0\cup {\mathcal P}_n^1)$
denotes the set of holes at level n. -
(iii)
 $G:=\varprojlim {\mathbb Z}/p_n{\mathbb Z}$
and
$G:=\varprojlim {\mathbb Z}/p_n{\mathbb Z}$
and
 $\Delta \colon {\mathbb Z} \rightarrow G$
, where
$\Delta \colon {\mathbb Z} \rightarrow G$
, where
 $\Delta (n) = (n+ p_1{\mathbb Z},n+ p_2{\mathbb Z},\ldots )$
denotes the diagonal embedding.
$\Delta (n) = (n+ p_1{\mathbb Z},n+ p_2{\mathbb Z},\ldots )$
denotes the diagonal embedding. -
(iv)
 $T\colon G \rightarrow G$
denotes the rotation by
$T\colon G \rightarrow G$
denotes the rotation by
 $\Delta (1)$
, that is,
$\Delta (1)$
, that is,
 $(Tg)_n = g_n + 1+p_n{\mathbb Z}$
for all
$(Tg)_n = g_n + 1+p_n{\mathbb Z}$
for all
 $n\in {\mathbb N}$
.
$n\in {\mathbb N}$
. -
(v) The topology on G is generated by the (open and closed) cylinder sets
 $$ \begin{align*}U_n(h) := \{g\in G : g_n = h_n\},\quad h\in G.\end{align*} $$
$$ \begin{align*}U_n(h) := \{g\in G : g_n = h_n\},\quad h\in G.\end{align*} $$
-
(vi)
 $V^i:=\bigcup _{n\in {\mathbb N}}\bigcup _{k\in {\mathcal P}_n^i\cap [0,p_n)}U_n(\Delta (k))$
for
$V^i:=\bigcup _{n\in {\mathbb N}}\bigcup _{k\in {\mathcal P}_n^i\cap [0,p_n)}U_n(\Delta (k))$
for
 $i=0,1$
.
$i=0,1$
. -
(vii) The window
 $W:=\overline {V^1}=G\setminus V^0$
is topologically regular, i.e.
$W:=\overline {V^1}=G\setminus V^0$
is topologically regular, i.e.
 $\overline {\operatorname {int}(W)}=W$
.
$\overline {\operatorname {int}(W)}=W$
. -
(viii)
 $\phi \colon G\rightarrow \{0,1\}^{\mathbb Z}$
is the coding function:
$\phi \colon G\rightarrow \{0,1\}^{\mathbb Z}$
is the coding function:
 $(\phi (g))_n = \mathbf {1}_W(g+\Delta (n))$
. Observe that
$(\phi (g))_n = \mathbf {1}_W(g+\Delta (n))$
. Observe that
 $\phi (\Delta (0))=\eta $
.
$\phi (\Delta (0))=\eta $
.
1.7 More background material and an outline of the paper
The odometer
![]() $(G,T)$
is the MEF of
$(G,T)$
is the MEF of
![]() $(X_{\eta },\sigma )$
, see [Reference Williams25]. Let
$(X_{\eta },\sigma )$
, see [Reference Williams25]. Let
![]() $F\colon X_\eta \to X_\eta $
be an automorphism commuting with
$F\colon X_\eta \to X_\eta $
be an automorphism commuting with
![]() $\sigma $
, and denote by
$\sigma $
, and denote by
![]() $\pi :(X_\eta ,\sigma )\to (G,T)$
that factor map onto the MEF which is uniquely determined by
$\pi :(X_\eta ,\sigma )\to (G,T)$
that factor map onto the MEF which is uniquely determined by
![]() $\pi (\eta )=\Delta (0)$
. Then there is
$\pi (\eta )=\Delta (0)$
. Then there is
![]() $y_F\in G$
such that the rotation
$y_F\in G$
such that the rotation
![]() $f:y\mapsto y+y_F$
on G represents F in the sense that
$f:y\mapsto y+y_F$
on G represents F in the sense that
![]() $\pi \circ F=f\circ \pi $
(see e.g. [Reference Donoso, Durand, Maass and Petite6, Lemma 2.4]). Observe that
$\pi \circ F=f\circ \pi $
(see e.g. [Reference Donoso, Durand, Maass and Petite6, Lemma 2.4]). Observe that
![]() $y_F=\pi (F(\eta ))$
.
$y_F=\pi (F(\eta ))$
.
Denote by
![]() $C_\phi $
the set of continuity points of
$C_\phi $
the set of continuity points of
![]() $\phi :G\to \{0,1\}^{\mathbb Z}$
. Then,
$\phi :G\to \{0,1\}^{\mathbb Z}$
. Then,
![]() $|\pi ^{-1}\{\pi (x)\}|=1$
if and only if
$|\pi ^{-1}\{\pi (x)\}|=1$
if and only if
![]() $\pi (x)\in C_\phi $
and, in this case,
$\pi (x)\in C_\phi $
and, in this case,
![]() $x=\phi (\pi (x))$
. This is folklore knowledge, but the reader may consult [Reference Keller and Richard21, Remark 4.2] and also [Reference Downarowicz, Kolyada, Manin and Ward8, §§5–7] for a related and more general perspective on this point.
$x=\phi (\pi (x))$
. This is folklore knowledge, but the reader may consult [Reference Keller and Richard21, Remark 4.2] and also [Reference Downarowicz, Kolyada, Manin and Ward8, §§5–7] for a related and more general perspective on this point.
Since F is a bijection respecting the fibre structure
![]() $X_\eta =\bigcup _{h\in G}\pi ^{-1}\{h\}$
, we have
$X_\eta =\bigcup _{h\in G}\pi ^{-1}\{h\}$
, we have
![]() $|\pi ^{-1}\{\pi (F(x))\}|=|\pi ^{-1}\{\pi (x)\}|$
for all
$|\pi ^{-1}\{\pi (F(x))\}|=|\pi ^{-1}\{\pi (x)\}|$
for all
![]() $x\in X_\eta $
. In particular,
$x\in X_\eta $
. In particular,
![]() $f(C_\phi )=C_\phi $
, that is,
$f(C_\phi )=C_\phi $
, that is,
![]() $C_\phi +y_F=C_\phi $
, see also [Reference Downarowicz, Kolyada, Manin and Ward8, Lemma 4.2]. As the set of discontinuities of the indicator function
$C_\phi +y_F=C_\phi $
, see also [Reference Downarowicz, Kolyada, Manin and Ward8, Lemma 4.2]. As the set of discontinuities of the indicator function
![]() $\mathbf {1}_W$
is precisely the boundary
$\mathbf {1}_W$
is precisely the boundary
![]() $\partial W$
, a moment’s reflection shows that
$\partial W$
, a moment’s reflection shows that
![]() $X_\eta \setminus C_\phi =\bigcup _{k\in {\mathbb Z}}\partial W+\Delta (k)$
, so
$X_\eta \setminus C_\phi =\bigcup _{k\in {\mathbb Z}}\partial W+\Delta (k)$
, so
We will use only this property of
![]() $y_F$
to investigate the nature of possible automorphisms F. It is quite natural to expect that this will be much facilitated if the union on the right-hand side of equation (1) is disjoint. Indeed, for general Toeplitz sequences, Bułatek and Kwiatkowski [Reference Bułatek and Kwiatkowski2] studied the centralizer problem under this assumption, because their condition (Sh) is equivalent to the disjointness condition
$y_F$
to investigate the nature of possible automorphisms F. It is quite natural to expect that this will be much facilitated if the union on the right-hand side of equation (1) is disjoint. Indeed, for general Toeplitz sequences, Bułatek and Kwiatkowski [Reference Bułatek and Kwiatkowski2] studied the centralizer problem under this assumption, because their condition (Sh) is equivalent to the disjointness condition
Namely, condition (Sh) is satisfied if and only if each T-orbit in G hits the set of discontinuities of
![]() $\phi $
at most once, which is clearly equivalent to condition (D), see also [Reference Downarowicz, Kwiatkowski and Lacroix9, remark after Definition 1].
$\phi $
at most once, which is clearly equivalent to condition (D), see also [Reference Downarowicz, Kwiatkowski and Lacroix9, remark after Definition 1].
As in [Reference Bułatek and Kwiatkowski2, Proposition 3], it follows that:
-
(1) each fibre over a point in the MEF contains either exactly one or exactly two points; and
-
(2) there exists
 $N\in {\mathbb N}$
such that
$N\in {\mathbb N}$
such that
 $\partial W+y_F\subseteq \bigcup _{|k|\leqslant N}\partial W+\Delta (k)$
.
$\partial W+y_F\subseteq \bigcup _{|k|\leqslant N}\partial W+\Delta (k)$
.
We will introduce a weaker disjointness condition which also implies condition (2), see Proposition 2.12:
 $$ \begin{align} &\text{for all } k\in{\mathbb Z}\setminus\{0\}: \partial W\cap(\partial W-\Delta(k))\nonumber\\ &\quad\text{ is nowhere dense with respect to the subspace topology of }\partial W. \end{align} $$
$$ \begin{align} &\text{for all } k\in{\mathbb Z}\setminus\{0\}: \partial W\cap(\partial W-\Delta(k))\nonumber\\ &\quad\text{ is nowhere dense with respect to the subspace topology of }\partial W. \end{align} $$
Moreover, we need a strengthened version of this condition which, in many examples, will help to show that
![]() $\partial W+y_F\subseteq \partial W+\Delta (k_0)$
for a single
$\partial W+y_F\subseteq \partial W+\Delta (k_0)$
for a single
![]() $k_0\in {\mathbb Z}$
:
$k_0\in {\mathbb Z}$
:
 $$ \begin{align} &\text{for all } k\in{\mathbb Z}\setminus\{0\}\ \text{ for all } \beta\in G: \partial W\cap(\partial W-\beta)\cap(\partial W-2\beta-\Delta(k))\nonumber\\ &\quad\text{is nowhere dense with respect to the subspace topology of }\partial W. \end{align} $$
$$ \begin{align} &\text{for all } k\in{\mathbb Z}\setminus\{0\}\ \text{ for all } \beta\in G: \partial W\cap(\partial W-\beta)\cap(\partial W-2\beta-\Delta(k))\nonumber\\ &\quad\text{is nowhere dense with respect to the subspace topology of }\partial W. \end{align} $$
Conditions (D′) and (DD′) and an additional growth restriction on the arithmetic structure, see equation (42), play essential roles for proving that the assumption of our basic Theorem 2.8 is satisfied. To prove conditions (D′) and (DD′), we assume in equation (AS) below that the sets of essential holes have some particular arithmetic structure motivated by the intended applications to
![]() ${\mathcal B}$
-free Toeplitz shifts, see Propositions 2.20, 2.28 and 2.30. We note here that the additional growth restriction excludes irregular Toeplitz shifts, see Remark 2.29. In Theorem 3.17, we show that
${\mathcal B}$
-free Toeplitz shifts, see Propositions 2.20, 2.28 and 2.30. We note here that the additional growth restriction excludes irregular Toeplitz shifts, see Remark 2.29. In Theorem 3.17, we show that
![]() ${\mathcal B}$
-free Toeplitz subshifts indeed satisfy the structural assumption in equation (AS).
${\mathcal B}$
-free Toeplitz subshifts indeed satisfy the structural assumption in equation (AS).
A characterization of the triviality of the centralizer is provided in [Reference Bułatek and Kwiatkowski2, Theorem 1]. The example
![]() ${\mathcal B}_1=\{2^nc_n:n\in {\mathbb N}\}$
with coprime odd
${\mathcal B}_1=\{2^nc_n:n\in {\mathbb N}\}$
with coprime odd
![]() $c_n>1$
from [Reference Dymek10] satisfies condition (D), but we were unable to evaluate the criterion from [Reference Bułatek and Kwiatkowski2, Theorem 1] for it. Instead, we will show that the example not only satisfies
$c_n>1$
from [Reference Dymek10] satisfies condition (D), but we were unable to evaluate the criterion from [Reference Bułatek and Kwiatkowski2, Theorem 1] for it. Instead, we will show that the example not only satisfies
![]() $\partial W+y_F\subseteq \bigcup _{|k|\leqslant N}\partial W+\Delta (k)$
, but that there exists a single integer
$\partial W+y_F\subseteq \bigcup _{|k|\leqslant N}\partial W+\Delta (k)$
, but that there exists a single integer
![]() $k_0$
such that
$k_0$
such that
![]() $\partial W+y_F\subseteq \partial W+\Delta (k_0)$
, i.e.
$\partial W+y_F\subseteq \partial W+\Delta (k_0)$
, i.e.
![]() $\partial W+(y_F-\Delta (k_0))\subseteq \partial W$
, see Example 3.20. The same holds for the example
$\partial W+(y_F-\Delta (k_0))\subseteq \partial W$
, see Example 3.20. The same holds for the example
![]() ${\mathcal B}_1'={\mathcal B}_1\cup \{c_1^2\}$
and for further generalizations of this kind. We shall see that this is the key to control the centralizer with modest efforts in Corollary 2.21: in the case of
${\mathcal B}_1'={\mathcal B}_1\cup \{c_1^2\}$
and for further generalizations of this kind. We shall see that this is the key to control the centralizer with modest efforts in Corollary 2.21: in the case of
![]() ${\mathcal B}_1$
, the centralizer is trivial (see also [Reference Dymek10]), while for
${\mathcal B}_1$
, the centralizer is trivial (see also [Reference Dymek10]), while for
![]() ${\mathcal B}_1'$
, our approach only yields that the
${\mathcal B}_1'$
, our approach only yields that the
![]() $c_1$
th iterate of each centralizer element is trivial. Indeed, we will show for this example that the centralizer has an element of order
$c_1$
th iterate of each centralizer element is trivial. Indeed, we will show for this example that the centralizer has an element of order
![]() $c_1$
, see Proposition 3.23 and Remark 3.24. More generally, we will show that elements of the centralizer can be of arbitrarily large finite order, see Corollary 3.25.
$c_1$
, see Proposition 3.23 and Remark 3.24. More generally, we will show that elements of the centralizer can be of arbitrarily large finite order, see Corollary 3.25.
Already, the example
![]() ${\mathcal B}_2=\{2^nc_n, 3^nc_n:n\in {\mathbb N}\}$
, with coprime
${\mathcal B}_2=\{2^nc_n, 3^nc_n:n\in {\mathbb N}\}$
, with coprime
![]() $c_n>1$
also coprime to
$c_n>1$
also coprime to
![]() $2$
and
$2$
and
![]() $3$
and satisfying
$3$
and satisfying
![]() $\prod _{n\in {\mathbb N}}(1-{1}/{c_n})>\tfrac 12$
, violates condition (Sh) but satisfies conditions (D′) and (DD′), see Example 3.21. In §3.6, we show that the shift determined by
$\prod _{n\in {\mathbb N}}(1-{1}/{c_n})>\tfrac 12$
, violates condition (Sh) but satisfies conditions (D′) and (DD′), see Example 3.21. In §3.6, we show that the shift determined by
![]() ${\mathcal B}_2$
has superpolynomial complexity (the same holds for
${\mathcal B}_2$
has superpolynomial complexity (the same holds for
![]() ${\mathcal B}_1$
), so that the results from [Reference Cyr and Kra4–Reference Donoso, Durand, Maass and Petite6] do not apply. We also deliver examples for which not all holes are essential, see Examples 3.27 and 3.29.
${\mathcal B}_1$
), so that the results from [Reference Cyr and Kra4–Reference Donoso, Durand, Maass and Petite6] do not apply. We also deliver examples for which not all holes are essential, see Examples 3.27 and 3.29.
2 The abstract regular Toeplitz case
2.1 A first basic theorem
Let
![]() $\eta \in \{0,1\}^{\mathbb Z}$
be a non-periodic Toeplitz sequence with period structure
$\eta \in \{0,1\}^{\mathbb Z}$
be a non-periodic Toeplitz sequence with period structure
![]() $p_1\mid p_2\mid p_3 \ldots \to \infty $
. That means for each
$p_1\mid p_2\mid p_3 \ldots \to \infty $
. That means for each
![]() $k\in {\mathbb Z}$
, there exists
$k\in {\mathbb Z}$
, there exists
![]() $n\ge 1$
such that
$n\ge 1$
such that
![]() $\eta _{|k+p_n{\mathbb Z}}$
is constant, but
$\eta _{|k+p_n{\mathbb Z}}$
is constant, but
![]() $\eta $
is not periodic. For
$\eta $
is not periodic. For
![]() $i=0,1$
, denote
$i=0,1$
, denote
![]() ${\mathcal P}_n^i=\{k\in {\mathbb Z}: \eta _{|k+p_n{\mathbb Z}}=i\}$
(we use this notation, because it is shorter than
${\mathcal P}_n^i=\{k\in {\mathbb Z}: \eta _{|k+p_n{\mathbb Z}}=i\}$
(we use this notation, because it is shorter than
![]() $\operatorname {Per}_{p_n}(\eta ,i)$
established in the literature) and
$\operatorname {Per}_{p_n}(\eta ,i)$
established in the literature) and
![]() ${\mathcal H}_n={\mathbb Z}\setminus ({\mathcal P}_n^0\cup {\mathcal P}_n^1)$
. Here,
${\mathcal H}_n={\mathbb Z}\setminus ({\mathcal P}_n^0\cup {\mathcal P}_n^1)$
. Here,
![]() ${\mathcal H}_n$
is called the set of holes at level n.
${\mathcal H}_n$
is called the set of holes at level n.
The odometer group
![]() $G=\varprojlim {\mathbb Z}/p_n{\mathbb Z}$
with the
$G=\varprojlim {\mathbb Z}/p_n{\mathbb Z}$
with the
![]() ${\mathbb Z}$
-action ‘addition of
${\mathbb Z}$
-action ‘addition of
![]() $1$
’ (
$1$
’ (
![]() $T:G\to G$
,
$T:G\to G$
,
![]() $(Tg)_n=g_n+1$
) is the MEF of the subshift
$(Tg)_n=g_n+1$
) is the MEF of the subshift
![]() $X_\eta $
, which is the orbit closure of
$X_\eta $
, which is the orbit closure of
![]() $\eta $
under the left shift
$\eta $
under the left shift
![]() $\sigma $
on
$\sigma $
on
![]() $\{0,1\}^{\mathbb Z}$
. In symbols,
$\{0,1\}^{\mathbb Z}$
. In symbols,
![]() $\pi :(X_\eta ,\sigma )\to (G,T)$
. Observe that
$\pi :(X_\eta ,\sigma )\to (G,T)$
. Observe that
![]() ${\mathcal H}_n\subseteq {\mathcal H}_N$
if
${\mathcal H}_n\subseteq {\mathcal H}_N$
if
![]() $n>N$
.
$n>N$
.
In [Reference Baake, Jäger and Lenz1], a cut and project scheme is associated with
![]() $\eta $
by specifying a compact and topologically regular window
$\eta $
by specifying a compact and topologically regular window
![]() $W\subseteq G$
: for
$W\subseteq G$
: for
![]() $h\in G$
, let
$h\in G$
, let
![]() $U_n(h)=\{g\in G: g_n=h_n\}$
and define
$U_n(h)=\{g\in G: g_n=h_n\}$
and define
 $$ \begin{align*} V^i=\bigcup_{n\in{\mathbb N}}\bigcup_{k\in{\mathcal P}_n^i\cap[0,p_n)}U_n(\Delta(k)) \end{align*} $$
$$ \begin{align*} V^i=\bigcup_{n\in{\mathbb N}}\bigcup_{k\in{\mathcal P}_n^i\cap[0,p_n)}U_n(\Delta(k)) \end{align*} $$
for
![]() $i=0,1$
. From [Reference Baake, Jäger and Lenz1, Theorem 1 and its proof], we see:
$i=0,1$
. From [Reference Baake, Jäger and Lenz1, Theorem 1 and its proof], we see:
-
(1)
 $W:=\overline {V^1}=G\setminus V^0$
is topologically regular, i.e.
$W:=\overline {V^1}=G\setminus V^0$
is topologically regular, i.e.
 $\overline {\operatorname {int}(W)}=W$
;
$\overline {\operatorname {int}(W)}=W$
; -
(2)
 $\partial W=G\setminus (V^0\cup V^1)$
;
$\partial W=G\setminus (V^0\cup V^1)$
; -
(3)
 $\Delta (k)\in V^i$
if and only if
$\Delta (k)\in V^i$
if and only if
 $\eta _k=i$
for
$\eta _k=i$
for
 $i=0,1$
and all
$i=0,1$
and all
 $k\in {\mathbb Z}$
, in particular
$k\in {\mathbb Z}$
, in particular
 $\eta _k=1$
if and only if
$\eta _k=1$
if and only if
 $\Delta (k)\in W$
.
$\Delta (k)\in W$
.
Lemma 2.1.
![]() $h\in \partial W$
if and only if
$h\in \partial W$
if and only if
![]() $h_N\in {\mathcal H}_N$
for all
$h_N\in {\mathcal H}_N$
for all
![]() $N\in {\mathbb N}$
.
$N\in {\mathbb N}$
.
Proof. We have
 $$ \begin{align*} h\not\in\partial W &\Leftrightarrow h\in\bigcup_{i\in\{0,1\}}V^i \Leftrightarrow h\in\bigcup_{i\in\{0,1\}}\bigcup_{n\in{\mathbb N}}\bigcup_{k\in{\mathcal P}_n^i\cap[0,p_n)}U_n(\Delta(k))\\ &\Leftrightarrow \text{there exists } i\in\{0,1\}\text{ there exists } n\in{\mathbb N}\text{ there exists }\\ &\qquad k\in{\mathcal P}_n^i\cap[0,p_n): h_n=k\\ &\Leftrightarrow \text{there exists } i\in\{0,1\}\text{ there exists } n\in{\mathbb N}: h_n\in{\mathcal P}_n^i\\ &\Leftrightarrow \text{there exists } n\in{\mathbb N}: h_n\not\in {\mathcal H}_n\\[-2.8pc] \end{align*} $$
$$ \begin{align*} h\not\in\partial W &\Leftrightarrow h\in\bigcup_{i\in\{0,1\}}V^i \Leftrightarrow h\in\bigcup_{i\in\{0,1\}}\bigcup_{n\in{\mathbb N}}\bigcup_{k\in{\mathcal P}_n^i\cap[0,p_n)}U_n(\Delta(k))\\ &\Leftrightarrow \text{there exists } i\in\{0,1\}\text{ there exists } n\in{\mathbb N}\text{ there exists }\\ &\qquad k\in{\mathcal P}_n^i\cap[0,p_n): h_n=k\\ &\Leftrightarrow \text{there exists } i\in\{0,1\}\text{ there exists } n\in{\mathbb N}: h_n\in{\mathcal P}_n^i\\ &\Leftrightarrow \text{there exists } n\in{\mathbb N}: h_n\not\in {\mathcal H}_n\\[-2.8pc] \end{align*} $$
Definition 2.2. (Essential holes)
The set of essential holes at level N is defined as
Definition 2.3. The minimal periods of
![]() ${\mathcal H}_n$
and
${\mathcal H}_n$
and
![]() ${\widetilde {\mathcal H}}_n$
are denoted by
${\widetilde {\mathcal H}}_n$
are denoted by
![]() $\tau _n$
and
$\tau _n$
and
![]() $\tilde {\tau }_n$
, respectively.
$\tilde {\tau }_n$
, respectively.
Remark 2.4.
-
(a)
 ${\widetilde {\mathcal H}}_n\subseteq {\widetilde {\mathcal H}}_N$
if
${\widetilde {\mathcal H}}_n\subseteq {\widetilde {\mathcal H}}_N$
if
 $n>N$
.
$n>N$
. -
(b)
 ${\mathcal H}_N$
and
${\mathcal H}_N$
and
 ${\widetilde {\mathcal H}}_N$
are
${\widetilde {\mathcal H}}_N$
are
 $p_N$
-periodic by definition—although this need not be their minimal period. (For
$p_N$
-periodic by definition—although this need not be their minimal period. (For
 ${\widetilde {\mathcal H}}_N$
, just observe that
${\widetilde {\mathcal H}}_N$
, just observe that
 $k\in {\widetilde {\mathcal H}}_N$
if and only if
$k\in {\widetilde {\mathcal H}}_N$
if and only if
 $k+p_N\in {\widetilde {\mathcal H}}_N$
.) Hence,
$k+p_N\in {\widetilde {\mathcal H}}_N$
.) Hence,
 $\tau _N\mid p_N$
and
$\tau _N\mid p_N$
and
 $\tilde {\tau }_N\mid p_N$
, so that expressions like ‘
$\tilde {\tau }_N\mid p_N$
, so that expressions like ‘
 $\tau _N\mid h_N$
’ or ‘
$\tau _N\mid h_N$
’ or ‘
 $\gcd (\tilde {\tau }_N,h_N)$
’ are well defined when
$\gcd (\tilde {\tau }_N,h_N)$
’ are well defined when
 $h_N\in {\mathbb Z}/p_N{\mathbb Z}$
. (This is consistent with the following general convention: an element z of an abelian group Z is divisible by
$h_N\in {\mathbb Z}/p_N{\mathbb Z}$
. (This is consistent with the following general convention: an element z of an abelian group Z is divisible by
 $n\in {\mathbb N}$
if
$n\in {\mathbb N}$
if
 $z\in nZ$
. If Z is a cyclic group and
$z\in nZ$
. If Z is a cyclic group and
 $z_1,z_2\in Z$
, then
$z_1,z_2\in Z$
, then
 $\gcd (z_1,z_2)$
is a generator of the subgroup of Z generated by
$\gcd (z_1,z_2)$
is a generator of the subgroup of Z generated by
 $z_1$
and
$z_1$
and
 $z_2$
. If
$z_2$
. If
 $Z={\mathbb Z}$
, then we choose
$Z={\mathbb Z}$
, then we choose
 $\gcd (z_1,z_2)$
to be positive by convention. Finally, if
$\gcd (z_1,z_2)$
to be positive by convention. Finally, if
 $n\in {\mathbb Z}$
and
$n\in {\mathbb Z}$
and
 $z+p{\mathbb Z}\in {\mathbb Z}/p{\mathbb Z}$
, then we understand by
$z+p{\mathbb Z}\in {\mathbb Z}/p{\mathbb Z}$
, then we understand by
 $\gcd (n,z+p{\mathbb Z})$
the (positive) generator of the group generated by n and
$\gcd (n,z+p{\mathbb Z})$
the (positive) generator of the group generated by n and
 $z+p{\mathbb Z}$
; this is the greatest common divisor of the numbers
$z+p{\mathbb Z}$
; this is the greatest common divisor of the numbers
 $n,z$
and p in the usual sense.)
$n,z$
and p in the usual sense.)
Lemma 2.5.
-
(a)
 $k\in {\widetilde {\mathcal H}}_N$
if and only if
$k\in {\widetilde {\mathcal H}}_N$
if and only if
 $U_N(\Delta (k))\cap \partial W\neq \emptyset $
.
$U_N(\Delta (k))\cap \partial W\neq \emptyset $
. -
(b)
 $h\in \partial W$
if and only if
$h\in \partial W$
if and only if
 $h_N\in {\widetilde {\mathcal H}}_N$
for all
$h_N\in {\widetilde {\mathcal H}}_N$
for all
 $N\in {\mathbb N}$
.
$N\in {\mathbb N}$
.
Proof. (a) Let
![]() $h\in U_N(\Delta (k))\cap \partial W$
. Then
$h\in U_N(\Delta (k))\cap \partial W$
. Then
![]() $k\in h_N+p_N{\mathbb Z}\subseteq {\mathcal H}_N+p_N{\mathbb Z}={\mathcal H}_N$
by Lemma 2.1, and for all
$k\in h_N+p_N{\mathbb Z}\subseteq {\mathcal H}_N+p_N{\mathbb Z}={\mathcal H}_N$
by Lemma 2.1, and for all
![]() $n\ge N$
, we have in view of Lemma 2.1:
$n\ge N$
, we have in view of Lemma 2.1:
![]() $h_n\in {\mathcal H}_n\cap (h_N+p_N{\mathbb Z})={\mathcal H}_n\cap (k+p_N{\mathbb Z})$
. For the reverse implication, let
$h_n\in {\mathcal H}_n\cap (h_N+p_N{\mathbb Z})={\mathcal H}_n\cap (k+p_N{\mathbb Z})$
. For the reverse implication, let
![]() $k\in {\widetilde {\mathcal H}}_N$
. We construct
$k\in {\widetilde {\mathcal H}}_N$
. We construct
![]() $h\in \partial W$
with
$h\in \partial W$
with
![]() $h_N=k\,\mod p_N$
: for
$h_N=k\,\mod p_N$
: for
![]() $j>N$
, there is
$j>N$
, there is
![]() $r_j\in {\mathcal H}_j\cap (k+p_N{\mathbb Z})$
. Let
$r_j\in {\mathcal H}_j\cap (k+p_N{\mathbb Z})$
. Let
![]() $h^{(j)}=\Delta (r_j)$
and fix any accumulation point h of the sequence
$h^{(j)}=\Delta (r_j)$
and fix any accumulation point h of the sequence
![]() $(h^{(j)})_j$
. Consider any
$(h^{(j)})_j$
. Consider any
![]() $n\ge N$
. For some sufficiently large
$n\ge N$
. For some sufficiently large
![]() $j_n\ge n$
, we have
$j_n\ge n$
, we have
![]() $h_n=h_n^{(j_n)}=r_{j_n}\,\mod p_n$
. Hence,
$h_n=h_n^{(j_n)}=r_{j_n}\,\mod p_n$
. Hence,
![]() $h_N\in r_{j_N}+p_N{\mathbb Z}=k+p_N{\mathbb Z}$
, so that
$h_N\in r_{j_N}+p_N{\mathbb Z}=k+p_N{\mathbb Z}$
, so that
![]() $h\in U_N(\Delta (k))$
, and
$h\in U_N(\Delta (k))$
, and
![]() $h_n\in r_{j_n}+p_n{\mathbb Z}\subseteq {\mathcal H}_{j_n}+p_n{\mathbb Z}\subseteq {\mathcal H}_n+p_n{\mathbb Z}={\mathcal H}_n$
, so that
$h_n\in r_{j_n}+p_n{\mathbb Z}\subseteq {\mathcal H}_{j_n}+p_n{\mathbb Z}\subseteq {\mathcal H}_n+p_n{\mathbb Z}={\mathcal H}_n$
, so that
![]() $h\in \partial W$
by Lemma 2.1.
$h\in \partial W$
by Lemma 2.1.
(b) We have
 $$ \begin{align*} h\in\partial W &\Leftrightarrow\text{for all } N\in{\mathbb N}:U_N(h)\cap\partial W\neq\emptyset\\&\Leftrightarrow\text{for all } N\in{\mathbb N}:U_N(\Delta(h_N))\cap\partial W\neq\emptyset\\&\Leftrightarrow\text{for all } N\in{\mathbb N}:h_N\in{\widetilde{\mathcal H}}_N\quad\text{by part (a).}\\[-2.9pc] \end{align*} $$
$$ \begin{align*} h\in\partial W &\Leftrightarrow\text{for all } N\in{\mathbb N}:U_N(h)\cap\partial W\neq\emptyset\\&\Leftrightarrow\text{for all } N\in{\mathbb N}:U_N(\Delta(h_N))\cap\partial W\neq\emptyset\\&\Leftrightarrow\text{for all } N\in{\mathbb N}:h_N\in{\widetilde{\mathcal H}}_N\quad\text{by part (a).}\\[-2.9pc] \end{align*} $$
The following simple lemma is basic for our approach.
Lemma 2.6.
-
(a) If
 $h+\beta {\mathbb Z}\subseteq \partial W$
for some
$h+\beta {\mathbb Z}\subseteq \partial W$
for some
 $h,\beta \in G$
, then
$h,\beta \in G$
, then
 $h_n+\gcd (\beta _n,\tilde {\tau }_n){\mathbb Z}\subseteq {\widetilde {\mathcal H}}_n$
for all
$h_n+\gcd (\beta _n,\tilde {\tau }_n){\mathbb Z}\subseteq {\widetilde {\mathcal H}}_n$
for all
 $n>0$
.
$n>0$
. -
(b) If
 $\partial W+\beta \subseteq \partial W$
for some
$\partial W+\beta \subseteq \partial W$
for some
 $\beta \in G$
, then
$\beta \in G$
, then
 $\tilde {\tau }_n\mid \beta _n$
for all
$\tilde {\tau }_n\mid \beta _n$
for all
 $n>0$
.
$n>0$
.
Proof. (a)
![]() $h_n+\beta _n{\mathbb Z}\subseteq {\widetilde {\mathcal H}}_n$
for all n by Lemma 2.5(b). As
$h_n+\beta _n{\mathbb Z}\subseteq {\widetilde {\mathcal H}}_n$
for all n by Lemma 2.5(b). As
![]() ${\widetilde {\mathcal H}}_n$
is
${\widetilde {\mathcal H}}_n$
is
![]() $\tilde {\tau }_n$
-periodic, this implies
$\tilde {\tau }_n$
-periodic, this implies
![]() $h_n+\gcd (\beta _n,\tilde {\tau }_n){\mathbb Z}\subseteq {\widetilde {\mathcal H}}_n$
.
$h_n+\gcd (\beta _n,\tilde {\tau }_n){\mathbb Z}\subseteq {\widetilde {\mathcal H}}_n$
.
(b) Let
![]() $j\in {\widetilde {\mathcal H}}_n$
. Then there is some
$j\in {\widetilde {\mathcal H}}_n$
. Then there is some
![]() $h\in U_n(\Delta (j))\cap \partial W$
by Lemma 2.5(a). Now,
$h\in U_n(\Delta (j))\cap \partial W$
by Lemma 2.5(a). Now,
![]() $h+\beta {\mathbb Z}\subseteq \partial W$
by assumption. As
$h+\beta {\mathbb Z}\subseteq \partial W$
by assumption. As
![]() $h_n=j$
, this implies, in view of part (a) of the lemma,
$h_n=j$
, this implies, in view of part (a) of the lemma,
![]() $j+\gcd (\beta _n,\tilde {\tau }_n){\mathbb Z}\subseteq {\widetilde {\mathcal H}}_n$
. As this holds for each
$j+\gcd (\beta _n,\tilde {\tau }_n){\mathbb Z}\subseteq {\widetilde {\mathcal H}}_n$
. As this holds for each
![]() $j\in {\widetilde {\mathcal H}}_n$
, we have
$j\in {\widetilde {\mathcal H}}_n$
, we have
![]() ${\widetilde {\mathcal H}}_n+\gcd (\beta _n,\tilde {\tau }_n){\mathbb Z}={\widetilde {\mathcal H}}_n$
, and as
${\widetilde {\mathcal H}}_n+\gcd (\beta _n,\tilde {\tau }_n){\mathbb Z}={\widetilde {\mathcal H}}_n$
, and as
![]() $\tilde {\tau }_n$
is the minimal period of
$\tilde {\tau }_n$
is the minimal period of
![]() ${\widetilde {\mathcal H}}_n$
, we conclude that
${\widetilde {\mathcal H}}_n$
, we conclude that
![]() $\tilde {\tau }_n\mid \beta _n$
.
$\tilde {\tau }_n\mid \beta _n$
.
Remark 2.7. If
![]() $h+\beta {\mathbb Z}\subseteq \partial W$
, Lemma 2.6 implies
$h+\beta {\mathbb Z}\subseteq \partial W$
, Lemma 2.6 implies
Therefore, the last lemma seems to be useful only for regular Toeplitz shifts, because for irregular ones,
![]() $\inf _n\boldsymbol {\delta }({\mathcal H}_n)>0$
so that no useful lower bound on
$\inf _n\boldsymbol {\delta }({\mathcal H}_n)>0$
so that no useful lower bound on
![]() $\gcd (\beta _n,\tilde {\tau }_n)$
can be expected.
$\gcd (\beta _n,\tilde {\tau }_n)$
can be expected.
Each automorphism F of
![]() $(X_\eta ,\sigma )$
determines an element
$(X_\eta ,\sigma )$
determines an element
![]() $y_F\in G$
such that
$y_F\in G$
such that
![]() $\pi (F(x))=\pi (x)+y_F$
for all
$\pi (F(x))=\pi (x)+y_F$
for all
![]() $x\in X_\eta $
. Observe that
$x\in X_\eta $
. Observe that
because F leaves the set of non-one-point fibres over the MEF invariant. We first focus on a stronger property than equation (3).
Theorem 2.8. Recall that
![]() $\tilde {\tau }_n$
denotes the minimal period of
$\tilde {\tau }_n$
denotes the minimal period of
![]() ${\widetilde {\mathcal H}}_n$
.
${\widetilde {\mathcal H}}_n$
.
-
(a) If an automorphism F of
 $(X_\eta ,\sigma )$
satisfies
$(X_\eta ,\sigma )$
satisfies
 $\partial W+y_F\subseteq \partial W+\Delta (k)$
for some
$\partial W+y_F\subseteq \partial W+\Delta (k)$
for some
 $k=k_F\in {\mathbb Z}$
, then
$k=k_F\in {\mathbb Z}$
, then
 $\tilde {\tau }_n\mid (y_F)_n-k_F$
. In particular, if infinitely many
$\tilde {\tau }_n\mid (y_F)_n-k_F$
. In particular, if infinitely many
 ${\widetilde {\mathcal H}}_n$
have minimal period
${\widetilde {\mathcal H}}_n$
have minimal period
 $p_n$
, then
$p_n$
, then
 $y_F=\Delta (k_F)$
.
$y_F=\Delta (k_F)$
. -
(b) Suppose that for each automorphism
 $F\in \operatorname {Aut}_\sigma (X_\eta )$
, there exists a unique
$F\in \operatorname {Aut}_\sigma (X_\eta )$
, there exists a unique
 $k_F\in {\mathbb Z}$
such that (4)
$k_F\in {\mathbb Z}$
such that (4) $$ \begin{align} \partial W+y_F\subseteq \partial W+\Delta(k_F). \end{align} $$
$$ \begin{align} \partial W+y_F\subseteq \partial W+\Delta(k_F). \end{align} $$
If
 $M:=\liminf _{n\to \infty }p_n/\tilde {\tau }_n<\infty $
, then where
$M:=\liminf _{n\to \infty }p_n/\tilde {\tau }_n<\infty $
, then where $$ \begin{align*} \operatorname{Aut}_\sigma(X_\eta)=\langle \sigma\rangle\oplus\operatorname{Tor}, \end{align*} $$
$$ \begin{align*} \operatorname{Aut}_\sigma(X_\eta)=\langle \sigma\rangle\oplus\operatorname{Tor}, \end{align*} $$
 $\operatorname {Tor}$
denotes the torsion group of
$\operatorname {Tor}$
denotes the torsion group of
 $\operatorname {Aut}_\sigma (X_\eta )$
. Moreover,
$\operatorname {Aut}_\sigma (X_\eta )$
. Moreover,
 $\operatorname {Tor}$
is a cyclic group (possibly trivial), whose order divides M. In particular, if infinitely many
$\operatorname {Tor}$
is a cyclic group (possibly trivial), whose order divides M. In particular, if infinitely many
 ${\widetilde {\mathcal H}}_n$
have minimal period
${\widetilde {\mathcal H}}_n$
have minimal period
 $p_n$
, then the centralizer of
$p_n$
, then the centralizer of
 $(X_\eta ,\sigma )$
is trivial.
$(X_\eta ,\sigma )$
is trivial.
Proof. (a) The first claim follows from Lemma 2.6(b), the second one is just a special case of this.
(b) In each residue class of
![]() $\operatorname {Aut}_\sigma (X_\eta )/\langle \sigma \rangle $
, there is exactly one element F for which the associated integer
$\operatorname {Aut}_\sigma (X_\eta )/\langle \sigma \rangle $
, there is exactly one element F for which the associated integer
![]() $k_F$
satisfying equation (4) equals
$k_F$
satisfying equation (4) equals
![]() $0$
. These elements F form a subgroup J of
$0$
. These elements F form a subgroup J of
![]() $\operatorname {Aut}_\sigma (X_\eta )$
. Suppose for a contradiction that there are
$\operatorname {Aut}_\sigma (X_\eta )$
. Suppose for a contradiction that there are
![]() $M+1$
different automorphisms
$M+1$
different automorphisms
![]() $F_1,\ldots ,F_{M+1}\in J$
. In view of Lemma 2.6(b), they all satisfy
$F_1,\ldots ,F_{M+1}\in J$
. In view of Lemma 2.6(b), they all satisfy
Hence, there exists arbitrarily large
![]() $n\in {\mathbb N}$
such that
$n\in {\mathbb N}$
such that
![]() $M=p_n/\tilde {\tau }_n$
and
$M=p_n/\tilde {\tau }_n$
and
It follows that there exist two different
![]() $i,j\in \{1,\ldots ,M+1\}$
for which
$i,j\in \{1,\ldots ,M+1\}$
for which
![]() $(y_{F_i})_{S_n}=(y_{F_j})_{S_n}$
for infinitely many n, which is only possible if
$(y_{F_i})_{S_n}=(y_{F_j})_{S_n}$
for infinitely many n, which is only possible if
![]() $y_{F_i}=y_{F_j}$
. In view of [Reference Donoso, Durand, Maass and Petite6, Lemma 2.4], this implies
$y_{F_i}=y_{F_j}$
. In view of [Reference Donoso, Durand, Maass and Petite6, Lemma 2.4], this implies
![]() $F_i=F_j\,\mod \langle \sigma \rangle $
, so that
$F_i=F_j\,\mod \langle \sigma \rangle $
, so that
![]() $i=j$
, which is a contradiction. Hence, J is a finite group of order
$i=j$
, which is a contradiction. Hence, J is a finite group of order
![]() $m\leqslant M$
, say
$m\leqslant M$
, say
![]() $J=\{F_1,\ldots ,F_m\}$
. In particular,
$J=\{F_1,\ldots ,F_m\}$
. In particular,
![]() $J\subseteq \operatorname {Tor}$
. However, if
$J\subseteq \operatorname {Tor}$
. However, if
![]() $F\in \operatorname {Tor}$
, then
$F\in \operatorname {Tor}$
, then
![]() $ry_F=\Delta (0)\in G$
for some positive integer r. Hence, with the integer
$ry_F=\Delta (0)\in G$
for some positive integer r. Hence, with the integer
![]() $k_F$
satisfying equation (4), we have
$k_F$
satisfying equation (4), we have
but
![]() $k_{Id}=0$
, so equation (4) implies
$k_{Id}=0$
, so equation (4) implies
![]() $k_F=0$
. It follows that
$k_F=0$
. It follows that
![]() $F\in J$
, and we proved that
$F\in J$
, and we proved that
![]() $J=\operatorname {Tor}$
. Then [Reference Donoso, Durand, Maass and Petite7, Theorem 3.2(2)] implies that
$J=\operatorname {Tor}$
. Then [Reference Donoso, Durand, Maass and Petite7, Theorem 3.2(2)] implies that
![]() $\operatorname {Tor}$
is cyclic, and
$\operatorname {Tor}$
is cyclic, and
![]() $\operatorname {Aut}_\sigma (X_\eta )=J\oplus \langle \sigma \rangle =\operatorname {Tor}\oplus \ \langle \sigma \rangle $
.
$\operatorname {Aut}_\sigma (X_\eta )=J\oplus \langle \sigma \rangle =\operatorname {Tor}\oplus \ \langle \sigma \rangle $
.
It remains to determine the order m of
![]() $\operatorname {Tor}$
: fix some
$\operatorname {Tor}$
: fix some
![]() $F\in \operatorname {Tor}$
. In view of equation (5),
$F\in \operatorname {Tor}$
. In view of equation (5),
for all
![]() $n\in {\mathbb N}$
. Hence,
$n\in {\mathbb N}$
. Hence,
![]() $F^M=\operatorname {id}_{X_\eta }$
, so that the order of F is a divisor of M.
$F^M=\operatorname {id}_{X_\eta }$
, so that the order of F is a divisor of M.
To apply this theorem, we need to verify the assumption in equation (4) and to determine the periods
![]() $\tilde {\tau }_n$
. So we focus next on finding sufficient conditions that imply
$\tilde {\tau }_n$
. So we focus next on finding sufficient conditions that imply
![]() $\partial W+ (y_F-\Delta (k)){\mathbb Z}\subseteq \partial W$
.
$\partial W+ (y_F-\Delta (k)){\mathbb Z}\subseteq \partial W$
.
2.2 The separated holes conditions and its variants
The separated holes condition (Sh) was introduced in [Reference Bułatek and Kwiatkowski2]. It requires
As mentioned in the introduction, it is equivalent to the disjointness condition
Indeed, it is even equivalent to the separated essential holes condition
As we do not make use of this equivalence, we leave it as an exercise.
The following variants of the separated essential holes condition, which allow to study Toeplitz subshifts that violate condition (Sh), will play important roles; however, so we provide proofs for the corresponding equivalences:
-
(i) weak disjointness condition (D′), equivalent to weak separated essential holes condition (Seh′):
(D′) $$ \begin{align} &\text{for all } k\in{\mathbb Z}\setminus\{0\}:\partial W\cap(\partial W-\Delta(k))\nonumber \\ &\quad\text{ is nowhere dense with respect to~the subspace topology of }\partial W. \end{align} $$
(Seh′)
$$ \begin{align} &\text{for all } k\in{\mathbb Z}\setminus\{0\}:\partial W\cap(\partial W-\Delta(k))\nonumber \\ &\quad\text{ is nowhere dense with respect to~the subspace topology of }\partial W. \end{align} $$
(Seh′) $$ \begin{align} &\text{for all } k\in{\mathbb Z}\setminus\{0\}:\text{there is no arithmetic progression }r+p_N{\mathbb Z}\text{ such that} \nonumber \\ &\quad\text{for all } n\ge N:\emptyset\neq(r+p_N{\mathbb Z})\cap{\widetilde{\mathcal H}}_n\subseteq{\widetilde{\mathcal H}}_n-k; \end{align} $$
$$ \begin{align} &\text{for all } k\in{\mathbb Z}\setminus\{0\}:\text{there is no arithmetic progression }r+p_N{\mathbb Z}\text{ such that} \nonumber \\ &\quad\text{for all } n\ge N:\emptyset\neq(r+p_N{\mathbb Z})\cap{\widetilde{\mathcal H}}_n\subseteq{\widetilde{\mathcal H}}_n-k; \end{align} $$
-
(ii) weak double disjointness condition (DD′), equivalent to weak double separated essential holes condition (DSeh′):
(DD′) $$ \begin{align} &\text{for all } k\in{\mathbb Z}\setminus\{0\}\quad \text{for all } \beta\in G: \partial W\cap(\partial W-\beta)\cap(\partial W-2\beta-\Delta(k))\nonumber\\ &\quad\text{is nowhere dense with respect to the subspace topology of }\partial W, \end{align} $$
(DSeh′)
$$ \begin{align} &\text{for all } k\in{\mathbb Z}\setminus\{0\}\quad \text{for all } \beta\in G: \partial W\cap(\partial W-\beta)\cap(\partial W-2\beta-\Delta(k))\nonumber\\ &\quad\text{is nowhere dense with respect to the subspace topology of }\partial W, \end{align} $$
(DSeh′) $$ \begin{align} &\text{for all } k\in{\mathbb Z}\setminus\{0\}\ \text{ for all } \beta\in G:\text{there is no arithmetic progression }r+p_N{\mathbb Z}\nonumber\\ &\quad\text{such that for all } n\ge N:\emptyset\neq(r+p_N{\mathbb Z})\cap{\widetilde{\mathcal H}}_n\subseteq ({\widetilde{\mathcal H}}_n-\beta_n)\cap({\widetilde{\mathcal H}}_n-2\beta_n-k). \end{align} $$
$$ \begin{align} &\text{for all } k\in{\mathbb Z}\setminus\{0\}\ \text{ for all } \beta\in G:\text{there is no arithmetic progression }r+p_N{\mathbb Z}\nonumber\\ &\quad\text{such that for all } n\ge N:\emptyset\neq(r+p_N{\mathbb Z})\cap{\widetilde{\mathcal H}}_n\subseteq ({\widetilde{\mathcal H}}_n-\beta_n)\cap({\widetilde{\mathcal H}}_n-2\beta_n-k). \end{align} $$
Observe that for
![]() $\beta =0$
conditions (DD′) and (DSeh′) reduce to conditions (D′) and (Seh′), respectively. Moreover, conditions (D) and (Sh) clearly imply conditions (D′) and (Seh′), respectively.
$\beta =0$
conditions (DD′) and (DSeh′) reduce to conditions (D′) and (Seh′), respectively. Moreover, conditions (D) and (Sh) clearly imply conditions (D′) and (Seh′), respectively.
In the following, we will assume condition (DD′)—indeed, for some results, only the weaker condition (D′) is needed. In the
![]() ${\mathcal B}$
-free setting, condition (DD′) will be verified under suitable assumptions in Proposition 2.30.
${\mathcal B}$
-free setting, condition (DD′) will be verified under suitable assumptions in Proposition 2.30.
Both equivalences above, namely
![]() $\lnot $
condition (D′)
$\lnot $
condition (D′)
![]() $\Leftrightarrow \lnot $
condition (Seh′) and
$\Leftrightarrow \lnot $
condition (Seh′) and
![]() $\lnot $
condition (DD′)
$\lnot $
condition (DD′)
![]() $\Leftrightarrow \lnot $
condition (DSeh′), follow immediately from the next lemma.
$\Leftrightarrow \lnot $
condition (DSeh′), follow immediately from the next lemma.
Lemma 2.9. Let
![]() $k\in {\mathbb Z}\setminus \{0\}$
,
$k\in {\mathbb Z}\setminus \{0\}$
,
![]() $\beta \in G$
,
$\beta \in G$
,
![]() $N>0$
and
$N>0$
and
![]() $r\in {\mathbb Z}$
. Then,
$r\in {\mathbb Z}$
. Then,
if and only if
Proof. Suppose that equation (6) holds. Then, for all
![]() $n\ge N$
, there is
$n\ge N$
, there is
![]() $r_n\in r+p_N{\mathbb Z}$
such that
$r_n\in r+p_N{\mathbb Z}$
such that
![]() $U_n(\Delta (r_n))\cap \partial W\neq \emptyset $
, whence
$U_n(\Delta (r_n))\cap \partial W\neq \emptyset $
, whence
![]() $r_n\in (r+p_N{\mathbb Z})\cap {\widetilde {\mathcal H}}_n$
in view of Lemma 2.5(a).
$r_n\in (r+p_N{\mathbb Z})\cap {\widetilde {\mathcal H}}_n$
in view of Lemma 2.5(a).
Now consider any
![]() $r_n\in (r+p_N{\mathbb Z})\cap {\widetilde {\mathcal H}}_n$
. By the inclusion in equation (6),
$r_n\in (r+p_N{\mathbb Z})\cap {\widetilde {\mathcal H}}_n$
. By the inclusion in equation (6),
 $$ \begin{align*} U_n(\Delta(r_n))&\cap\partial W\subseteq U_N(\Delta(r_n))\cap\partial W\\ &=U_N(\Delta(r))\cap\partial W\subseteq(\partial W-\beta)\cap(\partial W-2\beta-\Delta(k)), \end{align*} $$
$$ \begin{align*} U_n(\Delta(r_n))&\cap\partial W\subseteq U_N(\Delta(r_n))\cap\partial W\\ &=U_N(\Delta(r))\cap\partial W\subseteq(\partial W-\beta)\cap(\partial W-2\beta-\Delta(k)), \end{align*} $$
so that, by Lemma 2.5(a) again,
![]() $r_n+\beta _n\in {\widetilde {\mathcal H}}_n$
and
$r_n+\beta _n\in {\widetilde {\mathcal H}}_n$
and
![]() $r_n+2\beta _n+k\in {\widetilde {\mathcal H}}_n$
, which proves equation (7).
$r_n+2\beta _n+k\in {\widetilde {\mathcal H}}_n$
, which proves equation (7).
Conversely, suppose that equation (7) holds. For each
![]() $n\ge N$
, there is some
$n\ge N$
, there is some
![]() $r_n\in (r+p_N{\mathbb Z})\cap {\widetilde {\mathcal H}}_n$
, and we find a subsequence
$r_n\in (r+p_N{\mathbb Z})\cap {\widetilde {\mathcal H}}_n$
, and we find a subsequence
![]() $\Delta (r_{n_i})$
that converges to some
$\Delta (r_{n_i})$
that converges to some
![]() $h\in G$
. Hence, for each
$h\in G$
. Hence, for each
![]() $m>0$
, there is
$m>0$
, there is
![]() $n_i\ge m$
such that
$n_i\ge m$
such that
![]() $h_m\in r_{n_i}+p_m{\mathbb Z}\subseteq {\widetilde {\mathcal H}}_{n_i}+p_m{\mathbb Z}\subseteq {\widetilde {\mathcal H}}_m+p_m{\mathbb Z}={\widetilde {\mathcal H}}_m$
, so that
$h_m\in r_{n_i}+p_m{\mathbb Z}\subseteq {\widetilde {\mathcal H}}_{n_i}+p_m{\mathbb Z}\subseteq {\widetilde {\mathcal H}}_m+p_m{\mathbb Z}={\widetilde {\mathcal H}}_m$
, so that
![]() $h\in \partial W$
in view of Lemma 2.5(b). As
$h\in \partial W$
in view of Lemma 2.5(b). As
![]() $h_N\in r_{n_i}+p_N{\mathbb Z}=r+p_N{\mathbb Z}$
for some
$h_N\in r_{n_i}+p_N{\mathbb Z}=r+p_N{\mathbb Z}$
for some
![]() $n_i$
, this shows that
$n_i$
, this shows that
![]() $h\in U_N(\Delta (r))\cap \partial W$
.
$h\in U_N(\Delta (r))\cap \partial W$
.
Now consider any
![]() $h\in U_N(\Delta (r))\cap \partial W$
. Then, for all
$h\in U_N(\Delta (r))\cap \partial W$
. Then, for all
![]() $n\ge N$
,
$n\ge N$
,
![]() $U_n(h)\cap \partial W\neq \emptyset $
, so that
$U_n(h)\cap \partial W\neq \emptyset $
, so that
![]() $h_n\in (r+p_N{\mathbb Z})\cap {\widetilde {\mathcal H}}_n$
, where we used Lemma 2.5(a) once more. The inclusion in equation (7) then implies
$h_n\in (r+p_N{\mathbb Z})\cap {\widetilde {\mathcal H}}_n$
, where we used Lemma 2.5(a) once more. The inclusion in equation (7) then implies
![]() $h_n\in ({\widetilde {\mathcal H}}_n-\beta _n)\cap ({\widetilde {\mathcal H}}_n-2\beta _n-k)$
for all
$h_n\in ({\widetilde {\mathcal H}}_n-\beta _n)\cap ({\widetilde {\mathcal H}}_n-2\beta _n-k)$
for all
![]() $n\ge N$
. Now Lemma 2.5(b) shows that
$n\ge N$
. Now Lemma 2.5(b) shows that
![]() $h+\beta \in \partial W$
and
$h+\beta \in \partial W$
and
![]() $h+2\beta +\Delta (k)\in \partial W$
, which proves equation (6).
$h+2\beta +\Delta (k)\in \partial W$
, which proves equation (6).
Remark 2.10. Suppose that the condition (*) from [Reference Bułatek and Kwiatkowski3] holds, that is, for any
![]() $n\in {\mathbb N}$
and
$n\in {\mathbb N}$
and
![]() $s\in {\mathbb Z}$
,
$s\in {\mathbb Z}$
,
and recall that it implies triviality of the centralizer [Reference Bułatek and Kwiatkowski3, Theorem 1]. Here we show that it implies
![]() ${\widetilde {\mathcal H}}_n={\mathcal H}_n$
for all n, but mostly precludes property (Seh′): note first that
${\widetilde {\mathcal H}}_n={\mathcal H}_n$
for all n, but mostly precludes property (Seh′): note first that
Indeed, otherwise there are
![]() $n\in {\mathbb N}$
and
$n\in {\mathbb N}$
and
![]() $r\in {\mathcal H}_n$
such that
$r\in {\mathcal H}_n$
such that
![]() $r+sp_n\in {\mathcal H}_n\setminus {\mathcal H}_{n+1}$
for all
$r+sp_n\in {\mathcal H}_n\setminus {\mathcal H}_{n+1}$
for all
![]() $s\in {\mathbb Z}$
. However, then
$s\in {\mathbb Z}$
. However, then
![]() ${\mathcal H}_{n+1}=\emptyset $
in view of condition (*), which is excluded because we study only non-periodic Toeplitz sequences. A straightforward inductive application of condition (8) shows that for all
${\mathcal H}_{n+1}=\emptyset $
in view of condition (*), which is excluded because we study only non-periodic Toeplitz sequences. A straightforward inductive application of condition (8) shows that for all
![]() $n\in {\mathbb N}$
,
$n\in {\mathbb N}$
,
![]() $r\in {\mathcal H}_n$
and
$r\in {\mathcal H}_n$
and
![]() $m> n$
, there are integers
$m> n$
, there are integers
![]() $s_n,\ldots ,s_{m-1}$
such that
$s_n,\ldots ,s_{m-1}$
such that
![]() $r+s_np_n+\cdots +s_{m-1}p_{m-1}\in (r+p_n{\mathbb Z})\cap {\mathcal H}_m$
. Hence,
$r+s_np_n+\cdots +s_{m-1}p_{m-1}\in (r+p_n{\mathbb Z})\cap {\mathcal H}_m$
. Hence,
![]() ${\widetilde {\mathcal H}}_n={\mathcal H}_n$
for all
${\widetilde {\mathcal H}}_n={\mathcal H}_n$
for all
![]() $n\in {\mathbb N}$
. We claim
$n\in {\mathbb N}$
. We claim
Indeed, let
![]() $r,r'\in {\mathcal H}_N\cap [0,p_N)$
and
$r,r'\in {\mathcal H}_N\cap [0,p_N)$
and
![]() $s\in {\mathbb Z}$
. Suppose that
$s\in {\mathbb Z}$
. Suppose that
![]() $r+sp_N\in {\mathcal H}_n$
for some
$r+sp_N\in {\mathcal H}_n$
for some
![]() $n>N$
. Since for any
$n>N$
. Since for any
![]() $m\geq N$
we have
$m\geq N$
we have
![]() $r+sp_N\in [s_m'p_m,(s_m'+1)p_m)$
, where
$r+sp_N\in [s_m'p_m,(s_m'+1)p_m)$
, where
![]() $s_m'=[{sp_N}/{p_m}]$
, and
$s_m'=[{sp_N}/{p_m}]$
, and
![]() ${\mathcal H}_n\subseteq {\mathcal H}_{n-1}\subseteq \cdots \subseteq {\mathcal H}_N$
, by condition (*), we obtain
${\mathcal H}_n\subseteq {\mathcal H}_{n-1}\subseteq \cdots \subseteq {\mathcal H}_N$
, by condition (*), we obtain
![]() $[s_m'p_m,(s_m'+1)p_m)\cap {\mathcal H}_m\subseteq {\mathcal H}_{m+1}$
for any
$[s_m'p_m,(s_m'+1)p_m)\cap {\mathcal H}_m\subseteq {\mathcal H}_{m+1}$
for any
![]() $N\leq m< n$
. In particular, since
$N\leq m< n$
. In particular, since
![]() $[sp_N,(s+1)p_N)\subseteq [s_m'p_m,(s_m'+1)p_m)$
, we have
$[sp_N,(s+1)p_N)\subseteq [s_m'p_m,(s_m'+1)p_m)$
, we have
![]() $[sp_N,(s+1)p_N)\cap {\mathcal H}_m\subseteq {\mathcal H}_{m+1}$
for any
$[sp_N,(s+1)p_N)\cap {\mathcal H}_m\subseteq {\mathcal H}_{m+1}$
for any
![]() $N\leq m<n$
. Hence,
$N\leq m<n$
. Hence,
Of course,
![]() $r'+sp_N\in [sp_N,(s+1)p_N)\cap {\mathcal H}_N$
. So
$r'+sp_N\in [sp_N,(s+1)p_N)\cap {\mathcal H}_N$
. So
![]() $r'+sp_N\in {\mathcal H}_n={\widetilde {\mathcal H}}_n$
. The same arguments as above, with roles of r and
$r'+sp_N\in {\mathcal H}_n={\widetilde {\mathcal H}}_n$
. The same arguments as above, with roles of r and
![]() $r'$
interchanged, show that
$r'$
interchanged, show that
So equation (9) follows. Hence, if
![]() $[0,p_N)$
contains at least two holes at level N, then condition (Seh′) does not hold. If, however,
$[0,p_N)$
contains at least two holes at level N, then condition (Seh′) does not hold. If, however,
![]() ${\mathcal H}_n\cap [0,p_n)$
is a singleton for any
${\mathcal H}_n\cap [0,p_n)$
is a singleton for any
![]() $n\geq N$
, then the distance between consecutive holes at level n is
$n\geq N$
, then the distance between consecutive holes at level n is
![]() $p_n$
, so even condition (Sh) holds.
$p_n$
, so even condition (Sh) holds.
Remark 2.11. Given
![]() $k\in {\mathcal H}_N\setminus {\widetilde {\mathcal H}}_N$
, let
$k\in {\mathcal H}_N\setminus {\widetilde {\mathcal H}}_N$
, let
![]() $n_k\ge N$
be minimal such that
$n_k\ge N$
be minimal such that
![]() $(k+p_N{\mathbb Z})\cap {\mathcal H}_{n_k}=\emptyset $
. Clearly,
$(k+p_N{\mathbb Z})\cap {\mathcal H}_{n_k}=\emptyset $
. Clearly,
![]() $n_k$
depends only on the residue of k modulo
$n_k$
depends only on the residue of k modulo
![]() $p_N$
, so the
$p_N$
, so the
![]() $n_k$
are bounded, say, by
$n_k$
are bounded, say, by
![]() $m_N$
. Then, for
$m_N$
. Then, for
![]() $k\in {\mathcal H}_N$
,
$k\in {\mathcal H}_N$
,
![]() $k\in {\widetilde {\mathcal H}}_N$
if and only if
$k\in {\widetilde {\mathcal H}}_N$
if and only if
![]() $(k+p_N{\mathbb Z})\cap {\mathcal H}_{m_N}\neq \emptyset $
. More generally, for every
$(k+p_N{\mathbb Z})\cap {\mathcal H}_{m_N}\neq \emptyset $
. More generally, for every
![]() $n\ge m_N$
:
$n\ge m_N$
:
![]() $k\in {\widetilde {\mathcal H}}_N$
if and only if
$k\in {\widetilde {\mathcal H}}_N$
if and only if
![]() $(k+p_N{\mathbb Z})\cap {\mathcal H}_{n}\neq \emptyset $
. Hence, for every
$(k+p_N{\mathbb Z})\cap {\mathcal H}_{n}\neq \emptyset $
. Hence, for every
![]() $n\ge m_N$
,
$n\ge m_N$
,
![]() ${\widetilde {\mathcal H}}_N={\mathcal H}_{n}+p_N{\mathbb Z}$
. It follows that the minimal period
${\widetilde {\mathcal H}}_N={\mathcal H}_{n}+p_N{\mathbb Z}$
. It follows that the minimal period
![]() $\tilde {\tau }_N$
of
$\tilde {\tau }_N$
of
![]() ${\widetilde {\mathcal H}}_N$
divides
${\widetilde {\mathcal H}}_N$
divides
![]() $\gcd (\tau _n,p_N)$
for
$\gcd (\tau _n,p_N)$
for
![]() $n\ge m_N$
.
$n\ge m_N$
.
2.3 Consequences of the weak disjointness condition (D′)
Consider any automorphism F of
![]() $(X_\eta ,\sigma )$
. Recall from the introduction that
$(X_\eta ,\sigma )$
. Recall from the introduction that
![]() $\pi \circ F=f\circ \pi $
, where
$\pi \circ F=f\circ \pi $
, where
![]() $\pi :(X_\eta ,\sigma )\to (G,T)$
is the MEF-map and
$\pi :(X_\eta ,\sigma )\to (G,T)$
is the MEF-map and
![]() $f:G\to G, y\mapsto y+y_F$
for some
$f:G\to G, y\mapsto y+y_F$
for some
![]() $y_F\in G$
, and that
$y_F\in G$
, and that
![]() $\partial W+y_F\subseteq \bigcup _{k\in {\mathbb Z}}\partial W+\Delta (k)$
. Denote
$\partial W+y_F\subseteq \bigcup _{k\in {\mathbb Z}}\partial W+\Delta (k)$
. Denote
and
Proposition 2.12. Assume that the weak disjointness condition (D′) holds. Let the automorphism F of
![]() $(X_\eta ,\sigma )$
be described by a block code
$(X_\eta ,\sigma )$
be described by a block code
![]() $\{0,1\}^{[-m:m]}\to \{0,1\}$
. Then,
$\{0,1\}^{[-m:m]}\to \{0,1\}$
. Then,
 $$ \begin{align} \partial W+y_F\subseteq\bigcup_{k=-m}^m\partial W+\Delta(k). \end{align} $$
$$ \begin{align} \partial W+y_F\subseteq\bigcup_{k=-m}^m\partial W+\Delta(k). \end{align} $$
Proof. Recall from equation (3) that
![]() $\partial W+y_F \subseteq \bigcup _{k\in {\mathbb Z}}\partial W+\Delta (k)$
.
$\partial W+y_F \subseteq \bigcup _{k\in {\mathbb Z}}\partial W+\Delta (k)$
.
Let
![]() $y\in G$
and recall that
$y\in G$
and recall that
![]() $\pi \colon {X_\eta \to G}$
denotes the factor map onto the MEF. At the end of the proof, we show
$\pi \colon {X_\eta \to G}$
denotes the factor map onto the MEF. At the end of the proof, we show
 $$ \begin{align} |\pi^{-1}\{y\}|=2 \Leftrightarrow \text{there exists } j\in{\mathbb Z}:y+\Delta(j)\in R:=\partial W\setminus\bigcup_{k\in{\mathbb Z}\setminus\{0\}}\partial W+\Delta(k). \end{align} $$
$$ \begin{align} |\pi^{-1}\{y\}|=2 \Leftrightarrow \text{there exists } j\in{\mathbb Z}:y+\Delta(j)\in R:=\partial W\setminus\bigcup_{k\in{\mathbb Z}\setminus\{0\}}\partial W+\Delta(k). \end{align} $$
As
![]() $F\colon X_\eta \to X_\eta $
is a bijection that maps
$F\colon X_\eta \to X_\eta $
is a bijection that maps
![]() $\pi $
-fibres to
$\pi $
-fibres to
![]() $\pi $
-fibres and as
$\pi $
-fibres and as
![]() $\pi \circ F=f\circ \pi $
, it follows that when
$\pi \circ F=f\circ \pi $
, it follows that when
![]() $\pi ^{-1}\{y\}=\{x_1,x_2\}$
with
$\pi ^{-1}\{y\}=\{x_1,x_2\}$
with
![]() $x_1\neq x_2$
, then
$x_1\neq x_2$
, then
![]() $\pi ^{-1}\{f(y)\}=\{x_1'=F(x_1),x_2'=F(x_2)\}$
, and there are exactly one index
$\pi ^{-1}\{f(y)\}=\{x_1'=F(x_1),x_2'=F(x_2)\}$
, and there are exactly one index
![]() $j\in {\mathbb Z}$
such that
$j\in {\mathbb Z}$
such that
![]() $y+\Delta (j)\in \partial W$
and
$y+\Delta (j)\in \partial W$
and
![]() $(x_1)_j\neq (x_2)_j$
, and exactly one index
$(x_1)_j\neq (x_2)_j$
, and exactly one index
![]() $k\in {\mathbb Z}$
such that
$k\in {\mathbb Z}$
such that
![]() $f(y)+\Delta (k)\in \partial W$
and
$f(y)+\Delta (k)\in \partial W$
and
![]() $(x_1')_{k}\neq (x_2')_{k}$
. As F is described by a block code
$(x_1')_{k}\neq (x_2')_{k}$
. As F is described by a block code
![]() $\{0,1\}^{[-m:m]}\to \{0,1\}$
, it follows that
$\{0,1\}^{[-m:m]}\to \{0,1\}$
, it follows that
![]() $|j-k|\leqslant m$
. (This argument is taken from the proof of [Reference Bułatek and Kwiatkowski2, Corollary 1].)
$|j-k|\leqslant m$
. (This argument is taken from the proof of [Reference Bułatek and Kwiatkowski2, Corollary 1].)
Consider any
![]() $y\in R$
. Then the index j in equation (13) equals
$y\in R$
. Then the index j in equation (13) equals
![]() $0$
and
$0$
and
![]() $y+y_F\in \partial W-\Delta (k)$
for some k with
$y+y_F\in \partial W-\Delta (k)$
for some k with
![]() $|k|\leqslant m$
. In other words:
$|k|\leqslant m$
. In other words:
![]() $f(R)$
is contained in the closed set
$f(R)$
is contained in the closed set
![]() $\bigcup _{k=-m}^mT^k(\partial W)$
. Because of condition (D′), the set R defined in equation (13) is residual with respect to the subspace topology of
$\bigcup _{k=-m}^mT^k(\partial W)$
. Because of condition (D′), the set R defined in equation (13) is residual with respect to the subspace topology of
![]() $\partial W$
. Hence,
$\partial W$
. Hence,
 $$ \begin{align*} \partial W+y_F=f(\partial W)=f(\overline{R})\subseteq\overline{f(R)}\subseteq \bigcup_{k=-m}^mT^k(\partial W) =\bigcup_{k=-m}^m\partial W+\Delta(k). \end{align*} $$
$$ \begin{align*} \partial W+y_F=f(\partial W)=f(\overline{R})\subseteq\overline{f(R)}\subseteq \bigcup_{k=-m}^mT^k(\partial W) =\bigcup_{k=-m}^m\partial W+\Delta(k). \end{align*} $$
It remains to prove equation (13). Recall first that
![]() $|\pi ^{-1}\{y\}|=1$
if and only if
$|\pi ^{-1}\{y\}|=1$
if and only if
![]() $y\in C_\phi $
, so that
$y\in C_\phi $
, so that
![]() $|\pi ^{-1}\{y\}|>1$
if and only if
$|\pi ^{-1}\{y\}|>1$
if and only if
![]() $y\in \bigcup _{k\in {\mathbb Z}}\partial W+\Delta (k)$
. So all we must show is that (A)
$y\in \bigcup _{k\in {\mathbb Z}}\partial W+\Delta (k)$
. So all we must show is that (A)
![]() $|\pi ^{-1}\{y\}|>2$
if and only if (B)
$|\pi ^{-1}\{y\}|>2$
if and only if (B)
![]() $y+\Delta (j)\in \partial W\cap (\partial W+\Delta (k))$
for some
$y+\Delta (j)\in \partial W\cap (\partial W+\Delta (k))$
for some
![]() $j\in {\mathbb Z}$
and
$j\in {\mathbb Z}$
and
![]() $k\in {\mathbb Z}\setminus \{0\}$
.
$k\in {\mathbb Z}\setminus \{0\}$
.
Suppose first that part (A) holds, i.e. that there are at least three different points in
![]() $\pi ^{-1}\{y\}$
. As points in the same
$\pi ^{-1}\{y\}$
. As points in the same
![]() $\pi $
-fibre can differ only at positions k where
$\pi $
-fibre can differ only at positions k where
![]() $y+\Delta (k)\in \partial W$
, there must be at least two such positions, and that is part (B).
$y+\Delta (k)\in \partial W$
, there must be at least two such positions, and that is part (B).
Conversely, if part (B) holds and if
![]() $x=\phi (y)$
, then
$x=\phi (y)$
, then
![]() $x_j=x_{j-k}=1$
.
$x_j=x_{j-k}=1$
.
-
(i) As
 $\partial W\cup (\partial W+\Delta (k))$
is nowhere dense in G, there are arbitrarily small perturbations
$\partial W\cup (\partial W+\Delta (k))$
is nowhere dense in G, there are arbitrarily small perturbations
 $y'$
of y such that
$y'$
of y such that
 $y'+\Delta (j)\not \in \partial W\cup (\partial W+\Delta (k))$
, resulting in points
$y'+\Delta (j)\not \in \partial W\cup (\partial W+\Delta (k))$
, resulting in points
 $x'=\phi (y')$
with
$x'=\phi (y')$
with
 $x^{\prime }_j=x^{\prime }_{j-k}=0$
.
$x^{\prime }_j=x^{\prime }_{j-k}=0$
. -
(ii) As
 $\partial W\cap (\partial W+\Delta (k))$
is nowhere dense in
$\partial W\cap (\partial W+\Delta (k))$
is nowhere dense in
 $\partial W$
with respect to the subspace topology on
$\partial W$
with respect to the subspace topology on
 $\partial W$
(because of condition (D′)), there are arbitrarily small perturbations
$\partial W$
(because of condition (D′)), there are arbitrarily small perturbations
 $y'$
of y such that
$y'$
of y such that
 $y'+\Delta (j)\in \partial W\setminus (\partial W+\Delta (k))$
, resulting in
$y'+\Delta (j)\in \partial W\setminus (\partial W+\Delta (k))$
, resulting in
 $x'=\phi (y')$
with
$x'=\phi (y')$
with
 $x^{\prime }_j=1$
and
$x^{\prime }_j=1$
and
 $x^{\prime }_{j-k}=0$
.
$x^{\prime }_{j-k}=0$
.
Hence,
![]() $|\pi ^{-1}\{y\}|\geqslant 3$
, and that is part (A).
$|\pi ^{-1}\{y\}|\geqslant 3$
, and that is part (A).
Proposition 2.13. We have
![]() $K\neq \emptyset $
, and there is a countable collection
$K\neq \emptyset $
, and there is a countable collection
![]() $U_{{N_j}}(\Delta (r_j))$
,
$U_{{N_j}}(\Delta (r_j))$
,
![]() ${j\in {\mathbb N}}$
, of cylinder sets in G with the following properties: for each
${j\in {\mathbb N}}$
, of cylinder sets in G with the following properties: for each
![]() $j\in {\mathbb N}$
, there exists some
$j\in {\mathbb N}$
, there exists some
![]() $k_j\in {\mathbb Z}$
such that
$k_j\in {\mathbb Z}$
such that
and
 $$ \begin{align} \bigcup_{j\in{\mathbb N}}U_{{N_j}}(\Delta(r_j))\cap\partial W\quad \text{is dense in }\partial W. \end{align} $$
$$ \begin{align} \bigcup_{j\in{\mathbb N}}U_{{N_j}}(\Delta(r_j))\cap\partial W\quad \text{is dense in }\partial W. \end{align} $$
Proof. We start from the observation of equation (3), namely
![]() $\partial W+y_F\subseteq \bigcup _{k\in {\mathbb Z}}\partial W+\Delta (k)$
. This implies
$\partial W+y_F\subseteq \bigcup _{k\in {\mathbb Z}}\partial W+\Delta (k)$
. This implies
Hence,
![]() $M:=\bigcup _{k\in {\mathbb Z}}V_k\setminus \operatorname {int}_{\partial W}(V_k)$
is a meagre subset of the compact space
$M:=\bigcup _{k\in {\mathbb Z}}V_k\setminus \operatorname {int}_{\partial W}(V_k)$
is a meagre subset of the compact space
![]() $\partial W$
and
$\partial W$
and
![]() $\partial W=M\cup \bigcup _{k\in K}\operatorname {int}_{\partial W}(V_k)$
. Now Baire’s category theorem implies that
$\partial W=M\cup \bigcup _{k\in K}\operatorname {int}_{\partial W}(V_k)$
. Now Baire’s category theorem implies that
![]() $K\neq \emptyset $
. As
$K\neq \emptyset $
. As
![]() $\partial W$
is separable, there is a countable collection
$\partial W$
is separable, there is a countable collection
![]() $U_{{N_j}}(\Delta (r_j))$
,
$U_{{N_j}}(\Delta (r_j))$
,
![]() ${j\in {\mathbb N}}$
, of cylinder sets in G, for each of which there exists
${j\in {\mathbb N}}$
, of cylinder sets in G, for each of which there exists
![]() $k_j\in K$
such that
$k_j\in K$
such that
![]() $\emptyset \neq \partial W\cap U_{{N_j}}(\Delta (r_j))\subseteq \operatorname {int}_{\partial W}(V_{k_j})$
and such that
$\emptyset \neq \partial W\cap U_{{N_j}}(\Delta (r_j))\subseteq \operatorname {int}_{\partial W}(V_{k_j})$
and such that
 $$ \begin{align*} \partial W=M\cup\bigcup_{j\in{\mathbb N}}(\partial W\cap U_{{N_j}}(\Delta(r_j))). \end{align*} $$
$$ \begin{align*} \partial W=M\cup\bigcup_{j\in{\mathbb N}}(\partial W\cap U_{{N_j}}(\Delta(r_j))). \end{align*} $$
As M is meagre in
![]() $\partial W$
, these cylinder sets satisfy equation (15), and as
$\partial W$
, these cylinder sets satisfy equation (15), and as
also equation (14) holds.
Corollary 2.14. Assume that the weak disjointness condition (D′) holds. Let the automorphism F of
![]() $(X_\eta ,\sigma )$
be described by a block code
$(X_\eta ,\sigma )$
be described by a block code
![]() $\{0,1\}^{[-m:m]}\to \{0,1\}$
. Then the set K is contained in
$\{0,1\}^{[-m:m]}\to \{0,1\}$
. Then the set K is contained in
![]() $[-m,m]$
,
$[-m,m]$
,
![]() ${\operatorname {int}_{\partial W}(V_{k_i})\cap \operatorname {int}_{\partial W}(V_{k_j})=\emptyset }$
for any different
${\operatorname {int}_{\partial W}(V_{k_i})\cap \operatorname {int}_{\partial W}(V_{k_j})=\emptyset }$
for any different
![]() $k_i,k_j\in K$
, and
$k_i,k_j\in K$
, and
![]() $\partial W=\bigcup _{k\in K}V_k'$
, where
$\partial W=\bigcup _{k\in K}V_k'$
, where
![]() $V_k':=\overline {\operatorname {int}_{\partial W}(V_k)}$
.
$V_k':=\overline {\operatorname {int}_{\partial W}(V_k)}$
.
Proof. Let
![]() $K':=K\cap [-m,m]$
, m as in Proposition 2.12. Because of that proposition and Proposition 2.13,
$K':=K\cap [-m,m]$
, m as in Proposition 2.12. Because of that proposition and Proposition 2.13,
![]() $\partial W=\bigcup _{k\in K'}\overline {\operatorname {int}_{\partial W}(V_k)}$
. Suppose there are
$\partial W=\bigcup _{k\in K'}\overline {\operatorname {int}_{\partial W}(V_k)}$
. Suppose there are
![]() $k_i,k_j\in K$
such that
$k_i,k_j\in K$
such that
![]() $\operatorname {int}_{\partial W}(V_{k_i})\cap \operatorname {int}_{\partial W}(V_{k_j})\neq \emptyset $
. Then there is some cylinder set
$\operatorname {int}_{\partial W}(V_{k_i})\cap \operatorname {int}_{\partial W}(V_{k_j})\neq \emptyset $
. Then there is some cylinder set
![]() $U_{N}(\Delta (r))\cap \partial W$
contained in this intersection. Let
$U_{N}(\Delta (r))\cap \partial W$
contained in this intersection. Let
![]() $\tilde {U}:=(U_{N}(\Delta (r))\cap \partial W)+y_F-\Delta (k_i)$
. Then,
$\tilde {U}:=(U_{N}(\Delta (r))\cap \partial W)+y_F-\Delta (k_i)$
. Then,
![]() $\tilde {U}\subseteq \partial W$
and
$\tilde {U}\subseteq \partial W$
and
![]() $\tilde {U}+\Delta (k_i-k_j)\subseteq \partial W$
, so that
$\tilde {U}+\Delta (k_i-k_j)\subseteq \partial W$
, so that
![]() $\tilde {U}\subseteq \partial W\cap (\partial W+\Delta (k_j-k_i))$
. As
$\tilde {U}\subseteq \partial W\cap (\partial W+\Delta (k_j-k_i))$
. As
![]() $\tilde {U}$
is non-empty and open in the relative topology on
$\tilde {U}$
is non-empty and open in the relative topology on
![]() $\partial W$
, the weak disjointness assumption implies
$\partial W$
, the weak disjointness assumption implies
![]() $k_i=k_j$
. This also proves that
$k_i=k_j$
. This also proves that
![]() $K=K'\subseteq [-m,m]$
.
$K=K'\subseteq [-m,m]$
.
For later use, we note a further consequence of Proposition 2.13.
Corollary 2.15. Assume that
![]() $(\operatorname {int}_{\partial W}(V_{k_i})+(y_F-\Delta (k_i))\cap \operatorname {int}_{\partial W}(V_{k_j})\neq \emptyset $
for some
$(\operatorname {int}_{\partial W}(V_{k_i})+(y_F-\Delta (k_i))\cap \operatorname {int}_{\partial W}(V_{k_j})\neq \emptyset $
for some
![]() $k_i,k_j\in K$
. Then there exist
$k_i,k_j\in K$
. Then there exist
![]() $N\in {\mathbb N}$
(which can be chosen arbitrarily large) and
$N\in {\mathbb N}$
(which can be chosen arbitrarily large) and
![]() $r\in {\mathbb Z}$
such that
$r\in {\mathbb Z}$
such that
 $$ \begin{align} \emptyset\neq(U_{{N}}(\Delta(r))\cap\partial W)+(y_F-\Delta(k_i))\subseteq&\ \partial W\quad\text{and} \nonumber \\ \emptyset\neq(U_{{N}}(\Delta(r))\cap\partial W)+(y_F-\Delta(k_i))+(y_F-\Delta(k_j))\subseteq&\ \partial W. \end{align} $$
$$ \begin{align} \emptyset\neq(U_{{N}}(\Delta(r))\cap\partial W)+(y_F-\Delta(k_i))\subseteq&\ \partial W\quad\text{and} \nonumber \\ \emptyset\neq(U_{{N}}(\Delta(r))\cap\partial W)+(y_F-\Delta(k_i))+(y_F-\Delta(k_j))\subseteq&\ \partial W. \end{align} $$
Proof. Fix some cylinder set
![]() $U_{{N'}}(\Delta (r'))$
such that
$U_{{N'}}(\Delta (r'))$
such that
In view of Proposition 2.13, there are
![]() $N_i',N_j'\in {\mathbb N}$
and
$N_i',N_j'\in {\mathbb N}$
and
![]() $r_i',r_j'\in {\mathbb Z}$
such that
$r_i',r_j'\in {\mathbb Z}$
such that
and
 $$ \begin{align} (U_{{N_i'}}(\Delta(r_i'))\cap\partial W)+(y_F-\Delta(k_i))&\subseteq\partial W,\nonumber\\ (U_{{N_j'}}(\Delta(r_j'))\cap\partial W)+(y_F-\Delta(k_j))&\subseteq\partial W. \end{align} $$
$$ \begin{align} (U_{{N_i'}}(\Delta(r_i'))\cap\partial W)+(y_F-\Delta(k_i))&\subseteq\partial W,\nonumber\\ (U_{{N_j'}}(\Delta(r_j'))\cap\partial W)+(y_F-\Delta(k_j))&\subseteq\partial W. \end{align} $$
Because of equations (17) and (18), the set
![]() $U_{{N'}}(\Delta (r'))\cap U_{{N_i'}}(\Delta (r_i'))\cap (U_{{N_j'}}(\Delta (r_j'))-(y_F-\Delta (k_i)))$
contains a cylinder set
$U_{{N'}}(\Delta (r'))\cap U_{{N_i'}}(\Delta (r_i'))\cap (U_{{N_j'}}(\Delta (r_j'))-(y_F-\Delta (k_i)))$
contains a cylinder set
![]() $U_{N}(\Delta (r))$
for which
$U_{N}(\Delta (r))$
for which
![]() $U_{N}(\Delta (r))\cap \partial W\neq \emptyset $
and
$U_{N}(\Delta (r))\cap \partial W\neq \emptyset $
and
 $$ \begin{align*} \begin{aligned} (U_{{N}}(\Delta(r))\cap\partial W)+(y_F-\Delta(k_i))\subseteq&\ \partial W\quad\text{and}\\ (U_{{N}}(\Delta(r))\cap\partial W)+(y_F-\Delta(k_i))+(y_F-\Delta(k_j))\subseteq&\ \partial W. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (U_{{N}}(\Delta(r))\cap\partial W)+(y_F-\Delta(k_i))\subseteq&\ \partial W\quad\text{and}\\ (U_{{N}}(\Delta(r))\cap\partial W)+(y_F-\Delta(k_i))+(y_F-\Delta(k_j))\subseteq&\ \partial W. \end{aligned} \end{align*} $$
Clearly, N can be chosen arbitrarily large.
2.4 Consequences of the weak double disjointness condition (DD′)
The crucial step is now to show that
![]() $\operatorname {int}_{\partial W}(V_k)+(y_F-\Delta (k))\kern1.2pt{\subseteq}\kern1.2pt V_k$
for all
$\operatorname {int}_{\partial W}(V_k)+(y_F-\Delta (k))\kern1.2pt{\subseteq}\kern1.2pt V_k$
for all
![]() $k\kern1.2pt{\in}\kern1.2pt K$
under suitable assumptions.
$k\kern1.2pt{\in}\kern1.2pt K$
under suitable assumptions.
Proposition 2.16. Assume that the weak double disjointness condition (DD′) holds. Let the automorphism F of
![]() $(X_\eta ,\sigma )$
be described by a block code
$(X_\eta ,\sigma )$
be described by a block code
![]() $\{0,1\}^{[-m:m]}\to \{0,1\}$
. Then,
$\{0,1\}^{[-m:m]}\to \{0,1\}$
. Then,
![]() $V_k'+(y_F-\Delta (k))\subseteq V_k'$
for all
$V_k'+(y_F-\Delta (k))\subseteq V_k'$
for all
![]() $k\in K$
, the set K is contained in
$k\in K$
, the set K is contained in
![]() $[-m,m]$
and the sets
$[-m,m]$
and the sets
![]() $V_k'$
have pairwise disjoint interiors.
$V_k'$
have pairwise disjoint interiors.
Proof. It suffices to prove that
![]() $\operatorname {int}_{\partial W}(V_k)+(y_F-\Delta (k))\subseteq V_k'$
for all
$\operatorname {int}_{\partial W}(V_k)+(y_F-\Delta (k))\subseteq V_k'$
for all
![]() $k\in K$
. Suppose for a contradiction that there is
$k\in K$
. Suppose for a contradiction that there is
![]() $k_i\in K$
such that
$k_i\in K$
such that
![]() $\operatorname {int}_{\partial W}(V_{k_i})+(y_F-\Delta (k_i))\not \subseteq V_{k_i}'$
. By Proposition 2.13, there exists
$\operatorname {int}_{\partial W}(V_{k_i})+(y_F-\Delta (k_i))\not \subseteq V_{k_i}'$
. By Proposition 2.13, there exists
![]() $k_j\in K\setminus \{k_i\}$
such that
$k_j\in K\setminus \{k_i\}$
such that
![]() $(\operatorname {int}_{\partial W}(V_{k_i})+(y_F-\Delta (k_i)))\cap \operatorname {int}_{\partial W}(V_{k_j})\neq \emptyset $
. So we can apply Corollary 2.15. Hence, there are
$(\operatorname {int}_{\partial W}(V_{k_i})+(y_F-\Delta (k_i)))\cap \operatorname {int}_{\partial W}(V_{k_j})\neq \emptyset $
. So we can apply Corollary 2.15. Hence, there are
![]() $N\in {\mathbb N}$
and
$N\in {\mathbb N}$
and
![]() $r\in {\mathbb Z}$
such that, setting
$r\in {\mathbb Z}$
such that, setting
![]() $\beta =y_F-\Delta (k_i)$
,
$\beta =y_F-\Delta (k_i)$
,
In view of condition (DD′), this implies
![]() $k_i=k_j$
. The remaining assertions follow from Corollary 2.14.
$k_i=k_j$
. The remaining assertions follow from Corollary 2.14.
Remark 2.17. Suppose that the conclusions of Proposition 2.16 are satisfied (not necessarily condition (DD′)).
-
(a) For
 $k\in K$
, let
$k\in K$
, let
 ${\widetilde {\mathcal H}}_n^k:=\{j\in {\widetilde {\mathcal H}}_n: U_n(\Delta (j))\cap V_k'\neq \emptyset \}$
. Then,
${\widetilde {\mathcal H}}_n^k:=\{j\in {\widetilde {\mathcal H}}_n: U_n(\Delta (j))\cap V_k'\neq \emptyset \}$
. Then,
 ${\widetilde {\mathcal H}}_n=\bigcup _{k\in K}{\widetilde {\mathcal H}}_n^k$
by Lemma 2.5 and Corollary 2.14. (However, observe that this need not be a disjoint union, in general!)
${\widetilde {\mathcal H}}_n=\bigcup _{k\in K}{\widetilde {\mathcal H}}_n^k$
by Lemma 2.5 and Corollary 2.14. (However, observe that this need not be a disjoint union, in general!) -
(b)
 $j\in {\widetilde {\mathcal H}}_n^k$
if and only if
$j\in {\widetilde {\mathcal H}}_n^k$
if and only if
 $j+p_n\in {\widetilde {\mathcal H}}_n^k$
, that is, all
$j+p_n\in {\widetilde {\mathcal H}}_n^k$
, that is, all
 ${\widetilde {\mathcal H}}_n^k$
are
${\widetilde {\mathcal H}}_n^k$
are
 $p_n$
-periodic.
$p_n$
-periodic. -
(c) For each
 $n>0$
and
$n>0$
and
 $k\in K$
, we have
$k\in K$
, we have
 ${\widetilde {\mathcal H}}_n^k+\gcd ((y_F)_n-k,p_n){\mathbb Z}\subseteq {\widetilde {\mathcal H}}_n^k$
.
${\widetilde {\mathcal H}}_n^k+\gcd ((y_F)_n-k,p_n){\mathbb Z}\subseteq {\widetilde {\mathcal H}}_n^k$
.Proof of (c)
For each
 $j\in {\widetilde {\mathcal H}}_n^k$
, there exists
$j\in {\widetilde {\mathcal H}}_n^k$
, there exists
 $h\in U_n(\Delta (j))\cap V_k'$
. By assumption,
$h\in U_n(\Delta (j))\cap V_k'$
. By assumption,
 ${h+(y_F-\Delta (k)){\mathbb Z}\subseteq V_k'}$
, so that for all
${h+(y_F-\Delta (k)){\mathbb Z}\subseteq V_k'}$
, so that for all
 $t\in {\mathbb Z}$
,
$t\in {\mathbb Z}$
,  $$ \begin{align*} U_n(\Delta(j+((y_F)_n-k)t)\cap V_k'= U_n(\Delta(j)+(y_F-\Delta(k))t)\cap V_k'\neq\emptyset, \end{align*} $$
$$ \begin{align*} U_n(\Delta(j+((y_F)_n-k)t)\cap V_k'= U_n(\Delta(j)+(y_F-\Delta(k))t)\cap V_k'\neq\emptyset, \end{align*} $$
that is,
 $j+((y_F)_n-k){\mathbb Z}\subseteq {\widetilde {\mathcal H}}_n^k$
.
$j+((y_F)_n-k){\mathbb Z}\subseteq {\widetilde {\mathcal H}}_n^k$
.
Remark 2.18. Remark 2.17(c) can be used to show that
![]() $|K|=1$
and hence
$|K|=1$
and hence
![]() $\partial W+ (y_F-\Delta (k))\subseteq \partial W$
, whenever
$\partial W+ (y_F-\Delta (k))\subseteq \partial W$
, whenever
![]() $\boldsymbol {\delta }({\widetilde {\mathcal H}}_n)=o({1}/{\sqrt p_n})$
. This allows us to apply Theorem 2.8, which imposes restrictions on
$\boldsymbol {\delta }({\widetilde {\mathcal H}}_n)=o({1}/{\sqrt p_n})$
. This allows us to apply Theorem 2.8, which imposes restrictions on
![]() $y_F$
in terms of the minimal periods
$y_F$
in terms of the minimal periods
![]() $\tilde {\tau }_n$
of the sets
$\tilde {\tau }_n$
of the sets
![]() ${\widetilde {\mathcal H}}_n$
. (However, that is quite far from what holds in the
${\widetilde {\mathcal H}}_n$
. (However, that is quite far from what holds in the
![]() ${\mathcal B}$
-free setting.)
${\mathcal B}$
-free setting.)
Indeed, let
![]() $k,k'\in K$
and denote
$k,k'\in K$
and denote
![]() $\beta =y_F-\Delta (k)$
and
$\beta =y_F-\Delta (k)$
and
![]() $\beta '=y_F-\Delta (k')$
. Suppose for a contradiction that
$\beta '=y_F-\Delta (k')$
. Suppose for a contradiction that
![]() $k\neq k'$
. Then,
$k\neq k'$
. Then,
where
![]() $\langle s\rangle {p_n}$
denotes the subgroup generated by s in
$\langle s\rangle {p_n}$
denotes the subgroup generated by s in
![]() ${\mathbb Z}/p_n{\mathbb Z}$
, so that
${\mathbb Z}/p_n{\mathbb Z}$
, so that
 $$ \begin{align*} |{\widetilde{\mathcal H}}_n\cap[0,p_n)|^2&\ge |{\widetilde{\mathcal H}}_n^{k}\cap[0,p_n)|\cdot|{\widetilde{\mathcal H}}_n^{k'}\cap[0,p_n)|\\ &\ge |\langle (\gcd(\beta_n,p_n),\gcd(\beta_n',p_n))\rangle_{p_n\times p_n}|, \end{align*} $$
$$ \begin{align*} |{\widetilde{\mathcal H}}_n\cap[0,p_n)|^2&\ge |{\widetilde{\mathcal H}}_n^{k}\cap[0,p_n)|\cdot|{\widetilde{\mathcal H}}_n^{k'}\cap[0,p_n)|\\ &\ge |\langle (\gcd(\beta_n,p_n),\gcd(\beta_n',p_n))\rangle_{p_n\times p_n}|, \end{align*} $$
where
![]() $\langle (s,t)\rangle {p_n\times p_n}$
denotes the subgroup generated by
$\langle (s,t)\rangle {p_n\times p_n}$
denotes the subgroup generated by
![]() $(s,t)$
in
$(s,t)$
in
![]() $({\mathbb Z}/p_n{\mathbb Z})^2$
. Hence,
$({\mathbb Z}/p_n{\mathbb Z})^2$
. Hence,
 $$ \begin{align*} \begin{aligned} |{\widetilde{\mathcal H}}_n\cap[0,p_n)|^2 &\ge \operatorname{lcm}\bigg(\frac{p_n}{\gcd(\beta_n,p_n)},\frac{p_n}{\gcd(\beta_n',p_n)}\bigg) =\frac{p_n}{\gcd(\beta_n,\beta_n',p_n)}\\ &\ge \frac{p_n}{\gcd(\beta_n-\beta_n',p_n)} = \frac{p_n}{\gcd(k-k',p_n)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |{\widetilde{\mathcal H}}_n\cap[0,p_n)|^2 &\ge \operatorname{lcm}\bigg(\frac{p_n}{\gcd(\beta_n,p_n)},\frac{p_n}{\gcd(\beta_n',p_n)}\bigg) =\frac{p_n}{\gcd(\beta_n,\beta_n',p_n)}\\ &\ge \frac{p_n}{\gcd(\beta_n-\beta_n',p_n)} = \frac{p_n}{\gcd(k-k',p_n)}. \end{aligned} \end{align*} $$
However, the last denominator is at most
![]() $2m$
, so
$2m$
, so
 $$ \begin{align*} \frac{1}{2m\cdot p_n}\le \bigg(\frac{|{\widetilde{\mathcal H}}_n\cap[0,p_n)|}{p_n}\bigg)^2 =\boldsymbol{\delta}({\widetilde{\mathcal H}}_n)^2, \end{align*} $$
$$ \begin{align*} \frac{1}{2m\cdot p_n}\le \bigg(\frac{|{\widetilde{\mathcal H}}_n\cap[0,p_n)|}{p_n}\bigg)^2 =\boldsymbol{\delta}({\widetilde{\mathcal H}}_n)^2, \end{align*} $$
which is in contradiction to the assumption.
Here is an example of a Toeplitz sequence for which Remark 2.18 applies and for which
![]() $\tau _n$
and
$\tau _n$
and
![]() $\tilde {\tau }_n$
, the smallest periods of
$\tilde {\tau }_n$
, the smallest periods of
![]() ${\mathcal H}_n$
and
${\mathcal H}_n$
and
![]() ${\widetilde {\mathcal H}}_n$
, are different.
${\widetilde {\mathcal H}}_n$
, are different.
Example 2.19. Garcia and Hedlund [Reference Garcia and Hedlund14] gave the first example of a
![]() $0$
–
$0$
–
![]() $1$
non-periodic Toeplitz sequence. At each level n of their construction, there is exactly one hole in each interval of length
$1$
non-periodic Toeplitz sequence. At each level n of their construction, there is exactly one hole in each interval of length
![]() $p_n$
, so all holes are essential, and the centralizer is trivial because condition (*) is satisfied, see Remark 2.10. Our example is a modification of this construction: (to be precise, the example from [Reference Garcia and Hedlund14] is not really a Toeplitz sequence, because it is not periodic at position
$p_n$
, so all holes are essential, and the centralizer is trivial because condition (*) is satisfied, see Remark 2.10. Our example is a modification of this construction: (to be precise, the example from [Reference Garcia and Hedlund14] is not really a Toeplitz sequence, because it is not periodic at position
![]() $0$
. However, its orbit closure is minimal and contains many Toeplitz sequences. Our modification takes this into account.)
$0$
. However, its orbit closure is minimal and contains many Toeplitz sequences. Our modification takes this into account.)
let
![]() $r_n:=\sum _{j=0}^{n-1}2^{2j}=({2^{2n}-1})/{3}$
. Define a Toeplitz sequence in such a way that
$r_n:=\sum _{j=0}^{n-1}2^{2j}=({2^{2n}-1})/{3}$
. Define a Toeplitz sequence in such a way that
Observe that
![]() ${\mathcal H}_{n}=2^{2(n-1)}(4{\mathbb Z}-1)-r_{n-1}\subseteq {\mathcal H}_{n-1}$
, in particular,
${\mathcal H}_{n}=2^{2(n-1)}(4{\mathbb Z}-1)-r_{n-1}\subseteq {\mathcal H}_{n-1}$
, in particular,
![]() $\bigcap _{n\ge 1}{\mathcal H}_n=\emptyset $
. Here,
$\bigcap _{n\ge 1}{\mathcal H}_n=\emptyset $
. Here,
![]() ${\mathcal H}_{n-1}\setminus {\mathcal H}_{n}$
is the disjoint union of the residue classes
${\mathcal H}_{n-1}\setminus {\mathcal H}_{n}$
is the disjoint union of the residue classes
![]() $2^{2(n-1)}(4{\mathbb Z}-k)-r_{n-1}$
,
$2^{2(n-1)}(4{\mathbb Z}-k)-r_{n-1}$
,
![]() $k\in \{0,2,3\}$
, and the positions in each of these residue classes should be filled alternatingly with
$k\in \{0,2,3\}$
, and the positions in each of these residue classes should be filled alternatingly with
![]() $0$
and
$0$
and
![]() $1$
. Then all these positions have minimal period
$1$
. Then all these positions have minimal period
![]() $2^{2n+1}$
, and
$2^{2n+1}$
, and
![]() $(p_n)_{n\ge 1}=(2^{2n+1})_{n\ge 1}$
is a period structure for the resulting Toeplitz sequence.
$(p_n)_{n\ge 1}=(2^{2n+1})_{n\ge 1}$
is a period structure for the resulting Toeplitz sequence.
If
![]() $2^{2N}t-r_N\in {\mathcal H}_N$
and
$2^{2N}t-r_N\in {\mathcal H}_N$
and
![]() $n>N$
, then
$n>N$
, then
 $$ \begin{align*} \begin{aligned} (2^{2N}t-r_N+p_N{\mathbb Z})\cap{\mathcal H}_n &= ((2^{2N}t+(r_n-r_N)+p_N{\mathbb Z})\cap 2^{2n}{\mathbb Z})-r_n\\ &= 2^{2N}\bigg(\bigg(t+\frac{2^{2(n-N)}-1}{3}+2{\mathbb Z}\bigg)\cap 2^{2(n-N)}{\mathbb Z}\bigg)-r_n \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (2^{2N}t-r_N+p_N{\mathbb Z})\cap{\mathcal H}_n &= ((2^{2N}t+(r_n-r_N)+p_N{\mathbb Z})\cap 2^{2n}{\mathbb Z})-r_n\\ &= 2^{2N}\bigg(\bigg(t+\frac{2^{2(n-N)}-1}{3}+2{\mathbb Z}\bigg)\cap 2^{2(n-N)}{\mathbb Z}\bigg)-r_n \end{aligned} \end{align*} $$
is non-empty if and only if t is odd. Hence,
![]() ${\widetilde {\mathcal H}}_N=2^{2N}(2{\mathbb Z}+1)-r_N$
and
${\widetilde {\mathcal H}}_N=2^{2N}(2{\mathbb Z}+1)-r_N$
and
![]() $\tilde {\tau }_N=2^{2N+1}=p_N=2\tau _N$
. Notice that each interval of length
$\tilde {\tau }_N=2^{2N+1}=p_N=2\tau _N$
. Notice that each interval of length
![]() $p_n$
contains exactly two holes and the distance between them is
$p_n$
contains exactly two holes and the distance between them is
![]() ${p_n}/{2}$
. However,
${p_n}/{2}$
. However,
![]() $p_{n+1}=4p_n$
, so condition (*) is not satisfied. Nevertheless, the centralizer is trivial by Theorem 2.8 and Remark 2.18.
$p_{n+1}=4p_n$
, so condition (*) is not satisfied. Nevertheless, the centralizer is trivial by Theorem 2.8 and Remark 2.18.
2.5 Additional arithmetic structure (motivated by the
 ${\mathcal B}$
-free case)
${\mathcal B}$
-free case)
Throughout this subsection, F is again an automorphism of
![]() $(X_\eta ,\sigma )$
and
$(X_\eta ,\sigma )$
and
![]() $\pi (F(x))=\pi (x)+y_F$
for
$\pi (F(x))=\pi (x)+y_F$
for
![]() $x\in X_\eta $
. We start with a particularly simple situation based on the following (very strong) trivial intersection property: there are
$x\in X_\eta $
. We start with a particularly simple situation based on the following (very strong) trivial intersection property: there are
![]() $A_n\subseteq {\mathbb N}$
,
$A_n\subseteq {\mathbb N}$
,
![]() $n\in {\mathbb N}$
such that
$n\in {\mathbb N}$
such that
We will check this property for some non-trivial
![]() ${\mathcal B}$
-free examples, see Examples 3.20, 3.27 and 3.28, and also §3.4.
${\mathcal B}$
-free examples, see Examples 3.20, 3.27 and 3.28, and also §3.4.
Proposition 2.20. Suppose property (TI) is satisfied.
-
(a) Then the disjointness condition (D) holds, and there exists a unique
 $k\in {\mathbb Z}$
such that
$k\in {\mathbb Z}$
such that
 $\partial W+y_F\subseteq \partial W+\Delta (k)$
.
$\partial W+y_F\subseteq \partial W+\Delta (k)$
. -
(b)
 $\tilde {\tau }_n\mid (y_F)_n-k$
, where
$\tilde {\tau }_n\mid (y_F)_n-k$
, where
 $\tilde {\tau }_n$
is the minimal period of
$\tilde {\tau }_n$
is the minimal period of
 ${\widetilde {\mathcal H}}_n$
. In particular, if infinitely many
${\widetilde {\mathcal H}}_n$
. In particular, if infinitely many
 ${\widetilde {\mathcal H}}_n$
have minimal period
${\widetilde {\mathcal H}}_n$
have minimal period
 $p_n$
then
$p_n$
then
 $y_F=\Delta (k)$
.
$y_F=\Delta (k)$
.
Proof. (a) If there is some
![]() $y\in \partial W\cap (\partial W-\Delta (k))$
, then
$y\in \partial W\cap (\partial W-\Delta (k))$
, then
![]() $U_{N}(\Delta (y_N))\cap \partial W=U_{N}(y)\cap \partial W\neq \emptyset $
and
$U_{N}(\Delta (y_N))\cap \partial W=U_{N}(y)\cap \partial W\neq \emptyset $
and
![]() $U_{N}(\Delta (k+y_N))\cap \partial W=U_{N}(\Delta (k)+y)\cap \partial W\neq \emptyset $
, so that
$U_{N}(\Delta (k+y_N))\cap \partial W=U_{N}(\Delta (k)+y)\cap \partial W\neq \emptyset $
, so that
![]() $k=(k+y_N)-y_N\in {\widetilde {\mathcal H}}_N-{\widetilde {\mathcal H}}_N\subseteq {\mathcal M}_{A_N}-{\mathcal M}_{A_N}\subseteq \langle {\mathcal M}_{A_N}\rangle =\langle A_{N}\rangle $
for all
$k=(k+y_N)-y_N\in {\widetilde {\mathcal H}}_N-{\widetilde {\mathcal H}}_N\subseteq {\mathcal M}_{A_N}-{\mathcal M}_{A_N}\subseteq \langle {\mathcal M}_{A_N}\rangle =\langle A_{N}\rangle $
for all
![]() $N>0$
by Lemma 2.5a). Hence,
$N>0$
by Lemma 2.5a). Hence,
![]() $k=0$
in view of property (TI). If there are
$k=0$
in view of property (TI). If there are
![]() $y_1,y_2\in \partial W$
and
$y_1,y_2\in \partial W$
and
![]() $k_1,k_2\in {\mathbb Z}$
such that
$k_1,k_2\in {\mathbb Z}$
such that
![]() $y_i+y_F\in \partial W-\Delta (k_i)$
(
$y_i+y_F\in \partial W-\Delta (k_i)$
(
![]() $i=1,2$
), then
$i=1,2$
), then
![]() $U_N(\Delta (k_i+(y_i+y_F)_N))\cap \partial W\neq \emptyset $
(
$U_N(\Delta (k_i+(y_i+y_F)_N))\cap \partial W\neq \emptyset $
(
![]() $i=1,2$
), so that
$i=1,2$
), so that
![]() $k_2-k_1\in \langle A_N\rangle $
for all
$k_2-k_1\in \langle A_N\rangle $
for all
![]() $N>0$
as before. Hence,
$N>0$
as before. Hence,
![]() $k_2=k_1$
because of property (TI).
$k_2=k_1$
because of property (TI).
(b) This follows from part (a) of the lemma and from Theorem 2.8a).
Together with Theorem 2.8, this proposition yields the following corollary.
Corollary 2.21. Suppose that property (TI) is satisfied. If
![]() ${M\kern0.8pt{:=}\kern0.8pt\liminf _{n\to \infty }\kern-1pt p_n/\tilde {\tau }_n\kern0.8pt{<}\kern0.8pt\infty }$
, then
${M\kern0.8pt{:=}\kern0.8pt\liminf _{n\to \infty }\kern-1pt p_n/\tilde {\tau }_n\kern0.8pt{<}\kern0.8pt\infty }$
, then
where
![]() $\operatorname {Tor}$
denotes the torsion group of
$\operatorname {Tor}$
denotes the torsion group of
![]() $\operatorname {Aut}_\sigma (X_\eta )$
. It is a cyclic group (possibly trivial), whose order divides M. In particular, if infinitely many
$\operatorname {Aut}_\sigma (X_\eta )$
. It is a cyclic group (possibly trivial), whose order divides M. In particular, if infinitely many
![]() ${\widetilde {\mathcal H}}_n$
have minimal period
${\widetilde {\mathcal H}}_n$
have minimal period
![]() $p_n$
, then the centralizer of
$p_n$
, then the centralizer of
![]() $(X_\eta ,\sigma )$
is trivial.
$(X_\eta ,\sigma )$
is trivial.
If property (TI) is not satisfied, as is the case for more complex
![]() ${\mathcal B}$
-free examples, we need additional tools to verify the assumption in equation (4) of Theorem 2.8. The weak double disjointness condition (DD′) turns out to be instrumental along this way, and hence its verification under mild arithmetic assumptions in Proposition 2.30 will be an important step.
${\mathcal B}$
-free examples, we need additional tools to verify the assumption in equation (4) of Theorem 2.8. The weak double disjointness condition (DD′) turns out to be instrumental along this way, and hence its verification under mild arithmetic assumptions in Proposition 2.30 will be an important step.
We continue with some arithmetic preparations. For the sake of brevity, we sometimes write
![]() $u\vee v$
instead of
$u\vee v$
instead of
![]() $\operatorname {lcm}(u,v)$
. The following notation will be used repeatedly for positive integers a and k:
$\operatorname {lcm}(u,v)$
. The following notation will be used repeatedly for positive integers a and k:
For
![]() $A\subseteq {\mathbb N}$
and
$A\subseteq {\mathbb N}$
and
![]() $k\in {\mathbb N}$
, denote
$k\in {\mathbb N}$
, denote
and
If
![]() $A=A^{\textrm {prim}}$
, then A is called primitive.
$A=A^{\textrm {prim}}$
, then A is called primitive.
Remark 2.22. Let
![]() $r,\ell ,s,m\in {\mathbb Z}$
and assume that
$r,\ell ,s,m\in {\mathbb Z}$
and assume that
![]() $\gcd (m,\ell )\mid s-r$
. Then,
$\gcd (m,\ell )\mid s-r$
. Then,
where
![]() $x{\kern-1.5pt}\in{\kern-1.5pt} \{0,\ldots ,(\ell {\kern-1pt}\vee{\kern-1pt} m){\kern-1pt}-{\kern-1pt}1\}$
is defined uniquely by the first identity,
$x{\kern-1.5pt}\in{\kern-1.5pt} \{0,\ldots ,(\ell {\kern-1pt}\vee{\kern-1pt} m){\kern-1pt}-{\kern-1pt}1\}$
is defined uniquely by the first identity,
![]() $g{\kern-1pt}={\kern-1pt}\gcd (x, \ell \vee m)$
,
$g{\kern-1pt}={\kern-1pt}\gcd (x, \ell \vee m)$
,
![]() $\tilde {r}={x}/{g}$
, and
$\tilde {r}={x}/{g}$
, and
![]() $\tilde {\ell }={\ell \vee m}/{g}$
. Observe that
$\tilde {\ell }={\ell \vee m}/{g}$
. Observe that
![]() $\gcd (\tilde {r},\tilde {\ell })=1$
. This formula will be applied in several settings, so that one should keep in mind that
$\gcd (\tilde {r},\tilde {\ell })=1$
. This formula will be applied in several settings, so that one should keep in mind that
![]() $g,\tilde {r}$
and
$g,\tilde {r}$
and
![]() $\tilde {\ell }$
depend on
$\tilde {\ell }$
depend on
![]() $r,\ell ,s$
and m. For later use, observe also that
$r,\ell ,s$
and m. For later use, observe also that
Here is the proof of equation (24): as
![]() $x-r\in \ell {\mathbb Z}$
and
$x-r\in \ell {\mathbb Z}$
and
![]() $x-s\in m{\mathbb Z}$
, we have
$x-s\in m{\mathbb Z}$
, we have
![]() $\gcd (x,\ell )=\gcd (r,\ell )$
and
$\gcd (x,\ell )=\gcd (r,\ell )$
and
![]() $\gcd (x,m)=\gcd (s,m)$
. Hence,
$\gcd (x,m)=\gcd (s,m)$
. Hence,
We list some further consequences:
where we used
![]() $\gcd (a,g)\mid \gcd (a,\ell \vee m)$
for the last inclusion. Each subset
$\gcd (a,g)\mid \gcd (a,\ell \vee m)$
for the last inclusion. Each subset
![]() $Z\subseteq {\mathbb Z}$
holds
$Z\subseteq {\mathbb Z}$
holds
because
![]() $\gcd (\tilde {r},\tilde {\ell })=1$
. (Indeed, if
$\gcd (\tilde {r},\tilde {\ell })=1$
. (Indeed, if
![]() $a\in A$
,
$a\in A$
,
![]() $z\in Z$
and
$z\in Z$
and
![]() $x=\tilde {r}+z\tilde {\ell }\in a{\mathbb Z}$
, then
$x=\tilde {r}+z\tilde {\ell }\in a{\mathbb Z}$
, then
![]() $\gcd (a,\tilde {\ell })\mid \tilde {r}$
, so that
$\gcd (a,\tilde {\ell })\mid \tilde {r}$
, so that
![]() $\gcd (a,\tilde {\ell })\mid \gcd (\tilde {r},\tilde {\ell })=1$
, i.e.
$\gcd (a,\tilde {\ell })\mid \gcd (\tilde {r},\tilde {\ell })=1$
, i.e.
![]() $a\in A^{\perp {\tilde {\ell }}}$
.) Combining equations (23), (25) and (26) yields
$a\in A^{\perp {\tilde {\ell }}}$
.) Combining equations (23), (25) and (26) yields
Given a set
![]() $A\subseteq {\mathbb Z}$
, we denote by
$A\subseteq {\mathbb Z}$
, we denote by
![]() $\boldsymbol {\delta }(A):=\lim _{N\to \infty }({1}/{\log N})\sum _{k=1}^N({1}/{k})1_A(k)$
the logarithmic density of A (provided the limit exists).
$\boldsymbol {\delta }(A):=\lim _{N\to \infty }({1}/{\log N})\sum _{k=1}^N({1}/{k})1_A(k)$
the logarithmic density of A (provided the limit exists).
Lemma 2.23. Let
![]() $r,\ell ,s,m\in {\mathbb Z}$
and assume that
$r,\ell ,s,m\in {\mathbb Z}$
and assume that
![]() $\gcd (m,\ell )\mid s-r$
. Recall that
$\gcd (m,\ell )\mid s-r$
. Recall that
![]() ${\tilde {\ell }={\ell \vee m}/{g}}$
. Then,
${\tilde {\ell }={\ell \vee m}/{g}}$
. Then,
Proof. As in [Reference Hall15, Lemma 1.17], we have
As
![]() $g\cdot \tilde {\ell }=\ell \vee m$
, this together with equation (23) proves the identity in equation (28). As
$g\cdot \tilde {\ell }=\ell \vee m$
, this together with equation (23) proves the identity in equation (28). As
![]() $\boldsymbol {\delta }((r+\ell {\mathbb Z})\cap (s+m{\mathbb Z}))={1}/{\ell \vee m}$
, equation (29) follows at once. For the inequality in equation (28), observe that
$\boldsymbol {\delta }((r+\ell {\mathbb Z})\cap (s+m{\mathbb Z}))={1}/{\ell \vee m}$
, equation (29) follows at once. For the inequality in equation (28), observe that
![]() ${\mathcal M}_{(A^{\div g})^{\perp {\tilde {\ell }}}}\subseteq {\mathcal M}_{A^{\div g}}\subseteq {\mathcal M}_{A^{\div \ell \vee m}}$
by equation (25).
${\mathcal M}_{(A^{\div g})^{\perp {\tilde {\ell }}}}\subseteq {\mathcal M}_{A^{\div g}}\subseteq {\mathcal M}_{A^{\div \ell \vee m}}$
by equation (25).
Lemma 2.24. Assume that
![]() $(r+\ell {\mathbb Z})\cap (s+m{\mathbb Z})\cap [N,\infty )\subseteq {\mathcal M}_C$
for some
$(r+\ell {\mathbb Z})\cap (s+m{\mathbb Z})\cap [N,\infty )\subseteq {\mathcal M}_C$
for some
![]() $r,\ell ,s, m\in {\mathbb Z}$
satisfying
$r,\ell ,s, m\in {\mathbb Z}$
satisfying
![]() $\gcd (m,\ell )\mid s-r$
, some
$\gcd (m,\ell )\mid s-r$
, some
![]() $N\in {\mathbb N}$
and a finite set
$N\in {\mathbb N}$
and a finite set
![]() $C\subset {\mathbb N}$
. Then,
$C\subset {\mathbb N}$
. Then,
![]() ${c\mid \gcd (r,\ell )\vee \gcd (s,m)}$
for some
${c\mid \gcd (r,\ell )\vee \gcd (s,m)}$
for some
![]() $c\in C$
.
$c\in C$
.
Proof. Let
![]() $A:=(C^{\div g})^{\perp \tilde \ell }$
. In view of equation (27), our assumption implies
$A:=(C^{\div g})^{\perp \tilde \ell }$
. In view of equation (27), our assumption implies
![]() $(\tilde {r}+\tilde {\ell }{\mathbb Z})\cap [N,\infty )\subseteq {\mathcal M}_{A}={\mathcal M}_{A^{\textrm {prim}}}$
. As
$(\tilde {r}+\tilde {\ell }{\mathbb Z})\cap [N,\infty )\subseteq {\mathcal M}_{A}={\mathcal M}_{A^{\textrm {prim}}}$
. As
![]() $A^{\textrm {prim}}$
is taut, [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk12, Proposition 4.31] shows that there is
$A^{\textrm {prim}}$
is taut, [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk12, Proposition 4.31] shows that there is
![]() $a\in A^{\textrm {prim}}$
such that
$a\in A^{\textrm {prim}}$
such that
![]() $a\mid \gcd (\tilde {r},\tilde {\ell })=1$
, that is,
$a\mid \gcd (\tilde {r},\tilde {\ell })=1$
, that is,
![]() $1\in A$
. Hence, there is
$1\in A$
. Hence, there is
![]() $c\in C$
such that
$c\in C$
such that
![]() $c\mid g=\gcd (r,\ell )\vee \gcd (s,m)$
.
$c\mid g=\gcd (r,\ell )\vee \gcd (s,m)$
.
We will need a more detailed arithmetic characterization of the inclusion from Lemma 2.24 when C is a singleton and
![]() $s=0$
.
$s=0$
.
Lemma 2.25. Let
![]() $r,\ell ,a,c\in {\mathbb Z}$
satisfying
$r,\ell ,a,c\in {\mathbb Z}$
satisfying
![]() $\gcd (a,\ell )\mid r$
. Then the following conditions are equivalent:
$\gcd (a,\ell )\mid r$
. Then the following conditions are equivalent:
-
(a)
 $(r+\ell {\mathbb Z})\cap a{\mathbb Z}\subseteq c{\mathbb Z}$
;
$(r+\ell {\mathbb Z})\cap a{\mathbb Z}\subseteq c{\mathbb Z}$
; -
(b)
 $c\mid \gcd (r,\ell )\vee a$
;
$c\mid \gcd (r,\ell )\vee a$
; -
(c)
 $c\mid \ell \vee a$
and
$c\mid \ell \vee a$
and
 $\gcd (c,\ell )\mid r$
.
$\gcd (c,\ell )\mid r$
.
Proof. By Lemma 2.24, condition (a) implies condition (b). Conversely, condition (a) follows from condition (b), because
![]() $(r+\ell {\mathbb Z})\cap a{\mathbb Z}\subseteq (\gcd (r,\ell )\vee a){\mathbb Z}$
.
$(r+\ell {\mathbb Z})\cap a{\mathbb Z}\subseteq (\gcd (r,\ell )\vee a){\mathbb Z}$
.
Suppose that conditions (a) and (b) hold. By condition (b), we have
![]() $c\mid \gcd (r,\ell )\vee a\mid \ell \vee a$
. Since
$c\mid \gcd (r,\ell )\vee a\mid \ell \vee a$
. Since
![]() $\gcd (a,\ell )\mid r$
, we have
$\gcd (a,\ell )\mid r$
, we have
![]() $(r+\ell {\mathbb Z})\cap a{\mathbb Z}\neq \emptyset $
. So by condition (a), we get
$(r+\ell {\mathbb Z})\cap a{\mathbb Z}\neq \emptyset $
. So by condition (a), we get
![]() $r\in c{\mathbb Z}+\ell {\mathbb Z}=\gcd (c,\ell ){\mathbb Z}$
. Hence, condition (c) holds.
$r\in c{\mathbb Z}+\ell {\mathbb Z}=\gcd (c,\ell ){\mathbb Z}$
. Hence, condition (c) holds.
Finally suppose that condition (c) holds. Then,
 $$ \begin{align*} \gcd(c,\gcd(r,\ell)\vee a)&=\gcd(c,r,\ell)\vee\gcd(c,a)\\ &=\gcd(c,\ell)\vee\gcd(c,a)=\gcd(c,\ell\vee a)=c, \end{align*} $$
$$ \begin{align*} \gcd(c,\gcd(r,\ell)\vee a)&=\gcd(c,r,\ell)\vee\gcd(c,a)\\ &=\gcd(c,\ell)\vee\gcd(c,a)=\gcd(c,\ell\vee a)=c, \end{align*} $$
and condition (b) follows at once.
We will need to know the smallest periods of the difference of the sets of multiples.
Lemma 2.26. Assume that A and C are finite subsets of
![]() ${\mathbb N}$
and that the set A is primitive.
${\mathbb N}$
and that the set A is primitive.
-
(a) If
 $A=\{a\}$
and
$A=\{a\}$
and
 $a\not \in {\mathcal M}_C$
, then
$a\not \in {\mathcal M}_C$
, then
 $a\cdot \operatorname {lcm}((C^{\div a})^{\mathrm {prim}})$
is the minimal period of
$a\cdot \operatorname {lcm}((C^{\div a})^{\mathrm {prim}})$
is the minimal period of
 $a{\mathbb Z}\setminus {\mathcal M}_C$
.
$a{\mathbb Z}\setminus {\mathcal M}_C$
. -
(b) If the set
 $C^{\div a}=\{{c}/{\gcd (a,c)}:c\in C\}\subset {\mathbb N}\setminus \{1\}$
is primitive for every
$C^{\div a}=\{{c}/{\gcd (a,c)}:c\in C\}\subset {\mathbb N}\setminus \{1\}$
is primitive for every
 $a\in A$
, then
$a\in A$
, then
 $\operatorname {lcm}(A \cup C)$
is the minimal period of
$\operatorname {lcm}(A \cup C)$
is the minimal period of
 ${\mathcal M}_{A}\setminus {\mathcal M}_C$
.
${\mathcal M}_{A}\setminus {\mathcal M}_C$
.
Proof. (a) Let
![]() $a\in {\mathbb N}\setminus {\mathcal M}_C$
. Then,
$a\in {\mathbb N}\setminus {\mathcal M}_C$
. Then,
![]() $\emptyset \neq a{\mathbb Z}\setminus {\mathcal M}_C=a\cdot ({\mathbb Z}\setminus {\mathcal M}_{C^{\div a}})$
, and the claim follows from the observation that
$\emptyset \neq a{\mathbb Z}\setminus {\mathcal M}_C=a\cdot ({\mathbb Z}\setminus {\mathcal M}_{C^{\div a}})$
, and the claim follows from the observation that
![]() $\operatorname {lcm}((C^{\div a})^{\textrm {prim}})$
is the minimal period of
$\operatorname {lcm}((C^{\div a})^{\textrm {prim}})$
is the minimal period of
![]() ${\mathcal M}_{C^{\div a}}$
, see [Reference Kasjan, Keller and Lemańczyk18, Lemma 5.1b)].
${\mathcal M}_{C^{\div a}}$
, see [Reference Kasjan, Keller and Lemańczyk18, Lemma 5.1b)].
(b) Let T be the minimal period of
![]() ${\mathcal M}_A\setminus {\mathcal M}_C$
. Clearly,
${\mathcal M}_A\setminus {\mathcal M}_C$
. Clearly,
![]() $T|\operatorname {lcm}(A\cup C)$
. Now let
$T|\operatorname {lcm}(A\cup C)$
. Now let
![]() $a\in A$
. Since
$a\in A$
. Since
![]() $1\not \in C^{\div a}$
,
$1\not \in C^{\div a}$
,
![]() $a\in {\mathcal M}_A\setminus {\mathcal M}_C$
, so
$a\in {\mathcal M}_A\setminus {\mathcal M}_C$
, so
![]() $a+T{\mathbb Z}\subset {\mathcal M}_A$
. By Lemma 2.24 and primitivity of A, we get
$a+T{\mathbb Z}\subset {\mathcal M}_A$
. By Lemma 2.24 and primitivity of A, we get
![]() $a|T$
, so that
$a|T$
, so that
![]() $T+(a{\mathbb Z}\setminus {\mathcal M}_C)\subset a{\mathbb Z}\setminus {\mathcal M}_C$
for every
$T+(a{\mathbb Z}\setminus {\mathcal M}_C)\subset a{\mathbb Z}\setminus {\mathcal M}_C$
for every
![]() $a\in A$
and therefore
$a\in A$
and therefore
![]() $a\cdot \operatorname {lcm}((C^{\div a})^{\textrm {prim}})\mid T$
in view of part (a). Hence,
$a\cdot \operatorname {lcm}((C^{\div a})^{\textrm {prim}})\mid T$
in view of part (a). Hence,
![]() $\operatorname {lcm}(\{a\}\cup C)=a\operatorname {lcm}(C^{\div a})=a\operatorname {lcm}((C^{\div a})^{\textrm {prim}})\mid T$
for every
$\operatorname {lcm}(\{a\}\cup C)=a\operatorname {lcm}(C^{\div a})=a\operatorname {lcm}((C^{\div a})^{\textrm {prim}})\mid T$
for every
![]() $a\in A$
, so that
$a\in A$
, so that
![]() $\operatorname {lcm}(A\cup C)|T$
.
$\operatorname {lcm}(A\cup C)|T$
.
The following proposition is the ‘multi-tool’ of this section.
Proposition 2.27. Let
![]() $A_n$
and
$A_n$
and
![]() $S_n$
be sets of positive integers. Let
$S_n$
be sets of positive integers. Let
![]() $b\in {\mathbb Z}$
,
$b\in {\mathbb Z}$
,
![]() $n\geqslant N\geqslant 0$
,
$n\geqslant N\geqslant 0$
,
![]() $a\in A_n$
and
$a\in A_n$
and
![]() $r\in {\mathbb Z}$
be such that
$r\in {\mathbb Z}$
be such that
and
Assume that there is a subset
![]() $E_{n,a}$
of
$E_{n,a}$
of
![]() $A_n\setminus \{a\}$
for which
$A_n\setminus \{a\}$
for which
 $$ \begin{align} \sum_{a'\in E_{n,a}}\frac{1}{\varphi(a^{{\prime}\div a})}<\frac{1}{p_N}, \end{align} $$
$$ \begin{align} \sum_{a'\in E_{n,a}}\frac{1}{\varphi(a^{{\prime}\div a})}<\frac{1}{p_N}, \end{align} $$
where
![]() $\varphi $
is Euler’s totient function. Then there is
$\varphi $
is Euler’s totient function. Then there is
![]() $a'\in A_n\setminus E_{n,a}$
such that
$a'\in A_n\setminus E_{n,a}$
such that
If
![]() ${b}=\beta _n$
for some
${b}=\beta _n$
for some
![]() $\beta =\Delta (k)$
with
$\beta =\Delta (k)$
with
![]() $|k|<\gcd (a',a)$
for all
$|k|<\gcd (a',a)$
for all
![]() $a'\in A_n\setminus E_{n,a}$
, then
$a'\in A_n\setminus E_{n,a}$
, then
![]() $\beta =0$
.
$\beta =0$
.
Proof. In view of the assumption in equation (31), we have
where
![]() $D_{n,a}=A_n\setminus E_{n,a}$
. We prove below that equation (32) implies
$D_{n,a}=A_n\setminus E_{n,a}$
. We prove below that equation (32) implies
Hence and by equation (34), there is
![]() $a'\in D_{n,a}$
such that equation (33) holds. Hence,
$a'\in D_{n,a}$
such that equation (33) holds. Hence,
![]() ${b}=0$
or
${b}=0$
or
![]() $|{b}|\geqslant \gcd (a',\gcd (r,p_N)\vee a)\geqslant \gcd (a',a)$
. It remains to show that equation (32) implies the assumption in equation (35).
$|{b}|\geqslant \gcd (a',\gcd (r,p_N)\vee a)\geqslant \gcd (a',a)$
. It remains to show that equation (32) implies the assumption in equation (35).
Consider any
![]() $a\in A_n$
for which
$a\in A_n$
for which
![]() $ ((r+p_N{\mathbb Z})\cap (a{\mathbb Z})\setminus {\mathcal M}_{S_n})\neq \emptyset $
. Then
$ ((r+p_N{\mathbb Z})\cap (a{\mathbb Z})\setminus {\mathcal M}_{S_n})\neq \emptyset $
. Then
![]() $\gcd (a,p_N)\mid r$
, and Lemma 2.23 implies
$\gcd (a,p_N)\mid r$
, and Lemma 2.23 implies
where
Suppose for a contradiction that there is inclusion in equation (35). Then,
 $$ \begin{align*} (r+p_N{\mathbb Z})\cap(a{\mathbb Z})\setminus{\mathcal M}_{S_n} \subseteq\bigcup_{a'\in E_{n,a}}(-{b}+a'{\mathbb Z}), \end{align*} $$
$$ \begin{align*} (r+p_N{\mathbb Z})\cap(a{\mathbb Z})\setminus{\mathcal M}_{S_n} \subseteq\bigcup_{a'\in E_{n,a}}(-{b}+a'{\mathbb Z}), \end{align*} $$
so that
 $$ \begin{align} &\boldsymbol{\delta}((r+p_N{\mathbb Z})\cap(a{\mathbb Z})\setminus{\mathcal M}_{S_n})\nonumber\\ &\quad\leqslant \sum_{a'\in E_{n,a}}\boldsymbol{\delta}((r+p_N{\mathbb Z})\cap(-{b}+a'{\mathbb Z})\cap(a{\mathbb Z})\setminus{\mathcal M}_{S_n})\nonumber\\ &\quad\leqslant \sum_{a'\in E_{n,a}} \boldsymbol{\delta}((g_n{\mathbb Z})\cap(-{b}+a'{\mathbb Z})\setminus{\mathcal M}_{S_n})\nonumber \\ &\quad= \sum_{a'\in E_{n,a},\ \gcd(g_n,a')\mid{b}} \boldsymbol{\delta}((g_n{\mathbb Z})\cap(-{b}+a'{\mathbb Z})\setminus{\mathcal M}_{S_n})\nonumber \\ &\quad= \sum_{a'\in E_{n,a},\ \gcd(g_n,a')\mid{b}} \frac{1}{g_n\vee a'}(1- \boldsymbol{\delta}({\mathcal M}_{(S_n^{\div (g_n\vee\gcd({b},a'))})^{\perp{g_n\vee a'}/{g_n\vee\gcd({b},a')}}})). \end{align} $$
$$ \begin{align} &\boldsymbol{\delta}((r+p_N{\mathbb Z})\cap(a{\mathbb Z})\setminus{\mathcal M}_{S_n})\nonumber\\ &\quad\leqslant \sum_{a'\in E_{n,a}}\boldsymbol{\delta}((r+p_N{\mathbb Z})\cap(-{b}+a'{\mathbb Z})\cap(a{\mathbb Z})\setminus{\mathcal M}_{S_n})\nonumber\\ &\quad\leqslant \sum_{a'\in E_{n,a}} \boldsymbol{\delta}((g_n{\mathbb Z})\cap(-{b}+a'{\mathbb Z})\setminus{\mathcal M}_{S_n})\nonumber \\ &\quad= \sum_{a'\in E_{n,a},\ \gcd(g_n,a')\mid{b}} \boldsymbol{\delta}((g_n{\mathbb Z})\cap(-{b}+a'{\mathbb Z})\setminus{\mathcal M}_{S_n})\nonumber \\ &\quad= \sum_{a'\in E_{n,a},\ \gcd(g_n,a')\mid{b}} \frac{1}{g_n\vee a'}(1- \boldsymbol{\delta}({\mathcal M}_{(S_n^{\div (g_n\vee\gcd({b},a'))})^{\perp{g_n\vee a'}/{g_n\vee\gcd({b},a')}}})). \end{align} $$
The last equality follows from Lemma 2.23. Notice that
![]() $\gcd (g_n,a')\mid {b}$
implies
$\gcd (g_n,a')\mid {b}$
implies
 $$ \begin{align} \frac{g_n\vee a'}{g_n\vee\gcd({b},a')} = \frac{(g_n\vee a')\cdot\gcd(g_n,a')}{g_n\cdot\gcd({b},a')}=\frac{a'}{\gcd({b},a')}=a^{{\prime}\div b}. \end{align} $$
$$ \begin{align} \frac{g_n\vee a'}{g_n\vee\gcd({b},a')} = \frac{(g_n\vee a')\cdot\gcd(g_n,a')}{g_n\cdot\gcd({b},a')}=\frac{a'}{\gcd({b},a')}=a^{{\prime}\div b}. \end{align} $$
As
 $$ \begin{align} \frac{p_N\vee a}{a'\vee g_n} \leqslant \frac{p_N\vee a}{a'\vee a} = \frac{p_N^{\div a}}{a^{\prime\div a}}, \end{align} $$
$$ \begin{align} \frac{p_N\vee a}{a'\vee g_n} \leqslant \frac{p_N\vee a}{a'\vee a} = \frac{p_N^{\div a}}{a^{\prime\div a}}, \end{align} $$
equations (36), (37) and (38) together yield
 $$ \begin{align} \begin{aligned} 1-\boldsymbol{\delta}({\mathcal M}_{(S_n^{\div g_n})^{\perp(p_N^{\div g_n})}}) &\leqslant \sum_{a'\in E_{n,a}} \frac{p_N^{\div a}}{a^{\prime\div a}}(1- \boldsymbol{\delta}({\mathcal M}_{(S_n^{\div(g_n\vee\gcd({b},a'))})^{\perp{a^{\prime\div b}}}})). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} 1-\boldsymbol{\delta}({\mathcal M}_{(S_n^{\div g_n})^{\perp(p_N^{\div g_n})}}) &\leqslant \sum_{a'\in E_{n,a}} \frac{p_N^{\div a}}{a^{\prime\div a}}(1- \boldsymbol{\delta}({\mathcal M}_{(S_n^{\div(g_n\vee\gcd({b},a'))})^{\perp{a^{\prime\div b}}}})). \end{aligned} \end{align} $$
Denote
Then
![]() $R_n(a')\subseteq S_n^{\div g_n}$
trivially and we claim that
$R_n(a')\subseteq S_n^{\div g_n}$
trivially and we claim that
Indeed, each
![]() $b^{\div g_n}\in S_n^{\div g_n}\setminus R_n(a')$
, which is also coprime to
$b^{\div g_n}\in S_n^{\div g_n}\setminus R_n(a')$
, which is also coprime to
![]() $p_N^{\div g_n}$
, is coprime to
$p_N^{\div g_n}$
, is coprime to
![]() $a^{\prime \div g_n}$
and, a fortiori, to
$a^{\prime \div g_n}$
and, a fortiori, to
![]() $a^{\prime \div b}$
because
$a^{\prime \div b}$
because
![]() $\gcd (g_n,a')\mid b$
. Moreover,
$\gcd (g_n,a')\mid b$
. Moreover,
![]() $b^{\div g_n}={b\vee g_n}/{g_n}$
is a multiple of
$b^{\div g_n}={b\vee g_n}/{g_n}$
is a multiple of
![]() ${b\vee g_n\vee \gcd ({b},a')}/{g_n\vee \gcd ({b},a')}$
, so that the latter is also coprime to
${b\vee g_n\vee \gcd ({b},a')}/{g_n\vee \gcd ({b},a')}$
, so that the latter is also coprime to
![]() ${a^{\prime \div b}}$
. Therefore,
${a^{\prime \div b}}$
. Therefore,
so that Behrend’s inequality (see [Reference Hall15, Theorem 0.12] for a reference) yields
 $$ \begin{align*} \begin{aligned} 1-\boldsymbol{\delta}({\mathcal M}_{(S_n^{\div g_n})^{\perp(p_N^{\div g_n})}}) &\geqslant 1-\boldsymbol{\delta}({\mathcal M}_{R_n(a')\cup {\mathcal M}_{(S_n^{\div(g_n\vee\gcd({b},a'))})^{\perp{a^{\prime\div b}}}}})\\ &= 1-\boldsymbol{\delta}({\mathcal M}_{R_n(a')\cup {(S_n^{\div(g_n\vee\gcd({b},a'))})^{\perp{a^{\prime\div b}}}}})\\ &\geqslant (1-\boldsymbol{\delta}({\mathcal M}_{R_n(a')}))\cdot (1- \boldsymbol{\delta}({\mathcal M}_{(S_n^{\div(g_n\vee\gcd({b},a'))})^{\perp{a^{\prime\div b}}}})). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} 1-\boldsymbol{\delta}({\mathcal M}_{(S_n^{\div g_n})^{\perp(p_N^{\div g_n})}}) &\geqslant 1-\boldsymbol{\delta}({\mathcal M}_{R_n(a')\cup {\mathcal M}_{(S_n^{\div(g_n\vee\gcd({b},a'))})^{\perp{a^{\prime\div b}}}}})\\ &= 1-\boldsymbol{\delta}({\mathcal M}_{R_n(a')\cup {(S_n^{\div(g_n\vee\gcd({b},a'))})^{\perp{a^{\prime\div b}}}}})\\ &\geqslant (1-\boldsymbol{\delta}({\mathcal M}_{R_n(a')}))\cdot (1- \boldsymbol{\delta}({\mathcal M}_{(S_n^{\div(g_n\vee\gcd({b},a'))})^{\perp{a^{\prime\div b}}}})). \end{aligned} \end{align*} $$
Therefore, equation (40) leads to
 $$ \begin{align*} 1-\boldsymbol{\delta}({\mathcal M}_{(S_n^{\div g_n})^{\perp(p_N^{\div g_n})}}) \leqslant \sum_{a'\in E_{n,a}} \frac{{p_N}^{\div a}}{a^{\prime\div a}}\cdot \frac{1-\boldsymbol{\delta}({\mathcal M}_{(S_n^{\div g_n})^{\perp(p_N^{\div g_n})}})}{1-\boldsymbol{\delta}({\mathcal M}_{R_n(a')})}. \end{align*} $$
$$ \begin{align*} 1-\boldsymbol{\delta}({\mathcal M}_{(S_n^{\div g_n})^{\perp(p_N^{\div g_n})}}) \leqslant \sum_{a'\in E_{n,a}} \frac{{p_N}^{\div a}}{a^{\prime\div a}}\cdot \frac{1-\boldsymbol{\delta}({\mathcal M}_{(S_n^{\div g_n})^{\perp(p_N^{\div g_n})}})}{1-\boldsymbol{\delta}({\mathcal M}_{R_n(a')})}. \end{align*} $$
As
![]() $1-\boldsymbol {\delta }({\mathcal M}_{(S_n^{\div g_n})^{\perp (p_N^{\div g_n})}})>0$
, in view of equation (36), we can divide the last inequality by this expression, so that
$1-\boldsymbol {\delta }({\mathcal M}_{(S_n^{\div g_n})^{\perp (p_N^{\div g_n})}})>0$
, in view of equation (36), we can divide the last inequality by this expression, so that
 $$ \begin{align} \begin{aligned} 1 &\leqslant \sum_{a'\in E_{n,a}} \frac{p_N^{\div a}}{a^{\prime\div a}}\cdot \frac{1}{1-\boldsymbol{\delta}({\mathcal M}_{R_n(a')})} \leqslant \sum_{a'\in E_{n,a}} \frac{p_N^{\div a}}{a^{\prime\div a}}\cdot \frac{1}{1-\boldsymbol{\delta}({\mathcal M}_{\operatorname{Spec}(a^{\prime\div a})})}\\ &= \sum_{a'\in E_{n,a}} \frac{{p_N}^{\div a}}{a^{\prime\div a}}\cdot \prod_{p\mid a^{\prime\div a}}\frac{1}{1-\frac{1}{p}} \leqslant {p_N}\cdot \sum_{a'\in E_{n,a}}\frac{1}{\varphi(a^{\prime\div a})}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} 1 &\leqslant \sum_{a'\in E_{n,a}} \frac{p_N^{\div a}}{a^{\prime\div a}}\cdot \frac{1}{1-\boldsymbol{\delta}({\mathcal M}_{R_n(a')})} \leqslant \sum_{a'\in E_{n,a}} \frac{p_N^{\div a}}{a^{\prime\div a}}\cdot \frac{1}{1-\boldsymbol{\delta}({\mathcal M}_{\operatorname{Spec}(a^{\prime\div a})})}\\ &= \sum_{a'\in E_{n,a}} \frac{{p_N}^{\div a}}{a^{\prime\div a}}\cdot \prod_{p\mid a^{\prime\div a}}\frac{1}{1-\frac{1}{p}} \leqslant {p_N}\cdot \sum_{a'\in E_{n,a}}\frac{1}{\varphi(a^{\prime\div a})}, \end{aligned} \end{align} $$
where we used the fact that
![]() $R_n(a')\subseteq {\mathcal M}_{\operatorname {Spec}(a^{\prime \div g_n})}\subseteq {\mathcal M}_{\operatorname {Spec}(a^{\prime \div a})}$
. However, the last estimate contradicts the assumption in equation (32).
$R_n(a')\subseteq {\mathcal M}_{\operatorname {Spec}(a^{\prime \div g_n})}\subseteq {\mathcal M}_{\operatorname {Spec}(a^{\prime \div a})}$
. However, the last estimate contradicts the assumption in equation (32).
From now on, we assume that the sets
![]() ${\widetilde {\mathcal H}}_n$
have some particular arithmetic structure: there is a primitive set
${\widetilde {\mathcal H}}_n$
have some particular arithmetic structure: there is a primitive set
![]() $A_n$
of positive integers such that for each
$A_n$
of positive integers such that for each
![]() $a_n\in A_n$
, there is a set
$a_n\in A_n$
, there is a set
![]() $S_n=S_n(a_n)$
of positive integers satisfying
$S_n=S_n(a_n)$
of positive integers satisfying
Observe that
![]() $\min A_n\to \infty $
as
$\min A_n\to \infty $
as
![]() $n\to \infty $
, because
$n\to \infty $
, because
![]() $A_n\subseteq {\widetilde {\mathcal H}}_n\subseteq {\mathcal H}_n$
and
$A_n\subseteq {\widetilde {\mathcal H}}_n\subseteq {\mathcal H}_n$
and
![]() $\min {\mathcal H}_n\to \infty $
.
$\min {\mathcal H}_n\to \infty $
.
In the remaining part of this section, we prove the weak double disjointness condition (DD′) under the arithmetic structure assumption in equation (AS), which allows us to apply Proposition 2.16 in this situation. Later, in Theorem 3.17, we verify equation (AS) in the
![]() ${\mathcal B}$
-free setting. Recall from equation (11) the definition of the set
${\mathcal B}$
-free setting. Recall from equation (11) the definition of the set
![]() $K=\{k\in {\mathbb Z}: \operatorname {int}_{\partial W}(V_k)\neq \emptyset \}$
.
$K=\{k\in {\mathbb Z}: \operatorname {int}_{\partial W}(V_k)\neq \emptyset \}$
.
Proposition 2.28. Assume the condition in equation (AS). If
 $$ \begin{align} \lim_{n\to\infty} \sum_{a'\in A_n} \frac{1}{\varphi({a'})} =0, \end{align} $$
$$ \begin{align} \lim_{n\to\infty} \sum_{a'\in A_n} \frac{1}{\varphi({a'})} =0, \end{align} $$
then the weak disjointness condition (D′) is satisfied.
Moreover, if the automorphism F of
![]() $(X_\eta ,\sigma )$
is described by a block code
$(X_\eta ,\sigma )$
is described by a block code
![]() $\{0,1\}^{[-m:m]}\to \{0,1\}$
, then the set K is contained in
$\{0,1\}^{[-m:m]}\to \{0,1\}$
, then the set K is contained in
![]() $[-m,m]$
,
$[-m,m]$
,
![]() $\operatorname {int}_{\partial W}(V_{k_i})\cap \operatorname {int}_{\partial W}(V_{k_j})=\emptyset $
for any different
$\operatorname {int}_{\partial W}(V_{k_i})\cap \operatorname {int}_{\partial W}(V_{k_j})=\emptyset $
for any different
![]() $k_i,k_j\in K$
, and
$k_i,k_j\in K$
, and
![]() $\partial W=\bigcup _{k\in K}V_k'$
, where
$\partial W=\bigcup _{k\in K}V_k'$
, where
![]() $V_k':=\overline {\operatorname {int}_{\partial W}(V_k)}$
.
$V_k':=\overline {\operatorname {int}_{\partial W}(V_k)}$
.
Proof. Suppose for a contradiction that condition (D′) does not hold, equivalently that condition (Seh′) does not hold. Then there are
![]() $k\in {\mathbb Z}\setminus \{0\}$
and an arithmetic progression
$k\in {\mathbb Z}\setminus \{0\}$
and an arithmetic progression
![]() $r+p_N{\mathbb Z}$
such that for all
$r+p_N{\mathbb Z}$
such that for all
![]() $n\ge N$
,
$n\ge N$
,
Let
![]() $n\ge N$
. In view of property (AS), there is
$n\ge N$
. In view of property (AS), there is
![]() $a\in A_n$
such that
$a\in A_n$
such that
Let
![]() $E_{n,a}=\{a'\in A_n: \gcd (a',a)\leqslant |k|\}$
. Since
$E_{n,a}=\{a'\in A_n: \gcd (a',a)\leqslant |k|\}$
. Since
 $$ \begin{align*} \varphi(a^{\prime\div a})=a^{\prime\div a}\prod_{p\mid a^{\prime\div a}}\bigg(1-\frac{1}{p}\bigg)\geqslant\frac{1}{|k|}a'\prod_{p\mid a'}\bigg(1-\frac{1}{p}\bigg)=\frac{1}{|k|}\varphi(a') \end{align*} $$
$$ \begin{align*} \varphi(a^{\prime\div a})=a^{\prime\div a}\prod_{p\mid a^{\prime\div a}}\bigg(1-\frac{1}{p}\bigg)\geqslant\frac{1}{|k|}a'\prod_{p\mid a'}\bigg(1-\frac{1}{p}\bigg)=\frac{1}{|k|}\varphi(a') \end{align*} $$
for any
![]() $a'\in E_{n,a}$
, the assumption in equation (42) above implies the assumption in equation (32) of Proposition 2.27. So this proposition applies to the inclusion in equation (43), and there is
$a'\in E_{n,a}$
, the assumption in equation (42) above implies the assumption in equation (32) of Proposition 2.27. So this proposition applies to the inclusion in equation (43), and there is
![]() $a'\in A_n\setminus E_{n,a}$
such that
$a'\in A_n\setminus E_{n,a}$
such that
![]() $\gcd (a',a)\mid k$
. As
$\gcd (a',a)\mid k$
. As
![]() $|k|<\gcd (a',a)$
for all
$|k|<\gcd (a',a)$
for all
![]() $a'\in A_n\setminus E_{n,a}$
, this contradicts the assumption
$a'\in A_n\setminus E_{n,a}$
, this contradicts the assumption
![]() $k\in {\mathbb Z}\setminus \{0\}$
.
$k\in {\mathbb Z}\setminus \{0\}$
.
The remaining conclusions follow from Corollary 2.14.
Remark 2.29. Any
![]() ${\mathcal B}$
-free Toeplitz subshift satisfying equation (42) is regular, because
${\mathcal B}$
-free Toeplitz subshift satisfying equation (42) is regular, because
![]() ${\widetilde {\mathcal H}}_n\subseteq {\mathcal M}_{{\mathcal A}_{S_n}^{\infty }}$
and
${\widetilde {\mathcal H}}_n\subseteq {\mathcal M}_{{\mathcal A}_{S_n}^{\infty }}$
and
![]() $d({\mathcal M}_{{\mathcal A}_{S_n}^{\infty }})\leq \sum _{a\in {\mathcal A}_{S_n}^{\infty }}{1}/{a}\leq \sum _{a\in {\mathcal A}_{S_n}^{\infty }}{1}/{\varphi (a)}$
.
$d({\mathcal M}_{{\mathcal A}_{S_n}^{\infty }})\leq \sum _{a\in {\mathcal A}_{S_n}^{\infty }}{1}/{a}\leq \sum _{a\in {\mathcal A}_{S_n}^{\infty }}{1}/{\varphi (a)}$
.
Proposition 2.30. Assume the condition in equation (AS). If
 $$ \begin{align} \lim_{n\to\infty} \sum_{a'\in A_n\setminus\{a\}} \frac{1}{\varphi({a'}^{\div a})} =0\quad\text{for all choices of }a\in A_n\; (\text{where }{a'}^{\div a}={a'}/{\gcd(a',a)}), \end{align} $$
$$ \begin{align} \lim_{n\to\infty} \sum_{a'\in A_n\setminus\{a\}} \frac{1}{\varphi({a'}^{\div a})} =0\quad\text{for all choices of }a\in A_n\; (\text{where }{a'}^{\div a}={a'}/{\gcd(a',a)}), \end{align} $$
then the weak double disjointness condition (DD′)—and a fortiori condition (D′)—is satisfied.
Moreover, the conclusions of Proposition 2.28 can be complemented by
![]() $V_k'+(y_F-\Delta (k)){\mathbb Z}\subseteq V_k'$
for all
$V_k'+(y_F-\Delta (k)){\mathbb Z}\subseteq V_k'$
for all
![]() $k\in K$
.
$k\in K$
.
Proof. Suppose for a contradiction that condition (DD′) does not hold, equivalently that condition (DSeh′) does not hold. Then there are
![]() $k\in {\mathbb Z}\setminus \{0\}$
,
$k\in {\mathbb Z}\setminus \{0\}$
,
![]() $\beta \in G$
, an arithmetic progression
$\beta \in G$
, an arithmetic progression
![]() $r+p_N{\mathbb Z}$
, such that for all
$r+p_N{\mathbb Z}$
, such that for all
![]() $n\ge N$
,
$n\ge N$
,
Let
![]() $n\ge N$
. In view of the property in equation (AS), there is
$n\ge N$
. In view of the property in equation (AS), there is
![]() $a\in A_n$
such that
$a\in A_n$
such that
 $$ \begin{align} &\emptyset\neq(r+p_N{\mathbb Z})\cap a{\mathbb Z}\setminus{\mathcal M}_{S_n}+\beta_n\subseteq {\mathcal M}_{A_n}\quad\text{and }\nonumber\\ &\emptyset\neq(r+p_N{\mathbb Z})\cap a{\mathbb Z}\setminus{\mathcal M}_{S_n}+2\beta_n+k\subseteq {\mathcal M}_{A_n}. \end{align} $$
$$ \begin{align} &\emptyset\neq(r+p_N{\mathbb Z})\cap a{\mathbb Z}\setminus{\mathcal M}_{S_n}+\beta_n\subseteq {\mathcal M}_{A_n}\quad\text{and }\nonumber\\ &\emptyset\neq(r+p_N{\mathbb Z})\cap a{\mathbb Z}\setminus{\mathcal M}_{S_n}+2\beta_n+k\subseteq {\mathcal M}_{A_n}. \end{align} $$
Let
![]() $E_{n,a}= A_n\setminus \{a\}$
. In view of the assumption in equation (44), Proposition 2.27 applies to both inclusions in equation (45), and as
$E_{n,a}= A_n\setminus \{a\}$
. In view of the assumption in equation (44), Proposition 2.27 applies to both inclusions in equation (45), and as
![]() $A_n\setminus E_{n,a}=\{a\}$
, we can conclude that
$A_n\setminus E_{n,a}=\{a\}$
, we can conclude that
![]() $a\mid \beta _n$
and
$a\mid \beta _n$
and
![]() $a\mid 2\beta _n+k$
, so that
$a\mid 2\beta _n+k$
, so that
![]() $a\mid k$
. As
$a\mid k$
. As
![]() $a\in A_n$
and
$a\in A_n$
and
![]() $\min A_n\to \infty $
, this contradicts the assumption
$\min A_n\to \infty $
, this contradicts the assumption
![]() $k\in {\mathbb Z}\setminus \{0\}$
.
$k\in {\mathbb Z}\setminus \{0\}$
.
The final conclusion follows from Proposition 2.16.
Theorem 2.31. Assume the condition in equation (AS) and let the automorphism F of
![]() $(X_\eta ,\sigma )$
be described by a block code
$(X_\eta ,\sigma )$
be described by a block code
![]() $\{0,1\}^{[-m:m]}\to \{0,1\}$
. Under the assumption in equation (44) of Proposition 2.30, the following hold.
$\{0,1\}^{[-m:m]}\to \{0,1\}$
. Under the assumption in equation (44) of Proposition 2.30, the following hold.
-
(a) For each
 $n>0$
and each
$n>0$
and each
 $k\in K$
, there exists
$k\in K$
, there exists
 $a\in A_n$
such that
$a\in A_n$
such that  $$ \begin{align*} a\mid (y_F)_{n}-k. \end{align*} $$
$$ \begin{align*} a\mid (y_F)_{n}-k. \end{align*} $$
-
(b) For each
 $n>0$
and each
$n>0$
and each
 $a\in A_n$
, there exists some
$a\in A_n$
, there exists some
 $k\in K$
such that If
$k\in K$
such that If $$ \begin{align*} a\mid (y_F)_{n}-k. \end{align*} $$
$$ \begin{align*} a\mid (y_F)_{n}-k. \end{align*} $$
 $a>2m$
, then this
$a>2m$
, then this
 $k\in K$
is unique. Denote it by
$k\in K$
is unique. Denote it by
 $\kappa _n(a)$
.
$\kappa _n(a)$
.
-
(c) Suppose n is so large that
 $\min A_n>2m$
, and denote by
$\min A_n>2m$
, and denote by
 ${\mathcal G}_n$
the graph with vertices
${\mathcal G}_n$
the graph with vertices
 $A_n$
and edges
$A_n$
and edges
 $(a,a')$
whenever
$(a,a')$
whenever
 $\gcd (a,a')>2m$
. Then,
$\gcd (a,a')>2m$
. Then,
 $\kappa _n(a)=\kappa _n(a')$
for any two
$\kappa _n(a)=\kappa _n(a')$
for any two
 $a,a'$
in the same connected component of
$a,a'$
in the same connected component of
 ${\mathcal G}_n$
. In particular,
${\mathcal G}_n$
. In particular,
 $|K|=1$
if
$|K|=1$
if
 ${\mathcal G}_n$
is connected.
${\mathcal G}_n$
is connected. -
(d) If
 $|K|=1$
, say
$|K|=1$
, say
 $K=\{k\}$
, then, for each n,
$K=\{k\}$
, then, for each n,
 $(y_F)_n-k$
is a multiple of the minimal period
$(y_F)_n-k$
is a multiple of the minimal period
 $\tilde {\tau }_n$
of
$\tilde {\tau }_n$
of
 ${\widetilde {\mathcal H}}_n$
.
${\widetilde {\mathcal H}}_n$
. -
(e) If
 $|K|=1$
and
$|K|=1$
and
 $\tilde {\tau }_n=p_n$
for all n, then
$\tilde {\tau }_n=p_n$
for all n, then
 $(X_\eta ,\sigma )$
has a trivial centralizer.
$(X_\eta ,\sigma )$
has a trivial centralizer.
Proof. (a) Let
![]() $k\in K$
. Then
$k\in K$
. Then
![]() $V_k'+(y_F-\Delta (k)){\mathbb Z}\subseteq V_k'\subseteq \partial W$
by Proposition 2.30, and because of Lemma 2.5,
$V_k'+(y_F-\Delta (k)){\mathbb Z}\subseteq V_k'\subseteq \partial W$
by Proposition 2.30, and because of Lemma 2.5,
![]() $h_n+(y_F-\Delta (k))_n{\mathbb Z}\subseteq {\widetilde {\mathcal H}}_n\subseteq {\mathcal M}_{A_n}$
for each
$h_n+(y_F-\Delta (k))_n{\mathbb Z}\subseteq {\widetilde {\mathcal H}}_n\subseteq {\mathcal M}_{A_n}$
for each
![]() $h\in V_k'$
. It follows that there exists
$h\in V_k'$
. It follows that there exists
![]() $a'\in A_n$
such that
$a'\in A_n$
such that
![]() $a'\mid \gcd (h_{n},(y_F-\Delta (k))_{n})$
.
$a'\mid \gcd (h_{n},(y_F-\Delta (k))_{n})$
.
(b) Let
![]() $a\in A_n$
. Notice that
$a\in A_n$
. Notice that
![]() $a\not \in {\mathcal M}_{S_n(a)}$
. Otherwise,
$a\not \in {\mathcal M}_{S_n(a)}$
. Otherwise,
![]() $a{\mathbb Z}\subseteq {\mathcal M}_{S_n(a)}$
which contradicts equation (AS). So,
$a{\mathbb Z}\subseteq {\mathcal M}_{S_n(a)}$
which contradicts equation (AS). So,
![]() $a\in {\widetilde {\mathcal H}}_n$
and, by Lemma 2.5, there exists some
$a\in {\widetilde {\mathcal H}}_n$
and, by Lemma 2.5, there exists some
![]() $h\in U_{n}(\Delta (a))\cap \partial W$
. In particular,
$h\in U_{n}(\Delta (a))\cap \partial W$
. In particular,
![]() $h_{n}=a\in {\widetilde {\mathcal H}}_n$
. Because of Corollary 2.14, there exists
$h_{n}=a\in {\widetilde {\mathcal H}}_n$
. Because of Corollary 2.14, there exists
![]() $k\in K$
such that
$k\in K$
such that
![]() $h\in V_k'$
. As in the proof of part (a), it follows that there exists
$h\in V_k'$
. As in the proof of part (a), it follows that there exists
![]() $a'\in A_n$
such that
$a'\in A_n$
such that
![]() $a'\mid \gcd (h_{n},(y_F-\Delta (k))_{n})$
. As
$a'\mid \gcd (h_{n},(y_F-\Delta (k))_{n})$
. As
![]() $a'$
and
$a'$
and
![]() $a=h_n$
belong to the same primitive set
$a=h_n$
belong to the same primitive set
![]() $A_n$
, this implies
$A_n$
, this implies
![]() $a=a'\mid (y_F-\Delta (k))_{n}$
.
$a=a'\mid (y_F-\Delta (k))_{n}$
.
Suppose there is another
![]() $k'\in K$
such that
$k'\in K$
such that
![]() $a\mid (y_F-\Delta (k'))_{n}$
. Then
$a\mid (y_F-\Delta (k'))_{n}$
. Then
![]() $a\mid k-k'$
, so that
$a\mid k-k'$
, so that
![]() $k=k'$
or
$k=k'$
or
![]() $a\leqslant |k-k'|\leqslant 2m$
.
$a\leqslant |k-k'|\leqslant 2m$
.
(c) It suffices to prove that
![]() $\kappa _n(a)=\kappa _n(a')$
for every edge
$\kappa _n(a)=\kappa _n(a')$
for every edge
![]() $(a,a')$
of
$(a,a')$
of
![]() ${\mathcal G}_n$
, i.e. whenever
${\mathcal G}_n$
, i.e. whenever
![]() $\gcd (a,a')>2m$
. However, as part (b) implies
$\gcd (a,a')>2m$
. However, as part (b) implies
it follows that
![]() $\kappa _n(a)=\kappa _n(a')$
or
$\kappa _n(a)=\kappa _n(a')$
or
![]() $2m<\gcd (a,a')\leqslant |\kappa _n(a)-\kappa _n(a')|\leqslant 2m$
.
$2m<\gcd (a,a')\leqslant |\kappa _n(a)-\kappa _n(a')|\leqslant 2m$
.
(d) If
![]() $K=\{k\}$
, then
$K=\{k\}$
, then
![]() $\partial W=V_k'$
, that is,
$\partial W=V_k'$
, that is,
![]() $\partial W+(y_F-\Delta (k))\subseteq \partial W$
, and the claim follows from Lemma 2.6(b).
$\partial W+(y_F-\Delta (k))\subseteq \partial W$
, and the claim follows from Lemma 2.6(b).
(e) It follows from part (d) that
![]() $y_F=\Delta (k)$
for some
$y_F=\Delta (k)$
for some
![]() $k\in {\mathbb Z}$
.
$k\in {\mathbb Z}$
.
3 The
 ${\mathcal B}$
-free case
${\mathcal B}$
-free case
In this section, we will apply our results for general Toeplitz subshifts from §2 to minimal
![]() ${\mathcal B}$
-free subshifts.
${\mathcal B}$
-free subshifts.
3.1 Preparations
Let us start with the following notation and observations.
-
(i) For a finite subset
 $S\subset {\mathcal B}$
, define as in [Reference Kasjan, Keller and Lemańczyk18] As
$S\subset {\mathcal B}$
, define as in [Reference Kasjan, Keller and Lemańczyk18] As $$ \begin{align*} \ell_S:=\operatorname{lcm}(S)\quad\text{and}\quad {\mathcal A}_S:=\{\gcd(b,\ell_S):b\in{\mathcal B}\}. \end{align*} $$
$$ \begin{align*} \ell_S:=\operatorname{lcm}(S)\quad\text{and}\quad {\mathcal A}_S:=\{\gcd(b,\ell_S):b\in{\mathcal B}\}. \end{align*} $$
 ${\mathcal B}$
is primitive, S is a proper subset of
${\mathcal B}$
is primitive, S is a proper subset of
 ${\mathcal A}_S$
.
${\mathcal A}_S$
.
-
(ii) The set
 ${\mathcal B}$
is taut, if
${\mathcal B}$
is taut, if
 $\delta ({\mathcal M}_{{\mathcal B}\setminus \{b\}})<\delta ({\mathcal M}_{\mathcal B})$
for each
$\delta ({\mathcal M}_{{\mathcal B}\setminus \{b\}})<\delta ({\mathcal M}_{\mathcal B})$
for each
 $b\in {\mathcal B}$
.
$b\in {\mathcal B}$
.So a set is primitive if removing any single point from it changes its set of multiples, and a set is taut if removing any single point from it changes the logarithmic density of its set of multiples.
-
(iii) Let
 $S\subseteq S' \subset {\mathcal B}$
. From [Reference Kasjan, Keller and Lemańczyk18, equation (17)], we recall that (46)
$S\subseteq S' \subset {\mathcal B}$
. From [Reference Kasjan, Keller and Lemańczyk18, equation (17)], we recall that (46) $$ \begin{align} S\subseteq S'\subseteq{\mathcal A}_{S'}\subseteq{\mathcal M}_{{\mathcal A}_S}\quad\text{so that}\quad {\mathcal M}_S\subseteq{\mathcal M}_{S'}\subseteq{\mathcal M}_{{\mathcal A}_{S'}}\subseteq{\mathcal M}_{{\mathcal A}_S}. \end{align} $$
$$ \begin{align} S\subseteq S'\subseteq{\mathcal A}_{S'}\subseteq{\mathcal M}_{{\mathcal A}_S}\quad\text{so that}\quad {\mathcal M}_S\subseteq{\mathcal M}_{S'}\subseteq{\mathcal M}_{{\mathcal A}_{S'}}\subseteq{\mathcal M}_{{\mathcal A}_S}. \end{align} $$
-
(iv) A finite set
 $S\subset {\mathcal B}$
is saturated if
$S\subset {\mathcal B}$
is saturated if
 ${\mathcal A}_S\cap {\mathcal B}=S$
.
${\mathcal A}_S\cap {\mathcal B}=S$
. -
(v) For a finite set
 $S\subset {\mathcal B}$
, define
$S\subset {\mathcal B}$
, define
 $S^{\textrm {sat}}={\mathcal A}_S\cap {\mathcal B}$
.
$S^{\textrm {sat}}={\mathcal A}_S\cap {\mathcal B}$
.
Then
![]() $S\subseteq S^{\textrm {sat}}$
,
$S\subseteq S^{\textrm {sat}}$
,
![]() $S^{\textrm {sat}}$
is finite,
$S^{\textrm {sat}}$
is finite,
![]() $\operatorname {lcm}(S^{\textrm {sat}})\mid \operatorname {lcm}({\mathcal A}_S)=\operatorname {lcm}(S)$
, so that
$\operatorname {lcm}(S^{\textrm {sat}})\mid \operatorname {lcm}({\mathcal A}_S)=\operatorname {lcm}(S)$
, so that
![]() $\operatorname {lcm}(S^{\textrm {sat}})=\operatorname {lcm}(S)$
, and
$\operatorname {lcm}(S^{\textrm {sat}})=\operatorname {lcm}(S)$
, and
![]() ${\mathcal A}_{S^{\textrm {sat}}}={\mathcal A}_S$
, because
${\mathcal A}_{S^{\textrm {sat}}}={\mathcal A}_S$
, because
![]() $\gcd (b,\operatorname {lcm}(S^{\textrm {sat}}))=\gcd (b,\operatorname {lcm}(S))$
for each
$\gcd (b,\operatorname {lcm}(S^{\textrm {sat}}))=\gcd (b,\operatorname {lcm}(S))$
for each
![]() $b\in {\mathcal B}$
. In particular,
$b\in {\mathcal B}$
. In particular,
![]() ${\mathcal A}_{S^{\textrm {sat}}}\cap {\mathcal B}={\mathcal A}_S\cap {\mathcal B}=S^{\textrm {sat}}$
, so that
${\mathcal A}_{S^{\textrm {sat}}}\cap {\mathcal B}={\mathcal A}_S\cap {\mathcal B}=S^{\textrm {sat}}$
, so that
![]() $S^{\textrm {sat}}$
is saturated.
$S^{\textrm {sat}}$
is saturated.
Any filtration
![]() $S_1\subseteq S_2\subseteq \cdots $
of
$S_1\subseteq S_2\subseteq \cdots $
of
![]() ${\mathcal B}$
by finite sets yields a period structure
${\mathcal B}$
by finite sets yields a period structure
![]() $p_n=\operatorname {lcm}(S_n)$
for
$p_n=\operatorname {lcm}(S_n)$
for
![]() $X_{\eta }$
. The definition of the group G depends on the period structure, but G is naturally isomorphic with the inverse limit
$X_{\eta }$
. The definition of the group G depends on the period structure, but G is naturally isomorphic with the inverse limit
![]() $\lim \limits _{\leftarrow }{\mathbb Z}/\operatorname {lcm}(S){\mathbb Z}$
of the inverse system of cyclic groups
$\lim \limits _{\leftarrow }{\mathbb Z}/\operatorname {lcm}(S){\mathbb Z}$
of the inverse system of cyclic groups
![]() ${\mathbb Z}/\operatorname {lcm}(S){\mathbb Z}$
indexed by the finite subsets
${\mathbb Z}/\operatorname {lcm}(S){\mathbb Z}$
indexed by the finite subsets
![]() $S\subset {\mathcal B}$
ordered by the inclusion. Moreover, there is an injective group homomorphism
$S\subset {\mathcal B}$
ordered by the inclusion. Moreover, there is an injective group homomorphism
![]() $\lim \limits _{\leftarrow }{\mathbb Z}/\operatorname {lcm}(S){\mathbb Z}\rightarrow \prod _{b\in {\mathcal B}}{\mathbb Z}/b{\mathbb Z}$
given by
$\lim \limits _{\leftarrow }{\mathbb Z}/\operatorname {lcm}(S){\mathbb Z}\rightarrow \prod _{b\in {\mathcal B}}{\mathbb Z}/b{\mathbb Z}$
given by
![]() $(n_S)_{S\subset {\mathcal B}}\mapsto (n_{\{b\}}+b{\mathbb Z})_{b\in {\mathcal B}}$
. We can identify the group G with the image of this homomorphism, which consists of the elements
$(n_S)_{S\subset {\mathcal B}}\mapsto (n_{\{b\}}+b{\mathbb Z})_{b\in {\mathcal B}}$
. We can identify the group G with the image of this homomorphism, which consists of the elements
![]() $h=(h_b)_{b\in {\mathcal B}}\in \prod _{b\in {\mathcal B}}{\mathbb Z}/b{\mathbb Z}$
satisfying
$h=(h_b)_{b\in {\mathcal B}}\in \prod _{b\in {\mathcal B}}{\mathbb Z}/b{\mathbb Z}$
satisfying
![]() $h_b=h_{b'}\,\mod \gcd (b,b')$
for any
$h_b=h_{b'}\,\mod \gcd (b,b')$
for any
![]() $b,b'\in {\mathcal B}$
. Under this identification,
$b,b'\in {\mathcal B}$
. Under this identification,
![]() $\Delta :{\mathbb Z}\to \prod _{b\in {\mathcal B}}{\mathbb Z}/b{\mathbb Z}$
is given by
$\Delta :{\mathbb Z}\to \prod _{b\in {\mathcal B}}{\mathbb Z}/b{\mathbb Z}$
is given by
![]() $(\Delta (n))_b=n+ b{\mathbb Z}$
for
$(\Delta (n))_b=n+ b{\mathbb Z}$
for
![]() $b\in {\mathcal B}$
and
$b\in {\mathcal B}$
and
![]() $\overline {\Delta ({\mathbb Z})}\cong G$
. Given a sequence
$\overline {\Delta ({\mathbb Z})}\cong G$
. Given a sequence
![]() $(n_S)_{S\subset {\mathcal B}}$
of integers belonging to the inverse limit (that is, satisfying
$(n_S)_{S\subset {\mathcal B}}$
of integers belonging to the inverse limit (that is, satisfying
![]() $n_S\equiv n_{S'}\,\mod \operatorname {lcm}(S)$
whenever
$n_S\equiv n_{S'}\,\mod \operatorname {lcm}(S)$
whenever
![]() $S\subseteq S'$
), we denote by
$S\subseteq S'$
), we denote by
![]() $\lim \Delta (n_S)$
the element
$\lim \Delta (n_S)$
the element
![]() $h\in \overline {\Delta ({\mathbb Z})}\subseteq \prod _{b\in {\mathcal B}}{\mathbb Z}/b{\mathbb Z}$
such that
$h\in \overline {\Delta ({\mathbb Z})}\subseteq \prod _{b\in {\mathcal B}}{\mathbb Z}/b{\mathbb Z}$
such that
![]() $h_b= n_S\,\mod b$
for
$h_b= n_S\,\mod b$
for
![]() $b\in S\subset {\mathcal B}$
.
$b\in S\subset {\mathcal B}$
.
Remark 3.1. The coding function
![]() $\phi :G\to \{0,1\}^{\mathbb Z}$
defined in the introduction can be written as
$\phi :G\to \{0,1\}^{\mathbb Z}$
defined in the introduction can be written as
![]() $\phi (y)=\mathbf {1}_{{\mathbb Z}\setminus \bigcup _{b\in {\mathcal B}}(b{\mathbb Z}-y_b)}$
for any
$\phi (y)=\mathbf {1}_{{\mathbb Z}\setminus \bigcup _{b\in {\mathcal B}}(b{\mathbb Z}-y_b)}$
for any
![]() $y=(y_b)_{b\in {\mathcal B}}\in \overline {\Delta ({\mathbb Z})}\cong G$
. It is injective. Indeed, for
$y=(y_b)_{b\in {\mathcal B}}\in \overline {\Delta ({\mathbb Z})}\cong G$
. It is injective. Indeed, for
![]() $y\in G$
, denote
$y\in G$
, denote
![]() $I_y:=\{s\in {\mathbb Z}:(\phi (y))_s=1\}=\{s\in {\mathbb Z}:y+\Delta (s)\in W\}$
. As
$I_y:=\{s\in {\mathbb Z}:(\phi (y))_s=1\}=\{s\in {\mathbb Z}:y+\Delta (s)\in W\}$
. As
![]() $\overline {\operatorname {int}(W)}=W\subseteq \overline {\Delta ({\mathbb Z})}$
(see the introduction), we have
$\overline {\operatorname {int}(W)}=W\subseteq \overline {\Delta ({\mathbb Z})}$
(see the introduction), we have
![]() $W=\overline {\operatorname {int}(W)}\subseteq \overline {\{y+\Delta (s):s\in I_y\}}\subseteq W$
for each
$W=\overline {\operatorname {int}(W)}\subseteq \overline {\{y+\Delta (s):s\in I_y\}}\subseteq W$
for each
![]() $y\in G$
. Hence, if
$y\in G$
. Hence, if
![]() $\phi (y)=\phi (y')$
, then
$\phi (y)=\phi (y')$
, then
![]() $I_y=I_{y'}$
and
$I_y=I_{y'}$
and
However, W is aperiodic [Reference Kasjan, Keller and Lemańczyk18, Proposition 5.1], so
![]() $y=y'$
.
$y=y'$
.
Lemma 3.2. [Reference Kasjan, Keller and Lemańczyk18, Lemma 2.5]
Let
![]() $U = U_S(\Delta (n))$
for some
$U = U_S(\Delta (n))$
for some
![]() $S\subset {\mathcal B}$
and
$S\subset {\mathcal B}$
and
![]() $n\in {\mathbb Z}$
.
$n\in {\mathbb Z}$
.
-
(a) If
 $n\in \mathcal {M}_S$
, then
$n\in \mathcal {M}_S$
, then
 $U\cap W =\emptyset $
.
$U\cap W =\emptyset $
. -
(b) If
 $U\cap W=\emptyset $
, then
$U\cap W=\emptyset $
, then
 $n+\operatorname {lcm}(S)\cdot {\mathbb Z}\subseteq \mathcal {M}_{{\mathcal B}\cap {\mathcal A}_S}$
.
$n+\operatorname {lcm}(S)\cdot {\mathbb Z}\subseteq \mathcal {M}_{{\mathcal B}\cap {\mathcal A}_S}$
. -
(c) If S is saturated, then
 $n\in \mathcal {M}_S$
if and only if
$n\in \mathcal {M}_S$
if and only if
 $U\cap W = \emptyset $
if and only if
$U\cap W = \emptyset $
if and only if
 $n + lcm(S)\cdot {\mathbb Z}\subseteq \mathcal {M}_S$
.
$n + lcm(S)\cdot {\mathbb Z}\subseteq \mathcal {M}_S$
.
Lemma 3.3. [Reference Kasjan, Keller and Lemańczyk18, Lemma 3.1]
-
(a) For all
 $S\subset {\mathcal B}$
and
$S\subset {\mathcal B}$
and
 $n\in {\mathbb Z}$
we have:
$n\in {\mathbb Z}$
we have:
 $U_S(\Delta (n))\subseteq W\Leftrightarrow n\in {\mathcal F}_{{\mathcal A}_S}$
.
$U_S(\Delta (n))\subseteq W\Leftrightarrow n\in {\mathcal F}_{{\mathcal A}_S}$
. -
(b) If
 $(S_k)_k$
is a filtration of
$(S_k)_k$
is a filtration of
 ${\mathcal B}$
by finite sets and
${\mathcal B}$
by finite sets and
 $\lim _k \Delta (n_{S_k}) = h$
, then
$\lim _k \Delta (n_{S_k}) = h$
, then
 $h\in \operatorname {int}(W)$
if and only if
$h\in \operatorname {int}(W)$
if and only if
 $n_{S_k}\in {\mathcal F}_{{\mathcal A}_{S_k}}$
for some k.
$n_{S_k}\in {\mathcal F}_{{\mathcal A}_{S_k}}$
for some k.
Lemma 3.4. [Reference Kasjan, Keller and Lemańczyk18, Lemma 5.2]
Assume that
![]() $S\subseteq S'$
are finite subsets of
$S\subseteq S'$
are finite subsets of
![]() ${\mathcal B}$
, then
${\mathcal B}$
, then
![]() ${\mathcal A}_S = \{\gcd (a, \operatorname {lcm}(S))\ : a \in {\mathcal A}_{S'} \}$
.
${\mathcal A}_S = \{\gcd (a, \operatorname {lcm}(S))\ : a \in {\mathcal A}_{S'} \}$
.
Proposition 3.5. [Reference Kasjan, Keller and Lemańczyk18, Theorem B]
The following are equivalent.
-
(a) W is topologically regular, that is
 $W = \overline {\operatorname {int}(W)}$
.
$W = \overline {\operatorname {int}(W)}$
. -
(b) There are no
 $d\in {\mathbb N}$
and no infinite pairwise coprime set
$d\in {\mathbb N}$
and no infinite pairwise coprime set
 ${\mathcal A}\subset {\mathbb N}\setminus \{1\}$
such that
${\mathcal A}\subset {\mathbb N}\setminus \{1\}$
such that
 $d{\mathcal A}\subset {\mathcal B}$
.
$d{\mathcal A}\subset {\mathcal B}$
. -
(c)
 $\eta =\phi (0)$
is a Toeplitz sequence different from
$\eta =\phi (0)$
is a Toeplitz sequence different from
 $(\ldots , 0, 0, 0,\ldots )$
.
$(\ldots , 0, 0, 0,\ldots )$
. -
(d)
 $\{n\in {\mathbb N} \ : \forall _{S \subset {\mathcal B}}\ \exists _{S'\subset {\mathcal B}}\ :S \subseteq S' \ \text { and } \ n\in {\mathcal A}_{S'}\setminus S'\}=\emptyset $
.
$\{n\in {\mathbb N} \ : \forall _{S \subset {\mathcal B}}\ \exists _{S'\subset {\mathcal B}}\ :S \subseteq S' \ \text { and } \ n\in {\mathcal A}_{S'}\setminus S'\}=\emptyset $
.
Lemma 3.6. Each filtration
![]() $S_1\subset S_2\subset \cdots \nearrow {\mathcal B}$
has a sub-filtration of sets
$S_1\subset S_2\subset \cdots \nearrow {\mathcal B}$
has a sub-filtration of sets
![]() $S_{n_k}$
such that
$S_{n_k}$
such that
![]() $S_{n_1}^{\mathrm{sat}}\subset S_{n_2}^{\mathrm{sat}}\subset \cdots \nearrow {\mathcal B}$
is a filtration.
$S_{n_1}^{\mathrm{sat}}\subset S_{n_2}^{\mathrm{sat}}\subset \cdots \nearrow {\mathcal B}$
is a filtration.
Proof. Let
![]() $n_1=1$
. If
$n_1=1$
. If
![]() $n_1<n_2<\cdots <n_k$
are chosen, let
$n_1<n_2<\cdots <n_k$
are chosen, let
![]() $n_{k+1}=\min \{j\in {\mathbb N}: S_{n_k}^{\textrm {sat}}\subseteq S_j\}$
.
$n_{k+1}=\min \{j\in {\mathbb N}: S_{n_k}^{\textrm {sat}}\subseteq S_j\}$
.
This lemma allows us in the following to assume that a filtration is saturated without loosing generality.
3.2 Sets of holes
Now we describe the set of holes and the set of essential holes.
Proposition 3.7. Let
![]() $S \subset \mathcal {B}$
be saturated and taut and
$S \subset \mathcal {B}$
be saturated and taut and
![]() $s\in {\mathbb Z}$
. Then:
$s\in {\mathbb Z}$
. Then:
-
(a)
 $s\in {\mathcal M}_S \Leftrightarrow s+\ell _S{\mathbb Z}\subseteq {\mathcal M}_S \Leftrightarrow s+\ell _S{\mathbb Z}\subseteq {\mathcal M}_{\mathcal B}$
;
$s\in {\mathcal M}_S \Leftrightarrow s+\ell _S{\mathbb Z}\subseteq {\mathcal M}_S \Leftrightarrow s+\ell _S{\mathbb Z}\subseteq {\mathcal M}_{\mathcal B}$
; -
(b)
 $s\in {\mathcal F}_{{\mathcal A}_S} \Leftrightarrow s+\ell _S{\mathbb Z}\subseteq {\mathcal F}_{{\mathcal A}_S} \Leftrightarrow s+\ell _S{\mathbb Z}\subseteq {\mathcal F}_{{\mathcal B}}$
.
$s\in {\mathcal F}_{{\mathcal A}_S} \Leftrightarrow s+\ell _S{\mathbb Z}\subseteq {\mathcal F}_{{\mathcal A}_S} \Leftrightarrow s+\ell _S{\mathbb Z}\subseteq {\mathcal F}_{{\mathcal B}}$
.
In particular,
![]() $s \in {\mathbb Z}$
is not
$s \in {\mathbb Z}$
is not
![]() $\ell _S$
-periodic if and only if
$\ell _S$
-periodic if and only if
![]() $s \in \mathcal {M}_{{\mathcal A}_{S}} \setminus \mathcal {M}_{S}$
. Hence,
$s \in \mathcal {M}_{{\mathcal A}_{S}} \setminus \mathcal {M}_{S}$
. Hence,
![]() $\mathcal {M}_{{\mathcal A}_{S_n}} \setminus \mathcal {M}_{S_n}$
is the set of all holes (with respect to the period structure given by
$\mathcal {M}_{{\mathcal A}_{S_n}} \setminus \mathcal {M}_{S_n}$
is the set of all holes (with respect to the period structure given by
![]() $p_n=\operatorname {lcm}(S_n)$
) in
$p_n=\operatorname {lcm}(S_n)$
) in
![]() $\eta $
on level n. (Observe also that if
$\eta $
on level n. (Observe also that if
![]() ${\mathcal B}$
is primitive and
${\mathcal B}$
is primitive and
![]() $\eta $
is a Toeplitz sequence, then
$\eta $
is a Toeplitz sequence, then
![]() ${\mathcal B}$
is taut, see [Reference Kasjan, Keller and Lemańczyk18, Lemma 3.7].)
${\mathcal B}$
is taut, see [Reference Kasjan, Keller and Lemańczyk18, Lemma 3.7].)
Proof. (i) Let
![]() $s\in {\mathcal M}_S$
. Then
$s\in {\mathcal M}_S$
. Then
![]() $b \mid s$
for some
$b \mid s$
for some
![]() $b \in S$
. Since
$b \in S$
. Since
![]() $b \mid \ell _{S}$
,
$b \mid \ell _{S}$
,
![]() $s+\ell _{S} \mathbb {Z} \subseteq b \mathbb {Z} \subseteq \mathcal {M}_{S}$
.
$s+\ell _{S} \mathbb {Z} \subseteq b \mathbb {Z} \subseteq \mathcal {M}_{S}$
.
(ii) Let
![]() $s+\ell _S{\mathbb Z}\subseteq {\mathcal M}_{\mathcal B}$
. By [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk12, Proposition 4.31], the tautness of
$s+\ell _S{\mathbb Z}\subseteq {\mathcal M}_{\mathcal B}$
. By [Reference Dymek, Kasjan, Kułaga-Przymus and Lemańczyk12, Proposition 4.31], the tautness of
![]() ${\mathcal B}$
implies
${\mathcal B}$
implies
![]() $b \mid \gcd (s,\ell _S)$
for some
$b \mid \gcd (s,\ell _S)$
for some
![]() $b \in {\mathcal B}$
. Since S is saturated,
$b \in {\mathcal B}$
. Since S is saturated,
![]() $b\in S$
. So
$b\in S$
. So
![]() $s \in \mathcal {M}_{S}$
.
$s \in \mathcal {M}_{S}$
.
(iii) Let
![]() $s\in {\mathcal F}_{{\mathcal A}_S}$
. Assume for a contradiction that
$s\in {\mathcal F}_{{\mathcal A}_S}$
. Assume for a contradiction that
![]() $\gcd (b,\ell _S) \mid s+\ell _{S} k$
for some
$\gcd (b,\ell _S) \mid s+\ell _{S} k$
for some
![]() $k \in {\mathbb Z}$
and some
$k \in {\mathbb Z}$
and some
![]() $b \in {\mathcal B}$
. Since
$b \in {\mathcal B}$
. Since
![]() $\gcd (b,\ell _S) \mid \ell _{S}$
,
$\gcd (b,\ell _S) \mid \ell _{S}$
,
![]() $\gcd (b, \ell _{S}) \mid s$
, which contradicts
$\gcd (b, \ell _{S}) \mid s$
, which contradicts
![]() $s\in {\mathcal F}_{{\mathcal A}_S}$
. So
$s\in {\mathcal F}_{{\mathcal A}_S}$
. So
![]() $s+\ell _S{\mathbb Z}\subseteq {\mathcal F}_{{\mathcal A}_S}$
.
$s+\ell _S{\mathbb Z}\subseteq {\mathcal F}_{{\mathcal A}_S}$
.
(iv) Let
![]() $s+\ell _S{\mathbb Z}\subseteq {\mathcal F}_{\mathcal B}$
. Assume for a contradiction that
$s+\ell _S{\mathbb Z}\subseteq {\mathcal F}_{\mathcal B}$
. Assume for a contradiction that
![]() $\gcd (b,\ell _S)\mid s$
for some
$\gcd (b,\ell _S)\mid s$
for some
![]() $b\in {\mathcal B}$
. Then there is
$b\in {\mathcal B}$
. Then there is
![]() $x\in {\mathbb Z}$
such that
$x\in {\mathbb Z}$
such that
![]() $x\equiv 0\,\mod b$
and
$x\equiv 0\,\mod b$
and
![]() $x\equiv s\,\mod \ell _S$
, i.e.
$x\equiv s\,\mod \ell _S$
, i.e.
![]() $x\in b{\mathbb Z}\cap (s+\ell _S{\mathbb Z})$
, in contradiction to
$x\in b{\mathbb Z}\cap (s+\ell _S{\mathbb Z})$
, in contradiction to
![]() $s+\ell _S{\mathbb Z}\subseteq {\mathcal F}_{\mathcal B}$
. Hence,
$s+\ell _S{\mathbb Z}\subseteq {\mathcal F}_{\mathcal B}$
. Hence,
![]() $s\in {\mathcal F}_{{\mathcal A}_S}$
.
$s\in {\mathcal F}_{{\mathcal A}_S}$
.
Now part (a) follows from items (i) and (ii), while part (b) follows from items (iii) and (iv).
To describe the set of essential holes, we extract special elements of
![]() ${\mathcal A}_S$
.
${\mathcal A}_S$
.
Definition 3.8. Let
![]() $S\subset {\mathcal B}$
.
$S\subset {\mathcal B}$
.
-
(a) An element
 $b\in {\mathcal B}\setminus S$
is a source of an element
$b\in {\mathcal B}\setminus S$
is a source of an element
 $a\in {\mathcal A}_S$
if
$a\in {\mathcal A}_S$
if
 $a=\gcd (b,\operatorname {lcm}(S))$
.
$a=\gcd (b,\operatorname {lcm}(S))$
. -
(b)
 ${\mathcal A}_S^\infty :=\{a\in {\mathcal A}_S: a\text { has infinitely many sources}\}$
and
${\mathcal A}_S^\infty :=\{a\in {\mathcal A}_S: a\text { has infinitely many sources}\}$
and
 ${\mathcal A}_S^{\infty ,p}:=({\mathcal A}_S^\infty )^{\textrm {prim}}$
.
${\mathcal A}_S^{\infty ,p}:=({\mathcal A}_S^\infty )^{\textrm {prim}}$
.
We will use some basic properties of
![]() ${\mathcal A}_S^\infty $
.
${\mathcal A}_S^\infty $
.
Lemma 3.9.
-
(a)
 ${\mathcal A}_S^{\infty ,p}\subseteq {\mathcal A}_S^\infty \subseteq {\mathcal A}_S\setminus {\mathcal M}_S$
.
${\mathcal A}_S^{\infty ,p}\subseteq {\mathcal A}_S^\infty \subseteq {\mathcal A}_S\setminus {\mathcal M}_S$
. -
(b) Let
 $S\subset S'\subset {\mathcal B}$
and
$S\subset S'\subset {\mathcal B}$
and
 $a\in {\mathcal A}_S^\infty $
. There exists at least one
$a\in {\mathcal A}_S^\infty $
. There exists at least one
 $a'\in {\mathcal A}_{S'}^\infty $
such that
$a'\in {\mathcal A}_{S'}^\infty $
such that
 $a=\gcd (a',\ell _S)$
.
$a=\gcd (a',\ell _S)$
. -
(c) Let
 $S\subset S'\subset {\mathcal B}$
and
$S\subset S'\subset {\mathcal B}$
and
 $a'\in {\mathcal A}_{S'}^\infty $
. Then,
$a'\in {\mathcal A}_{S'}^\infty $
. Then,
 $\gcd (\ell _S,a')\in {\mathcal A}^{\infty }_S$
.
$\gcd (\ell _S,a')\in {\mathcal A}^{\infty }_S$
. -
(d) Let
 $S\subset S'\subset {\mathcal B}$
and
$S\subset S'\subset {\mathcal B}$
and
 $a\in {\mathcal A}_S^{\infty ,p}$
. There exists at least one
$a\in {\mathcal A}_S^{\infty ,p}$
. There exists at least one
 $a'\in {\mathcal A}_{S'}^{\infty ,p}$
such that
$a'\in {\mathcal A}_{S'}^{\infty ,p}$
such that
 $a=\gcd (a',\ell _S)$
. In particular,
$a=\gcd (a',\ell _S)$
. In particular,
 $|{\mathcal A}_{S'}^{\infty ,p}|\geqslant |{\mathcal A}_S^{\infty ,p}|$
.
$|{\mathcal A}_{S'}^{\infty ,p}|\geqslant |{\mathcal A}_S^{\infty ,p}|$
. -
(e) Let
 $S\subset S'\subset {\mathcal B}$
with
$S\subset S'\subset {\mathcal B}$
with
 $|{\mathcal A}_{S'}^{\infty ,p}|=|{\mathcal A}_S^{\infty ,p}|$
and
$|{\mathcal A}_{S'}^{\infty ,p}|=|{\mathcal A}_S^{\infty ,p}|$
and
 $a'\in {\mathcal A}_{S'}^{\infty ,p}$
. Then,
$a'\in {\mathcal A}_{S'}^{\infty ,p}$
. Then,
 $\gcd (a',\ell _S)\in {\mathcal A}_S^{\infty ,p}$
. (Without the extra assumption, this need not hold, see Example 3.29.)
$\gcd (a',\ell _S)\in {\mathcal A}_S^{\infty ,p}$
. (Without the extra assumption, this need not hold, see Example 3.29.)
Proof. (a) Let
![]() $a\in {\mathcal A}_S^\infty $
. If
$a\in {\mathcal A}_S^\infty $
. If
![]() $a=\gcd (b,\ell _S)\in {\mathcal M}_S$
for some
$a=\gcd (b,\ell _S)\in {\mathcal M}_S$
for some
![]() $b\in {\mathcal B}$
, then there is
$b\in {\mathcal B}$
, then there is
![]() $b'\in S$
such that
$b'\in S$
such that
![]() $b'\mid a\mid b$
, and the primitivity of
$b'\mid a\mid b$
, and the primitivity of
![]() ${\mathcal B}$
implies
${\mathcal B}$
implies
![]() $b=a=b'\in S$
. This contradicts to a having infinitely many sources.
$b=a=b'\in S$
. This contradicts to a having infinitely many sources.
(b) Let
![]() $a\in {\mathcal A}_S^\infty $
. There are infinitely many
$a\in {\mathcal A}_S^\infty $
. There are infinitely many
![]() $b\in {\mathcal B}\setminus S'$
such that
$b\in {\mathcal B}\setminus S'$
such that
![]() $a=\gcd (b,\ell _S)$
. Let
$a=\gcd (b,\ell _S)$
. Let
![]() $a_b':=\gcd (b,\ell _{S'})$
for these b. Then,
$a_b':=\gcd (b,\ell _{S'})$
for these b. Then,
![]() $\gcd (a^{\prime }_b,\ell _S)=\gcd (b,\ell _S)=a$
for all these b, and as
$\gcd (a^{\prime }_b,\ell _S)=\gcd (b,\ell _S)=a$
for all these b, and as
![]() ${\mathcal A}_{S'}$
is finite, there exists some
${\mathcal A}_{S'}$
is finite, there exists some
![]() $a'\in {\mathcal A}_{S'}$
such that
$a'\in {\mathcal A}_{S'}$
such that
![]() $a'=a^{\prime }_b$
for infinitely many of them. Hence,
$a'=a^{\prime }_b$
for infinitely many of them. Hence,
![]() $a'\in {\mathcal A}_{S'}^\infty $
.
$a'\in {\mathcal A}_{S'}^\infty $
.
(c) Clear.
(d) In the situation of item (b), suppose that
![]() $a\in {\mathcal A}_S^{\infty ,p}$
and that there is
$a\in {\mathcal A}_S^{\infty ,p}$
and that there is
![]() $a^{\prime }_0\in {\mathcal A}_{S'}^{\infty ,p}$
such that
$a^{\prime }_0\in {\mathcal A}_{S'}^{\infty ,p}$
such that
![]() $a^{\prime }_0\mid a'$
. Then,
$a^{\prime }_0\mid a'$
. Then,
![]() $a_0:=\gcd (a^{\prime }_0,\ell _S)\in {\mathcal A}_S^\infty $
and
$a_0:=\gcd (a^{\prime }_0,\ell _S)\in {\mathcal A}_S^\infty $
and
![]() $a_0\mid \gcd (a',\ell _S)=a$
. As
$a_0\mid \gcd (a',\ell _S)=a$
. As
![]() $a\in {\mathcal A}_S^{\infty ,p}$
, this implies
$a\in {\mathcal A}_S^{\infty ,p}$
, this implies
![]() $a_0=a$
, so that
$a_0=a$
, so that
![]() $\gcd (a_0',\ell _S)=a$
.
$\gcd (a_0',\ell _S)=a$
.
(e) This follows from item (d).
Lemma 3.10. Suppose that
![]() $S_1\subseteq S_2\subseteq \cdots \nearrow {\mathcal B}$
is a filtration by saturated sets. Then, for each
$S_1\subseteq S_2\subseteq \cdots \nearrow {\mathcal B}$
is a filtration by saturated sets. Then, for each
![]() $N\in {\mathbb N}$
,
$N\in {\mathbb N}$
,
and, for all
![]() $r\in {\mathbb Z}$
,
$r\in {\mathbb Z}$
,
More precisely, if
![]() $h\in U_{S_N}(\Delta (r))\cap \partial W$
, then
$h\in U_{S_N}(\Delta (r))\cap \partial W$
, then
![]() $h_{S_n}\in (r+\ell _{S_N}{\mathbb Z})\cap ({\mathcal M}_{{\mathcal A}_{S_n}^\infty }\setminus {\mathcal M}_{S_n})$
for all
$h_{S_n}\in (r+\ell _{S_N}{\mathbb Z})\cap ({\mathcal M}_{{\mathcal A}_{S_n}^\infty }\setminus {\mathcal M}_{S_n})$
for all
![]() $n\geqslant N$
.
$n\geqslant N$
.
Proof. Suppose there exists some
![]() $h\in U_{S_N}(\Delta (r))\cap \partial W$
. Then,
$h\in U_{S_N}(\Delta (r))\cap \partial W$
. Then,
![]() $h_{S_n}\in (r+\ell _{S_N}{\mathbb Z})\cap ({\mathcal M}_{{\mathcal A}_{S_n}}\setminus {\mathcal M}_{S_n})$
for all
$h_{S_n}\in (r+\ell _{S_N}{\mathbb Z})\cap ({\mathcal M}_{{\mathcal A}_{S_n}}\setminus {\mathcal M}_{S_n})$
for all
![]() $n\geqslant N$
, see Lemma 2.1 and Proposition 3.7. Hence,
$n\geqslant N$
, see Lemma 2.1 and Proposition 3.7. Hence,
![]() $r\not \in {\mathcal M}_{S_N}$
, and there are numbers
$r\not \in {\mathcal M}_{S_N}$
, and there are numbers
![]() $k_n\in {\mathbb Z}$
and
$k_n\in {\mathbb Z}$
and
![]() $b_n\in {\mathcal B}\setminus S_n (n\geqslant N)$
such that
$b_n\in {\mathcal B}\setminus S_n (n\geqslant N)$
such that
![]() $\gcd (b_n,\ell _{S_N})\mid \gcd (b_n,\ell _{S_n})\mid h_{S_n}=r+k_n\ell _{S_N}$
. In particular,
$\gcd (b_n,\ell _{S_N})\mid \gcd (b_n,\ell _{S_n})\mid h_{S_n}=r+k_n\ell _{S_N}$
. In particular,
![]() $\gcd (b_n,\ell _{S_N})\mid r$
for all
$\gcd (b_n,\ell _{S_N})\mid r$
for all
![]() $n\geqslant N$
, and as
$n\geqslant N$
, and as
![]() ${\mathcal A}_{S_N}$
is a finite set, there exist
${\mathcal A}_{S_N}$
is a finite set, there exist
![]() $a\in {\mathcal A}_{S_N}$
and infinitely many
$a\in {\mathcal A}_{S_N}$
and infinitely many
![]() $b_{n_i}$
such that
$b_{n_i}$
such that
![]() $\gcd (b_{n_i},\ell _{S_N})=a$
. It follows that
$\gcd (b_{n_i},\ell _{S_N})=a$
. It follows that
![]() $a\in {\mathcal A}_{S_N}^\infty $
and
$a\in {\mathcal A}_{S_N}^\infty $
and
![]() $a\mid r$
. This proves equation (47).
$a\mid r$
. This proves equation (47).
Observe that, trivially,
![]() $h\in U_{S_n}(\Delta (h_{S_n}))\cap \partial W$
for each
$h\in U_{S_n}(\Delta (h_{S_n}))\cap \partial W$
for each
![]() $n\geqslant N$
. Hence, we can apply equation (47) to n and
$n\geqslant N$
. Hence, we can apply equation (47) to n and
![]() $h_{S_n}$
instead of N and r, respectively. It follows that
$h_{S_n}$
instead of N and r, respectively. It follows that
![]() $h_{S_n}\in {\mathcal M}_{{\mathcal A}_{S_n}^\infty }\setminus {\mathcal M}_{S_n}$
. As
$h_{S_n}\in {\mathcal M}_{{\mathcal A}_{S_n}^\infty }\setminus {\mathcal M}_{S_n}$
. As
![]() $h_{S_n}=r+k_n\ell _{S_N}$
, this proves the ‘
$h_{S_n}=r+k_n\ell _{S_N}$
, this proves the ‘
![]() $\Rightarrow $
’-direction of equation (48) and also the final claim.
$\Rightarrow $
’-direction of equation (48) and also the final claim.
The ‘
![]() $\Leftarrow $
’-implication of equation (48) follows from Lemma 2.5 and Proposition 3.7, because
$\Leftarrow $
’-implication of equation (48) follows from Lemma 2.5 and Proposition 3.7, because
![]() ${\mathcal A}_{S_n}^\infty \subseteq {\mathcal A}_{S_n}$
for all
${\mathcal A}_{S_n}^\infty \subseteq {\mathcal A}_{S_n}$
for all
![]() $n\in {\mathbb N}$
.
$n\in {\mathbb N}$
.
Corollary 3.11. Suppose that
![]() $S_1\subseteq S_2\subseteq \cdots \nearrow {\mathcal B}$
is a filtration by saturated sets. Then, for each
$S_1\subseteq S_2\subseteq \cdots \nearrow {\mathcal B}$
is a filtration by saturated sets. Then, for each
![]() $n\in {\mathbb N}$
,
$n\in {\mathbb N}$
,
 $$ \begin{align*} m_G(\partial W)\le d({\mathcal M}_{{\mathcal A}_{S_n}^{\infty,p}})\le 1-\prod_{a\in{\mathcal A}_{S_n}^{\infty,p}}\bigg(1-\frac{1}{a}\bigg). \end{align*} $$
$$ \begin{align*} m_G(\partial W)\le d({\mathcal M}_{{\mathcal A}_{S_n}^{\infty,p}})\le 1-\prod_{a\in{\mathcal A}_{S_n}^{\infty,p}}\bigg(1-\frac{1}{a}\bigg). \end{align*} $$
Proof. For
![]() $n\in {\mathbb N}$
, denote by
$n\in {\mathbb N}$
, denote by
![]() ${\mathcal U}_n$
the family of all sets
${\mathcal U}_n$
the family of all sets
![]() $U_{S_n}(\Delta (r))$
that have non-empty intersection with
$U_{S_n}(\Delta (r))$
that have non-empty intersection with
![]() $\partial W$
and by
$\partial W$
and by
![]() $\bigcup {\mathcal U}_n$
the union of these sets. Then, equation (47) implies
$\bigcup {\mathcal U}_n$
the union of these sets. Then, equation (47) implies
![]() $m_G(\partial W) \le m_G(\bigcup {\mathcal U}_n) = {|{\mathcal U}_n|}/{\ell _{S_n}} \le d({\mathcal M}_{{\mathcal A}_{S_n}^\infty }\setminus {\mathcal M}_{S_n}) \le d({\mathcal M}_{{\mathcal A}_{S_n}^{\infty ,p}})$
for all n, and the second inequality is the Heilbronn–Rohrbach inequality [Reference Hall15, Theorem 0.9].
$m_G(\partial W) \le m_G(\bigcup {\mathcal U}_n) = {|{\mathcal U}_n|}/{\ell _{S_n}} \le d({\mathcal M}_{{\mathcal A}_{S_n}^\infty }\setminus {\mathcal M}_{S_n}) \le d({\mathcal M}_{{\mathcal A}_{S_n}^{\infty ,p}})$
for all n, and the second inequality is the Heilbronn–Rohrbach inequality [Reference Hall15, Theorem 0.9].
Remark 3.12. Fix the period structure given by
![]() $p_n=\operatorname {lcm}(S_n)$
. Then,
$p_n=\operatorname {lcm}(S_n)$
. Then,
by Proposition 3.7, Lemma 2.5(a) and equation (47) of Lemma 3.10. Moreover, equation (48) of Lemma 3.10 shows that
![]() $r\in {\widetilde {\mathcal H}}_N$
if and only if
$r\in {\widetilde {\mathcal H}}_N$
if and only if
![]() $\text { for all } n\geqslant N: (r+\ell _{S_N}{\mathbb Z})\cap ({\mathcal M}_{{\mathcal A}_{S_n}^\infty }\setminus {\mathcal M}_{S_n})\neq \emptyset $
. This characterization is also the starting point for verifying the structural assumption in equation (AS) on
$\text { for all } n\geqslant N: (r+\ell _{S_N}{\mathbb Z})\cap ({\mathcal M}_{{\mathcal A}_{S_n}^\infty }\setminus {\mathcal M}_{S_n})\neq \emptyset $
. This characterization is also the starting point for verifying the structural assumption in equation (AS) on
![]() ${\widetilde {\mathcal H}}_n$
from §2.5, see Proposition 3.16 and Theorem 3.17 below.
${\widetilde {\mathcal H}}_n$
from §2.5, see Proposition 3.16 and Theorem 3.17 below.
Remark 3.13. In the general Toeplitz case, one can easily construct a Toeplitz sequence for which not all holes are essential. We construct a
![]() ${\mathcal B}$
-free Toeplitz subshift with this property in Example 3.27. Moreover, the property
${\mathcal B}$
-free Toeplitz subshift with this property in Example 3.27. Moreover, the property
![]() ${\widetilde {\mathcal H}}_n={\mathcal H}_n$
may depend on the choice of the period structure, as we show in Example 3.28, and a
${\widetilde {\mathcal H}}_n={\mathcal H}_n$
may depend on the choice of the period structure, as we show in Example 3.28, and a
![]() ${\mathcal B}$
-free Toeplitz subshift for which
${\mathcal B}$
-free Toeplitz subshift for which
![]() ${\widetilde {\mathcal H}}_n\subsetneq {\mathcal M}_{{\mathcal A}_{S_n}^\infty }\setminus {\mathcal M}_{S_n}$
is provided in Example 3.29.
${\widetilde {\mathcal H}}_n\subsetneq {\mathcal M}_{{\mathcal A}_{S_n}^\infty }\setminus {\mathcal M}_{S_n}$
is provided in Example 3.29.
In the rest of this subsection, we show that the structural assumption in equation (AS) of Propositions 2.28 and 2.30 and of Theorem 2.31 is satisfied in the
![]() ${\mathcal B}$
-free setting.
${\mathcal B}$
-free setting.
Definition 3.14. Let
![]() $(S_n)_n$
be a filtration of
$(S_n)_n$
be a filtration of
![]() ${\mathcal B}$
by finite sets. An integer sequence
${\mathcal B}$
by finite sets. An integer sequence
![]() $(a_n)_{n\ge N}$
is called an
$(a_n)_{n\ge N}$
is called an
![]() $(a,{\mathcal A})$
-sequence, if
$(a,{\mathcal A})$
-sequence, if
![]() $a_N=a$
and if
$a_N=a$
and if
![]() $a_n\in {\mathcal A}_{S_n}{\setminus S_n}$
and
$a_n\in {\mathcal A}_{S_n}{\setminus S_n}$
and
![]() $\gcd (a_{n+1},\ell _{S_n})=a_n$
for all
$\gcd (a_{n+1},\ell _{S_n})=a_n$
for all
![]() $n\ge N$
.
$n\ge N$
.
Remark 3.15. If
![]() $(a_n)_{n\ge N}$
is an
$(a_n)_{n\ge N}$
is an
![]() $(a,{\mathcal A})$
-sequence, then
$(a,{\mathcal A})$
-sequence, then
![]() $a_n\in {\mathcal A}_{S_n}^\infty $
for all
$a_n\in {\mathcal A}_{S_n}^\infty $
for all
![]() $n\ge N$
. Indeed, suppose that
$n\ge N$
. Indeed, suppose that
![]() $a_m$
has only finitely many sources
$a_m$
has only finitely many sources
![]() $b_1,\ldots ,b_k$
for some
$b_1,\ldots ,b_k$
for some
![]() $m\geq N$
. Consider
$m\geq N$
. Consider
![]() $n\geq m$
such that
$n\geq m$
such that
![]() $b_1,\ldots ,b_k\in S_n$
. Since
$b_1,\ldots ,b_k\in S_n$
. Since
![]() $a_n\not \in S_n$
, there exists
$a_n\not \in S_n$
, there exists
![]() $b\in {\mathcal B}\setminus S_n$
such that
$b\in {\mathcal B}\setminus S_n$
such that
![]() $a_n=\gcd (b,\ell _{S_n})$
. Then
$a_n=\gcd (b,\ell _{S_n})$
. Then
![]() $a_m=\gcd (a_n,\ell _{S_m})=\gcd (b,\ell _{S_m})$
. So b is a source of
$a_m=\gcd (a_n,\ell _{S_m})=\gcd (b,\ell _{S_m})$
. So b is a source of
![]() $a_m$
different from
$a_m$
different from
![]() $b_1,\ldots ,b_k$
. This yields a contradiction. Note also that by Lemma 3.9(b), for every
$b_1,\ldots ,b_k$
. This yields a contradiction. Note also that by Lemma 3.9(b), for every
![]() $a\in {\mathcal A}_{S_N}^{\infty }$
there exists an
$a\in {\mathcal A}_{S_N}^{\infty }$
there exists an
![]() $(a,{\mathcal A})$
-sequence.
$(a,{\mathcal A})$
-sequence.
Proposition 3.16. Let
![]() $(S_n)_n$
be a filtration of
$(S_n)_n$
be a filtration of
![]() ${\mathcal B}$
by finite sets. Then, for all
${\mathcal B}$
by finite sets. Then, for all
![]() $N\in {\mathbb N}$
, the set
$N\in {\mathbb N}$
, the set
![]() ${\widetilde {\mathcal H}}_N$
is the union of sets
${\widetilde {\mathcal H}}_N$
is the union of sets
![]() $a{\mathbb Z}\setminus {\mathcal M}_{S_N((a_n)_{n\ge N})}$
, where the union extends over all
$a{\mathbb Z}\setminus {\mathcal M}_{S_N((a_n)_{n\ge N})}$
, where the union extends over all
![]() $(a,{\mathcal A})$
-sequences
$(a,{\mathcal A})$
-sequences
![]() $(a_n)_{n\ge N}$
and where
$(a_n)_{n\ge N}$
and where
Proof. Notice that in view of Remark 3.12,
Hence,
 $$ \begin{align*} \begin{aligned} r\not\in{\widetilde{\mathcal H}}_N \Leftrightarrow\, &\text{there exists } n\ge N: (r+\ell_{S_N}{\mathbb Z})\cap({\mathcal M}_{{\mathcal A}_{S_n}^{\infty}}\setminus{\mathcal M}_{S_n})=\emptyset\\\Leftrightarrow\, &\text{there exists } n\ge N\ \text{ for all } a_n\in{\mathcal A}_{S_n}^{\infty}: (r+\ell_{S_N}{\mathbb Z})\cap a_n{\mathbb Z}\subseteq{\mathcal M}_{S_n}\\\Leftrightarrow\, &(\text{there exists } n\ge N\ \text{ for all } a_n\in{\mathcal A}_{S_n}^{\infty}: (r+\ell_{S_N}{\mathbb Z})\cap a_n{\mathbb Z}\neq\emptyset\\&\Rightarrow \text{there exists } b\in S_n: (r+\ell_{S_N}{\mathbb Z})\cap a_n{\mathbb Z}\subseteq b{\mathbb Z})\\\Leftrightarrow\, &(\text{there exists } n\ge N\ \text{ for all } a_n\in{\mathcal A}_{S_n}^{\infty}: \gcd(a_n,\ell_{S_N})\mid r\\&\Rightarrow\text{there exists } b\in S_n: b\mid a_n\vee\ell_{S_N}\text{ and }\gcd(b,\ell_{S_N})\mid r). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} r\not\in{\widetilde{\mathcal H}}_N \Leftrightarrow\, &\text{there exists } n\ge N: (r+\ell_{S_N}{\mathbb Z})\cap({\mathcal M}_{{\mathcal A}_{S_n}^{\infty}}\setminus{\mathcal M}_{S_n})=\emptyset\\\Leftrightarrow\, &\text{there exists } n\ge N\ \text{ for all } a_n\in{\mathcal A}_{S_n}^{\infty}: (r+\ell_{S_N}{\mathbb Z})\cap a_n{\mathbb Z}\subseteq{\mathcal M}_{S_n}\\\Leftrightarrow\, &(\text{there exists } n\ge N\ \text{ for all } a_n\in{\mathcal A}_{S_n}^{\infty}: (r+\ell_{S_N}{\mathbb Z})\cap a_n{\mathbb Z}\neq\emptyset\\&\Rightarrow \text{there exists } b\in S_n: (r+\ell_{S_N}{\mathbb Z})\cap a_n{\mathbb Z}\subseteq b{\mathbb Z})\\\Leftrightarrow\, &(\text{there exists } n\ge N\ \text{ for all } a_n\in{\mathcal A}_{S_n}^{\infty}: \gcd(a_n,\ell_{S_N})\mid r\\&\Rightarrow\text{there exists } b\in S_n: b\mid a_n\vee\ell_{S_N}\text{ and }\gcd(b,\ell_{S_N})\mid r). \end{aligned} \end{align*} $$
The third equivalence follows from Lemma 2.24 and the last one from Lemma 2.25. Now, the first of the following two equivalences is immediate:
 $$ \begin{align} &\hspace{-5pt}r\in{\widetilde{\mathcal H}}_N\nonumber\\ &\Leftrightarrow \text{for all } n\ge N\quad\text{there exists } a_n\in{\mathcal A}_{S_n}^{\infty}: \gcd(a_n,\ell_{S_N})\mid r \quad\text{and}\nonumber\\ &\quad\qquad[\text{for all } b\in S_n: b\mid a_n\vee\ell_{S_N}\Rightarrow\gcd(b,\ell_{S_N})\nmid r]\notag\\ &\Leftrightarrow \text{there exists } a\in{\mathcal A}_{S_N}^{\infty} \quad\text{there exists }\text{ an }(a,{\mathcal A})\text{-sequence }(a_n)_{n\ge N}: a\mid r\quad\text{and }\\ &\quad\qquad \text{for all } b\in{\mathcal B}\quad \text{for all } n\ge N: b\mid a_n\vee\ell_{S_N}\Rightarrow\gcd(b,\ell_{S_N})\nmid r.\notag \end{align} $$
$$ \begin{align} &\hspace{-5pt}r\in{\widetilde{\mathcal H}}_N\nonumber\\ &\Leftrightarrow \text{for all } n\ge N\quad\text{there exists } a_n\in{\mathcal A}_{S_n}^{\infty}: \gcd(a_n,\ell_{S_N})\mid r \quad\text{and}\nonumber\\ &\quad\qquad[\text{for all } b\in S_n: b\mid a_n\vee\ell_{S_N}\Rightarrow\gcd(b,\ell_{S_N})\nmid r]\notag\\ &\Leftrightarrow \text{there exists } a\in{\mathcal A}_{S_N}^{\infty} \quad\text{there exists }\text{ an }(a,{\mathcal A})\text{-sequence }(a_n)_{n\ge N}: a\mid r\quad\text{and }\\ &\quad\qquad \text{for all } b\in{\mathcal B}\quad \text{for all } n\ge N: b\mid a_n\vee\ell_{S_N}\Rightarrow\gcd(b,\ell_{S_N})\nmid r.\notag \end{align} $$
The ‘
![]() $\Leftarrow $
’-direction of the second equivalence is obvious—just a matter of notation. For the ‘
$\Leftarrow $
’-direction of the second equivalence is obvious—just a matter of notation. For the ‘
![]() $\Rightarrow $
’-direction, we construct a suitable
$\Rightarrow $
’-direction, we construct a suitable
![]() $(a,{\mathcal A})$
-sequence
$(a,{\mathcal A})$
-sequence
![]() $(a_m')_{m\ge N}$
from the given numbers
$(a_m')_{m\ge N}$
from the given numbers
![]() $a_n$
: there is
$a_n$
: there is
![]() $a\in {\mathcal A}_{S_N}^\infty $
such that
$a\in {\mathcal A}_{S_N}^\infty $
such that
![]() $a=\gcd (a_n,\ell _{S_N})$
for infinitely many indices n. Obviously
$a=\gcd (a_n,\ell _{S_N})$
for infinitely many indices n. Obviously
![]() $a\mid r$
, and we choose
$a\mid r$
, and we choose
![]() $a_N'=a$
. Suppose inductively that suitable
$a_N'=a$
. Suppose inductively that suitable
![]() $a_N',\ldots ,a_m'$
are constructed in such a way that
$a_N',\ldots ,a_m'$
are constructed in such a way that
![]() $a_m'=\gcd (a_{n},\ell _{S_m})$
for infinitely many different indices
$a_m'=\gcd (a_{n},\ell _{S_m})$
for infinitely many different indices
![]() $n\ge m$
. Then there is an increasing subsequence
$n\ge m$
. Then there is an increasing subsequence
![]() $(a_{n_i})_i$
such that
$(a_{n_i})_i$
such that
![]() $\gcd (a_{n_i},\ell _{S_{m+1}})$
is the same value for all
$\gcd (a_{n_i},\ell _{S_{m+1}})$
is the same value for all
![]() $n_i\ge m+1$
. This common value is denoted by
$n_i\ge m+1$
. This common value is denoted by
![]() $a_{m+1}'$
. It satisfies
$a_{m+1}'$
. It satisfies
![]() $\gcd (a_{m+1}',\ell _{S_m})=\gcd (a_{n_i},\ell _{S_{m+1}},\ell _{S_m})=\gcd (a_{n_i},\ell _{S_m})=a_m'$
for all
$\gcd (a_{m+1}',\ell _{S_m})=\gcd (a_{n_i},\ell _{S_{m+1}},\ell _{S_m})=\gcd (a_{n_i},\ell _{S_m})=a_m'$
for all
![]() $n_i$
. Suppose now that
$n_i$
. Suppose now that
![]() $b\in {\mathcal B}$
,
$b\in {\mathcal B}$
,
![]() $n\ge N$
and
$n\ge N$
and
![]() $b\mid a_n\vee \ell _{S_N}$
. Fix
$b\mid a_n\vee \ell _{S_N}$
. Fix
![]() $n'\ge n$
such that
$n'\ge n$
such that
![]() $b\in S_{n'}$
. Then
$b\in S_{n'}$
. Then
![]() $b\mid a_{n'}\vee \ell _{S_n}$
, because
$b\mid a_{n'}\vee \ell _{S_n}$
, because
![]() $a_n\mid a_{n'}$
, and we conclude that
$a_n\mid a_{n'}$
, and we conclude that
![]() $\gcd (b,\ell _{S_N})\nmid r$
. The claim follows.
$\gcd (b,\ell _{S_N})\nmid r$
. The claim follows.
Theorem 3.17. Let
![]() $(S_n)_n$
be a filtration of
$(S_n)_n$
be a filtration of
![]() ${\mathcal B}$
by finite sets and let
${\mathcal B}$
by finite sets and let
![]() $N>0$
. For each
$N>0$
. For each
![]() $a\in {\mathcal A}_{S_N}^\infty $
, there exists a finite primitive set
$a\in {\mathcal A}_{S_N}^\infty $
, there exists a finite primitive set
![]() $S_N(a)$
of positive integers such that
$S_N(a)$
of positive integers such that
 $$ \begin{align} {\widetilde{\mathcal H}}_N=\bigcup_{a\in{\mathcal A}_{S_N}^\infty}a{\mathbb Z}\setminus{\mathcal M}_{S_N(a)} \end{align} $$
$$ \begin{align} {\widetilde{\mathcal H}}_N=\bigcup_{a\in{\mathcal A}_{S_N}^\infty}a{\mathbb Z}\setminus{\mathcal M}_{S_N(a)} \end{align} $$
and all sets
![]() $a{\mathbb Z}\setminus {\mathcal M}_{S_N(a)}$
are non-empty. (An explicit construction of the sets
$a{\mathbb Z}\setminus {\mathcal M}_{S_N(a)}$
are non-empty. (An explicit construction of the sets
![]() $S_N(a)$
is given in the proof.) In particular, the assumption in equation (AS) of Theorem 2.31 is satisfied.
$S_N(a)$
is given in the proof.) In particular, the assumption in equation (AS) of Theorem 2.31 is satisfied.
Proof. Consider any fixed
![]() $a\in {\mathcal A}_{S_N}^\infty $
. In view of Proposition 3.16, the set
$a\in {\mathcal A}_{S_N}^\infty $
. In view of Proposition 3.16, the set
![]() $S_N(a)$
must be constructed in such a way that
$S_N(a)$
must be constructed in such a way that
![]() ${\mathcal M}_{S_N(a)}=\bigcap {\mathcal M}_{S_N((a_n)_{n\ge N})}$
, where the intersection runs over all
${\mathcal M}_{S_N(a)}=\bigcap {\mathcal M}_{S_N((a_n)_{n\ge N})}$
, where the intersection runs over all
![]() $(a,{\mathcal A})$
-sequences with
$(a,{\mathcal A})$
-sequences with
![]() $a_N=a$
. As all sets
$a_N=a$
. As all sets
![]() $S_N((a_n)_{n\ge N})$
consist of divisors of
$S_N((a_n)_{n\ge N})$
consist of divisors of
![]() $\ell _{S_N}$
, this set is only a finite intersection, say of r sets of multiples
$\ell _{S_N}$
, this set is only a finite intersection, say of r sets of multiples
![]() ${\mathcal M}_{R_1},\ldots ,{\mathcal M}_{R_r}$
. Hence, we may choose as
${\mathcal M}_{R_1},\ldots ,{\mathcal M}_{R_r}$
. Hence, we may choose as
![]() $S_N(a)$
the primitivization of the set of all
$S_N(a)$
the primitivization of the set of all
![]() $c_1\vee \cdots \vee c_r$
, where
$c_1\vee \cdots \vee c_r$
, where
![]() $c_i\in R_i$
for
$c_i\in R_i$
for
![]() $i=1,\ldots ,r$
.
$i=1,\ldots ,r$
.
Suppose for a contradiction that
![]() $a{\mathbb Z}\subseteq {\mathcal M}_{S_N(a)}$
. Then,
$a{\mathbb Z}\subseteq {\mathcal M}_{S_N(a)}$
. Then,
![]() $a{\mathbb Z}\subseteq {\mathcal M}_{S_N((a_n)_{n\ge N})}$
for each
$a{\mathbb Z}\subseteq {\mathcal M}_{S_N((a_n)_{n\ge N})}$
for each
![]() $(a,{\mathcal A})$
-sequence
$(a,{\mathcal A})$
-sequence
![]() $(a_n)_{n\ge N}$
with
$(a_n)_{n\ge N}$
with
![]() $a_N=a$
. Hence, for each such sequence, there is
$a_N=a$
. Hence, for each such sequence, there is
![]() $b\in {\mathcal B}$
such that
$b\in {\mathcal B}$
such that
![]() $\gcd (b,\ell _{S_N})\mid a=\gcd (a_n,\ell _{S_N})$
and
$\gcd (b,\ell _{S_N})\mid a=\gcd (a_n,\ell _{S_N})$
and
![]() $b\mid a_n\vee \ell _{S_N}$
for some
$b\mid a_n\vee \ell _{S_N}$
for some
![]() $n\ge N$
. It follows that
$n\ge N$
. It follows that
![]() $b^{\div \ell _{S_N}}\mid (a_n\vee \ell _{S_N})^{\div \ell _{S_N}}=a_n^{\div \ell _{S_N}}$
, so that
$b^{\div \ell _{S_N}}\mid (a_n\vee \ell _{S_N})^{\div \ell _{S_N}}=a_n^{\div \ell _{S_N}}$
, so that
![]() $b=b^{\div \ell _{S_N}}\cdot \gcd (b,\ell _{S_N})\mid a_n^{\div \ell _{S_N}}\cdot \gcd (a_n,\ell _{S_N})=a_n$
. However, this is impossible, because
$b=b^{\div \ell _{S_N}}\cdot \gcd (b,\ell _{S_N})\mid a_n^{\div \ell _{S_N}}\cdot \gcd (a_n,\ell _{S_N})=a_n$
. However, this is impossible, because
![]() $a_n\in {\mathcal A}_{S_n}^\infty $
and
$a_n\in {\mathcal A}_{S_n}^\infty $
and
![]() ${\mathcal B}$
is primitive.
${\mathcal B}$
is primitive.
Remark 3.18.
-
(a) Each set
 $S_N((a_n)_{n\ge N})$
contains the set
$S_N((a_n)_{n\ge N})$
contains the set
 $S_N$
. Hence, each of the sets
$S_N$
. Hence, each of the sets
 ${\mathcal M}_{S_N(a)}$
contains
${\mathcal M}_{S_N(a)}$
contains
 ${\mathcal M}_{S_N}$
.
${\mathcal M}_{S_N}$
. -
(b) If
 $\sup _N|{\mathcal A}_{S_N}^\infty |<\infty $
, then, for sufficiently large N, there is at most one
$\sup _N|{\mathcal A}_{S_N}^\infty |<\infty $
, then, for sufficiently large N, there is at most one
 $(a,{\mathcal A})$
-sequence
$(a,{\mathcal A})$
-sequence
 $(a_n)_{n\ge N}$
for each
$(a_n)_{n\ge N}$
for each
 $a\in {\mathcal A}_{S_N}^\infty $
. Hence,
$a\in {\mathcal A}_{S_N}^\infty $
. Hence,
 ${\mathcal M}_{S_N(a)}={\mathcal M}_{S_N((a_n)_{n\ge N})}$
for each such a.
${\mathcal M}_{S_N(a)}={\mathcal M}_{S_N((a_n)_{n\ge N})}$
for each such a.
Under a special assumption (which is satisfied in all our examples except Example 3.29), we have a simplified description of the sets
![]() ${\widetilde {\mathcal H}}_n$
.
${\widetilde {\mathcal H}}_n$
.
Lemma 3.19. Assume that
![]() $(S_n)$
is a filtration of
$(S_n)$
is a filtration of
![]() ${\mathcal B}$
by finite saturated sets. Let
${\mathcal B}$
by finite saturated sets. Let
![]() $N\in {\mathbb N}$
. The following conditions are equivalent:
$N\in {\mathbb N}$
. The following conditions are equivalent:
-
(a)
 $\ell _{S_N}\vee a'\in {\mathcal F}_{{\mathcal B}\setminus S_N}$
for every
$\ell _{S_N}\vee a'\in {\mathcal F}_{{\mathcal B}\setminus S_N}$
for every
 $n>N$
and
$n>N$
and
 $a'\in {\mathcal A}_{S_n}^{\infty }$
;
$a'\in {\mathcal A}_{S_n}^{\infty }$
; -
(b)
 $S_N((a_n)_{n\geq N})=S_N$
for every
$S_N((a_n)_{n\geq N})=S_N$
for every
 $a\in {\mathcal A}_{S_N}^{\infty }$
and for all
$a\in {\mathcal A}_{S_N}^{\infty }$
and for all
 $(a,{\mathcal A})$
-sequences
$(a,{\mathcal A})$
-sequences
 $(a_n)_{n\ge N}$
.
$(a_n)_{n\ge N}$
.
If this the case,
![]() ${\widetilde {\mathcal H}}_N={\mathcal M}_{{\mathcal A}_{S_N}^{\infty }}\setminus {\mathcal M}_{S_N}$
.
${\widetilde {\mathcal H}}_N={\mathcal M}_{{\mathcal A}_{S_N}^{\infty }}\setminus {\mathcal M}_{S_N}$
.
Proof. Assume condition (a) and let
![]() $a\in {\mathcal A}_{S_N}^{\infty }$
. Let
$a\in {\mathcal A}_{S_N}^{\infty }$
. Let
![]() $\gcd (b,\ell _{S_N})\in S_N((a_n)_{n\geq N})$
for some
$\gcd (b,\ell _{S_N})\in S_N((a_n)_{n\geq N})$
for some
![]() $b\in {\mathcal B}$
and some
$b\in {\mathcal B}$
and some
![]() $(a,{\mathcal A})$
-sequence
$(a,{\mathcal A})$
-sequence
![]() $(a_n)_{n\ge N}$
. Then,
$(a_n)_{n\ge N}$
. Then,
![]() $b\mid a_n\vee \ell _{S_N}$
for some
$b\mid a_n\vee \ell _{S_N}$
for some
![]() $n\ge N$
and, as
$n\ge N$
and, as
![]() $a_n\in {\mathcal A}_{S_n}^{\infty }$
by Remark 3.15, condition (a) applied to
$a_n\in {\mathcal A}_{S_n}^{\infty }$
by Remark 3.15, condition (a) applied to
![]() $a'=a_n$
yields
$a'=a_n$
yields
![]() $b\in S_N$
.
$b\in S_N$
.
Conversely, assume that
![]() $b{\kern-1pt}\mid{\kern-1pt} \ell _{S_N}{\kern-1pt}\vee{\kern-1pt} a'$
for some
$b{\kern-1pt}\mid{\kern-1pt} \ell _{S_N}{\kern-1pt}\vee{\kern-1pt} a'$
for some
![]() $b{\kern-1pt}\in{\kern-1pt} {\mathcal B}\setminus S_N$
and
$b{\kern-1pt}\in{\kern-1pt} {\mathcal B}\setminus S_N$
and
![]() $a'{\kern-1pt}\in{\kern-1pt} {\mathcal A}_{S_{n_0}}^{\infty }$
, where
$a'{\kern-1pt}\in{\kern-1pt} {\mathcal A}_{S_{n_0}}^{\infty }$
, where
![]() $n_0{\kern-1pt}>{\kern-1pt} N$
. There exists an
$n_0{\kern-1pt}>{\kern-1pt} N$
. There exists an
![]() $(a',{\mathcal A})$
-sequence
$(a',{\mathcal A})$
-sequence
![]() $(a_n)_{n\ge n_0}$
(see Remark 3.15). Set
$(a_n)_{n\ge n_0}$
(see Remark 3.15). Set
![]() $a_n=\gcd (a_{n_0},\ell _{S_n})$
for
$a_n=\gcd (a_{n_0},\ell _{S_n})$
for
![]() $N\le n\le n_0$
. Then,
$N\le n\le n_0$
. Then,
![]() $(a_n)_{n\ge N}$
is an
$(a_n)_{n\ge N}$
is an
![]() $(a_N,{\mathcal A})$
-sequence such that
$(a_N,{\mathcal A})$
-sequence such that
![]() $a_{n_0}=a'$
. Moreover,
$a_{n_0}=a'$
. Moreover,
![]() $\gcd (\ell _{S_N},b)\in S((a_n)_{n\ge N})$
and
$\gcd (\ell _{S_N},b)\in S((a_n)_{n\ge N})$
and
![]() $\gcd (\ell _{S_N},b)\notin S_N$
as
$\gcd (\ell _{S_N},b)\notin S_N$
as
![]() $S_N$
is saturated. It follows that
$S_N$
is saturated. It follows that
![]() $S_N((a_n)_{n\geq N})\neq S_N$
.
$S_N((a_n)_{n\geq N})\neq S_N$
.
The remaining assertion follows by Proposition 3.16 and Remark 3.15.
3.3 Trivial centralizer
We start with an example for which the simple Proposition 2.20 guarantees a trivial centralizer.
Example 3.20. Let
![]() ${\mathcal B}=\{2^nc_n: n>0\}$
, where
${\mathcal B}=\{2^nc_n: n>0\}$
, where
![]() $(c_n)_n$
is a pairwise coprime sequence of odd integers. We will show that the corresponding
$(c_n)_n$
is a pairwise coprime sequence of odd integers. We will show that the corresponding
![]() ${\mathcal B}$
-free system has a trivial centralizer. Let
${\mathcal B}$
-free system has a trivial centralizer. Let
![]() $S_n=\{2^kc_k: 0<k\le n\}$
. The sets
$S_n=\{2^kc_k: 0<k\le n\}$
. The sets
![]() $S_n$
form a filtration by finite sets. Then,
$S_n$
form a filtration by finite sets. Then,
![]() $\ell _{S_n}=2^n\prod _{i=1}^nc_i$
and
$\ell _{S_n}=2^n\prod _{i=1}^nc_i$
and
![]() ${\mathcal A}_{S_n}^{\infty ,p}={\mathcal A}_{S_n}\setminus S_n=\{2^n\}$
. Notice that the property in equation (TI) is satisfied for
${\mathcal A}_{S_n}^{\infty ,p}={\mathcal A}_{S_n}\setminus S_n=\{2^n\}$
. Notice that the property in equation (TI) is satisfied for
![]() $A_n={\mathcal A}_{S_n}^{\infty }$
. Moreover, for each
$A_n={\mathcal A}_{S_n}^{\infty }$
. Moreover, for each
![]() $N>0$
, there is only one
$N>0$
, there is only one
![]() $(a,{\mathcal A})$
-sequence with
$(a,{\mathcal A})$
-sequence with
![]() $a\in {\mathcal A}_{S_N}^{\infty ,p}$
, namely the sequence
$a\in {\mathcal A}_{S_N}^{\infty ,p}$
, namely the sequence
![]() $(2^n)_{n\ge N}$
, and
$(2^n)_{n\ge N}$
, and
![]() $S_N((2^n)_{n\ge N})=S_N$
according to equation (49). Hence,
$S_N((2^n)_{n\ge N})=S_N$
according to equation (49). Hence,
![]() ${\widetilde {\mathcal H}}_N=2^N\setminus {\mathcal M}_{S_N}={\mathcal H}_N$
. So
${\widetilde {\mathcal H}}_N=2^N\setminus {\mathcal M}_{S_N}={\mathcal H}_N$
. So
![]() $\tilde {\tau }_n=\ell _{S_n}$
. By Proposition 2.20, the centralizer is trivial, as shown previously in [Reference Dymek10].
$\tilde {\tau }_n=\ell _{S_n}$
. By Proposition 2.20, the centralizer is trivial, as shown previously in [Reference Dymek10].
Next, we apply Theorem 2.31 to examples which violate properties (TI) and (Seh), and hence also condition (D).
Example 3.21. Let
![]() ${\mathcal B}=\{2^nc_n,3^nd_n: n>0\}$
, where
${\mathcal B}=\{2^nc_n,3^nd_n: n>0\}$
, where
![]() $(c_n)_n$
and
$(c_n)_n$
and
![]() $(d_n)_n$
are two sequences of integers coprime to
$(d_n)_n$
are two sequences of integers coprime to
![]() $2$
and
$2$
and
![]() $3$
, and such that the sequence
$3$
, and such that the sequence
![]() $(c_n\vee d_n)_{n>0}$
is pairwise coprime. We will show that the corresponding
$(c_n\vee d_n)_{n>0}$
is pairwise coprime. We will show that the corresponding
![]() ${\mathcal B}$
-free system has a trivial centralizer. Let
${\mathcal B}$
-free system has a trivial centralizer. Let
![]() $S_n=\{2^kc_k,3^kd_k: 0<k\le n\}$
. The sets
$S_n=\{2^kc_k,3^kd_k: 0<k\le n\}$
. The sets
![]() $S_n$
form a filtration by finite sets. Notice that
$S_n$
form a filtration by finite sets. Notice that
![]() $\ell _{S_n}=6^n\prod _{i=1}^n(c_i\vee d_i)$
and
$\ell _{S_n}=6^n\prod _{i=1}^n(c_i\vee d_i)$
and
![]() ${\mathcal A}_{S_n}^{\infty ,p}={\mathcal A}_{S_n}\setminus S_n=\{2^n,3^n\}$
. In particular,
${\mathcal A}_{S_n}^{\infty ,p}={\mathcal A}_{S_n}\setminus S_n=\{2^n,3^n\}$
. In particular,
![]() $\langle {\mathcal A}_{S_n}^\infty \rangle ={\mathbb Z}$
for all n, so that property (TI) is violated. Below we show that also condition (D) is violated, while Proposition 2.30 shows that conditions (D′) and (DD′) are satisfied.
$\langle {\mathcal A}_{S_n}^\infty \rangle ={\mathbb Z}$
for all n, so that property (TI) is violated. Below we show that also condition (D) is violated, while Proposition 2.30 shows that conditions (D′) and (DD′) are satisfied.
We claim
![]() ${\widetilde {\mathcal H}}_n={\mathcal H}_n={\mathcal M}_{{\mathcal A}_{S_n}^{\infty ,p}}\setminus {\mathcal M}_{S_n}$
. Indeed, suppose that
${\widetilde {\mathcal H}}_n={\mathcal H}_n={\mathcal M}_{{\mathcal A}_{S_n}^{\infty ,p}}\setminus {\mathcal M}_{S_n}$
. Indeed, suppose that
![]() $b\mid s^{n}\vee \ell _{S_N}$
for some
$b\mid s^{n}\vee \ell _{S_N}$
for some
![]() $b\in {\mathcal B}$
and some
$b\in {\mathcal B}$
and some
![]() $s\in \{2,3\}$
. Since
$s\in \{2,3\}$
. Since
![]() $c_j\nmid s^{n}\vee \ell _{S_N}$
and
$c_j\nmid s^{n}\vee \ell _{S_N}$
and
![]() $d_j\nmid s^{n}\vee \ell _{S_N}$
for any
$d_j\nmid s^{n}\vee \ell _{S_N}$
for any
![]() $j>N$
, we have
$j>N$
, we have
![]() $b\in S_N$
. So condition (a) from Lemma 3.19 holds, and the claim follows observing also Remark 3.12.
$b\in S_N$
. So condition (a) from Lemma 3.19 holds, and the claim follows observing also Remark 3.12.
In view of Theorem 3.17, the condition in equation (AS) is satisfied, so that Theorem 2.31 implies
![]() $|K|=1$
or
$|K|=1$
or
![]() $|K|=2$
. Below we will rule out the second possibility.
$|K|=2$
. Below we will rule out the second possibility.
(i) If
![]() $K=\{k\}$
, then
$K=\{k\}$
, then
![]() $\tilde {\tau }_n\mid (y_F)_n-k$
for all
$\tilde {\tau }_n\mid (y_F)_n-k$
for all
![]() $n>0$
, where
$n>0$
, where
![]() $\tilde {\tau }_n$
is the minimal period of
$\tilde {\tau }_n$
is the minimal period of
![]() ${\widetilde {\mathcal H}}_n$
, in this case, the minimal period of
${\widetilde {\mathcal H}}_n$
, in this case, the minimal period of
![]() ${\mathcal M}_{{\mathcal A}_{S_n}^\infty }\setminus {\mathcal M}_{S_n}$
. Since
${\mathcal M}_{{\mathcal A}_{S_n}^\infty }\setminus {\mathcal M}_{S_n}$
. Since
![]() $S_n^{\div 2^n}=\{c_k,3^kd_k: 0<k\leq n\}$
and
$S_n^{\div 2^n}=\{c_k,3^kd_k: 0<k\leq n\}$
and
![]() $S_n^{\div 3^n}=\{2^kc_k,d_k: 0<k\leq n\}$
are primitive, Lemma 2.26(b) applies. So
$S_n^{\div 3^n}=\{2^kc_k,d_k: 0<k\leq n\}$
are primitive, Lemma 2.26(b) applies. So
![]() $\tilde {\tau }_n=\operatorname {lcm}({\mathcal A}_{S_n}^\infty \cup S_n)=\operatorname {lcm}(S_n)$
, and the triviality of the centralizer follows from Theorem 2.31. (ii) Suppose for a contradiction that
$\tilde {\tau }_n=\operatorname {lcm}({\mathcal A}_{S_n}^\infty \cup S_n)=\operatorname {lcm}(S_n)$
, and the triviality of the centralizer follows from Theorem 2.31. (ii) Suppose for a contradiction that
![]() $|K|=2$
, say
$|K|=2$
, say
![]() $K=\{k_2=\kappa _n(2^n),k_3=\kappa _n(3^n)\}$
. Then by Theorem 2.31(b),
$K=\{k_2=\kappa _n(2^n),k_3=\kappa _n(3^n)\}$
. Then by Theorem 2.31(b),
![]() $2^n\mid (y_F)_n-k_2$
and
$2^n\mid (y_F)_n-k_2$
and
![]() $3^n\mid (y_F)_n-k_3$
for all
$3^n\mid (y_F)_n-k_3$
for all
![]() $n>0$
. For
$n>0$
. For
![]() $s\in \{2,3\}$
, the sets
$s\in \{2,3\}$
, the sets
![]() ${\widetilde {\mathcal H}}_n^{k_s}$
(defined in Remark 2.17(a)) and
${\widetilde {\mathcal H}}_n^{k_s}$
(defined in Remark 2.17(a)) and
![]() $s^n{\mathbb Z}\cap {\widetilde {\mathcal H}}_n^{k_s}$
are invariant under translation by
$s^n{\mathbb Z}\cap {\widetilde {\mathcal H}}_n^{k_s}$
are invariant under translation by
![]() $\gcd ((y_F)_n-k_s,p_n)$
, see Remark 2.17(c), because
$\gcd ((y_F)_n-k_s,p_n)$
, see Remark 2.17(c), because
![]() $s^n\mid p_n$
and
$s^n\mid p_n$
and
![]() $s^n\mid (y_F)_n-k_s$
. Hence, the same is true for the set
$s^n\mid (y_F)_n-k_s$
. Hence, the same is true for the set
![]() ${\widetilde {\mathcal H}}_n^{k_s}\setminus s^n{\mathbb Z}$
.
${\widetilde {\mathcal H}}_n^{k_s}\setminus s^n{\mathbb Z}$
.
We claim that
![]() ${\widetilde {\mathcal H}}_n^{k_s}\subseteq s^n{\mathbb Z}\cap {\widetilde {\mathcal H}}_n$
for
${\widetilde {\mathcal H}}_n^{k_s}\subseteq s^n{\mathbb Z}\cap {\widetilde {\mathcal H}}_n$
for
![]() $s=2,3$
. Indeed, if this is not the case, then for at least one
$s=2,3$
. Indeed, if this is not the case, then for at least one
![]() $s\in \{2,3\}$
and
$s\in \{2,3\}$
and
![]() $\bar s=5-s$
,
$\bar s=5-s$
,
so that
![]() $\gcd ((y_F)_n-k_s,p_n)$
must be a multiple of
$\gcd ((y_F)_n-k_s,p_n)$
must be a multiple of
![]() $\bar s^n$
. It follows that
$\bar s^n$
. It follows that
![]() $\bar s^n\mid (y_F)_n-k_s$
. Since we observed above that
$\bar s^n\mid (y_F)_n-k_s$
. Since we observed above that
![]() $\bar s^n\mid (y_F)_n-k_{\bar s}$
, we see that
$\bar s^n\mid (y_F)_n-k_{\bar s}$
, we see that
![]() $\bar s^n\mid k_s-k_{\bar s}=\pm (k_2-k_3)$
for all
$\bar s^n\mid k_s-k_{\bar s}=\pm (k_2-k_3)$
for all
![]() $n>0$
, which implies
$n>0$
, which implies
![]() $k_2=k_3$
in contradiction to
$k_2=k_3$
in contradiction to
![]() $|K|=2$
.
$|K|=2$
.
Moreover, as
![]() ${\widetilde {\mathcal H}}_n={\widetilde {\mathcal H}}_n^{k_s}\cup {\widetilde {\mathcal H}}_n^{k_{\bar s}}$
,
${\widetilde {\mathcal H}}_n={\widetilde {\mathcal H}}_n^{k_s}\cup {\widetilde {\mathcal H}}_n^{k_{\bar s}}$
,
Since we proved above that
![]() ${\widetilde {\mathcal H}}_n={\mathcal M}_{{\mathcal A}_{S_n}^{\infty ,p}}\setminus {\mathcal M}_{S_n}={\mathcal M}_{\{2^n,3^n\}}\setminus {\mathcal M}_{S_n}$
, this implies
${\widetilde {\mathcal H}}_n={\mathcal M}_{{\mathcal A}_{S_n}^{\infty ,p}}\setminus {\mathcal M}_{S_n}={\mathcal M}_{\{2^n,3^n\}}\setminus {\mathcal M}_{S_n}$
, this implies
equivalently,
Denote the minimal period of
![]() ${\widetilde {\mathcal H}}_n^{k_s}$
by
${\widetilde {\mathcal H}}_n^{k_s}$
by
![]() $\tilde {\tau }^{(s)}$
. Our goal is to prove that
$\tilde {\tau }^{(s)}$
. Our goal is to prove that
![]() $\gcd (\tilde {\tau }^{(2)},\tilde {\tau }^{(3)})>2m$
, because the fact that
$\gcd (\tilde {\tau }^{(2)},\tilde {\tau }^{(3)})>2m$
, because the fact that
![]() $\gcd (\tilde {\tau }^{(2)},\tilde {\tau }^{(3)})$
divides
$\gcd (\tilde {\tau }^{(2)},\tilde {\tau }^{(3)})$
divides
![]() $\gcd ((y_F)_n-k_2,(y_F)_n-k_{3})$
and hence also
$\gcd ((y_F)_n-k_2,(y_F)_n-k_{3})$
and hence also
![]() $k_{3}-k_2$
then shows that
$k_{3}-k_2$
then shows that
![]() $k_2=k_3$
, which is the desired contradiction. (Recall from Proposition 2.28 that
$k_2=k_3$
, which is the desired contradiction. (Recall from Proposition 2.28 that
![]() $K\subseteq [-m,m]$
.)
$K\subseteq [-m,m]$
.)
Observe first that
![]() $s^n\mid \tilde {\tau }^{(s)}$
and
$s^n\mid \tilde {\tau }^{(s)}$
and
![]() $t+\tilde {\tau }^{(s)}{\mathbb Z}\subseteq s^n{\mathbb Z}\setminus {\widetilde {\mathcal H}}_n^{k_s}\subseteq s^n{\mathbb Z}\cap {\mathcal M}_{S_n\cup \{\bar s^n\}}$
for each
$t+\tilde {\tau }^{(s)}{\mathbb Z}\subseteq s^n{\mathbb Z}\setminus {\widetilde {\mathcal H}}_n^{k_s}\subseteq s^n{\mathbb Z}\cap {\mathcal M}_{S_n\cup \{\bar s^n\}}$
for each
![]() $t\in s^n{\mathbb Z}\setminus {\widetilde {\mathcal H}}_n^{k_s}$
. Hence, there is
$t\in s^n{\mathbb Z}\setminus {\widetilde {\mathcal H}}_n^{k_s}$
. Hence, there is
![]() $b\in S_n\cup \{\bar s^n\}$
such that
$b\in S_n\cup \{\bar s^n\}$
such that
![]() $s^n\vee b\mid \gcd (t,\tilde {\tau }^{(s)})$
.
$s^n\vee b\mid \gcd (t,\tilde {\tau }^{(s)})$
.
-
(1) If the first inclusion in equation (52) is strict, there exists
 $t\in (s^n{\mathbb Z}\setminus {\widetilde {\mathcal H}}_n^{k_s})\setminus {\mathcal M}_{S_n}$
. Hence,
$t\in (s^n{\mathbb Z}\setminus {\widetilde {\mathcal H}}_n^{k_s})\setminus {\mathcal M}_{S_n}$
. Hence,
 $s^n\vee \bar s^n\mid \gcd (t,\tilde {\tau }^{(s)})$
.
$s^n\vee \bar s^n\mid \gcd (t,\tilde {\tau }^{(s)})$
. -
(2) The same arguments apply when the roles of s and
 $\bar s$
are interchanged.
$\bar s$
are interchanged.
Therefore, if
![]() $2^n{\mathbb Z}\cap {\mathcal M}_{S_n}\subsetneq 2^n{\mathbb Z}\setminus {\widetilde {\mathcal H}}_n^{k_2}$
or
$2^n{\mathbb Z}\cap {\mathcal M}_{S_n}\subsetneq 2^n{\mathbb Z}\setminus {\widetilde {\mathcal H}}_n^{k_2}$
or
![]() $3^n{\mathbb Z}\cap {\mathcal M}_{S_n}\subsetneq 3^n{\mathbb Z}\setminus {\widetilde {\mathcal H}}_n^{k_{3}}$
, then
$3^n{\mathbb Z}\cap {\mathcal M}_{S_n}\subsetneq 3^n{\mathbb Z}\setminus {\widetilde {\mathcal H}}_n^{k_{3}}$
, then
![]() $3^n\mid \gcd (\tilde {\tau }^{(2)}, \tilde {\tau }^{(3)})$
or
$3^n\mid \gcd (\tilde {\tau }^{(2)}, \tilde {\tau }^{(3)})$
or
![]() $2^n\mid \gcd (\tilde {\tau }^{(2)},\tilde {\tau }^{(3)})$
, respectively, and we are done.
$2^n\mid \gcd (\tilde {\tau }^{(2)},\tilde {\tau }^{(3)})$
, respectively, and we are done.
It remains to treat the case where
![]() $2^n{\mathbb Z}\cap {\mathcal M}_{S_n}= 2^n{\mathbb Z}\setminus {\widetilde {\mathcal H}}_n^{k_2}$
and
$2^n{\mathbb Z}\cap {\mathcal M}_{S_n}= 2^n{\mathbb Z}\setminus {\widetilde {\mathcal H}}_n^{k_2}$
and
![]() $3^n{\mathbb Z}\cap {\mathcal M}_{S_n}= 3^n{\mathbb Z}\setminus {\widetilde {\mathcal H}}_n^{k_{3}}$
. In this case,
$3^n{\mathbb Z}\cap {\mathcal M}_{S_n}= 3^n{\mathbb Z}\setminus {\widetilde {\mathcal H}}_n^{k_{3}}$
. In this case,
![]() $\tilde {\tau }^{(s)}$
is the smallest period of
$\tilde {\tau }^{(s)}$
is the smallest period of
![]() $s^n{\mathbb Z}\setminus {\mathcal M}_{S_n}$
, so
$s^n{\mathbb Z}\setminus {\mathcal M}_{S_n}$
, so
![]() $\tilde {\tau }^{(s)}=s^n\cdot \operatorname {lcm}((S_n^{\div s^n})^{\textrm {prim}})$
for
$\tilde {\tau }^{(s)}=s^n\cdot \operatorname {lcm}((S_n^{\div s^n})^{\textrm {prim}})$
for
![]() $s=2,3$
by Lemma 2.26(a), where
$s=2,3$
by Lemma 2.26(a), where
![]() $S_n^{\div 2^n}=\{c_i,3^id_i: 1\le i\le n\}$
and
$S_n^{\div 2^n}=\{c_i,3^id_i: 1\le i\le n\}$
and
![]() $S_n^{\div 3^n}=\{2^ic_i,d_i: 1\le i\le n\}$
.
$S_n^{\div 3^n}=\{2^ic_i,d_i: 1\le i\le n\}$
.
-
(a) If there are infinitely many
 $i\in {\mathbb N}$
such that
$i\in {\mathbb N}$
such that
 $c_i\nmid d_i$
, then there are infinitely many
$c_i\nmid d_i$
, then there are infinitely many
 $n\in {\mathbb N}$
such that
$n\in {\mathbb N}$
such that
 $3^n\mid \operatorname {lcm}((S_n^{\div 2^n})^{\textrm {prim}})$
, so that
$3^n\mid \operatorname {lcm}((S_n^{\div 2^n})^{\textrm {prim}})$
, so that
 $3^n\mid \gcd (\tilde {\tau }^{(2)},\tilde {\tau }^{(3)})$
.
$3^n\mid \gcd (\tilde {\tau }^{(2)},\tilde {\tau }^{(3)})$
. -
(b) Analogously, if there are infinitely many
 $i\in {\mathbb N}$
such that
$i\in {\mathbb N}$
such that
 $d_i \nmid c_i$
, then there are infinitely many
$d_i \nmid c_i$
, then there are infinitely many
 $n\in {\mathbb N}$
such that
$n\in {\mathbb N}$
such that
 $2^n\mid \operatorname {lcm}((S_n^{\div 3^n})^{\textrm {prim}})$
, so that
$2^n\mid \operatorname {lcm}((S_n^{\div 3^n})^{\textrm {prim}})$
, so that
 $2^n\mid \gcd (\tilde {\tau }^{(2)},\tilde {\tau }^{(3)})$
.
$2^n\mid \gcd (\tilde {\tau }^{(2)},\tilde {\tau }^{(3)})$
. -
(c) It remains to treat the case where
 $c_i=d_i$
except for finitely many
$c_i=d_i$
except for finitely many
 $i\in {\mathbb N}$
, say for
$i\in {\mathbb N}$
, say for
 $i<N$
. Then,
$i<N$
. Then,
 $c_N\cdot \cdots \cdot c_n\mid \gcd (\tilde {\tau }^{(2)},\tilde {\tau }^{(3)})$
for all
$c_N\cdot \cdots \cdot c_n\mid \gcd (\tilde {\tau }^{(2)},\tilde {\tau }^{(3)})$
for all
 $n\ge N$
.
$n\ge N$
.
We complete this example by showing (for suitable choices of
![]() $c_n=d_n$
) that conditions (Seh) and hence also (D) are violated. Suppose that
$c_n=d_n$
) that conditions (Seh) and hence also (D) are violated. Suppose that
![]() $\prod _{n\in {\mathbb N}}(1-{1}/{c_n})>\tfrac 12$
. Then, for any
$\prod _{n\in {\mathbb N}}(1-{1}/{c_n})>\tfrac 12$
. Then, for any
![]() $n\geq 1$
, the equation
$n\geq 1$
, the equation
![]() $3^nT-2^nM=1$
has solutions
$3^nT-2^nM=1$
has solutions
![]() $T,M$
with
$T,M$
with
so that there are holes with distance 1 (in the sense of [Reference Bułatek and Kwiatkowski2]), see Proposition 3.7. Indeed, there is a unique solution
![]() $X_0\in \{1,\ldots ,6^n-1\}$
of the equations
$X_0\in \{1,\ldots ,6^n-1\}$
of the equations
![]() $X\equiv 1\,\mod 2^n$
and
$X\equiv 1\,\mod 2^n$
and
![]() $X\equiv 0\,\mod 3^n$
. For
$X\equiv 0\,\mod 3^n$
. For
![]() $k=0,\ldots ,c_1\cdots c_n-1$
, let
$k=0,\ldots ,c_1\cdots c_n-1$
, let
![]() $X_k=X_0+k6^n$
,
$X_k=X_0+k6^n$
,
![]() $T_k={X_k}/{3^n}$
and
$T_k={X_k}/{3^n}$
and
![]() $M_k={X_k-1}/{2^n}$
. As all
$M_k={X_k-1}/{2^n}$
. As all
![]() $X_k$
are further solutions of the same two equations, and as the
$X_k$
are further solutions of the same two equations, and as the
![]() $c_i$
are pairwise coprime and also coprime to
$c_i$
are pairwise coprime and also coprime to
![]() $2$
and to
$2$
and to
![]() $3$
, exactly
$3$
, exactly
![]() $\gamma _n:=c_1\cdots c_n\prod _{i=1}^n(1-{1}/{c_i})$
of these solutions are
$\gamma _n:=c_1\cdots c_n\prod _{i=1}^n(1-{1}/{c_i})$
of these solutions are
![]() $\{c_1,\ldots ,c_n\}$
-free, and also exactly
$\{c_1,\ldots ,c_n\}$
-free, and also exactly
![]() $\gamma _n$
of the
$\gamma _n$
of the
![]() $c_1\cdots c_n$
numbers
$c_1\cdots c_n$
numbers
![]() $X_k-1$
are
$X_k-1$
are
![]() $\{c_1,\ldots ,c_n\}$
-free. Hence, exactly
$\{c_1,\ldots ,c_n\}$
-free. Hence, exactly
![]() $\gamma _n$
of the numbers
$\gamma _n$
of the numbers
![]() $T_k$
and
$T_k$
and
![]() $\gamma _n$
of the numbers
$\gamma _n$
of the numbers
![]() $M_k$
are
$M_k$
are
![]() $\{c_1,\ldots ,c_n\}$
-free. Since
$\{c_1,\ldots ,c_n\}$
-free. Since
![]() $2\gamma _n>c_1\cdots c_n$
, there exists at least one
$2\gamma _n>c_1\cdots c_n$
, there exists at least one
![]() $k\in \{0,\ldots ,c_1\cdots c_n-1\}$
such that
$k\in \{0,\ldots ,c_1\cdots c_n-1\}$
such that
![]() $T_k$
and
$T_k$
and
![]() $M_k$
are
$M_k$
are
![]() $\{c_1,\ldots ,c_n\}$
-free. This proves the claim.
$\{c_1,\ldots ,c_n\}$
-free. This proves the claim.
3.4 Non-trivial centralizer
The purpose of this section is to treat simple examples of the type
where
![]() $N\in {\mathbb N}\cup \{\infty \}$
, and the numbers
$N\in {\mathbb N}\cup \{\infty \}$
, and the numbers
![]() $c_n$
are odd and pairwise coprime. Observe that
$c_n$
are odd and pairwise coprime. Observe that
![]() ${\mathcal B}_1^1$
and
${\mathcal B}_1^1$
and
![]() ${\mathcal B}_1^2$
are the sets
${\mathcal B}_1^2$
are the sets
![]() ${\mathcal B}_1$
and
${\mathcal B}_1$
and
![]() ${\mathcal B}_1'$
from the introduction, respectively. Let
${\mathcal B}_1'$
from the introduction, respectively. Let
![]() $S_n=\{2^kc_k:k\leqslant n\}\cup \{2^{k-1}c_k^2: k\leqslant \min \{n,N-1\}\}$
. Then,
$S_n=\{2^kc_k:k\leqslant n\}\cup \{2^{k-1}c_k^2: k\leqslant \min \{n,N-1\}\}$
. Then,
![]() $\operatorname {lcm}(S_n)=2^nc_1^2\ldots c_n^2$
for
$\operatorname {lcm}(S_n)=2^nc_1^2\ldots c_n^2$
for
![]() $n<N$
,
$n<N$
,
![]() $\operatorname {lcm}(S_n)=2^nc_1^2\ldots c_{N-1}^2c_N\ldots c_n$
for
$\operatorname {lcm}(S_n)=2^nc_1^2\ldots c_{N-1}^2c_N\ldots c_n$
for
![]() $n\geq N$
and
$n\geq N$
and
![]() ${\mathcal A}_{S_n}=S_n\cup \{2^n\}$
, so that
${\mathcal A}_{S_n}=S_n\cup \{2^n\}$
, so that
![]() ${\mathcal A}_{S_n}\setminus S_n={\mathcal A}_{S_n}^{\infty }={\mathcal A}_{S_n}^{\infty ,p}=\{2^n\}$
. As
${\mathcal A}_{S_n}\setminus S_n={\mathcal A}_{S_n}^{\infty }={\mathcal A}_{S_n}^{\infty ,p}=\{2^n\}$
. As
![]() $\min ({\mathcal A}_{S_n}\setminus S_n)$
obviously tends to infinity, these are examples of Toeplitz type by Proposition 3.5(d). Along the same lines as in Example 3.21, one can show that all periods are essential and
$\min ({\mathcal A}_{S_n}\setminus S_n)$
obviously tends to infinity, these are examples of Toeplitz type by Proposition 3.5(d). Along the same lines as in Example 3.21, one can show that all periods are essential and
![]() ${\widetilde {\mathcal H}}_n={\mathcal H}_n=2^n{\mathbb Z}\setminus {\mathcal M}_{S_n}$
.
${\widetilde {\mathcal H}}_n={\mathcal H}_n=2^n{\mathbb Z}\setminus {\mathcal M}_{S_n}$
.
Let
![]() $\tilde {\tau }_n$
be the smallest period of
$\tilde {\tau }_n$
be the smallest period of
![]() ${\widetilde {\mathcal H}}_n={\mathcal H}_n$
. We will show that
${\widetilde {\mathcal H}}_n={\mathcal H}_n$
. We will show that
![]() $\tilde {\tau }_n={\operatorname {lcm}(S_n)}/{c_1\ldots c_{N-1}}$
. Notice that
$\tilde {\tau }_n={\operatorname {lcm}(S_n)}/{c_1\ldots c_{N-1}}$
. Notice that
![]() $2^nk\in {\mathcal M}_{S_n}$
if and only if
$2^nk\in {\mathcal M}_{S_n}$
if and only if
![]() $2^nk\in {\mathcal M}_{\{c_1,\ldots ,c_n\}}$
. So,
$2^nk\in {\mathcal M}_{\{c_1,\ldots ,c_n\}}$
. So,
![]() ${\widetilde {\mathcal H}}_n=2^n{\mathbb Z}\setminus {\mathcal M}_{\{c_1,\ldots ,c_n\}}$
. Since
${\widetilde {\mathcal H}}_n=2^n{\mathbb Z}\setminus {\mathcal M}_{\{c_1,\ldots ,c_n\}}$
. Since
![]() $c_1,\ldots ,c_n$
are odd and pairwise coprime, Lemma 2.26(a) implies
$c_1,\ldots ,c_n$
are odd and pairwise coprime, Lemma 2.26(a) implies
![]() $\tilde {\tau }_n=2^nc_1\ldots c_n={\operatorname {lcm}(S_n)}/{c_1\ldots c_{N-1}}$
.
$\tilde {\tau }_n=2^nc_1\ldots c_n={\operatorname {lcm}(S_n)}/{c_1\ldots c_{N-1}}$
.
Notice that property (TI) holds for
![]() $A_n={\mathcal A}_{S_n}^{\infty ,p}$
. By Proposition 2.20, there exists a unique
$A_n={\mathcal A}_{S_n}^{\infty ,p}$
. By Proposition 2.20, there exists a unique
![]() $k\in {\mathbb Z}$
such that
$k\in {\mathbb Z}$
such that
![]() $\partial W+y_F\subseteq \partial W+\Delta (k)$
, and
$\partial W+y_F\subseteq \partial W+\Delta (k)$
, and
![]() ${\operatorname {lcm}(S_n)}/{c_1\ldots c_{N-1}}=\tilde {\tau }_n\mid (y_F)_{S_n}-k$
. It follows at once that
${\operatorname {lcm}(S_n)}/{c_1\ldots c_{N-1}}=\tilde {\tau }_n\mid (y_F)_{S_n}-k$
. It follows at once that
![]() $y_F=\Delta (k)$
for
$y_F=\Delta (k)$
for
![]() ${\mathcal B}_1^1$
and that
${\mathcal B}_1^1$
and that
![]() $y_F-\Delta (k)$
has order at most
$y_F-\Delta (k)$
has order at most
![]() $\prod _{i=1}^{N-1}c_i$
in G in the case of
$\prod _{i=1}^{N-1}c_i$
in G in the case of
![]() ${\mathcal B}_1^N$
and finite N, while
${\mathcal B}_1^N$
and finite N, while
![]() $y_F-\Delta (k)$
may have any order in the case of
$y_F-\Delta (k)$
may have any order in the case of
![]() ${\mathcal B}_1^\infty $
.
${\mathcal B}_1^\infty $
.
In the remainder of this subsection, we show that such non-trivial centralizers as allowed above really exist. To this end, fix
![]() $N\in {\mathbb N}\cup \{\infty \}$
and
$N\in {\mathbb N}\cup \{\infty \}$
and
![]() $1\leq \ell <N$
, and consider
$1\leq \ell <N$
, and consider
![]() ${\mathcal B}_1^N$
as before. Denote
${\mathcal B}_1^N$
as before. Denote
![]() $p_m=\operatorname {lcm}(S_m)$
for any
$p_m=\operatorname {lcm}(S_m)$
for any
![]() $m\in {\mathbb N}$
. Let
$m\in {\mathbb N}$
. Let
We define
![]() $F_\ell \colon X_\eta \to \{0,1\}^{\mathbb Z}$
by
$F_\ell \colon X_\eta \to \{0,1\}^{\mathbb Z}$
by
 $$ \begin{align*} (F_\ell x)_s= \begin{cases} x_s&\text{ if }s\not\in c_\ell{\mathbb Z}-\pi_{\operatorname{lcm}(S_\ell)}(x),\\ x_{s+q}&\text{ if }s\in c_\ell{\mathbb Z}-\pi_{\operatorname{lcm}(S_\ell)}(x). \end{cases} \end{align*} $$
$$ \begin{align*} (F_\ell x)_s= \begin{cases} x_s&\text{ if }s\not\in c_\ell{\mathbb Z}-\pi_{\operatorname{lcm}(S_\ell)}(x),\\ x_{s+q}&\text{ if }s\in c_\ell{\mathbb Z}-\pi_{\operatorname{lcm}(S_\ell)}(x). \end{cases} \end{align*} $$
This map is continuous, because
![]() $\pi _{\operatorname {lcm}(S_\ell )}$
, the
$\pi _{\operatorname {lcm}(S_\ell )}$
, the
![]() $\ell $
th coordinate of the MEF map, is continuous. Recall that the MEF map
$\ell $
th coordinate of the MEF map, is continuous. Recall that the MEF map
![]() $\pi :X_\eta \to G$
is chosen such that
$\pi :X_\eta \to G$
is chosen such that
![]() $\pi (\eta )=\Delta (0)$
. As
$\pi (\eta )=\Delta (0)$
. As
![]() $\Delta (0)\in C_\phi $
[Reference Kasjan, Keller and Lemańczyk18, Lemma 3.5] for
$\Delta (0)\in C_\phi $
[Reference Kasjan, Keller and Lemańczyk18, Lemma 3.5] for
![]() ${\mathcal B}$
-free Toeplitz subshifts,
${\mathcal B}$
-free Toeplitz subshifts,
![]() $|\pi ^{-1}\{\pi (F(\eta ))\}|=|\pi ^{-1}\{\pi (\eta )\}|=1$
, that is,
$|\pi ^{-1}\{\pi (F(\eta ))\}|=|\pi ^{-1}\{\pi (\eta )\}|=1$
, that is,
![]() $\pi (F(\eta ))\in C_\phi $
and, observing also Remark 3.1,
$\pi (F(\eta ))\in C_\phi $
and, observing also Remark 3.1,
Lemma 3.22. Define
![]() $y\in G$
by
$y\in G$
by
 $$ \begin{align} y_b= \begin{cases}0&\text{if}\;b\neq 2^{\ell-1}c_{\ell}^2,\\ q&\text{if}\;b= 2^{\ell-1}c_{\ell}^2. \end{cases} \end{align} $$
$$ \begin{align} y_b= \begin{cases}0&\text{if}\;b\neq 2^{\ell-1}c_{\ell}^2,\\ q&\text{if}\;b= 2^{\ell-1}c_{\ell}^2. \end{cases} \end{align} $$
Then y coincides with the rotation
![]() $y_{F_\ell }$
associated to
$y_{F_\ell }$
associated to
![]() $F_\ell $
.
$F_\ell $
.
Proof. As
![]() $\pi _{\operatorname {lcm}(S_\ell )}(\eta )=0$
,
$\pi _{\operatorname {lcm}(S_\ell )}(\eta )=0$
,
 $$ \begin{align*} (F_\ell\eta)_s = \begin{cases} \eta_s&\text{if}\;s\notin c_{\ell}{\mathbb Z},\\ \eta_{s+q}&\text{if}\;s\in c_{\ell}{\mathbb Z}. \end{cases} \end{align*} $$
$$ \begin{align*} (F_\ell\eta)_s = \begin{cases} \eta_s&\text{if}\;s\notin c_{\ell}{\mathbb Z},\\ \eta_{s+q}&\text{if}\;s\in c_{\ell}{\mathbb Z}. \end{cases} \end{align*} $$
In view of equation (55) and of the injectivity of
![]() $\phi $
(see Remark 3.1), we must show that
$\phi $
(see Remark 3.1), we must show that
![]() $(F_\ell \eta )_s=0$
if and only if
$(F_\ell \eta )_s=0$
if and only if
![]() $s\in \bigcup _{b\in {\mathcal B}}(b{\mathbb Z}-y_b)$
for all
$s\in \bigcup _{b\in {\mathcal B}}(b{\mathbb Z}-y_b)$
for all
![]() $s\in {\mathbb Z}$
.
$s\in {\mathbb Z}$
.
(1) Assume that
![]() $s\notin c_{\ell }{\mathbb Z}$
. Then,
$s\notin c_{\ell }{\mathbb Z}$
. Then,
 $$ \begin{align*} (F_\ell\eta)_s=0\Leftrightarrow \eta_s=0 \Leftrightarrow s\in{\mathcal M}_{{\mathcal B}} \Leftrightarrow s\in 2^{\ell-1}c_\ell^2{\mathbb Z}\cup\bigcup_{b\in{\mathcal B}\setminus\{2^{\ell-1}c_\ell^2\}}(b{\mathbb Z}-y_b). \end{align*} $$
$$ \begin{align*} (F_\ell\eta)_s=0\Leftrightarrow \eta_s=0 \Leftrightarrow s\in{\mathcal M}_{{\mathcal B}} \Leftrightarrow s\in 2^{\ell-1}c_\ell^2{\mathbb Z}\cup\bigcup_{b\in{\mathcal B}\setminus\{2^{\ell-1}c_\ell^2\}}(b{\mathbb Z}-y_b). \end{align*} $$
As
![]() $s\not \in c_\ell {\mathbb Z}$
by assumption and
$s\not \in c_\ell {\mathbb Z}$
by assumption and
![]() $s+q\not \in c_\ell {\mathbb Z}$
because
$s+q\not \in c_\ell {\mathbb Z}$
because
![]() $c_\ell \mid q$
, this is equivalent to
$c_\ell \mid q$
, this is equivalent to
![]() $ s\in \bigcup _{b\in {\mathcal B}}(b{\mathbb Z}-y_b). $
$ s\in \bigcup _{b\in {\mathcal B}}(b{\mathbb Z}-y_b). $
(2) Now assume that
![]() $s\in c_{\ell }{\mathbb Z}$
. Let
$s\in c_{\ell }{\mathbb Z}$
. Let
![]() $T=\{2c_1,\ldots ,2^{\ell }c_{\ell }, c_1^2,\ldots ,2^{\ell -2}c_{\ell -1}^2\}$
. Observe that
$T=\{2c_1,\ldots ,2^{\ell }c_{\ell }, c_1^2,\ldots ,2^{\ell -2}c_{\ell -1}^2\}$
. Observe that
![]() $q=\operatorname {lcm}(T)$
and T is saturated. Observe also that
$q=\operatorname {lcm}(T)$
and T is saturated. Observe also that
![]() $(F_\ell \eta )_s=0$
if and only if
$(F_\ell \eta )_s=0$
if and only if
![]() $s+q\in {\mathcal M}_{{\mathcal B}}$
.
$s+q\in {\mathcal M}_{{\mathcal B}}$
.
So let
![]() $b\in {\mathcal B}$
and assume that
$b\in {\mathcal B}$
and assume that
![]() $b\mid s+q$
.
$b\mid s+q$
.
-
(i) If
 $b\in T$
, then
$b\in T$
, then
 $b\mid q$
, and hence
$b\mid q$
, and hence
 $s\in b{\mathbb Z}=b{\mathbb Z}-y_b$
.
$s\in b{\mathbb Z}=b{\mathbb Z}-y_b$
. -
(ii) If
 $b=2^{\ell -1}c^2_{\ell }$
, then
$b=2^{\ell -1}c^2_{\ell }$
, then
 $s\in b{\mathbb Z}-q=b{\mathbb Z}-y_b$
.
$s\in b{\mathbb Z}-q=b{\mathbb Z}-y_b$
. -
(iii) If
 $b\in {\mathcal B}\setminus (T\cup \{2^{\ell -1}c_{\ell }^2\})$
, then
$b\in {\mathcal B}\setminus (T\cup \{2^{\ell -1}c_{\ell }^2\})$
, then
 $2^{\ell }\mid b$
and, as
$2^{\ell }\mid b$
and, as
 $c_{\ell }\mid s$
and
$c_{\ell }\mid s$
and
 $2^{\ell }c_{\ell }\mid q$
, it follows that
$2^{\ell }c_{\ell }\mid q$
, it follows that
 $s\in 2^{\ell }c_{\ell }{\mathbb Z}=2^{\ell }c_{\ell }{\mathbb Z}-y_{2^{\ell }c_{\ell }}$
.
$s\in 2^{\ell }c_{\ell }{\mathbb Z}=2^{\ell }c_{\ell }{\mathbb Z}-y_{2^{\ell }c_{\ell }}$
.
We have proved that
![]() $ s\in \bigcup _{b\in {\mathcal B}}(b{\mathbb Z}-y_b). $
$ s\in \bigcup _{b\in {\mathcal B}}(b{\mathbb Z}-y_b). $
It remains to prove that if
![]() $s\in c_{\ell }{\mathbb Z}$
and
$s\in c_{\ell }{\mathbb Z}$
and
![]() $s\in \bigcup _{b\in {\mathcal B}}(b{\mathbb Z}-y_b)$
, then
$s\in \bigcup _{b\in {\mathcal B}}(b{\mathbb Z}-y_b)$
, then
![]() $s+q\in {\mathcal M}_{{\mathcal B}}$
. Indeed,
$s+q\in {\mathcal M}_{{\mathcal B}}$
. Indeed,
 $$ \begin{align*} s+q &\in \bigg(c_{\ell}{\mathbb Z}\cap \bigcup_{b\in{\mathcal B}}(b{\mathbb Z}-y_b)\bigg)+q\\ &= \bigg(\bigcup_{b\in T}(b\vee c_{\ell}){\mathbb Z}+q\bigg)\ \cup\ 2^{\ell-1}c^2_{\ell}{\mathbb Z}\ \cup\ \bigg(\bigcup_{b\in{\mathcal B}\setminus (T\cup\{2^{\ell-1}c^2_{\ell}\})}c_{\ell}b{\mathbb Z}+q\bigg)\\ &\subseteq \bigcup_{b\in T}b{\mathbb Z}\ \cup\ 2^{\ell-1}c^2_{\ell}{\mathbb Z}\ \cup\ 2^\ell c_\ell{\mathbb Z}\subseteq{\mathcal M}_{\mathcal B}, \end{align*} $$
$$ \begin{align*} s+q &\in \bigg(c_{\ell}{\mathbb Z}\cap \bigcup_{b\in{\mathcal B}}(b{\mathbb Z}-y_b)\bigg)+q\\ &= \bigg(\bigcup_{b\in T}(b\vee c_{\ell}){\mathbb Z}+q\bigg)\ \cup\ 2^{\ell-1}c^2_{\ell}{\mathbb Z}\ \cup\ \bigg(\bigcup_{b\in{\mathcal B}\setminus (T\cup\{2^{\ell-1}c^2_{\ell}\})}c_{\ell}b{\mathbb Z}+q\bigg)\\ &\subseteq \bigcup_{b\in T}b{\mathbb Z}\ \cup\ 2^{\ell-1}c^2_{\ell}{\mathbb Z}\ \cup\ 2^\ell c_\ell{\mathbb Z}\subseteq{\mathcal M}_{\mathcal B}, \end{align*} $$
because
![]() $\operatorname {lcm}(T\cup \{c_{\ell }\})=q$
and
$\operatorname {lcm}(T\cup \{c_{\ell }\})=q$
and
![]() $2^{\ell }\mid b$
for each
$2^{\ell }\mid b$
for each
![]() $b\in {\mathcal B}\setminus (T \cup \{2^{\ell -1}c_{\ell }^2\})$
.
$b\in {\mathcal B}\setminus (T \cup \{2^{\ell -1}c_{\ell }^2\})$
.
Proposition 3.23. For each
![]() $1\leqslant \ell <N\leqslant \infty $
, the map
$1\leqslant \ell <N\leqslant \infty $
, the map
![]() $F_\ell $
belongs to the centralizer of the
$F_\ell $
belongs to the centralizer of the
![]() ${\mathcal B}_1^N$
-free subshift. It satisfies
${\mathcal B}_1^N$
-free subshift. It satisfies
![]() $F_\ell ^{c_\ell }=\operatorname {id}_{X_\eta }$
, but
$F_\ell ^{c_\ell }=\operatorname {id}_{X_\eta }$
, but
![]() $F_\ell ^i\neq \operatorname {id}_{X_\eta }$
for all
$F_\ell ^i\neq \operatorname {id}_{X_\eta }$
for all
![]() $1\leqslant i<c_\ell $
.
$1\leqslant i<c_\ell $
.
Proof. We show first that
![]() $F_\ell (\eta )\in X_{\eta }$
. Recall that
$F_\ell (\eta )\in X_{\eta }$
. Recall that
![]() $\pi _{\operatorname {lcm}(S_\ell )}(\eta )=0$
. Fix
$\pi _{\operatorname {lcm}(S_\ell )}(\eta )=0$
. Fix
![]() $n\in {\mathbb N}$
and choose
$n\in {\mathbb N}$
and choose
![]() $t\geqslant \ell $
such that
$t\geqslant \ell $
such that
![]() $2^t>n$
. As
$2^t>n$
. As
![]() $\gcd (p_\ell ,{p_t}/{c_\ell })=q$
, there exists
$\gcd (p_\ell ,{p_t}/{c_\ell })=q$
, there exists
![]() $z\in {\mathbb Z}$
such that
$z\in {\mathbb Z}$
such that
We claim that
![]() $(F_\ell \eta )[-n,n]=\eta [-n+z,n+z]$
. Let
$(F_\ell \eta )[-n,n]=\eta [-n+z,n+z]$
. Let
![]() $s\in [-n,n]$
. There are two cases:
$s\in [-n,n]$
. There are two cases:
(1)
![]() $s\notin c_\ell {\mathbb Z}$
. Then,
$s\notin c_\ell {\mathbb Z}$
. Then,
![]() $2^{\ell -1}c_\ell ^2$
and
$2^{\ell -1}c_\ell ^2$
and
![]() $2^\ell c_\ell $
do not divide neither s nor
$2^\ell c_\ell $
do not divide neither s nor
![]() $s+z$
by the second of the congruences in equation (57).
$s+z$
by the second of the congruences in equation (57).
-
(i) Assume that
 $\eta _s=0$
. Then,
$\eta _s=0$
. Then,
 $2^{j-\varepsilon }c_j^{1+\varepsilon }\mid s$
for some
$2^{j-\varepsilon }c_j^{1+\varepsilon }\mid s$
for some
 $j\neq \ell $
and
$j\neq \ell $
and
 $\varepsilon \in \{0,1\}$
. Observe that
$\varepsilon \in \{0,1\}$
. Observe that
 $j\leqslant t$
, since
$j\leqslant t$
, since
 $|s|\le n<2^t$
. Then,
$|s|\le n<2^t$
. Then,
 $2^{j-\varepsilon }c_j^{1+\varepsilon }\mid s+z$
by the first of the congruences in equation (57), and hence
$2^{j-\varepsilon }c_j^{1+\varepsilon }\mid s+z$
by the first of the congruences in equation (57), and hence
 $\eta _{s+z}=0$
.
$\eta _{s+z}=0$
. -
(ii) Conversely, assume that
 $\eta _{s+z}=0$
. Then,
$\eta _{s+z}=0$
. Then,
 $2^{j-\varepsilon }c_j^{1+\varepsilon }\mid s+z$
for some
$2^{j-\varepsilon }c_j^{1+\varepsilon }\mid s+z$
for some
 $j\neq \ell $
and
$j\neq \ell $
and
 $\varepsilon \in \{0,1\}$
, and if
$\varepsilon \in \{0,1\}$
, and if
 $j\le t$
, then
$j\le t$
, then
 $2^{j-\varepsilon }c_j^{1+\varepsilon }\mid s$
by the first of the congruences in equation (57), and hence
$2^{j-\varepsilon }c_j^{1+\varepsilon }\mid s$
by the first of the congruences in equation (57), and hence
 $\eta _s=0$
. However,
$\eta _s=0$
. However,
 $j>t$
is impossible, because then
$j>t$
is impossible, because then
 $2^t\mid s+z$
, so that
$2^t\mid s+z$
, so that
 $2^t\mid s$
by the first of the congruences in equation (57) again, in contradiction to
$2^t\mid s$
by the first of the congruences in equation (57) again, in contradiction to
 $0<|s|<2^t$
.
$0<|s|<2^t$
.
We have shown that
![]() $\eta _{s+z}=\eta _s=(F_\ell \eta )_s$
.
$\eta _{s+z}=\eta _s=(F_\ell \eta )_s$
.
(2)
![]() $s\in c_\ell {\mathbb Z}$
. We use the fact that
$s\in c_\ell {\mathbb Z}$
. We use the fact that
![]() $z\equiv q \,\mod p_\ell $
in view of equation (57) repeatedly.
$z\equiv q \,\mod p_\ell $
in view of equation (57) repeatedly.
-
(i) Assume that
 $\eta _{s+q}=0$
, so that
$\eta _{s+q}=0$
, so that
 $2^{j-\varepsilon }c_j^{1+\varepsilon }\mid s+q$
for some
$2^{j-\varepsilon }c_j^{1+\varepsilon }\mid s+q$
for some
 $j\in {\mathbb N}$
and
$j\in {\mathbb N}$
and
 $\varepsilon \in \{0,1\}$
. If
$\varepsilon \in \{0,1\}$
. If
 $j\le \ell $
, then
$j\le \ell $
, then
 $2^{j-\varepsilon }c_j^{1+\varepsilon }\mid s+z$
because
$2^{j-\varepsilon }c_j^{1+\varepsilon }\mid s+z$
because
 $z\equiv q \,\mod p_\ell $
. If
$z\equiv q \,\mod p_\ell $
. If
 $j>\ell $
, then
$j>\ell $
, then
 $2^{\ell }\mid s+q$
, and hence
$2^{\ell }\mid s+q$
, and hence
 $2^{\ell }\mid s$
and
$2^{\ell }\mid s$
and
 $2^{\ell }c_\ell \mid s$
. As
$2^{\ell }c_\ell \mid s$
. As
 $z\equiv q \,\mod p_\ell $
, also
$z\equiv q \,\mod p_\ell $
, also
 $2^\ell c_\ell \mid z$
, so that
$2^\ell c_\ell \mid z$
, so that
 $2^\ell c_\ell \mid s+z$
. In both cases,
$2^\ell c_\ell \mid s+z$
. In both cases,
 $\eta _{s+z}=0$
.
$\eta _{s+z}=0$
. -
(ii) Conversely, assume that
 $\eta _{s+z}=0$
. The same arguments as before, with roles of q and z interchanged, show that
$\eta _{s+z}=0$
. The same arguments as before, with roles of q and z interchanged, show that
 $\eta _{s+q}=0$
.
$\eta _{s+q}=0$
.
We have shown that
![]() $\eta _{s+z}=\eta _{s+q}=(F_\ell \eta )_s$
, and thus the claim follows.
$\eta _{s+z}=\eta _{s+q}=(F_\ell \eta )_s$
, and thus the claim follows.
As
![]() $\pi (\eta )=\Delta (0)$
, we have
$\pi (\eta )=\Delta (0)$
, we have
![]() $\pi (\sigma ^k\eta )=\Delta (k)$
for any
$\pi (\sigma ^k\eta )=\Delta (k)$
for any
![]() $k\in {\mathbb Z}$
. So,
$k\in {\mathbb Z}$
. So,
![]() $\pi _{\operatorname {lcm}(S_\ell )}(\sigma ^k\eta )=k\,\mod p_\ell $
for any
$\pi _{\operatorname {lcm}(S_\ell )}(\sigma ^k\eta )=k\,\mod p_\ell $
for any
![]() $k\in {\mathbb Z}$
. Hence, for any
$k\in {\mathbb Z}$
. Hence, for any
![]() $k\in {\mathbb Z}$
,
$k\in {\mathbb Z}$
,
 $$ \begin{align*} (F_\ell(\sigma^k\eta))_s&=\begin{cases} (\sigma^k\eta)_s&\text{if }s\not\in c_\ell{\mathbb Z}-k,\\ (\sigma^k\eta)_{s+q}&\text{if }s\in c_\ell{\mathbb Z}-k, \end{cases}\\&=\begin{cases} \eta_{s+k}&\text{if }s+k\not\in c_\ell{\mathbb Z},\\ \eta_{s+q+k}&\text{if }s+k\in c_\ell{\mathbb Z}, \end{cases}=(F_\ell\eta)_{s+k}=(\sigma^k(F_\ell\eta))_s. \end{align*} $$
$$ \begin{align*} (F_\ell(\sigma^k\eta))_s&=\begin{cases} (\sigma^k\eta)_s&\text{if }s\not\in c_\ell{\mathbb Z}-k,\\ (\sigma^k\eta)_{s+q}&\text{if }s\in c_\ell{\mathbb Z}-k, \end{cases}\\&=\begin{cases} \eta_{s+k}&\text{if }s+k\not\in c_\ell{\mathbb Z},\\ \eta_{s+q+k}&\text{if }s+k\in c_\ell{\mathbb Z}, \end{cases}=(F_\ell\eta)_{s+k}=(\sigma^k(F_\ell\eta))_s. \end{align*} $$
So,
![]() $F_\ell (\sigma ^k\eta )\in X_\eta $
for each
$F_\ell (\sigma ^k\eta )\in X_\eta $
for each
![]() $k\in {\mathbb Z}$
. The denseness of the orbit of
$k\in {\mathbb Z}$
. The denseness of the orbit of
![]() $\eta $
and the continuity of
$\eta $
and the continuity of
![]() $F_\ell $
imply that
$F_\ell $
imply that
![]() $F_\ell (X_\eta )\subseteq X_\eta $
and
$F_\ell (X_\eta )\subseteq X_\eta $
and
![]() $F_\ell $
commutes with
$F_\ell $
commutes with
![]() $\sigma $
.
$\sigma $
.
Since
![]() $F_{\ell }$
corresponds to
$F_{\ell }$
corresponds to
![]() $y_{F_\ell }$
given by equation (56), and q has order
$y_{F_\ell }$
given by equation (56), and q has order
![]() $c_{\ell }$
in the group
$c_{\ell }$
in the group
![]() ${\mathbb Z}/2^{\ell -1}c^2_{\ell }{\mathbb Z}$
, it follows that
${\mathbb Z}/2^{\ell -1}c^2_{\ell }{\mathbb Z}$
, it follows that
![]() $F_{\ell }$
has order
$F_{\ell }$
has order
![]() $c_{\ell }$
.
$c_{\ell }$
.
This proves in particular that
![]() $F_\ell $
is a homeomorphism.
$F_\ell $
is a homeomorphism.
Remark 3.24. Consider the case
![]() $N<\infty $
. As the numbers
$N<\infty $
. As the numbers
![]() $c_1,\ldots ,c_{N-1}$
are pairwise coprime, the group generated by the automophisms
$c_1,\ldots ,c_{N-1}$
are pairwise coprime, the group generated by the automophisms
![]() $F_{1},\ldots ,F_{{N-1}}$
is cyclic of order
$F_{1},\ldots ,F_{{N-1}}$
is cyclic of order
![]() $c_1\ldots c_{N-1}$
. Let F be a generator of this group. Then, in view of Corollary 2.21,
$c_1\ldots c_{N-1}$
. Let F be a generator of this group. Then, in view of Corollary 2.21,
![]() $\operatorname {Aut}_\sigma (X_\eta )=\langle \sigma \rangle \oplus \langle F\rangle $
in the case of
$\operatorname {Aut}_\sigma (X_\eta )=\langle \sigma \rangle \oplus \langle F\rangle $
in the case of
![]() ${\mathcal B}^{N}_1$
.
${\mathcal B}^{N}_1$
.
Corollary 3.25. Consider
![]() ${\mathcal B}_1^\infty $
. Proposition 3.23 shows that the group
${\mathcal B}_1^\infty $
. Proposition 3.23 shows that the group
![]() $Aut_{\sigma }(X_{\eta })/\langle \sigma \rangle $
contains the infinite direct sum of finite cyclic groups
$Aut_{\sigma }(X_{\eta })/\langle \sigma \rangle $
contains the infinite direct sum of finite cyclic groups
Remark 3.26. One can show that the element
![]() $y\in G$
given by equation (56) satisfies the sufficient conditions from [Reference Bułatek and Kwiatkowski2, Theorem 1] for representing a (non-trivial) element of the centralizer of the
$y\in G$
given by equation (56) satisfies the sufficient conditions from [Reference Bułatek and Kwiatkowski2, Theorem 1] for representing a (non-trivial) element of the centralizer of the
![]() ${\mathcal B}_1^N$
-free subshift. However, the methods from [Reference Bułatek and Kwiatkowski2] do not limit the order of elements from this centralizer as in Theorem 2.8. It is shown in [Reference Bułatek and Kwiatkowski2] that Toeplitz subshifts with skeletons with equidistant holes have only elements of finite order in their centralizer. However, this does not apply to minimal
${\mathcal B}_1^N$
-free subshift. However, the methods from [Reference Bułatek and Kwiatkowski2] do not limit the order of elements from this centralizer as in Theorem 2.8. It is shown in [Reference Bułatek and Kwiatkowski2] that Toeplitz subshifts with skeletons with equidistant holes have only elements of finite order in their centralizer. However, this does not apply to minimal
![]() ${\mathcal B}$
-free subshifts, see Proposition 3.7.
${\mathcal B}$
-free subshifts, see Proposition 3.7.
3.5 Holes versus essential holes: examples
We start with an example for which there is no period structure such that all holes are essential and the centralizer is trivial.
Example 3.27. Assume that
![]() $c_1,\ldots ,c_n,\ldots ,q_1,\ldots ,q_n,\ldots $
are pairwise coprime natural numbers. Let
$c_1,\ldots ,c_n,\ldots ,q_1,\ldots ,q_n,\ldots $
are pairwise coprime natural numbers. Let
and set
![]() ${\mathcal B}=\{b_m:m\in {\mathbb N}\}$
. Let
${\mathcal B}=\{b_m:m\in {\mathbb N}\}$
. Let
![]() $(p_n)$
be any period structure for
$(p_n)$
be any period structure for
![]() $\eta =\eta _{{\mathcal B}}$
. Observe that for every
$\eta =\eta _{{\mathcal B}}$
. Observe that for every
![]() $m\in {\mathbb N}$
, there exists
$m\in {\mathbb N}$
, there exists
![]() $n,n'\in {\mathbb N}$
such that
$n,n'\in {\mathbb N}$
such that
Fix N such that
![]() $q_1|p_N$
and let
$q_1|p_N$
and let
Then,
![]() $q_{m+1}\nmid p_N$
and hence
$q_{m+1}\nmid p_N$
and hence
where
![]() $\varepsilon \in \{0,1\}$
. Note that
$\varepsilon \in \{0,1\}$
. Note that
We claim that
![]() $k\in {\mathcal H}_N\setminus {\widetilde {\mathcal H}}_N$
. Clearly,
$k\in {\mathcal H}_N\setminus {\widetilde {\mathcal H}}_N$
. Clearly,
![]() $k\in {\mathcal F}_{{\mathcal B}}$
, so
$k\in {\mathcal F}_{{\mathcal B}}$
, so
![]() $\eta _k=1$
. By the definition of k, it follows that
$\eta _k=1$
. By the definition of k, it follows that
![]() $(k+p_N{\mathbb Z})\cap b_{m+1}{\mathbb Z}\neq \emptyset $
, thus
$(k+p_N{\mathbb Z})\cap b_{m+1}{\mathbb Z}\neq \emptyset $
, thus
![]() $\eta $
is not constant along
$\eta $
is not constant along
![]() $k+p_N{\mathbb Z}$
and hence
$k+p_N{\mathbb Z}$
and hence
![]() $k\in {\mathcal H}_N$
. Now take
$k\in {\mathcal H}_N$
. Now take
![]() $n>N$
such that
$n>N$
such that
We claim that
![]() $(k+p_N{\mathbb Z})\cap {\mathcal H}_n=\emptyset $
. Let
$(k+p_N{\mathbb Z})\cap {\mathcal H}_n=\emptyset $
. Let
![]() $l\in {\mathbb Z}$
and assume first that
$l\in {\mathbb Z}$
and assume first that
![]() $k+lp_N\in {\mathcal F}_{{\mathcal B}}$
. Suppose that
$k+lp_N\in {\mathcal F}_{{\mathcal B}}$
. Suppose that
![]() $k+lp_N+l'p_n\in {\mathcal M}_{{\mathcal B}}$
for some
$k+lp_N+l'p_n\in {\mathcal M}_{{\mathcal B}}$
for some
![]() $l'\in {\mathbb Z}$
. So
$l'\in {\mathbb Z}$
. So
![]() $b\mid k+lp_N+l'p_n$
for some
$b\mid k+lp_N+l'p_n$
for some
![]() $b\in {\mathcal B}$
. By equations (58) and (59),
$b\in {\mathcal B}$
. By equations (58) and (59),
![]() $q_m\nmid b$
, so
$q_m\nmid b$
, so
![]() $b\in \{b_1,\ldots ,b_{m+1}\}$
. However then, by equation (59),
$b\in \{b_1,\ldots ,b_{m+1}\}$
. However then, by equation (59),
![]() $b\mid k+lp_N$
, which is a contradiction. It follows that
$b\mid k+lp_N$
, which is a contradiction. It follows that
![]() $k+lp_N\notin {\mathcal H}_n$
. Now assume that
$k+lp_N\notin {\mathcal H}_n$
. Now assume that
![]() $k+l p_N\in {\mathcal M}_{{\mathcal B}}$
. So,
$k+l p_N\in {\mathcal M}_{{\mathcal B}}$
. So,
![]() $b\mid k+l p_N$
for some
$b\mid k+l p_N$
for some
![]() $b\in {\mathcal B}$
. Then by equation (58),
$b\in {\mathcal B}$
. Then by equation (58),
![]() $b\in \{b_1,\ldots ,b_{m+1}\}$
, and hence
$b\in \{b_1,\ldots ,b_{m+1}\}$
, and hence
![]() $b\mid p_n$
and
$b\mid p_n$
and
![]() $k+lp_N+p_n{\mathbb Z}\subseteq {\mathcal M}_{{\mathcal B}}$
by equation (59). Again we see that
$k+lp_N+p_n{\mathbb Z}\subseteq {\mathcal M}_{{\mathcal B}}$
by equation (59). Again we see that
![]() $k+l p_N\notin {\mathcal H}_n$
. The claim follows.
$k+l p_N\notin {\mathcal H}_n$
. The claim follows.
Let
![]() $S_n=\{b_1,\ldots ,b_n\}$
. Then
$S_n=\{b_1,\ldots ,b_n\}$
. Then
![]() $p_n:=\operatorname {lcm}(S_n)=q_1\ldots q_nc_1\ldots {c_n}$
defines a period structure,
$p_n:=\operatorname {lcm}(S_n)=q_1\ldots q_nc_1\ldots {c_n}$
defines a period structure,
![]() ${{\mathcal A}_{S_n}\setminus S_n}=\{q_1\ldots q_{n-1},q_1\ldots q_n\}$
and
${{\mathcal A}_{S_n}\setminus S_n}=\{q_1\ldots q_{n-1},q_1\ldots q_n\}$
and
![]() ${\mathcal A}_{S_n}^\infty =\{q_1\ldots q_n\}$
. By Proposition 3.7, with respect to this period structure,
${\mathcal A}_{S_n}^\infty =\{q_1\ldots q_n\}$
. By Proposition 3.7, with respect to this period structure,
![]() ${\mathcal H}_n=q_1\ldots q_{n-1}{\mathbb Z}\setminus {\mathcal M}_{S_n}$
. Since
${\mathcal H}_n=q_1\ldots q_{n-1}{\mathbb Z}\setminus {\mathcal M}_{S_n}$
. Since
![]() $c_m\nmid \ell _{S_N}\vee q_1\ldots q_n$
for any
$c_m\nmid \ell _{S_N}\vee q_1\ldots q_n$
for any
![]() $m,n>N$
,
$m,n>N$
,
![]() $\ell _{S_N}\vee q_1\ldots q_n\in \mathcal {F}_{{\mathcal B}\setminus S_N}$
. So item (a) from Lemma 3.19 holds. Hence,
$\ell _{S_N}\vee q_1\ldots q_n\in \mathcal {F}_{{\mathcal B}\setminus S_N}$
. So item (a) from Lemma 3.19 holds. Hence,
![]() ${\widetilde {\mathcal H}}_n=q_1\ldots q_n{\mathbb Z}\setminus {\mathcal M}_{S_n}$
. Since
${\widetilde {\mathcal H}}_n=q_1\ldots q_n{\mathbb Z}\setminus {\mathcal M}_{S_n}$
. Since
![]() $S_n^{\div q_1\ldots q_n}=\{c_1,\ldots ,c_n\}$
and
$S_n^{\div q_1\ldots q_n}=\{c_1,\ldots ,c_n\}$
and
![]() $S_n^{\div q_1\ldots q_{n-1}}=\{c_1,\ldots ,c_{n-1},q_nc_n\}$
are both primitive, Lemma 2.26 shows that the minimal periods of
$S_n^{\div q_1\ldots q_{n-1}}=\{c_1,\ldots ,c_{n-1},q_nc_n\}$
are both primitive, Lemma 2.26 shows that the minimal periods of
![]() ${\widetilde {\mathcal H}}_n$
and
${\widetilde {\mathcal H}}_n$
and
![]() ${\mathcal H}_n$
are both equal
${\mathcal H}_n$
are both equal
![]() $p_n=q_1\ldots q_nc_1\ldots c_n$
, although
$p_n=q_1\ldots q_nc_1\ldots c_n$
, although
![]() ${\widetilde {\mathcal H}}_n\neq {\mathcal H}_n$
. Proposition 2.20 shows that the centralizer of
${\widetilde {\mathcal H}}_n\neq {\mathcal H}_n$
. Proposition 2.20 shows that the centralizer of
![]() $X_\eta $
is trivial.
$X_\eta $
is trivial.
We continue with an example for which the validity of the identities
![]() ${\widetilde {\mathcal H}}_n={\mathcal H}_n$
depends on the choice of the period structure.
${\widetilde {\mathcal H}}_n={\mathcal H}_n$
depends on the choice of the period structure.
Example 3.28. Assume that we have a collection
![]() $\{q_i,c_i,d_i: i\ge 1\}$
of pairwise coprime odd natural numbers greater than 1. Let
$\{q_i,c_i,d_i: i\ge 1\}$
of pairwise coprime odd natural numbers greater than 1. Let
for
![]() $i\ge 1$
and
$i\ge 1$
and
for
![]() $n\ge 1$
. Finally, we set
$n\ge 1$
. Finally, we set
Clearly,
![]() ${\mathcal B}$
contains no scaled copy of an infinite coprime set.
${\mathcal B}$
contains no scaled copy of an infinite coprime set.
The sets
![]() $S_n$
and
$S_n$
and
![]() $S^{\prime }_n$
are saturated and
$S^{\prime }_n$
are saturated and
and hence
and
It follows that
![]() ${\widetilde {\mathcal H}}_N={\mathcal H}_N=2^{N+1}({\mathbb Z}\setminus {\mathcal M}_{\{q_1,\ldots ,q_N\}})$
, where the sets of holes and essential holes are calculated with respect to the period structure
${\widetilde {\mathcal H}}_N={\mathcal H}_N=2^{N+1}({\mathbb Z}\setminus {\mathcal M}_{\{q_1,\ldots ,q_N\}})$
, where the sets of holes and essential holes are calculated with respect to the period structure
![]() $p_n=\operatorname {lcm}(S_n)$
. Indeed,
$p_n=\operatorname {lcm}(S_n)$
. Indeed,
by equation (61) and Proposition 3.7. Suppose that
![]() $b\mid \ell _{S_N}\vee 2^{n+1}$
for some
$b\mid \ell _{S_N}\vee 2^{n+1}$
for some
![]() $b\in {\mathcal B}$
and some
$b\in {\mathcal B}$
and some
![]() $n>N$
. Since
$n>N$
. Since
![]() $q_i\nmid \ell _{S_N}\vee 2^{n+1}$
for any
$q_i\nmid \ell _{S_N}\vee 2^{n+1}$
for any
![]() $i>N$
,
$i>N$
,
![]() $b\in S_N$
. So item (a) from Lemma 3.19 holds and the assertion follows. By Lemma 2.26(a), we obtain
$b\in S_N$
. So item (a) from Lemma 3.19 holds and the assertion follows. By Lemma 2.26(a), we obtain
![]() $\tilde {\tau }_N=\tau _N=2^{N+1}q_1\cdots q_N$
.
$\tilde {\tau }_N=\tau _N=2^{N+1}q_1\cdots q_N$
.
Let
![]() ${\mathcal H}^{\prime }_n$
,
${\mathcal H}^{\prime }_n$
,
![]() ${\widetilde {\mathcal H}}^{\prime }_n$
be the sets of holes and essential holes, respectively, calculated with respect to the period structure
${\widetilde {\mathcal H}}^{\prime }_n$
be the sets of holes and essential holes, respectively, calculated with respect to the period structure
![]() $p^{\prime }_n=\operatorname {lcm}(S^{\prime }_n)$
. We will show that
$p^{\prime }_n=\operatorname {lcm}(S^{\prime }_n)$
. We will show that
so that
![]() $\tilde {\tau }_N'=\tau _N'/c_{N+1}=2^{N+1}q_1\cdots q_{N+1}$
by Lemma 2.26(a).
$\tilde {\tau }_N'=\tau _N'/c_{N+1}=2^{N+1}q_1\cdots q_{N+1}$
by Lemma 2.26(a).
Indeed,
by equation (62) and Proposition 3.7. Let
![]() $n>N$
. (Notice that item (a) from Lemma 3.19 does not hold because
$n>N$
. (Notice that item (a) from Lemma 3.19 does not hold because
![]() $2^{N+2}q_{N+1}\mid 2^{n+1}\vee \operatorname {lcm}(S_N')$
and
$2^{N+2}q_{N+1}\mid 2^{n+1}\vee \operatorname {lcm}(S_N')$
and
![]() $2^{N+2}q_{N+1}\not \in S_N'$
.) Suppose that for some
$2^{N+2}q_{N+1}\not \in S_N'$
.) Suppose that for some
![]() $k\in {\mathbb Z}\setminus {\mathcal M}_{\{q_1,\ldots ,q_N,q_{N+1}c_{N+1}\}}$
,
$k\in {\mathbb Z}\setminus {\mathcal M}_{\{q_1,\ldots ,q_N,q_{N+1}c_{N+1}\}}$
,
Then, in particular,
By Lemma 2.24, there exists
![]() $b\in S_n'$
such that
$b\in S_n'$
such that
Since
![]() $k\in {\mathbb Z}\setminus {\mathcal M}_{\{q_1,\ldots ,q_N,q_{N+1}c_{N+1}\}}$
and
$k\in {\mathbb Z}\setminus {\mathcal M}_{\{q_1,\ldots ,q_N,q_{N+1}c_{N+1}\}}$
and
![]() $b\mid 2^{N+1}k\vee 2^{n+1}$
, we have
$b\mid 2^{N+1}k\vee 2^{n+1}$
, we have
![]() $b\in S_n'\setminus S_N'$
. However,
$b\in S_n'\setminus S_N'$
. However,
![]() $b\mid \operatorname {lcm}(S_N')\vee 2^{n+1}$
but
$b\mid \operatorname {lcm}(S_N')\vee 2^{n+1}$
but
![]() $q_i\nmid \operatorname {lcm}(S_N')\vee 2^{n+1}$
for any
$q_i\nmid \operatorname {lcm}(S_N')\vee 2^{n+1}$
for any
![]() $i>N+1$
,
$i>N+1$
,
![]() $d_{N+1}\nmid \operatorname {lcm}(S_N')\vee 2^{n+1}$
and
$d_{N+1}\nmid \operatorname {lcm}(S_N')\vee 2^{n+1}$
and
![]() $2^{N+1}q_{N+1}c_{N+1}\in S_N'$
. So,
$2^{N+1}q_{N+1}c_{N+1}\in S_N'$
. So,
![]() $b=2^{N+2}q_{N+1}$
and
$b=2^{N+2}q_{N+1}$
and
![]() $q_{N+1}\mid k$
. Conversely,
$q_{N+1}\mid k$
. Conversely,
for any
![]() $m\in {\mathbb Z}$
. Hence,
$m\in {\mathbb Z}$
. Hence,
 $$ \begin{align*} \begin{aligned} {\widetilde{\mathcal H}}_N'&=2^{N+1}{\mathbb Z}\setminus{\mathcal M}_{S_N'\cup\{2^{N+1}q_{N+1}\}}=2^{N+1}({\mathbb Z}\setminus{\mathcal M}_{((S_N'\cup\{2^{N+1}q_{N+1}\})^{\div 2^{N+1}})^{\textrm{prim}}})\\ &= 2^{N+1}({\mathbb Z}\setminus{\mathcal M}_{\{q_1,\ldots,q_N,q_{N+1}\}}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} {\widetilde{\mathcal H}}_N'&=2^{N+1}{\mathbb Z}\setminus{\mathcal M}_{S_N'\cup\{2^{N+1}q_{N+1}\}}=2^{N+1}({\mathbb Z}\setminus{\mathcal M}_{((S_N'\cup\{2^{N+1}q_{N+1}\})^{\div 2^{N+1}})^{\textrm{prim}}})\\ &= 2^{N+1}({\mathbb Z}\setminus{\mathcal M}_{\{q_1,\ldots,q_N,q_{N+1}\}}). \end{aligned} \end{align*} $$
For both filtrations, property (TI) from §2.5 is obviously satisfied so that Proposition 2.20 applies. However,
![]() $p_N/\tilde {\tau }_N=c_1\cdots c_N\cdot d_1\cdots d_N$
and
$p_N/\tilde {\tau }_N=c_1\cdots c_N\cdot d_1\cdots d_N$
and
![]() $p_N'/\tilde {\tau }_N'=c_1\cdots c_{N+1}\cdot d_1\cdots d_N$
are both unbounded in N, so that only very weak conclusions can be drawn from this proposition. In particular, no bound on the size of the centralizer can be deduced from it.
$p_N'/\tilde {\tau }_N'=c_1\cdots c_{N+1}\cdot d_1\cdots d_N$
are both unbounded in N, so that only very weak conclusions can be drawn from this proposition. In particular, no bound on the size of the centralizer can be deduced from it.
Finally, we provide an example for which
![]() ${\widetilde {\mathcal H}}_n\subsetneq {\mathcal M}_{{\mathcal A}_{S_n}^\infty }\setminus {\mathcal M}_{S_n}$
for any saturated filtration
${\widetilde {\mathcal H}}_n\subsetneq {\mathcal M}_{{\mathcal A}_{S_n}^\infty }\setminus {\mathcal M}_{S_n}$
for any saturated filtration
![]() $(S_n)$
of
$(S_n)$
of
![]() ${\mathcal B}$
, so that
${\mathcal B}$
, so that
![]() $S_n\subsetneq S_n(a)$
for some
$S_n\subsetneq S_n(a)$
for some
![]() $a\in {\mathcal A}_{S_n}^{\infty }$
(and hence also for some
$a\in {\mathcal A}_{S_n}^{\infty }$
(and hence also for some
![]() $a\in {\mathcal A}_{S_n}^{\infty ,p}$
), see Theorem 3.17 and Remark 3.18(a).
$a\in {\mathcal A}_{S_n}^{\infty ,p}$
), see Theorem 3.17 and Remark 3.18(a).
Example 3.29. Let
![]() $s_i, s^{\prime }_i, q_i, r_i, d_{i-1} (i\in {\mathbb N})$
be pairwise different primes. Let
$s_i, s^{\prime }_i, q_i, r_i, d_{i-1} (i\in {\mathbb N})$
be pairwise different primes. Let
and, for
![]() $m\in {\mathbb N}\cup \{0\}$
and
$m\in {\mathbb N}\cup \{0\}$
and
![]() $i\ge 2$
, let
$i\ge 2$
, let
 $$ \begin{align} b_{i,m}=\frac{1}{s^{\prime}_{i-1}}s_1\cdot s^{\prime}_1\cdot\ldots \cdot s_i\cdot s^{\prime}_i\cdot q_i\cdot r_i^m\cdot d_m. \end{align} $$
$$ \begin{align} b_{i,m}=\frac{1}{s^{\prime}_{i-1}}s_1\cdot s^{\prime}_1\cdot\ldots \cdot s_i\cdot s^{\prime}_i\cdot q_i\cdot r_i^m\cdot d_m. \end{align} $$
We set
Then,
![]() ${\mathcal B}$
is primitive. It is easy to show that
${\mathcal B}$
is primitive. It is easy to show that
![]() ${\mathcal B}$
contains no scaled copy of an infinite coprime set, so the
${\mathcal B}$
contains no scaled copy of an infinite coprime set, so the
![]() ${\mathcal B}$
-free shift is Toeplitz by Proposition 3.5.
${\mathcal B}$
-free shift is Toeplitz by Proposition 3.5.
Let
![]() $(S_n)$
be any saturated filtration of
$(S_n)$
be any saturated filtration of
![]() ${\mathcal B}$
by finite sets. With no loss of generality, we can assume that
${\mathcal B}$
by finite sets. With no loss of generality, we can assume that
![]() $b_1, b_{2,0}\in S_1$
. Let k be the minimal number such that
$b_1, b_{2,0}\in S_1$
. Let k be the minimal number such that
![]() $b_{k+1,0}\notin S_1$
. It follows that
$b_{k+1,0}\notin S_1$
. It follows that
![]() $b_{2,0},\ldots ,b_{k,0}\in S_1$
. Let n be maximal such that
$b_{2,0},\ldots ,b_{k,0}\in S_1$
. Let n be maximal such that
![]() $b_{k+1,0}\notin S_n$
. Then,
$b_{k+1,0}\notin S_n$
. Then,
and
Observe that
![]() $b_{k+1,m}\notin S_n$
for every
$b_{k+1,m}\notin S_n$
for every
![]() $m\in {\mathbb N}$
. Otherwise, as
$m\in {\mathbb N}$
. Otherwise, as
![]() $d_0|\ell _{S_n}$
and
$d_0|\ell _{S_n}$
and
![]() $S_n$
is saturated,
$S_n$
is saturated,
![]() $b_{k+1,0}\in S_n$
in contrast to our assumption. Thus,
$b_{k+1,0}\in S_n$
in contrast to our assumption. Thus,
![]() $r_{k+1}\nmid \ell _{S_n}$
. For m large enough, say for
$r_{k+1}\nmid \ell _{S_n}$
. For m large enough, say for
![]() $m\ge m_0$
, the number
$m\ge m_0$
, the number
![]() $\gcd (b_{k+1,m},\ell _{S_{n+1}})$
does not depend on m.
$\gcd (b_{k+1,m},\ell _{S_{n+1}})$
does not depend on m.
A case by case analysis of prime divisors of
![]() $b_{k+1,0}$
and
$b_{k+1,0}$
and
![]() $b_{k+1,m}$
shows that
$b_{k+1,m}$
shows that
Indeed,
![]() $s_i|b_{k+1,0}$
(respectively
$s_i|b_{k+1,0}$
(respectively
![]() $s_i'|b_{k+1,0}$
) if and only if
$s_i'|b_{k+1,0}$
) if and only if
![]() $s_i|b_{k+1,m}$
(respectively
$s_i|b_{k+1,m}$
(respectively
![]() $s_i'|b_{k+1,m}$
) for every
$s_i'|b_{k+1,m}$
) for every
![]() $i\in {\mathbb N}$
. Moreover,
$i\in {\mathbb N}$
. Moreover,
![]() $r_{k+1}\nmid \ell _{S_n}$
,
$r_{k+1}\nmid \ell _{S_n}$
,
![]() $d_0\nmid b_{k+1,m}$
and
$d_0\nmid b_{k+1,m}$
and
![]() $q_{k+1}$
divides both
$q_{k+1}$
divides both
![]() $b_{k+1,0}$
and
$b_{k+1,0}$
and
![]() $b_{k+1,m}$
.
$b_{k+1,m}$
.
We prove that
 $$ \begin{align} &\text{for all }{a\in{\mathcal A}_{S_{n+1}}^{\infty}:\gcd(a,\ell_{S_n})|\gcd(b_{k+1,0},\ell_{S_n})}\nonumber\\ &\quad\Leftrightarrow a=\gcd(b_{k+1,m},\ell_{S_{n+1}}) \quad\text{for}\; m\ge m_0. \end{align} $$
$$ \begin{align} &\text{for all }{a\in{\mathcal A}_{S_{n+1}}^{\infty}:\gcd(a,\ell_{S_n})|\gcd(b_{k+1,0},\ell_{S_n})}\nonumber\\ &\quad\Leftrightarrow a=\gcd(b_{k+1,m},\ell_{S_{n+1}}) \quad\text{for}\; m\ge m_0. \end{align} $$
In view of equation (68), it is enough to prove ‘
![]() $\Rightarrow $
’. We can assume that
$\Rightarrow $
’. We can assume that
![]() $a=\gcd (b_{i,m},\ell _{S_{n+1}})$
for some
$a=\gcd (b_{i,m},\ell _{S_{n+1}})$
for some
![]() $i>1$
and
$i>1$
and
![]() $m\in {\mathbb N}$
, and
$m\in {\mathbb N}$
, and
![]() $\gcd (b_{i,m},\ell _{S_n})=\gcd (a,\ell _{S_n})\mid \gcd (b_{k+1,0},\ell _{S_n})$
. As
$\gcd (b_{i,m},\ell _{S_n})=\gcd (a,\ell _{S_n})\mid \gcd (b_{k+1,0},\ell _{S_n})$
. As
![]() $s^{\prime }_k\nmid b_{k+1,0}$
and
$s^{\prime }_k\nmid b_{k+1,0}$
and
![]() $s^{\prime }_k|\ell _{S_n}$
, we have
$s^{\prime }_k|\ell _{S_n}$
, we have
![]() $i\le k-1$
or
$i\le k-1$
or
![]() $i=k+1$
. However,
$i=k+1$
. However,
![]() $i\le k-1$
implies that
$i\le k-1$
implies that
![]() $q_i\mid \gcd (b_{i,m},\ell _{S_n})\mid b_{k+1,0}$
, which is a contradiction. Thus,
$q_i\mid \gcd (b_{i,m},\ell _{S_n})\mid b_{k+1,0}$
, which is a contradiction. Thus,
![]() $i=k+1$
and since
$i=k+1$
and since
![]() $a\in {\mathcal A}_{S_{n+1}}^{\infty }$
,
$a\in {\mathcal A}_{S_{n+1}}^{\infty }$
,
![]() $a=\gcd (b_{k+1,m},\ell _{S_{n+1}})$
for
$a=\gcd (b_{k+1,m},\ell _{S_{n+1}})$
for
![]() $m\ge m_0$
.
$m\ge m_0$
.
Note that as
![]() $b_{k+1,0}\in S_{n+1}$
,
$b_{k+1,0}\in S_{n+1}$
,
Let
![]() $a\in {\mathcal A}_{S_{n+1}}^{\infty }$
be such that
$a\in {\mathcal A}_{S_{n+1}}^{\infty }$
be such that
![]() $(\gcd (b_{k+1,0},\ell _{S_n})+\ell _{S_n}{\mathbb Z})\cap a{\mathbb Z}\neq \emptyset $
. Then,
$(\gcd (b_{k+1,0},\ell _{S_n})+\ell _{S_n}{\mathbb Z})\cap a{\mathbb Z}\neq \emptyset $
. Then,
![]() $\gcd (a,\ell _{S_n})| \gcd (b_{k+1,0},\ell _{S_n})$
and by equation (69),
$\gcd (a,\ell _{S_n})| \gcd (b_{k+1,0},\ell _{S_n})$
and by equation (69),
![]() $a=\gcd (b_{k+1,m},\ell _{S_{n+1}})$
for
$a=\gcd (b_{k+1,m},\ell _{S_{n+1}})$
for
![]() $m\ge m_0$
. By equations (67) and (70),
$m\ge m_0$
. By equations (67) and (70),
It follows from Lemma 2.25 that
![]() $(\gcd (b_{k+1,0},\ell _{S_n})+\ell _{S_n}{\mathbb Z})\cap a{\mathbb Z}\subseteq b_{k+1,0}{\mathbb Z}$
. Hence,
$(\gcd (b_{k+1,0},\ell _{S_n})+\ell _{S_n}{\mathbb Z})\cap a{\mathbb Z}\subseteq b_{k+1,0}{\mathbb Z}$
. Hence,
which, because of Remark 3.12, implies
![]() $\gcd (b_{k+1,0},\ell _{S_n})\notin {\widetilde {\mathcal H}}_n$
. Moreover, by equation (68) and the primitivity of
$\gcd (b_{k+1,0},\ell _{S_n})\notin {\widetilde {\mathcal H}}_n$
. Moreover, by equation (68) and the primitivity of
![]() ${\mathcal B}$
,
${\mathcal B}$
,
![]() $\gcd (b_{k+1,0},\ell _{S_n})\in {\mathcal M}_{{\mathcal A}_{S_n}^{\infty }}\setminus {\mathcal M}_{S_n}$
. Thus,
$\gcd (b_{k+1,0},\ell _{S_n})\in {\mathcal M}_{{\mathcal A}_{S_n}^{\infty }}\setminus {\mathcal M}_{S_n}$
. Thus,
![]() $\gcd (b_{k+1,0},\ell _{S_n})\in {\mathcal M}_{{\mathcal A}_{S_n}^{\infty }}\setminus ({\mathcal M}_{S_n}\cup {\widetilde {\mathcal H}}_n)$
.
$\gcd (b_{k+1,0},\ell _{S_n})\in {\mathcal M}_{{\mathcal A}_{S_n}^{\infty }}\setminus ({\mathcal M}_{S_n}\cup {\widetilde {\mathcal H}}_n)$
.
We claim that
![]() $\eta $
is a regular Toeplitz sequence. Indeed, let
$\eta $
is a regular Toeplitz sequence. Indeed, let
![]() $S_n=\{b_1\}\cup \{b_{i,m}: 2\leq i{\kern-1pt}\leq{\kern-1pt} n, 0{\kern-1pt}\leq{\kern-1pt} m{\kern-1pt}\leq{\kern-1pt} n\}$
. Then,
$S_n=\{b_1\}\cup \{b_{i,m}: 2\leq i{\kern-1pt}\leq{\kern-1pt} n, 0{\kern-1pt}\leq{\kern-1pt} m{\kern-1pt}\leq{\kern-1pt} n\}$
. Then,
![]() $\ell _{S_n}{\kern-1pt}={\kern-1pt}s_1s_1'\ldots s_ns_n'q_1\ldots q _nr_1^n\ldots r_n^nd_0\ldots d_n$
and for
$\ell _{S_n}{\kern-1pt}={\kern-1pt}s_1s_1'\ldots s_ns_n'q_1\ldots q _nr_1^n\ldots r_n^nd_0\ldots d_n$
and for
![]() $b_{i,m}\not \in S_n$
,
$b_{i,m}\not \in S_n$
,
 $$ \begin{align*} \gcd(b_{i,m},\ell_{S_n})=\begin{cases} \dfrac{1}{s_{i-1}'}s_1s_1'\ldots s_is_i'q_ir_i^n &\text{if }i\leq n,m>n,\\ s_1s_1'\ldots s_{n-1}s_{n-1}'s_nd_m &\text{if } i=n+1,m\leq n,\\ s_1s_1'\ldots s_{n-1}s_{n-1}'s_n &\text{if } i=n+1,m>n,\\ s_1s_1'\ldots s_ns_n'd_m &\text{if }i>n+1,m\leq n,\\ s_1s_1'\ldots s_ns_n'&\text{if }i>n+1,m>n. \end{cases} \end{align*} $$
$$ \begin{align*} \gcd(b_{i,m},\ell_{S_n})=\begin{cases} \dfrac{1}{s_{i-1}'}s_1s_1'\ldots s_is_i'q_ir_i^n &\text{if }i\leq n,m>n,\\ s_1s_1'\ldots s_{n-1}s_{n-1}'s_nd_m &\text{if } i=n+1,m\leq n,\\ s_1s_1'\ldots s_{n-1}s_{n-1}'s_n &\text{if } i=n+1,m>n,\\ s_1s_1'\ldots s_ns_n'd_m &\text{if }i>n+1,m\leq n,\\ s_1s_1'\ldots s_ns_n'&\text{if }i>n+1,m>n. \end{cases} \end{align*} $$
Hence,
![]() ${\mathcal A}_{S_n}^{\infty ,p}=\{{1}/{s_{i-1}'}s_1s_1'\ldots s_is_i'q_ir_i^n: 2\leq i\leq n\}\cup \{s_1s_1'\ldots s_{n-1}s_{n-1}'s_n\}$
. Since
${\mathcal A}_{S_n}^{\infty ,p}=\{{1}/{s_{i-1}'}s_1s_1'\ldots s_is_i'q_ir_i^n: 2\leq i\leq n\}\cup \{s_1s_1'\ldots s_{n-1}s_{n-1}'s_n\}$
. Since
 $d({\mathcal M}_{{\mathcal A}_{S_n}^{\infty ,p}}){\kern2pt}\leq{\kern2pt} 1-\prod _{a\in {\mathcal A}_{S_n}^{\infty ,p}}(1-{1}/{a}){\kern2pt}\leq{\kern2pt} 1{\kern1pt}-{\kern1pt}(1{\kern1pt}-{\kern1pt}{1}/{\min _{2\leq i\leq n}{r_i}^n})^{n-1}(1-{1}/s_1s_1'\ldots s_{n-1} s_{n-1}'s_n)\to 0$
as
$d({\mathcal M}_{{\mathcal A}_{S_n}^{\infty ,p}}){\kern2pt}\leq{\kern2pt} 1-\prod _{a\in {\mathcal A}_{S_n}^{\infty ,p}}(1-{1}/{a}){\kern2pt}\leq{\kern2pt} 1{\kern1pt}-{\kern1pt}(1{\kern1pt}-{\kern1pt}{1}/{\min _{2\leq i\leq n}{r_i}^n})^{n-1}(1-{1}/s_1s_1'\ldots s_{n-1} s_{n-1}'s_n)\to 0$
as
![]() $n\to \infty $
, by Corollary 3.11,
$n\to \infty $
, by Corollary 3.11,
![]() $m_G(\partial W)=0$
. So the
$m_G(\partial W)=0$
. So the
![]() ${\mathcal B}$
-free Toeplitz shift is regular, see e.g. [Reference Downarowicz, Kolyada, Manin and Ward8, Theorem 13.1]. Similarly, one can show that the condition in equation (42) of Proposition 2.28 and Theorem 2.31 is satisfied for
${\mathcal B}$
-free Toeplitz shift is regular, see e.g. [Reference Downarowicz, Kolyada, Manin and Ward8, Theorem 13.1]. Similarly, one can show that the condition in equation (42) of Proposition 2.28 and Theorem 2.31 is satisfied for
![]() $A_n={\mathcal A}_{S_n}^{\infty ,p}$
. We do not attempt to determine the sets
$A_n={\mathcal A}_{S_n}^{\infty ,p}$
. We do not attempt to determine the sets
![]() ${\widetilde {\mathcal H}}_n$
(and their periods) according to the prescription in Theorem 3.17 explicitly.
${\widetilde {\mathcal H}}_n$
(and their periods) according to the prescription in Theorem 3.17 explicitly.
Note that
![]() $a_{n+1}=s_1 s_1'\cdots s_n s_n' s_{n+1}$
is an example of a number in
$a_{n+1}=s_1 s_1'\cdots s_n s_n' s_{n+1}$
is an example of a number in
![]() ${\mathcal A}_{S_{n+1}}^{\infty ,p}$
for which
${\mathcal A}_{S_{n+1}}^{\infty ,p}$
for which
![]() $\gcd (a_{n+1},\ell _{S_n})$
belongs to
$\gcd (a_{n+1},\ell _{S_n})$
belongs to
![]() ${\mathcal A}_{S_n}^\infty $
but not to
${\mathcal A}_{S_n}^\infty $
but not to
![]() ${\mathcal A}_{S_n}^{\infty ,p}$
, compare Lemma 3.9 items (c) and (e).
${\mathcal A}_{S_n}^{\infty ,p}$
, compare Lemma 3.9 items (c) and (e).
We complete this example by showing (for suitable choices of
![]() $d_i$
) that conditions (Seh) and hence also (D) (the equivalence of conditions (Seh) and (D) was claimed without proof in §2.2, see also Lemma 2.9) and property (TI), see Proposition 2.20, are violated. Let
$d_i$
) that conditions (Seh) and hence also (D) (the equivalence of conditions (Seh) and (D) was claimed without proof in §2.2, see also Lemma 2.9) and property (TI), see Proposition 2.20, are violated. Let
![]() $a_n=s_1s_1's_2s_2'\ldots s_{n-1}s_{n-1}'s_n$
and
$a_n=s_1s_1's_2s_2'\ldots s_{n-1}s_{n-1}'s_n$
and
![]() $a_n'=s_1s_2s_2'q_2r_2^n$
. Suppose that
$a_n'=s_1s_2s_2'q_2r_2^n$
. Suppose that
![]() $\prod _{n\geq 0}(1-{1}/{d_n})>\tfrac 12$
. Then the equation
$\prod _{n\geq 0}(1-{1}/{d_n})>\tfrac 12$
. Then the equation
![]() ${a_n}/{s_1s_2s_2'}T-{a_n'}/{s_1s_2s_2'}M=1$
has solutions
${a_n}/{s_1s_2s_2'}T-{a_n'}/{s_1s_2s_2'}M=1$
has solutions
![]() $T,M$
with
$T,M$
with
so that, for all n, there are holes with distance
![]() $s_1s_2s_2'$
(in the sense of [Reference Bułatek and Kwiatkowski2]) in
$s_1s_2s_2'$
(in the sense of [Reference Bułatek and Kwiatkowski2]) in
![]() ${\mathcal H}_n$
, see Proposition 3.7. Indeed, there is a unique solution
${\mathcal H}_n$
, see Proposition 3.7. Indeed, there is a unique solution
![]() $X_0\in \{1,\ldots ,{\operatorname {lcm}(a_n,a_n')}/ {s_1s_2s_2'}-1\}$
of the equations
$X_0\in \{1,\ldots ,{\operatorname {lcm}(a_n,a_n')}/ {s_1s_2s_2'}-1\}$
of the equations
![]() $X\equiv 1\,\mod {a_n}/{s_1s_2s_2'}$
and
$X\equiv 1\,\mod {a_n}/{s_1s_2s_2'}$
and
![]() $X\equiv 0\,\mod {a_n'}/{s_1s_2s_2'}$
. For
$X\equiv 0\,\mod {a_n'}/{s_1s_2s_2'}$
. For
![]() $k=0,\ldots ,d _0d_1\cdots d_n-1$
, let
$k=0,\ldots ,d _0d_1\cdots d_n-1$
, let
![]() $X_k=X_0+k{\operatorname {lcm}(a_n,a_n')}/{s_1s_2s_2'}$
,
$X_k=X_0+k{\operatorname {lcm}(a_n,a_n')}/{s_1s_2s_2'}$
,
![]() $T_k={X_ks_1s_2s_2'}/{a_n}$
and
$T_k={X_ks_1s_2s_2'}/{a_n}$
and
![]() $M_k={(X_k-1)s_1s_2s_2'}/{a_n'}$
. As all
$M_k={(X_k-1)s_1s_2s_2'}/{a_n'}$
. As all
![]() $X_k$
are further solutions of the same two equations, and as the
$X_k$
are further solutions of the same two equations, and as the
![]() $d_i$
are pairwise different primes, exactly
$d_i$
are pairwise different primes, exactly
![]() $\gamma _n:=d_0d_1\cdots d_n\prod _{i=0}^n(1-{1}/{d_i})$
of these solutions are
$\gamma _n:=d_0d_1\cdots d_n\prod _{i=0}^n(1-{1}/{d_i})$
of these solutions are
![]() $\{d_0,d_1,\ldots ,d_n\}$
-free, and also exactly
$\{d_0,d_1,\ldots ,d_n\}$
-free, and also exactly
![]() $\gamma _n$
of the
$\gamma _n$
of the
![]() $d_0d_1\cdots d_n$
numbers
$d_0d_1\cdots d_n$
numbers
![]() $X_k-1$
are
$X_k-1$
are
![]() $\{d_0,d_1,\ldots ,d_n\}$
-free. Hence, exactly
$\{d_0,d_1,\ldots ,d_n\}$
-free. Hence, exactly
![]() $\gamma _n$
of the numbers
$\gamma _n$
of the numbers
![]() $T_k$
and
$T_k$
and
![]() $\gamma _n$
of the numbers
$\gamma _n$
of the numbers
![]() $M_k$
are
$M_k$
are
![]() $\{d_0,d_1,\ldots ,d_n\}$
-free. Since
$\{d_0,d_1,\ldots ,d_n\}$
-free. Since
![]() $2\gamma _n>d_0d_1\cdots d_n$
, there exists at least one
$2\gamma _n>d_0d_1\cdots d_n$
, there exists at least one
![]() $k\in \{0,\ldots ,d_0d_1\cdots d_n-1\}$
such that
$k\in \{0,\ldots ,d_0d_1\cdots d_n-1\}$
such that
![]() $T_k$
and
$T_k$
and
![]() $M_k$
are
$M_k$
are
![]() $\{d_0,d_1,\ldots ,d_n\}$
-free, so then
$\{d_0,d_1,\ldots ,d_n\}$
-free, so then
![]() $a_nT_k$
and
$a_nT_k$
and
![]() $a_n'M_k$
are
$a_n'M_k$
are
![]() $S_n$
-free. This proves the claim.
$S_n$
-free. This proves the claim.
3.6 Superpolynomial complexity
We consider the example
![]() ${\mathcal B}={\mathcal B}_2=\{2^ic_i, 3^ic_i: i\in {\mathbb N}\}$
, where
${\mathcal B}={\mathcal B}_2=\{2^ic_i, 3^ic_i: i\in {\mathbb N}\}$
, where
![]() $c_i$
are odd pairwise coprime numbers not divisible by 3. Recall from Example 3.21 that our Theorem 2.31 applies to this
$c_i$
are odd pairwise coprime numbers not divisible by 3. Recall from Example 3.21 that our Theorem 2.31 applies to this
![]() ${\mathcal B}$
and ensures that the
${\mathcal B}$
and ensures that the
![]() ${\mathcal B}$
-free subshift has a trivial centralizer. Here we show that it has superpolynomial complexity.
${\mathcal B}$
-free subshift has a trivial centralizer. Here we show that it has superpolynomial complexity.
We denote by
![]() $\rho $
the complexity function of
$\rho $
the complexity function of
![]() $X_{\eta }$
for
$X_{\eta }$
for
![]() , that is,
, that is,
for
![]() $n\in {\mathbb N}$
.
$n\in {\mathbb N}$
.
Proposition 3.30. Assume that
![]() $2c_1< 2^2c_2< 2^3c_3<\cdots $
are such that
$2c_1< 2^2c_2< 2^3c_3<\cdots $
are such that
 $$ \begin{align} \sum_{i=1}^{\infty}\frac{1}{c_i}<\frac12, \end{align} $$
$$ \begin{align} \sum_{i=1}^{\infty}\frac{1}{c_i}<\frac12, \end{align} $$
and there exists a real number
![]() $\alpha>1$
such that
$\alpha>1$
such that
for
![]() $j\gg 0$
. Then, for each
$j\gg 0$
. Then, for each
![]() $\varepsilon \in (0,1)$
,
$\varepsilon \in (0,1)$
,
Remark 3.31. If
![]() $c_i$
is the square of the
$c_i$
is the square of the
![]() $(i+2)$
th odd prime number, for
$(i+2)$
th odd prime number, for
![]() $i\in {\mathbb N}$
(that is,
$i\in {\mathbb N}$
(that is,
![]() $c_1=25$
etc.), the assumptions of the proposition are satisfied (equation (73) holds for
$c_1=25$
etc.), the assumptions of the proposition are satisfied (equation (73) holds for
![]() $\alpha \geq 25$
).
$\alpha \geq 25$
).
Remark 3.32. For any
![]() $j\in {\mathbb N}$
, under the assumption in equation (72),
$j\in {\mathbb N}$
, under the assumption in equation (72),
This inequality is a consequence of the fact that the arithmetic mean of positive numbers is greater than or equal to their geometric mean.
The following lemma is elementary.
Lemma 3.33. For every
![]() $n,b\in {\mathbb N}$
and
$n,b\in {\mathbb N}$
and
![]() $k,r\in {\mathbb Z}$
:
$k,r\in {\mathbb Z}$
:
Let
 $$ \begin{align*} \delta=\frac12-\sum_{i=1}^{\infty}\frac{1}{c_i}. \end{align*} $$
$$ \begin{align*} \delta=\frac12-\sum_{i=1}^{\infty}\frac{1}{c_i}. \end{align*} $$
Given
![]() $n\in {\mathbb N}$
let
$n\in {\mathbb N}$
let
![]() $m_n=[\lg _2n]$
. Note that
$m_n=[\lg _2n]$
. Note that
![]() $\delta>0$
by equation (72) and
$\delta>0$
by equation (72) and
![]() $2^{m_n+1}>n$
.
$2^{m_n+1}>n$
.
Lemma 3.34. Assume that
![]() $j_0\in \{1,\ldots ,m_n\}$
satisfies
$j_0\in \{1,\ldots ,m_n\}$
satisfies
If
 $$ \begin{align*}[1,n]\cap (2^{j_0}c_{j_0}{\mathbb Z}+r)\subseteq \bigcup_{i=1}^{m_n}(2^ic_i{\mathbb Z}+s_i)\cup \bigcup_{i=1}^{m_n}(3^ic_i{\mathbb Z}+t_i) \end{align*} $$
$$ \begin{align*}[1,n]\cap (2^{j_0}c_{j_0}{\mathbb Z}+r)\subseteq \bigcup_{i=1}^{m_n}(2^ic_i{\mathbb Z}+s_i)\cup \bigcup_{i=1}^{m_n}(3^ic_i{\mathbb Z}+t_i) \end{align*} $$
for some
![]() $r,s_1,\ldots ,s_{m_n},t_1,\ldots ,t_{m_n} \in {\mathbb Z}$
, then
$r,s_1,\ldots ,s_{m_n},t_1,\ldots ,t_{m_n} \in {\mathbb Z}$
, then
![]() $r\equiv s_{j_0} \,\mod 2^{j_0}c_{j_0}$
.
$r\equiv s_{j_0} \,\mod 2^{j_0}c_{j_0}$
.
Proof. Suppose otherwise, then
![]() $(2^{j_0}c_{j_0}{\mathbb Z}+r)$
is disjoint to
$(2^{j_0}c_{j_0}{\mathbb Z}+r)$
is disjoint to
![]() $(2^{j_0}c_{j_0}{\mathbb Z}+s_{j_0})$
and hence
$(2^{j_0}c_{j_0}{\mathbb Z}+s_{j_0})$
and hence
 $$ \begin{align} [1,n]\cap (2^{j_0}c_{j_0}{\mathbb Z}+r) \subseteq \bigcup_{i\in\{1,\ldots,m_n\}\setminus\{j_0\}}(2^ic_i{\mathbb Z}+s_i)\cup \bigcup_{i=1}^{m_n}(3^ic_i{\mathbb Z}+t_i). \end{align} $$
$$ \begin{align} [1,n]\cap (2^{j_0}c_{j_0}{\mathbb Z}+r) \subseteq \bigcup_{i\in\{1,\ldots,m_n\}\setminus\{j_0\}}(2^ic_i{\mathbb Z}+s_i)\cup \bigcup_{i=1}^{m_n}(3^ic_i{\mathbb Z}+t_i). \end{align} $$
If follows that
 $$ \begin{align} & |[1,n]\cap (2^{j_0}c_{j_0}{\mathbb Z}+r)|\nonumber\\ &\quad\le \sum\limits_{i\in\{1,\ldots,m_n\}\setminus\{j_0\}}|[1,n]\cap(2^ic_i{\mathbb Z}+s_i)\cap (2^{j_0}c_{j_0}{\mathbb Z}+r)|\nonumber\\&\qquad + \sum\limits_{i=1}^{m_n}|[1,n]\cap(3^ic_i{\mathbb Z}+t_i)\cap (2^{j_0}c_{j_0}{\mathbb Z}+r)|. \end{align} $$
$$ \begin{align} & |[1,n]\cap (2^{j_0}c_{j_0}{\mathbb Z}+r)|\nonumber\\ &\quad\le \sum\limits_{i\in\{1,\ldots,m_n\}\setminus\{j_0\}}|[1,n]\cap(2^ic_i{\mathbb Z}+s_i)\cap (2^{j_0}c_{j_0}{\mathbb Z}+r)|\nonumber\\&\qquad + \sum\limits_{i=1}^{m_n}|[1,n]\cap(3^ic_i{\mathbb Z}+t_i)\cap (2^{j_0}c_{j_0}{\mathbb Z}+r)|. \end{align} $$
For
![]() $i\neq j_0$
,
$i\neq j_0$
,
![]() $(2^ic_i{\mathbb Z}+s_i)\cap (2^{j_0}c_{j_0}{\mathbb Z}+r)$
is either empty or equal to
$(2^ic_i{\mathbb Z}+s_i)\cap (2^{j_0}c_{j_0}{\mathbb Z}+r)$
is either empty or equal to
![]() $\operatorname {lcm}(2^ic_i,2^{j_0}c_{j_0}) {\mathbb Z}+r'$
for some
$\operatorname {lcm}(2^ic_i,2^{j_0}c_{j_0}) {\mathbb Z}+r'$
for some
![]() $r'\in {\mathbb Z}$
. Similarly, for
$r'\in {\mathbb Z}$
. Similarly, for
![]() $i=1,\ldots ,m_n$
,
$i=1,\ldots ,m_n$
,
![]() $(3^ic_i{\mathbb Z}+r_i)\cap (2^{j_0}c_{j_0}{\mathbb Z}+r)$
is either empty or equal to
$(3^ic_i{\mathbb Z}+r_i)\cap (2^{j_0}c_{j_0}{\mathbb Z}+r)$
is either empty or equal to
![]() $\operatorname {lcm}(3^ic_i,2^{j_0}c_{j_0}){\mathbb Z}+r"$
for some
$\operatorname {lcm}(3^ic_i,2^{j_0}c_{j_0}){\mathbb Z}+r"$
for some
![]() $r"\in {\mathbb Z}$
. Then, equation (75) and Lemma 3.33 yield
$r"\in {\mathbb Z}$
. Then, equation (75) and Lemma 3.33 yield
 $$ \begin{align} \frac{n}{2^{j_0}c_{j_0}}-1\le \sum_{i\in\{1,\ldots,m_n\}\setminus\{j_0\}}\bigg(\frac{n}{\operatorname{lcm}(2^ic_i,2^{j_0}c_{j_0})}+1\bigg)+\sum_{i=1}^{m_n}\bigg(\frac{n}{3^i2^{j_0}\operatorname{lcm}(c_i,c_{j_0})}+1\bigg). \end{align} $$
$$ \begin{align} \frac{n}{2^{j_0}c_{j_0}}-1\le \sum_{i\in\{1,\ldots,m_n\}\setminus\{j_0\}}\bigg(\frac{n}{\operatorname{lcm}(2^ic_i,2^{j_0}c_{j_0})}+1\bigg)+\sum_{i=1}^{m_n}\bigg(\frac{n}{3^i2^{j_0}\operatorname{lcm}(c_i,c_{j_0})}+1\bigg). \end{align} $$
For
![]() $i\neq j_0$
,
$i\neq j_0$
,
![]() $\operatorname {lcm}(2^ic_i,2^{j_0}c_{j_0})=2^{\max \{i,j_0\}}c_ic_{j_0}\ge 2^{j_0}c_ic_{j_0}$
and
$\operatorname {lcm}(2^ic_i,2^{j_0}c_{j_0})=2^{\max \{i,j_0\}}c_ic_{j_0}\ge 2^{j_0}c_ic_{j_0}$
and
![]() $\operatorname {lcm}(c_i,c_{j_0})\ge c_{j_0}$
for every i, thus
$\operatorname {lcm}(c_i,c_{j_0})\ge c_{j_0}$
for every i, thus
 $$ \begin{align} \frac{n}{2^{j_0}c_{j_0}}-1\le \sum_{i\in\{1,\ldots,m_n\}\setminus\{j_0\}}\bigg(\frac{n}{2^{j_0}c_ic_{j_0}}+1\bigg)+\sum_{i=1}^{m_n}\bigg(\frac{n}{3^i2^{j_0}c_{j_0}}+1\bigg), \end{align} $$
$$ \begin{align} \frac{n}{2^{j_0}c_{j_0}}-1\le \sum_{i\in\{1,\ldots,m_n\}\setminus\{j_0\}}\bigg(\frac{n}{2^{j_0}c_ic_{j_0}}+1\bigg)+\sum_{i=1}^{m_n}\bigg(\frac{n}{3^i2^{j_0}c_{j_0}}+1\bigg), \end{align} $$
which, as
![]() $\sum _{i=1}^{m_n}{1}/{3^i}< \tfrac 12$
, implies
$\sum _{i=1}^{m_n}{1}/{3^i}< \tfrac 12$
, implies
 $$ \begin{align} \frac{n}{2^{j_0}c_{j_0}}-1\le \frac{n}{2^{j_0}c_{j_0}}\bigg(\frac12+\sum_{i=1}^{m_n}\frac{1}{c_i}\bigg)+2m_n-1, \end{align} $$
$$ \begin{align} \frac{n}{2^{j_0}c_{j_0}}-1\le \frac{n}{2^{j_0}c_{j_0}}\bigg(\frac12+\sum_{i=1}^{m_n}\frac{1}{c_i}\bigg)+2m_n-1, \end{align} $$
and hence
 $$ \begin{align} \frac{\delta n}{2^{j_0}c_{j_0}}\le 2m_n. \end{align} $$
$$ \begin{align} \frac{\delta n}{2^{j_0}c_{j_0}}\le 2m_n. \end{align} $$
It follows that
which is in contrast to the assumption.
Let
![]() $n\in {\mathbb N}$
be big enough to satisfy
$n\in {\mathbb N}$
be big enough to satisfy
![]() $2c_1<{\delta n}/{2\lg _2n}$
, and let
$2c_1<{\delta n}/{2\lg _2n}$
, and let
![]() $j_n$
be the greatest natural number such that
$j_n$
be the greatest natural number such that
It follows by equation (81) that
![]() $j_n\le m_n$
. Moreover,
$j_n\le m_n$
. Moreover,
![]() $(j_n)$
is a non-decreasing (starting from n big enough) sequence such that
$(j_n)$
is a non-decreasing (starting from n big enough) sequence such that
![]() $\lim _{n\rightarrow +\infty }j_n=+\infty .$
$\lim _{n\rightarrow +\infty }j_n=+\infty .$
Let N be a natural number such that
![]() $c_j\le \alpha ^j$
for every
$c_j\le \alpha ^j$
for every
![]() $j\ge j_N$
and
$j\ge j_N$
and
![]() $2c_1<{\delta N}/{2\lg _2N}$
. If
$2c_1<{\delta N}/{2\lg _2N}$
. If
![]() $n\ge N$
, then
$n\ge N$
, then
 $$ \begin{align} j_n\ge \lg_{2\alpha}\bigg(\frac{\delta n}{2\lg_2n}\bigg)-1. \end{align} $$
$$ \begin{align} j_n\ge \lg_{2\alpha}\bigg(\frac{\delta n}{2\lg_2n}\bigg)-1. \end{align} $$
Indeed, otherwise
which is a contradiction with the choice of
![]() $j_n$
.
$j_n$
.
Lemma 3.35. For any sequence
![]() $\mathbf {r}=(r_1,\ldots ,r_{m_n})$
, there exists
$\mathbf {r}=(r_1,\ldots ,r_{m_n})$
, there exists
![]() $x_{\mathbf {r}}\in {\mathbb Z}$
such that
$x_{\mathbf {r}}\in {\mathbb Z}$
such that
 $$ \begin{align*} \begin{cases} x_{\mathbf{r}}\equiv 2^jr_j\,\mod 2^jc_j\;\;\text{for}\;j=1,\ldots,m_n,\\ x_{\mathbf{r}}\equiv 0\,\mod 2^{m_n+1}3^{m_n+1}. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} x_{\mathbf{r}}\equiv 2^jr_j\,\mod 2^jc_j\;\;\text{for}\;j=1,\ldots,m_n,\\ x_{\mathbf{r}}\equiv 0\,\mod 2^{m_n+1}3^{m_n+1}. \end{cases} \end{align*} $$
Moreover, if
![]() ${\mathbf {r}'}=(r^{\prime }_1,\ldots ,r^{\prime }_{m_n})$
is another sequence of integers and
${\mathbf {r}'}=(r^{\prime }_1,\ldots ,r^{\prime }_{m_n})$
is another sequence of integers and
where
![]() $x_{\mathbf {r}^{\prime }}$
is defined analogously, then
$x_{\mathbf {r}^{\prime }}$
is defined analogously, then
for
![]() $j\le j_n$
, provided
$j\le j_n$
, provided
![]() $n\ge N$
.
$n\ge N$
.
Proof. The existence of
![]() $x_{\mathbf {r}}$
follows by the Chinese Remainder Theorem. Assume equation (84). Since
$x_{\mathbf {r}}$
follows by the Chinese Remainder Theorem. Assume equation (84). Since
![]() $2^{m_n+1}3^{m_n+1}\mid x_{\mathbf {r}}$
,
$2^{m_n+1}3^{m_n+1}\mid x_{\mathbf {r}}$
,
![]() $2^{m_n+1}3^{m_n+1}\mid x_{\mathbf {r}^{\prime }}$
and
$2^{m_n+1}3^{m_n+1}\mid x_{\mathbf {r}^{\prime }}$
and
![]() $2^{m_n+1}>n$
, the sets
$2^{m_n+1}>n$
, the sets
![]() $[x_{\mathbf {r}}+1,x_{\mathbf {r}}+n]$
and
$[x_{\mathbf {r}}+1,x_{\mathbf {r}}+n]$
and
![]() $[x_{\mathbf {r}^{\prime }}+1,x_{\mathbf {r}^{\prime }}+n]$
are disjoint to
$[x_{\mathbf {r}^{\prime }}+1,x_{\mathbf {r}^{\prime }}+n]$
are disjoint to
![]() $\bigcup _{i> m_n}(2^ic_i{\mathbb Z}\cup 3^ic_i{\mathbb Z})$
. Therefore, equation (84) implies
$\bigcup _{i> m_n}(2^ic_i{\mathbb Z}\cup 3^ic_i{\mathbb Z})$
. Therefore, equation (84) implies
 $$ \begin{align*} [1,n]\cap\bigcup_{i=1}^{m_n}((2^ic_i{\mathbb Z}\cup 3^ic_i{\mathbb Z})-x_{\mathbf{r}})=[1,n]\cap\bigcup_{i=1}^{m_n}((2^ic_i{\mathbb Z}\cup 3^ic_i{\mathbb Z})-x_{\mathbf{r}^{\prime}}). \end{align*} $$
$$ \begin{align*} [1,n]\cap\bigcup_{i=1}^{m_n}((2^ic_i{\mathbb Z}\cup 3^ic_i{\mathbb Z})-x_{\mathbf{r}})=[1,n]\cap\bigcup_{i=1}^{m_n}((2^ic_i{\mathbb Z}\cup 3^ic_i{\mathbb Z})-x_{\mathbf{r}^{\prime}}). \end{align*} $$
In particular,
 $$ \begin{align*} [1,n]\cap(2^jc_j{\mathbb Z}-x_{\mathbf{r}})\subseteq \bigcup_{i=1}^{m_n}((2^ic_i{\mathbb Z}\cup 3^ic_i{\mathbb Z})-x_{\mathbf{r}^{\prime}}) \end{align*} $$
$$ \begin{align*} [1,n]\cap(2^jc_j{\mathbb Z}-x_{\mathbf{r}})\subseteq \bigcup_{i=1}^{m_n}((2^ic_i{\mathbb Z}\cup 3^ic_i{\mathbb Z})-x_{\mathbf{r}^{\prime}}) \end{align*} $$
for every
![]() $j=1,\ldots ,m_n$
. If
$j=1,\ldots ,m_n$
. If
![]() $j\le j_n$
, then
$j\le j_n$
, then
![]() $2^jc_j<{\delta n}/{2\lg _2n}$
and by Lemma 3.34, we conclude that
$2^jc_j<{\delta n}/{2\lg _2n}$
and by Lemma 3.34, we conclude that
![]() $x_{\mathbf {r}}\equiv x_{\mathbf {r}^{\prime }}\,\mod 2^jc_j$
. As
$x_{\mathbf {r}}\equiv x_{\mathbf {r}^{\prime }}\,\mod 2^jc_j$
. As
![]() $x_{\mathbf {r}}\equiv 2^jr_j \,\mod 2^jc_j$
and
$x_{\mathbf {r}}\equiv 2^jr_j \,\mod 2^jc_j$
and
![]() $x_{\mathbf {r}^{\prime }}\equiv 2^jr_j'\,\mod 2^jc_j$
, it follows that
$x_{\mathbf {r}^{\prime }}\equiv 2^jr_j'\,\mod 2^jc_j$
, it follows that
![]() $r_j\equiv r^{\prime }_j\,\mod c_j$
.
$r_j\equiv r^{\prime }_j\,\mod c_j$
.
Proof of Proposition 3.30
Take
![]() $n\geq N$
big enough. By Lemma 3.35, to every sequence
$n\geq N$
big enough. By Lemma 3.35, to every sequence
![]() $\mathbf {r}=(r_1,\ldots ,r_{m_n})$
of integers, we can associate a block of length n on
$\mathbf {r}=(r_1,\ldots ,r_{m_n})$
of integers, we can associate a block of length n on
![]() $\eta $
, and the remainders of
$\eta $
, and the remainders of
![]() $r_j$
modulo
$r_j$
modulo
![]() $c_j$
for
$c_j$
for
![]() $j\le j_n$
are determined uniquely by the block. (The choice is not unique. The conditions on
$j\le j_n$
are determined uniquely by the block. (The choice is not unique. The conditions on
![]() $x_{\mathbf {r}}$
given in Lemma 3.35 do not determine
$x_{\mathbf {r}}$
given in Lemma 3.35 do not determine
![]() $\eta [x_{\mathbf {r}}+1,x_{\mathbf {r}}+n]$
uniquely.) It follows that
$\eta [x_{\mathbf {r}}+1,x_{\mathbf {r}}+n]$
uniquely.) It follows that
Remark 3.32 yields that
We observed in equation (82) that
![]() $j_n\ge \lg _{2\alpha }({\delta n}/({2\lg _2n}))-1$
. Let
$j_n\ge \lg _{2\alpha }({\delta n}/({2\lg _2n}))-1$
. Let
![]() $0<\varepsilon <1$
. The right-hand side of this inequality is greater than
$0<\varepsilon <1$
. The right-hand side of this inequality is greater than
![]() $\lg _{2\alpha }(n^{\varepsilon })$
for
$\lg _{2\alpha }(n^{\varepsilon })$
for
![]() $n\gg 0$
. Thus, for n big enough, we have
$n\gg 0$
. Thus, for n big enough, we have
Putting this together with equations (85) and (86), we finish the proof of the proposition.
Remark 3.36. Analogous (even simpler) arguments can be applied to the example
![]() ${\mathcal B}_1^1$
, with the same conclusion about the complexity.
${\mathcal B}_1^1$
, with the same conclusion about the complexity.
Acknowledgements
The research of the first and second authors is supported by Narodowe Centrum Nauki grant UMO-2019/33/B/ST1/00364. We are indebted to Daniel Sell for several very helpful remarks and corrections to a previous version of this manuscript.