Hostname: page-component-5d84bcc8dc-2m954 Total loading time: 0 Render date: 2026-09-14T01:03:48.520Z Has data issue: false hasContentIssue false
  • English
  • Français

A classification of aperiodic order via spectral metrics and Jarník sets

Published online by Cambridge University Press:  13 March 2018

MAIK GRÖGER ,
MARC KESSEBÖHMER ,
ARNE MOSBACH ,
TONY SAMUEL  and
MALTE STEFFENS
MAIK GRÖGER
Affiliation:
Faculty of Mathematics and Computer Science, Friedrich-Schiller University Jena, Ernst-Abbe-Platz 2, 07743 Jena, Germany email maik.groeger@uni-jena.de
MARC KESSEBÖHMER
Affiliation:
Fachbereich 3 – Mathematik und Informatik, Universität Bremen, Bibliothekstraße 1, 28359 Bremen, Germany email mhk@math.uni-bremen.de, mosbach@uni-bremen.de, m.steffens@math.uni-bremen.de
ARNE MOSBACH
Affiliation:
Fachbereich 3 – Mathematik und Informatik, Universität Bremen, Bibliothekstraße 1, 28359 Bremen, Germany email mhk@math.uni-bremen.de, mosbach@uni-bremen.de, m.steffens@math.uni-bremen.de
TONY SAMUEL
Affiliation:
Mathematics Department, California Polytechnic State University, 1 Grand Avenue, San Luis Obispo, CA 93407, USA email ajsamuel@calpoly.edu Institut Mittag-Leffler, Auravägen 17, 182 60 Djursholm, Sweden
MALTE STEFFENS
Affiliation:
Fachbereich 3 – Mathematik und Informatik, Universität Bremen, Bibliothekstraße 1, 28359 Bremen, Germany email mhk@math.uni-bremen.de, mosbach@uni-bremen.de, m.steffens@math.uni-bremen.de
Get access Rights & Permissions [Opens in a new window]

Abstract

Given an 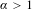$\unicode[STIX]{x1D6FC}>1$ and a $\unicode[STIX]{x1D703}$ with unbounded continued fraction entries, we characterize new relations between Sturmian subshifts with slope $\unicode[STIX]{x1D703}$ with respect to (i) an $\unicode[STIX]{x1D6FC}$-Hölder regularity condition of a spectral metric, (ii) level sets defined in terms of the Diophantine properties of $\unicode[STIX]{x1D703}$, and (iii) complexity notions which we call $\unicode[STIX]{x1D6FC}$-repetitiveness, $\unicode[STIX]{x1D6FC}$-repulsiveness and $\unicode[STIX]{x1D6FC}$-finiteness—generalizations of the properties known as linear repetitiveness, repulsiveness and power freeness, respectively. We show that the level sets relate naturally to (exact) Jarník sets and prove that their Hausdorff dimension is 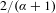$2/(\unicode[STIX]{x1D6FC}+1)$.

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 11 , November 2019 , pp. 3031 - 3065
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adamczewski, B.. On powers of words occurring in binary codings of rotations. Adv. Appl. Math. 34(1) (2005), 1–29.Google Scholar
Berthé, V. and Delecroix, V.. Beyond substitutive dynamical systems: S-adic expansions. Numeration and Substitution 2012 (RIMS Kôkyûroku Bessatsu, B46) . Res. Inst. Math. Sci. (RIMS), Kyoto, 2014, pp. 81–123.Google Scholar
Berthé, V.. S-adic expansions related to continued fractions. Natural Extension of Arithmetic Algorithms and S-adic System (RIMS Kôkyûroku Bessatsu, B58) . Res. Inst. Math. Sci. (RIMS), Kyoto, 2016, pp. 61–84.Google Scholar
Christensen, E. and Ivan, C.. Spectral triples for AF C ∗ -algebras and metrics on the Cantor set. J. Operator Theory 56(1) (2006), 17–46.Google Scholar
Christensen, E. and Ivan, C.. Sums of two dimensional spectral triples. Math. Scand. 100(1) (2007), 35–60.Google Scholar
Christensen, E., Ivan, C. and Lapidus, M. L.. Dirac operators and spectral triples for some fractal sets built on curves. Adv. Math. 217(1) (2008), 42–78.Google Scholar
Arnoux, P. and Rauzy, G.. Représentation géométrique de suites de complexité 2n + 1. Bull. Soc. Math. France 119(2) (1991), 199–215.Google Scholar
Baake, M. and Grimm, U.. Aperiodic Order: A Mathematical Invitation. Vol. 1 (Encyclopedia of Mathematics and its Applications, 149) . Cambridge University Press, Cambridge, 2013.Google Scholar
Baake, M. and Moody, R. V. (Eds). Directions in Mathematical Quasicrystals (CRM Monograph Series, 13) . American Mathematical Society, Providence, RI, 2000.Google Scholar
Bellissard, J. V. and Pearson, J.. Noncommutative Riemannian geometry and diffusion on ultrametric Cantor sets. J. Noncommut. Geom. 3(3) (2009), 447–480.Google Scholar
Bellissard, J. V., Marcolli, M. and Reihani, K.. Dynamical systems on spectral metric spaces. Preprint, 2010, arXiv:1008.4617.Google Scholar
Beresnevich, V.. Rational points near manifolds and metric Diophantine approximation. Ann. of Math. (2) 175(1) (2012), 187–235.Google Scholar
Beresnevich, V., Bernik, V., Dodson, M. and Velani, S.. Classical metric Diophantine approximation revisited. Analytic Number Theory. Essays in Honour of Klaus Roth. Ed. Chen, W. W. L. et al. . Cambridge University Press, Cambridge, 2009, pp. 38–61.Google Scholar
Bingham, N. H., Goldie, C. M. and Teugels, J. L.. Regular Variation (Encyclopedia of Mathematics and its Applications, 27) . Cambridge University Press, Cambridge, 1989.Google Scholar
Bugeaud, Y.. Sets of exact approximation order by rational numbers. Ann. of Math. (2) 327 (2003), 171–190.Google Scholar
Bugeaud, Y.. Sets of exact approximation order by rational numbers II. Unif. Distrib. Theory 3(2) (2008), 9–20.Google Scholar
Connes, A.. Noncommutative differential geometry. Inst. Hautes Études Sci. Publ. Math. 62 (1985), 257–360.Google Scholar
Connes, A.. Compact metric spaces, Fredholm modules, and hyperfiniteness. Ergod. Th. & Dynam. Sys. 9(2) (1989), 207–220.Google Scholar
Connes, A.. Noncommutative Geometry. Academic Press, San Diego, CA, 1994.Google Scholar
Dajani, K. and Kraaikamp, C.. Ergodic Theory of Numbers (Carus Mathematical Monographs, 29) . Mathematical Association of America, Washington, DC, 2002.Google Scholar
Damanik, D. and Lenz, D.. The index of Sturmian sequences. European J. Combin. 23(1) (2002), 23–29.Google Scholar
Diekert, V., Volkov, M. V. and Voronkov, A. (Eds). Computer science – theory and applications. Second Int. Symp. on Computer Science in Russia, CSR 2007 (Ekaterinburg, Russia, September 2007, Proceedings) .Google Scholar
Dreher, F., Kesseböhmer, M., Mosbach, A., Samuel, T. and Steffens, M.. Regularity of aperiodic minimal subshifts. Bull. Math. Sci. (2017), 1–22.Google Scholar
Durand, F.. Linearly recurrent subshifts have a finite number of non-periodic subshift factors. Ergod. Th. & Dynam. Sys. 20(4) (2000), 1061–1078.Google Scholar
Falconer, K. J.. Mathematical Foundations and Applications, 3rd edn. John Wiley & Sons, Chichester, 2014.Google Scholar
Falconer, K. and Samuel, T.. Dixmier traces and coarse multifractal analysis. Ergod. Th. & Dynam. Sys. 31(2) (2011), 369–381.Google Scholar
Fogg, N. P..Berthé, V., Ferenczi, S., Mauduit, C. and Siegel, A. (Eds). Substitutions in Dynamics, Arithmetics and Combinatorics (Lecture Notes in Mathematics, 1794) . Springer, Berlin, 2002.Google Scholar
Fuhrmann, G., Gröger, M. and Jäger, T.. Amorphic complexity. Nonlinearity 29(2) (2016), 528–565.Google Scholar
Gelfand, I. M. and Naĭmark, M. A.. On the imbedding of normed rings into the ring of operators in Hilbert space. Rec. Math. [Mat. Sbornik] N.S. 12(54) (1943), 197–213.Google Scholar
Grigorchuk, R., Lenz, D. and Nagnibeda, T.. Schreier graphs of Grigorchuk’s group and a substitution associated to a non-primitive subshift. Groups, Graphs and Random Walks (London Mathematical Society Lecture Note Series) . Eds. Ceccherini-Silberstein, T., Salvatori, M. and Sava-Huss, E.. Cambridge University Press, 2017.Google Scholar
Grigorchuk, R., Lenz, D. and Nagnibeda, T.. Spectra of Schreier graphs of Grigorchuk’s group and Schroedinger operators with aperiodic order. Math. Ann. (2017), doi:10.1007/s00208-017-1573-8.Google Scholar
Guido, D. and Isola, T.. Dimensions and singular traces for spectral triples, with applications to fractals. J. Funct. Anal. 203(2) (2003), 362–400.Google Scholar
Guido, D. and Isola, T.. Dimensions and spectral triples for fractals in ℝ N . Advances in Operator Algebras and Mathematical Physics (Theta Series in Advanced Mathematics, 5) . Theta, Bucharest, 2005, pp. 89–108.Google Scholar
Haynes, A., Koivusalo, H. and Walton, J.. Characterization of linearly repetitive cut and project sets. Nonlinearity, Vol. 31. 2018, pp. 515–539.Google Scholar
Ishimasa, T., Nissen, H. U. and Fukano, Y.. New ordered state between crystalline and amorphous in Ni–Cr particles. Phys. Rev. Lett. 55(5) (1985), 511–513.Google Scholar
Julien, A. and Putnam, I. F.. Spectral triples for subshifts. J. Funct. Anal. 270(3) (2016), 1031–1063.Google Scholar
Kaimanovich, V. A.. Random walks on Sierpiński graphs: hyperbolicity and stochastic homogenization. Fractals in Graz 2001 (Trends in Mathematics) . Birhäuser, Basel, 2003, pp. 145–183.Google Scholar
Kellendonk, J., Lenz, D. and Savinien, J.. A characterization of subshifts with bounded powers. Discrete Math. 313(24) (2013), 2881–2894.Google Scholar
Kellendonk, J. and Savinien, J.. Spectral triples and characterization of aperiodic order. Proc. Lond. Math. Soc. 104(1) (2012), 123–157.Google Scholar
Kesseböhmer, M. and Samuel, T.. Spectral metric spaces for Gibbs measures. J. Funct. Anal. 265(9) (2013), 1801–1828.Google Scholar
Khinchin, A. Ya.. Continued Fractions. Dover Publications, Mineola, NY, 1997.Google Scholar
Lapidus, M. L.. Towards a noncommutative fractal geometry? Laplacians and volume measures on fractals. Harmonic Analysis and Nonlinear Differential Equations (Contemporary Mathematics, 208) . American Mathematical Society, Providence, RI, 1997, pp. 211–252.10.1090/conm/208/02742Google Scholar
Lapidus, M. L.. Search of the Riemann Zeros. American Mathematical Society, Providence, RI, 2008.Google Scholar
Lagarias, J. C.. Geometric models for quasicrystals I. Delone sets of finite type. Discrete Comput. Geom. 21(29) (1999), 161–191.Google Scholar
Lagarias, J. C. and Pleasants, P. A. B.. Local complexity of Delone sets and crystallinity. Canad. Math. Bull. 45(4) (2002), 634–652.Google Scholar
Lagarias, J. C. and Pleasants, P. A. B.. Repetitive Delone sets and quasicrystals. Ergod. Th. & Dynam. Sys. 23(3) (2003), 831–867.Google Scholar
Lothaire, M.. Algebraic Combinatorics on Words (Encyclopedia of Mathematics and its Applications, 90) . Cambridge University Press, Cambridge, 2002.10.1017/CBO9781107326019Google Scholar
Lysenok, I. G.. A set of defining relations for a Grigorchuk group. Mat. Zametki 38 (1985), 503–516 (in Russian). Engl. Transl. Math. Notes 38 (1985), 784–792.Google Scholar
Moody, R. V. (Ed). The mathematics of long-range aperiodic order. Proceedings of the NATO Advanced Study Institute held in Waterloo (NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 489) . Kluwer Academic Publishers Group, Dordrecht, 1997, pp. 403–441.Google Scholar
Hedlund, G. A. and Morse, M.. Symbolic dynamics II: Sturmian trajectories. Amer. J. Math. 62 (1940), 1–42.Google Scholar
Patera, J. (Ed). Quasicrystals and Discrete Geometry (Fields Instititue Monographs, 10) . American Mathematical Society, Providence, RI, 1998.Google Scholar
Pavlović, B.. Defining metric spaces via operators from unital C ∗ -algebras. Pacific J. Math. 186(2) (1998), 285–313.Google Scholar
Rieffel, M. A.. Metrics on states from actions of compact groups. Doc. Math. 3 (1998), 215–229.Google Scholar
Rieffel, M. A.. Compact quantum metric spaces. Operator Algebras, Quantization, and Noncommutative Geometry (Contemporary Mathematics, 365) . American Mathematical Society, Providence, RI, 2004, pp. 315–330.Google Scholar
Savinien, J.. A metric characterisation of repulsive tilings. Discrete Comput. Geom. 54(3) (2015), 705–716.Google Scholar
Sharp, R.. Spectral triples and Gibbs measures for expanding maps on Cantor sets. J. Noncommut. Geom. 6(4) (2012), 801–817.Google Scholar
Shechtman, D., Blech, I., Gratias, D. and Cahn, J. W.. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 53(20) (1984), 1951–1953.Google Scholar