Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-05T23:27:37.176Z Has data issue: false hasContentIssue false
  • English
  • Français

Complete regularity of Ellis semigroups of $\mathbb{Z} $-actions

Part of: Semigroups Topological dynamics Connections with other structures, applications

Published online by Cambridge University Press:  13 November 2020

MARCY BARGE  and
JOHANNES KELLENDONK Open the ORCID record for JOHANNES KELLENDONK [Opens in a new window]
MARCY BARGE
Affiliation:
Montana State University, Department of Mathematical Sciences, Bozeman, MT59717, USA (e-mail: barge@math.montana.edu)
JOHANNES KELLENDONK*
Affiliation:
Univerisité de Lyon, Université Claude Bernard Lyon 1, Institute Camille Jordan, CNRS UMR 5208, 69622Villeurbanne, France
*
e-mail: kellendonk@math.univ-lyon1.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

It is shown that the Ellis semigroup of a 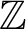$\mathbb Z$ -action on a compact totally disconnected space is completely regular if and only if forward proximality coincides with forward asymptoticity and backward proximality coincides with backward asymptoticity. Furthermore, the Ellis semigroup of a 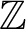$\mathbb Z$ - or 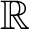$\mathbb R$ -action for which forward proximality and backward proximality are transitive relations is shown to have at most two left minimal ideals. Finally, the notion of near simplicity of the Ellis semigroup is introduced and related to the above.

Keywords

enveloping semigroupcompletely regular semigrouptopological dynamics

MSC classification

Primary: 54H20: Topological dynamics
Secondary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.) 20M17: Regular semigroups
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 12 , December 2021 , pp. 3593 - 3609
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akin, E., Auslander, J. and Glasner, E.. The Topological Dynamics of Ellis Actions ( Memoirs of the American Mathematical Society , 913). American Mathematical Society, Providence, RI, 2008.CrossRefGoogle Scholar
Aujogue, J.-B.. Ellis enveloping semigroup for almost canonical model sets of an Euclidean space. Algebr. Geom. Topol. 15(4) (2015), 2195–2237.CrossRefGoogle Scholar
Aujogue, J.-B., Barge, M., Kellendonk, J. and Lenz, D.. Equicontinuous factors, proximality and Ellis semigroup for Delone sets. Mathematics of Aperiodic Order (Progress in Mathematics 309). Birkhäuser/Springer, Basel, 2015, pp. 137–194.10.1007/978-3-0348-0903-0_5CrossRefGoogle Scholar
Auslander, J.. Minimal Flows and their Extensions ( North-Holland Mathematics Studies , 153, Notas de Matemática [Mathematical Notes], 122). North-Holland, Amsterdam, 1988.Google Scholar
Blanchard, F., Glasner, E., Kolyada, S. and Maass, A.. On Li-Yorke pairs . J. Reine Angew. Math. 547 (2002), 51–68.Google Scholar
Coven, E. M., Quas, A. and Yassawi, R.. Computing automorphism groups of shifts using atypical equivalence classes. Discrete Anal. 3 (2016), 28.Google Scholar
Dekking, F. M.. The spectrum of dynamical systems arising from substitutions of constant length. Z. Wahrscheinlichkeitsth. Verw. Geb. 41(3) (1977/1978), 221–239.10.1007/BF00534241CrossRefGoogle Scholar
Hindman, N. and Strauss, D.. Algebra in the Stone-Cech Compactification: Theory and Applications. Walter de Gruyter, Berlin, 2011.CrossRefGoogle Scholar
Howie, J. M.. Fundamentals of Semigroup Theory. Vol. 12. Clarendon, Oxford, 1995.Google Scholar
Kellendonk, J. and Yassawi, R.. The Ellis semigroup for bijective substitutions. Preprint, 2019, arXiv:math.DS1908.05690.Google Scholar
Petrich, M. and Reilly, N. R.. Completely Regular Semigroups. Vol. 27. John Wiley & Sons, New York, 1999.Google Scholar